Abstract
NdCl3 and CeCl3 are characterized by the very close proximity of their standard reduction potentials. Thus, they represent the most challenging salt mixtures with respect to decoupling electrochemical responses and calculating concentrations. The goals of this study include the determination of the apparent standard potentials of both Nd3+/Nd2+ and Ce3+/Ce in LiCl-KCl-CeCl3 or NdCl3 mixtures. Matrix and concentration effects on fundamental electrochemical properties are of particular interest, as these thermodynamic properties will impact the ability to use voltammetry to measure concentrations in unknown samples. Several LiCl-KCl-CeCl3 or NdCl3 mixtures with NdCl3/CeCl3 concentrations ranging from 4 to 10 wt% at 753 to 793 K have been explored. For apparent standard potential values of CeCl3, a good agreement was obtained with the literature data, except above 773 K.
1. Introduction
Numerous studies have focused on the research and development of the pyroprocessing technology for safe and proliferation resistance reprocessing of spent nuclear fuel [1,2]. Electrochemical-based methods of reductive extraction are used as pyrochemical separation processes [3,4,5]. Pyrochemical separation from molten salt is considered a suitable alternative method to aqueous processes for the separation of minor actinides from the rest of the fission products containing lathanides [6,7]. For this reason, the assessment of accurate electro- and thermochemical data of lathanides is of high importance. Success in the electrorefining process requires reliable data on the electrochemical behavior and thermodynamic data of lanthanides in these media. Recently, many studies on the electrochemical behavior of uranium using CV (Cyclic Voltammetry), CP (Cyclic Potentionmetry) and anodic stripping voltammetry in the LiCl-KCl eutectic salt have been focused on low concentrations up to ~4.7 wt% UCl3 [8]. Thermodynamic and transport properties of binary LnX3-MX systems have been investigated widely [9,10,11], where Ln = Ce, Nd, La, Pr, Gd; M = Li, Na, Cs, and X = F, Cl, I, and Br. The addition of lanthanide chloride to alkali metal chloride results in the formation of a variety of stoichiometric compounds. The formation of compounds and complexes in the molten salt system affects the electrical conductivity and other thermo-physical properties [12]. Recently, Castrillejo and coworkers reported the electrochemical behavior of a series of lanthanide elements in LiCl-KCl eutectic melt in the temperature range of 400–550 °C [7]. Most of the reports available in the open literature pertain to the electrochemical behavior of individual element of the lanthanide series at dilute concentrations [12]. Iizuka investigated chronopotentionmetry to determine diffusion coefficient of CeCl3 at various temperature. Marsden and Pesic measured apparent standard potentials and diffusion coefficients of CeCl3 by cyclic voltammetry methods [13,14]. Additionally, Novoselova conducted the emf method to determine the apparent standard redox potential of NdCl3 in fused LiCl-KCl eutectic at a different temperature [15,16,17]. However, the effect of the presence of multiple components along with moderate to high concentrations in the same electrolyte has not been largely investigated in detail. Furthermore, the thermodynamic properties of lanthanides in the LiCl-KCl are not known at various temperatures. In this report, we present results of an investigation of individual species electro-and thermo-physical properties of Nd3+/Nd and Ce3+/Ce in LiCl-KCl eutectic molten salt. The effects of NdCl3 and CeCl3 concentrations on the diffusion coefficient, activity coefficient and activation energy are currently being studied to enhance the fundamental knowledge of how electrochemical behavior, specifically for CeCl3 or NdCl3 contents ranging from 4 wt% to 10 wt% in LiCl-KCl eutectic salt at 753 to 793 K. Moreover, in ternary systems, there are various concentration-dependent effects that have not been previously reported in literature. Therefore, the main objective in this study is to explore electrochemical and thermodynamic behaviors of cerium (Ce) and neodymium (Nd) in high concentration ranges (4 wt% to 10 wt%) of LiCl-KCl eutectic salt by utilizing electrochemical transition techniques, such as cyclic voltammetry (CV) and chronopotentionmetry (CP).
2. Experimental
2.1. Electrochemical Apparatus and Electrodes
The eutectic LiCl–KCl was prepared by mixing LiCl (Alfa Aesar, Daejeon, Korea, 99.95% purity) and KCl (Alfa Aesar, 99.99% purity) in a 58.2:41.8 eutectic molar ratio followed by drying for more than 48 h at 572 K to remove residual water and melted under a high-purity argon atmosphere. This eutectic mixture was heated at 753 to 793 K with several LiCl-KCl mixtures containing NdCl3 and CeCl3 with concentrations ranging from 4 to 10 wt%. All the electrochemical measurements were carried out with Autolab/PGSTAT128N potentiostat. The data acquisition was controlled by NOVA 2.0 software for cyclic voltammetry. A three-electrode electrochemical cell was assembled in an alumina crucible, which was positioned in a graphite vessel and heated in an electric furnace. A chromel–alumel thermocouple was used for temperature measurement with an accuracy of ±1 °C. The reference electrode (RE) was self-assembled by a silver wire (1 mm diameter, 99.99% purity). The reference electrode consisted of a closed-end porous quartz tube, in which the LiCl-KCl eutectic salt containing 5 mol% AgCl was placed, and an Ag wire of 1.0 mm diameter was immersed into the molten bath. A glassy carbon rod of 2.0-mm diameter was used as a counter electrode (CE). The surface area of the glassy carbon counter electrode in contact with the salt phase was about 43.1 mm2. The working electrode (WE) consisted of a metallic tungsten (W) wire (1.0-mm diameter, 99.9% purity) dipped into a molten salt bath (Figure 1E).

Figure 1.
Experimental setup and instruments. (A) Ar atmosphere glove box. (B) Schematic diagram of experimental apparatus. (C) Oxygen and moisture monitoring. (D) Autolab/PGSTAT128N potentiostat (E) Electrode setup in glove box.
2.2. Determination of Active Electrode Area
The active surface of WE in contact with the LiCl-KCl eutectic was about 20.8 mm2. This active surface was determined by the following equation [18].
If that length is assumed to be the wetting height (h), then the contact angle (𝜃) of wetting can be calculated using the surface tension (𝛾) for LiCl-KCl (0.117 J/m2) [19], density (𝜌) of eutectic LiCl-KCl (1.62 g/cm3) [19] and the equation derived for a meniscus on a small cylinder. In order to maintain the same electrode area, the electrode was kept at a constant depth to the LiCl-KCl eutectic salt after each experiment. All of the electrochemical experiments were carried out in a glovebox with a high-purity argon gas atmosphere (H2O, O2 < 0.1 ppm) in the set up shown in Figure 1.
3. Results and Discussion
3.1. Determination of the Diffusion Coefficient of CeCl3 and NdCl3 in LiCl-KCl
The diffusion coefficient of Ce3+|Ce were calculated based on the modified Randles–sevcik equation according to the work of Hamel and co-workers [20]. Figure 2A shows representative cyclic voltammograms of a LiCl-KCl-4 wt% CeCl3 solution using a tungsten working electrode. A single, large peak is observed with the anodic peak being slightly larger and steeper than the cathodic peak, which is typical of a soluble-insoluble transition. As expected, peaks increase in magnitude as the scan rate increases. The electrochemical reversibility of the CeCl3 redox reaction was confirmed using CV. The reversibility of the redox reaction can be confirmed by plotting the cathodic peak currents as a function of the square root of the scan rate. In such a plot, a linear relationship between the peak currents vs. square root of the scan rate establishes reversibility. This relationship can be seen in Figure 2B. Figure 3A shows the diffusion coefficient of CeCl3 as a function of temperature, as calculated based on the Randles–sevcik equation. The diffusion coefficient varies 1.53% based on concentration and 3.2% based on temperature. Figure 3B. shows the diffusion coefficients match well with literature values at 753–763 K.
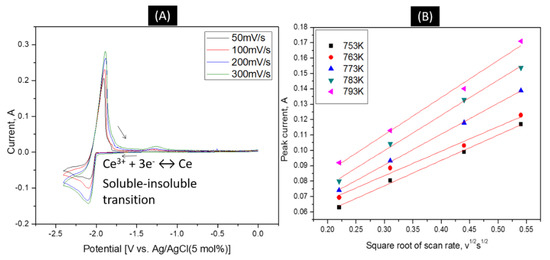
Figure 2.
(A) Cyclic voltammogram of 4 wt% Ce3+/Ce in LiCl-KCl eutectic salt at 773K. (B) Dependence of the current versus the square root of the scan rate according to the changing temperature in LiCl-KCl-CeCl3(XCeCl3 = 8.626 × 10−3).
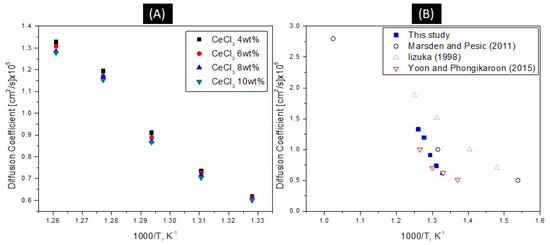
Figure 3.
(A) Diffusion coefficient of Ce3+ as a function of CeCl3 concentration and temperature in LiCl-KCl. (B) Comparison of values from literature.
These results obey the following the Arrhenius’ law, which is:
where is the activation energy. The linearity of the evolution of ln(D) versus 1/T is observed in Figure 4 with these results, which can be expressed as:
where D is in cm2/s and T in K for the 4 wt% CeCl3 case. From this relationship, the value of the activation energy is found to be 76.15 kJ/mol, and, as expected, the activation energy decreased as the CeCl3 concentration increased. It is expected that at a high concentration of CeCl3, there is enough analyte in solution to fully cover the working electrode. In the case of 4 wt% NdCl3 in LiCl-KCl solution, Figure 5 shows a series of CVs at different scan rates. While the large, sharp reduction and oxidation peaks look similar to the soluble–insoluble transition peaks seen in the CeCl3 studies, several broader peaks just to the right of the large peaks can be seen.
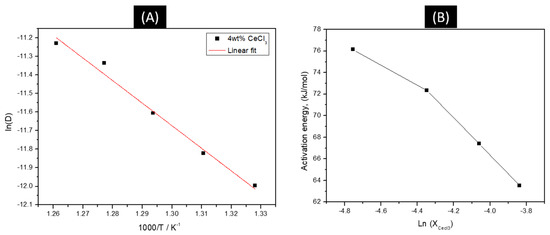
Figure 4.
(A) Linear relationship of the logarithm of CeCl3 diffusion coefficient vs. the reciprocal of the absolute temperature. (B) Activation energy as a function of CeCl3 concentration.
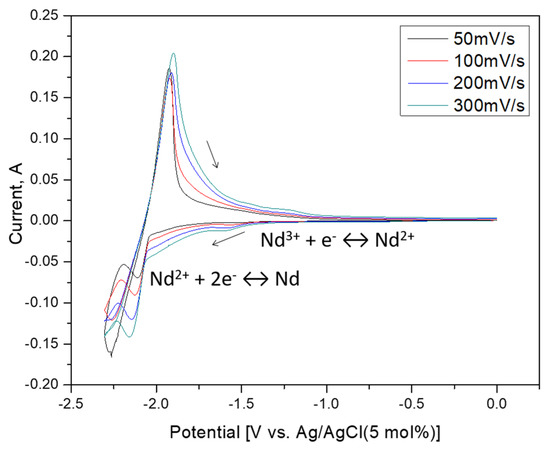
Figure 5.
Cyclic Voltammograms of 4 wt% NdCl3 in LiCl-KCl eutectic molten salt with scan rate; 50, 100, 200, 300 mV/s at 773 K.
These peaks can likely be associated with the Nd3+/Nd2+ soluble-soluble redox transition. The sharper peaks should be correlated with the potential scanning rates via the Berzins–Delahay relationship, reliable for a reversible soluble/insoluble systems [21,22,23].
where S is the electrode area in cm2, C0 is the solute concentration in moles/cm3, D is the diffusion coefficient in cm2 s−1, F is the Faraday constant (96,485 C), n is the number of exchanged electrons, v is the potential scanning rate in Vs−1 and T is the temperature in K. The linearity of Ip versus v1/2 proves that the electrochemical reduction process is controlled by the diffusion of Nd3+ ions in the solution. Figure 6 indicates the influence of the temperature on the value of diffusion coefficient from performing a series of cyclic voltammograms at several concentrations. At least 2.2% of the difference in the diffusion coefficient as a function of NdCl3 concentration and temperature, which can be up to 3.6%, can be seen in this graph. The resulting plot in Figure 7 obeys Arrhenius’ law and can be further expressed as follows for the 4 wt% NdCl3 case:
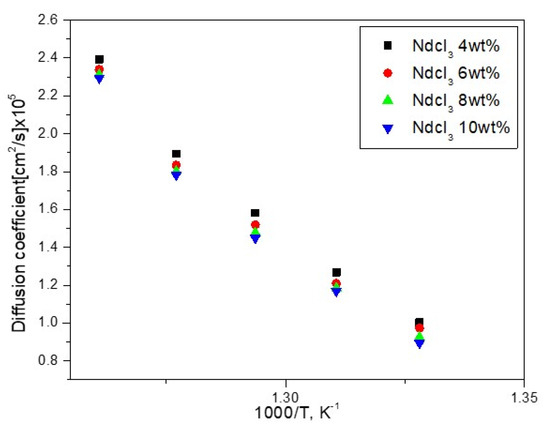
Figure 6.
Diffusion coefficient changes as a function of NdCl3 concentration in LiCl-KCl.
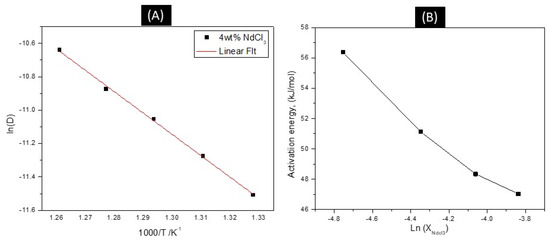
Figure 7.
(A) Linear relationship of the logarithm of NdCl3 diffusion coefficient vs. the reciprocal of absolute temperature. (B) Activation energy as a function of NdCl3 concentration.
In addition, the activation energy is found to be 56.37 kJ/mol and decreases as concentration increases.
3.2. Determination of the Apparent Standard Potential of CeCl3 and NdCl3 in LiCl-KCl
If it is assumed that the activity coefficient is constant over the range of concentrations tested, the apparent standard potential of cerium at 773 K can be calculated by plotting open circuit potential readings on a Nernst plot as shown in Figure 8A. In such a plot, the intercept is the apparent standard potential, E0 = −1.90132 V vs. Ag+|Ag reference scale (E0 = −3.0475 V vs. Cl−|Cl2). The same methods were used to create a Nernst plot as a function of temperature. Previous studies are shown for comparison, showing good agreement between these data sets, as shown Figure 8B. Using the slope from this plot, n was calculated to be 2.93, which is very close to the expected value of 3.0. In the case of Nd, due to the coexisting Nd2+ and Nd3+ oxidation states in LiCl-KCl eutectic molten salt, the usual method of calculating the apparent standard potential of the Nd3+ + 3e− Nd redox couple can no longer be applied since the exact amount of Nd3+ in the melt is unknown. However, a method applied to americium, which has +2 and +3 oxidation states, in a journal article by Fusselman and colleagues [22], can be used to provide a route to estimate the standard potential of both the +2 and +3 redox couple. The derivation is as follows:
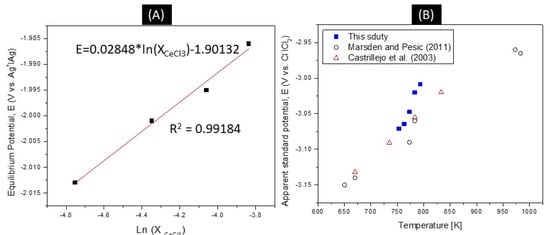
Figure 8.
(A) −1.901 V apparent standard potential vs. the 5 mol% Ag+│Ag reference scale at 773 K. (B) Comparison of values from literature [7,14].
Three redox couples exist in LiCl-KCl with dissolved Nd:
Nd2+ + 2e− Nd, + RTln (
Nd3+ + e Nd2+, + RTln (
Nd3+ + 3e− Nd, + RTln (
By substituting that
2+ Oxidation: ln (
Since the concentrations of Nd2+ and Nd3+ are unknown, these variables must be written in terms of total Nd ions, NdOx, which is known:
where is the ratio of 2+ ions to the total oxidized ions in the molten salt. Combining the equations:
Here, the apparent standard potential of the 2+ state is found by measuring the equilibrium potential of the cyclic voltammograms attained at each concentration and making a Nernst equation, as shown in Figure 9. The intercept of this plot is the apparent standard potential of the 2+ state, = −1.8582 V vs. Ag+|Ag reference (−3.0042 vs. Cl−|Cl2), which can then be used to calculate the .
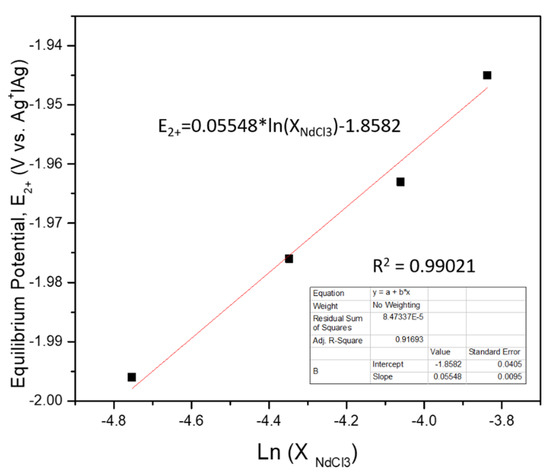
Figure 9.
−1.86 V apparent standard potential vs. the 5 mol% Ag+│Ag reference scale at 773 K.
3.3. Determination of the Activity Coefficient of CeCl3 and NdCl3 in LiCl-KCl
The activity coefficient can be extracted from the Nernstian plot and by rearranging the equation for apparent standard potential as shown below:
where is the experimentally determined apparent standard potential. In order for the above equation to be completely true, the measured apparent standard potential must be on the chlorine reference scale because the activity coefficient is in control of the full-cell reaction as opposed to the half-cell reaction. Once in the Cl−|Cl2 reference scale, the above equation can be written as:
where and is the standard-state Gibb’s free energy of the theoretical supercooled MClx-electrolyte in liquid state. The supercooled free energy may be calculated from the thermodynamic crystal data of MClx, the enthalpy of fusion data, and the heat capacity data in the liquid phase. While the supercooled state’s free energy may be calculated for any energy, the values for the free energy of the supercooled states of CeCl3, and NdCl3 were found in a paper by Patrick Masset and coworkers [24]. The Gibbs energy of formation of MClx in the supercooled states was derived from the crystal data (cr) of MClx (cr), the enthalpy of fusion (ΔfusH) and the heat capacity of the liquid phase (Cp) [25] according to the below Equation.
The selected thermodynamic data are summarized, and the calculated activity coefficients of CeCl3 and NdCl3 as a function of temperature are then given in Table 1.

Table 1.
Standard-state Gibb’s free energy of the theoretical supercooled value for NdCl3 and CeCl3 and activity coefficient as a function of temperature [14,24,25,26].
4. Conclusions
The present study collects the available thermochemical and electrochemical properties of CeCl3 and NdCl3 in the molten LiCl-KCl eutectic for pyroprocessing technology. The determination of the reaction mechanism was primarily investigated with cyclic voltammetry and was confirmed using Nernst plots. The results include the apparent standard potential, diffusion coefficient and the activity coefficient in the molten salt considered. The free Gibbs energies of formation, and the activity coefficients were derived from the electrochemical measurements. Apparent standard potential was determined through plotting the equilibrium potential, determined via cyclic voltammetry, of each concentration measurement against the natural logarithm of the concentration. The intercept of this Nernst plot was defined as the apparent standard potential. For apparent standard potential values of CeCl3, a good agreement was obtained with the literature data, except above 773 K. The activity coefficient can then be calculate based on the experimentally determined apparent standard potential and standard-state Gibb’s free energy.
Author Contributions
Conceptualization, S.K. and S.-h.L.; methodology, S.K.; software, S.-h.L.; validation, S.K.; investigation, S.K.; data curation, S.-h.L.; writing—original draft preparation, S.K.; writing—review and editing, S.K.; visualization, S.-h.L.; project administration, S.K. Both authors have read and agreed to the published version of the manuscript.
Funding
This study is supported by MOTIE and KETEP (No. 2018170201770).
Conflicts of Interest
Both authors declare no conflict of interest.
References
- IAEA-TECDOC-1648. Assessment of Partitioning Processes for Transmutation of Actinides; IAEA: Vienna, Austria, 2010. [Google Scholar]
- NEA. Pyrochemical Separations in Nuclear Applications, A Status Report; OECD Publications: Paris, France, 2004. [Google Scholar]
- Inoue, T.; Koch, L. Fuel cycle with pyro-process from the perspective of resisting proliferation. In Proceedings of the GLOBAL 2007, CD-ROM, Tsukuba, Ibaraki, Japan, 9–13 October 2005. [Google Scholar]
- Kim, T.J.; Ahn, D.H.; Paek, S.W.; Jung, Y. Study on electrodeposition of Ce(III) at a tungsten electrode in a LiCl-KCl molten salt solution. Int. J. Electrochem. Sci. 2013, 8, 9180–9186. [Google Scholar]
- Shirai, O.; Uehara, A.; Fujii, T.; Yamana, H. Thermochemical properties of the intermetallic compounds in the lanthanum–cadmium system. J. Nucl. Mater. 2005, 344, 142–145. [Google Scholar] [CrossRef]
- Sethi, R.S. Electrocoating from molten salts. J. Appl. Electrochem. 1979, 9, 411–426. [Google Scholar] [CrossRef]
- Castrillejo, Y.; Bermejo, M.R.; Barrado, A.I.; Pardo, R.; Barrado, E.; Martínez, A.M. Electrochemical behaviour of dysprosium in the eutectic LiCl–KCl at W and Al electrodes. Electrochim. Acta 2005, 50, 2047–2057. [Google Scholar] [CrossRef]
- Hoover, R.O.; Shaltry, M.R.; Martin, S.; Sridharan, K.; Phongikaroon, S. Electrochemical studies and analysis of 1–10wt% UCl3 concentrations in molten LiCl–KCl eutectic. J. Nucl. Mater. 2014, 452, 389–396. [Google Scholar] [CrossRef]
- Takagi, R.; Rycerz, L.; Gaune-Escard, M. Phase equilibrium in the LnCI3-mcl mixtures (Ln = Lanthanide; M = Alkali): Thermodynamics and electrical conductivity of the M3LnCI6 compounds. J. Alloys Compd. 1997, 257, 134. [Google Scholar] [CrossRef]
- Gong, W.; Gaune-Escard, M.; Rycerz, L. Thermodynamic assessment of LiCl—NdCl3 and LiCl—PrCl3 quasi-binary systems. J. Alloys Compd. 2005, 396, 92–99. [Google Scholar] [CrossRef]
- Rycerz, L.; Gaune-Escard, M. Mixing enthalpies of TbBr3-MBr liquid mixtures. Z. Nat. A 2001, 56, 859–864. [Google Scholar] [CrossRef]
- Misra, M.; Raja, K.S.; Jaques, A.V.; Baral, S. Effect of addition of multi-component lanthanides to LiCl-KCl eutectic on thermal and electrochemical properties. ECS Trans. 2010, 33, 351–360. [Google Scholar] [CrossRef]
- Iizuka, M. Diffusion coefficients of cerium and gadolinium in molten LiCl-KCl. J. Electrochem. Soc. 1998, 145, 84–88. [Google Scholar] [CrossRef]
- Marsden, K.C.; Pesic, B. Evaluation of the electrochemical behavior of CeCl3 in molten LiCl-KCl eutectic utilizing metallic ce as an anode. J. Electrochem. Soc. 2011, 158, F111–F120. [Google Scholar] [CrossRef]
- Novoselova, A.V.; Smolenskii, V.V. Electrochemical study of the properties of Nd(III) and Nd(II) ions in molten LiCl-KCl-CsCl eutectic and individual CsCl. Russ. J. Electrochem. 2013, 49, 931–937. [Google Scholar] [CrossRef]
- Kreysa, G. Electrochemical cell design and optimization procedures. J. Electroanal. Chem. Interfacial Electrochem. 1990, 283, 459–460. [Google Scholar] [CrossRef]
- Fukasawa, K.; Uehara, A.; Nagai, T.; Fujii, T.; Yamana, H. Electrochemical and spectrophotometric study on neodymium ions in molten alkali chloride mixtures. J. Alloys Compd. 2011, 509, 5112–5118. [Google Scholar] [CrossRef]
- Yu, Y.-X.; Gao, G.-H.; Li, Y.-G. Surface tension for aqueous electrolyte solutions by the modified mean spherical approximation. Fluid Phase Equilibria 2000, 173, 23–38. [Google Scholar] [CrossRef]
- Ito, H.; Hasegawa, Y.; Ito, Y. Densities of eutectic mixtures of molten alkali chlorides below 673 K. J. Chem. Eng. Data 2001, 46, 1203–1205. [Google Scholar] [CrossRef]
- Hamel, C.; Chamelot, P.; Taxil, P. Neodymium(lll) cathodic processes in molten fluorides. Electrochim. Acta 2004, 49, 4467–4476. [Google Scholar] [CrossRef]
- Gibilaro, M.; Massot, L.; Chamelot, P.; Taxil, P. Study of neodymium extraction in molten fluorides by electrochemical co-reduction with aluminium. J. Nucl. Mater. 2008, 382, 39–45. [Google Scholar] [CrossRef]
- Fusselman, S.P.; Roy, J.J.; Grimmett, D.L.; Grantham, L.F.; Krueger, C.L.; Nabelek, C.R.; Storvick, T.S.; Inoue, T.; Hijikata, T.; Kinoshita, K.; et al. Thermodynamic properties for rare earths and americium in pyropartitioning process solvents. J. Electrochem. Soc. 1999, 146, 2573–2580. [Google Scholar] [CrossRef]
- Morss, L.R.; Edelstein, N.M.; Fuger, J. The Chemistry of the Actinide and Transactinide Elements; Springer: New York, NY, USA, 2008. [Google Scholar]
- Masset, P.; Konings, R.J.; Malmbeck, R.; Serp, J.; Glatz, J.-P. Thermochemical properties of lanthanides (Ln=La,Nd) and actinides (An=U,Np,Pu,Am) in the molten LiCl–KCl eutectic. J. Nucl. Mater. 2005, 344, 173–179. [Google Scholar] [CrossRef]
- He, M.; Lu, G.; Kang, Z.; Zhang, Y. Thermodynamic assessment of the LiCl–KCl–CeCl3 system. Calphad 2015, 49, 1–7. [Google Scholar] [CrossRef]
- Toda, T.; Maruyama, T.; Moritani, K.; Moriyama, H.; Hayashi, H. Thermodynamic properties of lanthanides and actinides for reductive extraction of minor actinides. J. Nucl. Sci. Tech. 2009, 46, 18. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).