Abstract
This paper analyzes the effects of gamification in the social network of a massive online course. An educational social-networking platform gathered information about the contributions of participants and about the social networks that were formed during the course. A gamification layer with three game elements (points, badges, and leaderboard) was then implemented in the online learning platform. Social network analysis (SNA) and principal component analysis (PCA) were used to analyze the differences between a treatment and a comparison group (N = 591 and N = 427), using a set of 20 variables for each participant which quantified contributions to the learning platform as well as position and influence in the social network. The results of SNA show that gamification influences the structure of the social network of the course. The results also suggest that the variables cluster similarly for each group and that the linear combination of variables called the first component (F1) is a good descriptor of students’ work and position in the network. F1 can be used to build predictive models of course completion. The models show that the probability of passing the course increases more rapidly in the treatment (gamified) group.
1. Introduction
Gamification is the use of game elements in non-game contexts to promote participation and motivate action [1,2] Framing activities as a game through game elements, such as points, badges, and leaderboards, holds as much psychological power as the full game mechanics [3]. Gamification increases users’ performance of simple repetitive tasks [4], but findings of its motivational effects are contradictory [5]. Effectiveness is also in question, pointing to the necessity to align gamification with the goal of the activity and to address the psychological needs of the expected users at design time [6].
Educators are trying to harness the potential of gamification to design motivational learning experiences. Not surprisingly, education is the most common context in which gamification is implemented and reported [7,8,9]. Gamification can be used in traditional learning as well as blended and online learning. A recent literature review suggests that empirical studies equally addressed both online and regular courses, although online learning is considered a more promising field to apply gamification because it usually requires stronger motivation [10]. Since it intends to promote participation, gamification is particularly promising in massive online courses such as massive open online courses (MOOCs) in which the participation of instructors is limited, and feedback depends on the contributions of learners. Social networking presents a unique opportunity to develop peer support, thereby filling this instructional void [11]. E-learning can also take advantage of personalized and adaptive methods such as testing for measuring student performance [12], which can be used to tailor content and feedback. However, the effects of gamification in the MOOC context have not been thoroughly explored yet because it is being implemented in similar ways to those in small-scale contexts [13]. Since gamification and social networking serve different but complementary purposes, approaches combining both can result in motivationally-enhanced-social-learning experiences. Gamification can increase participation, as measured by contributions within the social network, resulting in increased social interaction and communication, which, in turn, would also result in motivational gains that fuel further participation.
Social network analysis (SNA) provides a set of measures for a social network and its participants. In their literature review, Cela et al. [14] pointed out that the application of SNA to e-learning environments is at a very early stage, although the number of studies is increasing. Network measures can be used to analyze the social interactions and the structure of the network in courses and the influence that different elements have on the network [15]. If gamification motivates participation in a social networked setting, it should be reflected in the contributions and in the structure of the social network, and SNA can be used to find such effects. Measures of each individual participant represent his/her position and influence in the network. Such measures can reflect the effects of gamification in the social network, but they also provide the means to analyze learning performance in relation to the contribution, position and influence in the network. Previous studies suggested that network metrics can be used to predict user behavior and characteristics [16].
This work sets out to study the effect of game mechanics (points, achievements, and leaderboards) in the social network of massive online courses in which the participation of facilitators is limited, and students have to take an active role in the learning platform. Since positioning in the network can also impact course completion, this study also aims to analyze the effects of gamification on course completion by building predictive models of it.
2. Related Work
Game elements such as achievements and badges serve several functions, for example, giving instructions, setting goals, and providing reputation, affirmation, and group identification [17]. Existing research presents mixed results regarding the impact of gamified elements such as badges, points, and leaderboards in learning outcomes. For instance, initial studies suggested a positive effect on the practical assignments but a negative effect on conceptual learning [18] of undergraduate students. Similarly, Hew et al. reported greater student contribution in the discussion forums but no significant difference in students’ recall of factual knowledge in an undergraduate course. They also found that the quality of the learning artifacts produced by students who used gamification mechanics was higher and that game mechanics also had a positive effect on motivating students to engage in more difficult tasks when compared to a control group [19]. Landers and Landers pointed to the necessity to study the effect of each game element on learning. They reported that students using the leaderboard spend more time on a task, and that time-on-task positively correlated with learning outcomes when compared with students who did not use the leaderboard [20]. Boticki et al. studied the effects of a gamified mobile application using badges in primary education. They found that the use of the app had a significant effect on learning, as measured by the quantity and quality of students’ contributions [21]. Contrastingly, other studies reported no effects or even adverse effects. For instance, Attali and Arieli-Attali studied the effect of points in computerized assessment. They found that points did not affect the accuracy of responses, although the speed of responses increased [22]. Hanus and Fox experimented with the effects of gamification in motivation using game elements aligned explicitly with learning objectives. They found that students who used gamification were less motivated in class and got lower grades than a control group [5]. When it comes to MOOCs, Qu et al. reported on student achievement based on temporal learning behavior in the learning platform [23].
Gamification addresses the psychological needs for competence, meaningfulness, and relatedness by providing timely feedback on learning progress and social experiences [24]. It also partially addresses the need for relatedness by providing recognition and status with elements such as badges. Social networks further support relatedness by facilitating communication and collaboration among participants. However, a significant limitation is that most of the existing research on the utility and effectiveness of social media in higher education is limited to self-reported data (e.g., surveys and questionnaires) and content analyses [25]. For instance, Hamid et al. analyzed students’ perceptions of social networks for learning and reported the following benefits: engaging with content, peer learning, promotion of critical thinking, self-directed learning, self-monitoring of learning progress, and interaction with lecturers [26]. Educational social-networking sites provide data for analysis, like the contributions of participants and the connections between them. SNA can then be used to mitigate the limitations of self-reported data by providing a set of measures that represents the student’s position and influence in the network. SNA also facilitates finding tendencies and patterns among participants in learning environments that can guide further analysis and even prompt intervention [15]. As participants create new bonds, the structure of the network and the positions of individual participants change over time [27]. The density and centrality of groups of students also increase over time when lecturers participate [28]. Cho et al. found that two centrality measures (degree and closeness centrality) were associated with students’ final grades [29]. Paredes and Chung also found that social learning is influenced by the relations, position and structure of the social network [30]. Shen et al. used SNA to describe interaction, explaining how it influences the sense of community of students in online learning environments [31]. Students in a structured network act as bridges, and they also trigger learning interactions, as compared with non-structured settings in which students mostly take passive roles and facilitators become the center of activity [32].
Still, the number of studies that bring together gamification and social networking is limited. De Lima and Zorrilla suggested that network metrics can be used as elements of gamification because they quantify the relevance of participants [33]. Simoes et al. presented a social gamification framework to assist teachers in creating motivational learning experiences fitted to learners’ needs [34], but the authors did not analyze the effects of it. Thom et al. reported the effects of removing gamification from an enterprise-social-networking site, finding that the number of contributions decreased significantly [35]. de-Marcos et al. compared gamification and social networking, concluding that both yielded similar results regarding learning performance for undergraduate courses; however, both approaches are best suited for practical assignments but not appropriate to convey conceptual knowledge [36,37]. The structure of gamification-driven educational social networks is a small world that resembles the features of similar networks analyzed in other domains. However, predictive models of learning success returned mixed results and were not very representative [38].
Existing research analyzed the structure of educational social-networks, changes over time, and the influence of other factors such as the intervention of teachers. It also informed about the effects of the social network on a variety of learning and other outcomes. This study contributes to the current state of the art (1) by analyzing how gamification influences the structure of the social network, and (2) by providing new models that describe learning success in terms of the contribution and positioning of individuals in the network. To the best of our knowledge, there are no previous works that study the former (number 1 above). Studies reporting the latter (number 2 above) offered mixed results that do not relate activity in the network and learning performance. Furthermore, most of the reported results focus on traditional or blended settings with a few participants, but our study reports the effects in a massive educational setting.
3. Materials and Methods
3.1. Research Questions
This study explores the following research questions related to gamification and social networking in a large MOOC-like educational setting:
RQ1. What is the influence of gamification on the structure of the social network in a large-scale online course?
RQ2. How does gamification relate to course completion in a large-scale online course?
To address the first research question, we explored the similarities and differences between basic educational networking and gamification-driven social networking, which may reflect the effect that gamification has on the social network. A gamification layer that includes achievements, points and a leaderboard is deployed on the top of a social networking site to explore such effect. We then studied the structure of the social network by examining the graph of connections between participants at the end of the course. SNA then provides a set of network metrics that can be used to compare the courses. Furthermore, SNA also provides a set of useful metrics to characterize each participant (student in this study). Metrics can be grouped using statistical methods to analyze the differences among groups of students that use different learning instruments.
The second objective of this study is to analyze the impact of gamification on learning success in a large-scale autonomous learning environment. Network measures of each participant can be used to build predictive models about learning success based on the student’s work in the course and on the student’s positioning in the network. Such models can also inform about differences among groups, providing further insights into the effect that gamification may have in the social network.
This study focuses on centrality measures to analyze the position and influence of participants in the network. The preeminent use in this study of centrality is based on previous evidence of the effect of such metrics in the learning and performance of students, as reported in Section 2. Alternatives may include segmentation measures and, particularly, community detection algorithms. This study also considers one of these measures (clustering coefficient).
3.2. Setting
The educational setting was the undergraduate online course, “Digital Skills for Teachers”, which is offered by an open university. The course uses a MOOC approach that requires autonomous and independent learning with a strong emphasis on the social and collaborative dimension. The level of involvement of each student depends on his/her interests and needs. Students have to work independently, exploring and finding relevant material, reflecting on their learning experience, and producing artifacts that show evidence of their competence and understanding of the topics. Students should also take an active role in the ongoing class dialog, contributing to the collaborative building of knowledge. The learning activities of the course are just a guide to support learning and facilitate collaboration and discussion of the course topics. The course is offered free of charge in Portuguese to teachers and teaching students worldwide.
The syllabus includes three learning modules: (1) searching and sharing online resources; (2) using digital tools in the classroom, and (3) promoting collaborative learning using digital tools. The course has a duration of 6 weeks. Students have to complete two assignments. The first consists of designing and building a learning experience based on the use of learning technologies (modules 1 and 2). The second assignment is an essay describing a cooperative/collaborative learning activity that includes the pedagogical use or design of new digital tools to support and facilitate learning (module 3). Assignments are anonymously peer-reviewed using a rubric by three other students. Students who get a positive assessment (pass) in both assignments obtain a digital certificate that acknowledges course completion.
3.3. Instruments
A social-networking educational online environment provides support for the pedagogical needs of the course. It uses the Moodle learning management system to centralize all course information and the Elgg social networking engine. Both platforms are integrated using a single sign-on service, offering a transparent learning environment which delivers the following tools and resources to participants: news, learning guide, dashboard, blogs, bookmarks, and an internal tweeting system. The basic version of the course measures the contributions of each participant including the number of blogs, tweets, “likes”, messages, comments, followers, and logins. A plugin deployed on the Elgg social networking engine provides the gamification features. It implements a set of thirteen achievements, points, and a leaderboard. Students get achievements for their participation and for interacting with the learning environment and with other participants. Achievements have a visual badge and a short description of the requirements to get them (Figure 1). For instance, the achievement, “iPopular”, is given to participants who are followed by at least 25 other participants. Points are given for completing the learning activities and for getting achievements. Points are then used to implement a leaderboard that students can use to compare their performance with other participants. Besides the measures provided by the educational social networking site, the gamification layer provided measures of the number of achievements and points for each participant.

Figure 1.
Social-networking educational gamified platform showing a subset of the achievements.
Self-determination theory [39] provided the theoretical background that guided the inclusion and design of the gamified social elements. These are designed to provide means to afford the basic needs of competence, autonomy, and relatedness in alignment with learning objectives. By providing gamification elements to address these affordances, we aim to motivate participation and interaction in the learning platform that may eventually result in students producing more and better assignments that increase course completion rates. Competence is the feeling of adequacy and possession of the skill, knowledge, or qualification required to complete the current task. Competence was acknowledged by the gamification system by providing points for completing the assignment. Autonomy is the feeling of freedom in one’s actions. By providing a set of thirteen different achievements, the gamified layer offers students different choices. Relatedness is the feeling of association and connection with other participants, and of being part of a community with common interests or goals. The social component of the system provided different opportunities for connection, such as following other participants. The social dimension was also emphasized by the peer-review, the social-based achievements, and competition through the leaderboard.
3.4. Participants
Experimentation included two instances of the course. A control group of 427 students used the social-networking online environment to take the course. The social-networking environment that included the gamification layer was used by the experimental group (591 students). Students were assigned to the group based on the date in which they enrolled, so a quasi-experimental design was used. Course contents and teachers were the same. Evaluation items and criteria were used consistently in both editions. Course contents and teachers were the same in both instances of the course. Evaluation items and criteria were used consistently in both editions. Table 1 presents the socio-demographic data of participants. It suggests that both groups are similar regarding the characteristics of learners. As registration was freely open in the two instances of the course, twenty-nine students participated in both editions, and three of them passed on their second try. Although the starting date was different in both editions, it was a short 6-week course starting in the middle of the term in both cases.

Table 1.
Geographic location, gender, educational background and occupation of participants as a percentage of the sample.
3.5. Measures
The interaction of participants in the social-networking online learning environment results in a set of measures that quantifies their participation. The social-networking online environment facilitates the gathering of the following measures: blogs, tweets, “likes”, messages (to other participants), comments (to any publication), followers, following, logins, and total interactions. All measures refer to the number of contributions made. The Elgg social networking engine implements a system of followers, similar to Twitter. For each participant, it is possible to know the number of followers that he/she has and the number that the participant is following. Total interactions return the number of actions (requests sent to the web server) that participants completed in the online environment. Most browsing actions in the learning system are not reflected in any of the previous measures. For instance, clicking on a particular link may be meaningful for the learner, but it is not recorded as a contribution because such action does not result in new information stored in the web server’s database. So, the total number of interactions is an estimate of the total amount of actions that participants perform in the learning platform. For the experimental group, the gamification layer gathers two additional measures about the interaction with the game elements: the number of achievements and the number of points that each participant earned.
SNA can be used to mine the social graph of participants, returning a set of network measures for each participant. Network measures quantify relevance in the network and the quality of connections. The definitions of measures used in this study are as follows: Degree is the total number of connections of a participant. Closeness centrality is the average of the shortest distance to all other participants in the network. Eccentricity is the largest distance between a participant and any other participant. Betweenness centrality reflects the number of shortest paths in the network in which a participant takes part. Eigenvector centrality is a measure of the influence of a participant in the network, based on relative scores to all other participants. Clustering coefficient returns the level of embeddedness of a participant with her neighbors. It is a measure of community formation (network segmentation) that can help to identify the level of connection of students within their local group. Clustering coefficient contrasts with the other centrality metrics that represent the position in the network.
Link analysis algorithms offer quantitative measures of the importance of a node, based not only on the quantity but also on the quality of edges. There are three of these metrics also used in this study; namely, PageRank, authority, and hub. PageRank [40] measures the importance of participants by considering the quantity and quality of links. The more important participants are likely to have more followers. Authority and hub also measure the importance of participants in the network. Both are computed using the Hyperlink-Induced Topic Search (HITS) algorithm [41]. Authority estimates the value of a participant as a function of his/her connections. A good authority is followed by many hubs. Hub estimates the value of the links to other participants. A good hub follows many participants.
Students credited or passed the course, getting a certificate; or they failed the course, based on learning performance as measured by the reviews of the learning artifacts. A binary variable called “Certificate” was included in the dataset. All measures were made when the instances of the course finished and reflected the activities and the structure of the social network of participants at the end of the course.
3.6. Analytical Tools
The primary instrument used to analyze the instances of the course was the principal component analysis (PCA) [42]. PCA determines the orthogonal axis of maximum variance by finding the eigenvalues and the eigenvector of the correlation matrix. Variables are projected onto those axes, calling these “factor loadings”. Observations, when projected onto the axis, are called “factor scores”. Factor loadings show how variables group together. The dimension of a dataset can be reduced when factor loadings of different variables are somewhat close in their biplot, indicating that the variables are very closely correlated. Furthermore, if the factors resulting from PCA are adequate and interpretable, then the factor scores can also be used to analyze correlations and build predictive models of desired outcomes. Since groups can be different, independent PCAs were carried out for each dataset (group).
The data gathered satisfy PCA assumptions. Firstly, all variables were measured at the continuous level. Second, we can assume a linear relation between variables since they all represent contributions to the learning platform, or they are measures of position in the social network. Third, Bartlett’s test of sphericity returned that data for both groups were suitable for data reduction (p < 0.001 in both cases). Fourth, the Kaiser–Meyer–Olkin (KMO) test returned 0.880 for the experimental group and 0.788 for the control group suggesting that data had sampling adequacy. Finally, no significant outliers were found. A Grubb’s test returned two possible outliers with a significantly high number of messages and interactions. Subsequent analysis showed that this was due to a mistake in data collection that added messages from other courses. Records were fixed and included in the dataset. We also checked that this error did not occur in other records.
The Gephi visualization-and-exploration software [43] was used to create the graphs that represent the social networks and to compute their global metrics. Gephi was also used to compute the individual metrics of each participant.
4. Results
4.1. Social Networks and Descriptive Statistics
The final structure of the social network of participants in each group is represented as a directed graph in which nodes are participants and edges are connections (followers). In massive online courses, many participants do not do any work and do not follow other participants. Two hundred and eighty-seven participants in the experimental group and 269 in the control group did not make any connection. Only nodes with edges are included to improve the readability of the graphs. A connected component is a subgraph in which all nodes are connected. Both instances of the course present only one central connected component. Figure 2 presents the central connected component of the experimental group (313 nodes), and Figure 3 shows the central connected component of the control group (167 nodes).
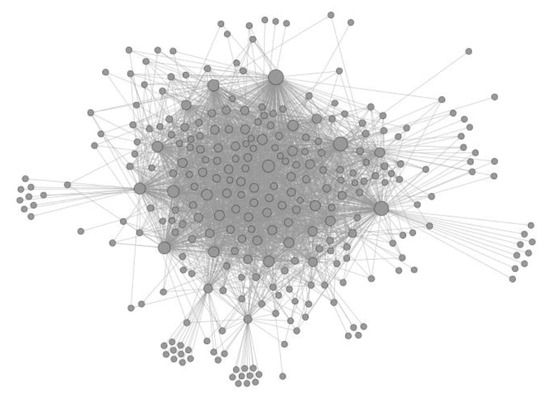
Figure 2.
The connected components of the social network for the experimental group. Nodes represent participants, and edges represent connections (followers). The size of each node is proportional to the degree (number of connections).
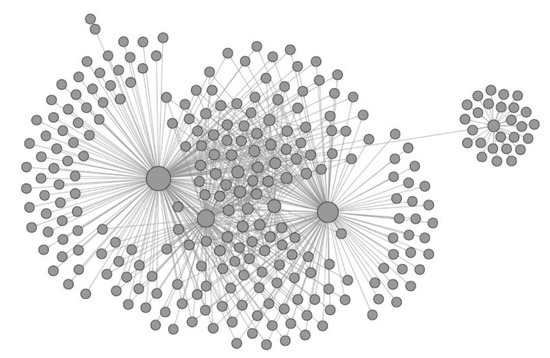
Figure 3.
The connected components of the social network for the control group. Nodes represent participants, and edges represent connections (followers). The size of each node is proportional to the degree (number of connections).
For the experimental group, we see that there is a central cluster with many nodes and many connections between them. There are also several hubs (nodes with many connections) and only a few nodes in the periphery with one or two connections. The density of connections makes it difficult to see if two particular nodes are connected. For the control group, we see only a few hubs with many connections and many nodes with only one or two connections. We observe three nodes with more than 100 connections; those correspond to the teachers. Contrastingly, in the experimental group, central nodes are both students and teachers. The five nodes with more than 130 connections comprise three students and two teachers, and the node with the most connections in the experimental group is a student. Although the differences in Figure 2 and Figure 3 could be attributed to the differences in the size of both groups (591 vs. 427), we can observe that the number of connections is 4.48 times larger for the treatment group, suggesting that something besides the size of the group shapes the final structure of the social network.
Table 2 presents descriptive statistics and network metrics—the average degree increases (5.33 for the experimental group and 1.64 for the control group). Graph density represents the ratio between the number of edges and the number of possible edges. A graph is complete (density = 1) if all possible edges between each pair of nodes are present. The experimental group graph has twice as much density as the control group. The number of participants with connections, the number of participants who passed, and the minimum number of connections to pass are also higher for the experimental group. The average path length (average shortest distance from one node to all others) decreases for the experimental group, suggesting that additional connections reduce the distance between participants.

Table 2.
Comparison of network metrics for the different instances of an online course.
4.2. Reduction in Dimensionality
The results of the PCA for the treatment group show that the first component (F1), which represents 68.44% of the variability, is associated with all variables except the Messages and the clustering coefficient (Table 3), suggesting that F1 is a measure of the students’ global work. Indeed, F1 is a weighted sum of different variables. The weights are proportional to the cosines between the variables and the principal component axis, that is, Pearson’s correlation between the variable and a principal component value. Table 3 also suggests that several variables can measure the same thing; i.e., the variables are associated with the same principal component with a similar square cosine. As the square root of 0.5 is 0.707, any square cosine greater than 0.5 indicates a strong correlation between the variable and the principal component. In Figure 4, we present the correlation plot of factor loadings for the treatment group. We can see that there are at least five clusters of variables, potentially meaning that the twenty variables described previously can be reduced to five or six if we select one representative variable per cluster. Each group represents closely correlated variables. For example, closeness centrality and eccentricity measure similar things.

Table 3.
Results of the PCA: squared cosines of the variables, eigenvalues, and variability of the factors. Values in bold correspond to the factor for which the squared cosine is the largest.
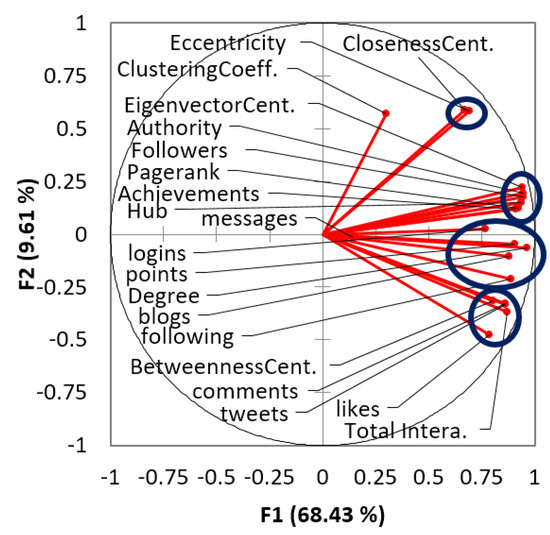
Figure 4.
Principal component analysis (PCA) factor loading biplot for the experimental group.
For the comparison group, the first component (55.36% of variability) includes all variables except Tweets, Messages, and eigenvector centrality (Table 3). Therefore, for both groups, F1 is associated with the most course activities and measures, suggesting that it is a functional characterization of the students’ work. The correlation plot of the comparison group (Figure 5) shows that variables are even more clustered, showing only 2 or 3 groups, which implies that for this group, most of the measurements taken measure similar constructs. In statistics, this is called collinearity, and it is a severe problem as it tends to make regression models biased to the current sample, meaning that the model seems to represent very well the current sample but will do so poorly if tried on additional data. In standard regression, collinear variables should be eliminated from the analysis. Going even further, we could also argue that those activities should be eliminated from the course as they achieve the same result over and over, but we will not go that far at this point. The use of the results of PCA to create predictive models, as shown in the next section, significantly reduces the effect of collinearity in variable prediction.
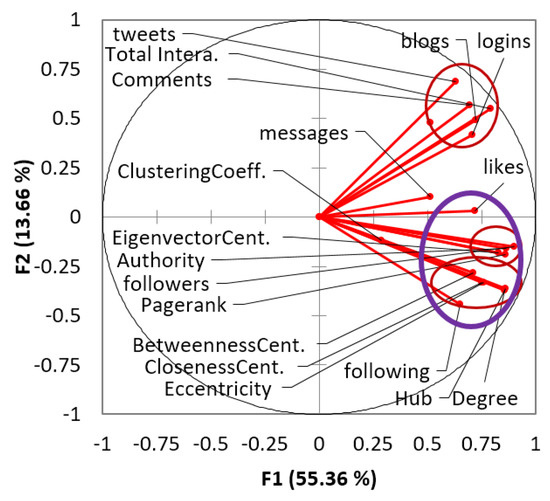
Figure 5.
PCA factor loading biplot for the control group.
If we compare the results of both groups, we can see that they are similar in terms of how variables group together and that, also in both cases, the first component (F1) is a good descriptor of students’ work since it includes most variables. We can use this information to build predictive models of course completion based on the activity completed by students as represented by F1. This can also provide valuable information to instructors monitoring future courses since we can focus only on a subset of 2–3 instead of all variables, or on F1 if they can perform a PCA, to analyze the results of the learning action. For instance, we could study the scores of students for F1 during the course to determine the levels of participation of students and decide whether to take further action to motivate them or even provide automated individual feedback based on the results of this score.
4.3. Predictive Models
Because for both groups, the first component (F1) includes most variables, we analyzed whether F1 (factor scores) can be used as a predictor of the probability of learning success. Remember that F1 is a weighted sum of variables. As the variable "Certificate" can have only two values (“1” for Certificate and “0” for course fail), testing the relationship is difficult, as shown in Figure 6A that plots Certificate vs. F1. Even though the relationship exists with R2 = 0.33, the binary nature of the Certificate makes the appreciation of the relationships hard to see.
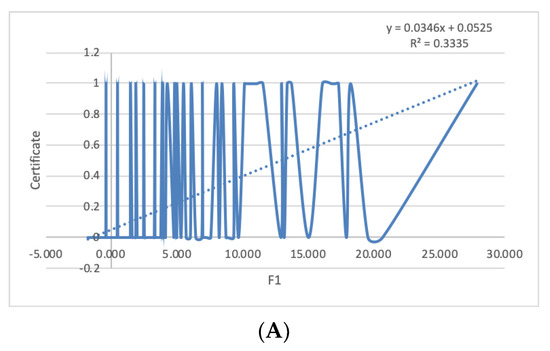
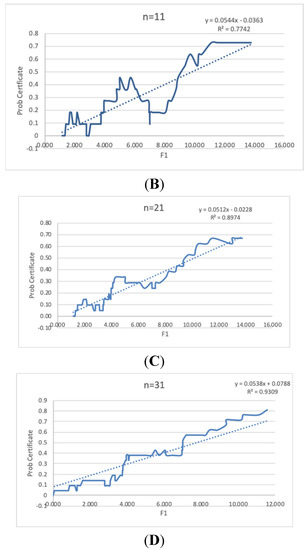
Figure 6.
The plot of Certificate probability vs. F1 with the linear fit for the experimental group with different sample sizes (n) of the probability estimate. (A)—without probability estimate (n = 1), (B)—with sample size n = 11, (C)—with sample size n = 21, (D)—with sample size n = 31
For a better characterization of the relationships, we introduced a new measure called the success probability, or in this case, the probability of getting the certificate. To estimate this probability, we ordered the dataset by F1 and sampled the certificate values above and below a given value of the variable F1, taking n samples that created a sliding window of samples. In essence, we considered each result (certificate or not) in the sample as a Bernoulli experiment and used the sample mean of the Certificate variable as an estimator for the probability, which is a well-known-maximum-likelihood estimator [44]. This estimator is similar to the Krichevsky–Trofimov estimator, which is used as a conditional estimator of the outcome of the next Bernoulli experiment [45]. However, since our dataset is not a time series and our objective is to create a global model for the success probability as a function of the variable F1, we used the sample mean of the current window, as shown in [46,47]. In general, n data points from the plots are lost (n/2 points at the beginning of the plot and n/2 at the end). Initially, we used n = 11, which is 11 samples from the ordered list, as the window size. The samples are taken, and then the number of successes (or certificates) is counted.
Assume is a measure which indicates that horizontal point is a success () or not (). When the horizontal coordinate is ordered, the probability of success at the horizontal point is estimated using Equation (1).
Equation (1): Probability of success (getting the certificate) at point .
Figure 6B plots the probability of Certificate vs. F1 with n = 11. Notice how the R2 statistic improved significantly (R2 = 0.77). The plot and the fit provide mathematical models to describe the student’s performance. Figure 6B shows that the probability of getting a certificate improves significantly when participation in the course increases, as measured by the variables that are part of F1. It is noteworthy that the plot of this figure has R2 of only 0.334 (Figure 6A) and that by using the certificate-probability estimate, the R2 increases to 0.774 with n = 11 (Figure 6B), which is a significant increase in model prediction capability. The sample size used to estimate the success probability was small, so tests were made with different values of n (Figure 6B–D). It was found that the behavior of the probability estimate was about the same, showing stability in the estimate. Naturally, the bigger the sample, the more precise the estimate will be. In Figure 7, we show the success probability estimator against F1 for the control group. We can appreciate that F1 can be used as a predictor of learning success for both groups. We also see that the steepness of the slope is higher in the experimental group (0.05 for experimental and 0.03 for control). This means that the probability of getting the certificate increases more rapidly in the experimental groups for students who engage in getting higher scores in the variables that are part of F1.
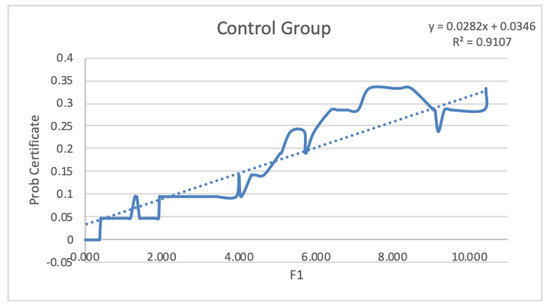
Figure 7.
The plot of Certificate probability vs. F1 with the linear fit for the control group with a sample size of the probability estimate n = 21.
5. Discussion and Conclusions
Regarding the influence of gamification in the structure of the social network (RQ1), we observe substantially more connections in the experimental group and many nodes with a large number of connections. This suggests a redistribution in the flow of communication among students that widens and changes the patterns of participation as previously reported [32], but that in this study is found in a massive online course. We also see that the social network of the gamified group presents the structural characteristics such as low density and short average paths that are also common in networks that involve human social interactions [48]. Descriptive statistics of the structural properties of the networks then suggest that there are differences between the treatment and comparison groups. However, we can also observe that the proportion of nodes with at least one connection is still small for each group (39% for comparison and 59% for treatment) and that the number of students that complete the course is a very small proportion, as is common in MOOCs. This suggests that a substantial number of students do not participate.
The results of the PCA show that F1 includes most variables for both groups, suggesting that F1 is a good representation of students’ work on the platform and students’ position and influence in the network. Personal activity and structural centrality in the educational social-network are correlated, as also shown in previous studies about social networking sites [49]. We also note that the variability explained by the first component (F1) is higher for the experimental group. This suggests that the gamification features and the two variables included to measure it (points and achievements) contribute to explaining the students’ work, providing a better statistical description of the gamified group.
To analyze the relationship between gamification and course completion (RQ2), we investigated the difference in overall success probability (the probability of getting a certificate) in both groups and found that probability increased from 3.28% in the comparison group to 5.25% in the treatment group. We further investigated the relationship between gamification and course completion by building a mathematical model to describe completion as a function of the amount of work, characterized as a function of the factor scores of F1 obtained from the PCA. The results suggest that F1 is a good predictor of the probability of completing the course for both groups. A closer examination of the models highlights the differences among groups. For students who engaged heavily, the probability of getting a certificate increased to almost 70% in the experimental group, while it was around 35% in the control group. This suggests that, besides the effect of gamification in participation and the structure of the network, gamification may also impact on learning success. Previous studies point to correlations between social networking and learning success [29] and between gamification-driven social networking and learning success [38,50], which our study confirms in a large-scale course. We also show that F1, in addition to being a good representation of a student’s work and position in the network, is a reliable estimator of the probability of success. Future work can community detection to further analyze the relationships between learning communities and their impact on course completion [51].
Our study has several limitations. First, it is essential to note that the causal relationship between the effect of social networking and gamification in learning performance is not proven. It may be that if students carry out the activities that increase the scores in the variables mentioned above, they will improve their chances of getting a certificate. However, it may also be that students who are responsible and motivated will get their certificates even if they do little work, and they do all the activities just because they are asked to do them. Our experiment is quasi-experimental because students were preassigned to experimental conditions based on the date in which they enrolled. Randomized-control trials need to be set up to check the causality of the relationships. Nevertheless, our analysis does point out the questions to address in those experiments. Another limitation of our study relates to generalization. Since the setting is a course on Digital Skills for Teachers, participants may be more motivated to learn and apply any digital skill just by their choice. Gamification is the very subject of the study, but it is also another digital skill in which participants are just interested and participate actively. In addition, only two cohorts of students and two social networks are studied. We suggest performing similar experiments to analyze whether and under which conditions the results reported here about the effect on the structure of the social network and on completion rates are found in other educational settings.
Author Contributions
Conceptualization, L.d.-M., R.V.R.-V. and J.-J.M.-H.; Methodology, L.d.-M., A.G.-C., E.G.-L. and A.M.T.; Software, A.G.-C. and R.V.R.-V.; Validation, L.d.-M., A.G.-C., E.G.-L., R.V.R.-V., A.M.T. and J.-J.M.-H.; Formal Analysis, A.G.-C. and J.-J.M.-H.; Investigation, E.G.-L. and J.-J.M.-H.; Resources, R.V.R.-V. and A.M.T.; Data Curation, L.d.-M.; Writing—Original Draft Preparation, L.d.-M. and R.V.R.-V.; Writing—Review & Editing, L.d.-M., A.G.-C., E.G.-L., R.V.R.-V., A.M.T. and J.-J.M.-H.; Visualization, L.d.-M., A.G.-C. and E.G.-L.; Supervision, E.G.-L.; Project Administration, J.-J.M.-H.; Funding Acquisition, A.G.-C. All authors have read and agreed to the published version of the manuscript.
Funding
Spanish Ministry of Economic Affairs and Digital Transformation (Grant TIN2014-54874-R) and Government of Comunidad de Madrid (Grant CM/JIN/2019-037).
Acknowledgments
Authors thank the support provided by the Junta de Comunidades de Castilla-La Mancha in the form of a postdoctoral training grant, and by the University of Alcala research mobility program.
Conflicts of Interest
The authors have no conflict of interest concerning this manuscript.
References
- Deterding, S.; Dixon, D.; Khaled, R.; Nacke, L. From game design elements to gamefulness: Defining “gamification”. In Proceedings of the 15th International Academic MindTrek Conference: Envisioning Future Media Environments, Tampere, Finland, 29–30 September 2011. [Google Scholar]
- Werbach, K.; Hunter, D. For the Win: How Game Thinking Can Revolutionize Your Business; Wharton Digital Press: Philadelphia, PA, USA, 2012. [Google Scholar]
- Lieberoth, A. Shallow Gamification: Testing Psychological Effects of Framing an Activity as a Game. Games Cult. 2014. [Google Scholar] [CrossRef]
- Mekler, E.D.; Brühlmann, F.; Opwis, K.; Tuch, A.N. Do points, levels and leaderboards harm intrinsic motivation? An empirical analysis of common gamification elements. In Proceedings of the First International Conference on Gameful Design, Research, and Applications, Toronto, ON, Canada, 2–4 October 2013. [Google Scholar]
- Hanus, M.D.; Fox, J. Assessing the effects of gamification in the classroom: A longitudinal study on intrinsic motivation, social comparison, satisfaction, effort, and academic performance. Comput. Educ. 2015, 80, 152–161. [Google Scholar] [CrossRef]
- Van Roy, R.; Zaman, B. Why Gamification Fails in Education and How to Make it Successful: Introducing Nine Gamification Heuristics Based on Self-Determination Theory. In Serious Games and Edutainment Application; Ma, M., Oikonomou, A., Eds.; Springer: Cham, Switzerland, 2017; Volume II, pp. 485–509. [Google Scholar]
- Hamari, J.; Koivisto, J.; Sarsa, H. Does Gamification Work?—A Literature Review of Empirical Studies on gamification. In Proceedings of the 47th Hawaii International Conference on System Sciences, Waikoloa, HI, USA, 6–9 January 2014. [Google Scholar]
- Seaborn, K.; Fels, D.I. Gamification in theory and action: A survey. Int. J. Hum.-Comput. Stud. 2015, 74, 14–31. [Google Scholar] [CrossRef]
- Martí-Parreño, J.; Méndez-Ibáñez, E.; Alonso-Arroyo, A. The use of gamification in education: A bibliometric and text mining analysis. J. Comput. Assist. Learn. 2016, 32, 663–676. [Google Scholar] [CrossRef]
- Dichev, C.; Dicheva, D. Gamifying education: What is known, what is believed and what remains uncertain: A critical review. Int. J. Educ. Technol. High. Educ. 2017, 14, 9. [Google Scholar] [CrossRef]
- Kellogg, S.; Booth, S.; Oliver, K. A social network perspective on peer supported learning in MOOCs for educators. Int. Rev. Res. Open Distrib. Learn. 2014, 15. [Google Scholar] [CrossRef]
- Melesko, J.; Novickij, V. Computer Adaptive Testing Using Upper-Confidence Bound Algorithm for Formative Assessment. Appl. Sci. 2019, 9, 4303. [Google Scholar] [CrossRef]
- Ortega-Arranz, A.; Muñoz-Cristóbal, J.A.; Martínez-Monés, A.; Bote-Lorenzo, M.L.; Asensio-Pérez, J.I. How Gamification Is Being Implemented in MOOCs? A Systematic Literature Review; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Cela, K.L.; Sicilia, M.A.; Sanchez, S. Social Network Analysis in E-Learning Environments: A Preliminary Systematic Review. Educ. Psychol. Rev. 2014, 27, 219–246. [Google Scholar] [CrossRef]
- Martınez, A.; Dimitriadis, Y.; Rubia, B.; Gomez, E.; De La Fuente, P. Combining qualitative evaluation and social network analysis for the study of classroom social interactions. Comput. Educ. 2003, 41, 353–368. [Google Scholar] [CrossRef]
- İş, H.; Tuncer, T. Interaction-Based Behavioral Analysis of Twitter Social Network Accounts. Appl. Sci. 2019, 9, 4448. [Google Scholar] [CrossRef]
- Antin, J.; Churchil, E.F. Badges in Social Media: A Social Psychological Perspective. In Proceedings of the ACM CHI 2011 Conference on Human Factors in Computing Systems; Gamification Workshop Proceedings: Vancouver, BC, Canada, 2011. [Google Scholar]
- Domínguez, A.; Saenz-De-Navarrete, J.; De-Marcos, L.; Fernández-Sanz, L.; Pagés, C.; Martínez-Herráiz, J.-J. Gamifying learning experiences: Practical implications and outcomes. Comput. Educ. 2013, 63, 380–392. [Google Scholar] [CrossRef]
- Hew, K.F.; Huang, B.; Chu, S.K.W.; Chiu, D.K.W. Engaging Asian students through game mechanics: Findings from two experiment studies. Comput. Educ. 2016, 92, 221–236. [Google Scholar] [CrossRef]
- Landers, R.N.; Landers, A.K. An Empirical Test of the Theory of Gamified Learning. Simul. Gaming 2014, 45, 769–785. [Google Scholar] [CrossRef]
- Boticki, I.; Baksa, J.; Seow, P.; Looi, C.-K. Usage of a mobile social learning platform with virtual badges in a primary school. Comput. Educ. 2015, 86, 120–136. [Google Scholar] [CrossRef]
- Attali, Y.; Arieli-Attali, M. Gamification in assessment: Do points affect test performance? Comput. Educ. 2015, 83, 57–63. [Google Scholar] [CrossRef]
- Shaojie, Q.; Li, K.; Wu, B.; Zhang, S.; Wang, Y. Predicting Student Achievement Based on Temporal Learning Behavior in MOOCs. Appl. Sci. 2019, 9, 5539. [Google Scholar] [CrossRef]
- Sailer, M.; Hense, J.U.; Mayr, S.K.; Mandl, H. How gamification motivates: An experimental study of the effects of specific game design elements on psychological need satisfaction. Comput. Hum. Behav. 2017, 69, 371–380. [Google Scholar] [CrossRef]
- Tess, P.A. The role of social media in higher education classes (real and virtual)—A literature review. Comput. Hum. Behav. 2013, 29, A60–A68. [Google Scholar] [CrossRef]
- Hamid, S.; Waycott, J.; Kurnia, S.; Chang, S. Understanding students’ perceptions of the benefits of online social networking use for teaching and learning. Internet High. Educ. 2015, 26, 1–9. [Google Scholar] [CrossRef]
- Lee, J.; Bonk, C.J. Social network analysis of peer relationships and online interactions in a blended class using blogs. Internet High. Educ. 2016, 28, 35–44. [Google Scholar] [CrossRef]
- Ergün, E.; Usluel, Y.K. An Analysis of Density and Degree-Centrality According to the Social Networking Structure Formed in an Online Learning Environment. Educ. Technol. Soc. 2016, 19, 34–46. [Google Scholar]
- Cho, H.; Gay, G.; Davidson, B.; Ingraffea, A.R. Social networks, communication styles, and learning performance in a CSCL community. Comput. Educ. 2007, 49, 309–329. [Google Scholar] [CrossRef]
- Paredes, W.C.; Chung, K.S.K. Modelling Learning & Performance: A Social Networks Perspective. In Proceedings of the 2nd International Conference on Learning Analytics and Knowledge, Vancouver, BC, Canada, 29 April–2 May 2012. [Google Scholar]
- Shen, D.; Nuankhieo, P.; Huang, X.; Amelung, C.; Laffey, J. Using Social Network Analysis to Understand Sense of Community in an Online Learning Environment. J. Educ. Comput. Res. 2008, 39, 17–36. [Google Scholar] [CrossRef]
- Aviv, R.; Erlich, Z.; Ravid, G.; Geva, A. Network Analysis of Knowledge Construction in Asynchronous Learning Networks. Online Learn. 2019, 7, 1–23. [Google Scholar] [CrossRef]
- De Lima, M.; Zorrilla, M. Social Networks and the Building of Learning Communities: An Experimental Study of a Social MOOC. Int. Rev. Res. Open Distrib. Learn. 2017, 18, 40–63. [Google Scholar] [CrossRef]
- Simões, J.; Redondo, R.D.; Vilas, A.F. A social gamification framework for a K-6 learning platform. Comput. Hum. Behav. 2013, 29, 345–353. [Google Scholar] [CrossRef]
- Thom, J.; Millen, D.R.; DiMicco, J. Removing Gamification from an Enterprise SNS. In Proceedings of the ACM Conference on Computer Supported Cooperative Work (CSCW), Seattle, WA, USA, 11–15 February 2012. [Google Scholar]
- De-Marcos, L.; Domínguez, A.; Saenz-De-Navarrete, J.; Pagés, C. An empirical study comparing gamification and social networking on e-learning. Comput. Educ. 2014, 75, 82–91. [Google Scholar] [CrossRef]
- De-Marcos, L.; Garcia-Lopez, E.; Garcia-Cabot, A. On the effectiveness of game-like and social approaches in learning: Comparing educational gaming, gamification & social networking. Comput. Educ. 2016, 95, 99–113. [Google Scholar] [CrossRef]
- De-Marcos, L.; García-López, E.; Garcia-Cabot, A.; Medina-Merodio, J.-A.; Domínguez, A.; Martínez-Herráiz, J.-J.; Diez, T. Social network analysis of a gamified e-learning course: Small-world phenomenon and network metrics as predictors of academic performance. Comput. Hum. Behav. 2016, 60, 312–321. [Google Scholar] [CrossRef]
- Ryan, R.M.; Deci, E.L. Self-determination theory and the facilitation of intrinsic motivation, social development, and well-being. Am. Psychol. 2000, 55, 68–78. [Google Scholar] [CrossRef]
- Brin, S.; Page, L. The anatomy of a large-scale hypertextual Web search engine. Comput. Netw. ISDN Syst. 1998, 30, 107–117. [Google Scholar] [CrossRef]
- Kleinberg, J.M. Authoritative sources in a hyperlinked environment. J. ACM 1999, 46, 604–632. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Principal Component Analysis; Springer: New York, NY, USA, 2002. [Google Scholar]
- Bastian, M.; Heymann, S.; Jacomy, M. Gephi: An Open Source Software for Exploring and Manipulating Networks. In Proceedings of the Third International AAAI Conference on Web and Social Media, San José, CA, USA, 17–19 May 2009; Available online: http://www.aaai.org/ocs/index.php/ICWSM/09/paper/view/154 (accessed on 16 October 2018).
- Wilks, S.S. Mathematical Statistics; John Wiley & Sons: New York, NY, USA, 1962. [Google Scholar]
- Belyaev, E.; Gilmutdinov, M.; Turlikov, A. Binary Arithmetic Coding System with Adaptive Probability Estimation by “Virtual Sliding Window”. In Proceedings of the IEEE Tenth International Symposium on Consumer Electronics, St. Petersburg, Russia, 28 June–1 July 2006. [Google Scholar]
- Krichevsky, R.; Trofimov, V. The performance of universal encoding. IEEE Trans. Inf. Theory 1981, 27, 199–207. [Google Scholar] [CrossRef]
- Leighton, F.; Rivest, R.L. Estimating a probability using finite memory. IEEE Trans. Inf. Theory 1986, 32, 733–742. [Google Scholar] [CrossRef]
- Chakrabarti, D.; Faloutsos, C. Graph mining. ACM Comput. Surv. 2006, 38, 2. [Google Scholar] [CrossRef]
- Klein, A.; Ahlf, H.; Sharma, V. Social activity and structural centrality in online social networks. Telemat. Inform. 2015, 32, 321–332. [Google Scholar] [CrossRef]
- De-Marcos, L.; Garcia-Cabot, A.; Garcia-Lopez, E. Towards the Social Gamification of e-Learning: A Practical Experiment. Int. J. Eng. Educ. 2017, 33, 66–73. [Google Scholar]
- Behera, R.K.; Rath, S.K.; Misra, S.; Damaševičius, R.; Maskeliūnas, R. Large Scale Community Detection Using a Small World Model. Appl. Sci. 2017, 7, 1173. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).