Evolving Matrix-Factorization-Based Collaborative Filtering Using Genetic Programming
Abstract
1. Introduction
2. Materials and Methods
2.1. Matrix Factorization
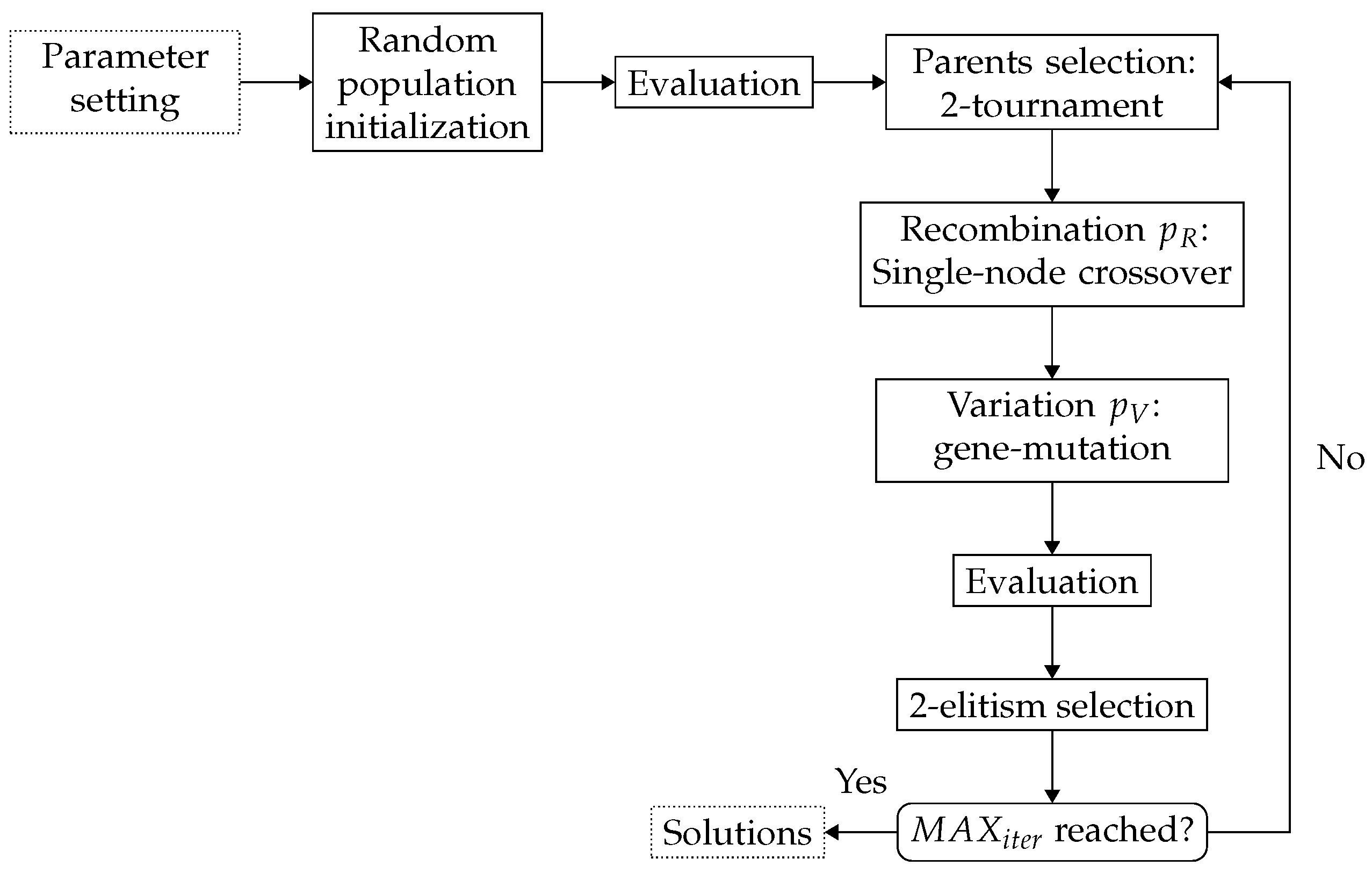
2.2. Genetic Programming
2.3. Experimental Setup
3. Results
3.1. Quality of the Recommender System Predictions
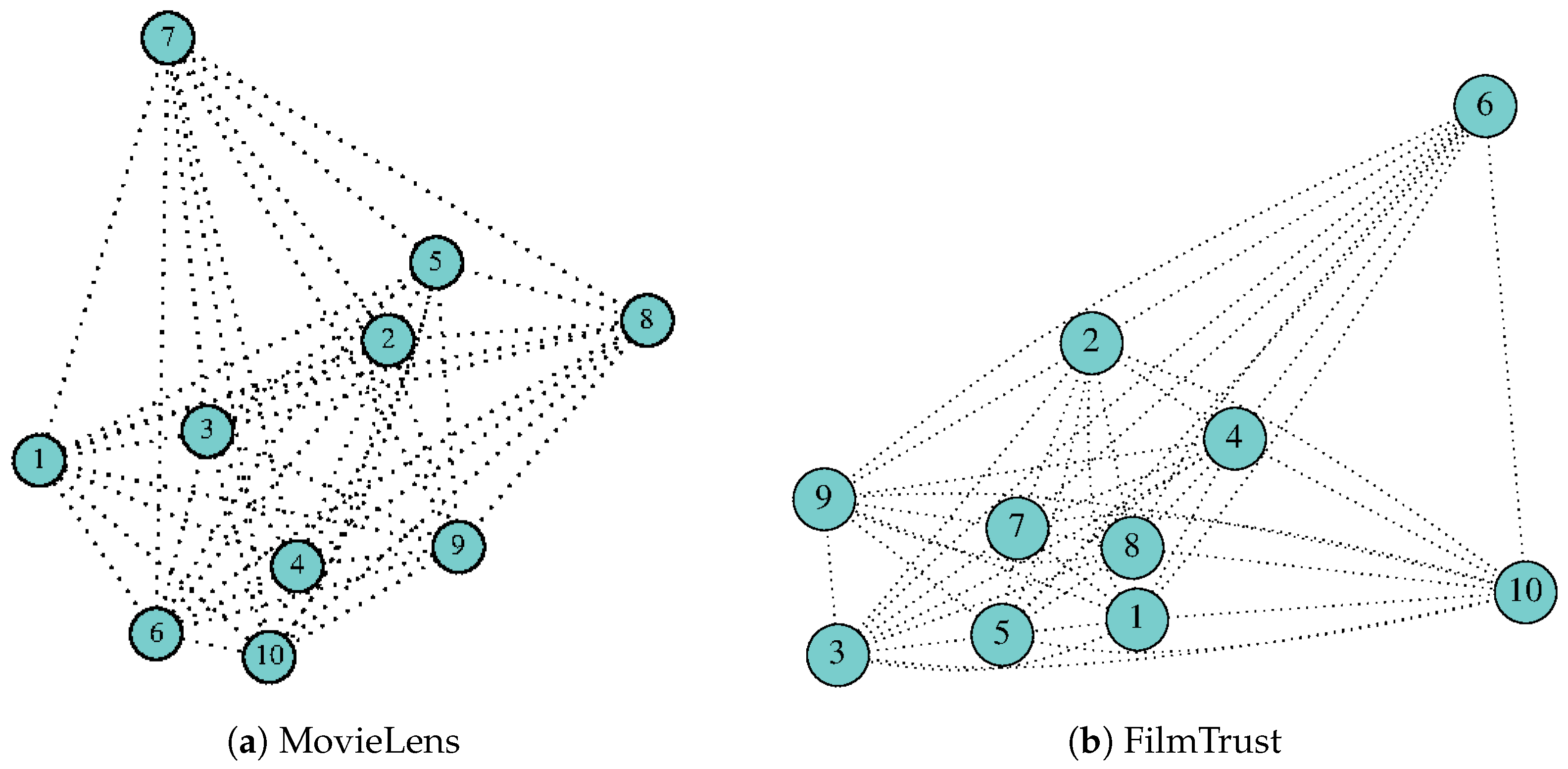
3.2. Results of the Evolutionary Method
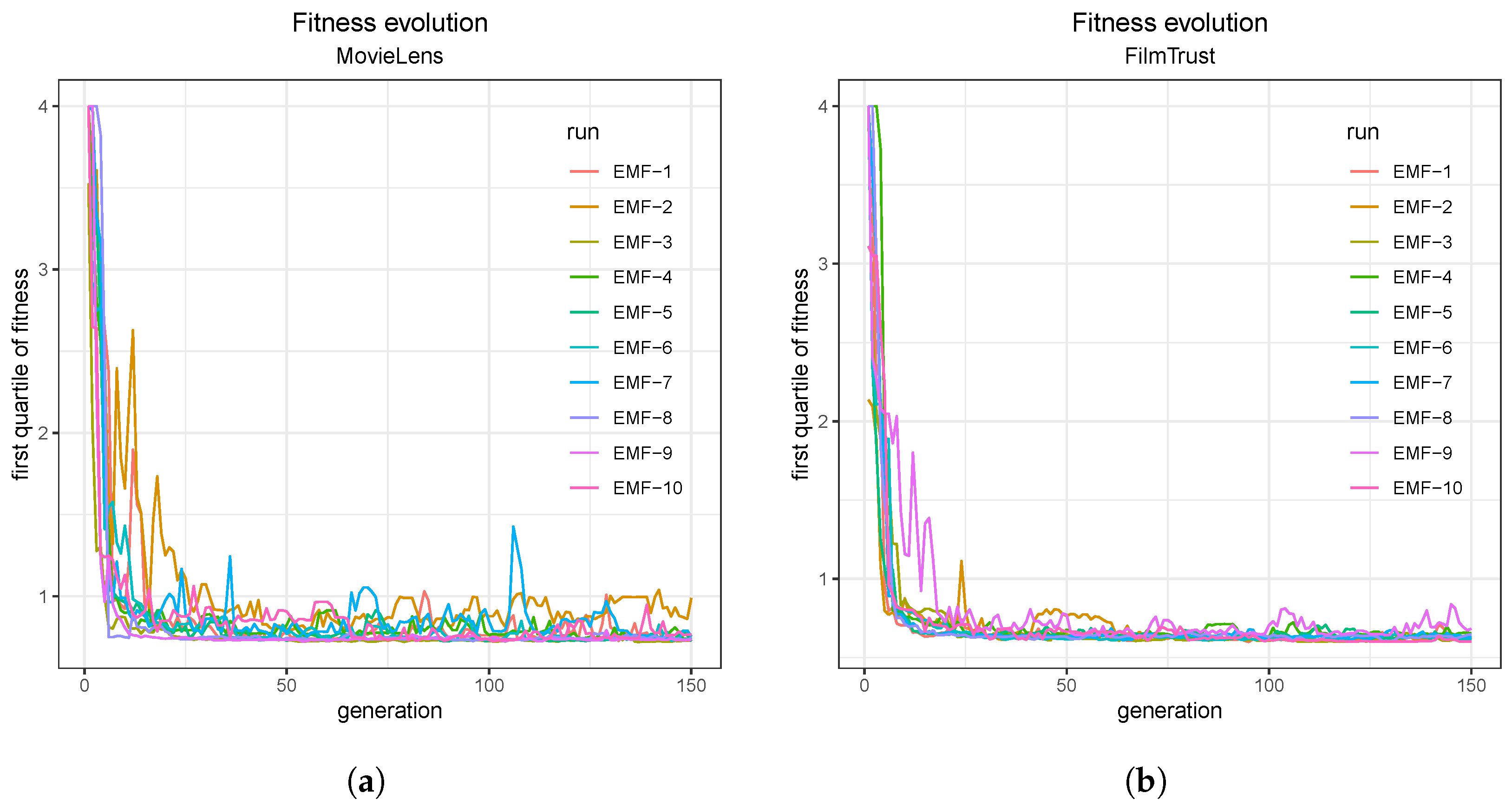
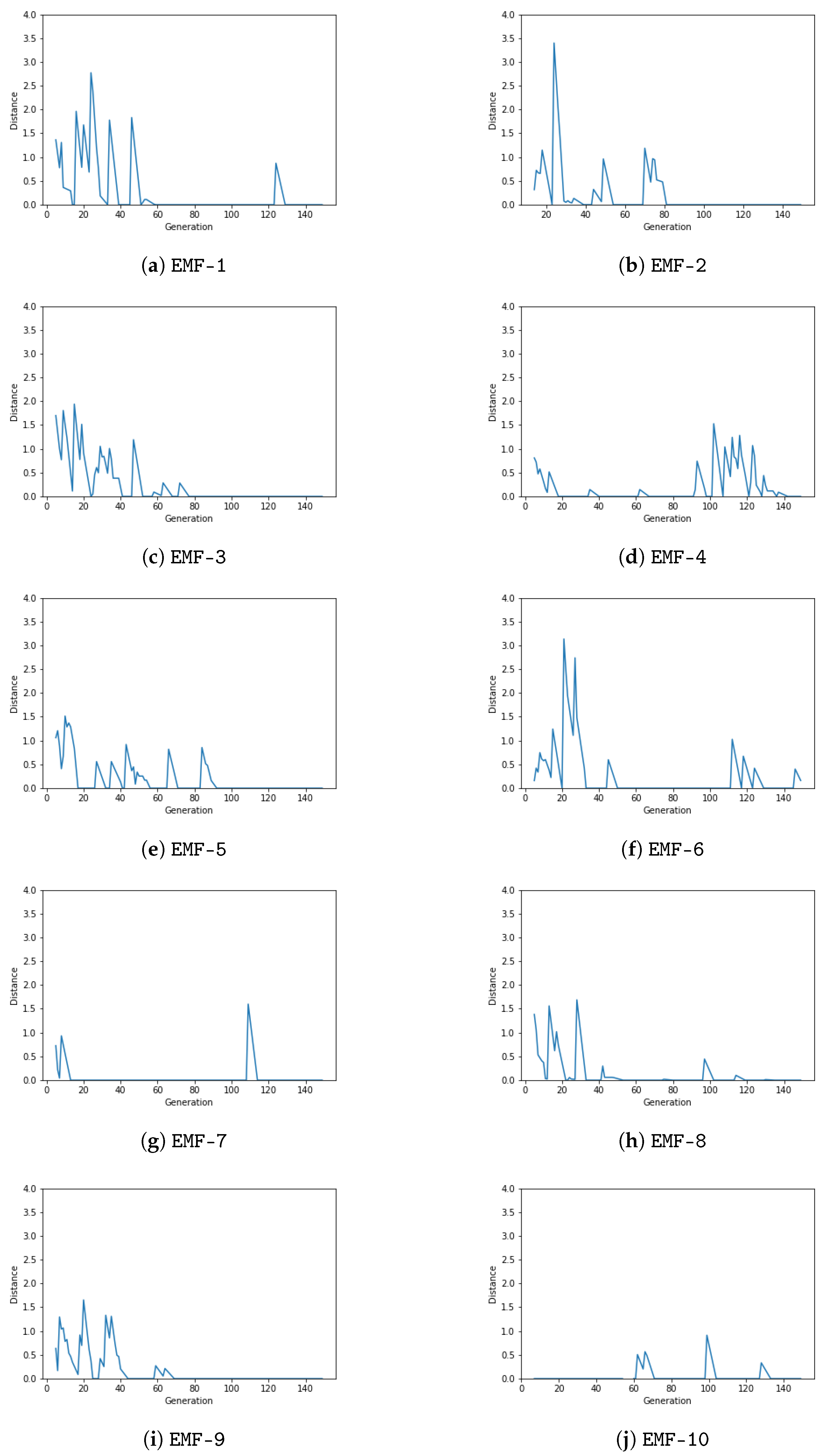
3.3. Convergence of the Evolutionary Method
4. Discussion
Author Contributions
Funding
Conflicts of Interest
Appendix A
- EMF-1: * - cos cos log exp atan- atan–exp–atan log expexp cos log cos log exp - exp cosexp–atan log atan sin cos cos atan atan exp - log exp atan cos log exp atan
- EMF-2: - + + exp sinexp + atancos One* +sin +sin + ++ + expexp + *sin + +* + * * One OneOne +* + * * One OneOne
- EMF-3: - - inv inv + inv inv + sin One cos Zero - inv inv + inv inv + sin atan–+ + * * cos Zero cos Zero + * inv inv –sin atan + + * + * inv inv –sin atan + + * cos Zero atan–+ + * inv + inv inv + sin One cos Zero cos Zero
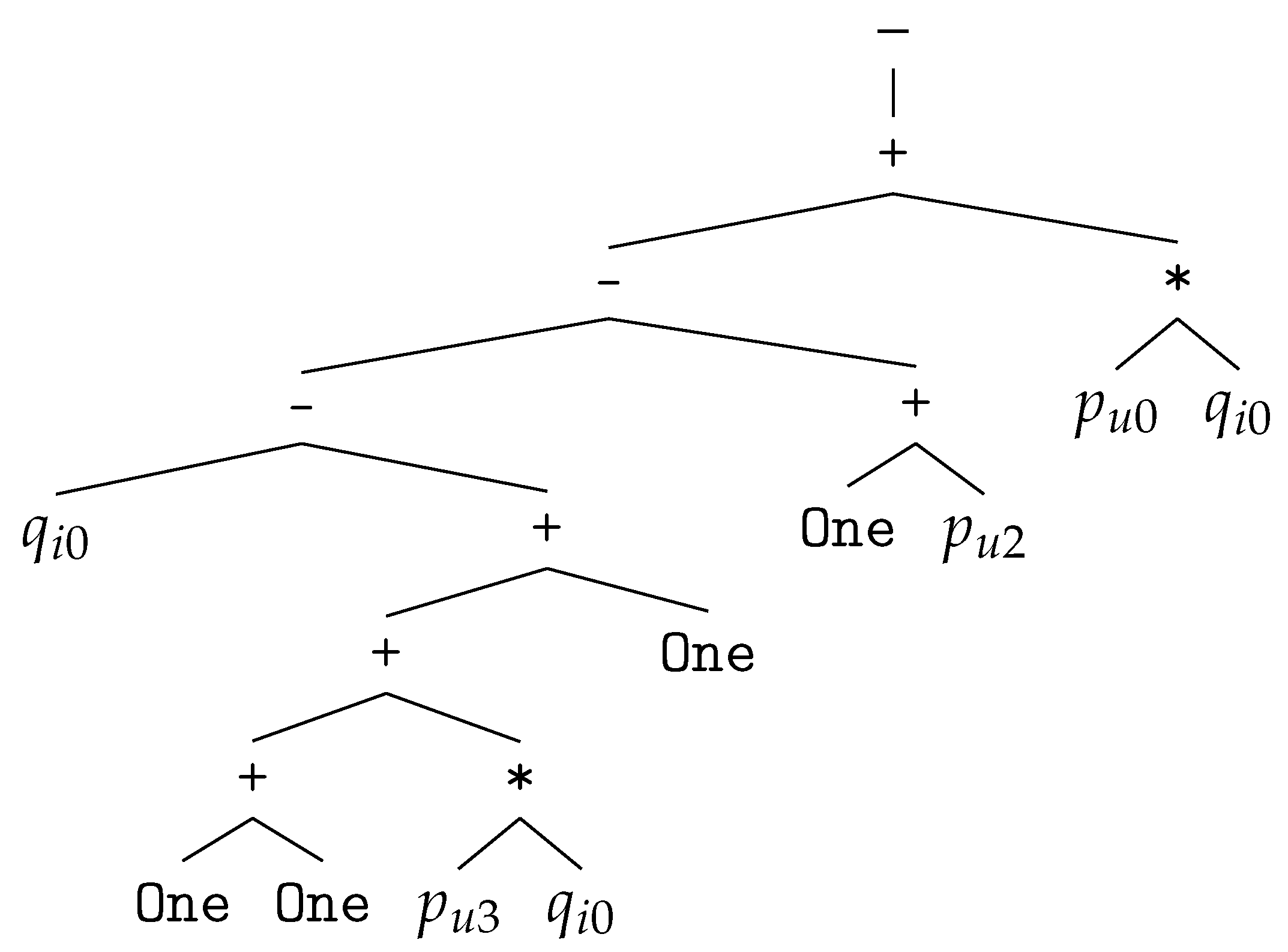
- EMF-4:–+ - - + + + One One * One + One *
- EMF-5:–– + + atan + + atan exp atan +–- exp exp atan exp
- EMF-6: log exp + exp atan exp atan - exp atan - expexp atan -
- EMF-7: * -–– cos–– atan inv– exp cos * atan–exp atan –
- EMF-8: - + -inv * cos sin -atan exp- cos -cos cos * - - * One –atan
- EMF-9: + exp- exp atan+ - Zero - exp+ *-
- EMF-10: exp atan pow pow * exp exp inv exp exp exp inv exp
- EMF-1: exp atan + cosexp + +
- EMF-2:–– + sin–– + One exp sin cos exp + –+ sin + sin exp sin–+ One exp sin cos–+ sin sin + One exp sin cos exp + –+ sin exp sin–sin
- EMF-3: inv exp atan -exp exp atan - exp - exp -exp atan -exp - - exp atan - exp - exp atan - exp exp atan - exp - exp - - exp exp atan - exp - exp - - exp atan - exp - exp atan - exp exp - exp atan - - - - -
- EMF-4: +exp cos
- EMF-5: exp atan - exp exp–
- EMF-6: exp atan ++ +atan ataninv
- EMF-7: + atan expexp cos
- EMF-8: + expexp cos sin exp–atan
- EMF-9: exp inv cos cos exp cos exp atan - * One exp *cos cos exp *exp atan - * One exp *cos
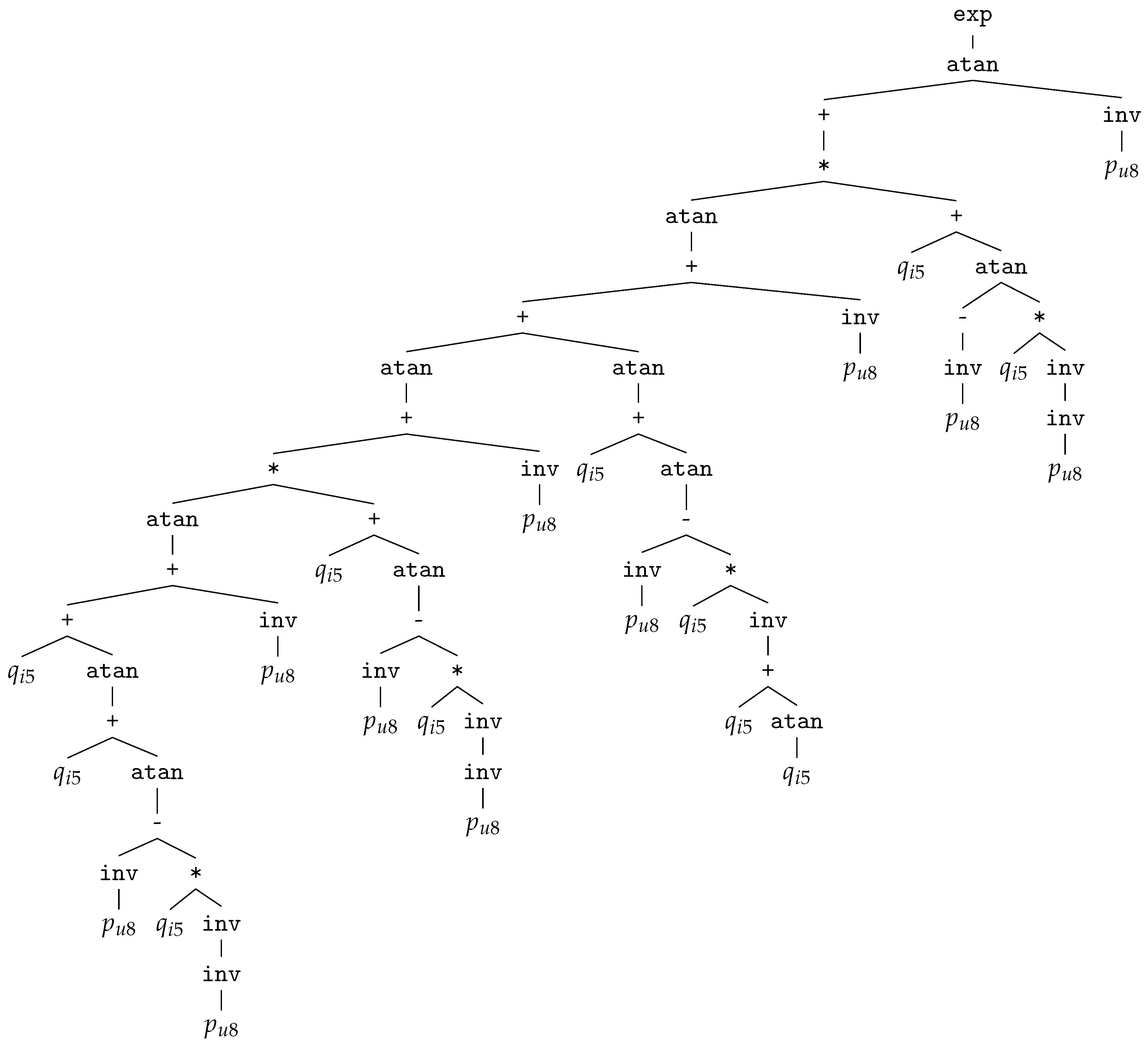
- EMF-10: exp atan + * atan + + atan + * atan + +atan +atan - inv*inv invinv+atan - inv*inv invinvatan +atan - inv*inv +ataninv+atan - inv*inv invinv
References
- Bobadilla, J.; Ortega, F.; Hernando, A.; Gutiérrez, A. Recommender systems survey. Knowl.-Based Syst. 2013, 46, 109–132. [Google Scholar] [CrossRef]
- Ricci, F.; Rokach, L.; Shapira, B. Introduction to recommender systems handbook. In Recommender Systems Handbook; Springer: Berlin, Germany, 2011; pp. 1–35. [Google Scholar]
- Wan, X.; Zhang, B.; Zou, G.; Chang, F. Sparse Data Recommendation by Fusing Continuous Imputation Denoising Autoencoder and Neural Matrix Factorization. Appl. Sci. 2019, 9, 54. [Google Scholar] [CrossRef]
- Melo, E. Improving Collaborative Filtering-Based Image Recommendation through Use of Eye Gaze Tracking. Information 2018, 9, 262. [Google Scholar] [CrossRef]
- Resnick, P.; Varian, H.R. Recommender systems. Commun. ACM 1997, 40, 56–59. [Google Scholar] [CrossRef]
- Ai, Q.; Azizi, V.; Chen, X.; Zhang, Y. Learning heterogeneous knowledge base embeddings for explainable recommendation. Algorithms 2018, 11, 137. [Google Scholar] [CrossRef]
- Adomavicius, G.; Tuzhilin, A. Toward the next generation of recommender systems: A survey of the state-of-the-art and possible extensions. IEEE Trans. Knowl. Data Eng. 2005, 17, 734–749. [Google Scholar] [CrossRef]
- Herlocker, J.L.; Konstan, J.A.; Borchers, A.; Riedl, J. An algorithmic framework for performing collaborative filtering. In 22nd Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, SIGIR 1999; Association for Computing Machinery, Inc.: New York, NY, USA, 1999; pp. 230–237. [Google Scholar]
- Schafer, J.B.; Frankowski, D.; Herlocker, J.; Sen, S. Collaborative filtering recommender systems. In The Adaptive Web; Springer: Berlin, Germany, 2007; pp. 291–324. [Google Scholar]
- Su, X.; Khoshgoftaar, T.M. A survey of collaborative filtering techniques. Adv. Artif. Intell. 2009, 2009. [Google Scholar] [CrossRef]
- Koren, Y.; Bell, R.; Volinsky, C. Matrix factorization techniques for recommender systems. Computer 2009, 42, 30–37. [Google Scholar] [CrossRef]
- Han, H.; Huang, M.; Zhang, Y.; Bhatti, U. An Extended-Tag-Induced Matrix Factorization Technique for Recommender Systems. Information 2018, 9, 143. [Google Scholar] [CrossRef]
- Bottou, L. Large-Scale Machine Learning with Stochastic Gradient Descent. In Proceedings of COMPSTAT’2010; Lechevallier, Y., Saporta, G., Eds.; Physica-Verlag HD: Heidelberg, Germany, 2010; pp. 177–186. [Google Scholar]
- Eiben, A.E.; Smith, J.E. Introduction to Evolutionary Computing; Springer: Berlin, Germany, 2003; Volume 53. [Google Scholar]
- Koza, J.R.; Koza, J.R. Genetic Programming: On the Programming of Computers by Means Of Natural Selection; MIT Press: Cambridge, MA, USA, 1992; Volume 1. [Google Scholar]
- González-Prieto, Á.; Lara-Cabrera, R.; Ortega, F. Symbolic Derivation. 2019. Available online: https://github.com/AngelGonzalezPrieto/sym-derivation (accessed on 15 January 2020). [CrossRef]
- Horváth, T.; de Carvalho, A.C.P.L.F. Evolutionary computing in recommender systems: A review of recent research. Nat. Comput. 2017, 16, 441–462. [Google Scholar] [CrossRef]
- Sadeghi, M.; Asghari, S.A. Recommender Systems Based on Evolutionary Computing: A Survey. J. Softw. Eng. Appl. 2017, 10, 407–421. [Google Scholar] [CrossRef]
- Belém, F.M.; Martins, E.F.; Almeida, J.M.; Gonçalves, M.A. Personalized and object-centered tag recommendation methods for Web 2.0 applications. Inf. Process. Manag. 2014, 50, 524–553. [Google Scholar] [CrossRef]
- Anand, D.; Bharadwaj, K.K. Adaptive user similarity measures for recommender systems: A genetic programming approach. In Proceedings of the 2010 3rd International Conference on Computer Science and Information Technology, Chengdu, China, 9–11 July 2010; Volume 8, pp. 121–125. [Google Scholar]
- Guimarães, A.; Costa, T.F.; Lacerda, A.; Pappa, G.L.; Ziviani, N. Guard: A genetic unified approach for recommendation. J. Inf. Data Manag. 2013, 4, 295. Available online: https://periodicos.ufmg.br/index.php/jidm/article/view/217 (accessed on 15 January 2020).
- Wilhelmstötter, F. JENETICS: Java Genetic Algorithm Library. 2012. Available online: http://jenetics.io/ (accessed on 15 January 2020).
- Harper, F.M.; Konstan, J.A. The movielens datasets: History and context. ACM Trans. Interact. Intell. Syst. (TIIS) 2016, 5, 19. [Google Scholar] [CrossRef]
- Guo, G.; Zhang, J.; Yorke-Smith, N. A Novel Bayesian Similarity Measure for Recommender Systems. In Proceedings of the 23rd International Joint Conference on Artificial Intelligence (IJCAI), Beijing, China, 3–9 August 2013; pp. 2619–2625. [Google Scholar]
- Mnih, A.; Salakhutdinov, R.R. Probabilistic matrix factorization. Adv. Neural Inf. Process. Syst. 2008, 1257–1264. Available online: http://papers.nips.cc/paper/3208-probabilistic-matrix-factorization.pdf (accessed on 15 January 2020).
- Lee, D.D.; Seung, H.S. Algorithms for non-negative matrix factorization. Adv. Neural Inf. Process. Syst. 2001, 13, 556–562. [Google Scholar]
- Hernando, A.; Bobadilla, J.; Ortega, F. A non negative matrix factorization for collaborative filtering recommender systems based on a Bayesian probabilistic model. Knowl.-Based Syst. 2016, 97, 188–202. [Google Scholar] [CrossRef]
- Rudin, W. Real and Complex Analysis; Mathematics Series; McGraw-Hill: New York, NY, USA, 1987. [Google Scholar]
- Ortega, F.; Zhu, B.; Bobadilla, J.; Hernando, A. CF4J: Collaborative filtering for Java. Knowl.-Based Syst. 2018, 152, 94–99. [Google Scholar] [CrossRef]
- Ellson, J.; Gansner, E.; Koutsofios, L.; North, S.; Woodhull, G.; Description, S.; Technologies, L. Graphviz— Open Source Graph Drawing Tools; Lecture Notes in Computer Science; Springer: Berlin, Germany, 2001; pp. 483–484. [Google Scholar]
- Herlocker, J.L.; Konstan, J.A.; Terveen, L.G.; Riedl, J.T. Evaluating collaborative filtering recommender systems. ACM Trans. Inf. Syst. (TOIS) 2004, 22, 5–53. [Google Scholar] [CrossRef]

| Operator | Arity | Function | Symbol |
|---|---|---|---|
| Sine | 1 | sin | |
| Cosine | 1 | cos | |
| Arctangent | 1 | atan | |
| Exponential | 1 | exp | |
| Logarithm | 1 | log | |
| Inverse | 1 | inv | |
| Sign | 1 | – | |
| Addition | 2 | + | |
| Subtraction | 2 | - | |
| Multiplication | 2 | * | |
| Power | 2 | pow |
| Dataset | #users | #items | #ratings | Rating Scale |
|---|---|---|---|---|
| MovieLens | 943 | 1682 | 100,000 | 1–5 |
| FilmTrust | 1508 | 2071 | 35,497 | 0.5–4.0 |
| Method | MAE | MSE |
|---|---|---|
| PMF | 0.7225 | 0.8492 |
| BiasedMF | 0.7160 | 0.8406 |
| NMF | 0.7672 | 0.9867 |
| BNMF | 0.7500 | 0.8860 |
| EMF-1 | 0.7256 | 0.8728 |
| EMF-2 | 0.7195 | 0.8332 |
| EMF-3 | 0.7210 | 0.8427 |
| EMF-4 | 0.7197 | 0.8282 |
| EMF-5 | 0.7195 | 0.8592 |
| EMF-6 | 0.7220 | 0.8377 |
| EMF-7 | 0.7255 | 0.8721 |
| EMF-8 | 0.7193 | 0.8442 |
| EMF-9 | 0.7161 | 0.8441 |
| EMF-10 | 0.7163 | 0.8381 |
| EMF (best) | 0.7161 | 0.8282 |
| EMF (worst) | 0.7256 | 0.8728 |
| EMF (avg) | 0.7205 | 0.8472 |
| Method | MAE | MSE |
|---|---|---|
| PMF | 0.7514 | 1.1321 |
| BiasedMF | 0.6277 | 0.7050 |
| NMF | 0.7950 | 1.3710 |
| BNMF | 0.6598 | 0.6987 |
| EMF-1 | 0.6046 | 0.6705 |
| EMF-2 | 0.6114 | 0.6653 |
| EMF-3 | 0.6013 | 0.6778 |
| EMF-4 | 0.6303 | 0.6780 |
| EMF-5 | 0.6109 | 0.6846 |
| EMF-6 | 0.6087 | 0.6808 |
| EMF-7 | 0.6108 | 0.6652 |
| EMF-8 | 0.6075 | 0.6672 |
| EMF-9 | 0.6209 | 0.7050 |
| EMF-10 | 0.5993 | 0.6581 |
| EMF (best) | 0.5993 | 0.6581 |
| EMF (worst) | 0.6303 | 0.7050 |
| EMF (avg) | 0.6105 | 0.6752 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lara-Cabrera, R.; González-Prieto, Á.; Ortega, F.; Bobadilla, J. Evolving Matrix-Factorization-Based Collaborative Filtering Using Genetic Programming. Appl. Sci. 2020, 10, 675. https://doi.org/10.3390/app10020675
Lara-Cabrera R, González-Prieto Á, Ortega F, Bobadilla J. Evolving Matrix-Factorization-Based Collaborative Filtering Using Genetic Programming. Applied Sciences. 2020; 10(2):675. https://doi.org/10.3390/app10020675
Chicago/Turabian StyleLara-Cabrera, Raúl, Ángel González-Prieto, Fernando Ortega, and Jesús Bobadilla. 2020. "Evolving Matrix-Factorization-Based Collaborative Filtering Using Genetic Programming" Applied Sciences 10, no. 2: 675. https://doi.org/10.3390/app10020675
APA StyleLara-Cabrera, R., González-Prieto, Á., Ortega, F., & Bobadilla, J. (2020). Evolving Matrix-Factorization-Based Collaborative Filtering Using Genetic Programming. Applied Sciences, 10(2), 675. https://doi.org/10.3390/app10020675







