Maximizing Demand Response Aggregator Compensation through Optimal RES Utilization: Aggregation in Johannesburg, South Africa
Abstract
1. Introduction
2. Materials and Methods
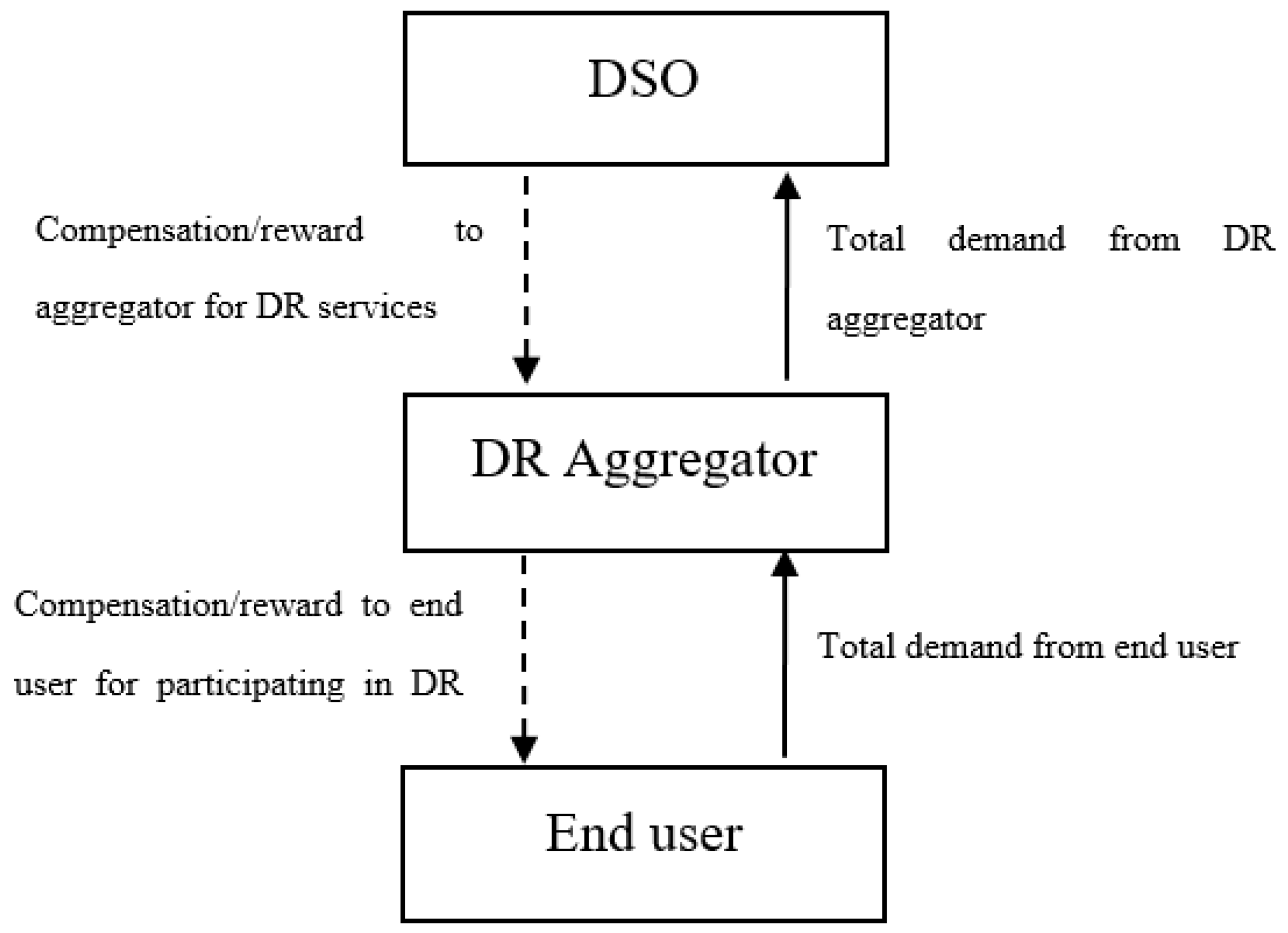
3. Proposed Methodology
- To provide demand side management services to the DSO, which results in a financial reward from the DSO.
- To ensure that end users reduce their electricity bill, which provides incentive for them to participate more actively in demand response programs.
3.1. Utilization of RES by the DSO
3.2. Utilization of RES by End Users
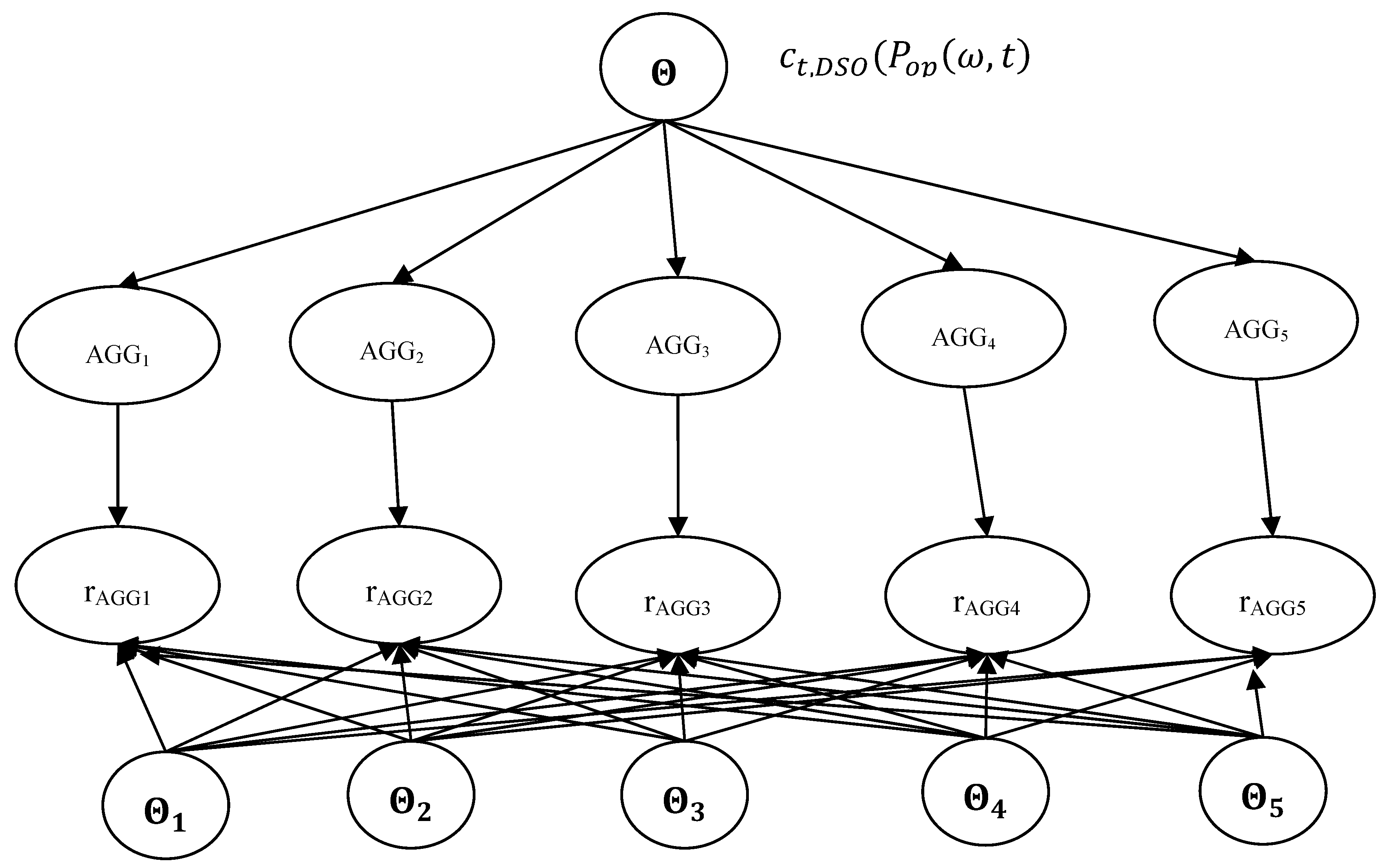
3.3. Objective Function Specification for Compensation Optimization
- Initialization of DSO savings, aggregator compensation, and end user reward.
- Estimation of appliance scheduling threshold by each aggregator.
- Aggregators announce the unit reward schedule for each time slot within the given day.
- Demand of each user within the aggregator is determined as well as the deviation from reference usage limits specified in (ii) and (iii).
- The operator announces the total demand for each aggregator cluster.
- The aggregator with the most cost savings is selected as the winner of the bid and removed from the competition.
| Algorithm 1. Procedure for rewarding the best-performing aggregator by DSO |
| Start under no DR program For each aggregator, determine the inelasticity coefficient for all shiftable appliances ) |
| Aggregators calculate the compensation from the objective function ) End |
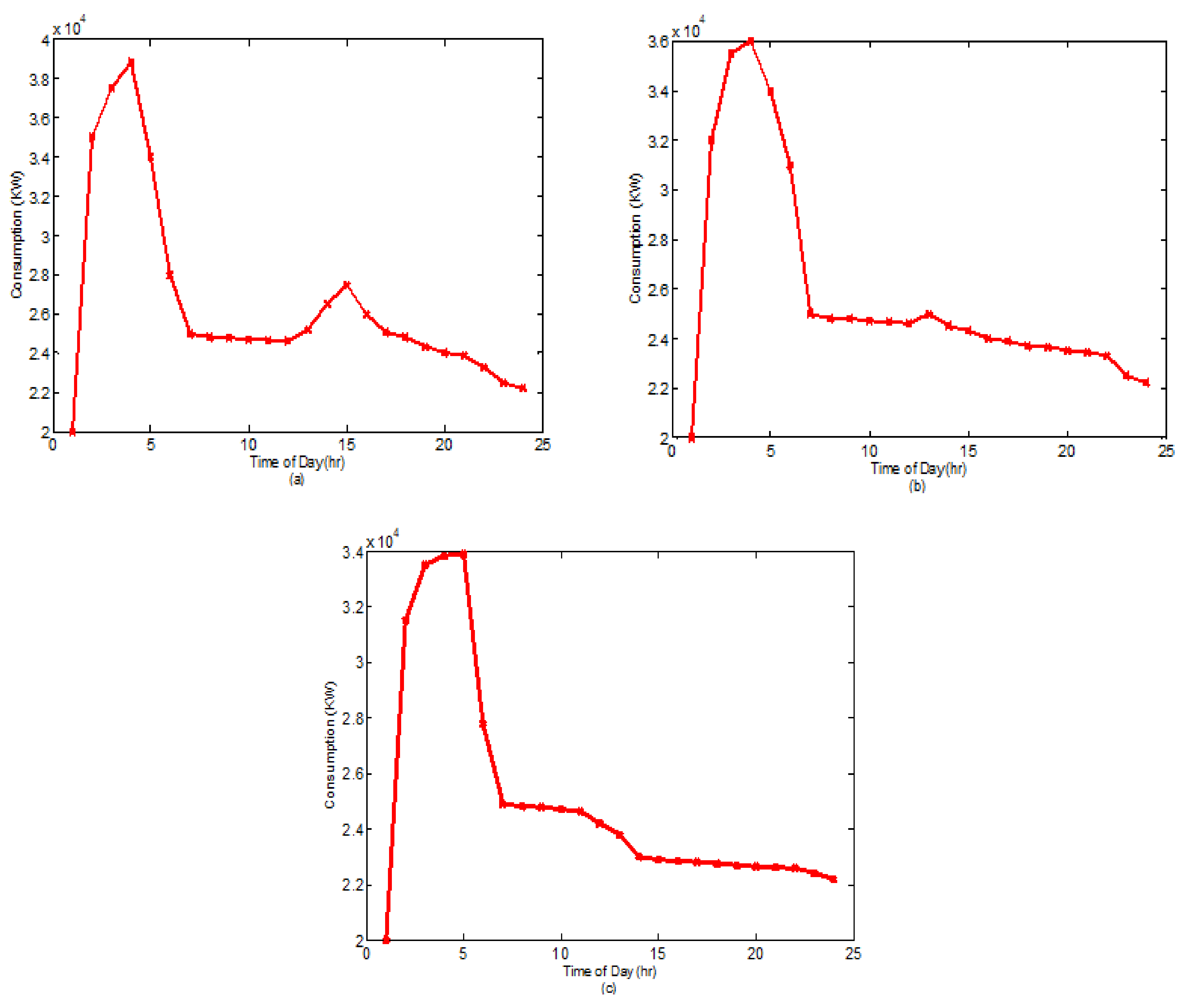
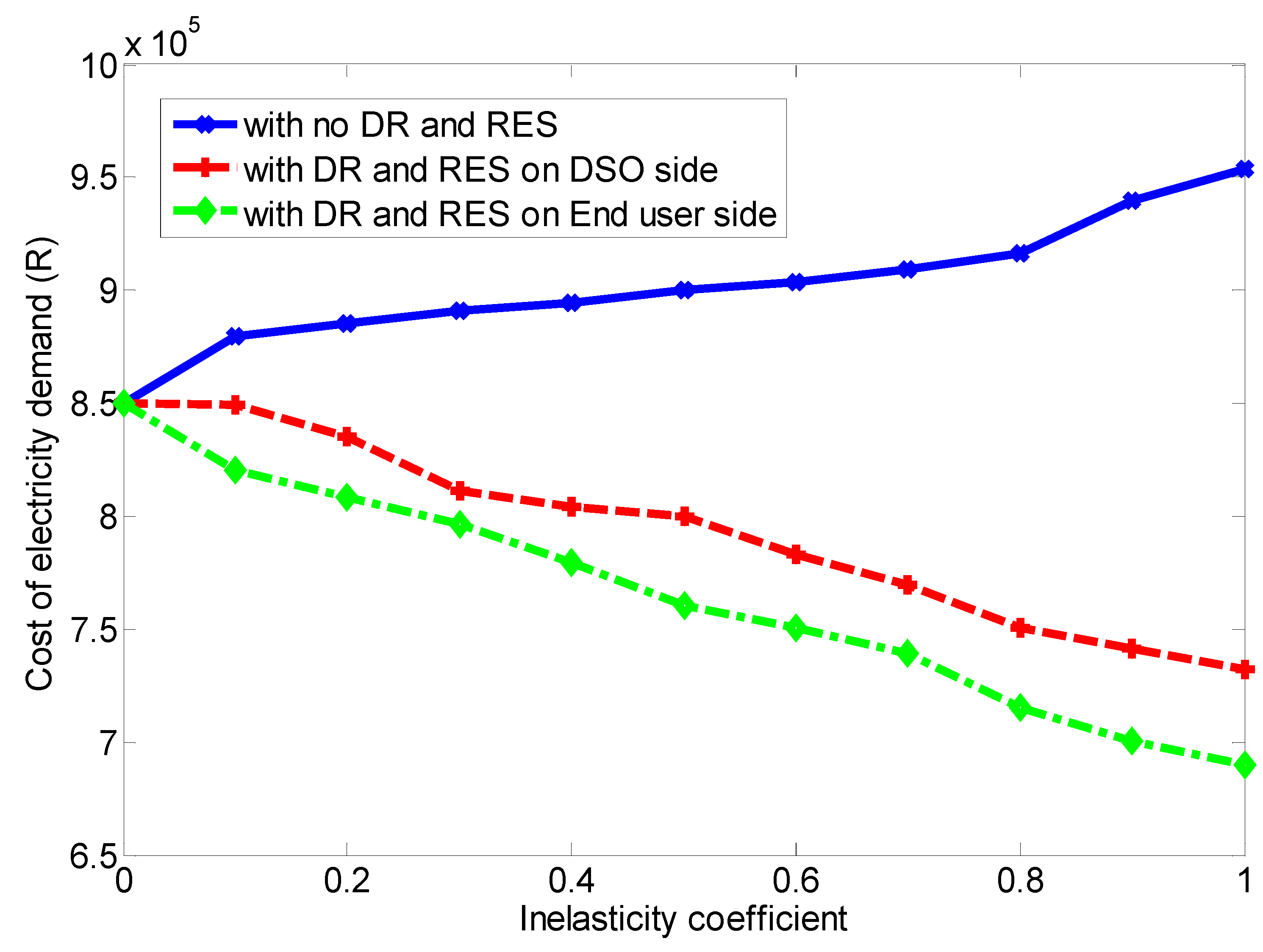
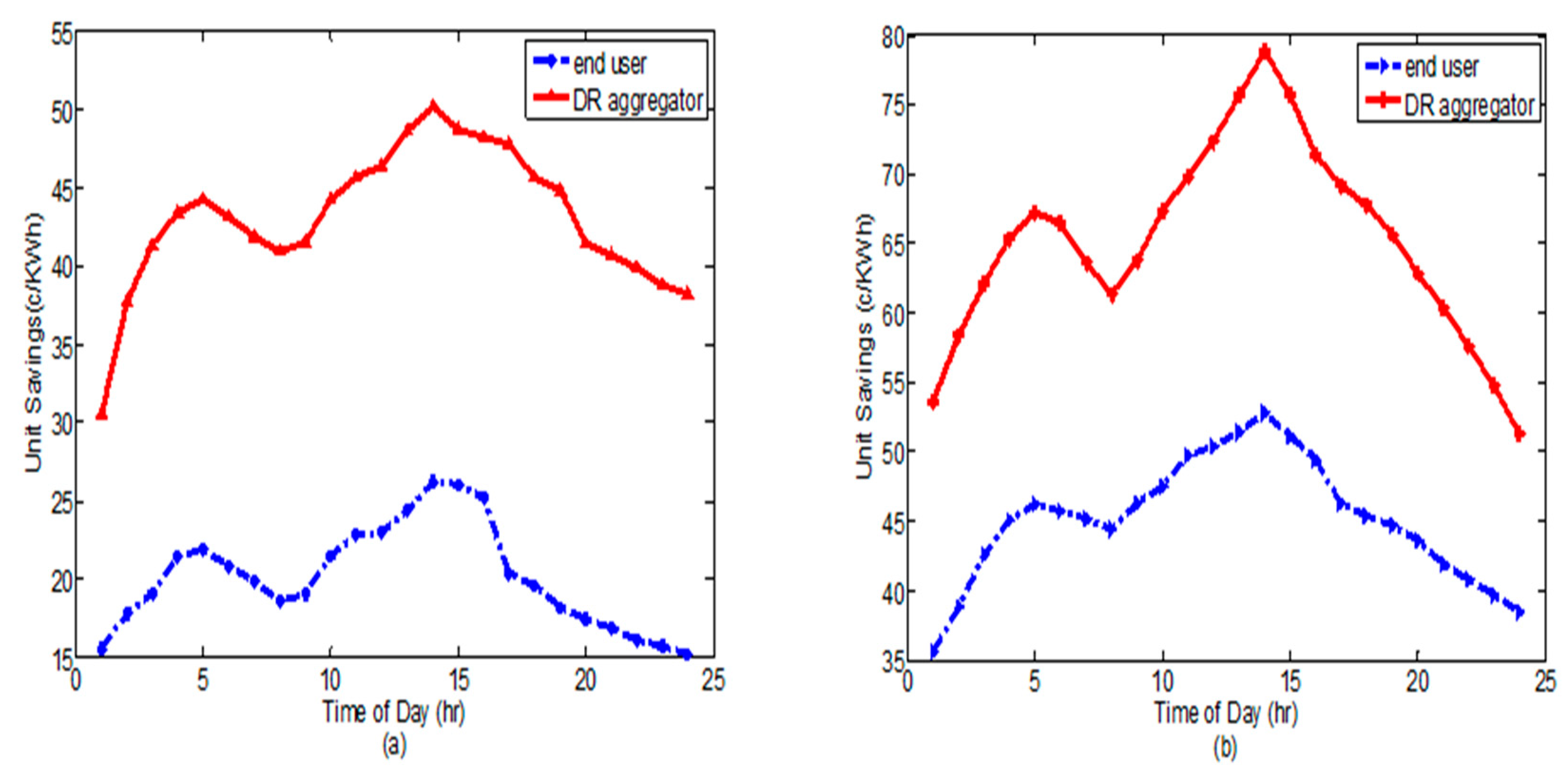
4. Results and Discussion
5. Conclusions
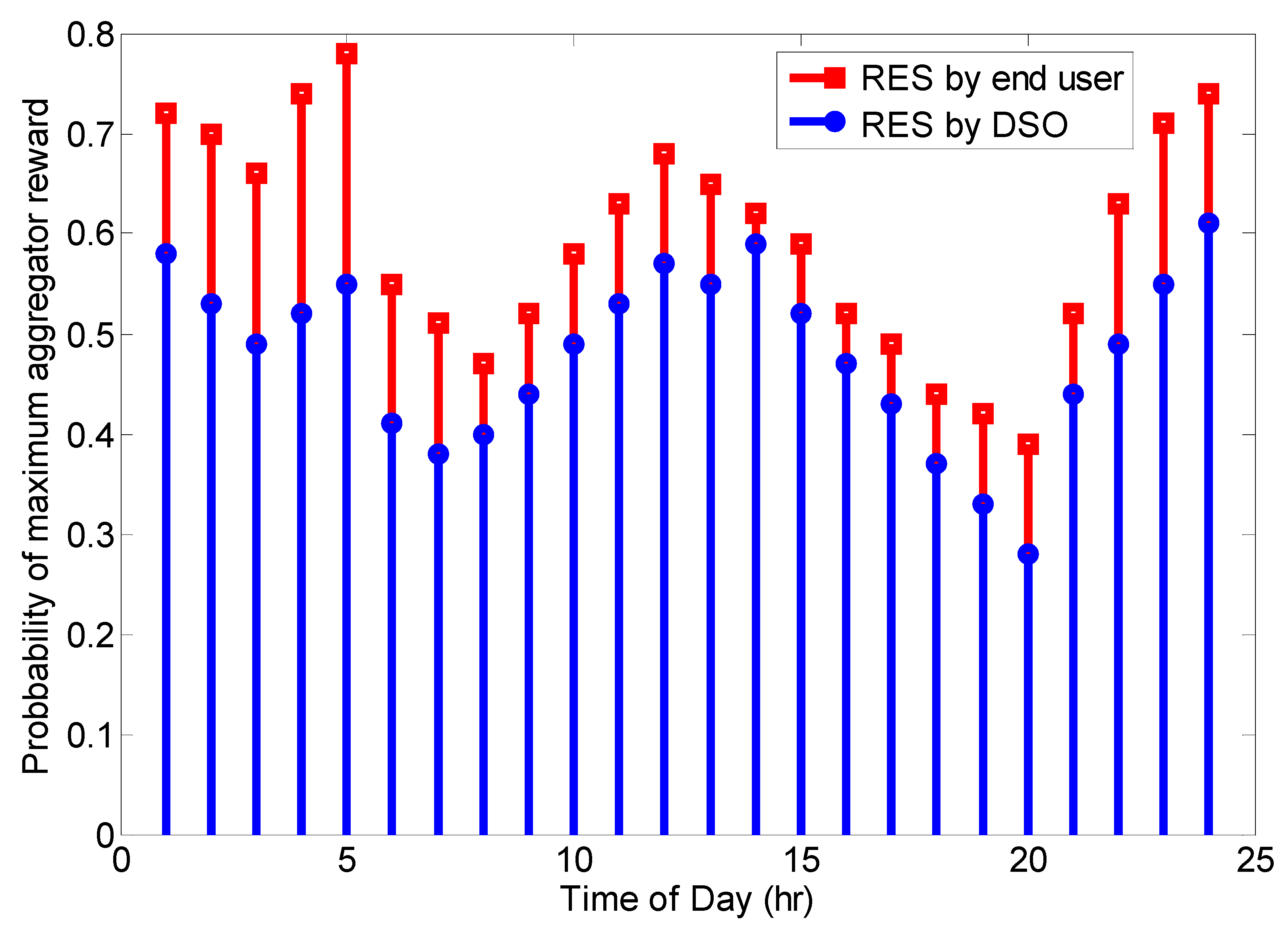
- Effective demand side management services have been provided to the DSO. This can be proved by the reduction in consumption of end users, which translates to cost savings for the DSO.
- Cost savings in terms of both total electricity demand and unit energy as end users participate in DR programs.
- DR aggregators have a positive impact in terms of maximizing financial benefits to both the DSO and end users. In particular, they ensure both unit energy savings and reduction in demand for end users while flattening the energy use profile during peak hours.
- Aggregators have maximized the benefits of incorporating renewable energy sources on both the DSO and end user side of the energy supply chain. Competition among aggregators results in the most cost-effective implementation of RES for both the DSO and end users.
- From the perspective of the end user, the financial benefits of participating in DR programs are significant in spite of the inconvenience caused by load shifting and curtailment. This is an incentive for end users to participate more actively in DR programs.
- The effect of plug-in electric vehicles has been observed as an improvement in load demand profile for end users during off-peak periods since they are largely in V2G mode.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| RES parameters | |
| DSO reward coefficient without demand response | |
| DSO reward coefficient due to energy purchased from solar farm | |
| DSO reward coefficient due to energy available from battery energy storage system | |
| SoC of battery at current time step | |
| SoC of battery at next time step | |
| Battery charging efficiency | |
| Battery discharging efficiency | |
| Battery self-discharge rate | |
| Self-discharging time step | |
| Battery charging time step | |
| Battery charging rate | |
| Battery charging power | |
| Battery discharging power | |
| Battery discharging time step | |
| Battery maximum allowed charging power level | |
| Battery maximum allowed discharging power level | |
| Battery charging status (0 = discharging, 1 = charging) | |
| Battery discharging status (0 = charging, 1 = discharging) | |
| PV module supplied power | |
| PV module thermal voltage | |
| PV module output current | |
| Number of PV module cascaded cells | |
| Boltzmann constant | |
| PV module irradiated temperature | |
| PV module electronic charge | |
| PV module output voltage | |
| Solar cell series current | |
| Solar cell series resistance | |
| Diode quality factor | |
| Solar cell parallel resistance | |
| Minimum real power requirement for EV m in aggregator j at time t | |
| Time slot duration | |
| Optimal power charging coefficients | |
| Nominal power charging coefficients | |
| Charging status of EV m in aggregator cluster j at time t (0 = commuting, 1 = plug-in) | |
| SoC of battery for EV m in aggregator cluster j at time t | |
| Battery capacity of EV m in aggregator cluster j at time t | |
| Efficiency of charger for EV m in aggregator cluster j at time t | |
| Optimal operational setpoint of EV m in aggregator j at time t | |
| Maximum power demand of EV m at time t | |
| Up regulator capacity by aggregator at time t | |
| Down regulator capacity by aggregator at time t | |
| Responsive reserve capacity by aggregator | |
| Operational setpoint of EV m in aggregator cluster j at time t | |
| Power discharged by battery of EV m in aggregator cluster j at time t | |
| Energy price at time t | |
| Battery degradation for EV m in aggregator cluster j at time t | |
| Minimum additional power draw of EV m in aggregator j at time t | |
| Maximum additional power draw of EV m in aggregator j at time t | |
| Maximum power draw of EV m in aggregator cluster j at time t | |
| Estimated operating point of EV m in aggregator cluster j at time t | |
| Expected reserve capacity response for EV m in aggregator cluster j at time t | |
| Initial SoC of EV m in aggregator cluster j at time t | |
| Tri-level distribution service parameters | |
| Financial reward to DSO for winter day | |
| Financial reward to DR aggregator for winter day | |
| Financial reward to end user for winter day | |
| Cost of electricity generation accruing to DSO without DR implementation | |
| Cost of electricity generation accruing to DSO with DR implementation | |
| Compensation received from DSO | |
| Compensation paid to end users | |
| Compensation received from DR aggregator | |
| Dissatisfaction (coefficient) | |
| DSO operating cost | |
| Financial reward to DR aggregator | |
| Financial compensation to end user | |
| Compensation factor for EV m in aggregator cluster j at time t (compensating for unplanned trips) | |
| Degradation cost of battery for EV m in aggregator cluster j | |
| Discharge due to battery efficiency of EV m in aggregator cluster j at time t | |
| Maximum forecast day-ahead net load | |
| Forecast day-ahead net load at time t | |
| Minimum forecast day-ahead net load | |
References
- Muhammad, N.; Mishra, Y. Retailer’s risk-aware trading framework with demand response aggregators in short-term electricity markets. IET Gener. Transm. Distrib. 2019, 13, 2611–2618. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Le, L.B. Risk-constrained profit maximization for microgrid aggregators with demand response. IEEE Trans. Smart Grid 2015, 6, 135–146. [Google Scholar] [CrossRef]
- Li, D.; Chiu, W.-Y.; Sun, H.; Vincent Poor, H. Multiobjective optimization for demand side management program in smart grid. IEEE Trans. Smart Grid 2018, 14, 1482–1490. [Google Scholar] [CrossRef]
- Li, Z.; Wang, S.; Zheng, X.; de Leon, F.; Hong, T. Dynamic demand response using customer coupons considering multiple load aggregators to simultaneously achieve efficiency and fairness. IEEE Trans. Smart Grid 2018, 9, 3112–3121. [Google Scholar] [CrossRef]
- Mahmoudi, N.; Saha, T.; Eghbal, M. Demand response application by strategic wind power producers. IEEE Trans. Power Syst. 2016, 31, 1227–1237. [Google Scholar] [CrossRef]
- Essiet, I.O.; Sun, Y.; Wang, Z. Analysis of the effect of parameter variation on a dynamic cost function for distributed energy resources: A DER-CAM case study. Appl. Sci. 2018, 8, 884. [Google Scholar] [CrossRef]
- Gkatzikis, L.; Koutsopoulos, I.; Salonidis, T. The role of aggregators in smart grid demand response markets. IEEE J. Sel. Areas Commun. 2013, 31, 1247–1257. [Google Scholar] [CrossRef]
- Richardson, I.; Thomson, M.; Infield, D.; Clifford, C. Domestic electricity use: A high-resolution energy demand model. Energy Build. 2010, 42, 1878–1887. [Google Scholar] [CrossRef]
- Di Somma, M.; Graditi, G.; Siano, P. Optimal bidding strategy for a DER aggregator in the day-ahead market in the presence of demand flexibility. IEEE Trans. Ind. Electr. 2019, 66, 1509–1519. [Google Scholar] [CrossRef]
- Faria, P.; Spinola, J.; Vale, Z. Aggregation and remuneration of electricity consumers and producers for the definition of demand-response programs. IEEE Trans. Ind. Inf. 2016, 12, 952–961. [Google Scholar] [CrossRef]
- Hansen, T.; Roche, R.; Suryanaranan, S.; Maciejewski, A.; Siegel, H.J. Heuristic Optimization for an aggregator-based resource allocation in the smart grid. IEEE Trans. Smart Grid 2015, 6, 1785–1794. [Google Scholar] [CrossRef]
- Henriquez, R.; Wenzel, G.; Olivares, D.; Negrete-Pincetic, M. Participation of demand response aggregators in electricity markets: Optimal portfolio management. IEEE Trans. Smart Grid 2018, 9, 4861–4871. [Google Scholar] [CrossRef]
- Jia, Y.; Mi, Z.; Yu, Y.; Song, Z.; Fan, H. Tri-level decision-making framework for strategic trading of demand response aggregator. IET Ren. Power Gener. 2019, 13, 2195–2206. [Google Scholar] [CrossRef]
- Salah, F.; Henriquez, R.; Wenzel, G.; Olivares, D.; Negrete-Pincetic, M.; Weinhardt, C. Portfolio design of a demand response aggregator with satisficing consumers. IEEE Trans. Smart Grid 2019, 10, 2475–2484. [Google Scholar] [CrossRef]
- Kies, A.; Schyska, B.U.; von Bremen, L. The demand side management potential to balance a highly renewable European power system. Energies 2016, 9, 955. [Google Scholar] [CrossRef]
- Behrangrad, M. A review of demand side management business models in the electricity market. Renew. Sust. Energy Rev. 2015, 47, 270–283. [Google Scholar] [CrossRef]
- Rashidizadeh-Kermani, H.; Vahedipour-Dahraie, M.; Anvari-Moghaddam, A.; Guerrero, J.M. A stochastic bi-level decision-making framework for a load-serving entity in day-ahead and balancing markets. Int. Trans. Electr. Energy Syst. 2019, 29, 1–20. [Google Scholar] [CrossRef]
- Sharifi, R.; Anvari-Moghaddam, A.; Fathi, S.H.; Guerrero, J.M.; Vahidinasab, V. Economic demand response model in liberalised electricity markets with respect to flexibility of consumers. IET Gener. Trans. Distrib. 2017, 4291–4298. [Google Scholar] [CrossRef]
- Anvari-Moghaddam, A.; Monsef, H.; Rahimi-Kian, A.; Guerrero, J.M.; Vasquez, J.C. Optimized energy management of a single-house residential micro-grid with automated demand response. In Proceedings of the 2015 IEEE Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015. [Google Scholar]
- Mohan, V.; Singh, J.G.; Ongsakul, W. Sortino ratio based portfolio optimization considering EVs and renewable energy in microgrid power market. IEEE Trans. Sustain. Energy 2017, 8, 219–229. [Google Scholar] [CrossRef]
- Carpinelli, G.; Mottola, F.; Proto, D. Optimal scheduling of a microgrid with demand response resources. IET Gener.Trans. Distrib. 2014, 8, 1891–1899. [Google Scholar] [CrossRef]
- Kardakos, E.G.; Simoglou, C.K.; Bakirtzis, A.G. Optimal offering strategy of a virtual power plant: A stochastic bi-level approach. IEEE Trans. Smart Grid 2016, 7, 794–806. [Google Scholar] [CrossRef]
- Diekerhof, M.; Peterssen, F.; Monti, A. Hierarchical distributed robust optimization for demand response services. IEEE Trans. Smart Grid 2018, 9, 6018–6029. [Google Scholar] [CrossRef]
- Brusco, G.; Burgio, A.; Menniti, D.; Pinnarelli, A.; Sorrentino, N. Energy management system for an energy district with demand response availability. IEEE Trans. Smart Grid 2014, 5, 2385–2393. [Google Scholar] [CrossRef]
- Zhang, Y.; Giannakis, G.B. Distributed stochastic market clearing with high-penetration wind power. IEEE Trans. Power Syst. 2016, 31, 895–906. [Google Scholar] [CrossRef]
- Mhanna, S.; Chapman, A.; Verbic, G. A fast distributed algorithm for large-scale demand response aggregation. IEEE Trans. Smart Grid 2016, 7, 2094–2107. [Google Scholar] [CrossRef]
- Bahrami, S.; Amini, M.H.; Shafie-Khah, M.; Catalão, J.P.S. A decentralized renewable generation management and demand response in power distribution networks. IEEE Trans. Sustain. Energy 2018, 9, 1783–1797. [Google Scholar] [CrossRef]
- Anjos, M.F.; Lodi, A.; Tanneau, M. A decentralized framework for the optimal coordination of distributed energy resources. IEEE Trans. Power Syst. 2019, 34, 349–359. [Google Scholar] [CrossRef]
- Lu, T.; Wang, Z.; Wang, J.; Ai, Q.; Wang, C. A data-driven Stackelberg market strategy for demand response-enabled distribution systems. IEEE Trans. Smart Grid 2019, 10, 2345–2357. [Google Scholar] [CrossRef]
- Rashidizadeh-Kermani, H.; Vahedipour-Dahraie, M.; Anvari-Moghaddam, A.; Guerrero, J.M. Stochastic risk-constrained decision-making approach for a retailer in a competitive environment with flexible demand side resources. Int. Trans. Electr. Energy Syst. 2019, 29, 1–21. [Google Scholar] [CrossRef]
- Esmaeili, S.; Anvari-Moghaddam, A.; Jadid, S. Retail market equilibrium and interactions among reconfigurable networked microgrids. Sustain. Cities Soc. 2019, 49, 1–14. [Google Scholar] [CrossRef]
- Motoring Technology. There Are 1000 Electric Vehicles on SA Roads. Available online: https://www.itweb.co.za/content/mQwkoq6Kb2gv3r9A (accessed on 11 November 2019).
- Essiet, I.O.; Sun, Y.; Wang, Z. Optimized energy consumption model for smart home using improved differential evolution algorithm. Energy 2019, 172, 354–365. [Google Scholar] [CrossRef]
- Mohammadi, M.; Talebpour, F.; Safaee, E.; Ghadimi, N.; Abedinia, O. Small-scale building load forecast based on hybrid forecast engine. Neural Process. Lett. 2018, 48, 329–351. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Y.; He, H.; Ren, S.; Weng, W. Real-time demand side management for a microgrid considering uncertainties. IEEE Trans. Smart Grid 2019, 10, 3401–3414. [Google Scholar] [CrossRef]
- Karfopoulos, E.L.; Panourgias, K.A.; Hatziargyriou, N.D. Distributed coordination of electric vehicles providing V2G regulation services. IEEE Trans. Power Syst. 2016, 31, 2834–2846. [Google Scholar]
- Schedule of Approved Electricity Tariffs for FY2019/20. Available online: www.citypower.co.za (accessed on 28 September 2019).
| Appliance | Rating (KW) | Number | Operating Time (h) | Schedule | Energy Usage Sharing |
|---|---|---|---|---|---|
| Geyser | 3.5 | 1 | 06:00–07:00, 19:00–20:00 | Shiftable | Smart plug |
| Electric kettle | 2.0 | 1 | 07:00–09:00 | Shiftable | Smart plug |
| Toaster | 1.5 | 1 | 07:00–08:00 | Shiftable | Smart plug |
| Microwave oven | 1.0 | 1 | 18:00–20:00 | Shiftable | Smart plug |
| Dishwasher | 1.0 | 1 | 08:00–09:00, 21:00–22:00 | Shiftable | Smart plug |
| Vacuum cleaner | 1.7 | 1 | 21:00–23:00 | Shiftable | Smart plug |
| Electric iron | 1.2 | 1 | 06:00–07:00, 22:00–23:00 | Shiftable | Smart plug |
| Washing machine | 0.33 | 1 | 22:00–00:00 | Shiftable | Smart plug |
| TV | 0.065 | 1 | 07:00–09:00, 18:00–23:00 | Shiftable | Smart plug |
| Pool heater | 2.5 | 1 | 20:00–22:00 | Shiftable | Smart plug |
| Electric stove/oven | 4.0 | 1 | 07:00–08:00, 18:00–20:00 | Shiftable | Smart plug |
| Refrigerator | 0.25 | 1 | 00:00–00:00 | Non-shiftable | Smart plug |
| Lights | 0.024 | 10 | 06:00–08:00, 18:00–23:00 | Shiftable | Zigbee enabled |
| Bedroom heater | 0.8 | 1 | 23:00–06:00 | Shiftable | Smart plug |
| Miscellaneous loads | 1.0 | - | 07:00–09:00, 18:00–23:00 | Shiftable | Smart plug |
| Parameter | Setting |
|---|---|
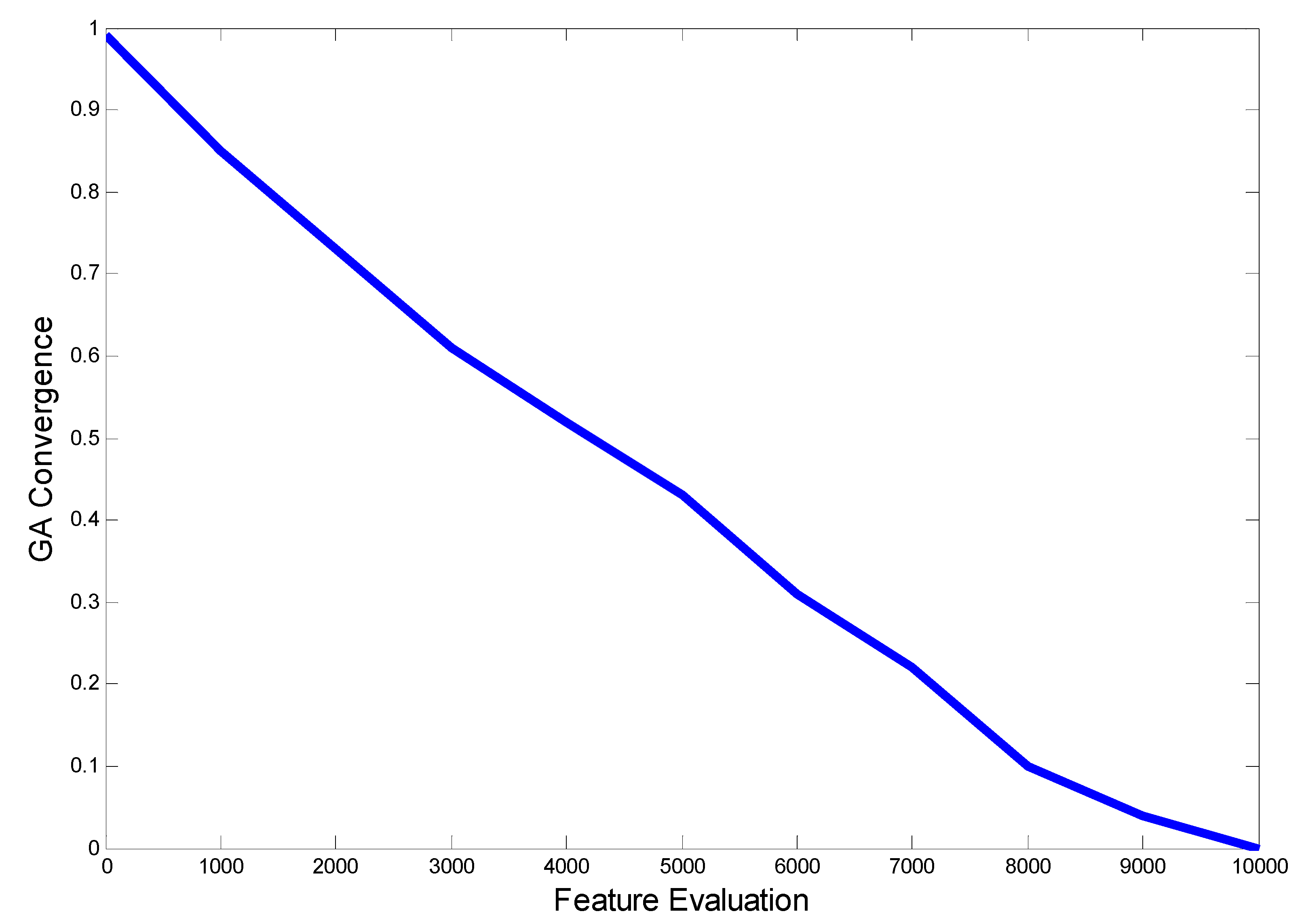
| Number of feature evaluations (FEs) | 10,000 |
| Number of particles | 500 |
| Mutation rate | 1/n |
| Cross over rate | 0.5–1.0 |
| Number of dimensions | 50 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Essiet, I.O.; Sun, Y. Maximizing Demand Response Aggregator Compensation through Optimal RES Utilization: Aggregation in Johannesburg, South Africa. Appl. Sci. 2020, 10, 594. https://doi.org/10.3390/app10020594
Essiet IO, Sun Y. Maximizing Demand Response Aggregator Compensation through Optimal RES Utilization: Aggregation in Johannesburg, South Africa. Applied Sciences. 2020; 10(2):594. https://doi.org/10.3390/app10020594
Chicago/Turabian StyleEssiet, Ima O., and Yanxia Sun. 2020. "Maximizing Demand Response Aggregator Compensation through Optimal RES Utilization: Aggregation in Johannesburg, South Africa" Applied Sciences 10, no. 2: 594. https://doi.org/10.3390/app10020594
APA StyleEssiet, I. O., & Sun, Y. (2020). Maximizing Demand Response Aggregator Compensation through Optimal RES Utilization: Aggregation in Johannesburg, South Africa. Applied Sciences, 10(2), 594. https://doi.org/10.3390/app10020594





