Numerical Simulation of an InP Photonic Integrated Cross-Connect for Deep Neural Networks on Chip
Abstract
1. Introduction
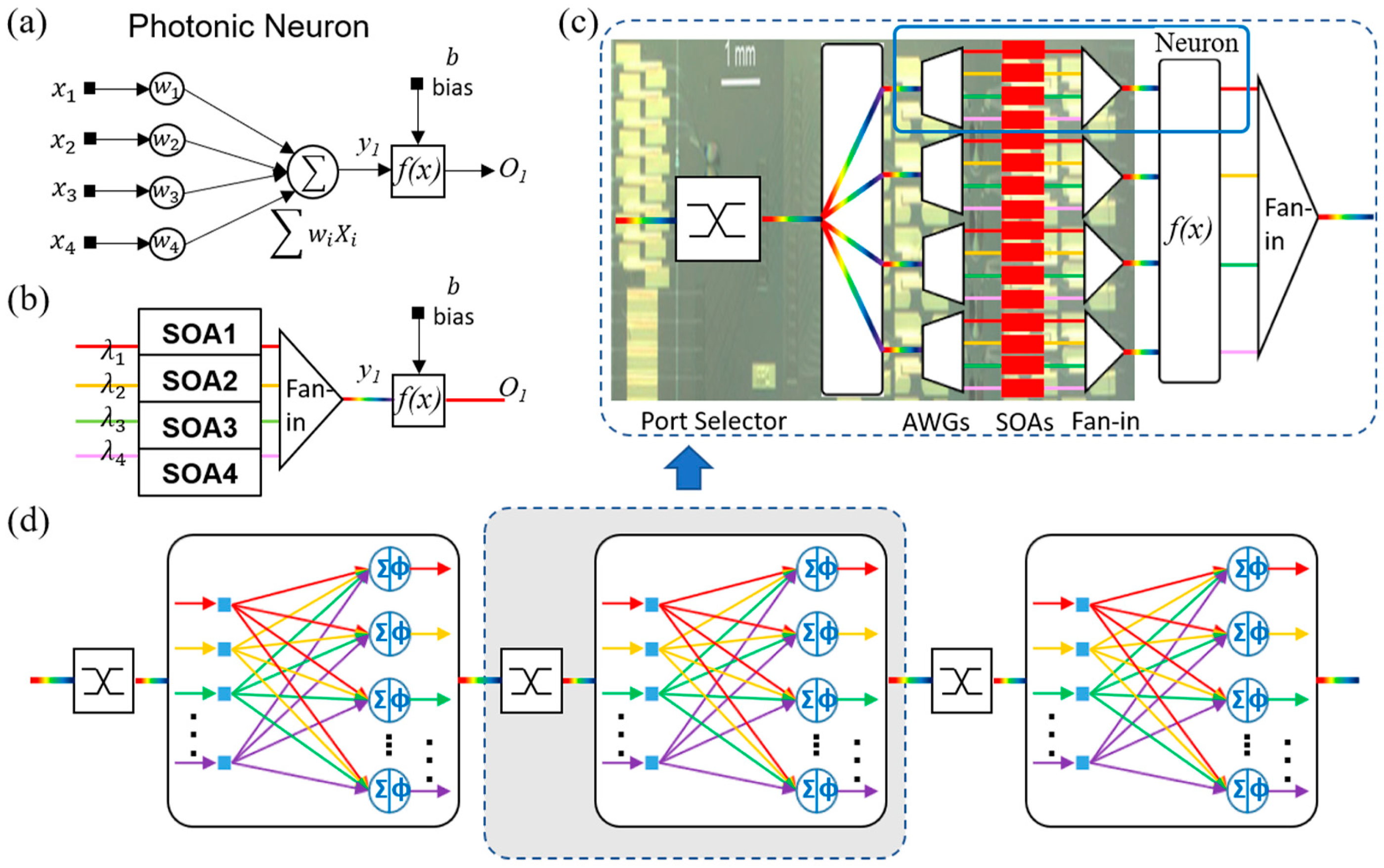
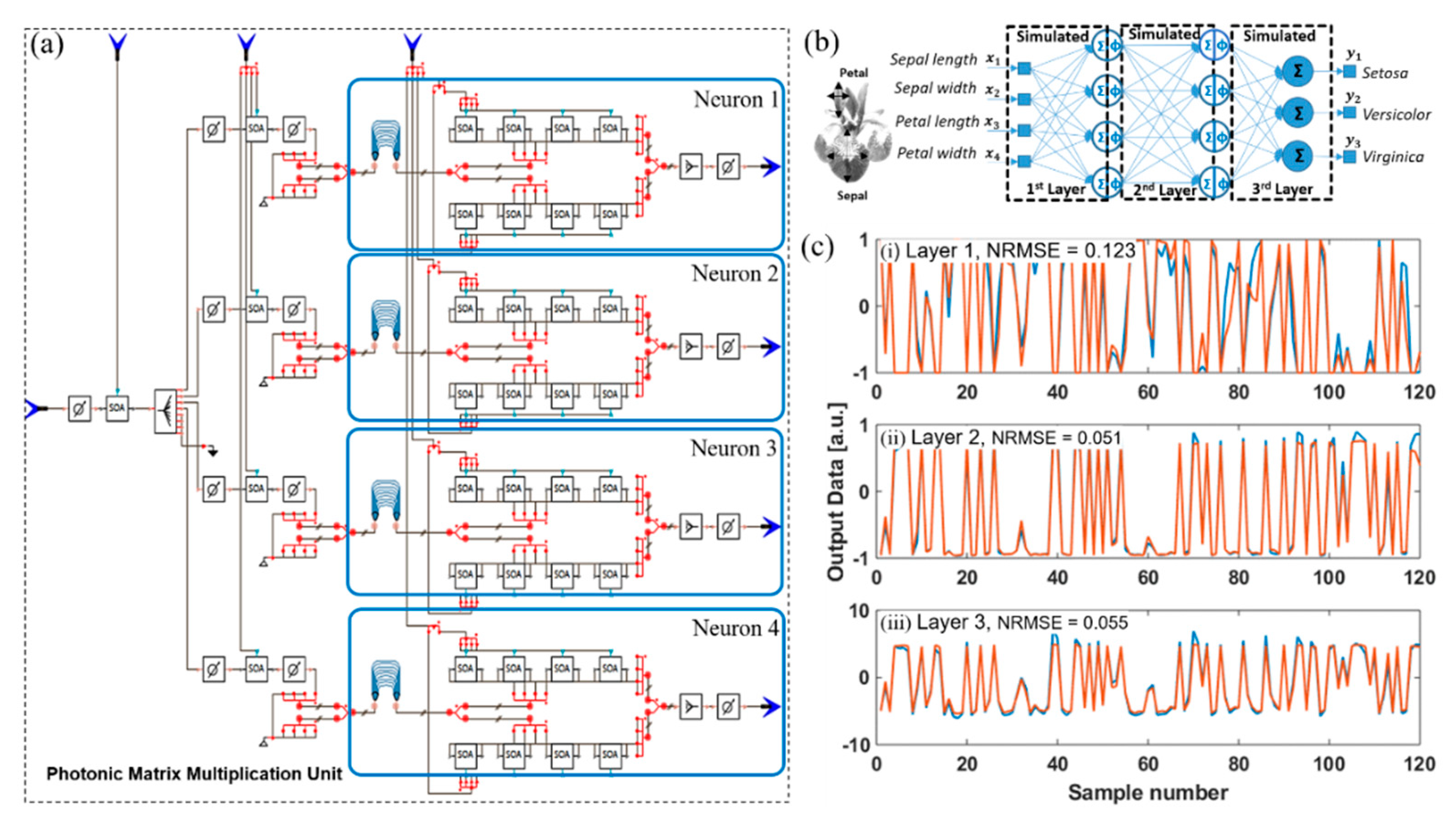
2. Photonic Deep Neural Network with Weight-SOAs
3. Optical Cross-Connect: Implementation and Simulation
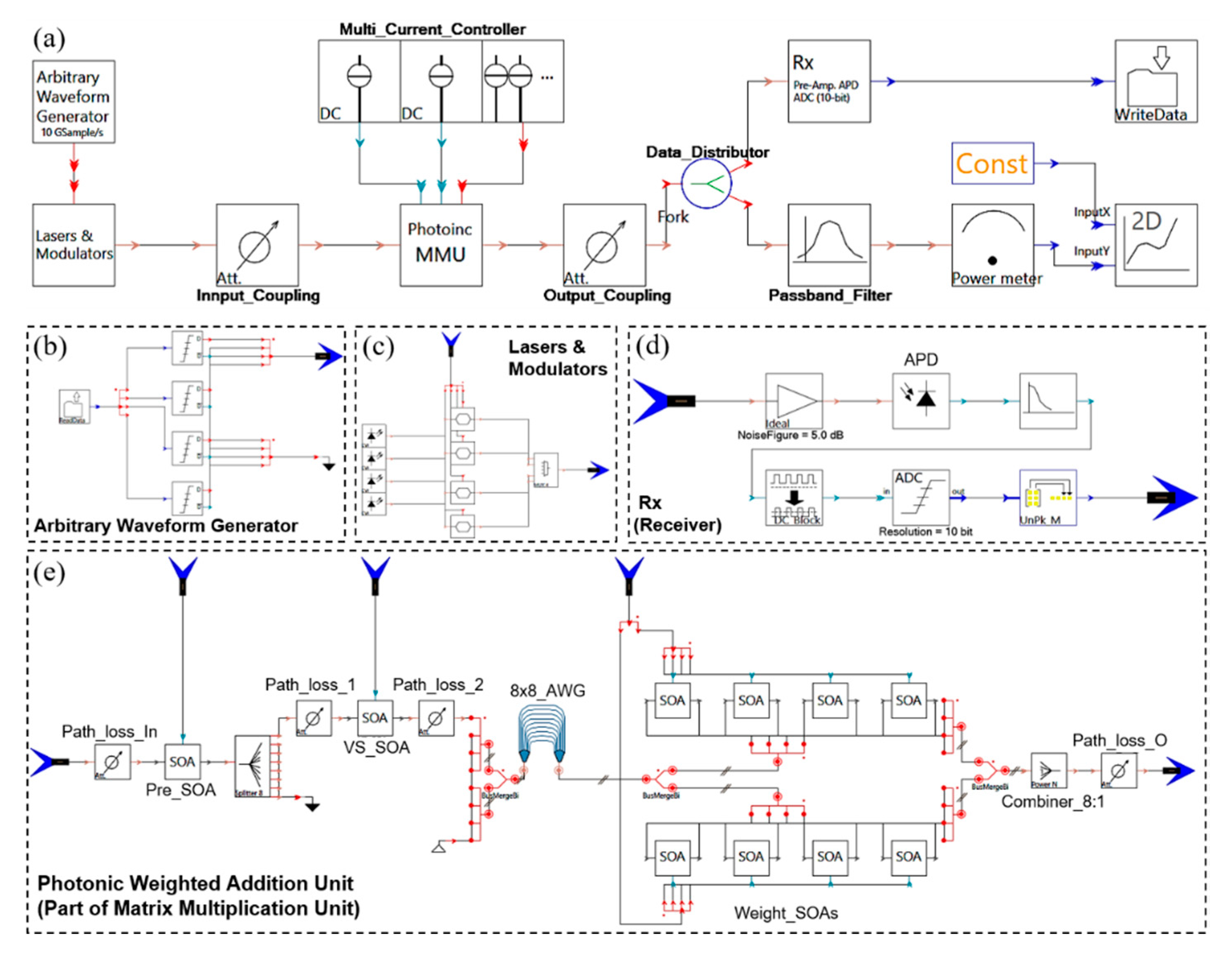
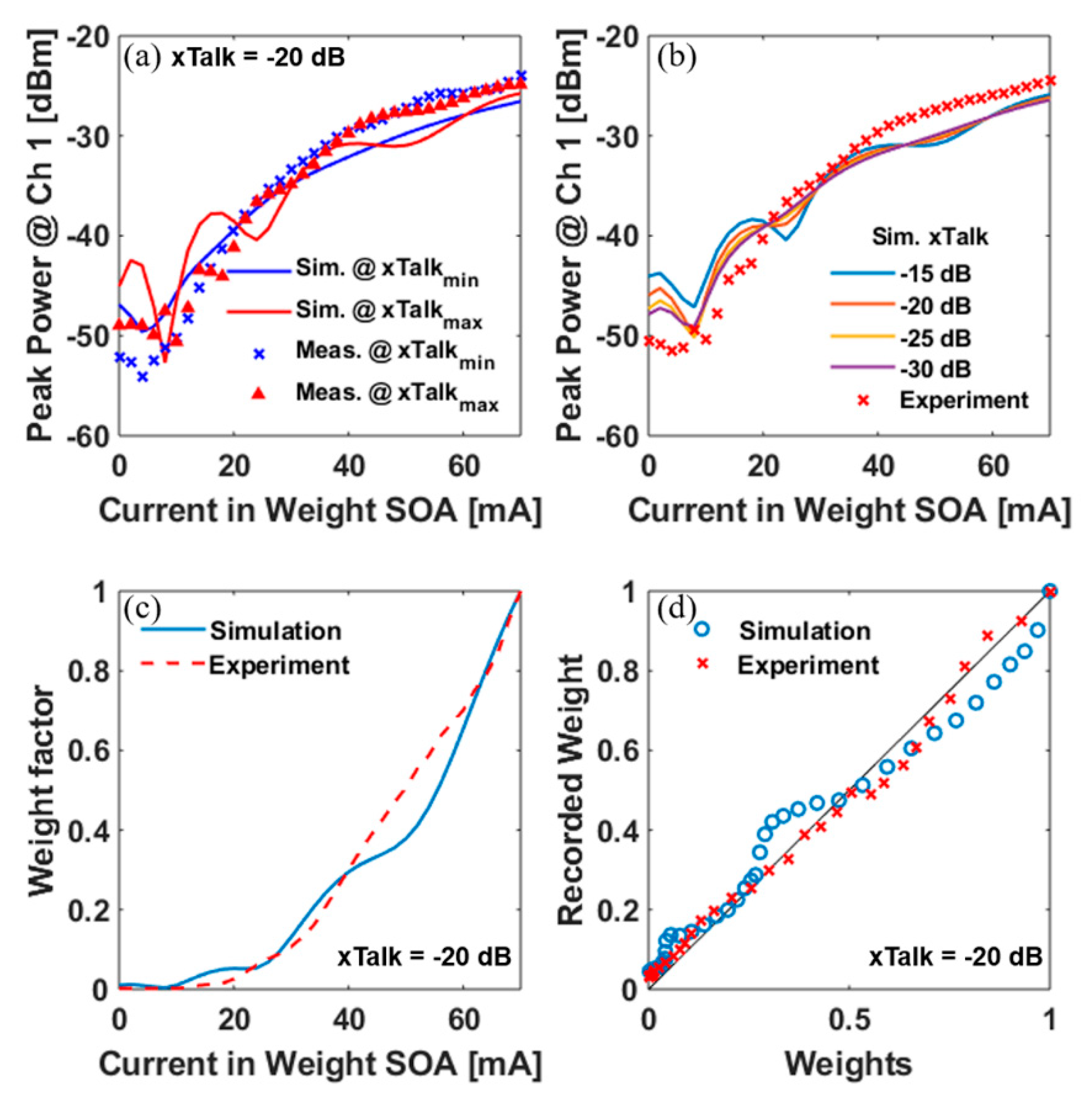
4. Implementation of Weight Calibration and Weighted Addition
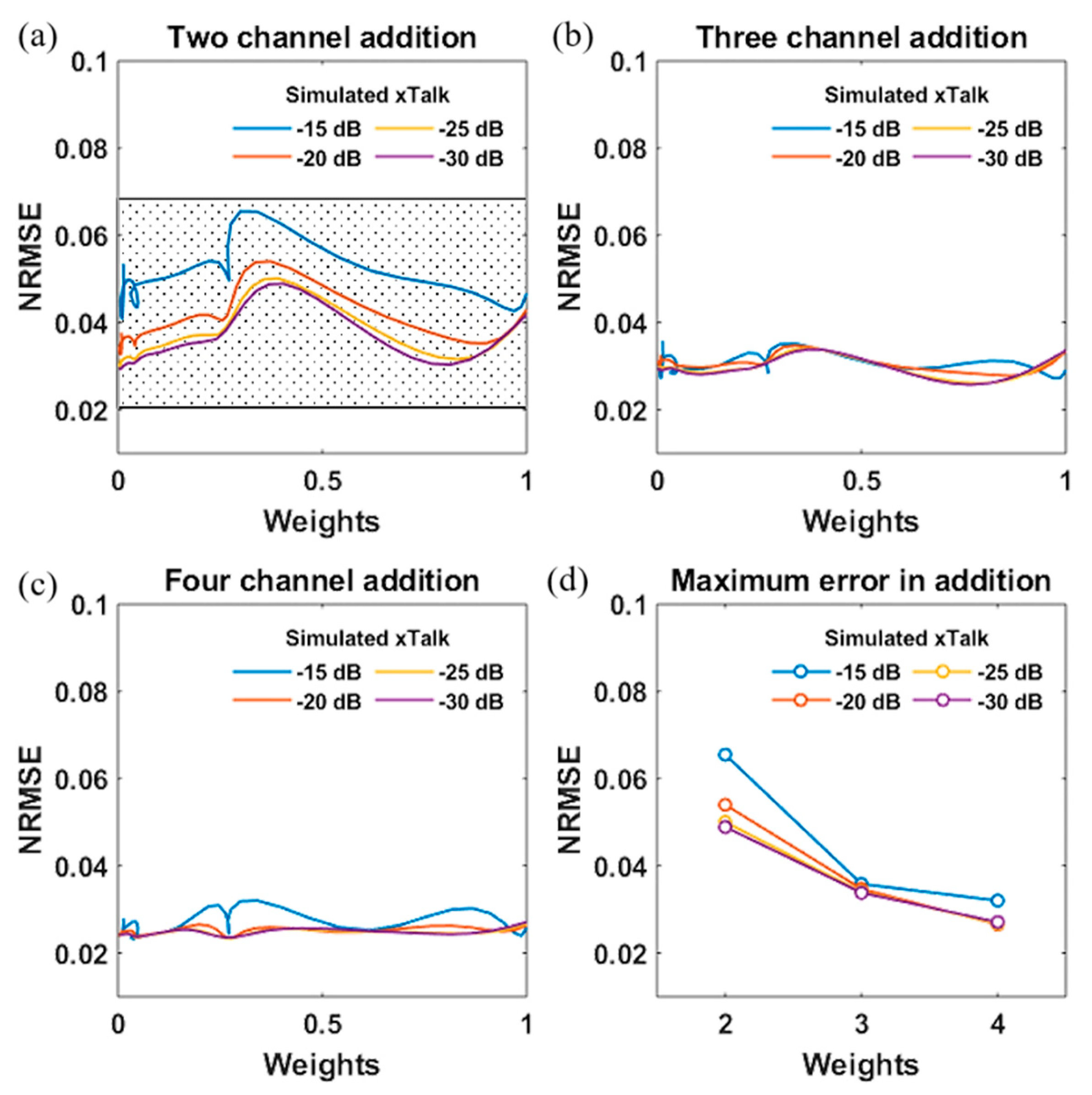
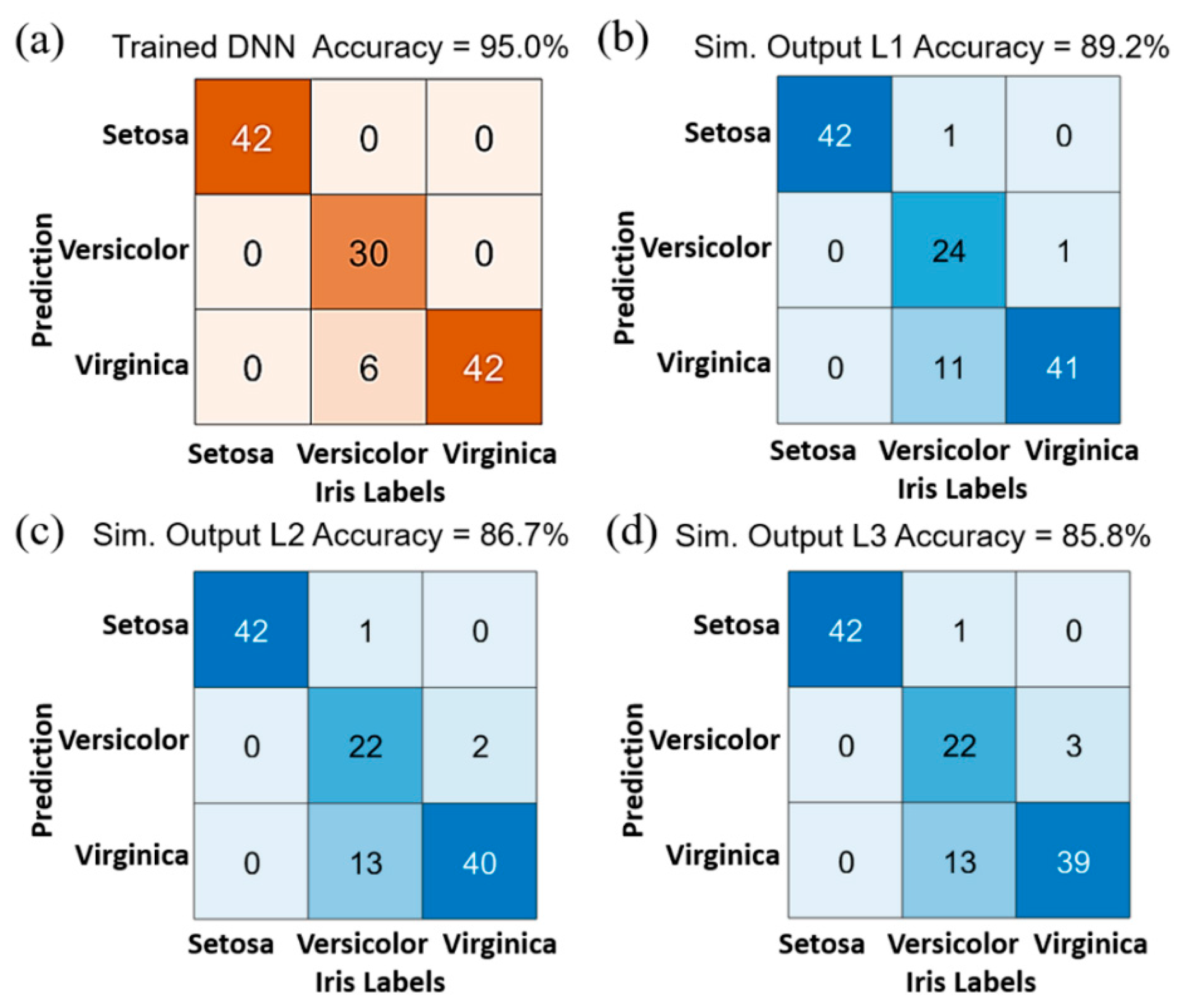
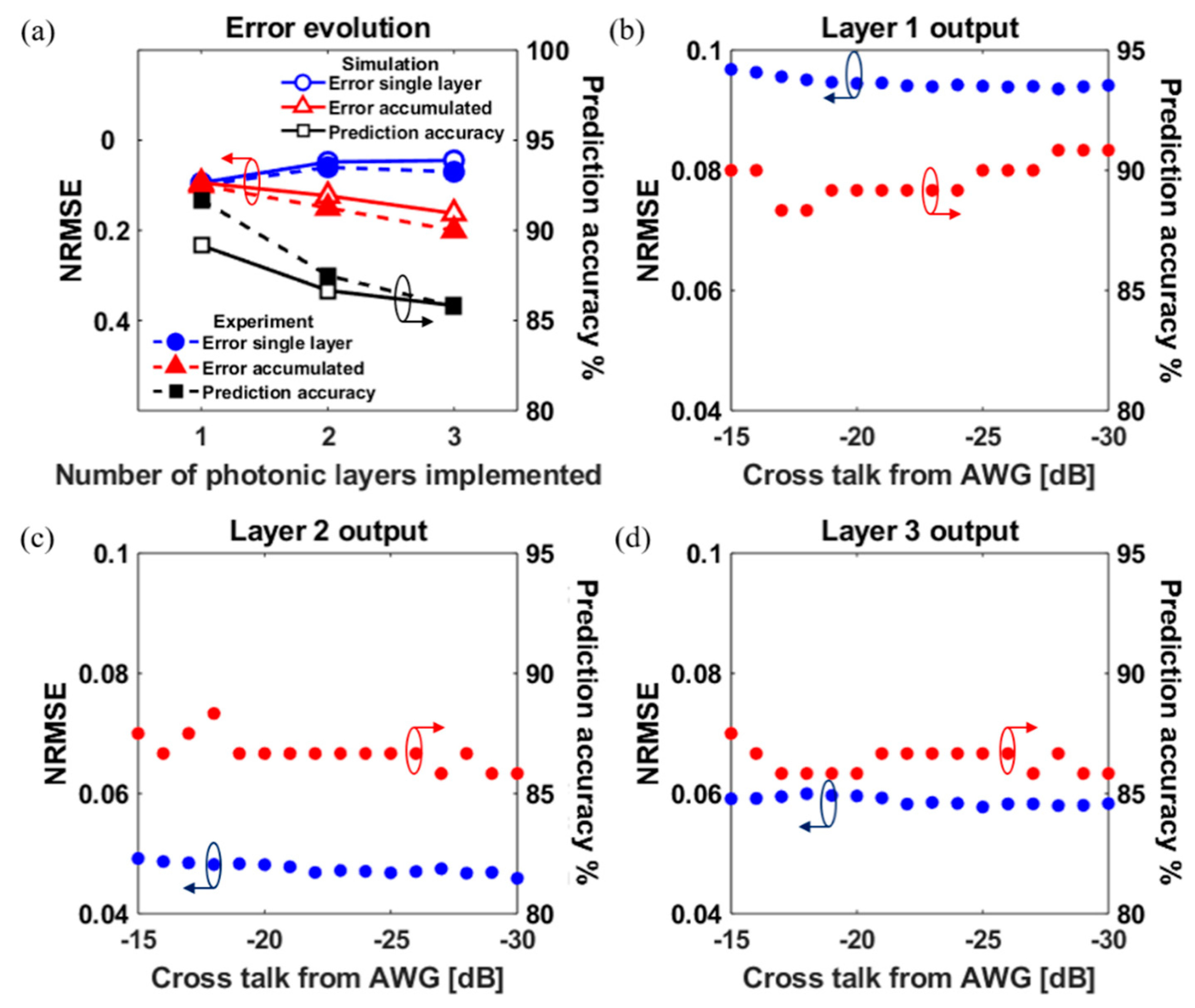
5. Image Classification via a Three-Layer Photonic Deep Neural Network
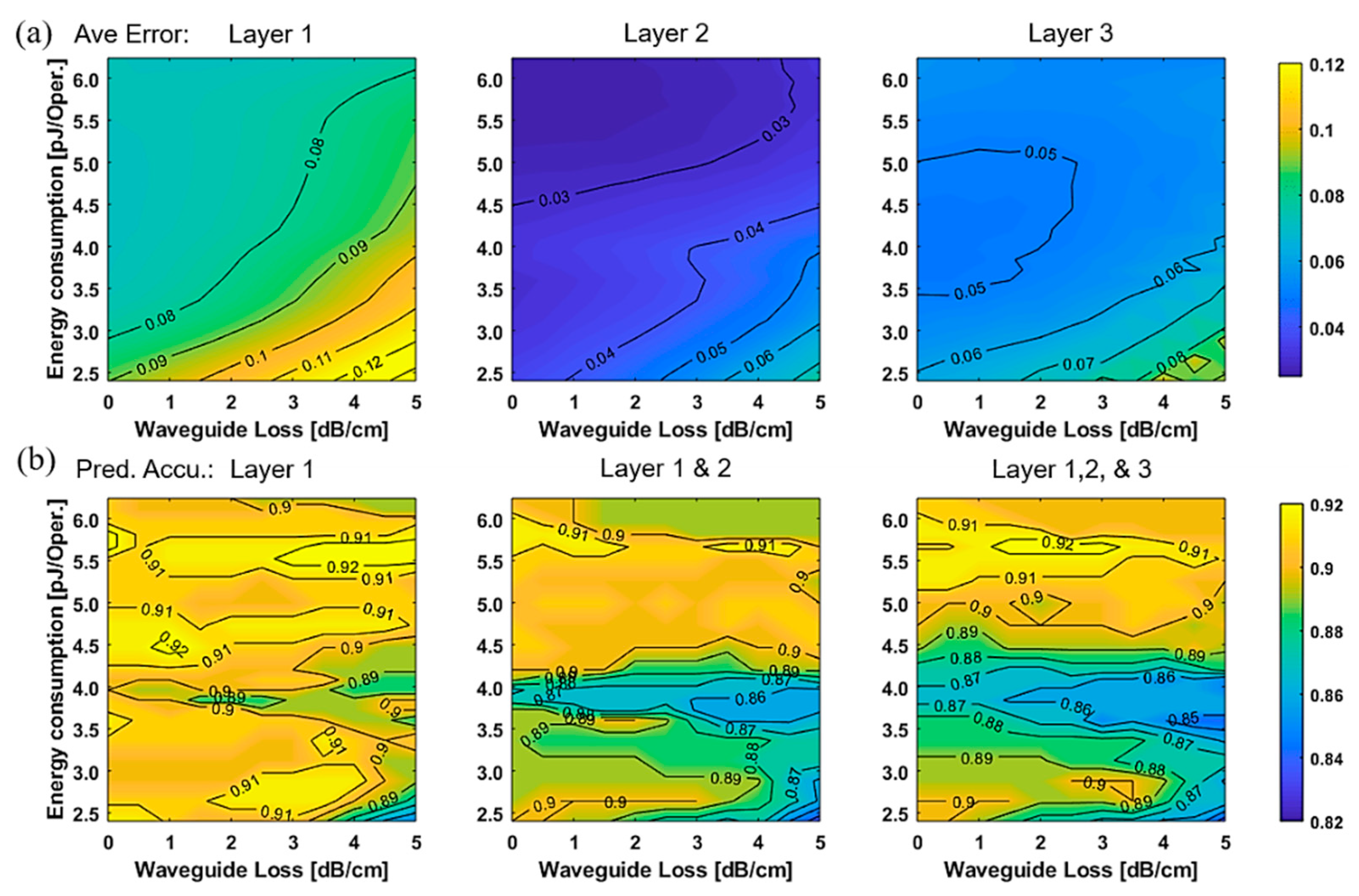
5.1. Energy Consumption Versus Physical Layer Impairments
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- McAfee, A.; Brynjolfsson, E. Big Data: the Management Revolution. Harv. Bus. Rev. 2012, 90, 60–66, 68, 128. [Google Scholar] [PubMed]
- Philip Chen, C.L.; Zhang, C.-Y. Data-Intensive Applications, Challenges, Techniques and Technologies: A Survey on Big Data. Inf. Sci. (Ny) 2014, 275, 314–347. [Google Scholar] [CrossRef]
- Masci, J.; Meier, U.; Cire, D. Stacked Convolutional Auto-Encoders for Hierarchical Feature Extraction. In Proceedings of the Artificial Neural Networks and Machine Learning-ICANN 2011; Honkela, T., Duch, W., Girolami, M., Kaski, S., Eds.; Springer: Berlin, Germany, 2011; pp. 52–59. [Google Scholar]
- Lawrence, S.; Giles, C.L.; Tsoi, A.C.; Back, A.D. Face Recognition: A Convolutional Neural-Network Approach. IEEE Trans. Neural Netw. 1997, 8, 98–113. [Google Scholar] [CrossRef]
- Hill, T.; O’Connor, M.; Remus, W. Neural Network Models for Time Series Forecasts. Manag. Sci. 1996, 42, 1082–1092. [Google Scholar] [CrossRef]
- Chow, T.T.; Zhang, G.Q.; Lin, Z.; Song, C.L. Global Optimization of Absorption Chiller System by Genetic Algorithm and Neural Network. Energy Build. 2002, 34, 103–109. [Google Scholar] [CrossRef]
- Zeng, H.; Edwards, M.D.; Liu, G.; Gifford, D.K. Convolutional Neural Network Architectures for Predicting DNA–Protein Binding. Bioinformatics 2016, 32, i121–i127. [Google Scholar] [CrossRef]
- Ball, N.M.; Brunner, R.J. Data Mining and Machine Learning in Astronomy. Int. J. Mod. Phys. D 2010, 19, 1049–1106. [Google Scholar] [CrossRef]
- Cannas, B.; Fanni, A.; Marongiu, E.; Sonato, P. Disruption Forecasting at JET Using Neural Networks. Nucl. Fusion 2004, 44, 68–76. [Google Scholar] [CrossRef]
- Fischer, M.M.; Gopal, S. Artificial Neural Networks: A New Approach to Modeling Interregional Telecommunication Flows. J. Reg. Sci. 1994, 34, 503–527. [Google Scholar]
- Akopyan, F.; Sawada, J.; Cassidy, A.; Alvarez-Icaza, R.; Arthur, J.; Merolla, P.; Imam, N.; Nakamura, Y.; Datta, P.; Nam, G.J.; et al. TrueNorth: Design and Tool Flow of a 65 mW 1 Million Neuron Programmable Neurosynaptic Chip. IEEE Trans. Comput. Des. Integr. Circuits Syst. 2015, 34, 1537–1557. [Google Scholar] [CrossRef]
- Benjamin, B.V.; Gao, P.; McQuinn, E.; Choudhary, S.; Chandrasekaran, A.R.; Bussat, J.; Alvarez-Icaza, R.; Arthur, J.V.; Merolla, P.A.; Boahen, K. Neurogrid: A Mixed-Analog-Digital Multichip System for Large-Scale Neural Simulations. Proc. IEEE 2014, 102, 699–716. [Google Scholar] [CrossRef]
- Furber, S.B.; Galluppi, F.; Temple, S.; Plana, L.A. The SpiNNaker Project. Proc. IEEE 2014, 102, 652–665. [Google Scholar] [CrossRef]
- Neckar, A.; Fok, S.; Benjamin, B.V.; Stewart, T.C.; Oza, N.N.; Voelker, A.R.; Eliasmith, C.; Manohar, R.; Boahen, K. Braindrop: A Mixed-Signal Neuromorphic Architecture with a Dynamical Systems-Based Programming Model. Proc. IEEE 2019, 107, 144–164. [Google Scholar] [CrossRef]
- Zhang, C.; Li, P.; Sun, G.; Guan, Y.; Xiao, B.; Cong, J. Optimizing FPGA-Based Accelerator Design for Deep Convolutional Neural Networks. In Proceedings of the FPGA 2015–2015 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Monterey, CA, USA, 22–24 February 2015; ACM Press: New York, NY, USA, 2015; pp. 161–170. [Google Scholar]
- Han, S.; Liu, X.; Mao, H.; Pu, J.; Pedram, A.; Horowitz, M.A.; Dally, W.J. EIE: Efficient Inference Engine on Compressed Deep Neural Network. In Proceedings of the 2016 ACM/IEEE 43rd Annual International Symposium on Computer Architecture (ISCA), Seoul, Korea, 18–22 June 2016; pp. 243–254. [Google Scholar]
- Jouppi, N.P.; Borchers, A.; Boyle, R.; Cantin, P.; Chao, C.; Clark, C.; Coriell, J.; Daley, M.; Dau, M.; Dean, J.; et al. In-Datacenter Performance Analysis of a Tensor Processing Unit. In Proceedings of the Proceedings-International Symposium on Computer Architecture, Toronto, ON, Canada, 24–28 June 2017; ACM Press: New York, NY, USA, 2017; pp. 1–12. [Google Scholar]
- Kravtsov, K.S.; Fok, M.P.; Prucnal, P.R.; Rosenbluth, D. Ultrafast All-Optical Implementation of a Leaky Integrate-and-Fire Neuron. Opt. Express 2011, 19, 2133–2147. [Google Scholar] [CrossRef]
- Bueno, J.; Maktoobi, S.; Froehly, L.; Fischer, I.; Jacquot, M.; Larger, L.; Brunner, D. Reinforcement Learning in a Large-Scale Photonic Recurrent Neural Network. Optica 2018, 5, 756–760. [Google Scholar] [CrossRef]
- Nakayama, J.; Kanno, K.; Uchida, A. Laser Dynamical Reservoir Computing with Consistency: An Approach of a Chaos Mask Signal. Opt. Express 2016, 24, 8679–8692. [Google Scholar] [CrossRef]
- Stabile, R.; Rohit, A.; Williams, K.A. Monolithically Integrated 8 × 8 Space and Wavelength Selective Cross-Connect. J. Light. Technol. 2014, 32, 201–207. [Google Scholar] [CrossRef]
- Smit, M.; Leijtens, X.; Ambrosius, H.; Bente, E.; van der Tol, J.; Smalbrugge, B.; de Vries, T.; Geluk, E.-J.; Bolk, J.; van Veldhoven, R.; et al. An Introduction to InP-Based Generic Integration Technology. Semicond. Sci. Technol. 2014, 29, 083001. [Google Scholar] [CrossRef]
- Vandoorne, K.; Dambre, J.; Verstraeten, D.; Schrauwen, B.; Bienstman, P. Parallel Reservoir Computing Using Optical Amplifiers. IEEE Trans. Neural Netw. 2011, 22, 1469–1481. [Google Scholar] [CrossRef]
- Vandoorne, K.; Mechet, P.; Van Vaerenbergh, T.; Fiers, M.; Morthier, G.; Verstraeten, D.; Schrauwen, B.; Dambre, J.; Bienstman, P. Experimental Demonstration of Reservoir Computing on a Silicon Photonics Chip. Nat. Commun. 2014, 5, 3541. [Google Scholar] [CrossRef]
- Shen, Y.; Harris, N.C.; Skirlo, S.; Prabhu, M.; Baehr-Jones, T.; Hochberg, M.; Sun, X.; Zhao, S.; Larochelle, H.; Englund, D.; et al. Deep Learning with Coherent Nanophotonic Circuits. Nat. Photonics 2017, 11, 441–446. [Google Scholar] [CrossRef]
- Tait, A.N.; De Lima, T.F.; Zhou, E.; Wu, A.X.; Nahmias, M.A.; Shastri, B.J.; Prucnal, P.R. Neuromorphic Photonic Networks Using Silicon Photonic Weight Banks. Sci. Rep. 2017, 7, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Shi, B.; Calabretta, N.; Stabile, R. Deep Neural Network Through an InP SOA-Based Photonic Integrated Cross-Connect. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 1–11. [Google Scholar] [CrossRef]
- Peng, H.-T.; Nahmias, M.A.; de Lima, T.F.; Tait, A.N.; Shastri, B.J. Neuromorphic Photonic Integrated Circuits. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 1–15. [Google Scholar] [CrossRef]
- Nahmias, M.A.; Peng, H.-T.; de Lima, T.F.; Huang, C.; Tait, A.N.; Shastri, B.J.; Prucnal, P.R. A TeraMAC Neuromorphic Photonic Processor. In Proceedings of the 2018 IEEE Photonics Conference (IPC), Reston, VA, USA, 30 September–4 October 2018; pp. 1–2. [Google Scholar]
- Mourgias-Alexandris, G.; Tsakyridis, A.; Passalis, N.; Tefas, A.; Vyrsokinos, K.; Pleros, N. An all-Optical Neuron with Sigmoid Activation Function. Opt. Express 2019, 27, 9620. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-Based Learning Applied to Document Recognition. Proc. IEEE 1998, 86, 2278–2323. [Google Scholar] [CrossRef]
- Lowery, A.J. Amplified Spontaneous Emission in Semiconductor Laser Amplifiers. Validity of the Transmission-Line Laser Model. IEE Proc. Part J. Optoelectron. 1990, 137, 241–247. [Google Scholar] [CrossRef]
- Stabile, R.; Rohit, A.; Williams, K.A. Dynamic Multi-Path WDM Routing in a Monolithically Integrated 8 × 8 Cross-Connect. Opt. Express 2014, 22, 435–442. [Google Scholar] [CrossRef]
- Fisher, R.A. The Use of Multipe Measurements in Taxonomic Problems. Ann. Eugen. 1936, 7, 179–188. [Google Scholar] [CrossRef]
- Chan, T.-H.; Jia, K.; Gao, S.; Lu, J.; Zeng, Z.; Ma, Y. PCANet: A Simple Deep Learning Baseline for Image Classification? IEEE Trans. Image Process. 2015, 24, 5017–5032. [Google Scholar] [CrossRef]
| Parameters | Value | Unit | Parameters | Value | Unit |
|---|---|---|---|---|---|
| Device Section Length | 1000 × 10−6 | m | Nonlinear Gain Coefficient | 1.0 × 10−23 | m3 |
| Active Region Type | MQW | Nonlinear Gain Time Constant | 5.00 × 10−13 | s | |
| Active Region Width | 2.0 × 10−6 | m | Carrier Density Transparency | 1.0 × 1024 | m−3 |
| Active Region Thickness | 250 × 10−6 | m | Linear Recombination | 1.0 × 108 | s−1 |
| Active Region Thickness MQW | 100 × 10−6 | m | Bimolecular Recombination | 1.0 × 10−16 | m3/s |
| Active Region Thickness SCH | 200 × 10−6 | m | Auger Recombination | 2.1 × 10−41 | m6/s |
| Current Injection Efficiency | 1 | Carrier Capture Time Constant | 3.0 × 10−11 | s | |
| Nominal Frequency | 193.7 | THz | Carrier Escape Time Constant | 1.0 × 10−10 | s |
| Group Index | 3.52 | Initial Carrier Density | 8.0 × 1023 | m−3 | |
| Polarization Model | TE | Chirp Model | Linewidth Factor | ||
| Internal Loss | 3000 | m−1 | Linewidth Factor | 3 | |
| Confinement Factor | 0.3 | Linewidth Factor MQW | 3 | ||
| Confinement Factor MQW | 0.07 | Differential Index | −1.0 × 10−26 | m3 | |
| Confinement Factor SCH | 0.56 | Differential Index MQW | −1.0 × 10−26 | m3 | |
| Gain Shape Model | Flat | Differential Index SCH | −1.5 × 10−26 | m3 | |
| Gain Model | Logarithmic | Carrier Density Ref. Index | 1.0 × 1024 | m−3 | |
| Gain Coefficient Linear | 4.00 × 10−20 | m2 | Noise Model | Inversion Parameter | |
| Gain Coefficient Logarithmic | 6.9 × 104 | m−1 | Inversion Parameter | 1.2 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, B.; Calabretta, N.; Stabile, R. Numerical Simulation of an InP Photonic Integrated Cross-Connect for Deep Neural Networks on Chip. Appl. Sci. 2020, 10, 474. https://doi.org/10.3390/app10020474
Shi B, Calabretta N, Stabile R. Numerical Simulation of an InP Photonic Integrated Cross-Connect for Deep Neural Networks on Chip. Applied Sciences. 2020; 10(2):474. https://doi.org/10.3390/app10020474
Chicago/Turabian StyleShi, Bin, Nicola Calabretta, and Ripalta Stabile. 2020. "Numerical Simulation of an InP Photonic Integrated Cross-Connect for Deep Neural Networks on Chip" Applied Sciences 10, no. 2: 474. https://doi.org/10.3390/app10020474
APA StyleShi, B., Calabretta, N., & Stabile, R. (2020). Numerical Simulation of an InP Photonic Integrated Cross-Connect for Deep Neural Networks on Chip. Applied Sciences, 10(2), 474. https://doi.org/10.3390/app10020474






