Thermally Stratified Darcy Forchheimer Flow on a Moving Thin Needle with Homogeneous Heterogeneous Reactions and Non-Uniform Heat Source/Sink

Abstract

This study discusses the flow of viscous fluid past a moving thin needle in a Darcy–Forchheimer permeable media. The novelty of the envisioned mathematical model is enhanced by adding the effects of a non-uniform source/sink amalgamated with homogeneous–heterogeneous (hh) reactions. The MATLAB bvp4c function is employed to solve the non-linear ordinary differential equations (ODEs), which are obtained via similarity transformations. The outcomes of numerous parameters are explicitly discussed graphically. The drag force coefficient and heat transfer rate are considered and discussed accordingly. It is comprehended that higher estimates of variable source/sink boost the temperature profile.

1. Introduction

The phenomenon of stratification is the result of concentrations and temperature variations or fluid having different densities. Stratification is an essential phenomenon in terms of heat and mass transfer. Thermal stratification in reservoirs such as oceans, rivers, groundwater helps in reducing the amalgamation of water and oxygen. Stratification plays a major role in keeping a balance between hydrogen and oxygen to rationalize the breeding of species. Ramzan et al. [1] discussed double stratification on an inclined stretched cylinder with a chemical reaction on a Jeffery magnetic nanofluid. Hayat et al. [2] investigated the results of thermal stratification with Cattaneo–Christov (CC) heat flux on a stretching flow. Mukhopadhyay et al. [3] examined a mixed convection flow with the impact of thermal stratification on a stretching cylinder. Eichhorn et al. [4] inspected natural convection on cylinders and isothermal spheres immersed in a stratified fluid. Kumar et al. [5] analyzed the thermal stratification effect in a fluid that was saturated in a porous enclosure with free convection. Many scholars have shown a huge interest in stratification, as cited in [6,7,8,9,10,11,12].

Chemical reactions have extensive applications and are categorized as homogeneous–heterogeneous (hh) reactions. Some reactions progress slowly, so a catalyst plays a key role in enhancing the rate of a chemical reaction. The relation shared by hh reactions is somewhat perplexing. As the rate of fabrication and incineration of reactant species fluctuates with time. Chemical reactions have a wide range of applications such as the formation of fog, the assembly of ceramics, polymers, crop damage through freezing, and the orchards of fruit trees. There has been extensive research that has discussed hh reactions, including that by Ramzan et al. [13], who examined the influence of hh reactions with CC heat flux on an magneto hydro dynamic (MHD) 3D Maxwell fluid with convective boundary conditions. Lu et al. [14] reported CC heat flux on the unsteady flow of a nanofluid with hh reactions. Suleman et al. [15] numerically studied hh reactions past a stretched cylinder with Newtonian heating and their impact on a silver–water nanofluid. More research on hh reactions is mentioned in [14,16,17,18,19,20,21,22].

A fluid flow through a porous medium is of extreme significance due to its appearance in the movement of water in reservoirs, the processing of mines and minerals, agriculture, the petroleum industry, the production of oil and gas, the insulation of thermal processes, and cooling reactors. Enormous problems involving porous mediums have been described with classical Darcy’s theory [23]. Darcy’s expression is only applicable to situations of small velocity and low porosity, as it lacks the capability of dealing with inertia and boundary effects at a high flow rate. Flows with a Reynold number $\left(>1\right)$ are non-linear due to their higher velocities. The impact of inertia and boundary layer cannot be neglected, as a porous medium mostly involves relatively higher velocities. Forchheimer [24] added the term of square velocity in order to make Darcy’s law more conveniently applicable. Muskat [25] later recognized this term as Forchheimer’s term. Majeed et al. [26] examined a numerical study of the Darcy–Forchheimer (DF) flow with slip condition of the momentum of order two and chemically reactive species. Ganesh et al. [27] scrutinized a thermally stratified porous medium on a stretching/shrinking surface with a DF flow and a second-order slip on a hydromagnetic nanofluid. Abbasi et al. [28] detected a DF flow with a CC heat flux in a viscoelastic fluid with a porous medium. Recent research works involving the Darcy flow include [29,30].

In many physical problems, variable source/sink plays an important role in controlling the transfer of heat. Gireesha et al. [31] perceived the transfer of heat and mass on a chemically reacting Casson fluid with variable heat source/sink on an occupied MHD boundary layer. Saravanti et al. [32] discussed non-linear thermal radiation on a nanofluid with a slip condition on a stretching vertical cylinder involving a variable heat source/sink. Mabood et al. [33] presented Soret effects and non-Darcy convective flows with radiation on an MHD micropolar fluid over a stretchable surface with a variable heat source/sink. Studies involving variable sources/sinks were carried out by researchers such as Sandeep et al. [34] and Reddy et al. [35].

Despite all the aforementioned research, the impacts of a Darcy–Forchheimer flow, when amalgamated with thermal stratification past a thin needle, have been barely described. In this paper, the novelty of the envisaged mathematical model is boosted with variable source/sink effects combined with homogeneous–heterogeneous reactions. The aforementioned model is numerically handled. The impression of pertinent parameters is graphically illustrated with requisite deliberations.

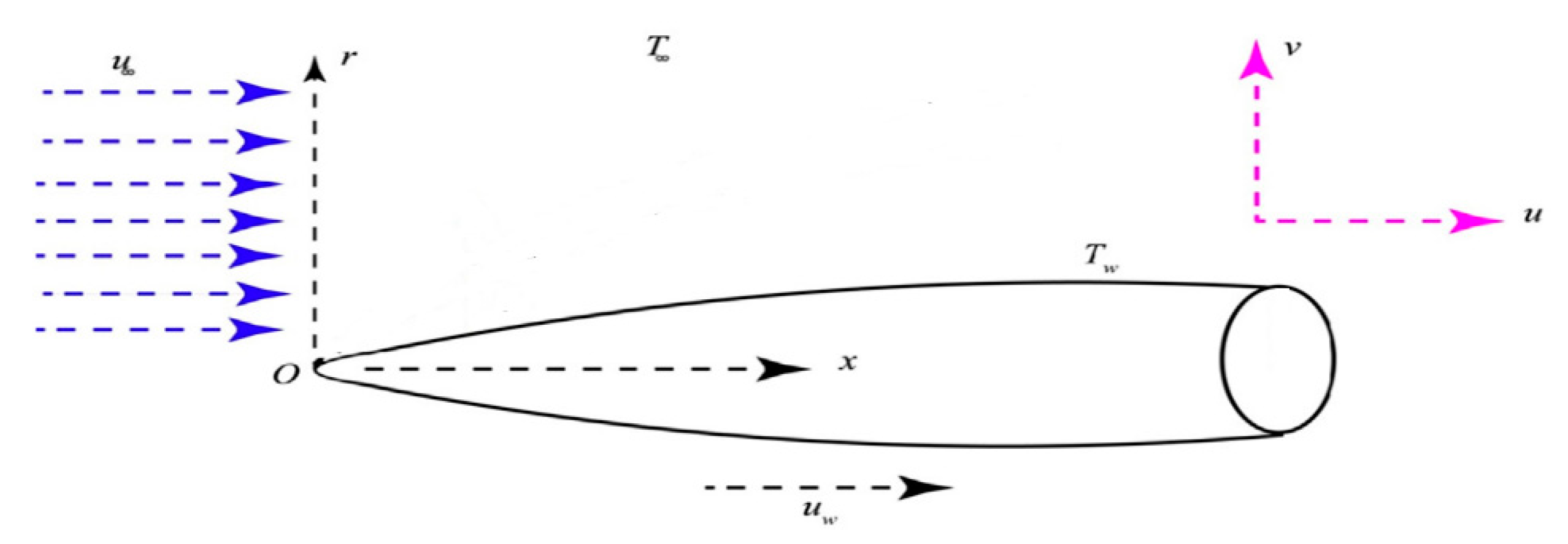
2. Mathematical Formulation

Consider a steady, two dimensional, laminar, incompressible fluids over a thin moving needle. The influence of variable heat source/sink and hh reactions should also be considered. The geometry of the problem and its cylindrical coordinates $\left(x,r\right)$ are demonstrated in Figure 1. The axial direction $x$ is parallel to the moving thin needle, and radial direction $r$ is in the direction of the flow that is normal to it. The width of the needle is smaller than the thickness of the boundary layer formed over it. The impact of the curvature in the transverse direction is of utmost prominence, as the anticipation of the needle is thin. The pressure variation is unkempt along the surface of the needle [36,37,38].

Let $r=R\left(x\right)={\left(\frac{\nu nx}{U}\right)}^{0.5}$ stipulate the radius of the needle. Following Chaudhary and Merkin [39,40], the cubic autocatalysis homogeneous reaction is stated as:

$$A^{\ast }+2B^{\ast }\to 3B^{\ast },rate=k_c{a}^{\ast }{b}^{\ast },$$

(1)

and on a catalyst surface, the heterogeneous reaction is indicated as:

$$A^{\ast }\to B^{\ast },rate=k_s{a}^{\ast },$$

(2)

where $A^{\ast },B^{\ast }$ are two chemical species with $k_c,k_s$ as the respective concentrations of these chemical species.

Keeping in view the prior assumptions, the non-linear partial differential equations (PDEs) that govern the problem are as follows [2,41,42,43]:

$$\frac{\partial \left(ru\right)}{\partial x}+\frac{\partial \left(rv\right)}{\partial r}=0,$$

(3)

$$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial r}=\frac{\nu }{r}\frac{\partial }{\partial r}\left(r\frac{\partial u}{\partial r}\right)-F{u}^2,$$

(4)

$$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial r}=\frac{\alpha }{r}\frac{\partial }{\partial r}\left(r\frac{\partial T}{\partial r}\right)+\frac{1}{\rho C_p}{h}^{‴},$$

(5)

$$u\frac{\partial a^{\ast }}{\partial x}+v\frac{\partial a^{\ast }}{\partial r}=D_A\left(\frac{{\partial }^2{a}^{\ast }}{\partial r^2}+\frac{1}{r}\frac{\partial a^{\ast }}{\partial r}\right)-k_c{a}^{\ast }{b}^{\ast 2},$$

(6)

$$u\frac{\partial b^{\ast }}{\partial x}+v\frac{\partial b^{\ast }}{\partial r}=D_B\left(\frac{{\partial }^2{b}^{\ast }}{\partial r^2}+\frac{1}{r}\frac{\partial b^{\ast }}{\partial r}\right)+k_c{a}^{\ast }{b}^{\ast 2},$$

(7)

The suitable associated boundary conditions [11,44,45,46] are:

$$u=u_w,v=0,T=T_w=T_0+ex,D_A\frac{\partial a^{\ast }}{\partial r}=k_s{a}^{\ast },D_B\frac{\partial b^{\ast }}{\partial r}=-k_s{a}^{\ast }, \mathrm{at} r=R(x)$$

$$u\to u_{\infty },T\to T_{\infty }=T_0+fx,a^{\ast }\to a_0,b^{\ast }\to 0 \mathrm{as} r\to \infty .$$

(8)

The variable heat source/sink $h^{‴}$ [47] is articulated as:

$$h^{‴}=\frac{\kappa u_w}{x\nu }\left(C\left(T_w-T_0\right)f^{\prime }\left(\zeta \right)+D\left(T-T_{\infty }\right)\right).$$

(9)

3. Similarity Transformations

In order to obtain ODEs for Equations (3)–(7), the following non dimensional parameters are used [48,49]:

$$\psi =\nu xf\left(\zeta \right),\zeta =\frac{U{r}^2}{\nu x},\theta \left(\zeta \right)=\frac{T-T_0}{T_w-T_{\infty }},g\left(\zeta \right)=\frac{a^{\ast }}{a_0},m\left(\zeta \right)=\frac{b^{\ast }}{a_0}.$$

(10)

Equation (3) is satisfied by utilizing Equations (8) and (9). Equations (4)–(7) are converted into the following ODEs:

$$2f^{″}+2\zeta f^{‴}+f{f}^{″}-F_r{f^{\prime }}^2=0,$$

(11)

$$4{\theta }^{\prime }+4\zeta {\theta }^{″}+2\mathrm{Pr}\left(f{\theta }^{\prime }-f^{\prime }\theta -f^{\prime }S\right)+\lambda \left(C{f}^{\prime }\left(\zeta \right)+D\theta \right)\left(\zeta \right)=0,$$

(12)

$$\frac{1}{Sc}\left(2g^{\prime }+\zeta g^{″}\right)+f{g}^{\prime }-Kg{m}^2=0,$$

(13)

$$\frac{\beta }{Sc}\left(2m^{\prime }+\zeta m^{″}\right)+f{m}^{\prime }+Kg{m}^2=0.$$

(14)

The non-dimensional form of these parameters is [50,51]:

$$F_r=\frac{C_{b}x}{\sqrt{k}},\mathrm{Pr}=\frac{\nu }{\alpha },S=\frac{f}{e},Sc=\frac{\nu }{D_A},\beta =\frac{D_B}{D_A},K=\frac{k_1{a}_0^{2}x}{u_w},K_s=\frac{k_s}{D_A}\sqrt{\frac{\nu x}{U_0}}.$$

(15)

The modified boundary conditions are given as:

$$f(\zeta )=\frac{\lambda }{2}\zeta ,f^{\prime }(\zeta )=\frac{\lambda }{2},\theta (\zeta )=1-S,g^{\prime }(\zeta )=K_{s}g(\zeta ),\beta m^{\prime }(n)=-K_{s}g(\zeta ), \mathrm{as} \zeta =n$$

$$f^{\prime }(\zeta )\to \frac{1-\lambda }{2},\theta \left(\zeta \right)\to 0,g\left(\zeta \right)\to 1,m\left(\zeta \right)\to 0 \mathrm{as} \zeta \to \infty$$

(16)

Since $U=u_w+u_{\infty }\ne 0$, $\lambda =0$ and corresponds to a needle that behaves to be static in a flowing nanofluid. On the other hand, $\lambda =1$ indicates the approach of dynamic needle in a deskbound ambient fluid. When $\lambda$ varies between zero and one, i.e., ($0<\lambda <1$), the movement of the needle is similar to the direction of fluid. For $\lambda <0$, the needle moves toward the negative $x$-axis, and the free stream velocity moves towards positive $x$-axis; for $\lambda >1$, it is vice-versa.

For simplicity, a comparison can be drawn between $A^{\ast }$ and $B^{\ast }$ in terms of size of diffusion coefficients. Thus, the diffusion coefficients $D_A$ and $D_B$ are equal [52], i.e., $\beta =1$.

$$g\left(\zeta \right)+m\left(\zeta \right)=1.$$

(17)

Now, Equations (13) and (14) yield:

$$\frac{1}{Sc}\left(2\zeta g^{″}+2g^{\prime }\right)+f{g}^{\prime }-Kg{m}^2=0,$$

(18)

with the boundary conditions:

$$g^{\prime }\left(\zeta \right)=K_{s}g(\zeta ), \mathrm{as} \zeta =n$$

$$g(\zeta )\to 1 \mathrm{as} \zeta \to \infty$$

(19)

The physical quantity of noteworthy attention are the drag force coefficient $C_f$ and the rate of heat transfer $N{u}_x$, which are specified as follows:

$$C_f=\frac{{\tau }_w}{\rho U^2},\hspace{1em}{\tau }_w=\mu {\left(\frac{\partial u}{\partial r}\right)}_{r=R(x)},$$

(20)

$$N{u}_x=\frac{x{q}_w}{k\left(T_w-T_{\infty }\right)},q_w=-k{\left(\frac{\partial T}{\partial r}\right)}_{r=R(x)}.$$

(21)

By using Equation (8), Equations (20) and (21) can be transmuted as:

$$C_f{\mathrm{Re}}_x^{1/2}=4n^{1/2}{f}^{″}\left(n\right),N{u}_x{\mathrm{Re}}_x^{-1/2}=-2n^{1/2}{\theta }^{\prime }\left(n\right).$$

(22)

4. Numerical Methodology

The non-linear ODEs (11), (12), and (18), in combination with ODEs (16) and (19), are solved by employing MATLAB bvp4c. The following numerical code converts the problem into first order ODEs.

$$\begin{array}{l}{y}_1=f(\zeta )\\ y_2=f^{\prime }(\zeta )\\ y_3=f^{″}(\zeta )\\ f^{‴}(\zeta )=y{y}_1=\frac{1}{2\eta }\left[F_r{\left(y_2\right)}^2-y_1{y}_3-2y_3\right]\\ y_4=\theta \left(\zeta \right)\\ y_5={\theta }^{\prime }\left(\zeta \right)\\ {\theta }^{″}\left(\zeta \right)=y{y}_2=\frac{1}{4\eta }\left[-2\mathrm{Pr}\left(y_1{y}_5-y_2{y}_4-y_{2}S\right)-4y_5-\lambda \left(C{y}_2+D{y}_4\right)\right]\\ y_6=g\left(\zeta \right)\\ y_7=g^{\prime }\left(\zeta \right)\\ g^{″}\left(\zeta \right)=y{y}_3=\frac{1}{4\eta }\left[Sc\left(K{y}_6{\left(1-y_6\right)}^2-y_1{y}_7-2y_7\right)\right]\end{array}$$

(23)

and the boundary conditions take the form:

$$\begin{array}{l}{y}_1(0)=\frac{\lambda }{2}n,y_2(0)=\frac{\lambda }{2},y_4(0)=1-S,y_7(0)=K_s{y}_6(0),\\ y_2(\infty )\to \frac{1-\lambda }{2},y_4(\infty )\to 0,y_6(\infty )\to 1.\end{array}$$

(24)

5. Graphical Analysis

This section exhibits the behavior of innumerable parameters on velocity $f^{\prime }\left(\zeta \right)$, temperature $\theta \left(\zeta \right)$ and concentration $g\left(\zeta \right)$ profile.

Figure 2 illustrates the performance on $f^{\prime }\left(\zeta \right)$ or the velocity ratio parameter $\lambda$. In our models, the velocity profile shows an increasing behavior near the surface of the needle for $0\le \lambda \le 0.5$; however, for $\lambda >0.5$, when it’s far away from the needle surface, a decreasing nature is observed. Figure 3 displays the result on $f^{\prime }\left(\zeta \right)$ for inertia coefficient $F_r$. This figure illustrates that the inertial forces increase with growth in $F_r$. A downfall of $f^{\prime }\left(\zeta \right)$ appears as diminution of thickness of the boundary layer for different values of $F_r$ that oppose the fluid motion. The influence of $\lambda$ on $\theta \left(\zeta \right)$ is highlighted in Figure 4. An up rise for increasing values of $\lambda$ as heat intensely intrudes inside the fluid can be seen for $\theta \left(\zeta \right)$. Figure 5 describes the impact of the Prandtl number $\mathrm{Pr}$ on $\theta \left(\zeta \right)$. $\mathrm{Pr}$ is the ratio of momentum to thermal diffusivity, so, as values of Pr increase, the momentum diffusion and thermal diffusion drop. The outcome of larger values of $\mathrm{Pr}$ results in the diminution of $\theta \left(\zeta \right)$ and the thermal boundary layer. Figure 6a,b illustrates the result of non-uniform source parameter on $\theta \left(\zeta \right)$. As $C>0,D>0$ corresponds to the internal heat source, an escalation can be analyzed for the strengthening the conduct of $C,D$ for the thermal boundary layer. Higher values of $C,D$ respond as heat generators, which are energy, and whose output is in the form of an increasing temperature profile $\theta \left(\zeta \right)$. In Figure 7a,b, $C<0,D<0$ behave as heat sinks that are the parameters that control the flow and transfer of heat. Additionally, decreasing values act as absorbers of heat for a non-uniform heat sink. This shows a reduction in the thickness of the boundary layer, and $\theta \left(\zeta \right)$ exhibits a downfall. The response of different values of the thermal stratification parameter $S$ on the temperature profile $\theta \left(\zeta \right)$ can be noticed in Figure 8. It is noticed that the $\theta \left(\zeta \right)$ shows a deteriorating nature for larger values of $S$ due to the difference between the surface temperature and the ambient temperature. Figure 9, Figure 10 and Figure 11 provide analyses of homogeneous reaction strength $K$, heterogeneous reaction strength $K_s$, and the Schmidt number $Sc$. The outcome of $K$ and $K_s$ on the concentration profile $g\left(\zeta \right)$ is shown in Figure 9 and Figure 10. As the homogeneous and heterogeneous reaction reactants are utilized such that the concentration profile decreases for higher values of $K$ and $K_s$. An analysis of $Sc$ is shown in Figure 11 for the concentration profile of $g\left(\zeta \right)$. As $Sc$ is the ratio of momentum diffusion to mass diffusion, higher values of $Sc$ boost momentum diffusivity and lower mass diffusivity. Due to this impact, escalation in the concentration profile $g\left(\zeta \right)$ is seen.

Figure 12 the drag force coefficient C_f is plotted against thermal stratification $S$ and inertia coefficient F_r. An increasing behavior of C_f is seen for higher values of $S$. For higher values of F_r, the drag force coefficient C_f reduces. Figure 13 depicts the effect of P_r and $S$ on the heat transfer rate Nu_x. It is noted that Nu_x is an increasing function of P_r. For escalating values of $S$, the heat transfer rate decreases. The graphical result of Nu_x versus $Sc$ for varying $K$ is shown in Figure 14. It is observed that heat transfer rate increases for higher values of $Sc$, whereas Nu_x is a diminishing function of $K_s$.

Table 1. Comparison of $f^{″}\left(n\right)$ for varied estimates of $n$ done by Ishaq et al. [38] and Rida et al. [45].

$\mathit{n}$	${\mathit{f}}^{″}\left(\mathit{n}\right)$
	[38]	[45]	Present
0.10	01.2888	01.2888171	01.2888188
0.010	08.4924	08.4924360	08.4924389
0.0010	062.1637	062.163672	062.163677

depicts the numerically calculated values of $f^{″}\left(n\right)$ for numerous estimates of $n$ done by Ishak et al. [38] and Rida et al. [45], but in limiting cases. An outstanding harmony between the results is found. That also validates the current exploration results.

6. Conclusions

In this paper, the impact of variable heat sources/sinks on a Darcy–Forchheimer fluid flow with an hh reaction and thermal stratification on a moving thin needle is examined. MATLAB bvp4c was used to solve the dimensionless equations governing the problem. The foremost findings of this study are as follows:

❖

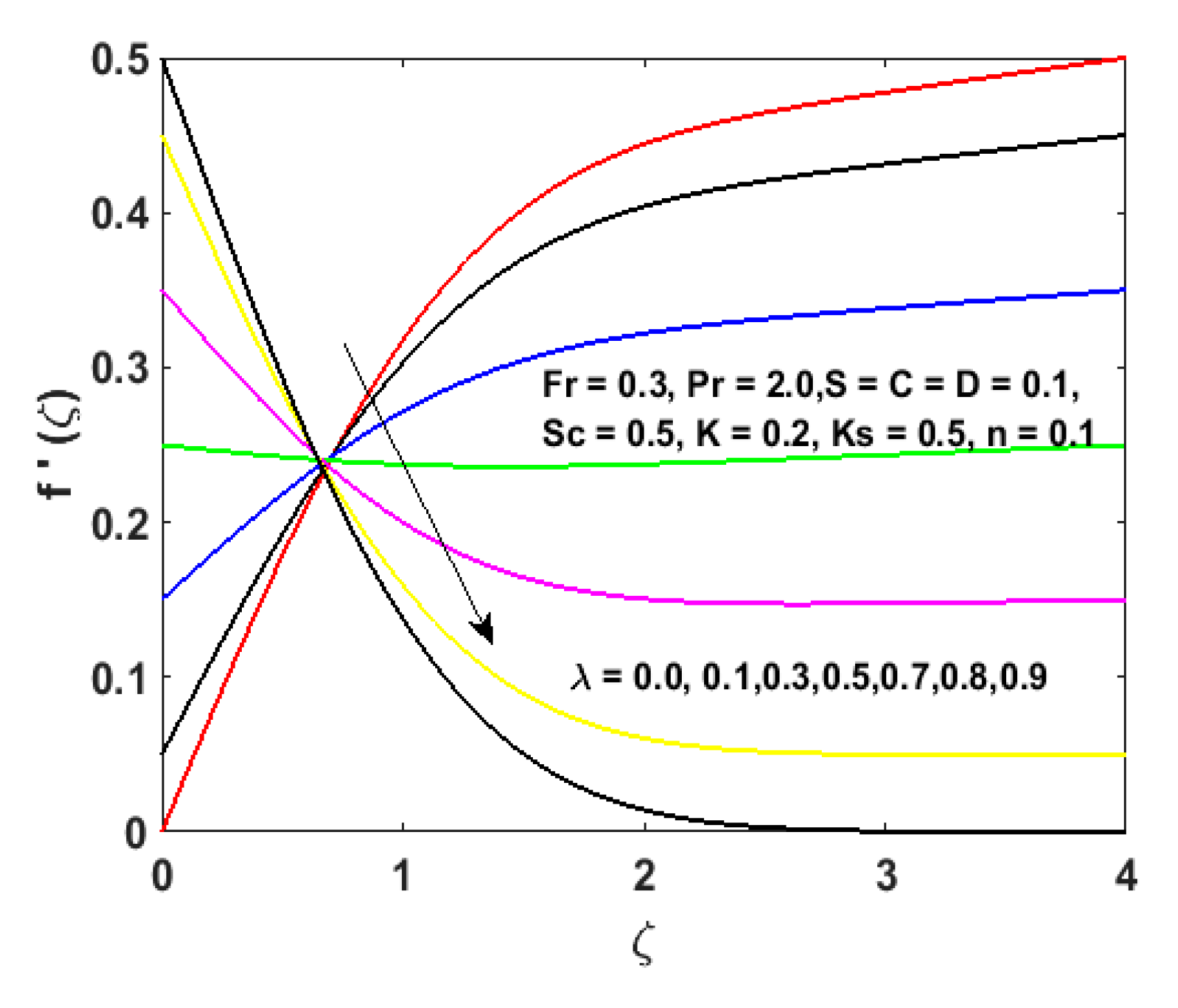
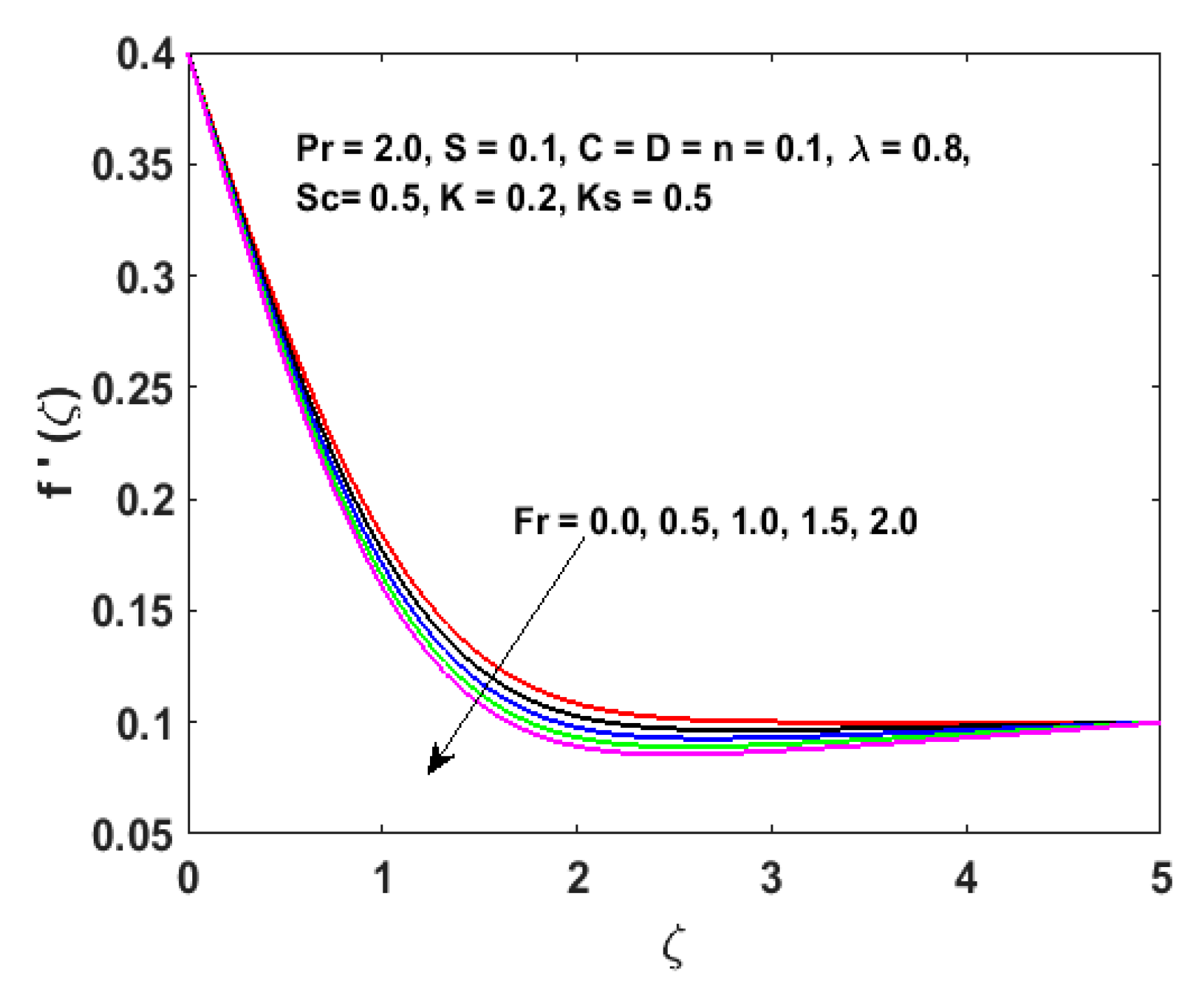
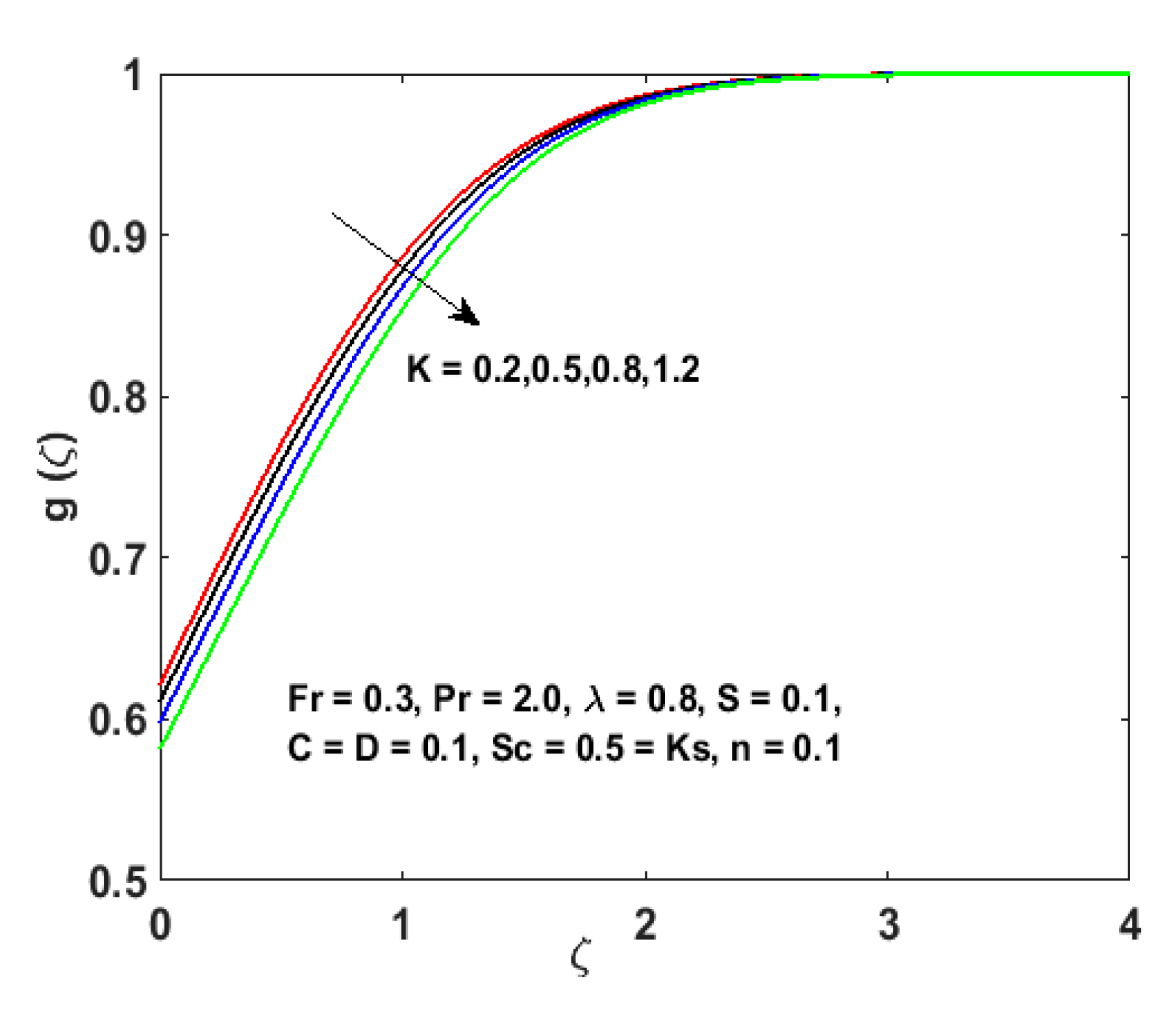
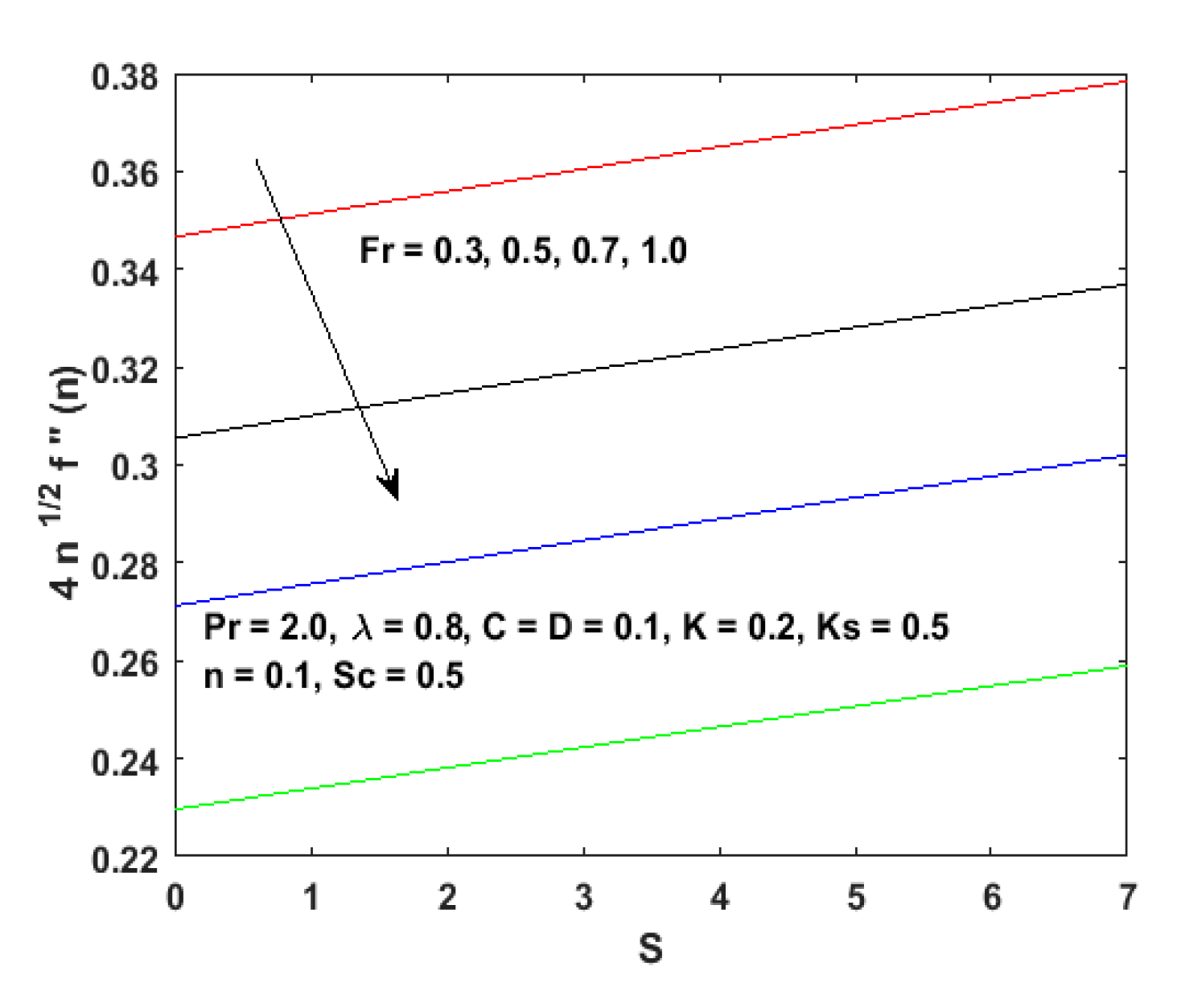
Higher values of $F_r$ result in the decline of velocity distribution as well as the thickness of the boundary layer.

❖

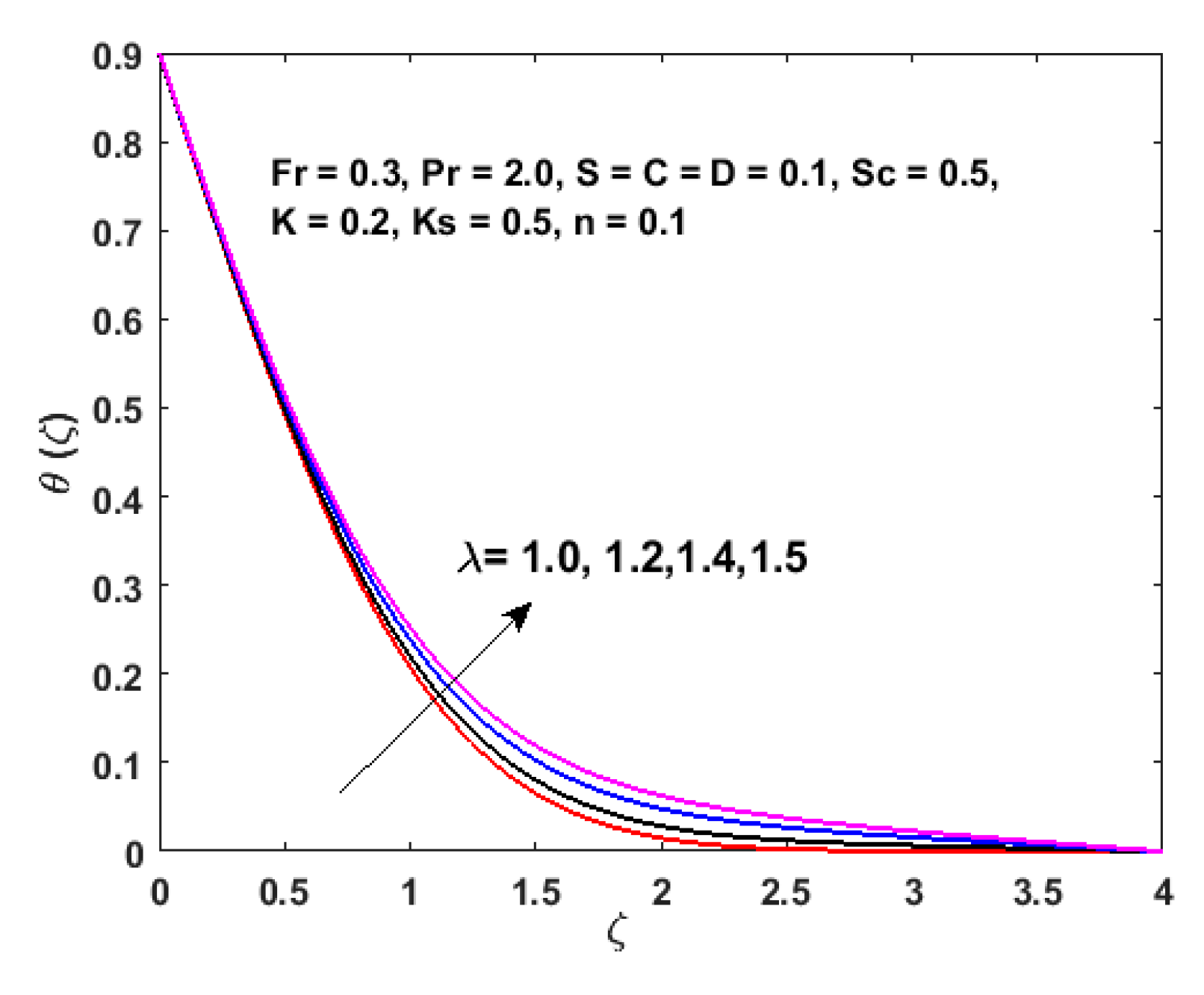
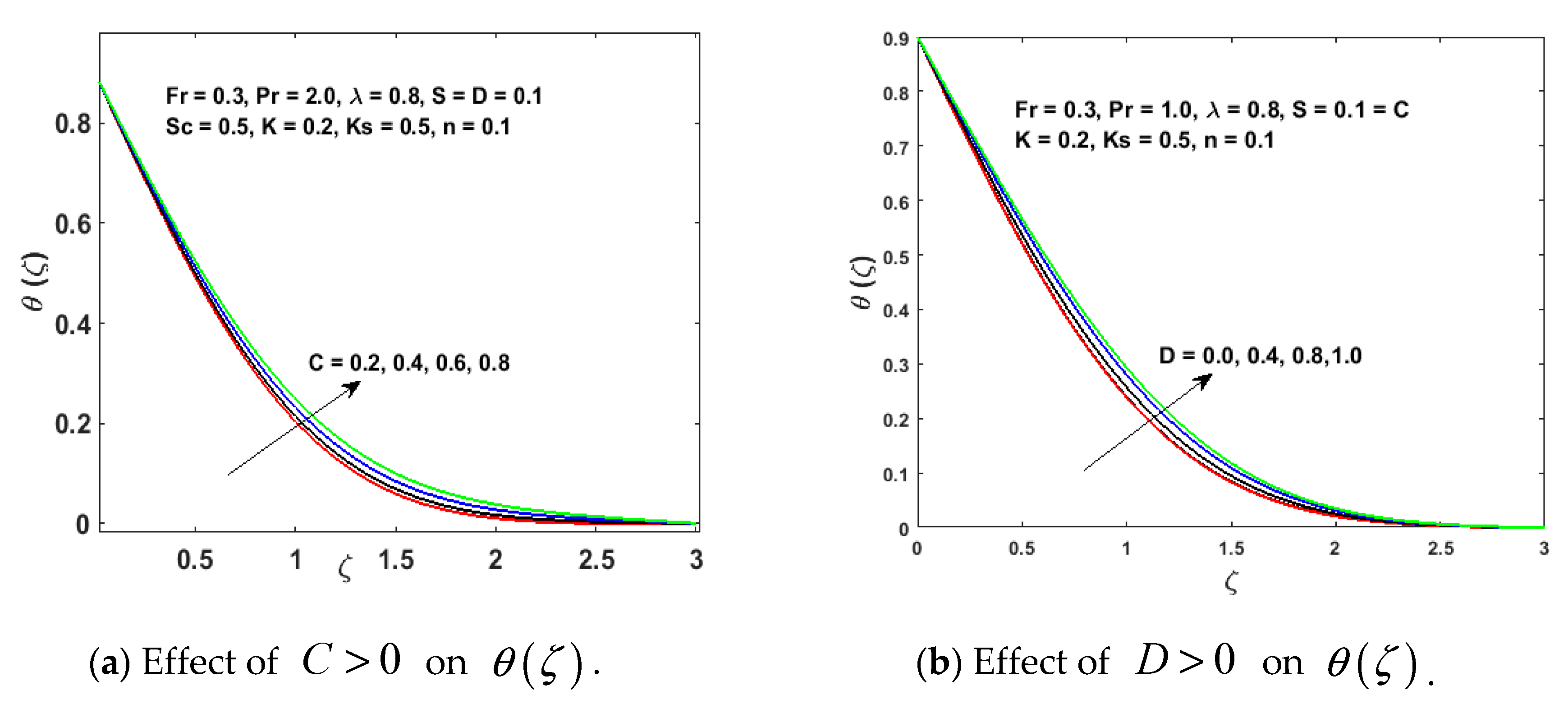
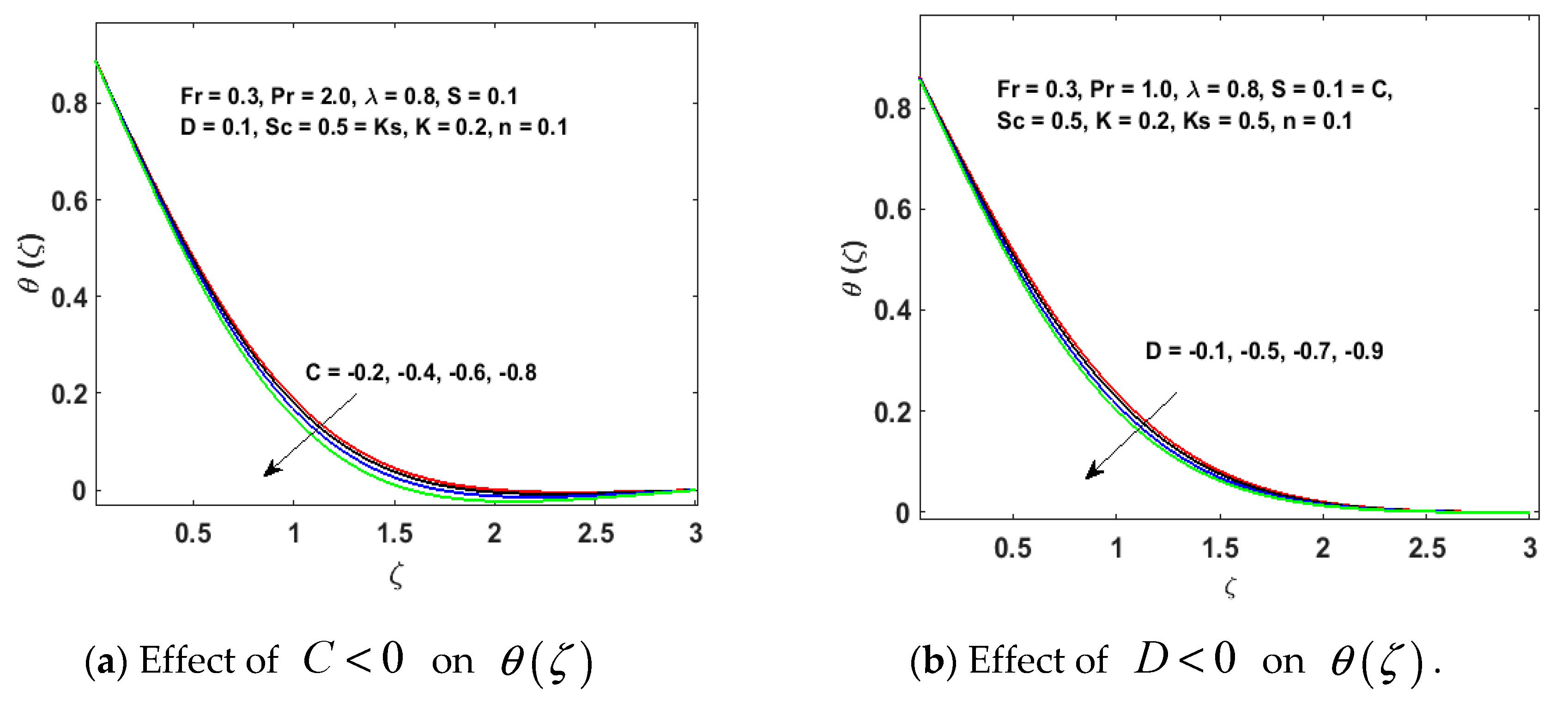
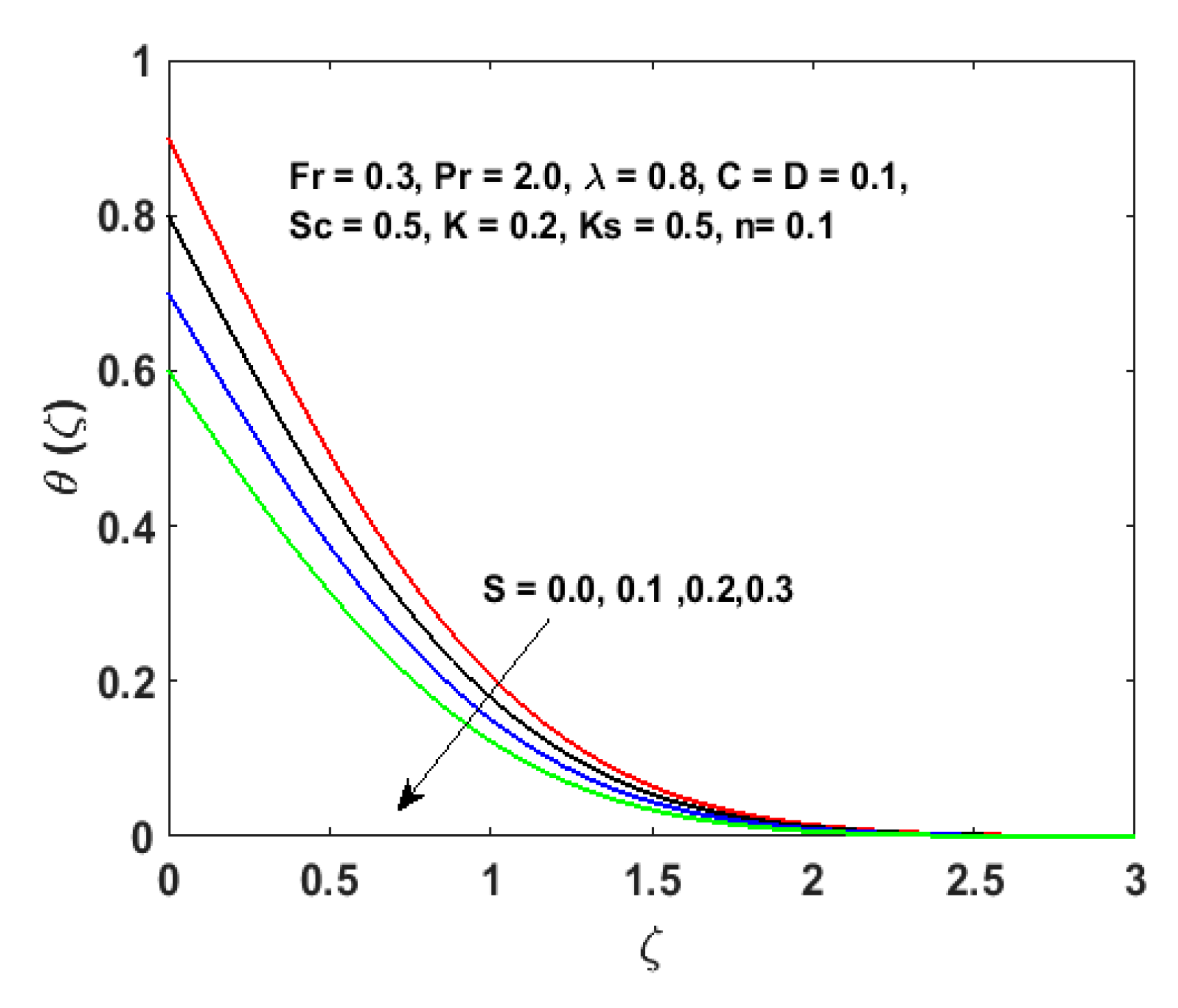
Increments of $S$ and $\mathrm{Pr}$ diminish the thermal boundary layer and temperature field.

❖

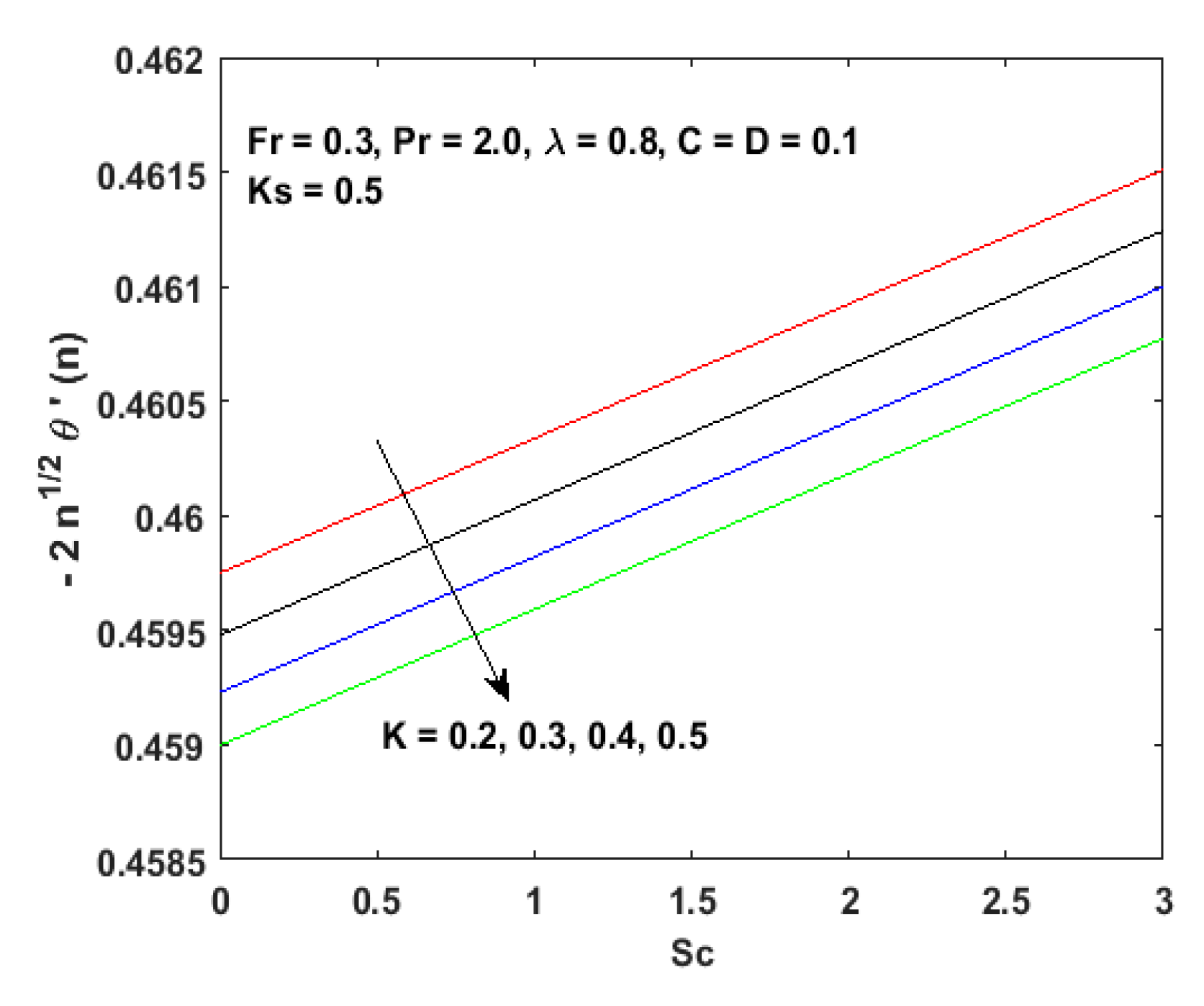
The temperature field increases for non-uniform heat sources $C,D>0$ as they respond to heat generators, while $C,D<0$ signifies variable heat sinks that absorb heat and affirm the decline of $\theta \left(\zeta \right)$ and boundary layer thickness.

❖

The concentration distribution is lessened with upgraded values of $K$ and $K_s$ that are the homogeneous and heterogeneous parameters,

❖

The concentration profile increases for larger estimates of the Schmidt number.