Application of the Theory of Convex Sets for Engineering Structures with Uncertain Parameters
Abstract
1. Introduction
2. Problem Formulation
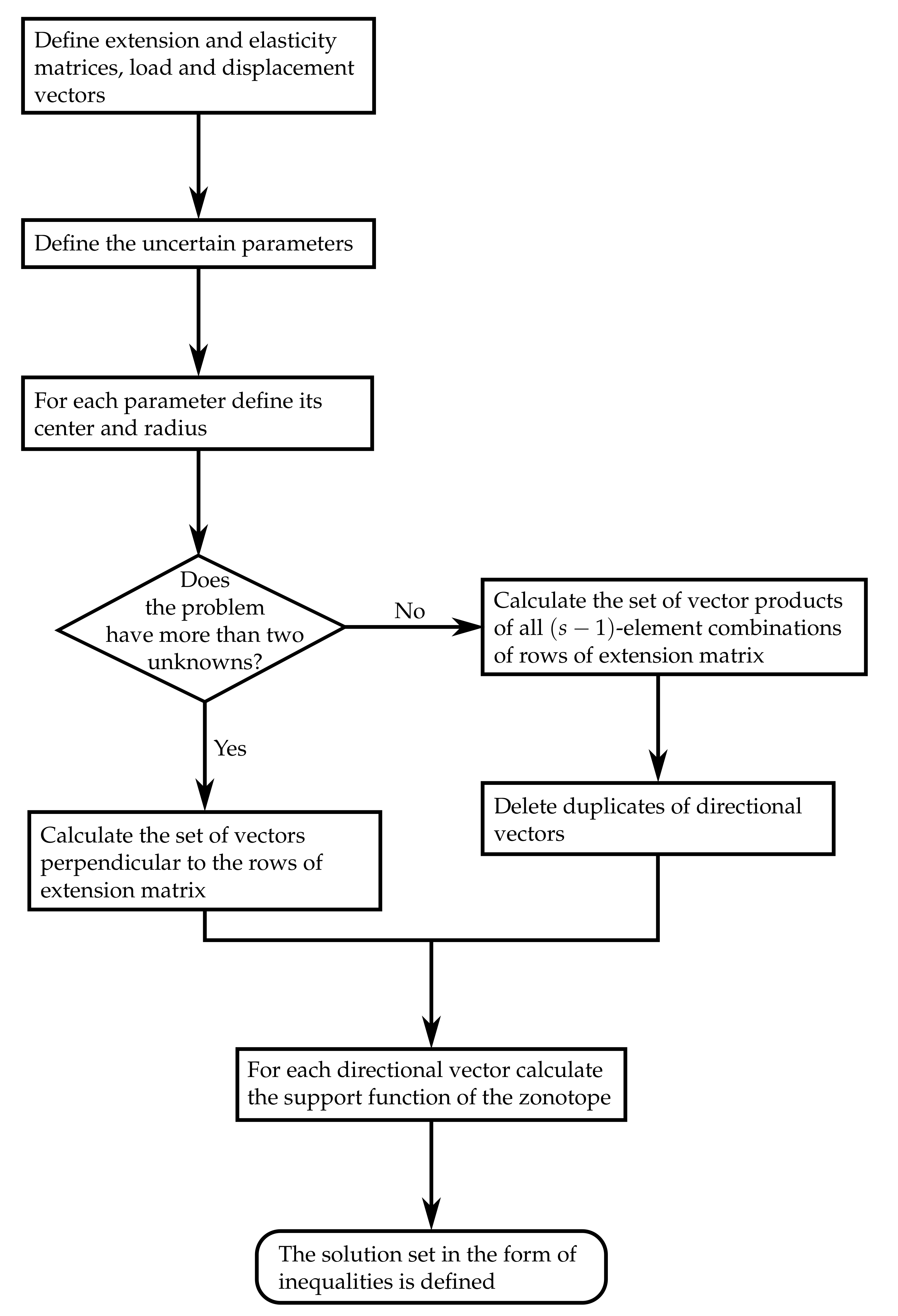
3. Description of the Solution Sets for Bar Structures
3.1. Trusses
3.2. Frames
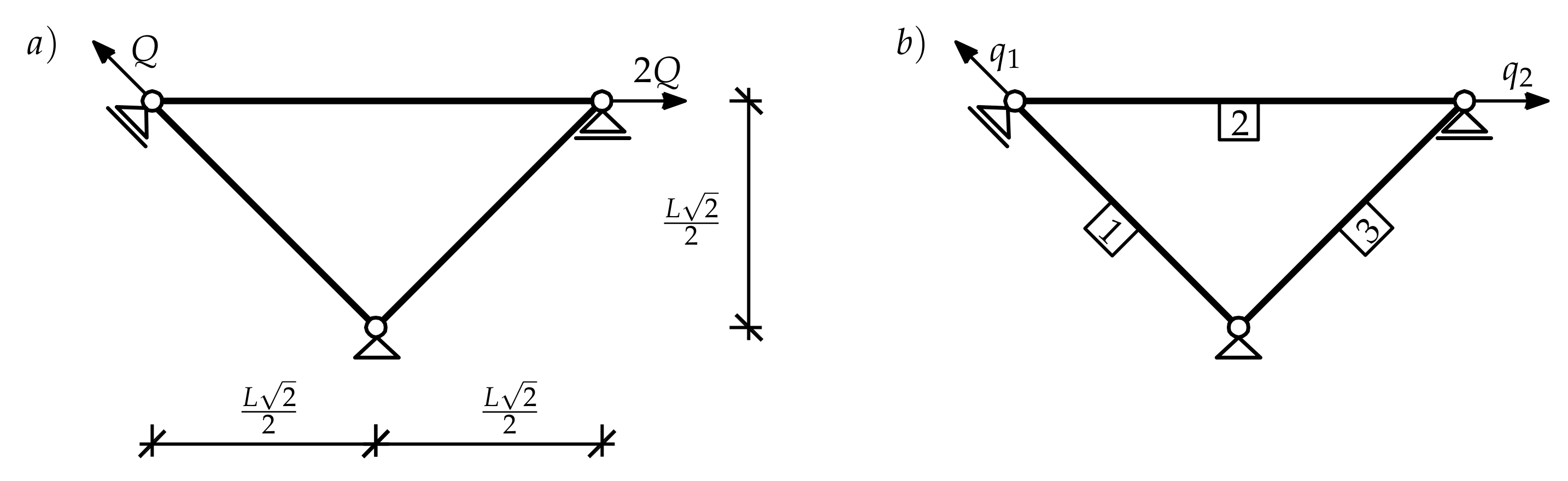
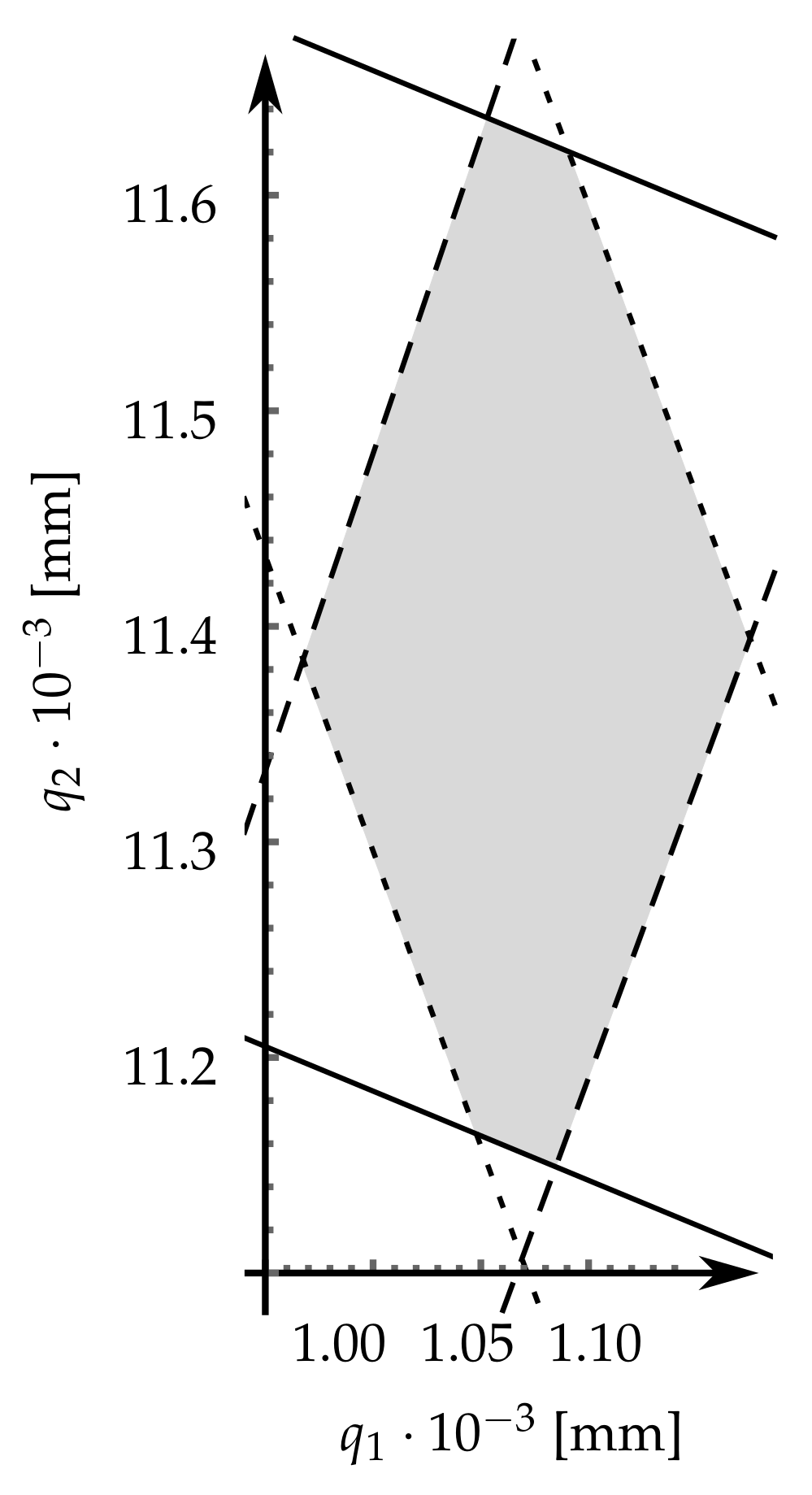
4. Illustrative Example
5. Numerical Example
6. Practical Implications
7. Conclusions
Funding
Conflicts of Interest
Appendix A. Basic Notions and Notations
Appendix B. Vectors ui Obtained for Ten-Bar Truss
References
- Pełczyński, J. On Mathematical Descriptions of Uncertain Parameters in Engineering Structures. Arch. Civ. Eng. 2018, 64, 2–19. [Google Scholar] [CrossRef]
- Moens, D.; Vandepitte, D. A survey of non-probabilistic uncertainty treatment in finite element analysis. Comput. Methods Appl. Mech. Eng. 2005, 194, 1527–1555. [Google Scholar] [CrossRef]
- Radoń, U. Reliability analysis of Mises truss. Arch. Civ. Mech. Eng. 2011, 11, 723–738. [Google Scholar] [CrossRef]
- Stefanou, G. The stochastic finite element method: Past, present and future. Comput. Methods Appl. Mech. Eng. 2009, 198, 1031–1051. [Google Scholar] [CrossRef]
- Korkmaz, K.A.; Demir, F.; Tekeli, H. Uncertainty modelling of critical column buckling for reinforced concrete buildings. Sadhana 2011, 36, 267. [Google Scholar] [CrossRef]
- Guo, S.X.; Lu, Z.Z. A non-probabilistic robust reliability method for analysis and design optimization of structures with uncertain-but-bounded parameters. Appl. Math. Model. 2015, 39, 1985–2002. [Google Scholar] [CrossRef]
- Smith, A.P.; Garloff, J.; Werkle, H. Verified solution for a simple truss structure with uncertain node locations. In Proceedings of the 18th International Conference on the Application of Computer Science and Mathematics in Architecture and Civil Engineering, Weimar, Germany, 7–9 July 2009. [Google Scholar]
- Wang, L.; Xiong, C.; Wang, X.; Xu, M.; Li, Y. A dimension-wise method and its improvement for multidisciplinary interval uncertainty analysis. Appl. Math. Model. 2018, 59, 680–695. [Google Scholar] [CrossRef]
- Xiong, C.; Wang, L.; Liu, G.; Shi, Q. An iterative dimension-by-dimension method for structural interval response prediction with multidimensional uncertain variables. Aerosp. Sci. Technol. 2019, 86, 572–581. [Google Scholar] [CrossRef]
- Wang, L.; Liu, Y.; Liu, Y. An inverse method for distributed dynamic load identification of structures with interval uncertainties. Adv. Eng. Softw. 2019, 131, 77–89. [Google Scholar] [CrossRef]
- Niczyj, J. Multi-Criterion Reliability Optimization and Technical Assessment of Bar Structures on the Background of Fuzzy Set Theory; Szczecin Univ. of Technology Publishers: Szczecin, Poland, 2003. (In Polish) [Google Scholar]
- De Mulder, W.; Moens, D.; Vandepitte, D. Modeling uncertainty in the context of finite element models with distance-based interpolation. In Proceedings of the 1st International Symposium on Uncertainty Quantification and Stochastic Modeling, Maresias, Brazil, 16 February–2 March 2012. [Google Scholar]
- Harirchian, E.; Lahmer, T. Improved Rapid Visual Earthquake Hazard Safety Evaluation of Existing Buildings Using a Type-2 Fuzzy Logic Model. Appl. Sci. 2020, 10, 2375. [Google Scholar] [CrossRef]
- Fink, T. BIM for Structural Engineering. In Building Information Modeling; Springer: Berlin, Germany, 2018; pp. 329–336. [Google Scholar]
- Alizadehsalehi, S.; Hadavi, A.; Huang, J.C. From BIM to extended reality in AEC industry. Autom. Constr. 2020, 116, 103254. [Google Scholar] [CrossRef]
- Muhanna, R.L.; Mullen, R.L.; Zhang, H. Interval finite element as a basis for generalized models of uncertainty in engineering mechanics. Reliab. Comput. 2007, 13, 173–194. [Google Scholar] [CrossRef]
- Shary, S.P. On optimal solution of interval linear equations. SIAM J. Numer. Anal. 1995, 32, 610–630. [Google Scholar] [CrossRef]
- Lewiński, T. On algebraic equations of elastic trusses, frames and grillages. J. Theor. Appl. Mech. 2001, 39, 307–322. [Google Scholar]
- Pełczyński, J.; Gilewski, W. Algebraic Formulation for Moderately Thick Elastic Frames, Beams, Trusses, and Grillages within Timoshenko Theory. Math. Probl. Eng. 2019, 2019, 7545473. [Google Scholar] [CrossRef]
- Dessombz, O.; Thouverez, F.; Laîné, J.P.; Jézéquel, L. Analysis of mechanical systems using interval computations applied to finite element methods. J. Sound Vib. 2001, 239, 949–968. [Google Scholar] [CrossRef]
- Neumaier, A.; Pownuk, A. Linear systems with large uncertainties, with applications to truss structures. Reliab. Comput. 2007, 13, 149–172. [Google Scholar] [CrossRef]
- Du, J.; Du, Z.; Wei, Y.; Zhang, W.; Guo, X. Exact response bound analysis of truss structures via linear mixed 0-1 programming and sensitivity bounding technique. Int. J. Numer. Methods Eng. 2018, 116, 21–42. [Google Scholar] [CrossRef]
- Gilewski, W.; Pełczyński, J.; Rzeżuchowski, T.; Wąsowski, J. Truss structures with uncertain parameters–geometrical interpretation of the solution based on properties of convex sets. In Theoretical Foundations of Civil Engineering Vol. 7: Structural Mechanics; Jemioło, S., Gajewski, M., Eds.; Warsaw University of Technology Publisher House: Warszawa, Poland, 2016; pp. 41–52. [Google Scholar]
- Pełczyński, J.; Rzeżuchowski, T.; Wąsowski, J. Description of united solution sets by inequalities for truss structures. In Proceedings of the 4th ECCOMAS Young Investigators Conference (YIC 2017), Milan, Italy, 13–15 September 2017. [Google Scholar]
- Rzeżuchowski, T.; Wąsowski, J. Characterization of AE solution sets of parametric linear systems based on the techniques of convex sets. Linear Algebra Appl. 2017, 533, 468–490. [Google Scholar] [CrossRef]

© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pełczyński, J. Application of the Theory of Convex Sets for Engineering Structures with Uncertain Parameters. Appl. Sci. 2020, 10, 6864. https://doi.org/10.3390/app10196864
Pełczyński J. Application of the Theory of Convex Sets for Engineering Structures with Uncertain Parameters. Applied Sciences. 2020; 10(19):6864. https://doi.org/10.3390/app10196864
Chicago/Turabian StylePełczyński, Jan. 2020. "Application of the Theory of Convex Sets for Engineering Structures with Uncertain Parameters" Applied Sciences 10, no. 19: 6864. https://doi.org/10.3390/app10196864
APA StylePełczyński, J. (2020). Application of the Theory of Convex Sets for Engineering Structures with Uncertain Parameters. Applied Sciences, 10(19), 6864. https://doi.org/10.3390/app10196864




