On the Use of a Simplified Slip Limit Equation to Predict Screw Self-Loosening of Dental Implants Subjected to External Cycling Loading
Abstract
Featured Application
Abstract
1. Introduction
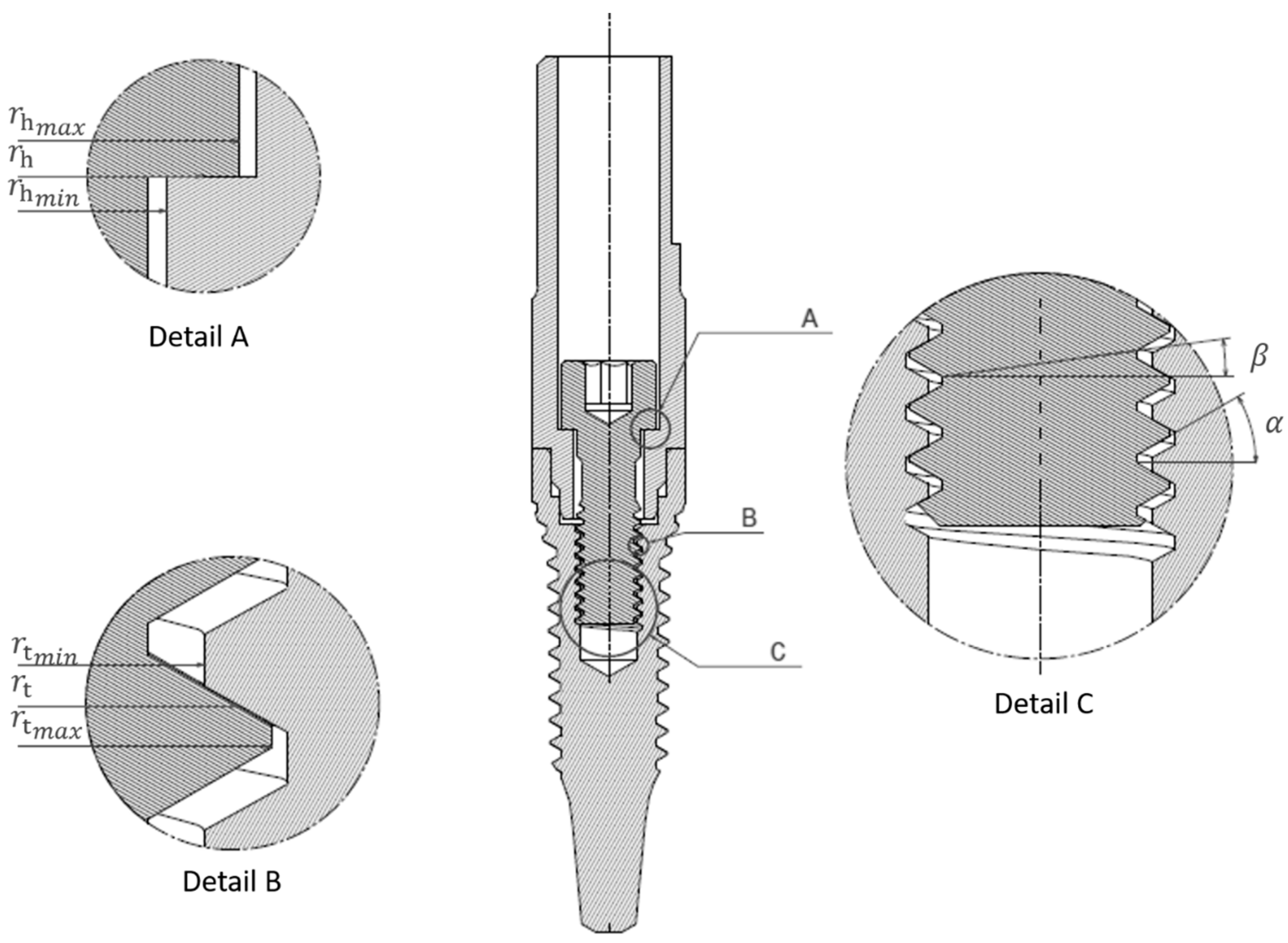
2. Materials and Methods
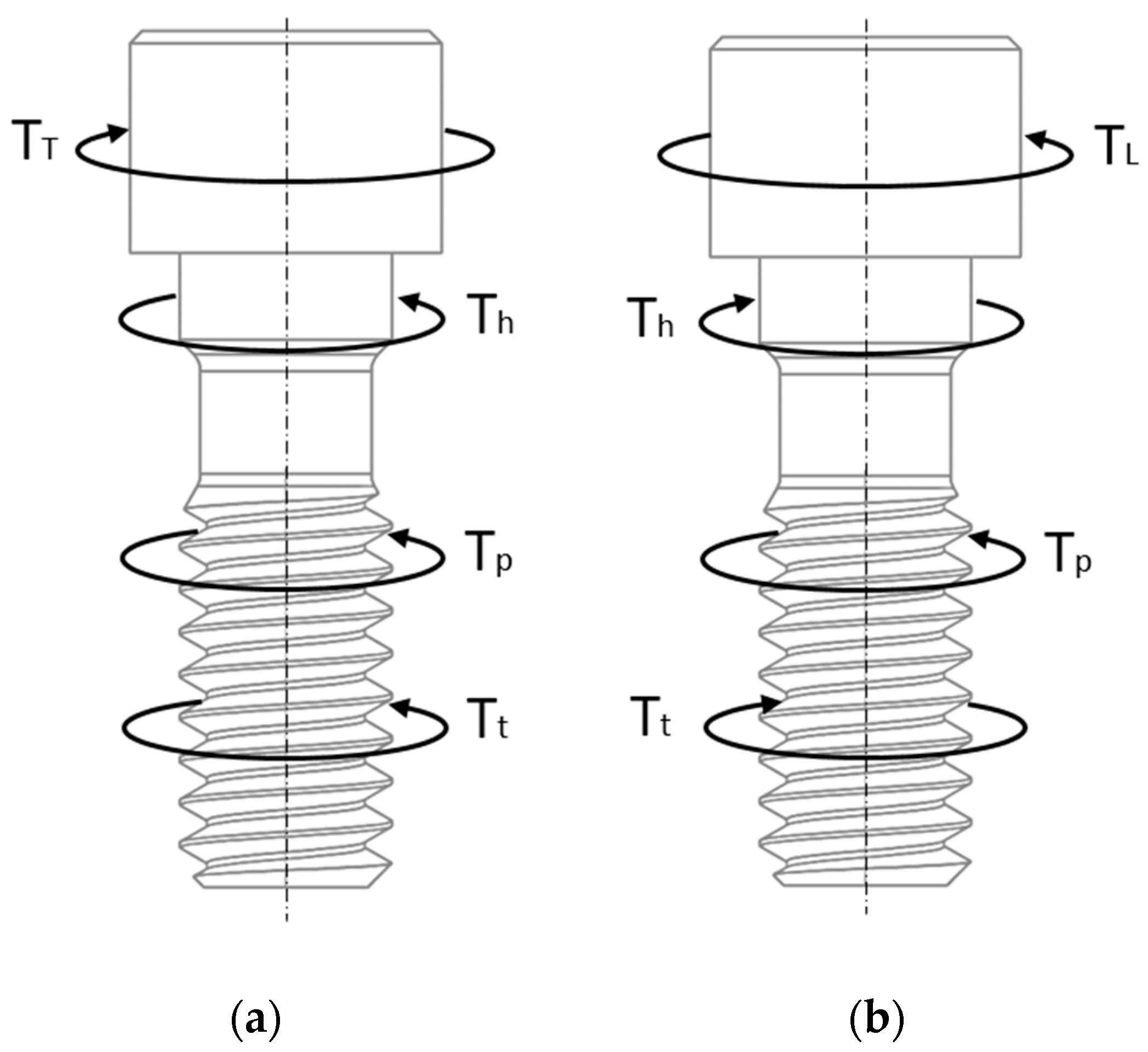
2.1. Background: Loosening Torque
2.2. Simplified Model for the Loosening Torque
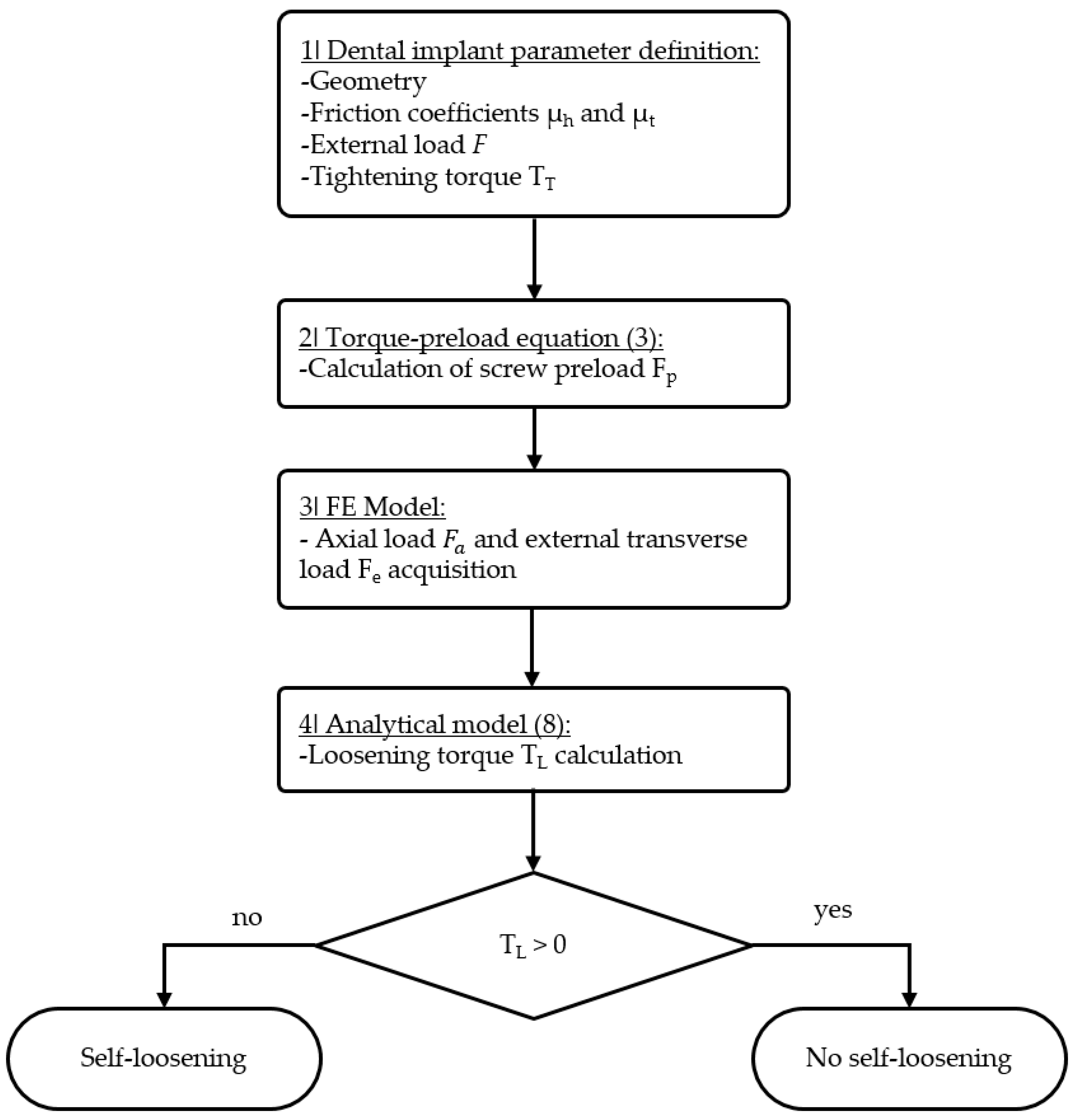
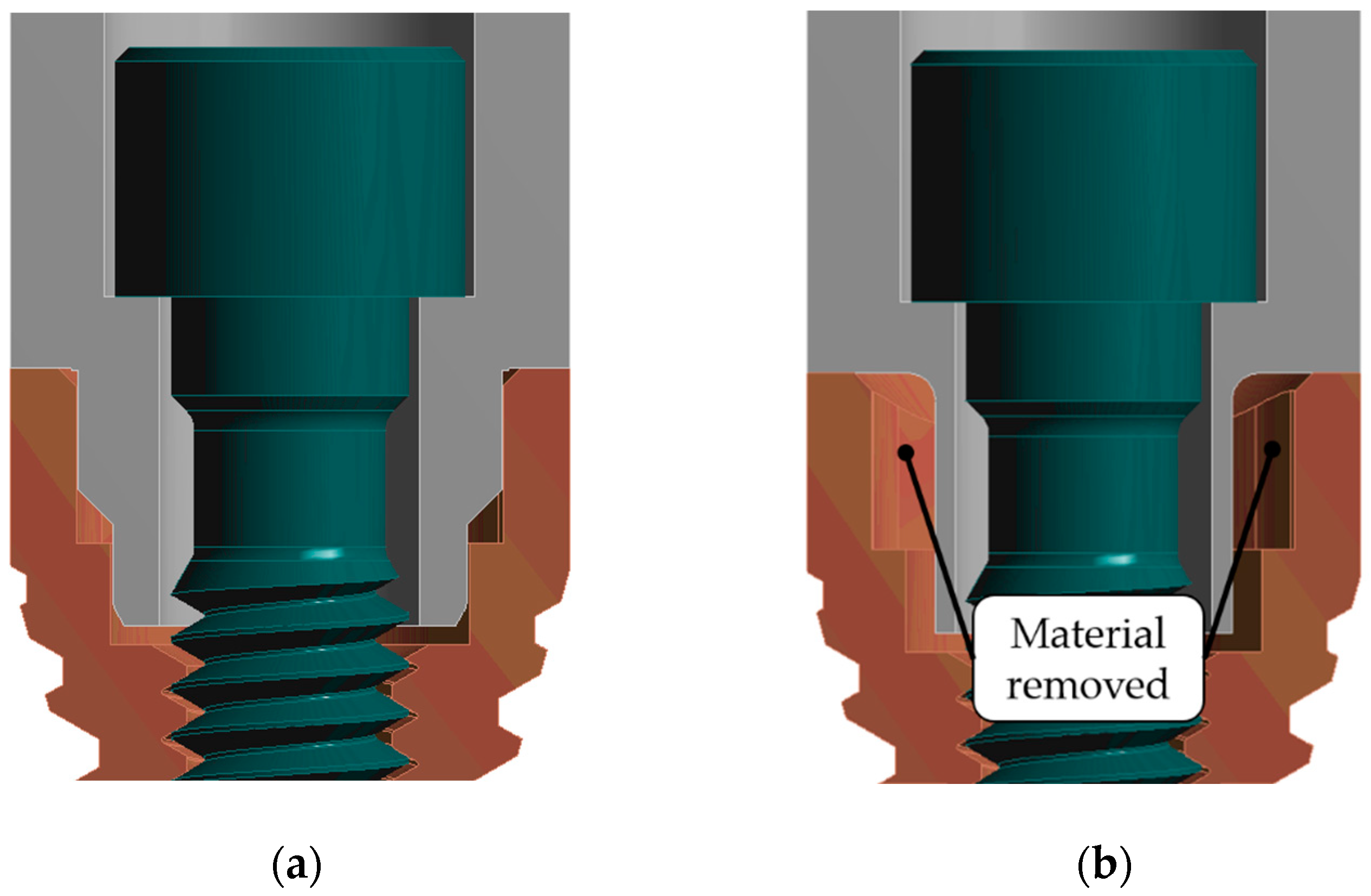
2.3. Methodology to Study Self-Loosening in Dental Implants
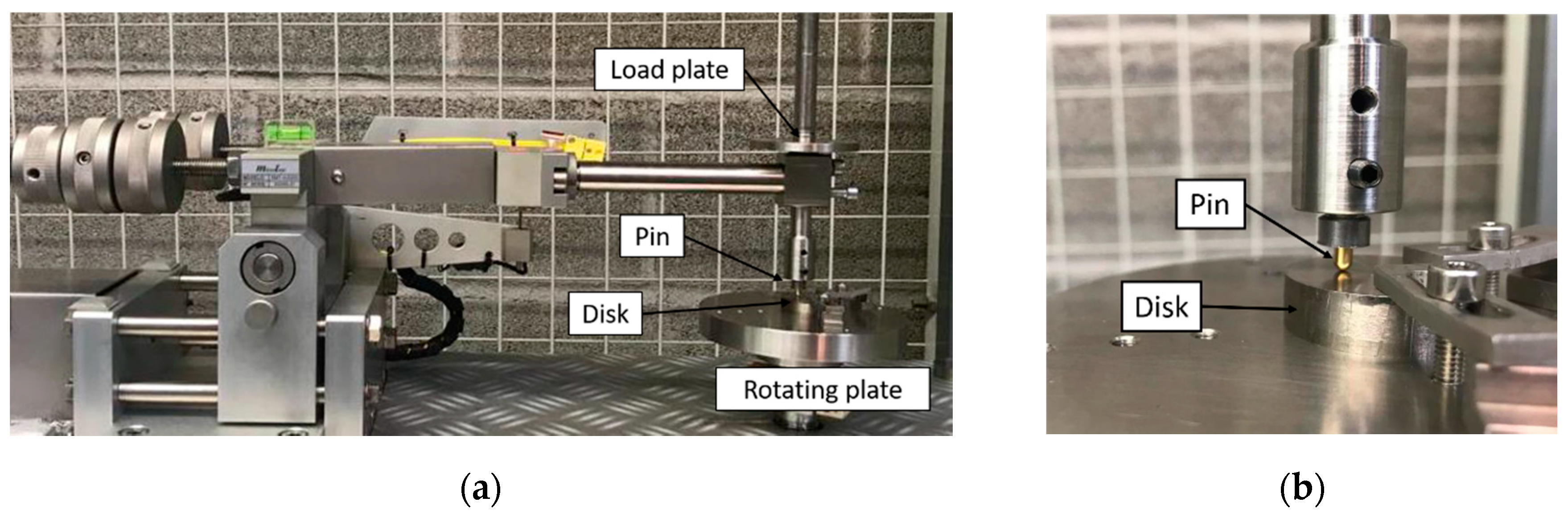
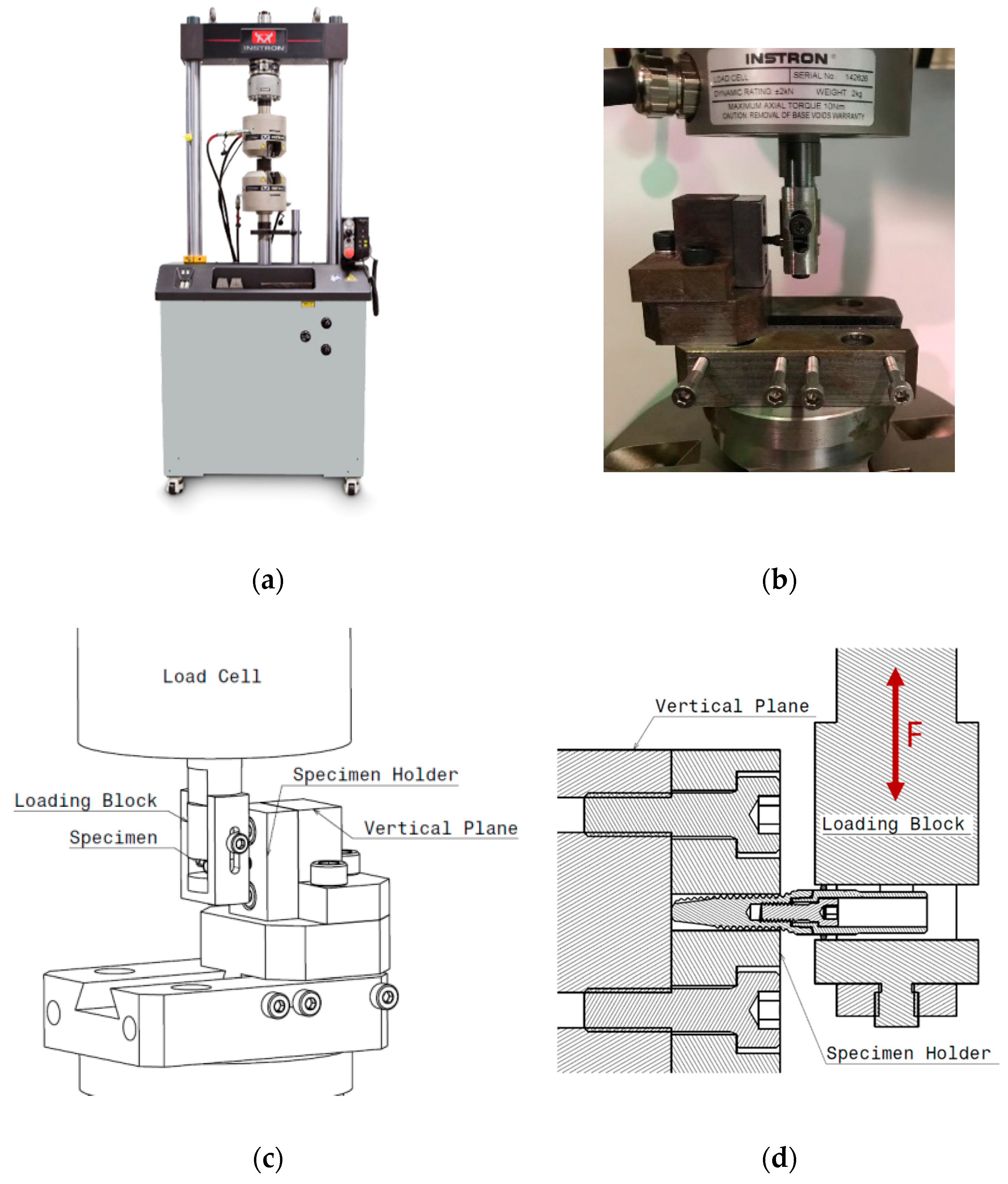
2.4. Experimental Setup
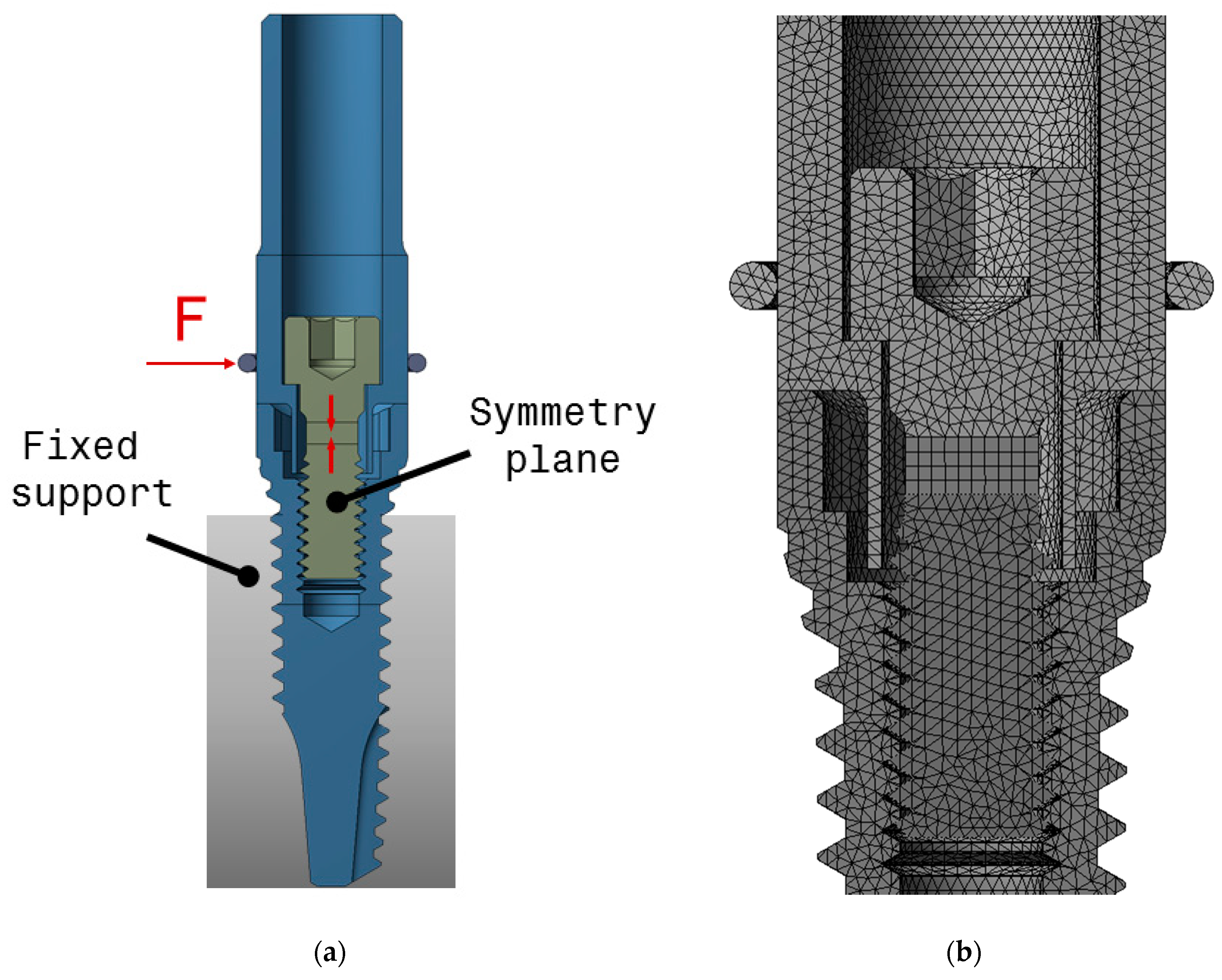
2.5. Finite Element Model
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Patterson, E.A.; Johns, R.B. Theoretical analysis of the fatigue life of fixture screws in osseointegrated dental implants. Int. J. Oral Maxillofac. Implants 1992, 7, 26–33. [Google Scholar]
- Bickford, J.H. Introduction to the Design and Behavior of Bolted Joints. In Introduction to the Design and Behavior of Bolted Joints; CRC Press: New York, NY, USA, 2008; pp. 1–14. [Google Scholar]
- Barbosa, G.S.; da Silva-Neto, J.P.; Simamoto-Júnior, P.C.; das Neves, F.D.; da Gloria Chiarello de Mattos, M.; Ribeiro, R.F. Evaluation of screw loosening on new abutment screws and after successive tightening. Braz. Dent. J. 2011, 22, 51–55. [Google Scholar] [CrossRef] [PubMed]
- Theoharidou, A.; Petridis, H.; Tzannas, K.; Garefis, P. Abutment screw loosening in single-implant restorations: A systematic review. Int. J. Oral Maxillofac. Implants 2007, 23, 681–690. [Google Scholar]
- Dixon, D.L.; Breeding, L.C.; Sadler, J.P.; McKay, M.L. Comparison of screw loosening, rotation, and deflection among three implant designs. J. Prosthet. Dent. 1995, 74, 270–278. [Google Scholar] [CrossRef]
- Mericske-Stern, R.; Geering, A.H.; Bürgin, W.B.; Graf, H. Three-dimensional force measurements on mandibular implants supporting overdentures. Int. J. Oral Maxillofac. Implants 1998, 13, 36–43. [Google Scholar]
- Stüker, R.A.; Teixeira, E.R.; Beck, J.C.P.; Da Costa, N.P. Preload and torque removal evaluation of three different abutment screws for single standing implant restorations. J. Appl. Oral Sci. 2008, 16, 55–58. [Google Scholar] [CrossRef]
- Zeno, H.A.; Buitrago, R.L.; Sternberger, S.S.; Patt, M.E.; Tovar, N.; Coelho, P.; Kurtz, K.S.; Tuminelli, F.J. The Effect of Tissue Entrapment on Screw Loosening at the Implant/Abutment Interface of External- and Internal-Connection Implants: An In Vitro Study. J. Prosthodont. 2016, 25, 216–223. [Google Scholar] [CrossRef]
- Paepoemsin, T.; Reichart, P.A.; Chaijareenont, P.; Strietzel, F.P.; Khongkhunthian, P. Removal torque evaluation of three different abutment screws for single implant restorations after mechanical cyclic loading. Oral Implantol. 2016, 9, 213–221. [Google Scholar]
- Schwarz, M.S. Mechanical complications of dental implants. Clin. Oral Implants Res. 2000, 11, 156–158. [Google Scholar] [CrossRef]
- Jeng, M.-D.; Lin, Y.-S.; Lin, C.-L. Biomechanical Evaluation of the Effects of Implant Neck Wall Thickness and Abutment Screw Size: A 3D Nonlinear Finite Element Analysis. Appl. Sci. 2020, 10, 3471. [Google Scholar] [CrossRef]
- Khraisat, A.; Abu-Hammad, O.; Dar-Odeh, N.; Al-Kayed, A.M. Abutment screw loosening and bending resistance of external hexagon implant system after lateral cyclic loading. Clin. Implant Dent. Relat. Res. 2004, 6, 157–164. [Google Scholar] [CrossRef] [PubMed]
- Chaar, M.S.; Att, W.; Strub, J.R. Prosthetic outcome of cement-retained implant-supported fixed dental restorations: A systematic review. J. Oral Rehabil. 2011, 38, 697–711. [Google Scholar] [CrossRef]
- Jung, R.E.; Pjetursson, B.E.; Glauser, R.; Zembic, A.; Zwahlen, M.; Lang, N.P. A systematic review of the 5-year survival and complication rates of implant-supported single crowns. Clin. Oral Implants Res. 2008, 19, 119–130. [Google Scholar] [CrossRef] [PubMed]
- Simon, R.L. Single implant-supported molar and premolar crowns: A ten-year retrospective clinical report. J. Prosthet. Dent. 2003, 90, 517–521. [Google Scholar] [CrossRef] [PubMed]
- Aboyoussef, H.; Weiner, S.; Ehrenberg, D. Effect of an antirotation resistance form on screw loosening for single implant-supported crowns. J. Prosthet. Dent. 2000, 83, 450–455. [Google Scholar] [CrossRef]
- Cavazos, E.; Bell, F.A. Preventing loosening of implant abutment screws. J. Prosthet. Dent. 1996, 75, 566–569. [Google Scholar] [CrossRef]
- Kirov, D.; Stoichkov, B. Factors affecting the abutment screw loosening. J. IMAB–Annu. Proceeding Sci. Pap. 2017, 23, 1505–1509. [Google Scholar] [CrossRef]
- Arshad, M.; Shirani, G.; Refoua, S.; Yeganeh, M.R. Comparative study of abutment screw loosening with or without adhesive material. J. Adv. Prosthodont. 2017, 9, 99–103. [Google Scholar] [CrossRef]
- Yeo, I.-S.; Lee, J.-H.; Kang, T.-J.; Kim, S.-K.; Heo, S.-J.; Koak, J.-Y.; Park, J.-M.; Lee, S.-Y. The Effect of Abutment Screw Length on Screw Loosening in Dental Implants with External Abutment Connections After Thermocycling. Int. J. Oral Maxillofac. Implants 2014, 29, 59–62. [Google Scholar] [CrossRef]
- Wu, T.; Fan, H.; Ma, R.; Chen, H.; Li, Z.; Yu, H. Effect of lubricant on the reliability of dental implant abutment screw joint: An in vitro laboratory and three-dimension finite element analysis. Mater. Sci. Eng. C 2017, 75, 297–304. [Google Scholar] [CrossRef]
- Elias, C.N.; Figueira, D.C.; Rios, P.R. Influence of the coating material on the loosing of dental implant abutment screw joints. Mater. Sci. Eng. C 2006, 26, 1361–1366. [Google Scholar] [CrossRef]
- Park, C.I.; Choe, H.C.; Chung, C.H. Effects of surface coating on the screw loosening of dental abutment screws. Met. Mater. Int. 2004, 10, 549. [Google Scholar] [CrossRef]
- Yao, K.T.; Kao, H.C.; Cheng, C.K.; Fang, H.W.; Yip, S.W.; Hsu, M.L. The effect of clockwise and counterclockwise twisting moments on abutment screw loosening. Clin. Oral Implants Res. 2012, 23, 1181–1186. [Google Scholar] [CrossRef] [PubMed]
- Siamos, G.; Winkler, S.; Boberick, K.G. The relationship between implant preload and screw loosening on implant-supported prostheses. J. Oral Implantol. 2002, 28, 67–73. [Google Scholar] [CrossRef]
- Lang, L.A.; Kang, B.; Wang, R.F.; Lang, B.R. Finite element analysis to determine implant preload. J. Prosthet. Dent. 2003, 90, 539–546. [Google Scholar] [CrossRef] [PubMed]
- Norton, M.R. Assessment of cold welding properties of the internal conical interface of two commercially available implant systems. J. Prosthet. Dent. 1999, 81, 159–166. [Google Scholar] [CrossRef]
- Junker, G.H. New criteria for self-loosening of fasteners under vibration. SAE Trans. 1969, 78, 314–335. [Google Scholar]
- Junker, G.H. Criteria for Self Loosening of Fasteners Under Vibration. Aircr. Eng. Aerosp. Technol. 1973, 44, 14–16. [Google Scholar] [CrossRef]
- Haviland, G.S. Unraveling the Myths of Fastener World; SAE Technical Papers; SAE International: Warrendale, PA, USA, 1981. [Google Scholar]
- Nassar, S.A.; Yang, X. A mathematical model for vibration-induced loosening of preloaded threaded fasteners. J. Vib. Acoust. 2009, 131, 2–13. [Google Scholar] [CrossRef]
- Nassar, S.A.; Xianjie, Y. Novel formulation of the tightening and breakaway torque components in threaded fasteners. J. Press. Vessel Technol. Trans. ASME 2007, 129, 653–663. [Google Scholar] [CrossRef]
- Fort, V.; Bouzid, A.H.; Gratton, M. Analytical Modeling of Self-Loosening of Bolted Joints Subjected to Transverse Loading. J. Press. Vessel Technol. Trans. ASME 2019, 141, 1–11. [Google Scholar] [CrossRef]
- Motosh, N. Development of design charts for bolts preloaded up to the plastic range. J. Manuf. Sci. Eng. Trans. ASME 1976, 98, 849–951. [Google Scholar] [CrossRef]
- Juvinall, R.C.; Saunders, H. Fundamentals of Machine Component Design, 5th ed.; John Wiley & Sons, INC: Hoboken, NJ, USA, 2012; Chapter 10; pp. 411–471. ISBN 13 9781118012895. [Google Scholar]
- Armentia, M.; Abasolo, M.; Coria, I.; Albizuri, J. Fatigue Design of Dental Implant Assemblies: A Nominal Stress Approach. Metals 2020, 10, 744. [Google Scholar] [CrossRef]
- ISO 14801:2007 Dentistry. Dynamic Fatigue Test for Endosseous Dental Implants; ISO: Geneva, Switzerland, 2007. [Google Scholar]
- Horváth, P.; Tóth, P. Nondestructive Bolt Preload Measurement. Athens J. Τechnology Eng. 2018, 5, 91–110. [Google Scholar] [CrossRef]
- Little, R. Manual on Statistical Planning and Analysis, 17th ed.; ASTM International: Philadelphia, PA, USA, 1975. [Google Scholar]
- Guda, T.; Ross, T.A.; Lang, L.A.; Millwater, H.R. Probabilistic analysis of preload in the abutment screw of a dental implant complex. J. Prosthet. Dent. 2008, 100, 183–193. [Google Scholar] [CrossRef]
- Kim, S.K.; Lee, J.B.; Koak, J.Y.; Heo, S.J.; Lee, K.R.; Cho, L.R.; Lee, S.S. An abutment screw loosening study of a Diamond Like Carbon-coated CP titanium implant. J. Oral Rehabil. 2005, 32, 346–350. [Google Scholar] [CrossRef] [PubMed]
- Sun, F.; Wang, L.; Li, X.C.; Cheng, W.; Lin, Z.; Ba, D.C.; Song, G.Q.; Sun, C.S. Effect of surface modification on the long-term stability of dental implant abutment screws by plasma nitriding treatment. Surf. Coat. Technol. 2020, 399, 126089. [Google Scholar] [CrossRef]
- Bulaqi, H.A.; Mousavi Mashhadi, M.; Geramipanah, F.; Safari, H.; Paknejad, M. Effect of the coefficient of friction and tightening speed on the preload induced at the dental implant complex with the finite element method. J. Prosthet. Dent. 2015, 113, 405–411. [Google Scholar] [CrossRef]
- Yang, X.; Nassar, S.A.; Wu, Z. Criterion for preventing self-loosening of preloaded cap screws under transverse cyclic excitation. J. Vib. Acoust. 2011, 133, 041013. [Google Scholar] [CrossRef]



| Ti 6Al 4V ELI (TI GR5) | TI CP4 | ||
|---|---|---|---|
| Composition | Wt.% | Composition | Wt.% |
| Al | 5.5–6.5 | N(max) | 0.05 |
| V | 3.5–4.5 | C(max) | 0.08 |
| Fe(max) | 0.25 | Fe(max) | 0.5 |
| O(max) | 0.13 | O(max) | 0.4 |
| C(max) | 0.08 | H(max) | 0.0125 |
| N(max) | 0.05 | - | - |
| H(max) | 0.012 | - | - |
| 10 | 64.5 | 217.7 | 36.1 |
| 15 | 96.7 | 326.1 | 53.7 |
| 20 | 128.3 | 433.9 | 72.6 |
| Error (%) | |||
|---|---|---|---|
| 10 | 67.9 | 5.9 | 5 |
| 15 | 100.8 | 9.9 | 4.1 |
| 20 | 138.9 | 6.2 | 7.6 |
| Source of Variation | SS | DoF | MS | F | p-Value | Fcrit |
|---|---|---|---|---|---|---|
| Between groups | 0.75 | 2 | 0.38 | 1.29 | 0.28 | 3.11 |
| Within groups | 23.48 | 81 | 0.29 | |||
| Total | 24.23 | 83 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Armentia, M.; Abasolo, M.; Coria, I.; Bouzid, A.-H. On the Use of a Simplified Slip Limit Equation to Predict Screw Self-Loosening of Dental Implants Subjected to External Cycling Loading. Appl. Sci. 2020, 10, 6748. https://doi.org/10.3390/app10196748
Armentia M, Abasolo M, Coria I, Bouzid A-H. On the Use of a Simplified Slip Limit Equation to Predict Screw Self-Loosening of Dental Implants Subjected to External Cycling Loading. Applied Sciences. 2020; 10(19):6748. https://doi.org/10.3390/app10196748
Chicago/Turabian StyleArmentia, Mikel, Mikel Abasolo, Ibai Coria, and Abdel-Hakim Bouzid. 2020. "On the Use of a Simplified Slip Limit Equation to Predict Screw Self-Loosening of Dental Implants Subjected to External Cycling Loading" Applied Sciences 10, no. 19: 6748. https://doi.org/10.3390/app10196748
APA StyleArmentia, M., Abasolo, M., Coria, I., & Bouzid, A.-H. (2020). On the Use of a Simplified Slip Limit Equation to Predict Screw Self-Loosening of Dental Implants Subjected to External Cycling Loading. Applied Sciences, 10(19), 6748. https://doi.org/10.3390/app10196748





