An Optimal Power Control Strategy for Grid-Following Inverters in a Synchronous Frame
Abstract
1. Introduction
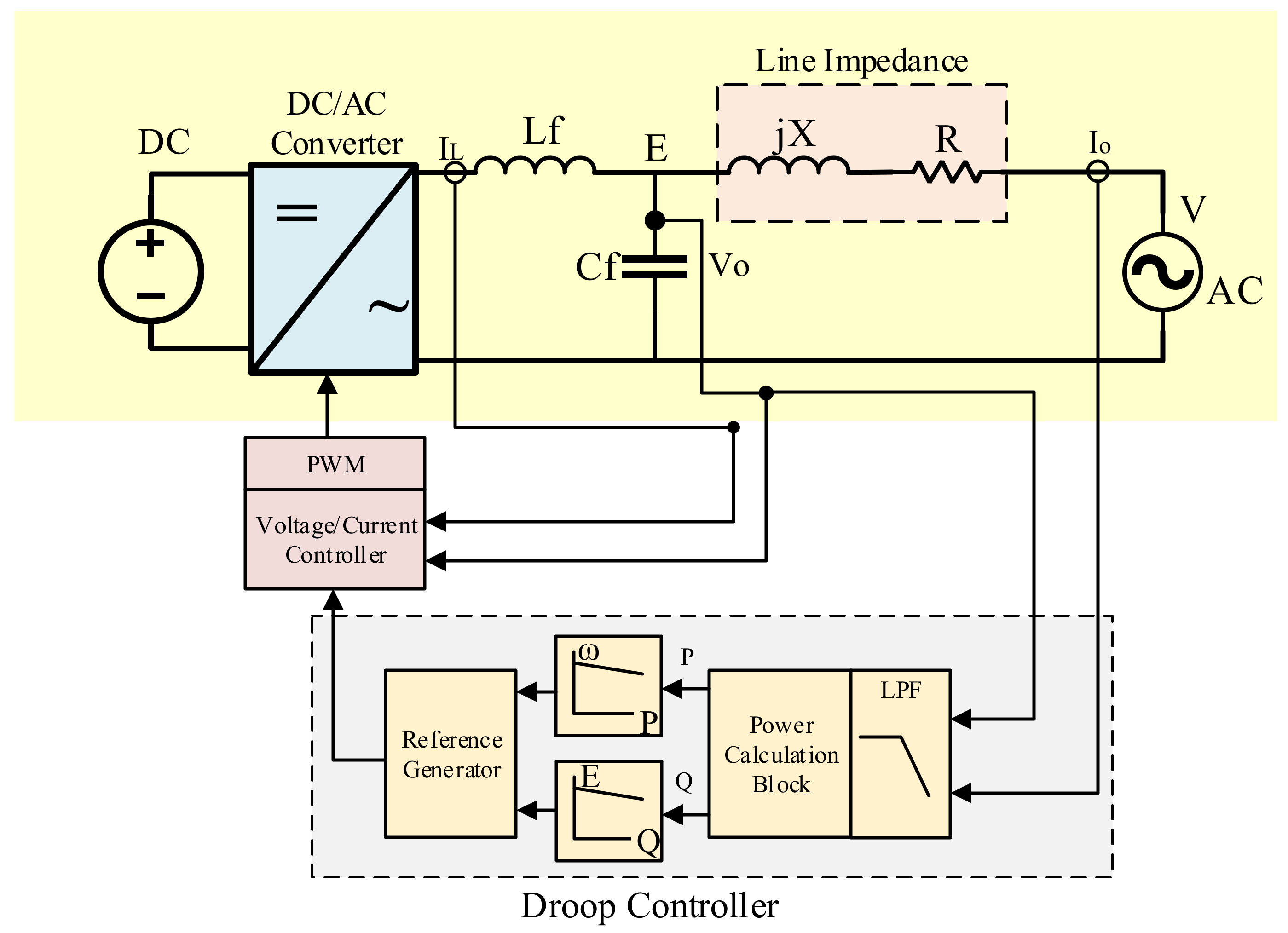
2. Mathematical Model
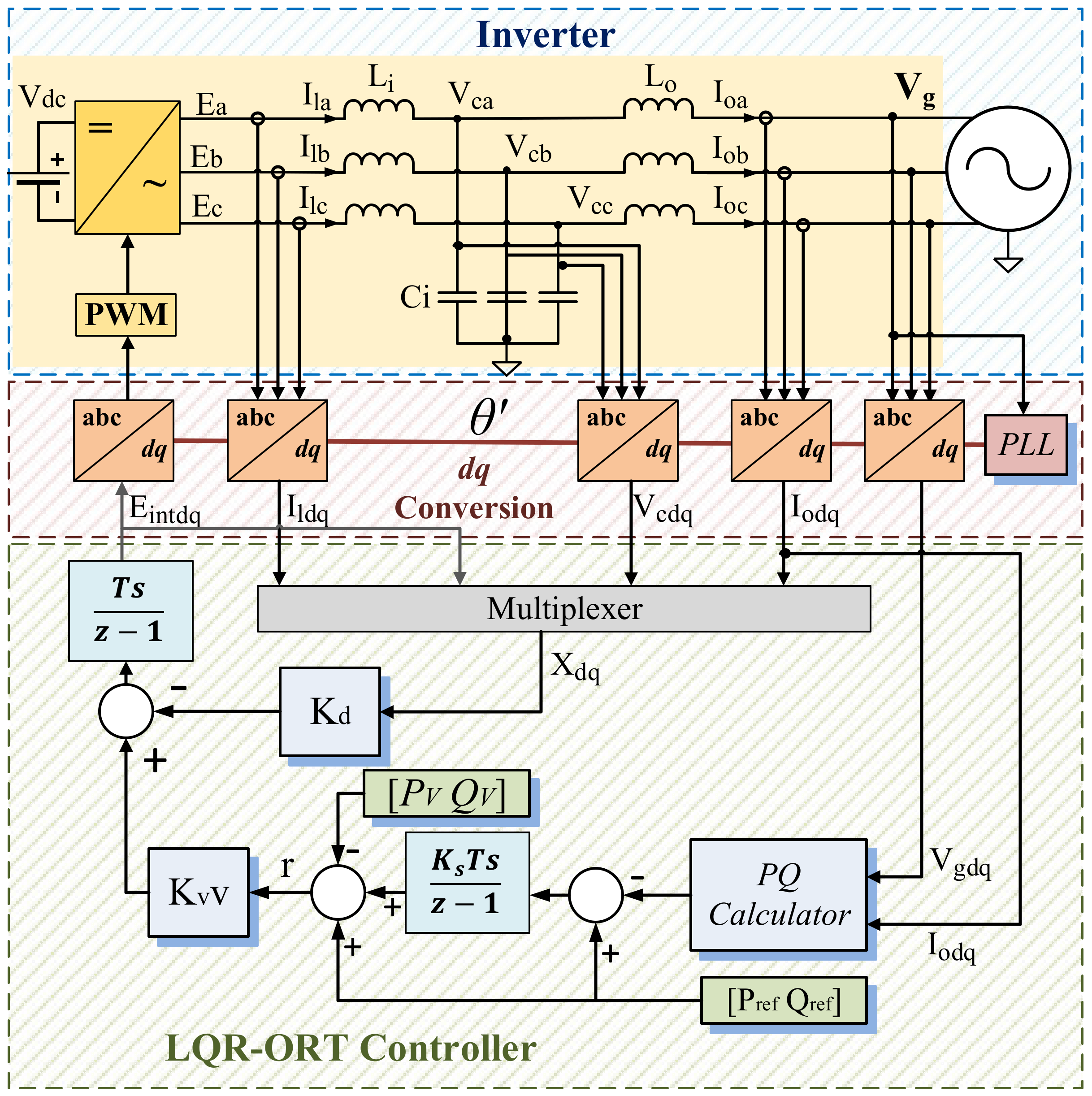
3. Discrete LQR-ORT Controller Design
3.1. Computation of Suboptimal LQR Controller
3.2. Optimal Reference Tracking Matrix
3.3. Main Grid Power Contribution Calculation Using Superposition Principle
4. Simulation and Experimental Results
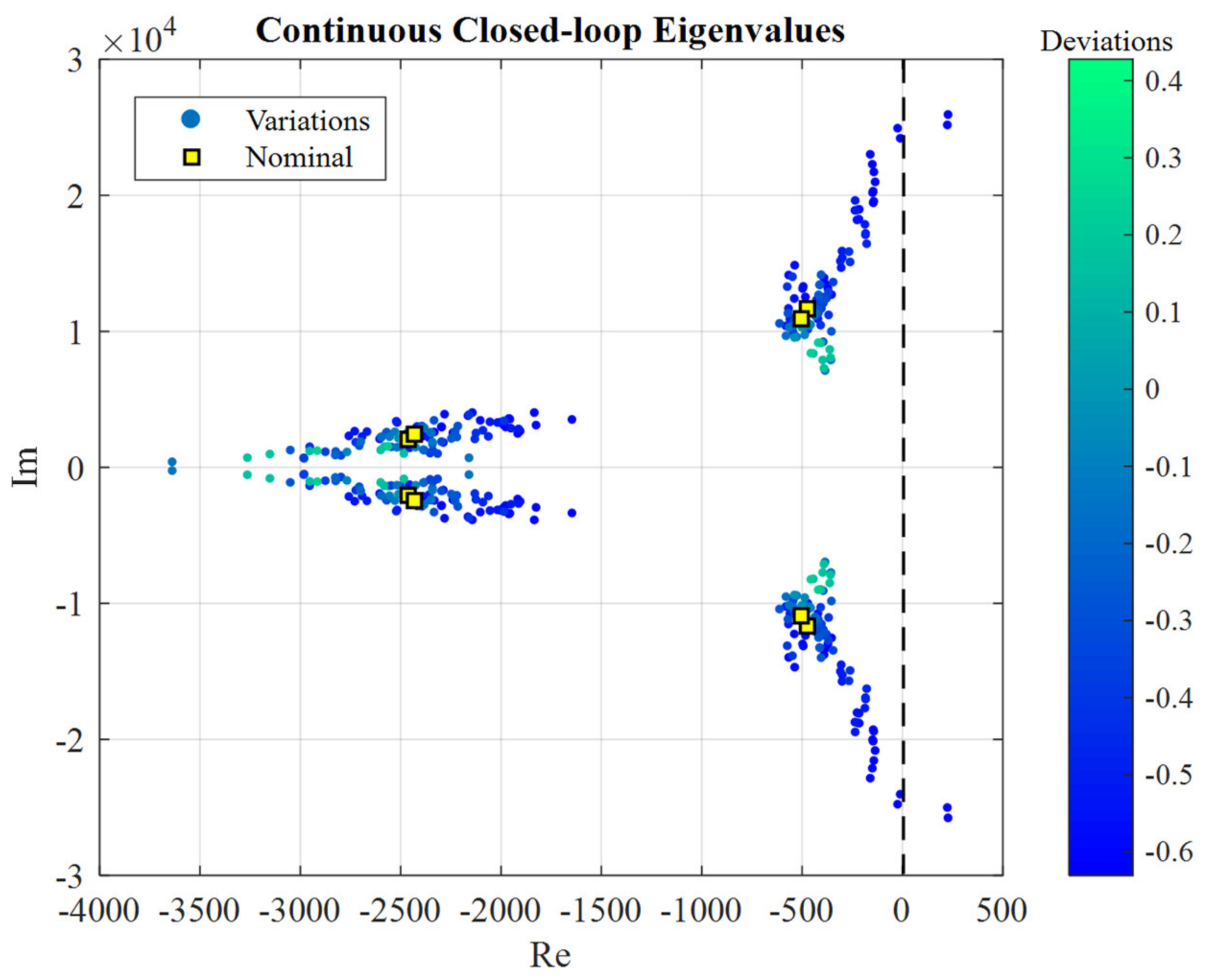
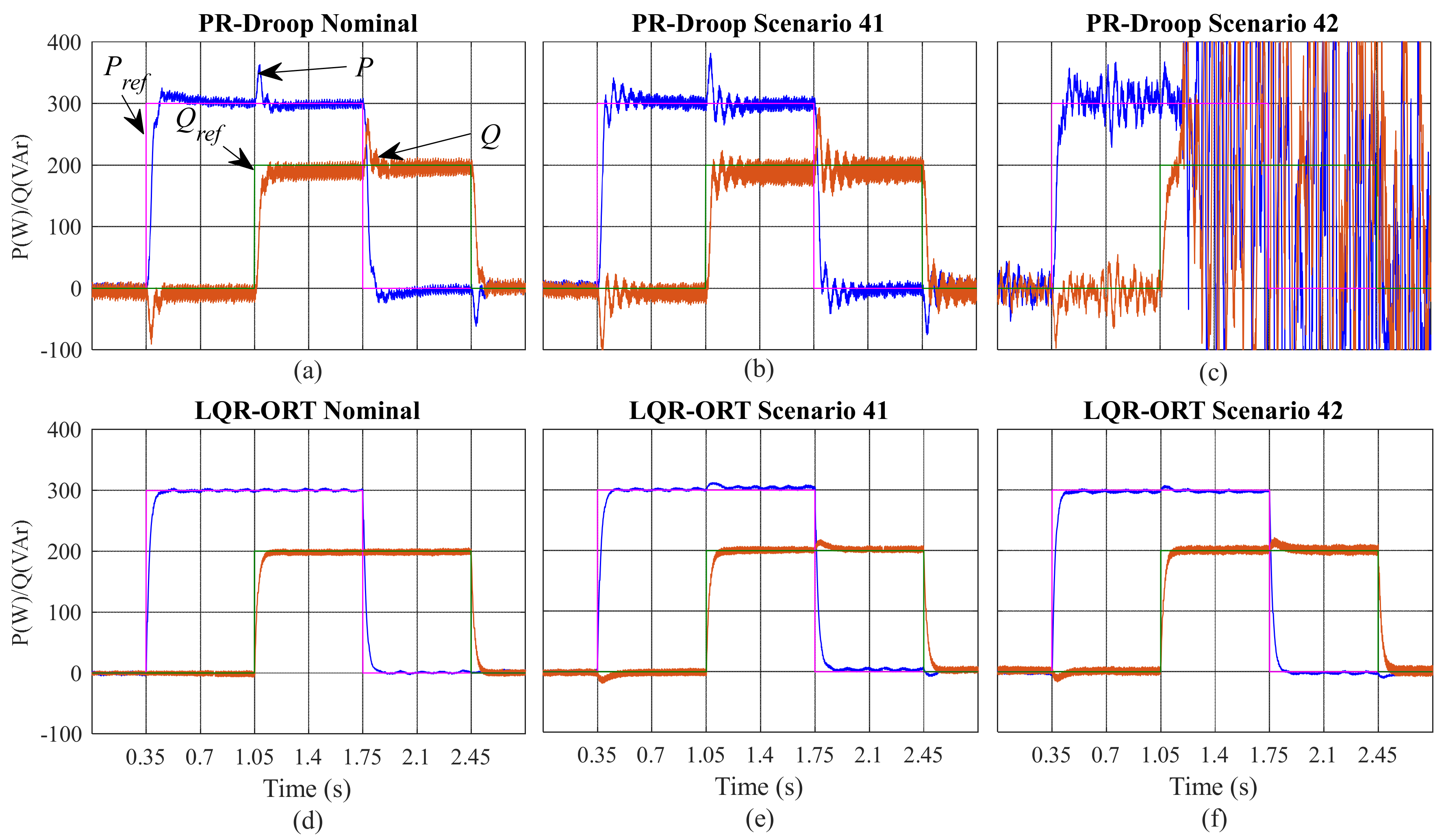
4.1. Robustness and Stability Analysis
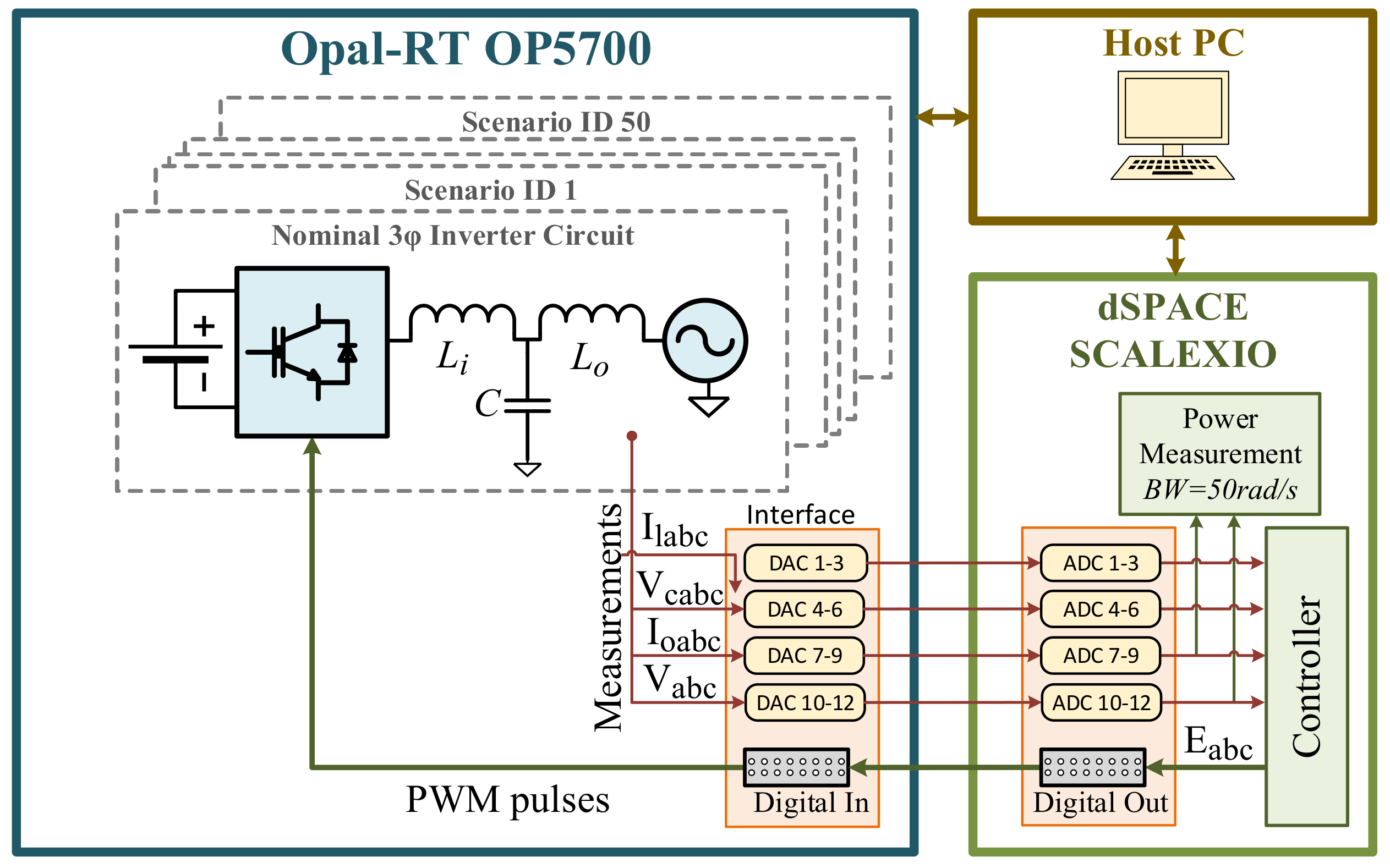
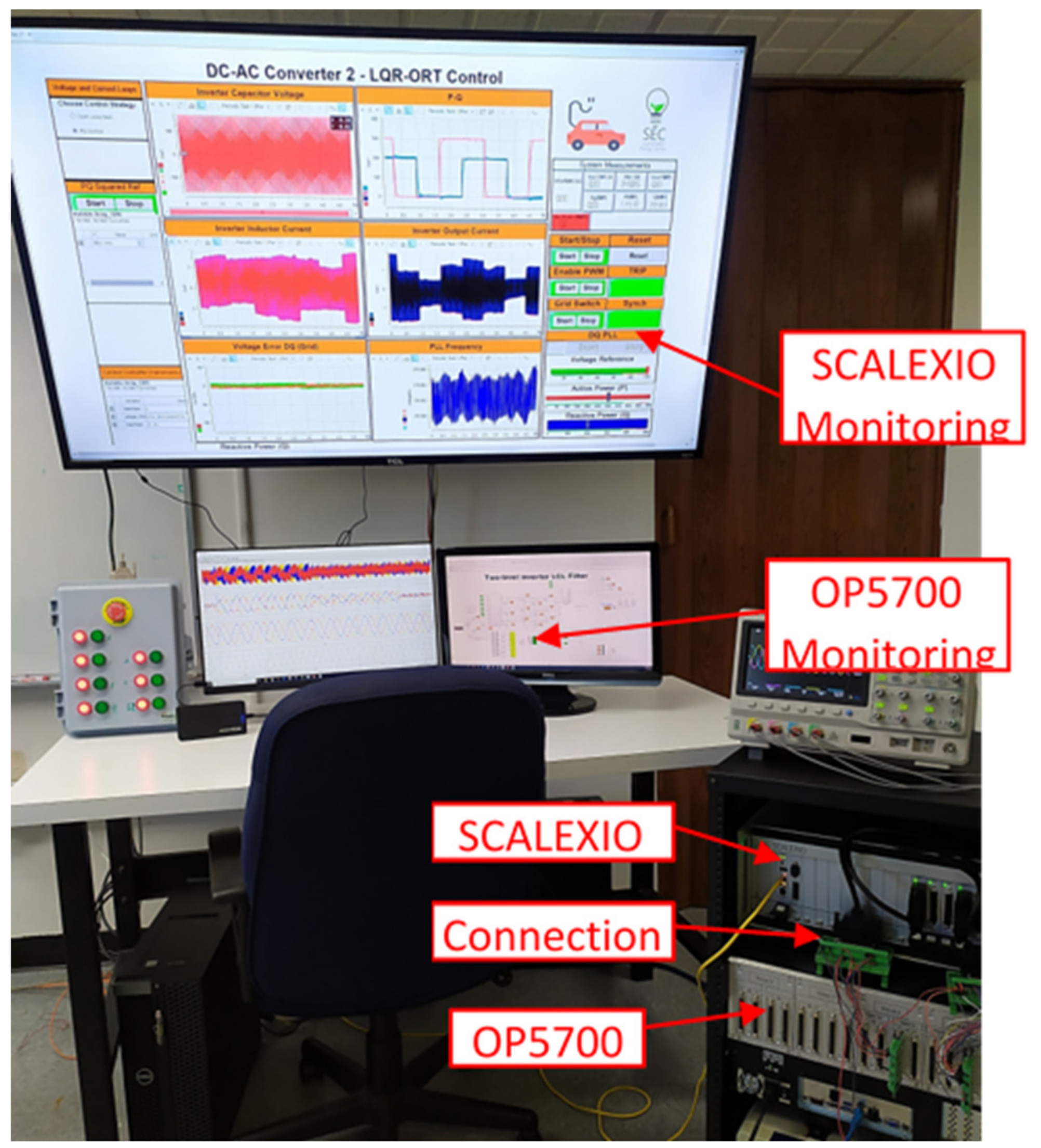
4.2. HIL Experimental Robustness Assessment
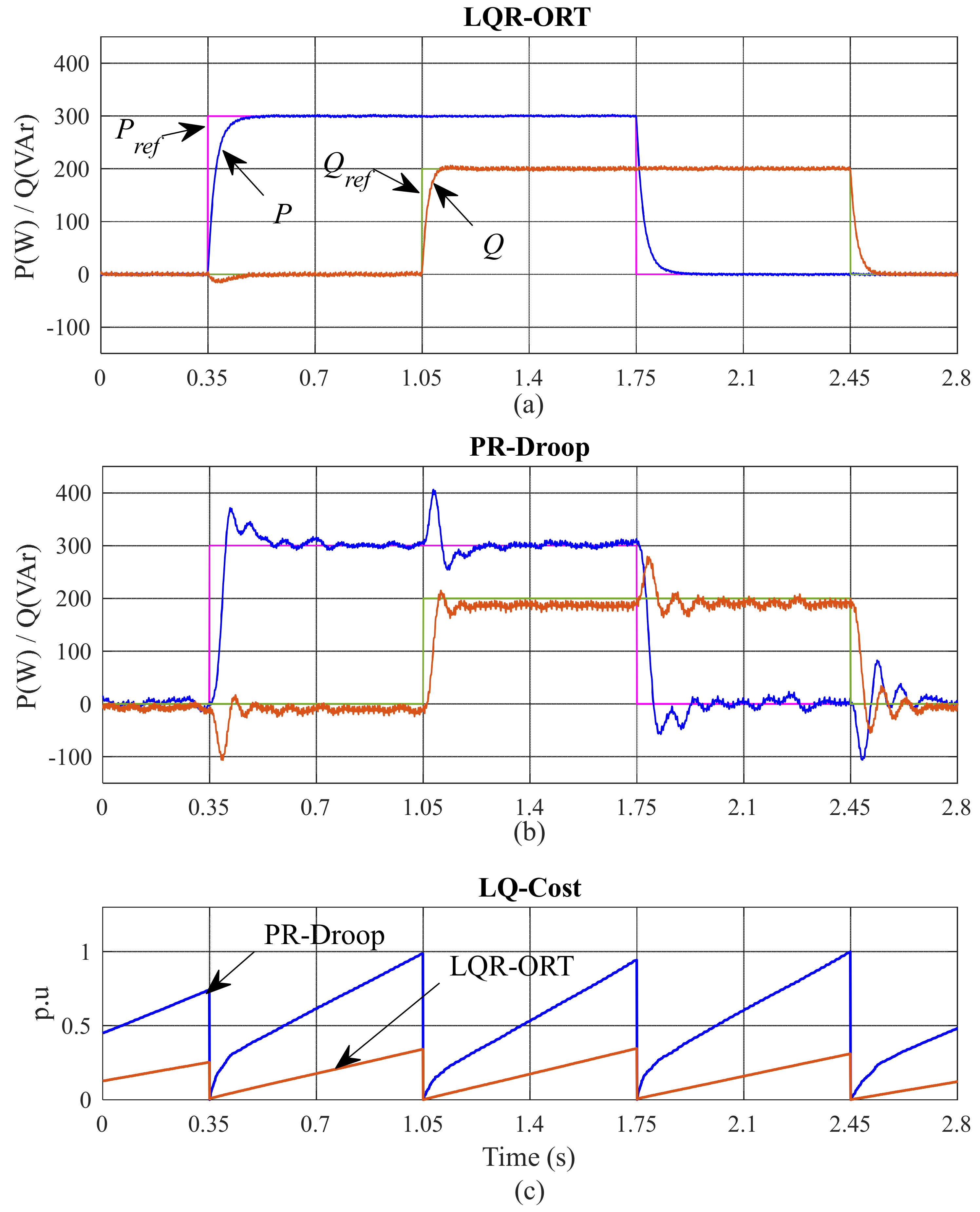
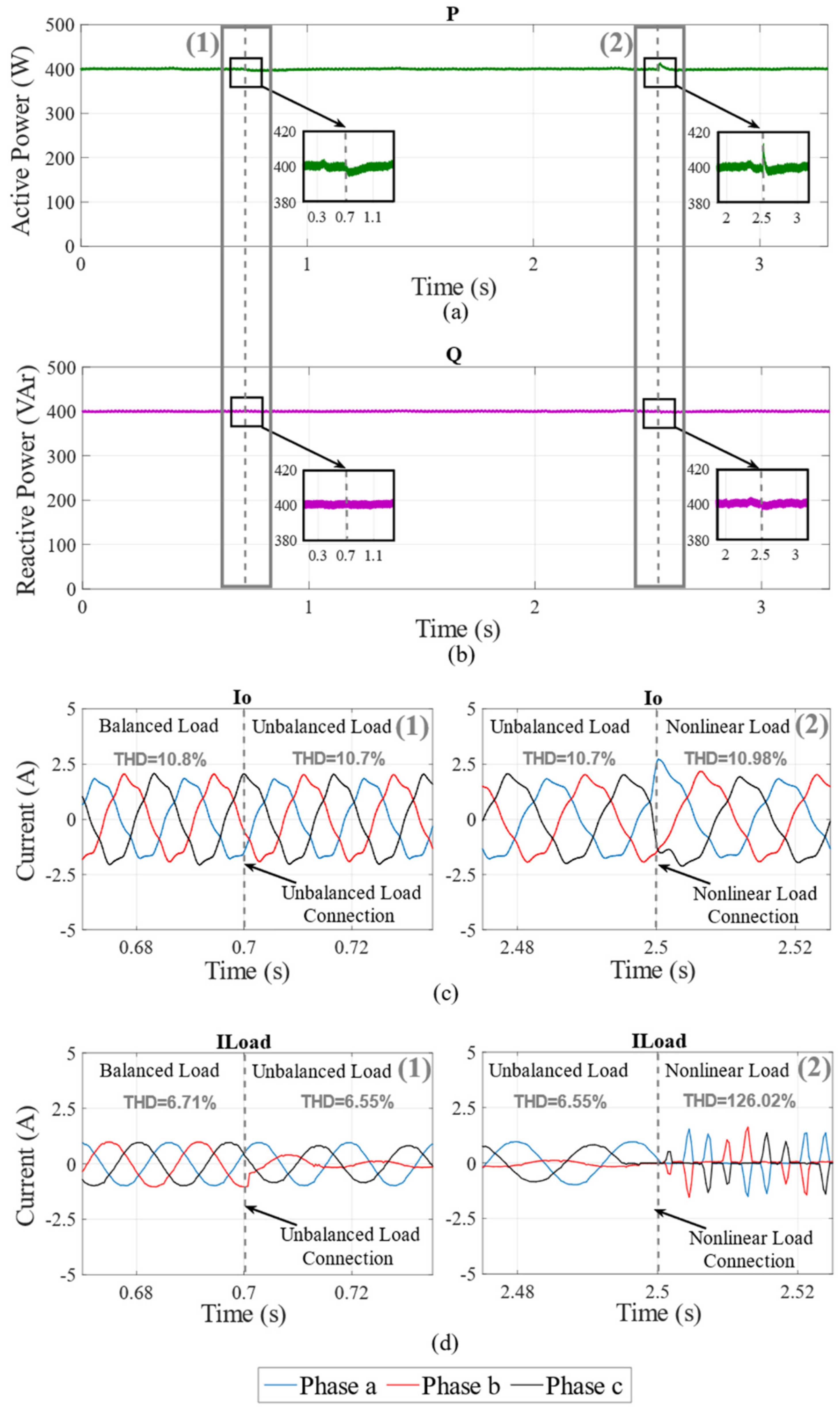
4.3. Experimental Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; De Vicuña, L.G.; Castilla, M. Hierarchical control of droop-controlled AC and DC microgrids—A general approach toward standardization. IEEE Trans. Ind. Electron. 2011, 58, 158–172. [Google Scholar] [CrossRef]
- Pogaku, N.; Prodanović, M.; Green, T.C. Modeling, analysis and testing of autonomous operation of an inverter-based microgrid. IEEE Trans. Power Electron. 2007, 22, 613–625. [Google Scholar] [CrossRef]
- Han, H.; Hou, X.; Yang, J.; Wu, J.; Su, M.; Guerrero, J.M. Review of Power Sharing Control Strategies for Islanding Operation of AC Microgrids. IEEE Trans. Smart Grid 2016, 7, 200–215. [Google Scholar] [CrossRef]
- Lasseter, R.H. MicroGrids. In Proceedings of the 2002 IEEE Power Engineering Society, Winter Meeting Conference Proceedings, New York, NY, USA, 27–31 January 2002; Cat. No.02CH37309. Volume 1, pp. 305–308. [Google Scholar]
- Coelho, E.A.A.; Cortizo, P.C.; Garcia, P.F.D. Small signal stability for single phase inverter connected to stiff AC system. In Proceedings of the Conference Record of the 1999 IEEE Industry Applications Conference Thirty-Forth IAS Annual Meeting, Phoenix, AZ, USA, 3–7 October 1999; Cat. No.99CH36370. Volume 4, pp. 2180–2187. [Google Scholar]
- Sao, C.K.; Lehn, P.W. Autonomous Load Sharing of Voltage Source Converters. IEEE Trans. Power Deliv. 2005, 20, 1009–1016. [Google Scholar] [CrossRef]
- Sao, C.K.; Lehn, P.W. Control and power management of converter fed microgrids. IEEE Trans. Power Syst. 2008, 23, 1088–1098. [Google Scholar] [CrossRef]
- Borup, U.; Blaabjerg, F.; Enjeti, P.N. Sharing of nonlinear load in parallel-connected three-phase converters. IEEE Trans. Ind. Appl. 2001, 37, 1817–1823. [Google Scholar] [CrossRef]
- Rokrok, E.; Golshan, M.E.H. Adaptive voltage droop scheme for voltage source converters in an islanded multibus microgrid. IET Gener. Transm. Distrib. 2010, 4, 562. [Google Scholar] [CrossRef]
- Marwali, M.N.; Jung, J.-W.; Keyhani, A. Control of Distributed Generation Systems—Part II: Load Sharing Control. IEEE Trans. Power Electron. 2004, 19, 1551–1561. [Google Scholar] [CrossRef]
- Majumder, R.; Chaudhuri, B.; Ghosh, A.; Majumder, R.; Ledwich, G.; Zare, F. Improvement of stability and load sharing in an autonomous microgrid using supplementary droop control loop. IEEE Trans. Power Syst. 2010, 25, 796–808. [Google Scholar] [CrossRef]
- Avelar, H.J.; Parreira, W.A.; Vieira, J.B.; de Freitas, L.C.G.; Coelho, E.A.A. A state equation model of a single-phase grid-connected inverter using a droop control scheme with extra phase shift control action. IEEE Trans. Ind. Electron. 2012, 59, 1527–1537. [Google Scholar] [CrossRef]
- Vasquez, J.C.; Guerrero, J.M.; Savaghebi, M.; Eloy-Garcia, J.; Teodorescu, R. Modeling, analysis, and design of stationary-reference-frame droop-controlled parallel three-phase voltage source inverters. IEEE Trans. Ind. Electron. 2013, 60, 1271–1280. [Google Scholar]
- Xiao, W.; Kanjiya, P.; Kirtley, J.L.; Kan’an, N.H.; Zeineldin, H.H.; Khadkikar, V. A modified control topology to improve stability margins in micro-grids with droop controlled IBDG. In Proceedings of the 3rd Renewable Power Generation Conference (RPG 2014), Naples, Italy, 24–25 September 2014; p. 5. [Google Scholar]
- Zhang, J.; Chen, J.; Chen, X.; Gong, C. Modelling, analysis and design of droop-controlled parallel three phase voltage source inverter using dynamic phasors method. In Proceedings of the IEEE Transportation Electrification Conference Expo, ITEC Asia-Pacific 2014, Beijing, China, 31 August–3 September 2014; pp. 1–6. [Google Scholar]
- Han, Y.; Shen, P.; Zhao, X.; Guerrero, J.M. Control Strategies for Islanded Microgrid Using Enhanced Hierarchical Control Structure With Multiple Current-Loop Damping Schemes. IEEE Trans. Smart Grid 2017, 8, 1139–1153. [Google Scholar]
- Tuladhar, A.; Jin, H.; Unger, T.; Mauch, K. Parallel operation of single phase inverter modules with no control interconnections. In Proceedings of the APEC 97—Applied Power Electronics Conference, Atlanta, GA, USA, 23–27 February 1997; Volume 1, pp. 94–100. [Google Scholar]
- Lewis, F.L.; Vrabie, D.L.; Syrmos, V.L. Optimal Control; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012. [Google Scholar]
- Dannehl, J.; Fuchs, F.W.; Thøgersen, P.B. PI state space current control of grid-connected PWM converters with LCL filters. IEEE Trans. Power Electron. 2010, 25, 2320–2330. [Google Scholar]
- Busada, C.A.; Jorge, S.G.; Leon, A.E.; Solsona, J.A. Current Controller Based on Reduced Order Generalized Integrators for Distributed Generation Systems. IEEE Trans. Ind. Electron. 2012, 59, 2898–2909. [Google Scholar]
- Eren, S.; Bakhshai, A.; Jain, P. Control of three-phase voltage source inverter for renewable energy applications. In Proceedings of the 2011 IEEE 33rd International Telecommunications Energy Conference, Amsterdam, The Netherlands, 9–13 October 2011; pp. 1–4. [Google Scholar]
- Eren, S.; Bakhshai, A.; Jain, P. Control of grid-connected voltage source inverter with LCL filter. In Proceedings of the 2012 Twenty-Seventh Annual IEEE Applied Power Electronics Conference Exposition, Orlando, FL, USA, 5–9 February 2012; pp. 1516–1520. [Google Scholar]
- Dirscherl, C.; Fessler, J.; Hackl, C.M.; Ipach, H. State-feedback controller and observer design for grid-connected voltage source power converters with LCL-filter. In Proceedings of the 2015 IEEE Conference on Control and Applications CCA 2015—Proceedings, Sydney, Australia, 21–23 September 2015; pp. 215–222. [Google Scholar]
- Khajehoddin, S.A.; Karimi-Ghartemani, M.; Ebrahimi, M. Optimal and Systematic Design of Current Controller for Grid-Connected Inverters. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 1. [Google Scholar]
- Yang, S.; Lei, Q.; Peng, F.Z.; Qian, Z. A robust control scheme for grid-connected voltage-source inverters. IEEE Trans. Ind. Electron. 2011, 58, 202–212. [Google Scholar]
- Maccari, L.A.; Massing, J.R.; Schuch, L.; Rech, C.; Pinheiro, H.; Montagner, V.F.; Oliveira, R.C.L.F. Robust Hinf Control for Grid Connected PWM Inverters with LCL Filters. In Proceedings of the Industry Applications (INDUSCON), 2012 10th IEEE/IAS International Conference, Fortaleza, Brazil, 5–7 November 2012; pp. 1–6. [Google Scholar]
- Ashtinai, N.A.; Azizi, S.M.; Khajehoddin, S.A. Control design in μ-synthesis framework for grid-connected inverters with higher order filters. In Proceedings of the ECCE 2016—IEEE Energy Conversion Congress & Exposition Proceedings, Milwaukee, WI, USA, 18–22 September 2016; pp. 1–6. [Google Scholar]
- Maccari, L.A.; Massing, J.R.; Schuch, L.; Rech, C.; Pinheiro, H.; Oliveira, R.C.L.F.; Montagner, V.F. LMI-Based Control for Grid-Connected Converters With LCL Filters Under Uncertain Parameters. IEEE Trans. Power Electron. 2014, 29, 3776–3785. [Google Scholar]
- Patarroyo-Montenegro, J.F.; Castellà, M.; Andrade, F.; Kampouropoulos, K.; Romeral, L.; Vasquez-Plaza, J. An Optimal Tracking Power Sharing Controller for Inverter-Based Generators in Grid-connected Mode. In Proceedings of the IECON Proceedings, Industrial Electronics Society Conference, Lisbon, Portugal, 14–17 October 2019. [Google Scholar]
- Pou, J. Modulation and Control of Three-phase PWM Multilevel Converters. Ph.D. Thesis, Departament D’Enginyeria Electronica, Universitat Politècnica de Catalunya, Barcelona, Spain, November 2002. [Google Scholar]
- Lu, M.; Wang, X.; Loh, P.C.; Blaabjerg, F.; Dragicevic, T. Graphical Evaluation of Time-Delay Compensation Techniques for Digitally Controlled Converters. IEEE Trans. Power Electron. 2018, 33, 2601–2614. [Google Scholar]
- Teodorescu, R.; Liserre, M.; Pedro, R. Grid Converters for Photovoltaic and Wind Power Systems; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Shaked, U. Guaranteed stability margins for the discrete-time linear quadratic optimal regulator. IEEE Trans. Automat. Contr. 1986, 31, 162–165. [Google Scholar]
- Arvanitis, K.G.; Kalogeropoulos, G.; Giotopoulos, S. Guaranteed stability margins and singular value properties of the discrete-time linear quadratic optimal regulator. IMA J. Math. Control Inf. 2001, 18, 299–324. [Google Scholar]
- Blight, J.D.; Dailey, R.L.; Gangsaas, D. Practical control law design for aircraft using multivariable techniques. Int. J. Control 1994, 59, 93–137. [Google Scholar] [CrossRef]
- Stengel, R.F.; Ryan, L.E. Stochastic robustness of linear time-invariant control systems. IEEE Trans. Automat. Contr. 1991, 36, 82–87. [Google Scholar] [CrossRef]
- Patarroyo-Montenegro, J.F.; Salazar-Duque, J.E.; Alzate-Drada, S.I.; Vasquez-Plaza, J.D.; Andrade, F. An AC Microgrid Testbed for Power Electronics Courses in the University of Puerto Rico at Mayagüez. In Proceedings of the 2018 IEEE ANDESCON, Santiago de Cali, Colombia, 22–24 August 2018; pp. 1–6. [Google Scholar] [CrossRef]



| Parameter | Symbol | Value |
|---|---|---|
| Grid Voltage | 120 | |
| DC bus Voltage | 350 | |
| Grid Frequency | 60 Hz | |
| Output Inductance | 1.8 mH | |
| Input Inductance | 1.8 mH | |
| Filter Capacitance | 8.8 | |
| Switching Frequency | 10 | |
| Sampling Period | 100 | |
| Error Weighting Matrix | ||
| Input Weighting Matrix | ||
| Inner Integrator Gain | 1 | |
| Outer Integrator Gain | 5 | |
| SOGI gain | 0.7 | |
| PLL Proportional Gain | 0.28307 | |
| PLL Integral Gain | 7.5102 |
| ID | C | Li | Lo | Max Deviation | LQR-ORT Stable | PR-Droop Stable |
|---|---|---|---|---|---|---|
| Nom | 8.8 | 1.8 | 1.8 | 0% | Yes | Yes |
| 1 | 12.6 | 2.87 | 2.57 | 42.8% | Yes | Yes |
| 27 | 10.85 | 2.92 | 1.06 | −41.0% | Yes | Yes |
| 28 | 5.97 | 1.03 | 2.79 | −42.7% | Yes | No |
| 29 | 5.47 | 0.95 | 2.58 | −47.3% | No | No |
| 30 | 14.03 | 1.73 | 0.92 | −48.9% | Yes | Yes |
| 31 | 4.32 | 1.91 | 2.16 | −50.9% | Yes | Yes |
| 32 | 4.25 | 1.79 | 2.90 | −51.7% | Yes | Yes |
| 33 | 11.09 | 2.39 | 0.86 | −52.4% | Yes | No |
| 34 | 13.96 | 0.85 | 1.97 | −52.7% | Yes | No |
| 35 | 5.93 | 0.85 | 1.96 | −53.0% | No | No |
| 36 | 4.40 | 2.53 | 0.85 | −53.0% | Yes | Yes |
| 37 | 14.33 | 2.39 | 0.82 | −54.2% | No | No |
| 38 | 3.94 | 1.96 | 1.27 | −55.3% | Yes | No |
| 39 | 11.12 | 1.89 | 0.78 | −56.6% | Yes | Yes |
| 40 | 3.82 | 1.96 | 1.33 | −56.7% | Yes | No |
| 41 | 9.82 | 1.44 | 0.76 | −58.0% | Yes | Yes |
| 42 | 12.21 | 0.74 | 1.80 | −58.6% | Yes | No |
| 43 | 4.32 | 1.33 | 0.73 | −59.7% | No | No |
| 44 | 10.75 | 0.72 | 2.30 | −59.8% | Yes | No |
| 45 | 3.52 | 1.62 | 1.42 | −60.0% | Yes | No |
| 46 | 3.51 | 1.63 | 1.40 | −60.1% | No | No |
| 47 | 3.48 | 1.91 | 1.00 | −60.4% | Yes | No |
| 48 | 11.97 | 0.67 | 2.59 | −62.6% | Yes | No |
| 49 | 3.50 | 0.67 | 1.40 | −62.7% | No | No |
| 50 | 3.25 | 1.36 | 0.86 | −63.1% | No | No |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Patarroyo-Montenegro, J.F.; Vasquez-Plaza, J.D.; Andrade, F.; Fan, L. An Optimal Power Control Strategy for Grid-Following Inverters in a Synchronous Frame. Appl. Sci. 2020, 10, 6730. https://doi.org/10.3390/app10196730
Patarroyo-Montenegro JF, Vasquez-Plaza JD, Andrade F, Fan L. An Optimal Power Control Strategy for Grid-Following Inverters in a Synchronous Frame. Applied Sciences. 2020; 10(19):6730. https://doi.org/10.3390/app10196730
Chicago/Turabian StylePatarroyo-Montenegro, Juan F., Jesus D. Vasquez-Plaza, Fabio Andrade, and Lingling Fan. 2020. "An Optimal Power Control Strategy for Grid-Following Inverters in a Synchronous Frame" Applied Sciences 10, no. 19: 6730. https://doi.org/10.3390/app10196730
APA StylePatarroyo-Montenegro, J. F., Vasquez-Plaza, J. D., Andrade, F., & Fan, L. (2020). An Optimal Power Control Strategy for Grid-Following Inverters in a Synchronous Frame. Applied Sciences, 10(19), 6730. https://doi.org/10.3390/app10196730








