1. Introduction
Copper is one of the first metal products to be listed on the world’s main foreign exchange markets: The London Metal Exchange (LME), Commodity Exchange Market of New York (COMEX) and Shanghai Futures Exchange (SHFE). Copper price is determined by the supply and demand dynamics on the metal exchanges, especially the London Metal Exchange. Although it may be strongly influenced by the currency exchange rate and the investment flow, the factors that can cause fluctuations in volatile prices are partially associated with changes in the activity of the economic cycle [
1].
There are many reasons for wanting to make predictions about the price of copper. On the one hand, copper, among other natural elements (e.g., silver), has a high electrical and thermal conductivity. On the other hand, it is cheaper than silver and more resistant to corrosion. Therefore, copper is the preferred metal option for electrical and electronic applications, both domestically and for more general industrial uses. Given the importance of the construction and telecommunications sectors in a modern economy, the changes in copper price can be perceived as an early indicator of global economic performance and have a significant impact factor on the performance of related companies [
2].
With regard to the copper market, any variation in its demand translates entirely into price fluctuations. Market participants see it as an early sign of changes in global production. Thus, it affects mining companies in their investment plans, traders, investors, agents involved in the copper mining business and governments dependent on the copper mining industry. To illustrate this, we can consider the particular case of Chile. As the world’s leading copper producer and exporter, Chile produced an estimated 5.6 million metric tons of copper in 2019 [
3]. The Chilean government made copper the main point of reference for the country’s structural budget rule introduced in 2000, trying to reduce the exposure of fluctuations in Chile’s gross domestic product (GDP) to the oscillation of the price of copper [
4].
There are several studies which currently include copper (and other metals) as one of the products of interest in the evaluations of the prediction to improve the forecasts of price, such as [
5,
6,
7,
8,
9]. Our study applies a copper price prediction technique using support vector regression (SVR) [
10,
11,
12]. This work explores the potential of the SVR with external recurrences to make predictions at 5, 10, 15, 20 and 30 days into the future in the copper closing price at the London Metal Exchange. The best model for each forecast interval is performed using a grid search and balanced cross-validation.
The paper is distributed as follows:
Section 2 presents the related works.
Section 3 presents the proposed model. The data used and the methodology are presented in
Section 4 and
Section 5, respectively.
Section 6 shows the results and analysis.
Section 7 shows the discussion. Finally,
Section 8 presents the conclusions.
2. Related Works
In the general case of the financial time series, the support vector machine (SVM) and SVR methods are widely used for making forecasts [
13]. Basically, when the SVM method extends to nonlinear regression problems, it is called SVR [
10,
11,
12]. The SVR method belonging to the field of data statistics was first proposed by Vapnik et al. [
10] at the end of the twentieth century. A characteristic of this method is that it solves the problems of “high dimensionality” and “overlearning” to a certain degree. Furthermore, it achieves a significant effect in solving the problem of small samples. Consequently, support vector regression is used to solve the prediction problems of nonlinear data in engineering areas.
It is important to consider some works, such as the work done by Kim [
14], which presents daily forecasts (using SVR) of the trend of change in the Korean Composite Stock Price Index (KOSPI), in which it uses 2928 days of data between January 1989 and December 1998. In another work, Kao et al. [
15] use SVR to predict the stock index of the São Paulo State Stock Exchange (BOVESPA), the Shanghai Stock Exchange Composite (SSEC) and the Dow Jones, using data from April 2006 to April 2010. Similarly, Kazem et al. [
16] predict the market prices of Microsoft, Intel and the National Bank shares using a set of data from November 2007 to November 2011. In these works, the prediction is always a day before and depends on a certain amount of past data (
l), i.e., if
is the price foretold in
, it has
.
Additionally, we must consider the work of Patel et al. [
17], which proposes to make predictions 10, 15 and 30 days in advance using a two-stage system based on SVR, neural networks and random forests, which are trained with nine technical indexes. Among these indicators is the stochastic index
, that compares the closing price at a particular time with the price range during a given period, and
, which is the first moving average. In addition, it uses the relative strength index (RSI) that indicates the price change rate and the average data rate, among others. The author uses historical data from January 2003 to December 2012 of the CNX Nifty stock index and S&P BSE Sensex.
On the other hand, several studies include copper and other metals as products of interest in the evaluations of the prediction to improve the forecasts of price. Such studies employ different methods and mathematical models such as autoregressive integrated moving average (ARIMA) models combined with wavelets [
18], meta-heuristics models [
19,
20], neural networks models [
2,
21] and hybrid models [
5,
6,
7,
8,
9]. The Fourier transform [
22] is used to analyze the variability of the prices of various metals. In addition, there are works in the literature that study the relationships of commodity and asset price models, such as the case of oil prices and their effects on copper and silver prices [
23].
3. Support Vector Regression Model
Given a data set of
N elements
, where
is the
i-th element in a space of
n dimensions,
and
(
) is the actual value for
, a nonlinear function is defined as
. To map the entry data,
is an
space of high dimension called space of features that determines the nonlinear transformation
. So, in a high-dimensional space, there exists a linear function
f that makes it possible to relate the entry data
and output
. That linear function, the SVR function, is presented in Equation (
1),
where
represents the foretold values;
and
. The SVR minimizes the empiric risk, shown in Equation (
2)
where
is a cost function. In the case of the
-SVR, a loss function
-insensitive is used [
10,
24], defined in Equation (
3),
is used to determine the nonlinear function
in the
space to find a function that can fit current training data with a deviation less than or equal to
(see
Figure 1a). This function minimizes the training error between the data training, and the function
-insensitive is provided by Equation (
4) [
11,
25].
subject to restrictions (for all,
):
Equation (
4) punishes the training errors of
and
Y through the function
-insensitive (
Figure 1b). The parameter
C determines the compromise between the complexity of the model, expressed by the vector
W and the points that fulfill the condition
in Equation (
3). If
, the model has a small margin and is adjusted to the data. If
, the model has a big margin, which is why it is softened. Finally,
represents the training errors greater than
and
the errors less than
(see
Figure 1a).
To solve this regression problem, we can replace the internal product of Equation (
1) by functions of kernel
. This makes it possible to perform such an operation in a superior dimension, using low-dimensional space data input without knowing the transformation
[
26], as it is shown in Equation (
6). This is called the kernel trick.
The parameters
and
are Lagrange multipliers associated with the problem of quadratic optimization. Several types of functions can be used as kernel [
27], but in this work, we will be using the Gaussian function of a radial base (RBF) [
28]:
The parameters of the kernel function, the regularization constant C and of the loss function are considered the parameters of design for the SVR to use. Furthermore, they are obtained from a data set that is different from the training data.
4. Data Description
There are three major stock exchanges where the copper is traded: LME, COMEX and SHFE. Similar to [
6,
7], we use the price of copper given by LME, which is widely considered as a reference index for world prices of this metal [
29]. The time series used in this research has 2971 daily data of copper prices in US dollars per metric ton from 2 January 2006 until 2 January 2018, as shown in
Figure 2. (These data were obtained through a trial subscription on
www.lme.com in January 2018. Currently, a membership must be paid for to get updated data.) Similar time ranges of copper price have been used in [
6,
7,
20].
5. Methodology
The methodology used in this research contains four steps. Step 1 is focused on preparing the data. Steps 2 and 3 explain the training and prediction stages. Finally, step 4 details the performance measures used.
5.1. Step 1: Data Pre-Processing
In the first place, the data is normalized with the min–max normalization (MMN) method [
30] within the range of 0 to 1. Then, a suitable range has to be determined for the SVR hyperparameter
, which is related to the margin of tolerance of punishment for errors in training. For this, it is necessary to know the level of noise
N that the time series has. It has an average
= 3.66 ×
, a root-mean-square value
and a range between
. These characteristics allow us to define a conservative interval for
.
Finally, the series of
Figure 2 is divided into two series,
and
, each one with 50% of the data, which will be used for training and evaluating alternately.
5.2. Step 2: Parameters Adjust and Training
In the case of the prediction of time series with SVR, it is assumed that the actual value
is a function of its previous
L values
and the hyperparameter of the SVR
. Hence, the model has four parameters:
L, the number of prior values to predict the actual value and the three hyperparameters of the SVR. The range of each one is shown in
Table 1.
The
i-th model of the SVR (
) is defined by the set of parameters
. To adjust these parameters, it is made into a grid search, according to the recommendation of Hsu et al. [
31] and its computational design shows in Algorithm 1. For all combinations of parameters
, the model
is trained with the series
and is tested with the series
, and vice versa. Then, for each training and testing, the set of parameters
with the least mean squared error (MSE) between the predicted and the original data is selected. This process of training/testing is made using the balanced cross-validation method proposed by McCarthy [
32].
| Algorithm 1: Algorithm design for grid search to find the best testing models. |
![Applsci 10 06648 i001 Applsci 10 06648 i001]() |
5.3. Step 3: Prediction
To make the prediction at
days,
(with its best set of parameters
) takes a vector of
past values, taking into account the previous predicted values if they correspond with
as the value to predict in
days and
being the vector that contains the previous
values that are used in the prediction. Then, you have
and
given by the expression of Equation (
8).
5.4. Step 4: Performance Measures
For each prediction interval, the effectiveness of the prediction model will be determined through performance measures such as MSE and RMSE. These performance measures have been used in previous prediction work [
33,
34,
35]. Furthermore, the correlation coefficient between the predicted value and the actual value will be used. The computational design of step 3 and step 4 is shown in Algorithm 2.
| Algorithm 2: Algorithm design for the prediction and performance measures steps. |
![Applsci 10 06648 i002 Applsci 10 06648 i002]() |
For the implementation of the training and adjustment system, R, version 3.4.4 was used with the library
e1071 [
36] for the basic training functions and the library
doParallel [
37] for parallelizing the search of parameters.
Shapiro–Wilk normality tests will be used to (1) select the correlation coefficient (Pearson or Spearman) between the predicted values and the real values of the time series and (2) select the method of comparison of the means (Wilcoxon rank-sum test or two-sample t-test) of the errors for the different prediction time horizons. For all tests, a p-value < 0.05 is considered significant.
6. Results and Analysis
In the experiments, the best models were explored in a grid choosing the best (MSE minor) for each
p prediction interval.
Table 2 shows the parameters for the best SVR, according to the MSE index, for each prediction interval of
p according to the training set and test. Additionally, the correlation index
between the real data and the predicted data and the root-mean-square error (RMSE) is shown. In
Table 2,
means that to train the SVR, the set
is used, and it is tested in the set
, with
, where
p is the prediction interval, with
.
It is interesting to note that the amount of previous data (
L) is independent of the prediction interval that is made, as well as the parameters of the SVR that remain practically intact. The adjustment capacity for the five-day prediction of the
time series for the 2017 period is shown in
Figure 3.
The best prediction capacity is obtained during the training with the series
, which is temporarily the oldest. The training could have been enhanced due to the level of noise of this series. The RMS value of the noise of series
is
, which is higher than the one of the series
,
. For example, for a five-day prediction, training with
gives
if training with
,
. Furthermore, the dispersion of the MSE is less compared to the training based on the most recent part of the series (see
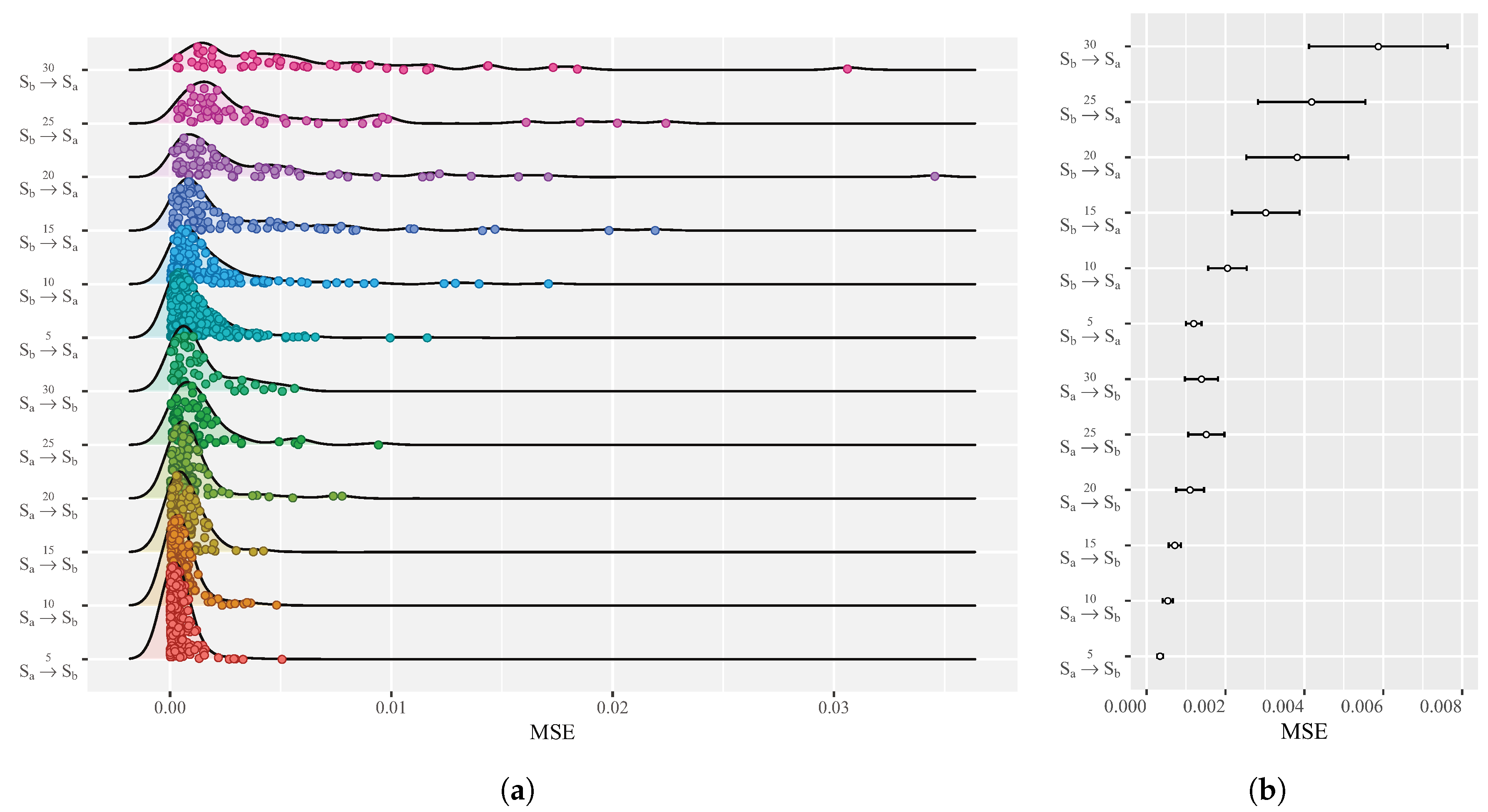
Figure 4a).
In
Figure 4a, we show the distribution of the MSE obtained in the predictions summarized in
Table 2, which will allow us to evaluate the capabilities of prediction statistically. In addition, the confidence intervals are shown in
Figure 4b, with a 5% significance for the mean estimation of the MSE of the sample obtained from the simulation—that is, intervals built at 95% confidence.
Table 3 presents the differences of means of the MSE between groups in the lower triangle, and the symbols of confidence indicators in the upper triangle. With concern to the combination of pairs in the test of the hypothesis of mean differences for MSE, it is obtained in the simulation for the different prediction time intervals and the two time series
and
. Furthermore, the average difference of the MSE can be visually appreciated according to the 95% confidence interval (see
Figure 4b). The previous results are presented in
Figure 4b and
Table 3. For the comparison of means of the MSE between groups, the Wilcoxon rank-sum test was used, because according to the Shapiro–Wilk test, they do not fit a normal distribution, with
p-value ≤ 1.73 × 10
for all groups.
7. Discussion
As a result of the search for training parameters for the SVR models and the search for the best prediction models for different forecasting intervals, it was determined that the amount of previous data of the time series that are needed (
for the best models) is independent of the prediction interval. Similar values have been used in the literature in similar time series, but without justification based on a parameter search that minimizes the prediction error. For example, a value of
is used in [
8,
9],
in [
5] and
in [
15].
Our results show that the presented model is able to predict copper price volatilities near reality (see
Figure 3). Similar results are obtained compared to other works, such as:
In [
9], an analysis on the dynamics of real prices for main industrial metals is presented. Using monthly data, the authors estimated linear and threshold autoregressive models. For the nonlinear models, they assumed that the dynamics of metal prices depend on their deviation from the recursive mean. We use a monthly prediction (30 days) to compare the best RMSE value obtained in both works. Our RMSE (
) is similar to the RMSE (
) obtained in that work.
In [
8], the authors use time series models to predict the prices of Shanghai copper futures. This work introduces the application of X12-ARIMA-GARCH family models in futures price analysis and forecasting. To compare their results with ours, we use a short prediction period (5 and 10 days) and compare the RMSE obtained. In the same period, our RMSE (
and
) are similar to the RMSE (
and
) in that work.
In [
5], a hybrid model is proposed to provide an accurate model for predictions of copper prices. The proposed model combines the adaptive neuro-fuzzy inference system and genetic algorithm. Our work presents an RMSE (
) similar to the GA-ANFIS method (
), presented in that work. This is due to the granularity of the training and prediction data. It is interesting to note that in that work, a method based on SVM is shown whose error (
) is high compared to our work. The difference is that in our work, a regression was used with an exhaustive search of its parameters.
In [
20], a Bat algorithm was used to predict the copper price volatility. The copper price was estimated using time series and Bat algorithms. The time series function used in this work is similar in our work. Under those conditions, the prediction error is
. With the method proposed in this work, a maximum error of
is achieved (see
Table 2).
Finally, we can observe in
Figure 4a that there are significant differences of the MSE at 95% confidence, between
and
in each of the prediction intervals 5, 10, 15, 20, 25 and 30 days. In contrast, for the prediction
, there are no significant differences in the MSE between the prediction intervals 5, 10, 15, 20, 25 and 30 days. This allows us to show the robustness of the prediction in the short and medium-term since the prediction at the five-day interval has not lost performance over the 30-day prediction interval, considering it, in this case, as a medium-term. This is useful for the decision-making process for mining companies and traders. On the other hand, to affect the decision-making process for investors and the government, it is necessary to have reliable long-term forecasts.
8. Conclusions
In this work, the construction of a model was presented based on SVR that allows making a prediction of the closing value of copper in the Metal London Stock Exchange, as the RMSE was equal to or less than the for prediction periods of 5 and 10 days. The method consists of finding the best model through a search in a grid, wherein each model is trained and tested through use of the balancing methods in cross-validation. For the training process, only the data of closing price of the series are used. The results indicate that the model of the SVR can be used regardless of the number of days of the prediction, and this can be done with only three actual values.Additionally, we observed that more current data negatively impact the MSE. This phenomenon must be studied in the future, but there is a signal that this can be explained through the level of noise and the amount of data of the training time series.
The importance of price prediction will depend on the interest of the agents and their objectives in short, medium and long-term prediction periods. Our work aims for short-term predictions of 5 days, 10, ..., up to 30 days. These predictions will interest brokers and investors who seek to take advantage of the periodic variations with active portfolio management. For medium-term predictions, such as monthly and annual predictions, governments may be more interested in their national budget, as is the case in Chile, which is an economy whose income and tax revenues come from copper mining. In the long-term (more than one year), investors and mining companies will be more interested in their long-term investment plans, such as the process of improvement, expansion, a search of new deposits that give value to their investments, or institutional or private investors with long-term investment horizons with buy and hold investment strategies.
For future work, it is necessary to apply the method to other time series of the stock index—for example, Standard & Poor’s 500 (S&P 500), Dow Jones, National Association of Securities Dealers Automated Quotation (NASDAQ) and BOVESPA. Furthermore, we can apply the method to others commodities like gold, silver, brent crude oil and corn to determine if it is possible to make forecasts with an error margin similar to the one found in this work.
Author Contributions
Conceptualization, G.A., R.C. and M.C.; formal analysis, G.A.; funding acquisition, M.C.; investigation, G.A. and R.C.; methodology, G.A., R.C., C.F.-C. and M.C.; project administration, M.C.; software, G.A. and R.C.; supervision, M.C.; validation, C.F.-C.; visualization, G.A. and R.C.; writing—original draft, G.A. and R.C.; writing—review and editing, C.F.-C. All authors have read and agreed to the published version of the manuscript.
Funding
This research is parcialy founded for Fondecyt project #1181659.
Acknowledgments
We are grateful to the Universidad de Santiago de Chile (USACH) and to Parcialy founded for Fondecyt project #1181659. Furthermore, the authors thank Paul Soper for the style correction of the language. Finally, the authors thank the referees for their valuable comments, which greatly improved the content and readability of the work.
Conflicts of Interest
The authors declare that there is no conflict of interest in the publication of this paper.
Abbreviations
The following abbreviations are used in this manuscript:
| ARIMA | Autoregressive integrated moving average |
| BOVESPA | São Paulo State Stock Exchange |
| COMEX | Commodity Exchange Market of New York |
| GDP | Gross domestic product |
| KOSPI | Korean Composite Stock Price Index |
| LME | London Metal Exchange |
| MMN | Min–max normalization |
| MSE | Mean squared error |
| NASDAQ | National Association of Securities Dealers Automated Quotation |
| RBF | Gaussian function of a radial base |
| RMSE | Root-mean-square error |
| RSI | Relative strength index |
| SHFE | Shanghai Futures Exchange |
| S&P 500 | Standard & Poor’s 500 |
| SSEC | Shanghai Stock Exchange Composite |
| SVM | Support vector machine |
| SVR | Support vector regression |
References
- Oglend, A.; Asche, F. Cyclical non-stationarity in commodity prices. Empir. Econ. 2016, 51, 1465–1479. [Google Scholar] [CrossRef]
- Lasheras, F.S.; de Cos Juez, F.J.; Sánchez, A.S.; Krzemień, A.; Fernández, P.R. Forecasting the COMEX copper spot price by means of neural networks and ARIMA models. Resour. Policy 2015, 45, 37–43. [Google Scholar] [CrossRef]
- Ebert, L.; Menza, T.L. Chile, copper and resource revenue: A holistic approach to assessing commodity dependence. Resour. Policy 2015, 43, 101–111. [Google Scholar] [CrossRef]
- Spilimbergo, A. Copper and the Chilean Economy, 1960–1998. Policy Reform 2002, 5, 115–126. [Google Scholar] [CrossRef]
- Alameer, Z.; Abd Elaziz, M.; Ewees, A.A.; Ye, H.; Jianhua, Z. Forecasting copper prices using hybrid adaptive neuro-fuzzy inference system and genetic algorithms. Nat. Resour. Res. 2019, 28, 1385–1401. [Google Scholar] [CrossRef]
- Hu, Y.; Ni, J.; Wen, L. A hybrid deep learning approach by integrating LSTM-ANN networks with GARCH model for copper price volatility prediction. Phys. A Stat. Mech. Appl. 2020, 557, 124907. [Google Scholar] [CrossRef]
- García, D.; Kristjanpoller, W. An adaptive forecasting approach for copper price volatility through hybrid and non-hybrid models. Appl. Soft Comput. 2019, 74, 466–478. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Z. Research on Shanghai Copper Futures Price Forecast Based on X12-ARIMA-GARCH Family Models. In Proceedings of the 2020 International Conference on Computer Information and Big Data Applications (CIBDA), Guiyang, China, 17–19 April 2020; pp. 304–308. [Google Scholar]
- Rubaszek, M.; Karolak, Z.; Kwas, M. Mean-reversion, non-linearities and the dynamics of industrial metal prices. A forecasting perspective. Resour. Policy 2020, 65, 101538. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995; p. 188. [Google Scholar] [CrossRef]
- Drucker, H.; Burges, C.J.; Kaufman, L.; Smola, A.; Vapnik, V. Support vector regression machines. Adv. Neural Inf. Process. Syst. 1997, 9, 155–161. [Google Scholar]
- Vapnik, V.; Golowich, S.E.; Smola, A.J. Support Vector Method for Function Approximation, Regression Estimation and Signal Processing. In Advances in Neural Information Processing Systems 9; Mozer, M.C., Jordan, M.I., Petsche, T., Eds.; MIT Press: Cambridge, MA, USA, 1997; pp. 281–287. [Google Scholar]
- Jaramillo, J.A.; Velásquez, J.D.; Franco, C.J. Research in Financial Time Series Forecasting with SVM: Contributions from Literature. IEEE Latin Am. Trans. 2017, 15, 145–153. [Google Scholar] [CrossRef]
- Kim, K.J. Financial time series forecasting using support vector machines. Neurocomputing 2003, 55, 307–319. [Google Scholar] [CrossRef]
- Kao, L.J.; Chiu, C.C.; Lu, C.J.; Chang, C.H. A hybrid approach by integrating wavelet-based feature extraction with MARS and SVR for stock index forecasting. Decis. Support Syst. 2013, 54, 1228–1244. [Google Scholar] [CrossRef]
- Kazem, A.; Sharifi, E.; Hussain, F.K.; Saberi, M.; Hussain, O.K. Support vector regression with chaos-based firefly algorithm for stock market price forecasting. Appl. Soft Comput. J. 2013, 13, 947–958. [Google Scholar] [CrossRef]
- Patel, J.; Shah, S.; Thakkar, P.; Kotecha, K. Predicting stock market index using fusion of machine learning techniques. Expert Syst. Appl. 2015, 42, 2162–2172. [Google Scholar] [CrossRef]
- Kriechbaumer, T.; Angus, A.; Parsons, D.; Rivas Casado, M. An improved wavelet-ARIMA approach for forecasting metal prices. Resour. Policy 2014, 39, 32–41. [Google Scholar] [CrossRef]
- Seguel, F.; Carrasco, R.; Adasme, P.; Alfaro, M.; Soto, I. A Meta-heuristic Approach for Copper Price Forecasting. In Information and Knowledge Management in Complex Systems; IFIP Advances in Information and Communication Technology; Liu, K., Nakata, K., Li, W., Galarreta, D., Eds.; Springer International Publishing: Toulouse, France, 2015; Volume 449, pp. 156–165. [Google Scholar] [CrossRef]
- Dehghani, H.; Bogdanovic, D. Copper price estimation using bat algorithm. Resour. Policy 2018. [Google Scholar] [CrossRef]
- Carrasco, R.; Vargas, M.; Soto, I.; Fuentealba, D.; Banguera, L.; Fuertes, G. Chaotic time series for copper’s price forecast: Neural networks and the discovery of knowledge for big data. In Digitalisation, Innovation, and Transformation; Liu, K., Nakata, K., Li, W., Baranauskas, C., Eds.; Springer: Cham, Switzerland; London, UK, 2018; Volume 527, pp. 278–288. [Google Scholar] [CrossRef]
- Khalifa, A.; Miao, H.; Ramchander, S. Return distributions and volatility forecasting in metal futures markets: Evidence from gold, silver, and copper. J. Futures Mark. 2011, 31, 55–80. [Google Scholar] [CrossRef]
- Fernandez-Perez, A.; Fuertes, A.M.; Miffre, J. Harvesting Commodity Styles: An Integrated Framework. In Proceedings of the INFINITI Conference on International Finance, València, Spain, 11–12 June 2017. [Google Scholar]
- Cristianini, N.; Shawe-Taylor, J. An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Shokri, S.; Sadeghi, M.T.; Marvast, M.A.; Narasimhan, S. Improvement of the prediction performance of a soft sensor model based on support vector regression for production of ultra-low sulfur diesel. Pet. Sci. 2015, 12, 177–188. [Google Scholar] [CrossRef]
- Wu, C.H.; Ho, J.M.; Lee, D.T. Travel-time prediction with support vector regression. IEEE Trans. Intell. Transp. Syst. 2004, 5, 276–281. [Google Scholar]
- Yeh, C.Y.; Huang, C.W.; Lee, S.J. A multiple-kernel support vector regression approach for stock market price forecasting. Expert Syst. Appl. 2011, 38, 2177–2186. [Google Scholar] [CrossRef]
- Vert, J.P.; Tsuda, K.; Schölkopf, B. A primer on kernel methods. Kernel Methods Comput. Biol. 2004, 47, 35–70. [Google Scholar]
- Watkins, C.; McAleer, M. Econometric modelling of non-ferrous metal prices. J. Econ. Surv. 2004, 18, 651–701. [Google Scholar] [CrossRef]
- Singh, D.; Singh, B. Investigating the impact of data normalization on classification performance. Appl. Soft Comput. J. 2019. [Google Scholar] [CrossRef]
- Hsu, C.W.; Chang, C.C.; Lin, C.J. A Practical Guide to Support Vector Classification; Technical Report; National Taiwan University: Taipei, Taiwan, 2003. [Google Scholar]
- McCarthy, P.J. The Use of Balanced Half-Sample Replication in Cross-Validation Studies. J. Am. Stat. Assoc. 1976, 71, 596–604. [Google Scholar] [CrossRef]
- Atsalakis, G.S. Using computational intelligence to forecast carbon prices. Appl. Soft Comput. 2016, 43, 107–116. [Google Scholar] [CrossRef]
- Henríquez, J.; Kristjanpoller, W. A combined Independent Component Analysis–Neural Network model for forecasting exchange rate variation. Appl. Soft Comput. 2019, 83, 105654. [Google Scholar] [CrossRef]
- Kim, H.Y.; Won, C.H. Forecasting the volatility of stock price index: A hybrid model integrating LSTM with multiple GARCH-type models. Expert Syst. Appl. 2018, 103, 25–37. [Google Scholar] [CrossRef]
- Meyer, D.; Dimitriadou, E.; Hornik, K.; Weingessel, A.; Leisch, F.; Chang, C.C.; Lin, C.C. e1071: Misc Functions of the Department of Statistics, Probability Theory Group (Formerly: E1071), TU Wien. R Package Version 1.7-3. 2019. Available online: https://CRAN.R-project.org/package=e1071 (accessed on 26 November 2019).
- Analytics, R.; Weston, S. doParallel: Foreach Parallel Adaptor for the Parallel Package, R Package Version 1.0.14; 2014. Available online: https://CRAN.R-project.org/package=doParallel (accessed on 2 August 2019).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).