Buckling of Planar Micro-Structured Beams
Abstract
1. Introduction
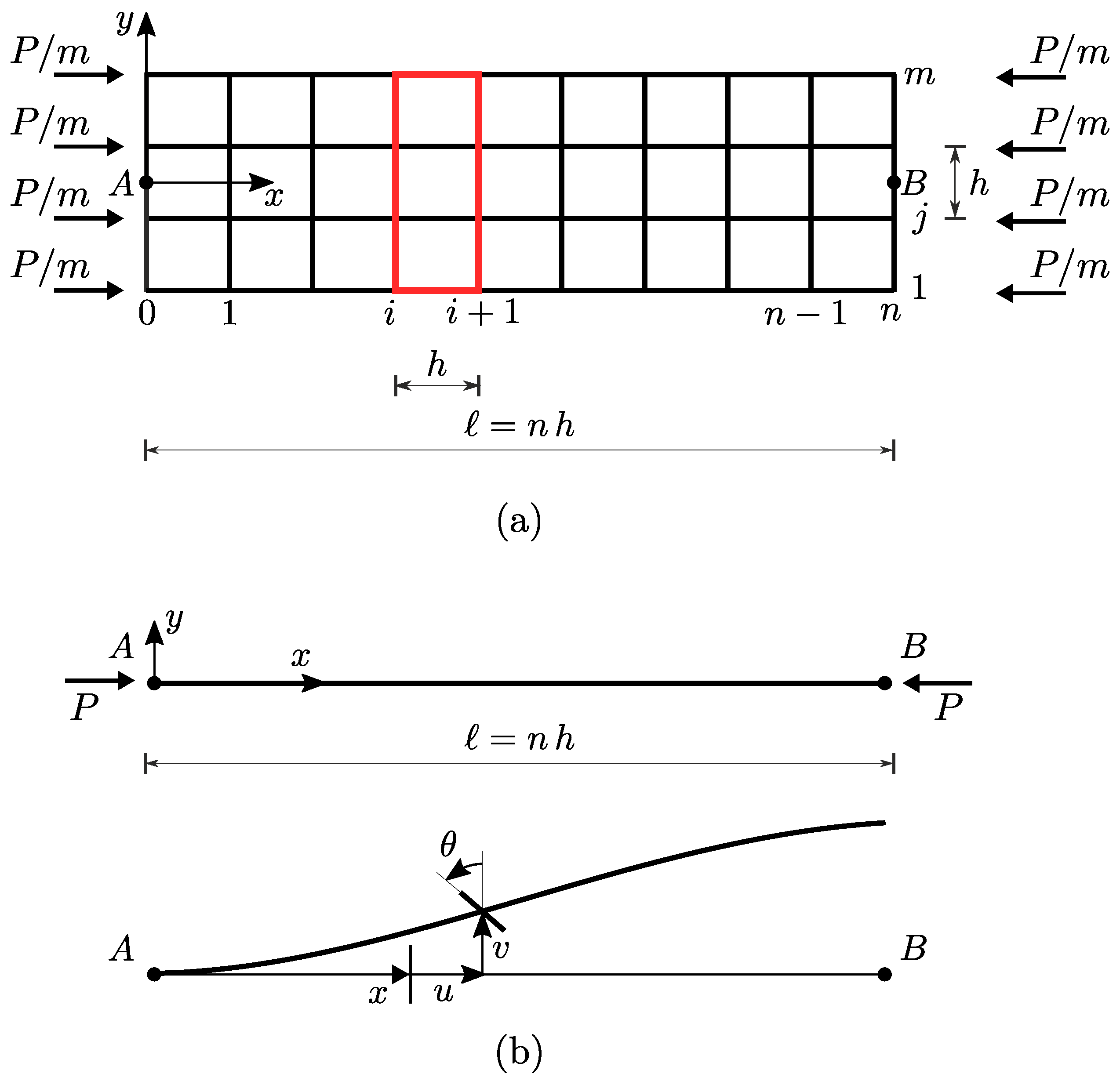
2. Model
- clamp (C) at H: ;
- hinge (H) at H: ;
- horizontal roller (R) at H: ;
- horizontal slider (S) at H: .
- free (F) at H: ;
- hinge (H) at H: ;
- horizontal roller (R) at H: ;
- horizontal slider (S) at H: .
- hinge at A, horizontal roller at B (H-R):
- clamp at A, free at B (C-F):
- clamp at A, horizontal roller at B (C-R):
- clamp at A, horizontal slider at B (C-S):
- finding the general solution of Equation (7)-a, namely the characteristic exponents , , with f a function of P, and the associated eigenvectors, which depends on four arbitrary constants;
- enforcing the boundary conditions (7)-b,c, which provide a (homogeneous) system of linear algebraic equations in the four arbitrary constants;
- zeroing the determinant of the matrix of the coefficients of the linear system, which gives a transcendent equation in P, whose smallest root is .
3. Elastic and Inertial Constant Identifications
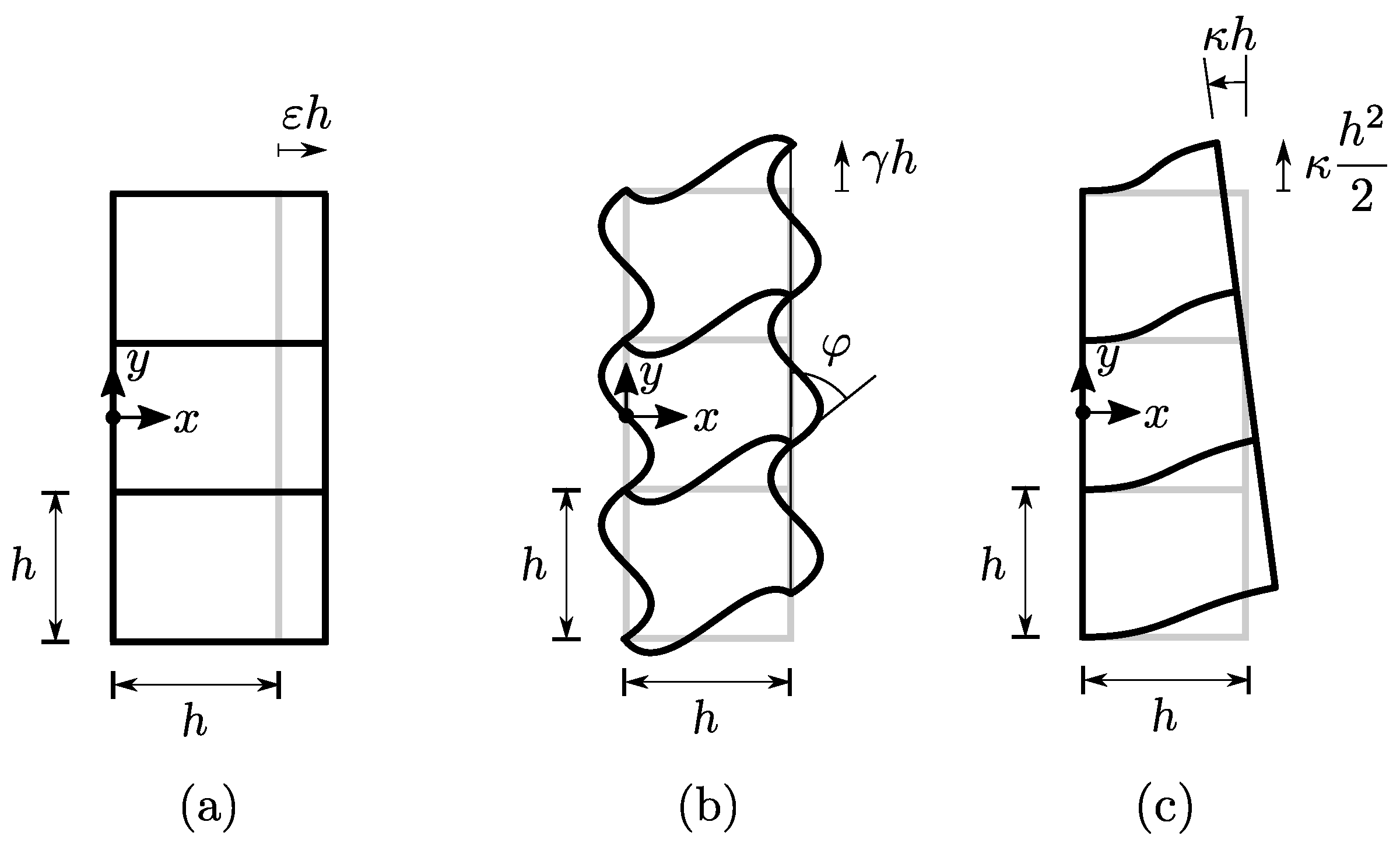
- an extensional mode (), in which axially translates;
- a shear mode (), in which transversely translates;
- a flexural modes (), in which rotates around the z-axis and transversely translates.
Analytical Identification of the Elastic Constants
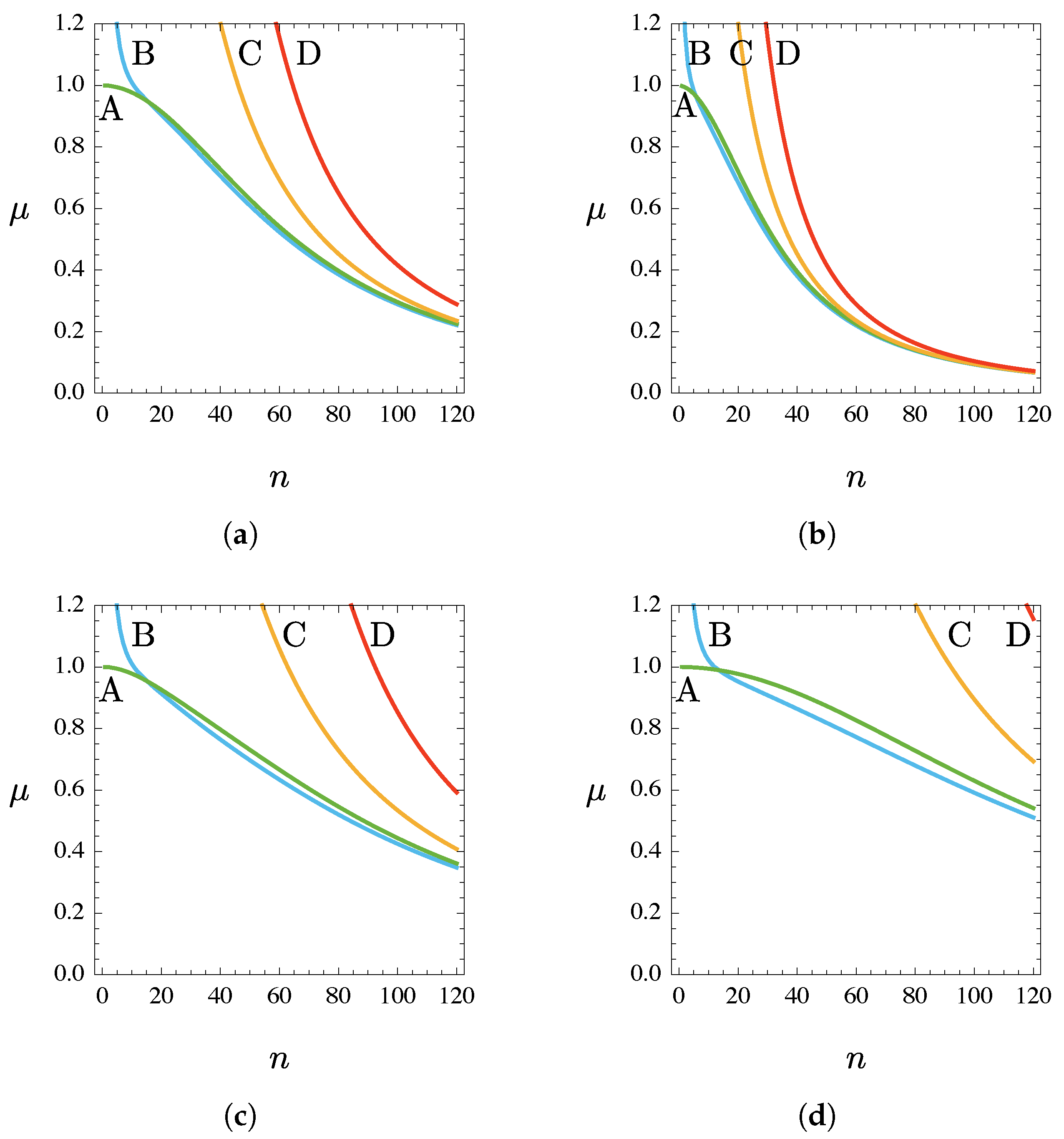
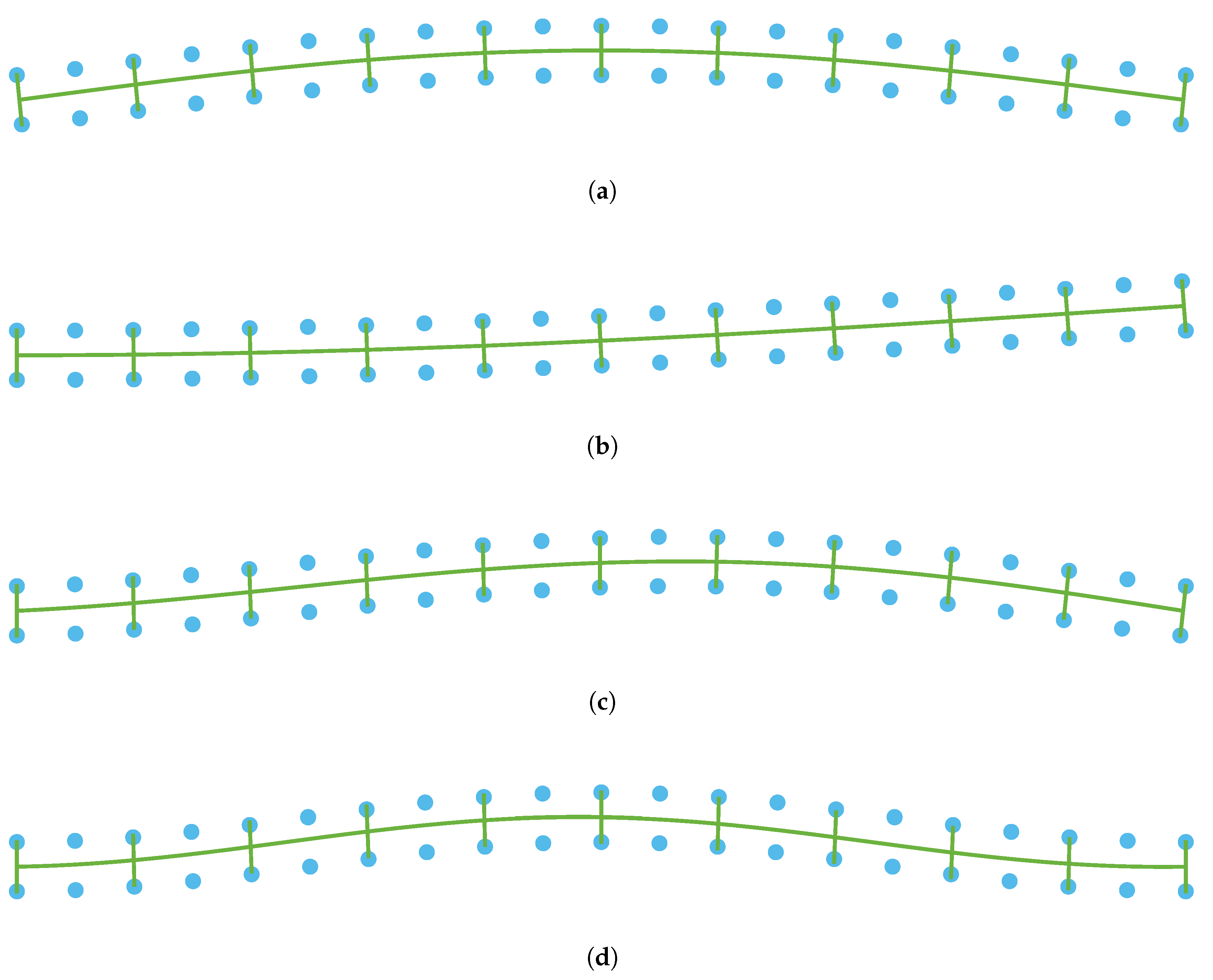
4. Numerical Results
5. Conclusions and Perspectives
- An excellent agreement between the critical loads and modes of the equivalent beam model, with respect to finite-element analyses has been found, providing a sufficient number of cell is considered. This finding is independent from the boundary conditions.
- The geometric effect of the prestress has been introduced both in the equilibrium and constitutive equations of the coarse model. The second aspect, accounting for micro-effects, is shown to be crucial to correctly describe the buckling behavior of the here analyzed micro-structured beams.
- The corrective factors provide a significant correction of the elastic operator, revealing their essential contribution in the proper modeling of planar grid beams.
Author Contributions
Funding
Conflicts of Interest
References
- Maconachie, T.; Leary, M.; Lozanovski, B.; Zhang, X.; Qian, M.; Faruque, O.; Brandt, M. SLM lattice structures: Properties, performance, applications and challenges. Mater. Des. 2019, 183, 108137. [Google Scholar] [CrossRef]
- Nazir, A.; Abate, K.M.; Kumar, A.; Jeng, J.Y. A state-of-the-art review on types, design, optimization, and additive manufacturing of cellular structures. Int. J. Adv. Manuf. Technol. 2019, 104, 3489–3510. [Google Scholar] [CrossRef]
- Ngo, T.D.; Kashani, A.; Imbalzano, G.; Nguyen, K.T.Q.; Hui, D. Additive manufacturing (3D printing): A review of materials, methods, applications and challenges. Compos. Part B Eng. 2018, 143, 172–196. [Google Scholar] [CrossRef]
- Mieszala, M.; Hasegawa, M.; Guillonneau, G.; Bauer, J.; Raghavan, R.; Frantz, C.; Kraft, O.; Mischler, S.; Michler, J.; Philippe, L. Micromechanics of amorphous metal/polymer hybrid structures with 3D cellular architectures: Size effects, buckling behavior, and energy absorption capability. Small 2017, 13, 1602514. [Google Scholar] [CrossRef]
- Eugster, S.; Steigmann, D.; Dell’Isola, F. Continuum theory for mechanical metamaterials with a cubic lattice substructure. Math. Mech. Complex Syst. 2019, 7, 75–98. [Google Scholar] [CrossRef]
- Barchiesi, E.; Spagnuolo, M.; Placidi, L. Mechanical metamaterials: A state of the art. Math. Mech. Solids 2019, 24, 212–234. [Google Scholar] [CrossRef]
- Vangelatos, Z.; Komvopoulos, K.; Grigoropoulos, C.P. Vacancies for controlling the behavior of microstructured three-dimensional mechanical metamaterials. Math. Mech. Solids 2019, 24, 511–524. [Google Scholar] [CrossRef]
- Casalotti, A.; D’Annibale, F.; Rosi, G. Multi-scale design of an architected composite structure with optimized graded properties. Compos. Struct. 2020, 112608. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F.; Zhang, J.; Triantafillou, T.C. Failure surfaces for cellular materials under multiaxial loads I. Modelling. Int. J. Mech. Sci. 1989, 31, 635–663. [Google Scholar] [CrossRef]
- Triantafillou, T.C.; Zhang, J.; Shercliff, T.L.; Gibson, L.J.; Ashby, M.F. Failure surfaces for cellular materials under multiaxial loads II. Comparison of models with experiment. Int. J. Mech. Sci. 1989, 31, 665–678. [Google Scholar] [CrossRef]
- Triantafyllidis, N.; Schraad, M.W. Onset of failure in aluminum honeycombs under general in-plane loading. J. Mech. Phys. Solids 1998, 46, 1089–1124. [Google Scholar] [CrossRef]
- Zhu, H.X.; Mills, N.J. The in-plane non-linear compression of regular honeycombs. Int. J. Solids Struct. 2000, 37, 1931–1949. [Google Scholar] [CrossRef]
- Chung, J.; Waas, A.M. In-plane biaxial crush response of polycarbonate honeycombs. J. Eng. Mech. 2001, 127, 180–193. [Google Scholar] [CrossRef]
- Yang, M.Y.; Huang, J.S. Elastic buckling of regular hexagonal honeycombs with plateau borders under biaxial compression. Compos. Struct. 2005, 71, 229–237. [Google Scholar] [CrossRef]
- Cricrì, G.; Perrella, M.; Calì, C. Honeycomb failure processes under in-plane loading. Compos. Part B Eng. 2013, 45, 1079–1090. [Google Scholar] [CrossRef]
- Ohno, N.; Okumura, D.; Niikawa, T. Long-wave buckling of elastic square honeycombs subject to in-plane biaxial compression. Int. J. Mech. Sci. 2004, 46, 1697–1713. [Google Scholar] [CrossRef]
- He, Y.; Zhou, Y.; Liu, Z.; Liew, K.M. Buckling and pattern transformation of modified periodic lattice structures. Extreme Mech. Lett. 2018, 22, 112–121. [Google Scholar] [CrossRef]
- Hu, N.; Burgueño, R. Buckling-induced smart applications: Recent advances and trends. Smart Mater. Struct. 2015, 24, 063001. [Google Scholar] [CrossRef]
- Askar, A.; Cakmak, A.S. A structural model of a micropolar continuum. Int. J. Eng. Sci. 1968, 6, 583–589. [Google Scholar] [CrossRef]
- Noor, A.K. Continuum modeling for repetitive lattice structures. Appl. Mech. Rev. 1988, 41, 285–296. [Google Scholar] [CrossRef]
- Tollenaere, H.; Caillerie, D. Continuous modeling of lattice structures by homogenization. Adv. Eng. Softw. 1998, 29, 699–705. [Google Scholar] [CrossRef]
- Boutin, C.; dell’Isola, F.; Giorgio, I.; Placidi, L. Linear pantographic sheets: Asymptotic micro-macro models identification. Math. Mech. Complex Syst. 2017, 5, 127–162. [Google Scholar] [CrossRef]
- dell’Isola, F.; Eremeyev, V.A.; Porubov, A. Advances in Mechanics of Microstructured Media and Structures; Springer: Berlin, Germany, 2018; Volume 87. [Google Scholar]
- Di Nino, S.; Luongo, A. A simple homogenized orthotropic model for in-plane analysis of regular masonry walls. Int. J. Solids Struct. 2019, 167, 156–169. [Google Scholar] [CrossRef]
- Boutin, C.; Hans, S.; Chesnais, C. Generalized Beams and Continua. Dynamics of Reticulated Structures. In Mechanics of Generalized Continua: One Hundred Years After the Cosserats; Maugin, G.A., Metrikine, A.V., Eds.; Springer: New York, NY, USA, 2010; pp. 131–141. [Google Scholar]
- Dos Reis, F.; Ganghoffer, J.F. Construction of micropolar continua from the asymptotic homogenization of beam lattices. Comput. Struct. 2012, 112, 354–363. [Google Scholar] [CrossRef]
- Giorgio, I.; Rizzi, N.L.; Turco, E. Continuum modelling of pantographic sheets for out-of-plane bifurcation and vibrational analysis. Proc. R. Soc. A Math. Phys. Eng. Sci. 2017, 473, 20170636. [Google Scholar] [CrossRef]
- dell’Isola, F.; Seppecher, P.; Spagnuolo, M.; Barchiesi, E.; Hild, F.; Lekszycki, T.; Giorgio, I.; Placidi, L.; Andreaus, U.; Cuomo, M.; et al. Advances in pantographic structures: Design, manufacturing, models, experiments and image analyses. Contin. Mech. Thermodyn. 2019, 31, 1231–1282. [Google Scholar] [CrossRef]
- dell’Isola, F.; Seppecher, P.; Alibert, J.J.; Lekszycki, T.; Grygoruk, R.; Pawlikowski, M.; Steigmann, D.; Giorgio, I.; Andreaus, U.; Turco, E.; et al. Pantographic metamaterials: An example of mathematically driven design and of its technological challenges. Contin. Mech. Thermodyn. 2019, 31, 851–884. [Google Scholar] [CrossRef]
- De Angelo, M.; Barchiesi, E.; Giorgio, I.; Abali, B.E. Numerical identification of constitutive parameters in reduced-order bi-dimensional models for pantographic structures: Application to out-of-plane buckling. Arch. Appl. Mech. 2019, 89, 1333–1358. [Google Scholar] [CrossRef]
- Ohno, N.; Okumura, D.; Noguchi, H. Microscopic symmetric bifurcation condition of cellular solids based on a homogenization theory of finite deformation. J. Mech. Phys. Solids 2002, 50, 1125–1153. [Google Scholar] [CrossRef]
- Chajes, M.J.; Romstad, K.M.; McCallen, D.B. Analysis of multiple-bay frames using continuum model. J. Struct. Eng. 1993, 119, 522–546. [Google Scholar] [CrossRef]
- Chajes, M.J.; Finch, W.W.; Kirby, J.T. Dynamic analysis of a ten-story reinforced concrete building using a continuum model. Comput. Struct. 1996, 58, 487–498. [Google Scholar] [CrossRef]
- Chajes, M.J.; Zhang, L.; Kirby, J.T. Dynamic analysis of tall building using reduced-order continuum model. J. Struct. Eng. 1996, 122, 1284–1291. [Google Scholar] [CrossRef]
- Zalka, K.A. Mode coupling in the torsional-flexural buckling of regular multistorey buildings. Struct. Des. Tall Spec. Build. 1994, 3, 227–245. [Google Scholar] [CrossRef]
- Zalka, K.A. Buckling analysis of buildings braced by frameworks, shear walls and cores. Struct. Des. Tall Spec. Build. 2002, 11, 197–219. [Google Scholar] [CrossRef]
- Boutin, C.; Hans, S. Homogenisation of periodic discrete medium: Application to dynamics of framed structures. Comput. Geotech. 2003, 30, 303–320. [Google Scholar] [CrossRef]
- Hans, S.; Boutin, C. Dynamics of discrete framed structures: A unified homogenized description. J. Mech. Mater. Struct. 2008, 3, 1709–1739. [Google Scholar] [CrossRef]
- Chesnais, C.; Boutin, C.; Hans, S. Structural Dynamics and Generalized Continua. In Mechanics of Generalized Continua; Altenbach, H., Maugin, G., Erofeev, V., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 57–76. [Google Scholar]
- Cluni, F.; Gioffrè, M.; Gusella, V. Dynamic response of tall buildings to wind loads by reduced order equivalent shear-beam models. J. Wind Eng. Ind. Aerodyn. 2013, 123, 339–348. [Google Scholar] [CrossRef]
- Potzta, G.; Kollár, L. Analysis of building structures by replacement sandwich beams. Int. J. Solids Struct. 2003, 40, 535–553. [Google Scholar] [CrossRef]
- Zalka, K.A. Global Structural Analysis of Buildings; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Piccardo, G.; Tubino, F.; Luongo, A. A shear–shear torsional beam model for nonlinear aeroelastic analysis of tower buildings. Zeitschrift für Angewandte Mathematik und Physik 2015, 66, 1895–1913. [Google Scholar] [CrossRef]
- Piccardo, G.; Tubino, F.; Luongo, A. Equivalent nonlinear beam model for the 3-D analysis of shear-type buildings: Application to aeroelastic instability. Int. J. Non-Linear Mech. 2016, 80, 52–65. [Google Scholar] [CrossRef]
- Piccardo, G.; Tubino, F.; Luongo, A. Equivalent timoshenko linear beam model for the static and dynamic analysis of tower buildings. Appl. Math. Model. 2019, 71, 77–95. [Google Scholar] [CrossRef]
- Ferretti, M. Flexural torsional buckling of uniformly compressed beam-like structures. Contin. Mech. Thermodyn. 2018, 30, 977–993. [Google Scholar] [CrossRef]
- D’Annibale, F.; Ferretti, M.; Luongo, A. Shear-shear-torsional homogenous beam models for nonlinear periodic beam-like structures. Eng. Struct. 2019, 184, 115–133. [Google Scholar] [CrossRef]
- Di Nino, S.; Luongo, A. Nonlinear aeroelastic behavior of a base-isolated beam under steady wind flow. Int. J. Non-Linear Mech. 2020, 119, 103340. [Google Scholar] [CrossRef]
- Ferretti, M.; D’Annibale, F.; Luongo, A.; Ferretti, M.; D’Annibale, F.; Luongo, A. Buckling of tower buildings on elastic foundation under compressive tip forces and self-weight. Continuum Mech. Thermodyn. 2020. [Google Scholar] [CrossRef]
- Luongo, A.; Zulli, D. Free and forced linear dynamics of a homogeneous model for beam-like structures. Meccanica 2020, 55, 907–925. [Google Scholar] [CrossRef]
- Luongo, A.; D’Annibale, F.; Ferretti, M. Shear and flexural factors for homogenized beam models of planar frames. Eng. Struct. 2020. submitted. [Google Scholar]
- Ferretti, M.; D’Annibale, F.; Luongo, A. Modeling beam-like planar structures by a one-dimensional continuum: An analytical-numerical method. J. Appl. Comput. Mech. 2020, in press. [Google Scholar]
- Luongo, A. Statics, Dynamics, Buckling and Aeroelastic Stability of Planar Cellular Beams. In Modern Trends in Structural and solid Mechanics; Challamel, N., Kaplunov, J., Takewaki, I., Eds.; ISTE-Wiley: London, UK, 2020. [Google Scholar]
- D’Annibale, F.; Ferretti, M.; Luongo, A. Static and dynamic responses of micro-structured beams. Appl. Sci. 2020. submitted. [Google Scholar]
- Luongo, A.; Zulli, D. Mathematical Models of Beams and Cables; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Elishakoff, I. Handbook on Timoshenko-Ehrenfest Beam and Uflyand-Mindlin Plate Theories; World Scientific: Singapore, 2020. [Google Scholar]
- Antman, S.S. The theory of rods. In Linear Theories of Elasticity and Thermoelasticity; Springer: Berlin, Germany, 1973; pp. 641–703. [Google Scholar]
- Antman, S.S. Nonlinear Problems of Elasticity; Springer: Berlin, Germany, 2005. [Google Scholar]
- Capriz, G. A Contribution to the Theory of Rods. Riv. Mat. Univ. Parma 1981, 7, 489–506. [Google Scholar]
- Altenbach, H.; Bîrsan, M.; Eremeyev, V.A. Cosserat-type rods. In Generalized Continua from the Theory to Engineering Applications; Springer: Berlin, Germany, 2013; pp. 179–248. [Google Scholar]
- Steigmann, D.J.; Faulkner, M.G. Variational theory for spatial rods. J. Elast. 1993, 33, 1–26. [Google Scholar] [CrossRef]


[] | [] | [] |
|---|---|---|
| 4905 |
| Case Study I | Case Study II | ||
|---|---|---|---|
| m | [] | [] | [] |
|---|---|---|---|
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | |||
| 6 | |||
| 7 | |||
| 8 | |||
| 9 | |||
| 10 | |||
| 11 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferretti, M.; D’Annibale, F. Buckling of Planar Micro-Structured Beams. Appl. Sci. 2020, 10, 6506. https://doi.org/10.3390/app10186506
Ferretti M, D’Annibale F. Buckling of Planar Micro-Structured Beams. Applied Sciences. 2020; 10(18):6506. https://doi.org/10.3390/app10186506
Chicago/Turabian StyleFerretti, Manuel, and Francesco D’Annibale. 2020. "Buckling of Planar Micro-Structured Beams" Applied Sciences 10, no. 18: 6506. https://doi.org/10.3390/app10186506
APA StyleFerretti, M., & D’Annibale, F. (2020). Buckling of Planar Micro-Structured Beams. Applied Sciences, 10(18), 6506. https://doi.org/10.3390/app10186506






