Abstract
Predicting pillar stability in underground mines is a critical problem because the instability of the pillar can cause large-scale collapse hazards. To predict the pillar stability for underground coal and stone mines, two new models (random tree and C4.5 decision tree algorithms) are proposed in this paper. Pillar stability depends on the parameters: width of the pillar (W), height of the pillar (H), W/H ratio, uniaxial compressive strength of the rock (σucs), and pillar stress (σp). These parameters are taken as input variables, while underground mines pillar stability as output. Various performance indices, i.e., accuracy, precision, recall, F-measure, Matthews correlation coefficient (MCC) were used to evaluate the performance of the models. The performance evaluation of the established models showed that both models were able to predict pillar stability with reasonable accuracy. Results of the random tree and C4.5 decision tree were also compared with available models of support vector machine (SVM) and fishery discriminant analysis (FDA). The results show that the proposed random tree provides a reliable and feasible method of evaluating the pillar stability for underground mines.
1. Introduction
Pillars are essential structural units of most underground mines, used to ensure safety and economically maximize the extraction of the ore body. Coates [1] defined the pillars as “the in-situ rock between two or more underground openings”. Their primary purpose is to provide safe access to the working area and to support the weight of overburden material between adjacent underground openings temporarily or permanently, and drilling room of ceilings during excavation and mining [2,3,4,5,6,7]. Instable pillars may significantly increase workers’ safety hazards and sudden roof collapse [8]. Additionally, with the increase in mining depth, the failure of the pillar becomes more frequent and critical owing to increased ground stresses. The determination of pillar stability is, therefore, important for attaining efficient and safe mining.
Several researchers have developed numerous methods for understanding and predicting pillar failures in thee past several decades. Pillar stability is generally evaluated using a factor of safety (FoS), which is the ratio between the pillar strength and the load imposed on the pillar structure. Theoretically, when the FoS ratio is greater than 1, the pillar is considered stable. However, studies suggest that pillar with FoS above this threshold may still fail due to non-regular geometries, uncertain material properties, and differences in mining operations [7,9].
In literature, numerical simulation methods are mostly used to predict the pillar stability that allows for consideration of material properties and complex boundary conditions. Shnorhokian et al. [10] used FLAC3D with mining sequence scenarios to predict pillar stability. Griffiths et al. [11] integrated the random field theory coupled with an elasto-plastic finite element method (FEM) for predicting pillar stability. In their study, Jaiswal et al. [12] used three-dimensional FEM analysis to investigate the stress-strain behavior of coal pillars. Li et al. [13] developed the Finite-Discrete Element Method (FDEM) to examine the failure modes and mechanical behavior of pillars. Mortazavi et al. [14] used the fast Lagrangian analysis of continua (FLAC) to investigate the pillar failure mechanism of pillar and non-linear rock behavior. Owing to the anisotropic nature of rock mass and complicated non-linear characteristics, it is difficult to accurately evaluate the model inputs and constitutive equations in the numerical simulation techniques [11].
With the increasing availability of pillar stability cases, machine learning (ML) algorithms have been successfully applied for pillar stability assessment with greater accuracy compared to most available methods. Tawadrous and Katsabanis [15] in their study, utilized artificial neural networks (ANN) to explore the stability characteristics of the surface crown pillars. Ding et al. [16] examine the applicability of the stochastic gradient boosting (SGB) model for predicting pillar stability. Study results demonstrated that the proposed model outperformed random forest (RF), multilayer neural perceptron (MPNN) and support vector machine (SVM). Wattimena [9] presented the multinomial logistic regression (MLR) for predicting the pillar’s stability. Ghasemi et al. [17] used SVM and J48 algorithms to develop pillar stability plots. Both models acquired acceptable prediction performance. Zhou et al. [18] used SVM and fishery discriminant analysis (FDA) for determining the pillar stability of underground mines. Zhou et al. [19] compared six different supervised machine learning algorithms for pillar stability analysis. Study results showed that SVM and RF performed much better. While most of the implemented ML techniques have been implemented successfully to predict the stability of the pillar, they also have some shortcomings. For example, the optimum model structure (such as the number of hidden layers and model inputs, training algorithms, and transfer functions) the a priori requirements when adopting the ANN approach. Typically, this is achieved through a trial and error process. Another main drawback of the ANN model is the black-box nature of the prediction process. Further, the relationship between input and output variables is given in terms of a matrix of weight and biases that cannot be accessed and easily undertood by the user [20]. Recently, decision trees i.e., random trees (RT) and C4.5 decision trees (DT) have been effectively applied in various domains and applications such as in the assessment of soil liquefaction potential [21,22], landslide susceptibility [23], classification of power quality problem [24] and surface settlement prediction owing to tunneling [25], however, their application in rock mechanics and mining are limited.
The main purpose of this study is to predict the pillar stability of underground coal and stone mines. To achieve this objective, RT and C4.5 DT algorithms are implemented to develop two models for pillar stability prediction. A critical review of existing literature suggests that despite the successful implementation of these techniques in various domains, their implementation in the analysis of rock mechanic mining is scarcely explored. Unlike other soft computing methods, RT and C4.5 DT algorithms can provide an easy-to-use, comprehensible tree structure.
The remainder of this paper is organized as follows: Section 2 briefly provides the description of datasets used for pillars stability for underground mines. Section 3 presents the methodology used to predict pillars stability for underground mine; an overview of the random tree and C4.5 decision tree techniques. Section 4 presents the development of the prediction models. Detailed results of the proposed models are discussed by performance criteria and comparisons with similar previous models are presented in Section 5, followed by conclusions and recommendations in Section 6.
2. Description of Database
This study utilized the pillar stability database previously collected by Jaiswal and Shrivastva [26], Mohan et al. [27] and Esterhuizen et al. [28] to determine and compare the performance of the proposed random tree and C4.5 decision tree models. The data recently referenced by Zhou et al. [18] comprised of a total of 46 pillar cases from USA underground stone mines and Indian coal mines which are shown in Table 1. The database contains pillar width (W), pillar height (H), the pillar W/H ratio, pillar stress (σp), and uniaxial compressive strength of the rock (σucs). The range of values associated with each input variable is shown in Table 2. It has been widely accepted, among the researchers such as Goodman [29], that the input factors selected by Zhou et al. [18] is a complete and suitable set to predict the pillar stability. The same factors have been widely used as significant factors by other researchers (e.g., Liang et al. [30]). Table 2 provides the descriptive statistics of each input parameter. The distribution of pillar case histories database is stable (14 cases) and failed (32 cases) according to the failure process and the instability mechanism of pillars. Figure 1 shows three common failure mechanisms for a naturally fractured pillar [31]. These include: (a) failure with the lateral kinematic release of pre-formed blocks because of rising vertical load and lack of confinement, (b) failure resulting from the buildup of inclined shear fractures that transect the pillar, and is prevailing in pillar with relatively low W/H ratio, and (c) failure along with transgressive fractures where the fracture inclination angle with the principal loading axis of the pillar exceeds the angle of friction. In all of these mechanisms, a pillar’s mechanical response is directly related to the geological structures of the ground and those effects are most notable for the slender pillars. Although, wider pillars are more likely to collapse by a combination of brittle and shearing processes. Geological discontinuities in rock strata are of fundamental importance for analyzing the strength, permeability, and deformability. Characterization of the discontinuity in geometry (i.e., spatial connectivity, persistence length, and aperture, etc.) is the first step towards better understanding of rock masses overall behavior [32]. It is generally agreed that discontinuities in rock profile significanrly affect their strength properties. Due to misjudgment of the effect of discontinuities on rock strength, several examples may be quoted from the relevant rock failure literature. Jessu and Spearing [33] reported that discontinuities have a substantial influence with an increase in pillar inclination even at larger W/H ratios. Shang et al. [34] attempted to address the problems of the tensile strength of incipient rock discontinuities and quantified this parameter based on laboratory test results. These indicators are considered the main parameters for quantitatively discovering the activities in the context of the pillar, but data collection is the main challenge faced for their applicability. Hence, the five parameters are considered in the current study.

Table 1.
Summary of pillar stability data Reprinted with permission from Ref. [18]. Copyright © 2011 The Nonferrous Metals Society of China, Elsevier Ltd.

Table 2.
Descriptive statistics of the pillar stability data.
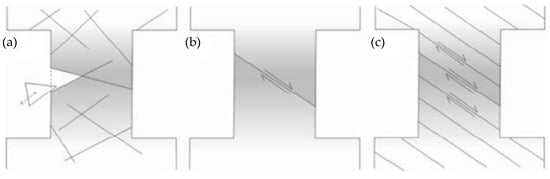
Figure 1.
Schematic for typical failure mechanism of a naturally fractured pillar (after Nordlund et al. [31]): (a) disintegration of rock blocks; (b) formation of inclined shear fractures transecting the pillar; and (c) transgressive fractures.
For implementing the random tree and C4.5 DT in this research study, a total of 40 datasets were considered for the training dataset, and the other six datasets were considered as the testing datasets. The testing and training datasets are the same as used by Zhou et al. [18].
3. Methodology
There are several data mining and machine learning (ML) algorithms available, among which random tree and C4.5 DT are the most frequently used algorithms for classification [24]. They represent decision trees that use strategies to divide and conquer in form of induction learning. The tree representation in these models helps to classify patterns in datasets, which are organized hierarchically in a collection of inter-connected nodes. The internal nodes evaluate each input attribute/feature in relation to a decision constant, thereby deciding what will be the next descending node. The nodes that are considered to be leaves are aimed to identify the instances that reach them as per the corresponding label [35].
3.1. Random Tree
Random trees were initially proposed by Leo Breiman and Adele Cutler. The algorithm can address both regression and classification tasks [36,37]. It is a decision tree, developed through a stochastic cycle. It makes use of a bagging concept to create a random dataset to construct a decision tree. Using the best split of all attributes, every node is split in the standard tree. In a random tree model, each node is split using the best at that node from the sub-set of randomly selected attributes. It also provides an option to estimate the class probabilities. A typical random tree structure is shown in Figure 2.
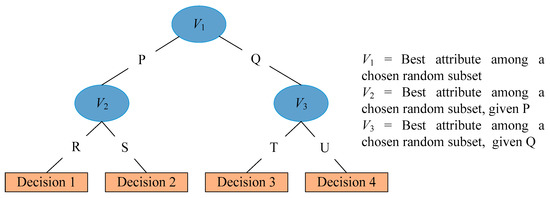
Figure 2.
Structure of random tree [24].
3.2. C4.5 Decision Tree
Commercial version 4.5 (C4.5), was proposed by Quinlan [38], is a widely known machine learning algorithm that is primarily used to develop decision trees. The method uses an entropy-based measure as the selection criteria that yield a good classification accuracy in minimal time. It is is an extension of the ID3 algorithm that also operates the divide-and-conquer policy [38]. The method’s main improvements include the pruning methodology and excellent processing of numeric attributes, missing values and noisy data. The C4.5 algorithm usually consists of two processes; preparation of thee decision tree, and making the rules (structure and design). Then measuring the entropy, and calculating the highest attribute for information gain.
The entropy formula is shown below, where S is entropy, and p in the output is a class proportion.
In addition, the attribute with the highest gain value is used as the root attribute. Gain (S, A) is presented in Equation (2) where, S is a case set; A is a case attribute; |Si| is a number of cases to i and |S| is number of cases in the set.
C4.5 algorithm develops a DT using the recursive-splitting and top-down and technique. The tree structure of C4.5 consists of a root node, internal nodes, and leaf-nodes. The root node encompasses all the input data. An internal node usually has two or more branches and is accompanied by a decision function. While the leaf node denotes the output of given input parameters. J48 is an open-source Java implementation of the C4.5 DT algorithm on the WEKA data- mining platform. The simple tree structure of C4.5 DT is as shown in Figure 3. Table 3 outlines the key differences between the two data mining algorithms adopted for the current study.
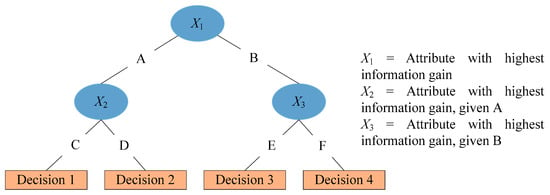
Figure 3.
Decision tree induced by the C4.5 algorithm [24].

Table 3.
Differences between a random tree and a C4.5 decision tree.
4. Development of Prediction Models
In this paper, the C4.5 decision tree and random tree algorithms were used to develop models for predicting underground mine pillar stability. The input variables were the width of the pillar (W), height of the pillar (H), W/H ratio, the pillar stress (σp), and uniaxial compressive strength of the rock (σucs). Pillar stability (PS) (dependent variable) was the sole output variable. The train-and-test approach, which is one of the most widely used techniques for establishing the predictive performance of ML algorithms for a given database, was used to develop the models. In this research study, the dataset used by Zhou et al. [18] was used as the training and testing datase for the proposed models. The working procedure for pillar stability prediction using the proposed models is shown in Figure 4.
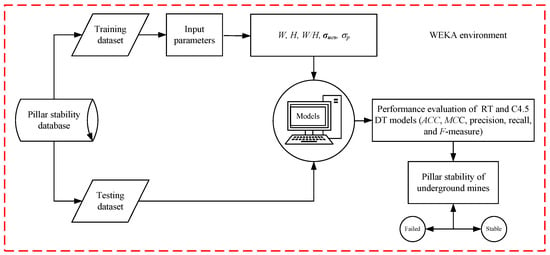
Figure 4.
Working procedure for the prediction of pillar stability using a random tree and C4.5 decision tree (DT).
To develop the proposed models, C4.5 DT and random tree algorithms are implemented based on training data on the Waikato Environment for Knowledge Analysis (WEKA) tool. The training dataset in ARFF form (attribute relation file format) was loaded in WEKA to train the adopted models which are subsequently tested by using a testing dataset based on the given training dataset. The optimal value of the C4.5 DT model parameters, including the confidence factor and the minimum number of instances per leaf, were calculated by the trial-and-error method to achieve the highest classification accuracy. The C4.5 DT algorithm’s optimal value for confidence factor was 0.25 and that of the minimum instances per leaf was found to be 2. Figure 5 and Figure 6 represent the random tree and C4.5 DT models based on the training dataset. As shown in the figure, the size of the random tree is 11 including a root node, 4 internal nodes, and 6 leaves, while the size of the C4.5 DT was 5 including a root-node, 1 internal node, and 3 leaves. The leaf node shows the stable and the failed class of underground mines. The value in the parentheses with each leaf node denotes the number of cases at that leaf. It is evident that for leaves, few instances are misclassified, which are clearly specified after a slash (see Figure 5 and Figure 6).
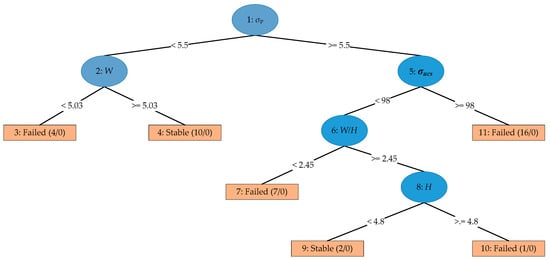
Figure 5.
The random tree for prediction of underground mines pillar stability.
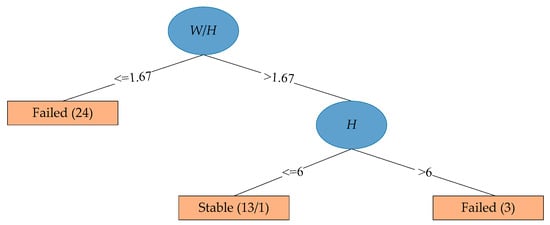
Figure 6.
Decision tree model generated by the C4.5 algorithm for prediction of underground mines pillar stability.
The performance of the trained pillar stability models was estimated using a number of statistical classification evaluation criteria such as counts of true-positive (TP), true-negative (TN), false-positive (FP), and false-negative (FN). These counts together form the confusion matrix shown in Table 4.

Table 4.
Confusion matrix for the binary class problem.
Consider that the failure of the underground mine pillar is actually positive then TP and TN represent the number of failed and stable instances that were predicted correctly. FN and FP occur when the outputs are incorrectly predicted as negative and positive, respectively. From the confusion matrix outcomes, the following classification evaluation metrics were used for comparing the prediction performance of the models [39,40,41]:
Accuracy (ACC) is the sum of TP and TN that shows the percentage of correctly classified instances among all of the data. This metric assesses the overall prediction effectiveness of the model. ACC may be deceptive, owing to the imbalanced dataset since it may produce a high value when the failed pillar samples in the majority class are favorably predicted. Therefore, in this study, other evaluation metrics including precision, recall, F-measure, and MCC were used to further assess the model’s performance. Precision is referred to as positive predicted value; recall is referred to as the true positive rate; F-measure represents a broad index that measures the performance of both recall and precision that ranged from 0 (worst value) to 1 (best value). MCC [41] represents the extent of correlation between observed and predicted classes of failed and stable cases. It is one of the standard metrics used by statisticians that takes values from −1 to 1. An MCC value of “−1” shows complete disagreement (strong negative association), “1” indicate the complete agreement (strong positive association), and “0” represent that the prediction was not related with the ground truth (very weak or no correlation between dependent and independent variable).
5. Results and Discussion
Several performance measures based on a confusion matrix were made using training and testing datasets for underground mines in order to quantify the performance measures of the proposed models. The performance results of the random tree and C4.5 DT were obtained and compared with FDA and SVM models available in the literature based on the same training and testing datasets. The confusion matrix of each model was then determined, which is shown in Table 5. Table 5 also shows the pillar stability prediction results from a couple of previous studies.

Table 5.
Confusion matrices results for training and testing datasets.
The values along the main diagonal show the number of correctly predicted cases. It may be noted from the results of Table 5 that most of the cases were accurately classified using the random tree and C4.5 DT. Based on Table 6, the overall accuracy, recall, precision, F-measure were calculated using Equations (3)–(7), which are given in Table 6. All models have good performance in training and testing the pillar stability of underground mines datasets, according to the result obtained. Furthermore, the overall accuracy, recall, precision, F-measure and MCC for stable and failed classes of the random tree and SVM models on training and testing datasets were found at par. Furthermore, a major drawback of SVM is the black-box nature of the model and the fact that correlation between input and output variables of the system are given in terms of a matrix of weight and biases which make it very challenging for users to access and understand the prediction process [19]. Decision tree algorithms i.e., random tree and C4.5, are quite transparent, and model and internal parameters need not be configured either. The SVM model is a black-box model that can show the input data and the results of the subsequent classification. However, because of its own characteristics, the black-box model cannot demonstrate the internal data mining mechanism, so the useful information relating to pillar stability is difficult to obtain for system operators [35,42]. Random tree and C4.5 DT are white-box models that are more intuitive and interpretable than ones with the black-box model i.e., the SVM model. Due to tree-like structures, the proposed models can not only obtain accurate classification results, but can also show the internal mechanism for classification results. Although, C4.5 DT and FDA possessed the same accuracy, MCC, precision, recall and F-measure for failed and stable pillars on the testing dataset, the training performances were different. Comparing their values of MCC, recall, precision, F-measure for failed and stable pillars, the C4.5 DT performed better than FDA in the training dataset. Therefore, based on their training and testing performances and bearing in mind the black-box nature of the SVM model, the random tree model is relatively better SVM and RBF models available in literature due to their easier application and of a clear graphical outcome. Although the proposed method produces desirable results for predictions, certain shortcomings should be discussed in the future.

Table 6.
Comparison of results of the developed random tree and C4.5 decision tree with available fishery discriminant analysis (FDA) and support vector machine (SVM) models.
The dataset is relatively unbalanced and small. Generally, if the dataset is limited it will affect model generalization and reliability. While random tree and C4.5 algorithms perform well with limited data sets, the performance of predictions on a larger dataset could be better. However, the developed models can always be updated to yield better results, as new data becomes available. Moreover, the dataset is unbalanced, owing to the fact that there are more failed cases than stable cases. Therefore, the establishment of a larger and more balanced pillar stability database is important. Other variables could also affect the prediction results. Numerous factors influence the stability of the pillar, such as external environments and the inherent characteristics of the pillar. While the five factors used in the current study, to some extent, may characterize the fundamental conditions for pillar stability, few other factors like underground water, joints, and blasting disturbance may also influence pillar stability. Analyzing the influence of these factors on the results of predictions is important.
6. Conclusions and Recommendations for Future Work
In this paper, a random tree and C4.5 DT models were applied to predict underground mines’ pillar stability. The models were trained and tested using the pillar stability database of underground mines collected from the USA and India. The developed models predict the pillar stability using the most important input variables such as pillar width (W), pillar height (H), pillar W/H ratio, uniaxial compressive strength, and average pillar stress. The main findings of this study are as follows:
- Unlike most soft computing techniques, the developed models are very simple to use and do not require exhaustive training. The proposed models present an explicit relationship between explanatory (input) and target (output) variables. Study results reveal that relationships obtained are compatible with engineering judgments and intuitions.
- The classification accuracy of the random tree and C4.5 DT is 100% and 95.65%, respectively during the training and testing phases, which indicates that both models are efficient and reliable for practical applications.
- Compared to the SVM model, the developed random tree model shows at par results and the random tree model application is easier due to a simple graphical outcome, while the information gained by the SVM algorithm during the training phase is implicitly processed that make it very difficult to explain well the overall structure of the network. So, it may be argued that the SVM model has little insight into the fundamental mechanism of the current problem.
- The comparison of the developed models’ performances showed that the random tree model achieved more reliable predictions than the C4.5 DT model.
- It is evident that the proposed models are open to further development in the future and that the acquisition of more data will improve the capacity for prediction.
For future research, it is recommended to work with a larger and more balanced pillar stability database to further evaluate the reliability of these models for the prediction of pillar stability. These models can also be refined by considering additional parameters pertaining to ground type and structural geology.
Author Contributions
Conceptualization M.A., X.-W.T., N.A.A.-S.; methodology M.A., X.-W.T., H.M.A.-A.; software M.A., F.A.; validation M.A., X.-W.T., N.A.A.-S.; formal analysis M.A., F.A., A.J., H.M.A.-A.; investigation M.A., A.J., F.A.; resources H.M.A.-A., X.-W.T., N.A.A.-S.; data curation M.A., F.A.; writing—original draft preparation M.A., A.J.; writing—review and editing M.A., A.J., N.A.A.-S.; supervision X.-W.T., N.A.A.-S., H.M.A.-A.; project administration X.-W.T., N.A.A.-S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors acknowledge and appreciate the support provided by the King Fahd University of Petroleum and Minerals (KFUPM).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Coates, D.F. Rock mechanics principles. In Geoscience Abstracts; American Society Photogrammetry: Bethesda, MD, USA, 1966. [Google Scholar]
- Brady, B.H.; Brown, E.T. Rock Mechanics: For Underground Mining; Springer Science & Business Media: Berlin, Germany, 1993. [Google Scholar]
- Tesarik, D.; Seymour, J.; Yanske, T. Long-Term stability of a backfilled room-and-pillar test section at the Buick Mine, Missouri, USA. Int. J. Rock Mech. Min. Sci. 2009, 46, 1182–1196. [Google Scholar] [CrossRef]
- Najafi, M.; Jalali, S.; Bafghi, A.Y.; Sereshki, F. Prediction of the confidence interval for stability analysis of chain pillars in coal mines. Saf. Sci. 2011, 49, 651–657. [Google Scholar] [CrossRef]
- Salamon, M. Stability, instability and design of pillar workings. Proc. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1970, 7, 613–631. [Google Scholar] [CrossRef]
- Košťák, B. Pillar strength prediction from representative sample of hard rock. Proc. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1971, 8, 523–526. [Google Scholar] [CrossRef]
- Deng, J.; Yue, Z.; Tham, L.; Zhu, H. Pillar design by combining finite element methods, neural networks and reliability: A case study of the Feng Huangshan copper mine, China. Int. J. Rock Mech. Min. Sci. 2003, 40, 585–599. [Google Scholar] [CrossRef]
- Wang, J.-A.; Shang, X.; Ma, H. Investigation of catastrophic ground collapse in Xingtai gypsum mines in China. Int. J. Rock Mech. Min. Sci. 2008, 45, 1480–1499. [Google Scholar] [CrossRef]
- Wattimena, R. Predicting the stability of hard rock pillars using multinomial logistic regression. Int. J. Rock Mech. Min. Sci. (1997) 2014, 71, 33–40. [Google Scholar] [CrossRef]
- Shnorhokian, S.; Mitri, H.S.; Moreau-Verlaan, L. Stability assessment of stope sequence scenarios in a diminishing ore pillar. Int. J. Rock Mech. Min. Sci. 2015, 74, 103–118. [Google Scholar] [CrossRef]
- Griffiths, D.; Fenton, G.A.; Lemons, C.B. Probabilistic analysis of underground pillar stability. Int. J. Numer. Anal. Methods Geomech. 2002, 26, 775–791. [Google Scholar] [CrossRef]
- Jaiswal, A.; Sharma, S.; Shrivastva, B. Numerical modeling study of asymmetry in the induced stresses over coal mine pillars with advancement of the goaf line. Int. J. Rock Mech. Min. Sci. (1997) 2004, 41, 859–864. [Google Scholar] [CrossRef]
- Li, L.; Tang, C.; Wang, S.; Yu, J. A coupled thermo-hydrologic-mechanical damage model and associated application in a stability analysis on a rock pillar. Tunn. Undergr. Space Technol. 2013, 34, 38–53. [Google Scholar] [CrossRef]
- Mortazavi, A.; Hassani, F.; Shabani, M. A numerical investigation of rock pillar failure mechanism in underground openings. Comput. Geotech. 2009, 36, 691–697. [Google Scholar] [CrossRef]
- Tawadrous, A.; Katsabanis, P. Prediction of surface crown pillar stability using artificial neural networks. Int. J. Numer. Anal. Methods Geomech. 2007, 31, 917–931. [Google Scholar] [CrossRef]
- Ding, H.; Li, G.; Dong, X.; Lin, Y. Prediction of pillar stability for underground mines using the stochastic gradient boosting technique. IEEE Access 2018, 6, 69253–69264. [Google Scholar] [CrossRef]
- Ghasemi, E.; Kalhori, H.; Bagherpour, R. Stability assessment of hard rock pillars using two intelligent classification techniques: A comparative study. Tunn. Undergr. Space Technol. 2017, 68, 32–37. [Google Scholar] [CrossRef]
- Zhou, J.; Li, X.-B.; Shi, X.-Z.; Wei, W.; Wu, B.-B. Predicting pillar stability for underground mine using Fisher discriminant analysis and SVM methods. Trans. Nonferr. Met. Soc. China 2011, 21, 2734–2743. [Google Scholar] [CrossRef]
- Zhou, J.; Li, X.; Mitri, H.S. Comparative performance of six supervised learning methods for the development of models of hard rock pillar stability prediction. Nat. Hazards 2015, 79, 291–316. [Google Scholar] [CrossRef]
- Javadi, A.A.; Ahangar-Asr, A.; Johari, A.; Faramarzi, A.; Toll, D. Modelling stress-strain and volume change behaviour of unsaturated soils using an evolutionary based data mining technique, an incremental approach. Eng. Appl. Artif. Intell. 2012, 25, 926–933. [Google Scholar] [CrossRef]
- Ahmad, M.; Tang, X.-W.; Qiu, J.-N.; Ahmad, F. Evaluating seismic soil liquefaction potential using Bayesian belief network and C4. 5 Decision Tree Approaches. Appl. Sci. 2019, 9, 4226. [Google Scholar] [CrossRef]
- Ahmad, M.; Tang, X.-W.; Qiu, J.-N.; Gu, W.-J.; Ahmad, F. A hybrid approach for evaluating CPT-based seismic soil liquefaction potential using Bayesian belief networks. J. Cent. South Univ. 2020, 27, 500–516. [Google Scholar] [CrossRef]
- Bui, D.T.; Ho, T.C.; Revhaug, I.; Pradhan, B.; Nguyen, D.B. Landslide susceptibility mapping along the national road 32 of Vietnam using GIS-based J48 decision tree classifier and its ensembles. In Cartography from Pole to Pole; Springer: Cham, Switzerland, 2014; pp. 303–317. [Google Scholar]
- Kiranmai, S.A.; Laxmi, A.J. Data mining for classification of power quality problems using WEKA and the effect of attributes on classification accuracy. Prot. Control Mod. Power Syst. 2018, 3, 29. [Google Scholar] [CrossRef]
- Dindarloo, S.R.; Siami-Irdemoosa, E. Maximum surface settlement based classification of shallow tunnels in soft ground. Tunn. Undergr. Space Technol. 2015, 49, 320–327. [Google Scholar] [CrossRef]
- Jaiswal, A.; Shrivastva, B. Numerical simulation of coal pillar strength. Int. J. Rock Mech. Min. Sci. 2009, 46, 779–788. [Google Scholar] [CrossRef]
- Mohan, G.M.; Sheorey, P.; Kushwaha, A. Numerical estimation of pillar strength in coal mines. Int. J. Rock Mech. Min. Sci. 2001, 38, 1185–1192. [Google Scholar] [CrossRef]
- Esterhuizen, G.; Dolinar, D.; Ellenberger, J. Pillar strength in underground stone mines in the United States. Int. J. Rock Mech. Min. Sci. 2011, 48, 42–50. [Google Scholar] [CrossRef]
- Goodman, R.E. Introduction to Rock Mechanics; Wiley: New York, NY, USA, 1989; Volume 2. [Google Scholar]
- Liang, W.; Luo, S.; Zhao, G.; Wu, H. Predicting hard rock pillar stability using GBDT, XGBoost, and LightGBM algorithms. Mathematics 2020, 8, 765. [Google Scholar] [CrossRef]
- Nordlund, E.; Radberg, G.; Jing, L. Determination of failure modes in jointed pillars by numerical modelling. In Proceedings of the Conference on Fractured and Jointed Rock Masses, Lake Tahoe, CA, USA, 3 June 1992; pp. 345–350. [Google Scholar]
- Shang, J.; West, L.; Hencher, S.; Zhao, Z. Geological discontinuity persistence: Implications and quantification. Eng. Geol. 2018, 241, 41–54. [Google Scholar] [CrossRef]
- Jessu, K.; Spearing, A. Performance of inclined pillars with a major discontinuity. Int. J. Min. Sci. Technol. 2019, 29, 437–443. [Google Scholar] [CrossRef]
- Shang, J.; Hencher, S.; West, L. Tensile strength of geological discontinuities including incipient bedding, rock joints and mineral veins. Rock Mech. Rock Eng. 2016, 49, 4213–4225. [Google Scholar] [CrossRef]
- Witten, I.H.; Frank, E. Data Mining: Practical Machine Learning Tools and Techniques, 2nd ed.; Morgen Kaufmann: San Francisco, CA, USA, 2005. [Google Scholar]
- Kalmegh, S. Analysis of weka data mining algorithm reptree, simple cart and randomtree for classification of indian news. Int. J. Innov. Sci. Eng. Technol. 2015, 2, 438–446. [Google Scholar]
- Hamsagayathri, P.; Sampath, P. Performance analysis of breast cancer classification using decision tree classifiers. Int. J. Curr. Pharm. Res. 2017, 9, 19–25. [Google Scholar] [CrossRef]
- Quinlan, J.R. C4.5: Programming for Machine Learning; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1993. [Google Scholar]
- Sokolova, M.; Japkowicz, N.; Szpakowicz, S. Beyond accuracy, F-score and ROC: A family of discriminant measures for performance evaluation. In Proceedings of the Australasian Joint Conference on Artificial Intelligence, Hobart, Australia, 4–8 December 2006; pp. 1015–1021. [Google Scholar]
- Powers, D.M. Evaluation: From precision, recall and F-measure to ROC, informedness, markedness and correlation. J. Mach. Learn. Technol. 2011, 2, 37–63. [Google Scholar]
- Matthews, B.W. Comparison of the predicted and observed secondary structure of T4 phage lysozyme. Biochim. Biophys. Acta (BBA) Protein Struct. 1975, 405, 442–451. [Google Scholar] [CrossRef]
- Zaki, M.J.; Meira, W. Data Mining and Analysis: Fundamental Concepts and Algorithms; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).