Improved SP-MCTS-Based Scheduling for Multi-Constraint Hybrid Flow Shop

Abstract

As a typical non-deterministic polynomial (NP)-hard combinatorial optimization problem, the hybrid flow shop scheduling problem (HFSSP) is known to be a very common layout in real-life manufacturing scenarios. Even though many metaheuristic approaches have been presented for the HFSSP with makespan criterion, there are limitations of the metaheuristic method in accuracy, efficiency, and adaptability. To address this challenge, an improved SP-MCTS (single-player Monte-Carlo tree search)-based scheduling is proposed for the hybrid flow shop to minimize the makespan considering the multi-constraint. Meanwhile, the Markov decision process (MDP) is applied to transform the HFSSP into the problem of shortest time branch path. The improvement of the algorithm includes the selection policy blending standard deviation, the single-branch expansion strategy and the 4-Rule policy simulation. Based on this improved algorithm, it could accurately locate high-potential branches, economize the resource of the computer and quickly optimize the solution. Then, the parameter combination is introduced to trade off the selection and simulation with the intention of balancing the exploitation and exploration in the search process. Finally, through the analysis of the calculated results, the validity of improved SP-MCTS (ISP-MCTS) for solving the benchmarks is proven, and the ISP-MCTS performs better than the other algorithms in solving large-scale problems.

1. Introduction

The flow shop scheduling problem (FSSP) has been a very active research field, since it was first proposed by Johnson [1]. In the FSSP, a set of n jobs have to be processed on m single-machine stages, where each job follows the same route of stages. In production, the FSSP may result in overloading some stages and blocking some jobs [2]. When parallel machines are introduced in some of the stage, the standard flow shop layout becomes a hybrid flow shop (HFS) for these questioners in many real-life manufacturing scenarios. Given its practical interest, the hybrid flow shop scheduling problem (HFSSP) is widely used in today’s manufacturing and production systems, such as heavy industry, light industry and other industrial systems. Taking into account the computation complexity, more researchers have conducted in-depth research in this field, since HFSSP has been proved as a non-deterministic polynomial (NP)-hard problem [3]. Simultaneously, production scheduling has been proved to play an important role for improving productivity and responsiveness in the manufacturing system [4]. Therefore, developing more efficient algorithms for this problem is significant.

Ribas and Ruizad [5] discussed HFSSP in depth, and the methods for solving the HFSSP were divided into the exact algorithm, heuristic method and meta-heuristic algorithm. The exact algorithm used to be the most common solution. In 1970s, the branch and bound algorithm (B&B) was proposed by Arthanary and Ramaswamy [6] to solve the two-stage HFSSP. Portmann and Vignier [7] combined the B&B algorithm with the genetic algorithm to solve HFSSP, and the performance of the algorithm was significantly improved. Neron et al. [8] applied energy reasoning and global operations to improve the efficiency of branch definition. Since 1998, many heuristics have been applied to solve HFSSP problems. Gupta and Tunc [9] proposed a heuristic algorithm for solving the minimum completion time of the two-stage HFSSP problem. Kahraman et al. [10] introduced an efficient parallel greedy heuristic algorithm for solving multi-task HFSSP problems. Lin and Liao [11] took a two-step label manufacturing company as an example to minimize the maximum delay of total weight. Heydari and Fakhrzad [12] proposed a heuristic algorithm for minimizing the total time of advance processing and delay processing. In addition, Paternina-Arboleda [13] developed a heuristic method for identifying and continuously solving bottleneck processes. In summary, the heuristic algorithm can quickly construct the scheduling solution, but the quality of the solution is difficult to guarantee.

In recent years, various meta-heuristics have also been developed for solving the HFSSP. Researchers have further studied the application of meta-heuristic algorithms for HFSSP. The taboo algorithm proposed by Nowicki and Smutnick [14] defines the specific neighborhood through critical paths for search optimization. Alaykyran et al. [15] proposed a modified ant colony optimization algorithm to solve HFSSP. Furthermore, Kahraman et al. [16] developed a genetic algorithm which is better than the B&B method. Liao et al. [17] proposed a particle optimization algorithm, which makes the hybrid discrete particle swarm optimization algorithm and the bottleneck heuristic algorithm to fully explore the bottleneck stage, and combine the simulated annealing algorithm to avoid the local optimal solution. Then, the superiority of the algorithm is illustrated by a comparison of examples. Recently, Marichelvama et al. [18] optimized the HFSSP using the algorithm of Nawaz, Enscore and Ham (NEH) heuristic method, and subsequently applied the CS (cuckoo search) algorithm to quickly search and improve on the basis of the optimized solution. Pan et al. [19] proposed an effective artificial bee colony optimization algorithm, and solved the optimal scheduling solution by hybrid representation method. Li et al. [20] used the variable neighborhood algorithm (HVNS) combined with the chemical reaction optimization algorithm and the distribution estimation algorithm to solve the HFSSP. In the meantime, the algorithm was studied and adjusted to locate the potential region, and search for the optimal solution. Cui and Gu [21] applied the vector notation to model HFSSP, and further proposed an improved discrete artificial bee colony (IDABC) algorithm. Meanwhile, the validity of the IDABC algorithm was verified by using the benchmark problems. Komaki et al. [22] proposed heuristic algorithms and two metaheuristic techniques based on an artificial immune system for a two-stage assembly hybrid flow shop scheduling problem. Zhang and Chen [23] developed a discrete differential evolution (DDE) algorithm with a modified crossover operator to solve larger sized problems. Other algorithms, such as Quantum-inspired immune algorithm (QIA) [24], Artificial immune system (AIS) [25], have also been applied to solve HFSSP. In addition, there are a lot of non-classical methods for solving this kind of large and complex problems. In order to solve the flow shop problem of the minimized makespan, Ramanan et al. [26] proposed a feed forward back propagation neural network to solve the problem. Tkachenko and Izonin [27,28] used neural-like structures based on the geometric transformations model as a universal approximator to implement principles of training and self-training, and thus provided the repeatability of training results and large and small training samples as a satisfactory solution. Gupta et al. [29] investigated the use of these training algorithms as competitive neural network learning tools to minimize makespan in a flow shop. In the studies mentioned above, although the meta-heuristic algorithms were widely used to solve HFSSP, it still has some disadvantages when encountering large problems, such as complex algorithm frameworks, a lack of real-state mapping and incomplete neighborhood structures [30].

In order to solve these disadvantages, some scholars adopted machine learning to study HFSSP for achieving an efficient scheduling. Monte-Carlo tree search (MCTS) algorithms heuristically build an asymmetric partial search tree by applying machine learning, and then search through the potential branches to solve the optimal strategy by continuously traversing [31]. Therefore, Chaslot et al. [32] first introduced MCTS for solving production-related problems. A MCTS-based algorithm for the multi-objective flexible job shop scheduling problem was presented by Wu et al. [33], and it was improved by incorporating the Variable Neighborhood Descent Algorithm and other techniques, like rapid action value, which can estimate the heuristic and transposition table. Chou et al. [34] used the improved MCTS algorithm to solve the multi-objective flexible shop scheduling problem, and search the minimum completion time by the adaptive value game comparison. Furuoka and Matsumoto [35] used an MCTS-based algorithm to find good schedules for a re-entrant scheduling problem. Although good efforts have been made in the above studies, and MCTS is a series of two-person zero-sum game decision-making methods, there are still limitations in the performance and learning efficiency when solving shop floor scheduling problems.

For minimizing the makespan, the HFSSP scheduling approach using improved SP-MCTS (single-player Monte-Carlo tree search) is proposed in this paper. Schadd et al. [36] proposed a new machine learning algorithm, which is named the SP-MCTS algorithm. Schadd et al. [37] applied the algorithm to solve the single-machine puzzle game, and the application algorithm achieved good results in the standardized test. Shimpei et al. [38] verified the effectiveness of the new simulation policy through data experiments, calibrated the relationship between the search method and parameters, and demonstrated the application potential of the SP-MCTS algorithm in actual scheduling.

Through the above review, the improved SP-MCTS (ISP-MCTS) algorithm was successfully applied in the scheduling problems. Therefore, this paper applies ISP-MCTS to solve HFSSP, and the organization of this paper is as follows. In Section 2, the flow shop scheduling problem is introduced, and the mathematical model is established. Then, the improvement scheme of SP-MCTS is introduced in detail in Section 3. In Section 4, the calibration of the algorithm parameters is performed. In Section 5, the experimental results and the comparison are presented. Finally, the conclusions are discussed in Section 6.

2. Hybrid Flow Shop Scheduling Problem

The HFSSP is described as follows: a set of n jobs J = {1, 2,…, n} must be processed by the s-stage, i.e., O_j1→O_j2,…, O_js, S = {1, 2,…, s}. Each stage k ∈S, has M_k ≥ 1 identical parallel machines, and each job j can be processed in any one of the M_k parallel machines. At the same time, the processing time of the job j in the stage k (O_jk) with deterministic processing time P_jk. Under known the parameters and assumptions, the scheduling policy is solved to minimize the maximum completion time for processing n jobs.

2.1. Assumption

The HFSSP problem satisfies the following assumptions:

• At the beginning, each job release time is 0.
• Job j can only be processed once in each stage.
• Each process of job j can only be processed in one machine, and each machine can only process one job at a time.
• There are infinite buffers in the adjacent two stages. Job setup time and the travel time between consecutive stages are included in the processing time P_js or are ignored.

2.2. Symbol Definition

The notation of the HFSSP model is shown as follows:

• P_jk is the processing time of job j at stage k.
• D_jk is the start processing time of job j at stage k.
• BM denotes a very large number, the traditional “Big M”.
• x_jik if job j is assigned to machine i at stage k, then x_jik = 1, otherwise x_jik = 0.
• y_jj’k if job j is processed earlier than j’ at stage k, then y_jj’k = 1, otherwise y_jj’k = 0.

2.3. Mathematical Model

Using the above notation, the mathematical relationship of HFSSP is formulated as follows:

$$\min \left(C_{\max }\right)=\underset{j\in J}{\max }\left(D_{js}+p_{js}\right)$$

(1)

$${\displaystyle \sum _{i=1}^{m_k}}{x}_{jik}=1,\forall j\in J,k\in S$$

(2)

$$D_{1j}\ge 0,\forall j\in J$$

(3)

$$D_{k+1,j}-D_{kj}\ge p_{kj},\forall j\in J,k,k+1\in S$$

(4)

$$y_{j{j}^{\prime }k}+y_{j^{\prime }jk}\le 1,\forall j,j^{\prime }\in J,k\in S$$

(5)

$$D_{k{j}^{\prime }}-\left(D_{kj}+p_{kj}\right)+BM\cdot \left(3-y_{j{j}^{\prime }k}-x_{kji}-x_{k{j}^{\prime }i}\right)\ge 0,\forall j,j^{\prime }\in J,k\in S,i\in \left\{1,2,\cdots ,M_k\right\}$$

(6)

$$x_{jik}\in \left\{0,1\right\},j\in J,k\in S,i\in \left\{1,\cdots ,M_k\right\}$$

(7)

$$y_{j{j}^{\prime }k}\in \left\{0,1\right\},j,j^{\prime }\in J,k\in S$$

(8)

The objective function (1) is to minimize the maximum completion time. Constraints (2) ensures that each job completes all the processing stages and can only be assigned to one machine in each stage. Equation (3) ensures that the first stage start time of each job is greater than or equal to 0. Equation (4) indicates that when the job is processed in two consecutive stages, the next process can be started after the previous process is completed. Equations (5) and (6) describe the sequential constraints of different jobs in the same machine. When two jobs are processed, the previous job must be finished before the following job can be started. Equations (7) and (8) define the value ranges of decision variables.

3. ISP-MCTS Algorithm Design

The MCTS is based on the Monte Carlo simulation to build an asymmetric search tree, and subsequently find the “best” action in the current state [39]. The SP-MCTS algorithm derived from MCTS is proposed to solve HFSSP, and HFSSP is seen as a single-player optimization problem. In the solving process, the processing machines are regarded as starred positions (drop points), and the rules are formulated according to the constraint relationship in the mathematical model. With the goal of maximizing the score, the entire search process includes four phases of selection, expansion, simulation and backpropagation, as shown in Figure 1.

3.1. HFSSP Model

According to Markov decision processes (MDP), the model of HFSSP is established [40,41]: (1) s is a series of state matrix of the HFSSP, describing the relationship between the job state and stage. s₁ and s_goal represent the initial state and completion state in the HFSSP. s₁, s₂,…, s_goal are used to describe the job production process through various stages. (2) a is the set of scheduling policies in each state s, the scheduling policy sets a₁, a₂,…, a_v are extracted under each state s₁, s₂,…, s_goal. A is the current scheduling policy selected from set a. Therefore, A₁, A₂,…, A_v are the policies corresponding to each state of s₁ to s_goal, selected from the policy sets of a₁, a₂,…, a_v. (3) T(s, A, s’) = 1, the scheduling policy A is selected, and the probability that the state is converted from s to s’ is 1.

According to the design methodology of the above MDP model, the relationship between the HFSSP field environment and the model state is established. The matrix model S_n×m satisfies the following conditions: (1) n represents the number of jobs, and m represents the number of stages. (2) The first column and the m th column of the matrix are on-line stage and offline stage respectively, the second to the m-1 th columns represent the processing stages. (3) The number of jobs being processed must be less than or equal to the number of parallel machines in the stage. (4) The job in the same row is processed according to the sequence of stages, so the job in the next column cannot be started until the job in the current column is completed. (5) For any job, there is P_i1 = 0, P_im = ∞. In Figure 1, S is a 4 × 4 state matrix, which is the problem of four jobs and four-stage HFSSP. In this matrix, stage 1 and stage 4 are the online stage and offline stage, respectively, and stage 2 and stage 3 have two parallel processing machines. When the state is searched to the k th state matrix, the element s_k(i,j) = 0 means the job i is not in the machine of the stage j, and s_k(i,j) = 1 represents that the job i is processing in the stage j. s_k(i,j) = 2 represents that the job i has finished processing in the j th stage and waits for scheduling. a_kx represents the scheduling policy set (A_k1, A_k2, … A_ku) in the s_k state. If the element A_k1(i,j) = 1, it represents that the job i is dispatched from the machine in the stage j to the processing machine in the stage j + 1.

As shown in Figure 1, the HFSSP coding model was designed according to the above description. The specific model evolution process is described as follows:

Step 1:

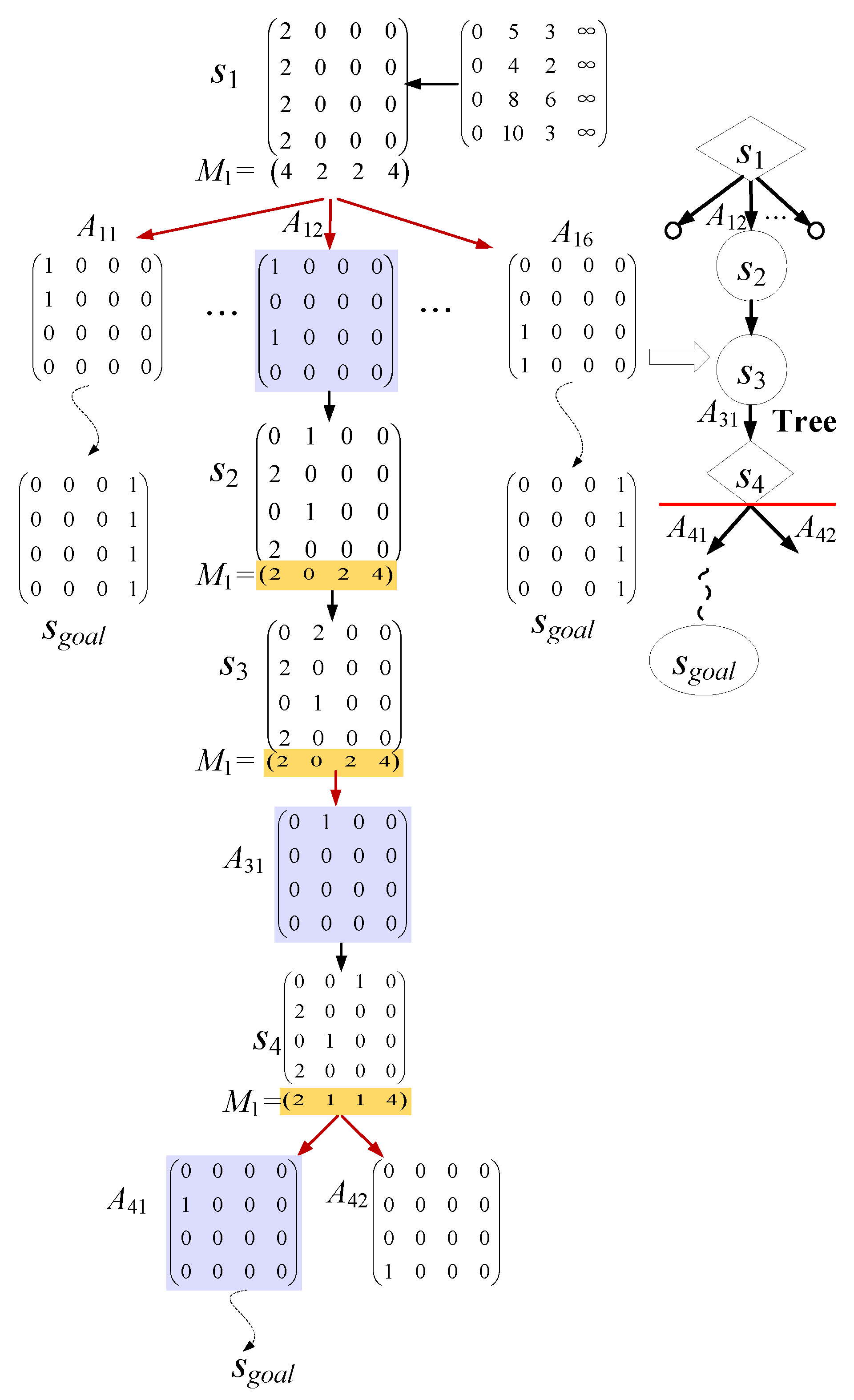
Construct the n × m matrix of the initial state s₁ and the completion state s_goal. In Figure 1, M is the number of parallel machines in each stage, M₁ is the number of idle machines in each stage during the process, and the matrix evolves from s₁ to s_goal.

Step 2:

According to the state of the job and the occupancy of the machine, the available scheduling policy set has a_k = (A_kγ, A_kβ,…, A_kδ) during searching for the k-floor shop state node s_k. Meanwhile, the search method is selected on the basis of the traversal times N(s_k) of the state node s_k. Details are shown as follows: ① when N(s_k) ≤ P (P is the critical value of the simulation times), heuristic rules are applied to select the scheduling policy for searching to the s_goal state; ② as shown in Figure 1, when N(k) > P, the selection policy of the SP-MCTS algorithm is used to evaluate the policy set a_k and select the scheduling policy A_k. After executing strategy A_k, it will search from state s_k to s_k+1.

Step 3:

If s_k+1 ≠ s_goal, step 2 is repeated for state evolution until the s_goal.

3.2. ISP-MCTS Algorithm Optimization Process

In this paper, the HFSSP scheduling process is constructed as a tree structure. For the SP-MCTS algorithm, there are disadvantages such as poor branch positioning accuracy and slow convergence speed. Therefore, the SP-MCTS algorithm is improved as follows:

3.2.1. Selection

The relationship between balanced depth exploration and breadth exploration is constantly explored in the existing state tree nodes, so that each exploration can reach a better solution as far as possible. The UCT (upper confidence bounds applied to trees) algorithm [33] is used to select the scheduling policy, and the improvements are as follows:

$$Q^{\oplus }(s,a)=Q(s,a)+c\sqrt{2\ln N(s)/N(s,a)}+\sqrt{\left({\displaystyle \sum q{(s,a)}^2-N(s,a)\times }Q{(s,a)}^2+D\right)/N(s,a)}$$

(9)

$${\pi }_{UCT}(s)=\underset{a}{\arg \max }{Q}^{\oplus }(s,a)$$

(10)

The first two terms of the UCT algorithm in Equation (9) are reserved. N(s) represents the total times of that the state s is accessed, and N(s, a) represents the times during which the policy a is selected in the state s. Q(s, a) represents the average score of the policy a that is executed multiple times in state s. Considering a third item here, indicating the deviation obtained after the policy a is executed, where ∑q(s, a)² represents the sum of the squared results which achieves at the state s, constant D is used to ensure that policies with few choices are not underestimated [32]. The purpose of the deviation term without the particularity of the neighborhood is to fully consider the change in range of the score when the policy is selected, and select the policy by using Equation (10) in the end. As shown in Figure 1, taking node s₁ as an example, when N(s₁) > P, every policy in the set (A₁₁, A₁₂,…, A₁₆) is evaluated according to Equation (9), and the policy is selected on the basis of Equation (10).

3.2.2. Expansion

When N(s) > P, the branch node is expanded. As shown in Figure 1, if s₁ node N(s₁) > P, the scheduling policy A₁₂ is selected, and the node s₁ is updated to s₂. If s₂ is not a node in the tree, s₂ is added to the tree as a node.

Single-branch node continuous expansion: considering the existence of optional policy uniqueness and state self-updating in HFSSP operation, the single-branch node continuous expansion method is designed. After s₂ is expanded as shown in Figure 1, the state needs to be self-updated while the job finishes processing, so the state evolves to s₃. It can be seen that in s₃, the scheduling policy only has A₃₁. At this time, the node s₃ is continuously expanded, and then the state evolves to the s₄, and the number of policies (A₄₁, A₄₂) is more than 1. Therefore, node s₄ is expanded into the tree, and heuristic rules are applied to search the scheduling policy from nodes s₄ to s_goal. As shown in Figure 1, the states s₂→s₄ are continuously expanded to avoid multiple meaningless explorations while effectively utilizing computing resources.

3.2.3. Simulation

Heuristic rules are used to simulate s_goal from the leaf node s. When the tree searches from the A₁₂ branch to the s₄ leaf node, as shown in Figure 1, s₄ is used as the simulation initial state. Then, the heuristic rule is applied to search for s_goal. Therefore, the root node s₁ is used as the starting leaf node of the program. Each simulation policy is obtained by different heuristic rule.

According to the literature [19] heuristic rules comparison results, four heuristic rules (4-Rule) are selected as the simulation policy. These four heuristic rules are: (1) NEH_LPT(λ) forward heuristic rule for λ = n × 50%; (2) NEH_SPTB(λ) forward heuristic rule for λ = n × 35%; (3) shortest processing time (SPT); and (4) longest processing time (LPT). Before the simulation policy is applied, with probability ε a random move is played, ε = 0.005.

3.2.4. Backpropagation

When the simulation is completed, the backpropagation is performed according to the simulation result. Starting from leaf node s₄, as shown in Figure 1, each child node goes back to its parent node until root node s₁ is reached. The information is updated as follows:

$$N(s)\leftarrow N(s)+1$$

(11)

$$N(s,a)\leftarrow N(s,a)+1$$

(12)

$$Q\left(s,a\right)\leftarrow Q\left(s,a\right)+\left(z-Q\left(s,a\right)\right)/N(s,a)$$

(13)

$${\displaystyle \sum }q{\left(s,a\right)}^2\leftarrow {\displaystyle \sum }q{\left(s,a\right)}^2+z^2$$

(14)

Equation (11) represents the total number of times the node s was accessed. Equation (12) records the times that the policy a is executed under the node s. Equation (13) updates the average score of the execution policy a at node s. Equation (14) is used to calculate the sum of the squared score.

3.2.5. Evaluation and Policy Set

The application of ISP-MCT to solve the HFSSP is different from the game-type MCTS problem. In the ISP-MCTS scheduling search, the first iteration time T₁ is used as the benchmark, and the quality of each subsequent iteration is T_n − T₁ as the evaluation score. When T_n − T₁ ≤ 0, the score is T₁ − T_n+1, and if T_n − T₁ > 0, the score is 0. Therefore, the optimization purpose is to select the highest scoring policy set.

3.3. The Complete Process of ISP-MCTS

Through the selection policy and the simulation policy, the root node searches from s₁ to s_goal. The algorithm is based on the node average score design selection algorithm and takes the maximum score (T_min) for the optimization purpose. Therefore, the pseudo code of the ISP-MCTS for solving HFSSP is described as Algorithm 1.

Algorithm 1 The main procedure of ISP-MCTS
1:	Initialize: C, D, T1, s1, P, N = 0, sgoal, s = s1.
2:		While the halting criterion is not satisfied do
3:		Step 1: Selection and expansion
4:		if N(s) ≤ P then
5:		go to step 2
6:		else The improved UCT in Section 3.2.1 is applied to select the scheduling policy a
7:		Update state s→s’
8:		if the state s’ is a node in the tree then
9:		s = s1, return Step 1
10:		else s’ is expanded to a leaf node in the tree
11:		end if
12:		if The new expanded leaf node s has one optional policy or no one
13:		N(s) = P + 1, return Step 1
14:		else go to step 2
15:		end if
16:		end if
17:		Step 2: Simulation
18:		The node s’ is taken as the simulation start state.
19:		Selecting the simulation policy
20:		Simulation to sgoal, the completion time Tn is obtained, go to Step 3
21:		Step 3: Update simulation policy
22:		if Tn < Tmin then
23:		The policy set (A1γ, A2β,…, Avδ) from s1→sgoal is recorded, Tmin = Tn
24:		go to step 4
25:		else go to step 4
26:		end if
27:		Step 4: Backpropagation
28:		The information from the leaf node s to the root node s1 branch path node is updated according to Equation (11)→(14)
29:
30:		if The halting criterion is not satisfied
31:		Output the optimal policy set, Tmin
32:		else s = s1, return Step 1
33:		end if
34:		end while

4. Calibration of the Proposed Algorithms

4.1. Simulation Policy Verificationᾱ

In order to verify the simulation policy mentioned above, a set of instances are generated: n∈{20,40,60,80,100}, s∈{4,6,8}. Ten instances are generated for each combination of n and s, and a total of 150 instances are obtained. The processing time is generated from the uniform distribution [1], and the number of parallel machines M_k are generated from the uniform distribution [1,5]. The three simulation policies were constructed in comparison with 4-Rule in Section 3.2.3. The comparison policies are: 4-Rule without continuous expansion (N-Expan), NEH-LPT(λ) and random policy (Random). Simulation threshold: P = 4, taken the combination of expansion and exploration parameters as C = 0.5, D = 10,000.

These proposed algorithms were coded in MATLAB 2016a, and run on Intel Core i5-3470 3.2 GHz PC with 4 GB memory. The ISP-MCTS limited their run time to 30 n × s ms and ran two fixed replications. The minimum completion time C_min is the optimal result of all simulation policies under the current instance. The deviation between the final solution of each simulation policy and C_min is as shown in the following Equation (15):

RPI(C_i) = (C_i − C_min)/C_min × 100%,

(15)

In Equation (15), C_i is the solution value of the current simulation policy. The average relative percentage increase (ARPI) of the 10 sets of problems under each n and s combination is shown in

Table 1. Comparison results for the RPI values of the four simulation policies.

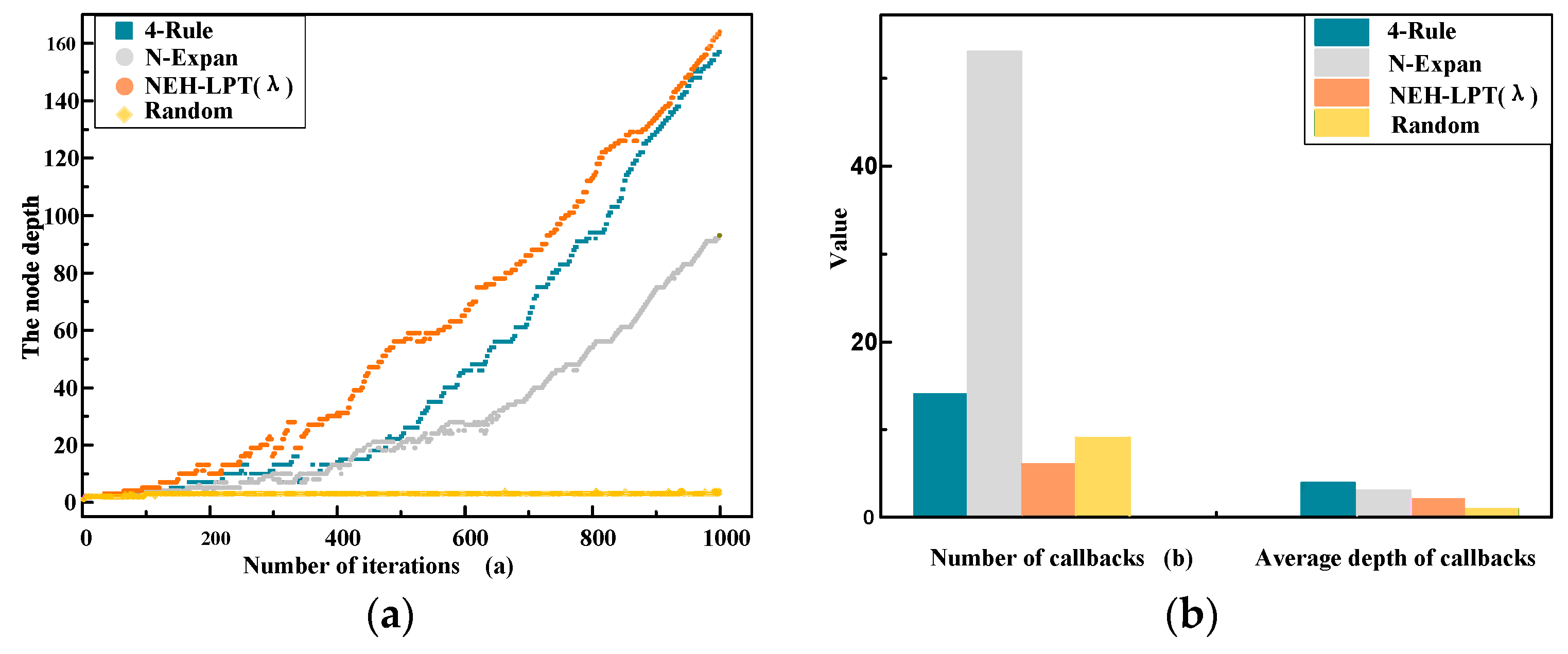
Problem	4-Rule	N-Expan	NEH-LPT(λ)	Random
20 × 4	0.01	0.02	4.92	12.23
20 × 6	0.03	0.04	4.37	13.11
20 × 8	0.15	0.29	5.76	14.45
40 × 4	0.08	0.12	4.11	10.17
40 × 6	0.14	0.37	4.77	13.67
40 × 8	0.11	0.28	5.67	15.42
60 × 4	0.04	0.16	4.52	12.83
60 × 6	0.07	0.52	4.87	14.17
60 × 8	0.13	0.31	5.12	17.85
80 × 4	0.02	0.47	2.31	11.77
80 × 6	0.03	0.17	7.57	13.46
80 × 8	0.06	0.24	6.86	15.52
100 × 4	0.03	0.23	3.18	12.83
100 × 6	0.08	0.29	3.57	17.51
100 × 8	0.07	0.61	6.85	21.84
Ave.	0.07	0.275	4.963	14.455

Notes: RPI: Relative percentage increase. NEH-LPT: the algorithm of Nawaz, Enscore and Ham - longest processing time.

. It can be seen that the average deviation of 4-Rule in the four-simulation policy is the smallest, with the average deviation of 0.07%. Meanwhile, the average deviation of the solution of the 4-Rule simulation policy is better than the simulation policy of the comparison.

Simulation policies were analyzed using a 40 × 6 case instance. Figure 2a shows the relationship between the number of iterations and the node depth. The number of callbacks and average depth of callbacks for each simulation policy are shown in Figure 2b. From Figure 2, NEH-LPT(λ) has the greater heuristic depth than the other three simulation policies throughout the iteration. In the iterative process, the number of NEH-LPT(λ) callbacks are the least, and the average depth of NEH-LPT(λ) callbacks are less than the two algorithms of 4-Rule and N-Expan. Therefore, it can be concluded that the NEH-LPT(λ) can easily fall into local minimum. The evaluation positioning is not accurate, and the N-Expan has a high callback frequency in the heuristic process. Therefore, the search depth of the N-Expan is less than 4-Rule. The Random has the least depth of search. From Figure 2b, since 4-Rule has the largest average callback depth, the 4-Rule can be used to accurately locate the branch area within a limited number of callbacks.

A single-factor analysis of variance (ANOVA) was carried out, where the type of simulation policy in

Table 2. The hypothesis tests of 4-Rule with other heuristic schemes.

	N-Expan and 4-Rule	NEH-LPT(λ) and 4-Rule	Random and 4-Rule
p-Value	0.00	0.00	0.00
Significant? (p < 0.05)	Yes	Yes	Yes

is considered to be a factor. The 4-Rule and the other three simulation policies are analyzed by multi-comparison method using the least significant difference (LSD) procedure. It indicates that the 4-Rule is significantly better than the other three simulation policies of N-Expan, NEH-LPT(λ) and Random. Therefore, the heuristic advantage of the 4-Rule is verified, and the 4-Rule is selected as the simulation policy.

4.2. Parameter Setting

The Benchmark problems [42] and Liao problems [17] were introduced to verify the performance of the ISP-MCT algorithm. The scale of the problems ranged from 10 jobs of 5 stages to 30 jobs of 10 stages. In this section, the parameter combination (C,D) is optimized in three segments according to the search space magnitude. The order of magnitude is 0–10⁵, 10⁵–10⁶ and 10⁶–5 × 10⁶. The parameter combination (0.1, 32) focuses on the development of potential nodes during the search process. Parameter combination (1, 20,000) in the search process considers the exploration ability of unknown regions, and the combination of parameters (0.5, 10,000) in the search process takes into account the expansion and exploration capabilities. As shown in

Table 3. Results of improved single-player Monte-Carlo tree search (ISP-MCTS) for the different settings.

(C,D)	(0.1, 32)	(0.5, 10,000)	(1, 20,000)
0–105(j15c5d2) (~10 s)
Average completion time	84.83	85.14	88.27
Standard deviation	0.53	1.27	2.50
Average depth	57	19	11
105–106(j30c5e4) (~100 s)
Average completion time	570.9	567.3	581.1
Standard deviation	3.51	2.77	4.73
Average depth	207	73	14
106–5 × 106(j30c5e1) (~200 s)
Average completion time	482.7	465.3	480.5
Standard deviation	3.56	2.72	3.21
Average depth	289	98	27

, j15c5d2 is selected for optimization analysis at each stage, and each parameter combination is operated independently for 20 times to obtain an average score. The depth is the distance between the deepest node and the root node, and the average depth is the average of 20 independent running depths.

As shown in Table 3, in the order of magnitude of 10⁵–10⁶, 10⁶–5 × 10⁶ within the specified time limit, the ISP-MCTS obtains the minimum average completion time and standard deviation, when the parameter combination is (0.1, 32). When applying the parameter combination (0.1, 32), the ISP-MCTS finds the minimum average completion time. The average depth of the search tree at the parameter combination (0.1, 32) is 57, then most of the nodes generated in the scheduling of the 15 jobs of 5 stages have been extended to the tree by the ISP-MCTS. Compared with the other two sets of parameters (0.5, 10,000) and (1, 20,000), the parameter combination (0.1, 32) expands the node deeper.

In the order of magnitude 10⁵~10⁶, 10⁶~5 × 10⁶ within the specified time limit, when the parameter combination is (0.5, 10,000), the ISP-MCTS finds that the average minimum completion time is optimal, and the algorithm stability is better than other combinations.

With the increasing magnitude and search time, the exploratory parameter combination advantage becomes more and more obvious. Therefore, at the order of magnitude of 10⁶–5 × 10⁶, the exploration parameter (1, 20,000) was significantly better than the parameter combination (0.1, 32).

It can be observed from the above that the order of magnitude is 0–10⁵ within the specified time limit. When the parameter combination is (0.1, 32), the ISP-MCTS algorithm has the highest solution quality and the best stability. Therefore, when the order of magnitude is 10⁵~10⁶ or 10⁶~5 × 10⁶, the algorithm selects the parameter combination (0.5, 10,000).

5. Calculation Results and Analysis

According to the machine layout, the Benchmark problems is divided into two groups: (1) 47 a and b problems; and (2) 30 c and d problems. The ISP-MCTS algorithm was programmed in MATLAB 2016a and run on a central processing unit (CPU)-i5-3470(3.20GHZ) with 4.0 GB Main Memory. Six algorithms HVNS [20], IDABC [21], particle swarm optimization (PSO) [17], AIS [25], genetic algorithm (GA) [16] and B&B [8] are selected as comparison algorithms. The calculation results of the above comparison algorithm are obtained from the source literature. The HVNS algorithm sets the maximum running time to 100 s and takes the minimum completion time of 20 independent results under the same conditions. The IDABC algorithm also limits their runtime to 1600 s and runs 20 times independently. The maximum running time of the algorithms B&B, AIS, GA and PSO in the literature is limited to 1600 s. The minimum C_max is obtained as the final solution by independently operating 20 times under the same conditions, and thus the CPU time corresponding to C_max is recorded for each problem. The performance of each algorithm is compared by “%Deviation”, and the deviation between the lower bound LB and each algorithm C_max is obtained by using Equation (16), as shown in

Table 4. Comparison results for the type a and type b problems.

Problem	LB	ISP-MCTS		IDABC		HVNS		PSO		GA		AIS		B&B
		Cmax	CPU	Cmax	CPU	Cmax	CPU	Cmax	CPU	Cmax	CPU	Cmax	CPU	Cmax	CPU
j10c5a2	88	88	0.003	88	0.002	88	0.004	88	0.002	88	0.000	88	1	88	13
j10c5a3	117	117	0.003	117	0.003	117	0.004	117	0.002	117	0.000	117	1	117	7
j10c5a4	121	121	0.002	121	0.003	121	0.002	121	0.003	121	0.015	121	1	121	6
j10c5a5	122	122	0.004	122	0.005	122	0.003	122	0.013	122	0.000	122	1	122	11
j10c5a6	110	110	0.022	110	0.009	110	0.024	110	0.174	110	0.015	110	4	110	6
j10c5b1	130	130	0.003	130	0.003	130	0.003	130	0.003	130	0.000	130	1	130	13
j10c5b2	107	107	0.003	107	0.004	107	0.003	107	0.003	107	0.000	107	1	107	6
j10c5b3	109	109	0.003	109	0.003	109	0.003	109	0.012	109	0.000	109	1	109	9
j10c5b4	122	122	0.003	122	0.003	122	0.004	122	0.025	122	0.000	122	2	122	6
j10c5b5	153	153	0.003	153	0.003	153	0.003	153	0.001	153	0.000	153	1	153	6
j10c5b6	115	115	0.003	115	0.004	115	0.002	115	0.001	115	0.000	115	1	115	11
j10c10a1	139	139	0.031	139	0.009	139	0.227	139	0.055	139	0.015	139	1	139	41
j10c10a2	158	158	0.337	158	0.009	158	0.354	158	0.87	158	0.125	158	18	158	21
j10c10a3	148	148	0.036	148	0.008	148	0.225	148	0.017	148	0.047	148	1	148	58
j10c10a4	149	149	0.010	149	0.007	149	0.007	149	0.085	149	0.141	149	2	149	21
j10c10a5	148	148	0.006	148	0.006	148	0.006	148	0.102	148	0.000	148	1	148	36
j10c10a6	146	146	0.282	146	0.008	146	0.264	146	0.239	146	0.156	146	4	146	20
j10c10b1	163	163	0.006	163	0.007	163	0.006	163	0.013	163	0.000	163	1	163	36
j10c10b2	157	157	0.114	157	0.009	157	0.104	157	0.221	157	0.131	157	1	157	66
j10c10b3	169	169	0.007	169	0.007	169	0.006	169	0.014	169	0.000	169	1	169	19
j10c10b4	159	159	0.012	159	0.005	159	0.068	159	0.021	159	0.015	159	1	159	20
j10c10b5	165	165	0.007	165	0.007	165	0.005	165	0.037	165	0.016	165	1	165	33
j10c10b6	165	165	0.008	165	0.006	165	0.005	165	0.056	165	0.016	165	1	165	34
j15c5a1	178	178	0.007	178	0.016	178	0.006	178	0.060	178	0.031	178	1	178	18
j15c5a2	165	165	0.005	165	0.018	165	0.005	165	0.005	165	0.015	165	1	165	35
j15c5a3	130	130	0.008	130	0.017	130	0.005	130	0.006	130	0.015	130	1	130	34
j15c5a4	156	156	0.010	156	0.019	156	0.005	156	0.013	156	0.015	156	2	156	21
j15c5a5	164	164	0.005	164	0.016	164	0.003	164	0.004	164	0.046	164	1	164	34
j15c5a6	178	178	0.007	178	0.016	178	0.005	178	0.006	178	0.032	178	1	178	38
j15c5b1	170	170	0.007	170	0.012	170	0.005	170	0.003	170	0.015	170	1	170	16
j15c5b2	152	152	0.005	152	0.015	152	0.003	152	0.005	152	0.015	152	1	152	25
j15c5b3	157	157	0.006	157	0.014	157	0.006	157	0.030	157	0.015	157	1	157	15
j15c5b4	147	147	0.010	147	0.017	147	0.007	147	0.000	147	0.015	147	1	147	37
j15c5b5	166	166	0.100	166	0.020	166	0.088	166	0.086	166	0.016	166	2	166	20
j15c5b6	175	175	0.007	175	0.018	175	0.004	175	0.016	175	0.015	175	1	175	23
j15c10a1	236	236	0.011	236	0.033	236	0.008	236	0.018	236	0.015	236	1	236	40
j15c10a2	200	200	0.120	200	0.048	200	0.339	200	0.214	200	0.015	200	30	200	154
j15c10a3	198	198	0.130	198	0.032	198	0.313	198	0.171	198	0.063	198	4	198	45
j15c10a4	225	225	0.070	225	0.034	225	0.212	225	0.072	225	0.031	225	12	225	78
j15c10a5	182	182	0.011	182	0.036	182	0.008	182	0.509	182	0.016	182	2	183	c
j15c10a6	200	200	0.052	200	0.033	200	0.024	200	0.468	200	0.031	200	2	200	44
j15c10b1	222	222	0.026	222	0.048	222	0.009	222	0.017	222	0.031	222	3	222	70
j15c10b2	187	187	0.009	187	0.044	187	0.008	187	0.012	187	0.047	187	1	187	80
j15c10b3	222	222	0.009	222	0.039	222	0.008	222	0.007	222	0.015	222	1	222	80
j15c10b4	221	221	0.009	221	0.037	221	0.008	221	0.007	221	0.016	221	1	221	84
j15c10b5	200	200	0.109	200	0.048	200	0.045	200	0.135	200	0.094	200	1	200	84
j15c10b6	219	219	0.010	219	0.037	219	0.009	219	0.006	219	0.031	219	1	219	67
AVE			0.035		0.017		0.052		0.082		0.028		2.574		35.674

Notes: CPU: The CPU time of the algorithm in seconds. ISP-MCTS: Improved single-player Monte-Carlo tree search. IDABC: Improved discrete artificial bee colony algorithm. HVNS: Hybrid variable neighborhood search. PSO: Particle swarm optimization. GA: Genetic algorithm. AIS: Artificial immune system. B&B: Branch-and-bound algorithm. GA_R: Genetic algorithm (Ruiz, R). ISA: Improved simulated annealing. ABC_P: Artificial bee colony algorithm with permutation.

and

Table 5. Comparison results for type c and d problems.

Problem	LB	ISP-MCTS		IDABC		HVNS		PSO		GA		AIS		B&B
		Cmax	CPU	Cmax	CPU	Cmax	CPU	Cmax	CPU	Cmax	CPU	Cmax	CPU	Cmax	CPU
j10c5c1	68	68	0.275	68	0.017	68	0.792	68	0.332	68	0.031	68	32	68	28
j10c5c2	74	74	0.633	74	0.055	74	0.752	74	0.535	74	0.016	74	4	74	19
j10c5c3	71	71	0.752	72	a	72	0.141(a)	71	36.997	71	0.016	72	a	71	240
j10c5c4	66	66	0.161	66	0.005	66	0.631	66	0.215	66	0.031	66	3	66	1017
j10c5c5	78	78	0.382	78	0.004	78	0.129	78	0.122	78	0.094	78	14	78	42
j10c5c6	69	69	0.527	69	0.004	69	0.226	69	0.405	69	0.000	69	12	69	4865
j10c5d1	66	66	0.268	66	0.005	66	0.148	66	0.185	66	0.046	66	5	66	6490
j10c5d2	73	73	0.271	73	0.069	73	0.142	73	1.158	73	0.110	73	31	73	2617
j10c5d3	64	64	0.277	64	0.007	64	0.157	64	0.098	64	0.015	64	15	64	481
j10c5d4	70	70	0.895	70	0.003	70	0.675	70	0.337	70	0.000	70	5	70	393
j10c5d5	66	66	1.576	66	0.009	66	1.382	66	0.515	66	0.031	66	1446	66	1627
j10c5d6	62	62	0.276	62	0.009	62	0.135	62	0.383	62	0.062	62	8	62	6861
j10c10c1	113	114	2.822(a)	115	a	115	0.571(a)	115	a	115	a	115	a	127	c
j10c10c2	116	117	0.414(a)	119	a	117	0.448(a)	117	a	117	a	119	a	116	1100
j10c10c3	98	108	2.706(a)	116	a	116	0.698(a)	116	a	116	a	116	a	133	c
j10c10c4	103	112	2.315(a)	120	a	120	0.461(a)	120	a	120	a	120	a	135	c
j10c10c5	121	125	2.831(a)	125	a	125	2.125(a)	125	a	125	a	126	a	145	c
j10c10c6	97	105	2.663(a)	106	a	106	0.343(a)	106	a	106	a	106	a	112	c
j15c5c1	85	85	1.179	85	0.127	85	1.128	85	4.205	85	0.031	85	774	85	2131
j15c5c2	90	90	0.785	90	27	90	0.491	90	1198	91	a	91	a	90	184
j15c5c3	87	87	0.511	87	0.048	87	0.502	87	2.398	87	0.109	87	16	87	202
j15c5c4	89	89	0.653	89	0.038	89	0.569	89	2.208	89	0.000	89	317	90	c
j15c5c5	73	74	2.197(a)	74	a	74	1.968(a)	74	a	75	a	74	a	84	c
j15c5c6	91	91	0.370	91	0.027	91	0.180	91	0.191	91	0.047	91	19	91	57
j15c5d1	167	167	0.005	167	0.020	167	0.004	167	0	167	0.015	167	1	167	24
j15c5d2	82	84	1.133(a)	84	a	84	0.915(a)	84	a	84	a	84	a	85	c
j15c5d3	77	82	2.171(a)	82	a	82	1.356(a)	82	a	83	a	83	a	96	c
j15c5d4	61	84	0.672(a)	84	a	84	1.325(a)	84	a	84	a	84	a	101	c
j15c5d5	67	79	1.559(a)	79	a	79	0.585(a)	79	a	80	a	80	a	97	c
j15c5d6	79	81	1.683(a)	81	a	81	1.123(a)	81	a	82	a	82	a	87	c
AVE			0.544		1.615		0.473		73.43		0.038		168.88		455.23

. The statistical analysis results are shown in

Table 6. Performance summary of the different algorithms.

Algorithm	a and b Problems		c and d Problems
	Solved	Deviation	Solved	Deviation
ISP-MCTS	47	0	18	3.40%
IDABC	47	0	17	4.00%
HVNS	47	0	17	4.00%
PSO	47	0	18	3.95%
GA	47	0	17	4.17%
AIS	47	0	16	4.26%
B&B	46	0.12%	18	9.32%

:

$$\%\mathrm{deviation}=\left(\frac{C_{\max }-LB}{LB}\right)\times 100\%$$

(16)

5.1. Comparison of Carlier and Neron’s Benchmarks

From Table 4 and Table 5, only the B&B algorithm does not obtain the optimal solution when solving the problem of j15c10a5 in the 47 a and b problems. The PSO and B&B algorithms, respectively, solve the optimal solutions of 18 problems in 30 c and d problems, and the average deviation of the solutions is 3.95% and 9.32%, respectively. As shown in Table 6, the IDABC, HVNS and GA algorithms solve the optimal solutions for the 17 problems in the 30 c and d problems, and the average deviation of the solutions are 4.00%, 4.00% and 4.17%, respectively. The AIS algorithm solves the optimal solution of 16 problems in 30 c and d problems, and the average deviation of the solution is 4.26%. The ISP-MCTS algorithm proposed in this paper solves the optimal solution of 18 problems in 30 c and d problems, and the average deviation of the solution is 3.4%. Therefore, the solution quality of the ISP-MCTS algorithm for solving c and d problems is better than the other six algorithms. It can be seen from Table 4 and Table 5 that the average CPU time of the ISP-MCTS algorithm is much smaller than that of the the PSO and B&B algorithms. From the above comparison, the ISP-MCTS algorithm has a better solution and efficient optimization ability than the other six algorithms when solving Carlier and Neron problems.

5.2. Comparison of Liao’s Benchmarks

From the discussion in Section 5.1, the average completion time of the three algorithms of IDABC, HVNS and PSO for solving Carlier and Neron’s benchmarks is smaller than that of GA, AIS, and B&B algorithms. Therefore, the algorithms IDABC, HVNS and PSO are selected as the comparison algorithms to solve the Liao problems in this section. In the source literature, the IDABC algorithm was coded in Visual C++ and run on an Intel Pentium 3.06 GHz PC with 2 GB RAM under the Windows 7 operating system, and each problem was tested 20 times and the termination criterion for all the tests was the computation time 100 s. The running environment of the HVNS algorithm in the literature [20] was Intel Core i5 3.3 GHz PC with 4 GB of memory. The algorithm PSO was used to solve the Liao problems, and the algorithm limited its run time to 200 s and each problem runs 20 times independently. The ISP-MCTS algorithm is used to solve the Liao problems in the computer running environment proposed in this paper, and the execution time for each problem is limited to 200 s.

As shown in

Table 7. Comparison results for the ten harder problems.

Problem	ISP-MCTS				IDABC				HVNS						PSO
	Ave.	Min.	Std.	CPU	Ave.	Min.	Std.	CPU	Ave.	Min.	Std.	CPU	Ave.	Min.	Std.	CPU
j30c5e1	463.2	462	0.81	14.52	465.2	463	1.80	57	465.41	464	1.34	29.16	474.70	471	1.42	96.16
j30c5e2	616.0	616	0	10.32	616.0	616	0	2	616.22	616	0.32	11.69	616.25	616	0.44	55.28
j30c5e3	594.7	593	0.97	20.37	596.4	593	1.70	49	598.51	595	3.32	27.33	610.25	602	4.70	64.56
j30c5e4	565.3	563	1.23	18.53	566.2	565	1.60	39	568.32	566	1.44	37.00	577.10	575	1.52	86.98
j30c5e5	600.9	600	0.77	17.23	602.0	600	1.60	58	603.75	601	1.26	21.32	606.80	605	1.11	79.84
j30c5e6	602.8	600	1.44	17.06	603.1	601	1.80	55	607.01	603	3.32	33.39	612.50	605	3.49	67.99
j30c5e7	626.4	626	0.31	18.23	626.0	626	0	19	627.34	626	0.83	27.37	630.60	629	0.75	87.18
j30c5e8	674.4	674	0.69	22.69	674.7	674	0.90	55	676.40	674	2.23	31.40	684.20	678	2.50	97.67
j30c5e9	643.1	642	0.76	21.37	643.7	642	1.00	67	645.28	643	1.66	33.81	654.65	651	1.87	83.80
j30c5e10	574.2	573	1.09	23.81	576.3	573	1.50	76	581.33	577	3.97	29.72	599.75	594	5.28	77.46
Ave.	596.1	594.9	0.83	18.41	596.9	595.3	1.19	47.7	598.96	596.5	1.97	28.22	606.68	602.6	2.31	79.69

, the average completion time of the ISP-MCTS solution is smaller than that of the IDABC, HVNS and PSO, and the ISP-MCTS further updates the best solution of the three problems in Liao problems. The nonparametric test is proposed, and the null hypothesis H₀ assumes that μ_ISP-MCTS ≥ μ_IDABC, and the alternative hypothesis H₁: μ_ISP-MCTS < μ_IDABC with 0.05 significance level. Similarly, the hypotheses H_0’:μ_ISP-MCTS ≥ μ_HVNS, H_1’:μ_ISP-MCTS < μ_HVNS. H_0’’:μ_ISP-MCTS ≥ μ_PSO, H_1’’:μ_ISP-MCTS < μ_PSO. As shown in

Table 8. Comparison results for the ten harder problems.

	ISP-MCTS and IDABC	ISP-MCTS and HVNS	ISP-MCTS and PSO
p-Value	0.12	0.018	0
Significant? (p < 0.05)	NO	Yes	Yes

, the ISP-MCTS algorithm performs significantly better than the PSO and AIS algorithms, and has certain advantages in terms of solution quality and stability compared with the HVNS algorithm.

The six effective algorithms for solving HFSSP in recent years were selected for comparison with ISP-MCTS. The algorithms were: HVNS [20], IDABC [21], PSO [17], GA_R [2], ISA [43] and artificial bee colony with permutation (ABC_P) [21]. In the computer operating environment of this study, each algorithm solved 150 problems in Section 4.1. For the comparison algorithms, HVNS, DABC, and PSO solved the same problems as reported in the literature, whereas GA_R, ISA, and ABC_P were used to solve complex HFSSP, and the ability to solve these algorithms was verified. The above algorithms directly select the optimal parameter combination of the source literature. All the algorithm runtimes were limited to the maximum CPU (t = ρ mn s) time, and ρ is: 10, 20, 30. All the above algorithms are programmed in MATLAB 2016a, and each of the 150 examples is run independently for 10 times, and the average of 10 running results is taken as the solution of each example. When ρ = 30, the best solution C_min found by any algorithm is used to calculate the relative percentage increase (RPI). The results are shown in

Table 9. Computational results of the algorithms (ρ = 10).

Problem	ISP-MCTS	IDABC	HVNS	PSO	GAR	ISA	ABCp
20 × 4	0.03	0.03	0.31	0.71	1.01	0.68	0.38
20 × 6	0.12	0.11	0.24	0.77	1.27	0.78	0.69
20 × 8	0.33	0.34	0.61	1.03	1.21	1.18	0.82
40 × 4	0.03	0.03	0.22	0.31	0.52	0.34	0.49
40 × 6	0.04	0.03	0.15	0.22	0.71	0.29	0.77
40 × 8	0.17	0.18	0.66	0.98	1.39	1.12	1.13
60 × 4	0.11	0.13	0.11	0.33	0.51	0.35	0.48
60 × 6	0.16	0.16	0.23	0.41	0.61	0.47	0.55
60 × 8	0.21	0.25	0.42	0.67	1.10	0.71	1.04
80 × 4	0.06	0.06	0.11	0.20	0.35	0.21	0.33
80 × 6	0.20	0.21	0.24	0.46	0.65	0.52	0.60
80 × 8	0.12	0.12	0.33	0.55	0.61	0.32	0.52
100 × 4	0.00	0.01	0.03	0.05	0.18	0.05	0.11
100 × 6	0.05	0.05	0.10	0.23	0.41	0.27	0.38
100 × 8	0.09	0.11	0.18	0.51	0.62	0.35	0.57
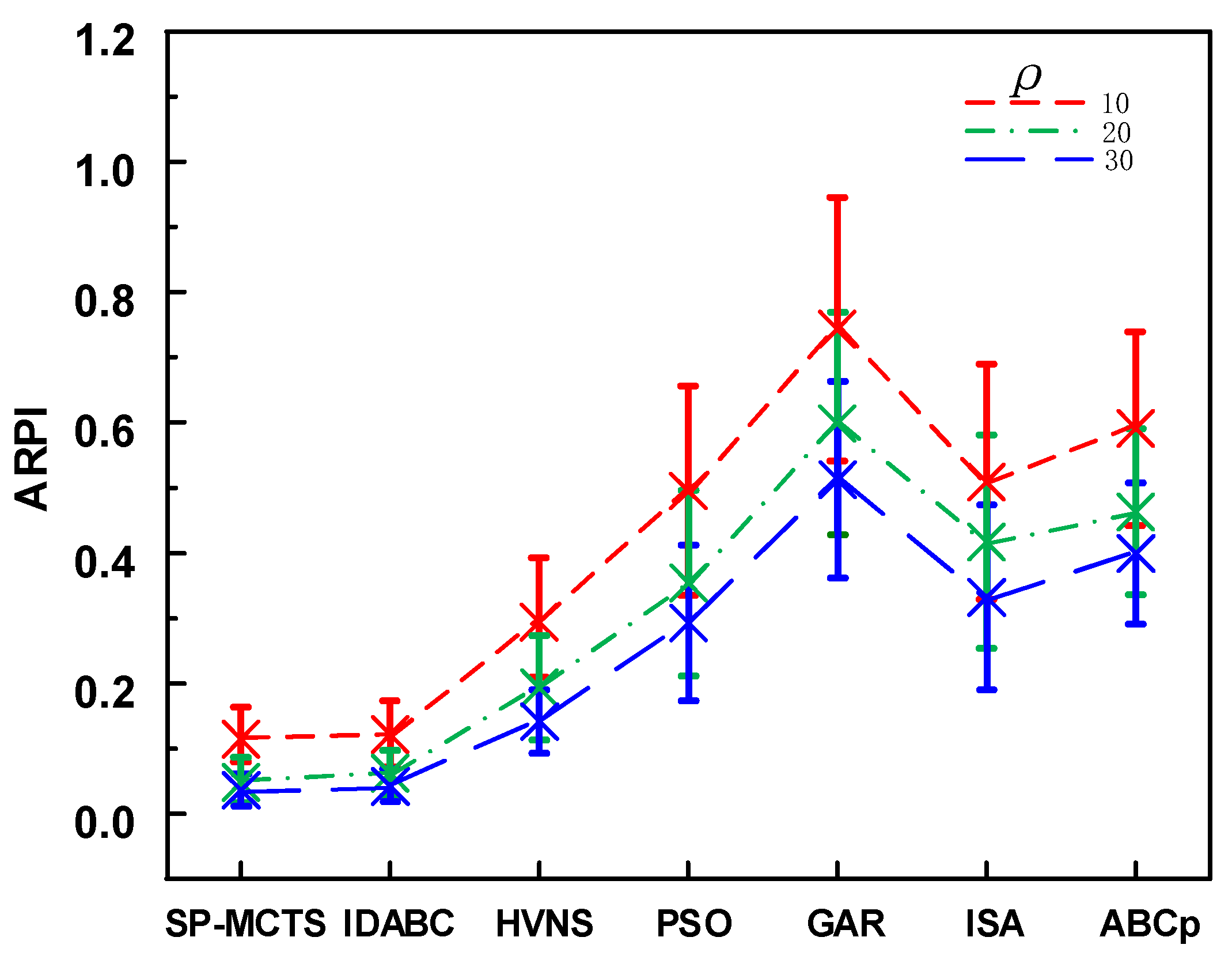
Ave.	0.115	0.121	0.263	0.495	0.743	0.509	0.591

,

Table 10. Computational results of the algorithms (ρ = 20).

Problem	ISP-MCTS	IDABC	HVNS	PSO	GAR	ISA	ABCp
20 × 4	0.02	0.01	0.27	0.62	0.88	0.57	0.29
20 × 6	0.04	0.06	0.16	0.68	1.03	0.66	0.57
20 × 8	0.21	0.23	0.47	0.89	0.96	1.01	0.44
40 × 4	0.02	0.03	0.15	0.24	0.41	0.29	0.36
40 × 6	0.01	0.02	0.11	0.15	0.56	0.17	0.51
40 × 8	0.10	0.13	0.53	0.73	1.15	1.01	0.99
60 × 4	0.05	0.07	0.09	0.21	0.47	0.31	0.42
60 × 6	0.06	0.10	0.17	0.33	0.48	0.36	0.51
60 × 8	0.12	0.13	0.31	0.42	0.92	0.62	0.93
80 × 4	0.02	0.02	0.08	0.11	0.29	0.18	0.31
80 × 6	0.09	0.13	0.17	0.23	0.65	0.46	0.48
80 × 8	0.05	0.09	0.25	0.33	0.47	0.28	0.42
100 × 4	0.00	0.00	0.02	0.03	0.13	0.03	0.09
100 × 6	0.02	0.02	0.07	0.11	0.28	0.16	0.31
100 × 8	0.06	0.06	0.21	0.39	0.46	0.31	0.48
Ave.	0.058	0.073	0.204	0.365	0.609	0.428	0.474

and

Table 11. Computational results of the algorithms (ρ = 30).

Problem	ISP-MCTS	IDABC	HVNS	PSO	GAR	ISA	ABCp
20 × 4	0.00	0.00	0.15	0.43	0.76	0.49	0.22
20 × 6	0.03	0.03	0.12	0.51	0.97	0.58	0.52
20 × 8	0.17	0.21	0.29	0.77	0.82	0.91	0.41
40 × 4	0.00	0.01	0.11	0.12	0.33	0.21	0.27
40 × 6	0.01	0.01	0.09	0.11	0.41	0.14	0.42
40 × 8	0.06	0.09	0.35	0.62	0.95	0.75	0.86
60 × 4	0.02	0.02	0.06	0.17	0.36	0.26	0.36
60 × 6	0.04	0.05	0.13	0.31	0.41	0.27	0.44
60 × 8	0.05	0.06	0.18	0.37	0.75	0.45	0.74
80 × 4	0.00	0.00	0.07	0.09	0.24	0.11	0.26
80 × 6	0.03	0.05	0.14	0.18	0.55	0.32	0.37
80 × 8	0.05	0.05	0.16	0.27	0.43	0.19	0.34
100 × 4	0.00	0.00	0.02	0.03	0.09	0.01	0.08
100 × 6	0.01	0.01	0.06	0.09	0.26	0.11	0.28
100 × 8	0.04	0.04	0.19	0.32	0.35	0.18	0.41
Ave.	0.034	0.042	0.141	0.293	0.512	0.332	0.399

.

As shown in Table 9, Table 10 and Table 11, the ISP-MCTS solution quality is better than that of the other six algorithms. When ρ = 10, the average deviation of ISP-MCTS in the seven algorithms is the smallest, and the value is 0.115. The average deviation of the ISP-MCTS algorithm is less than IDABC (0.121), HVNS (0.263), PSO (0.495), GA_R (0.743), ISA (0.509), and ABC_P (0.591). Therefore, the solution quality of the ISP-MCTS algorithm is better than the other six algorithms. When ρ = 20 and ρ = 30, the average deviation of all algorithms is improved through comparing to ρ = 10. At the same time, the ISP-MCTS algorithm still has the smallest deviation among all algorithms, so the validity of the ISP-MCTS algorithm can be verified.

Here, a multi-factor analysis of variance was used to further compare the seven algorithms, and the algorithm type and ρ were taken as factors. From the mean graph and the two-factor Tukey HSD test (95% confidence interval) as shown in Figure 3, the ISP-MCTS algorithm is significantly better than the HVNS, PSO, GA_R, ISA, and ABC_P algorithms at different CPU times. According to the above average variance value, the superiority of the ISP-MCTS algorithm in solving the HFSSP problem was verified.

6. Conclusions

• This paper analyzed the HFSSP operation mechanism, and proposed a tree search algorithm based on SP-MCTS to solve HFSSP. In order to solve the problem of HFSSP by SP-MCTS algorithm, the three steps of selection, expansion and simulation were improved respectively. The improvement of the algorithm included the selection blending standard deviation, the single-branch expansion strategy and the 4-Rule policy simulation. The results show that these improvements can quickly and accurately locate high-potential branches, and obtain the optimal solution.
• The 4-Rule simulation policy was selected based on a comparative analysis of the problems, and the 4-Rule can give an accurate evaluation of the leaf nodes during the search process, thus improving the search efficiency of the algorithm. According to the magnitude of the search, the combination of the parameters C and D was determined to ensure the convergence speed of the algorithm.
• The experimental results of the standard problems show that the ISP-MCTS algorithm is effective, and the optimal solutions of 47 class a and class b problems can be obtained at 100%. The ISP-MCTS algorithm solved the optimal solution of 18 problems in the c and d problems, and the average deviation was 3.4%, which was lower than the other five comparison algorithms. This proves that the ISP-MCTS algorithm has certain advantages in solving the HFSSP problems. According to the statistical analysis results of each algorithm to solve the Liao problems, the ISP-MCTS performance is obviously better than the HVNS and PSO algorithms, and it has a certain superiority in solution quality and stability compared with the IDABC algorithm.
• Through the comparison of large-scale random problems, it shows that the ISP-MCTS algorithm is superior to the comparison algorithms in terms of CPU time, solution quality and stability.