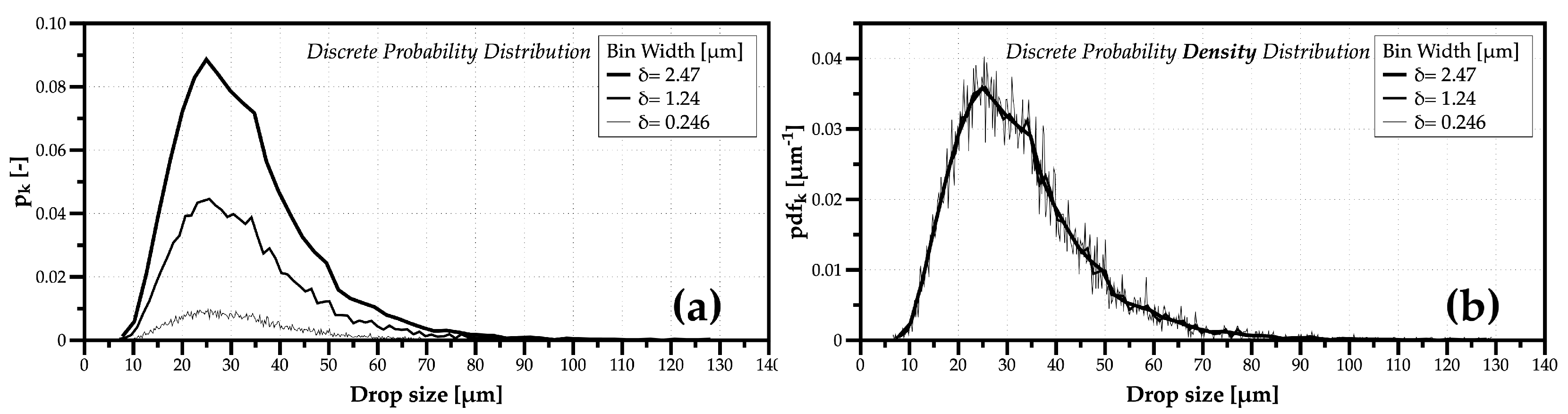
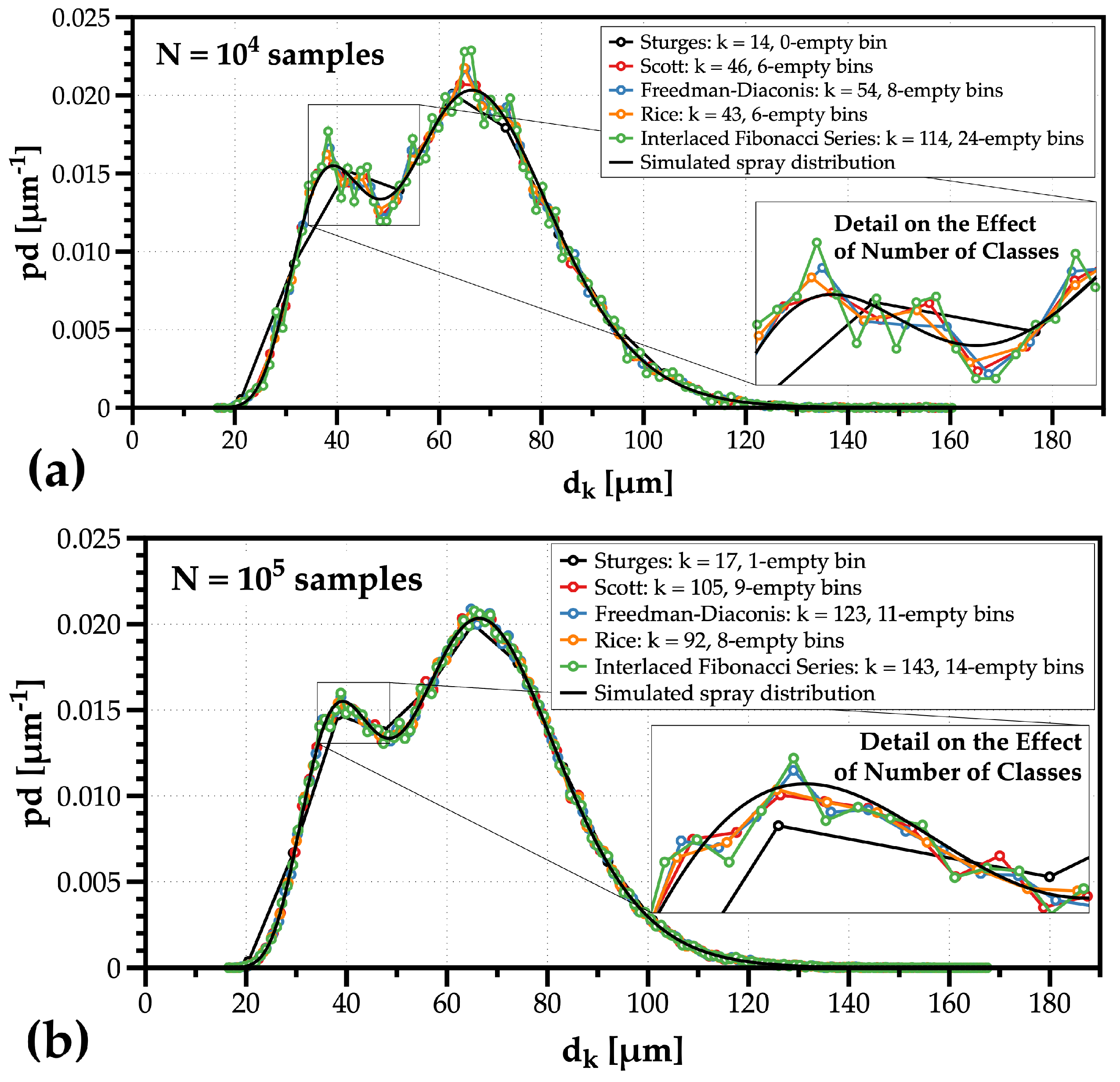
2.1. Defining Enoughness in Large Data Samples
An experimentalist stops a measurement based of criteria related to a statistical uncertainty. The definition of statistical uncertainty contains three conditions:
it is maximum for a uniform distribution where all classes have the same probability;
a small variation in the probability of a class generates a small variation in the uncertainty;
and, finally, it depends on the distribution itself.
The common measure used for the statistical uncertainty considers the standard deviation (
) and the sample size (
N) as
with
as the coefficient associated with the confidence interval considered (e.g.,
for a 95% Confidence Interval). When the mean value (
) is different from zero, dividing
by the mean provides the uncertainty in percentage. Since the standard deviation depends on the spray characteristics, reducing the statistical uncertainty implies adding more data to increase
N. However, as argued by Panao [
10], if the spray begins to operate in a different way and the distribution changes, the statistical uncertainty as defined in Equation (
4) continues to decrease, without providing any evidence to the experimentalist about the changes occurring in the spray. In a certain sense, it fails to comply to the third condition defining a statistical uncertainty because it is more sensitive to the sample size than the distribution itself. For this reason, an approach based on information theory is a better option.
In information theory, the Shannon entropy complies to all the aforementioned characteristics of a statistical uncertainty. Considering the probability values of any discrete distribution (
), the expression for calculating the Shannon entropy
H is
As an example, if we consider drop size, the minimum value corresponds to a monosize spray with all droplets having the same size, thus,
, and
. The maximum value occurs for a hypothetical spray where all droplets have the same probability of being present, corresponding to a uniform distribution with
k classes, each for a different drop size. Therefore, the maximum Shannon entropy is
. In sprays, while measuring size and velocity, considering the Shannon entropy normalized by its maximum value,
, it tends to stabilize (see Panao [
10] for details). The meaning is that adding more data does not mean adding more information because the shape and scale of the distribution stabilized. However, as argued in Panao [
10], the
enoughness requires a criterion with interpretative value and proposes the
excess entropy (
) because, as defined in Feldman et al. [
11], it is what best captures the nature of convergence of the entropy rate as the amount of memory gained, or the cost of amnesia if all data would suddenly be lost. To evaluate the evolution of
while measuring,
one calculates the entropy rate that quantifies the difference between the normalized Shannon entropy with adding one value the N samples and the Shannon entropy with N samples-;
considers the limit when , which is ;
and the excess entropy is formulated as
In the case of spray data, the stabilization implies
= 0, thus, it simplifies
. The method proposed is setting a convergence criterion–
and stop measuring when
, considering the number of samples corresponding to the median as the minimum required (see Panao [
10] for more details).
Once the experimentalist has enough information and organizes the spray data with histograms of drop velocity and weighted distributions of drop sizes, depending on the physical process under analysis, one of the methods to avoid losing information of the measured distributions is fitting data to known mathematical or empirical distribution functions. However, the question is whether such fitting can provide further insight into liquid atomization mechanisms. This is the topic explored in the next sub-section.
2.2. Underlying Physics of Probability Distribution Functions Applied to Sprays
An important consideration when characterizing sprays is the effect of the interaction between droplets and the continuous phase on the local (or even overall) size and velocity distributions. This interaction involves different transport phenomena, with momentum and energy exchanges between the dispersed phase (spray) and the carrier phase (surrounding environment), generating eventual secondary breakup of the spray droplets leading to changes in the shape and scale of drop size distributions, or acceleration (positive or negative) captured by changes in local velocity probability distributions. However, the physical reason why a certain distribution function might fit better than another is still open for further research.
This work advances an argument in favor of distinguishing between modeling and characterizing drop size distributions. The purpose of modeling drop size distributions is to
predict them from the information of the atomizer geometry and operating conditions. The simulation of sprays using a numerical approach [
12], or a statistical or stochastic approach [
13] can produce data on the droplets characteristics, but it is different from statistically processing such data. Therefore, according to Déchelette et al. [
14], there are four methods for modeling drop size distributions:
However, the purpose of characterizing a spray is to describe, as accurately as possible, the polydispersion of sizes and velocities of its droplets. This description aims at obtaining mean quantities for analyzing heat transfer and flow processes—or its aim is to improve our understanding of the nature underlying the atomization mechanisms.
There are two categories of probability distribution functions used to describe droplets’ characteristics: mathematical and empirical. Lefebvre and McDonell [
15] provide a synthesis of the main probability distributions in each category. Except for the Rosin–Rammler or Weibull, the Nukiyama–Tanasawa and Upper-Limit empirical distribution functions are complex and problems arise when determining the best-fit values for their parameters. As to the mathematical distribution functions, the simplest is the Log-Normal, while the Log-Hyperbolic is also complex and problems arise with finding the best fitting parameters. One distribution absent from Lefebvre and McDonell [
15] and other review works is the Gamma distribution function which Villermaux et al. [
16] associated with the distribution of droplets resulting from the fragmentation of ligaments, generating a spray, reviewed later in this section.
While most research on spray characterization focuses on the fitting process, few works such as Villermaux [
17] and Villermaux et al. [
16] address the meaning of the mathematical distribution function used and the physical background for such fitting. As mentioned in the Introduction, instead of focusing our attention on probability or probability density functions, we propose a greater focus on cumulative distribution functions (
). Therefore, any comparison between different
becomes universal and if such distribution properly describes the local or global experimental results, its digitization to simulate a spray is relatively accessible.
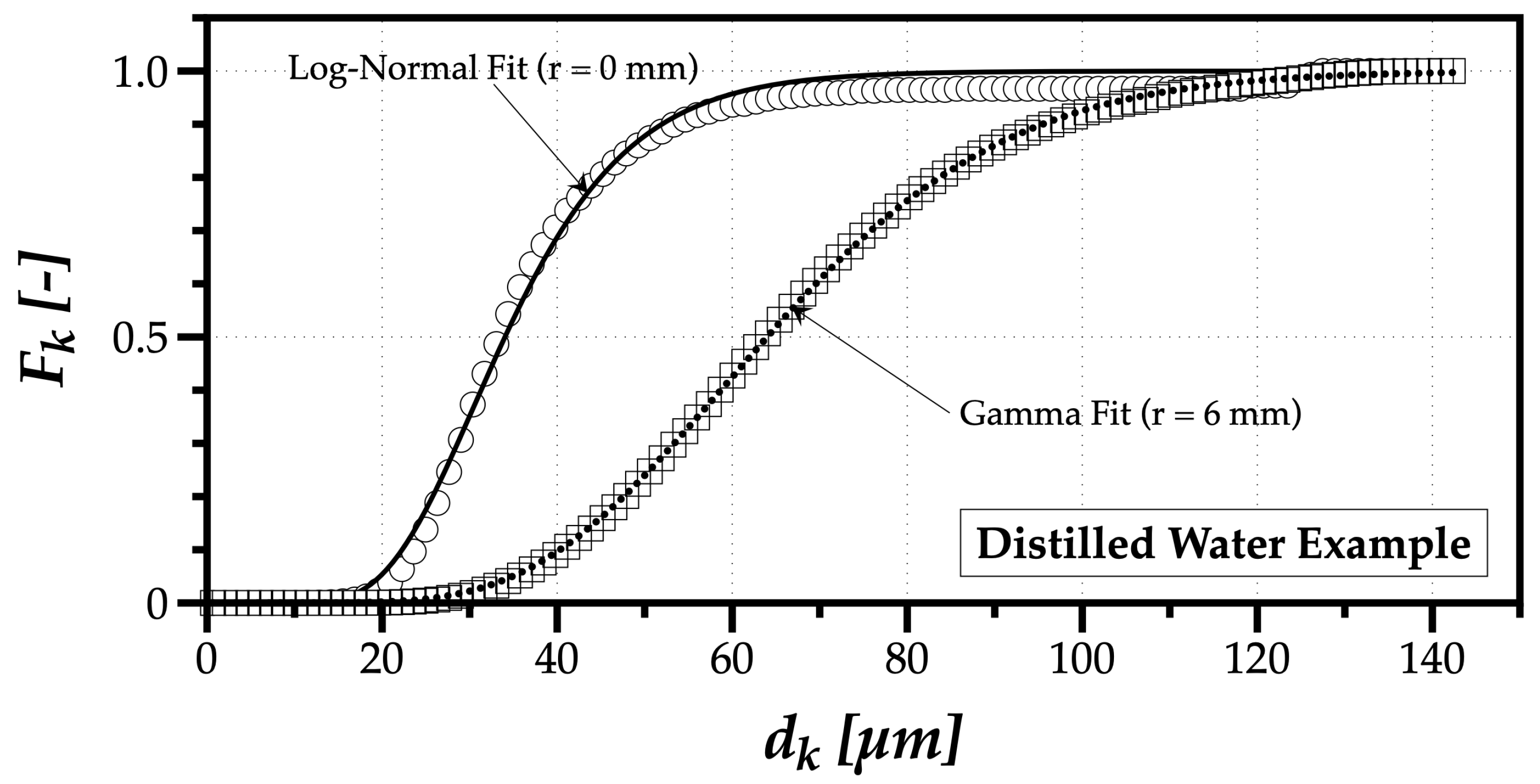
In the case of the Log-Normal distribution, its cumulative form given by
includes
as the scale parameter, the geometric mean diameter, and
as the shape parameter of the distribution. Applied to spray characterization, the reason for using a Log-Normal distribution function is related to the multiplicative effect of subsequent stages of droplets breaking up during atomization, as a cascade process, where one drop breaks into two or more and so on. However, if we consider the interaction between droplets and the continuous gaseous phase, in time, the dragging of droplets leads to secondary flows which eventually produce a vortical effect on the transport of subsequent droplets. Namely, smaller droplets, with lower response times, dragged by secondary flows, may return to upward locations, redistributing the counts of certain drop size classes in locations further downstream of the spray trajectory. Therefore, even if it is not the result of a multiplicative breakup process, the presence of these smaller drops affects the probability distributions describing the spray, having an effect similar to that of a cascade of multiple breakup stages. One could even speculate whether or not the reason for a Log-Normal distribution best fitting experimental results expresses the way the multiphase flow organizes the transport of droplets according to their size in a cascade pattern.
Besides several breakup stages and transport phenomena, some atomization processes result from the disintegration of liquid sheets or jets into ligaments, and those ligaments further fragmenting into droplets. In this case, Villermaux et al. [
16] argues each ligament constituted of several blobs, and when it fragments into several droplets, the size distribution that reasonably fits is a Gamma probability distribution function, which cumulative form is expressed by
with
a and
b as the shape and scale parameter, respectively. In this case, a characteristic size corresponds the product of both:
.
Considering empirical distribution functions, this work focuses on the Weibull distribution, first applied to describe the distribution of drop sizes by Rosin and Rammler,
where
is a scale parameter related to a characteristic drop size and
q is the shape parameter and considered a measure of the spreading in drop sizes. The accuracy of this empirical probability distribution is best related to drop size distributions with fewer smaller droplets or narrower size distributions [
15].
A final note considers the Nukiyama–Tanasawa empirical distribution that is often used to fit experimental data. Here, particular attention is given to the work of Li and Tankin [
18] that derived the expression using an information-theory approach, and for the spray liquid volume, its cumulative form results in
where
q is also the shape parameter.
The average quantities referred to so far are related to moments in probability distributions, but considering the cumulative distribution, any quantity corresponds to a representative diameter, generally expressed as , where x is the type of distribution, and w is the percent cumulative value related to the representative diameter. Therefore, if the cumulative distribution is
number-based, represents the size containing w% of the droplets in the spray;
area-based, represents the size containing w% of the spray surface area;
volume-based, represents the size containing w% of the liquid spray volume.
One of the most relevant representative diameters corresponds to 50% (, or ) because dividing the classes by that number allows a better comparison between cumulative distributions, useful for analyzing the effect of parametric variations in the spray.
2.3. Introducing Drop Size Diversity in a Spray
Drop size distributions are a way to organize the data acquired to characterize a spray. The characterization of the diversity of drop sizes answers two distinct questions: (1) how many different sizes are relevant in a spray; (2) and how different are the relevant sizes in a spray. The word relevant links to the probability of presence of certain drop size classes relative to others.
In the known textbook on
Atomization and Sprays, Lefebvre and McDonell [
15] refer to this diversity as
drop spray dispersion associated with the size range of droplets. On the other hand, several research articles address the different sizes of the spray droplets as a
polydispersed spray. In the authors’ opinion, these are two different things, which is why we introduce the concept of
Drop Size Diversity (DSD) measured by two different degrees:
the polydispersion degree to quantify the multitude of different sizes that are relevant in a spray. Thus, the maximum for the case where all different sizes have the same probability of being present in the spray, and
the heterogeneity degree to quantify how different are the relevant sizes in the spray. Therefore, it is related with the size range or size dispersion.
The challenge is to devise the right indicators to measure both degrees. Among the several indicators available and synthesized in Lefebvre and McDonell [
15], the most known and used indicator is the
Relative Span obtained from the representative diameters of a volume-based cumulative size distribution (
with
as the fraction of the spray liquid volume) as
Considering the normalization of a representative diameter by the value representing half of the liquid volume-
-as
, the interpretation of Equation (
10) relative to the range of drop sizes corresponds to a difference-
which is equal to zero when all droplets in the spray have the same size, and maximum when all droplets have the same probability of occurrence (a limit unrealistic case).
Panao [
19] proposed a different approach based on information theory, through the concept of the normalized Shannon entropy, already defined in
Section 2.1 as
In the information theory terminology applied to spray characterization, a spray where all droplets have the same size,
, resulting in a null normalized Shannon entropy,
, while an unrealistic spray with all classes having the same probability of presence (uniform distribution),
, because the Shannon entropy–numerator in Equation (
11)–is maximum.
Finally, García et al. [
20] proposed a third approach based on the standard deviation of the volume-weighted drop size distribution expressed as
where
and
are the second- and first-order moments of the volume-weighted drop size distribution, respectively. The authors compared this standard deviation with Shannon entropy and found inconsistencies. They state that the Shannon entropy has a main drawback, since the information of the drop sizes representing each class is not explicitly included; thus, if these probability values would be randomly rearranged, the H value would be the same. This is an important insight because it allows to understand the difference between polydispersion and size dispersion in a spray.
To compare the three approaches, consider the simulation of a spray mixing two monosize droplet streams of
m and
m. A weight parameter
w, varying between 0 and 1, sets the percentage of drops present in the mixed spray from each of the monosize sources. Therefore, if
, all droplets have the size of
m, and if
, all droplets have
m.
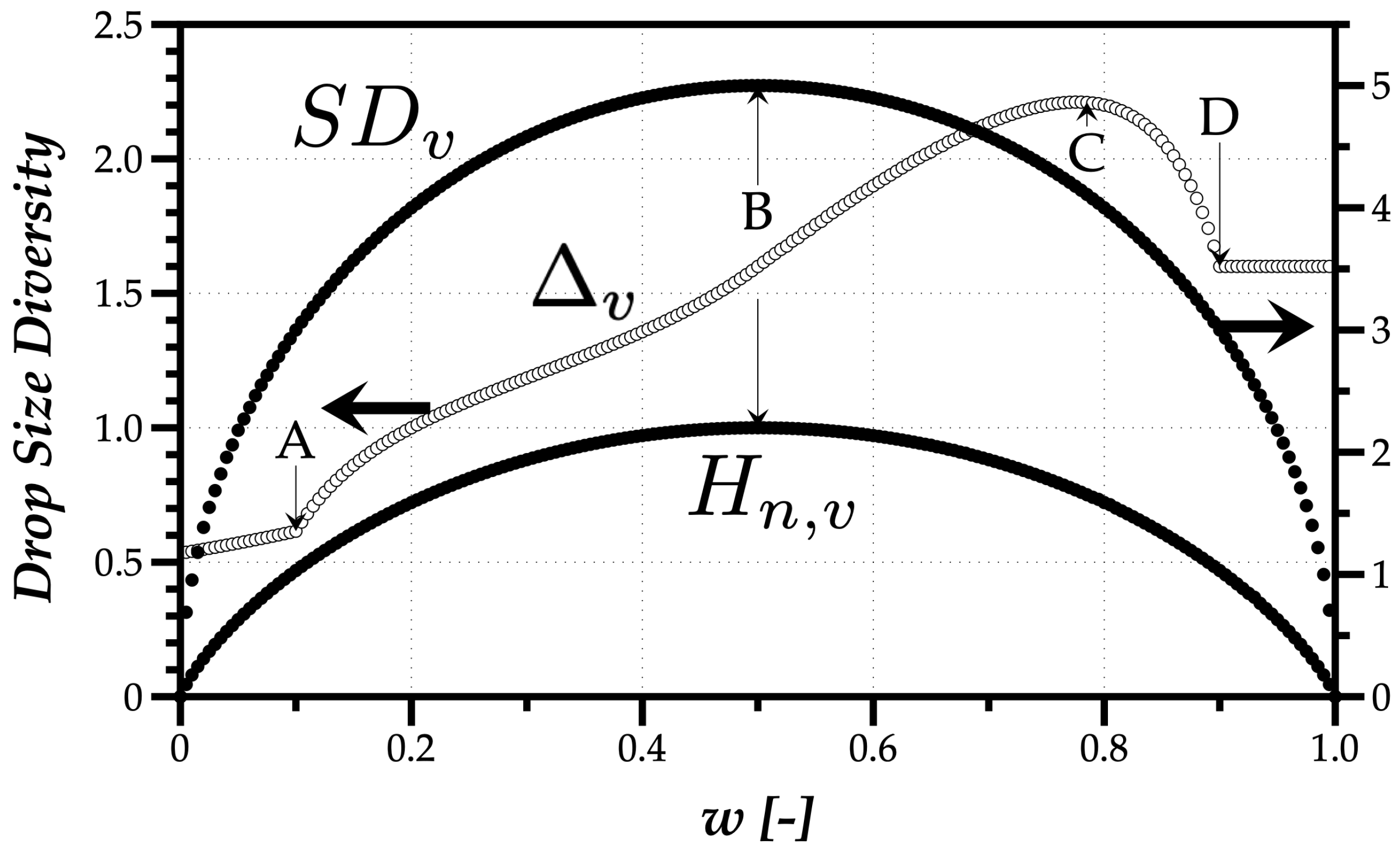
Figure 3 shows the result for the Relative Span (
), normalized Shannon entropy based on the volume-weight drop size distribution (
), and the volume-weighted standard deviation (
) with the variation of the weight
w attributed to the presence of droplets from each monosize source.
In the extreme cases where all droplets have the same size, the absence of polydispersed sizes results in null values for all indicators. However, while a small portion of droplets of a different size leads to a discontinuity in
, the normalized Shannon entropy and the volume-weighted standard deviation show a continuous behavior. In
Figure 3, points A and D in
mark the limits of 10% and 90% of the spray volume, meaning until A, 10
m droplets do not make 10% of the spray volume, and, at point D, these small droplets reached the mark of 90% of the spray volume. The maximum value of
at point C has no evident meaning.
The evolution of is simple to interpret. The maximum normalized Shannon, , occurs when all droplets have the same probability of being present in the spray (), corresponding to the uniform distribution. It is noteworthy that has no discontinuities as , and the variation with w shows a transition between the monosize spray droplets with m to the monosize spray of m droplets. It means that the size of droplets has no influence on , only their relevancy in the spray. On the contrary, the volume-weighted standard deviation depends on the maximum distance between relevant drop size in the spray. In this case, with an evolution similar to , the maximum occurs at m corresponding to the maximum distance between a mean quantity (15 m) and the sizes of the monodispersed sprays (10 and 20 m).
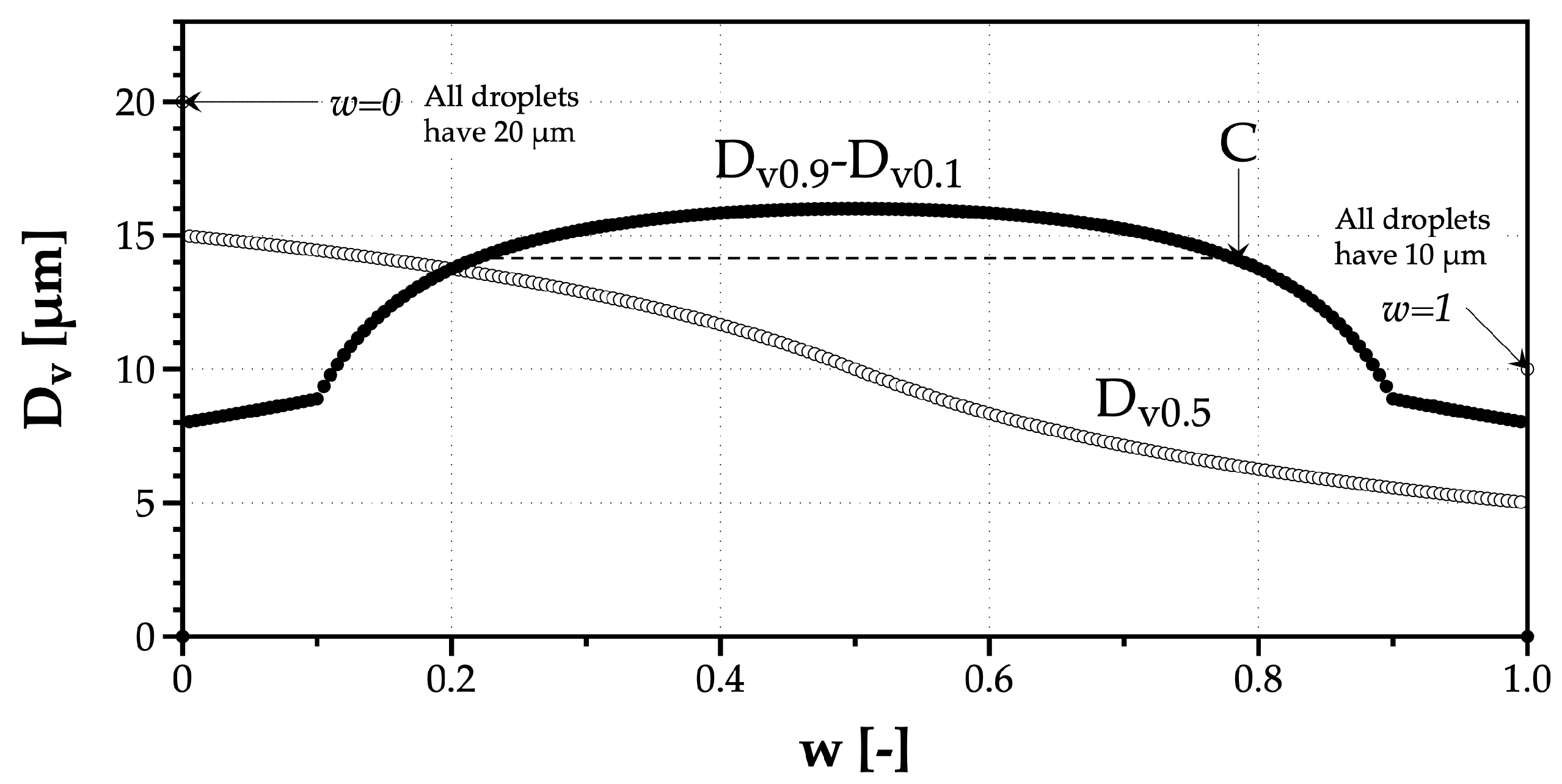
The Relative Span raises several questions, eventually pointing to its limitation if used to quantify the droplets size diversity. Namely, the values depend on drop sizes. Why would a monosize spray of smaller droplets, with a small portion of a monosize spray of larger droplets have a higher Relative Span? In fact,
Figure 4 helps to understand why this outcome is a result of the evolution of the diameter representing 50% of the liquid volume of the spray (
).
The first observation from
Figure 4 is the similarity between the other indicators (
) and the evolution of the difference
D–
D, in the numerator of
, as a function of
w with a maximum value at
. However, because the relative span normalizes this difference by
, which continues to decrease as the number of 10
m droplets in the mixed spray increases,
grows and indicates, for no reason, an increase of the drop size diversity until point C, when it is not the case. This theoretical example shows the limitations of using the relative span as a reliable tool to quantify the drop size diversity in a spray.
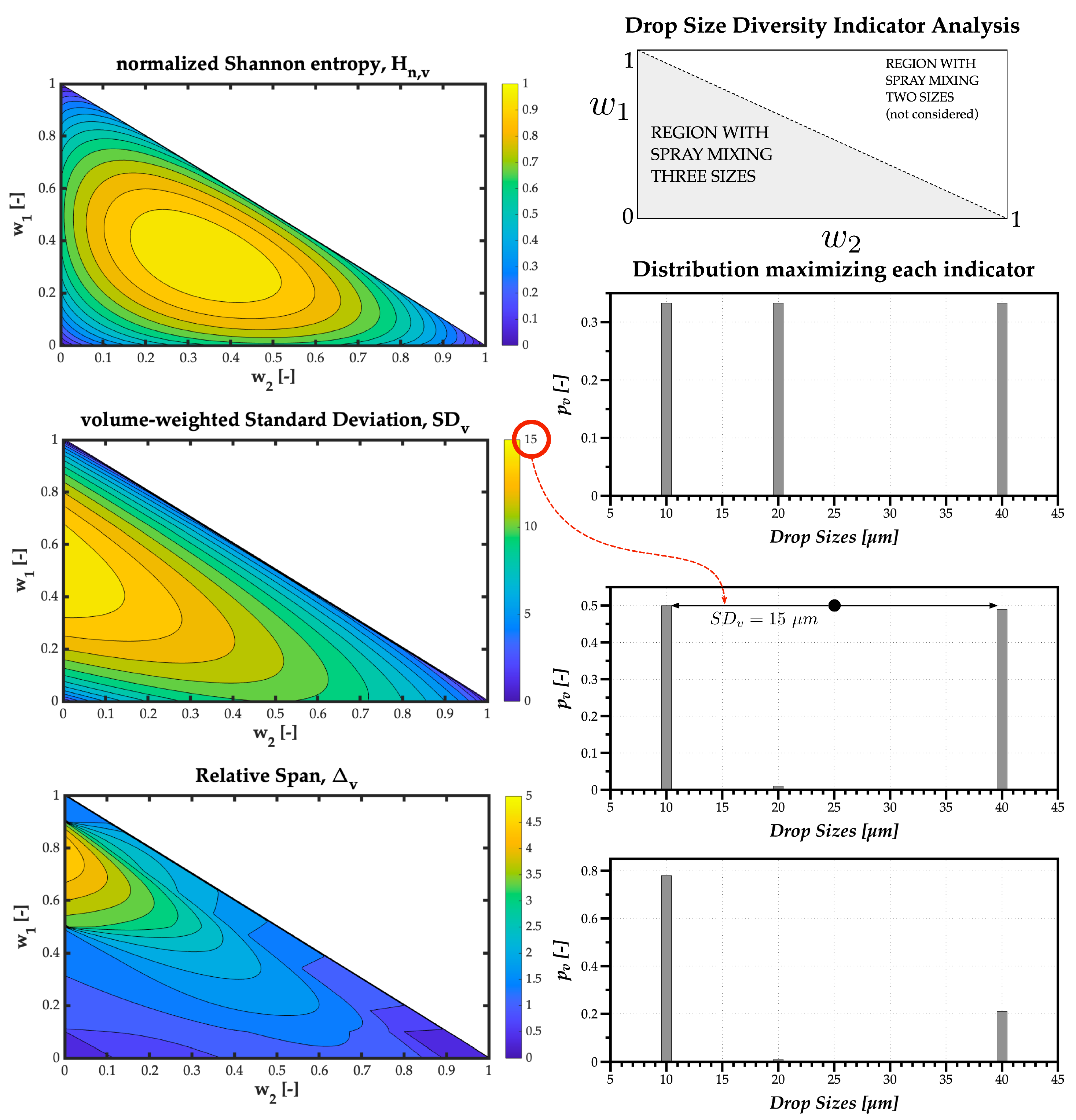
Although for the previous example, the and led to the same value of w = 0.5 corresponding to the maximum polydispersion and heterogeneity degrees, the parameters express different meanings relative to the drop size diversity. Therefore, a second theoretical simulation uses three monosize stream of droplets with 10, 20, and 40 m, with weights , and , respectively, varying from 0.01 to 0.98 to ensure that a percentage of all three sizes, no matter how small, is present in the spray.
Figure 5 shows the contour plots for each Drop Size Diversity indicator as a function of
and
, and plots on the right are the distributions corresponding to the maximum value obtained by each indicator. This simulation clarifies the difference between the polydispersion and heterogeneity degrees. Namely, the maximum normalized Shannon entropy obtained for the maximum number of droplets relevant in the spray corresponds to the uniform distribution where all relevant drop sizes have the same probability of being present in the spray—thus an adequate parameter to quantify the polydispersion degree.
The results for the volume-weighted standard deviation prove a maximum for the maximum difference between relevant drop sizes. In this case, between 10 m and 40 m droplets, with the standard deviation value of 15 m relative to the mid-point around 25 m—thus an adequate parameter to quantify the heterogeneity degree.
The results for the relative span show its meaning is closer to the heterogeneity degree, expressed by previous authors as size dispersion. However, it is a limited parameter to evaluate Drop Size Diversity, as shown by the distribution representing its maximum value closer to 5, which is difficult to interpret.
The next step would be to simulate a spray resulting from the mixture of two polydispersed sprays, for example, using the Log-Normal distribution with different geometric mean diameters (
) and equal shape parameters
(see Equation (
1)), and change the mixing through the weight parameter
w to simulate the transition between distributions.
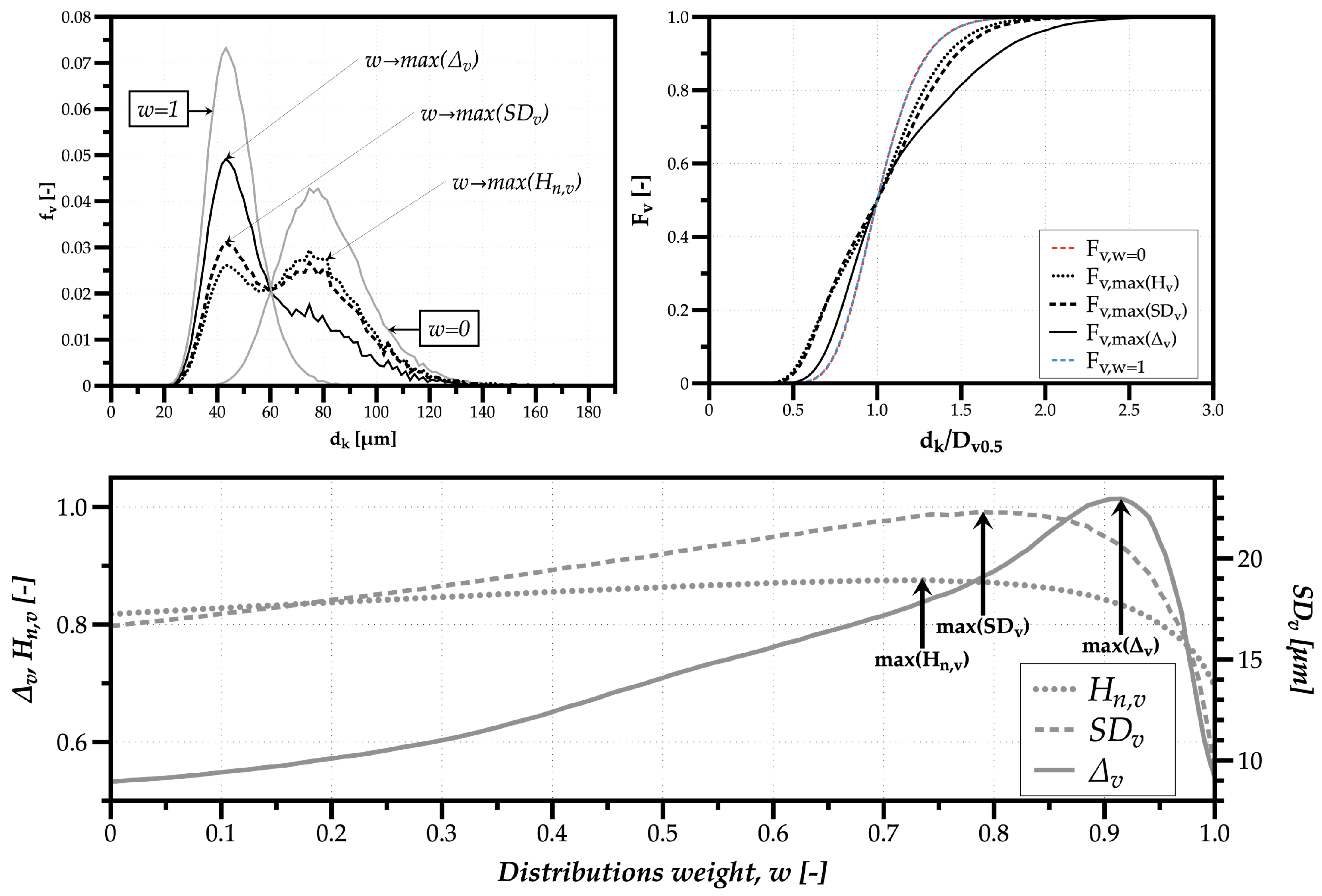
Considering a total sample of
droplets, the simulated spray fixes the shape of both distributions mixed with
, and uses distinct geometric mean diameters of
m and 70
m to mix sprays around larger and smaller drop sizes. The weight
corresponds to the Log-Normal distribution of
m and
to the distribution around smaller sizes.
Figure 6 shows on the top left the volume-weighted drop size distributions simulated with
w = 0, 1 and the distributions corresponding the the maximum values obtained for the normalized Shannon entropy (
), volume-weighted standard deviation (
), and relative span (
). The number of classes used the Rice Rule (see
Section 1). On the top right are the corresponding volume-based cumulative drop size distributions. Below is the comparison of all indicators for the Drop Size Diversity with the variation of the weight
w attributed to each distribution.
The first observation concerns the results obtained for each distribution with w = 0 and w = 1. Since the Log-Normal shape parameter is the same for both distributions, the cumulative distributions are equal when classes are divided by , which is why one obtains equal values for the relative span .
The second observation are the implications of probability values for each isolated distribution for the normalized Shannon entropy and the volume-weighted standard deviation. Namely, the lower probability values for the distribution with larger diameters, indicates a higher number of relevant droplets in the spray relative to the distribution with smaller drop sizes, . Accordingly, the values for and are higher for w = 0 compared to w = 1.
The third and final observation concerns the distribution with the highest polydispersion degree obtained through the maximum value for , where the similarity of the two peak values of prove a balanced mixing between clusters of droplets from each of the original distributions, resulting in a spray with a larger polydispersion of drop sizes. Concerning the volume-weighted standard deviation, the distribution with the maximum heterogeneity degree is similar to the distribution with maximum polydispersion—however, with 5.5% more droplets around the distribution of smaller sizes since it produces a slight increase in the largest difference between the smallest and largest relevant size classes in the mixed spray. As to the relative span, due to a decrease of as droplets from the distribution with smaller sizes begin to constitute the larger part of spray liquid volume, the maximum reached only at has no apparent physical reason. In this sense, in this work, the advice is to gradually cease to use the relative spam as an indicator to characterize drop size diversity.
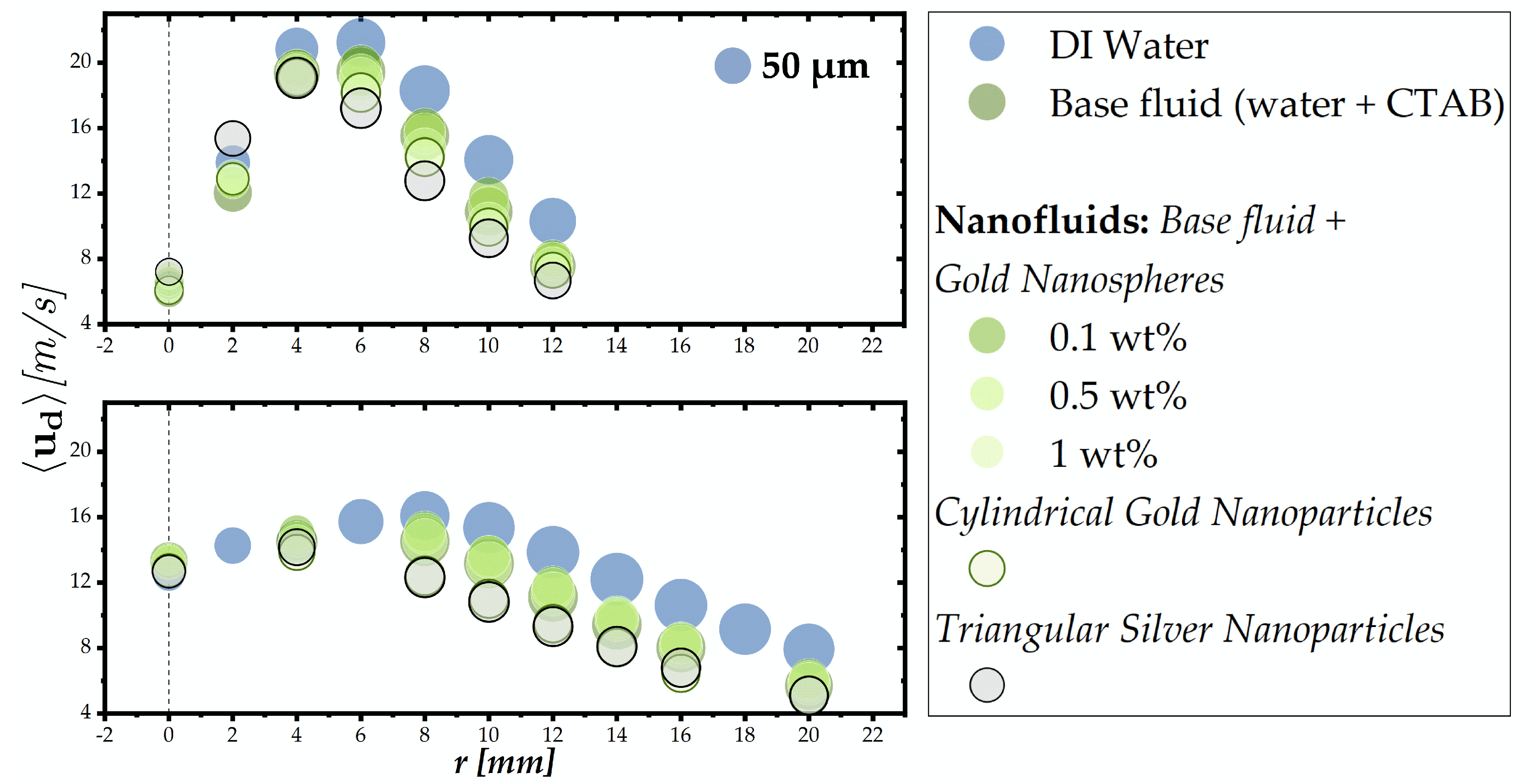
The following and final section applies the guidelines outlined above to the characterization of nanofluid sprays generated by a pressure-swirl atomizer.