1. Introduction
In Western tonal music, tension is the anticipation a musical composition creates in a listener’s mind for relaxation or release. The tonal tension is a perceptive phenomenon that can be produced by the combination of different musical properties, such as dynamics, reiteration or rhythm. The balance between tension and relaxation in a composition is usually denominated tonal tension profile, which can be represented with a curve. The movement between tense music and relaxed music keeps the music moving forward. Therefore it is an essential element for the composers to capture the receptor’s attention while they are listening.
The tonal tension profile usually depends on the different musical elements that are part of the musical fragment. One of the most important elements are chord progressions [
1,
2]. Chord progressions consist of sequences of chords (a set of notes that can be played together) that are played throughout the music. Over the past decades, there are some theoretical proposals that aimed to regulate tension of chord progressions through their particular elements, such as consonance, musical tension and voice leading. Riemann [
3], Schoenberg [
4], and Schenker [
5], among others, have discussed these principles extensively and proposed rules to create chord progressions.
In music composition, creating chord progressions which reflects a tonal tension profile commonly requires years of musical training. To make this process easier, technological solutions have been proposed to automatically model and analyze chord progressions, following different paradigms including statistical learning [
6,
7,
8,
9], rules [
10,
11,
12,
13], grammars [
14,
15], and biological principles [
16,
17,
18,
19].
In particular, genetic programming, genetic algorithms and artificial immune systems have been applied successfully to this field to create tools that can assist users into generating chord progressions [
20]. One of the first works to apply evolutionary computation [
16] proposed Vox Populi which uses genetic algorithms to evolve a population of chords by maximizing multiple musical criteria and following some users’ preferences. Mcdermott et al. [
21] propose a genetic algorithm that creates music represented by graphs. Sciera et al. [
22] present a meta-composer, capable of creating chord progressions based on a hybrid genetic algorithm.Fukumoto et al. [
17] apply genetic algorithms to automatically create chord progressions according to the user’s feelings. Herremans et al. [
23] propose an expert system to compose counterpoint based on different optimization functions. More recently, we [
24] proposed ChordAIS, a system that makes use a standard Artificial Immune System (AIS) called opt-ainet to iteratively generate the next chord in a given sequence by optimizing an objective function. Although all of them obtained positive results, the mentioned proposals do not follow or capture tonal tension profiles or curves. For such purposes, the proposals would require a hierarchical analysis of the whole chord progression.
To address this limitation, several authors propose new works in which the tonal properties of a chord are measured by considering not only on the previous chords but also their hierarchical relationships, typically represented as a tree structure [
25]. Granroth et al. [
26] propose a system that generates chord progressions by learning the most common structures from an annotated corpus. It works in a jazz context, thus it does not follow western tonal principles and they did not apply bioinspired algorithms. Herremans et al. [
27] present a chord generator to create progressions according to a tension profile. The authors use hybrid optimization with a function based on the spiral array representation. However, the work does not analyze how the properties of chords can influence the selection of a chord progression or another, and, although they applied a bio-inspired algorithm with successful results, it is not focused to help a novice composer or a user.
In this work, we propose a new system called ChordAIS-Gen, that assists the user to generate chord progressions by applying genetic programming (GP). To improve the performance of GP, we incorporate some properties derived from the Artificial Immune System [
28]. At last, the system is capable of offering chord progressions with different musical properties but adapted to a tonal tension profile given as an input. To evaluate the musical features of chord progressions, we depart from the conceptual basis of Lerdahl’s model and computationally generate an objective function that captures this tonal tension profile. In this work, tonal pitch indicators inspired by Lerdahl’s model are computed using the Tonal Interval Space (TIS) by Bernardes et al. [
13], a multidimensional space based on the discrete Fourier transform, where hierarchical tonal pitch relations are expressed as distances.
It is important to note that the application of the GP joined to an AIS has not been deeply explored. We aim to exploit the GP properties to create hierarchical structures that govern the chord progressions. Likewise, we also aim to take advantage of the immune properties of the AIS to generate multiple solutions different from one another. Therefore, while most state-of-the-art approaches propose a unique solution to the generation of chord progressions, the system proposed in this work is capable of proposing multiple different and good quality candidate chords. Furthermore, the lack of hierarchical structure has been a long identified problem in the field of generative music [
29]. ChordAIS-Gen addresses both linear and hierarchical dependencies of chord progressions and also aims to improve the accuracy of tonal indicators by adopting the perceptually-inspired TIS.
We carried out different experiments to evaluate the chords progressions created by performing a usability test with users. We also evaluated if the algorithm developed can get good solutions for our particular problem. In this case, we used a listening test to validate the candidates proposed by our system. We compared our model with two previous models: Lerdahl’s proposal [
30] and ChordAIS, a previous work [
24]. Lerdahl’s proposal captures similar musical properties as in this present work, but in a different topological space. With that comparison we aim to know if TIS is a good solution to capture musical properties. ChordAIS uses TIS to compute musical properties. However, the features captured differ from our work. ChordAIS measures the consonance and relatedness to the previous chord, key and harmonic function to create a chord progression. With this comparison we aim for the inclusion of new musical properties in the measure improves the results.
Additionally, we compared the performance of our algorithm against the classical version of GP and AIS. Finally, we aim to validate if the function can capture the tonal tension profile of a progression. Therefore, we created a listening test and asked the participants to select and rate the curve that fits best with the tonal tension profile. The correlation between the association of the curve made by the system and the subjective ratings will support our final conclusions.
This paper is organized as follows:
Section 2 reviews the topological space used to represent music in this work and the musical paradigm followed.
Section 3 describes the overall system with the integration of the fitness function and the bioinspired algorithm, along with the general workflow of ChordAIS-Gen.
Section 4 details the musical properties captured by the function, while
Section 5 exposes the technical information of the algorithm proposed. In
Section 6, we give information about the experiments performed to evaluate our proposal, followed by the results and a discussion. Finally,
Section 7 presents the conclusions and discusses future work.
3. System Overview
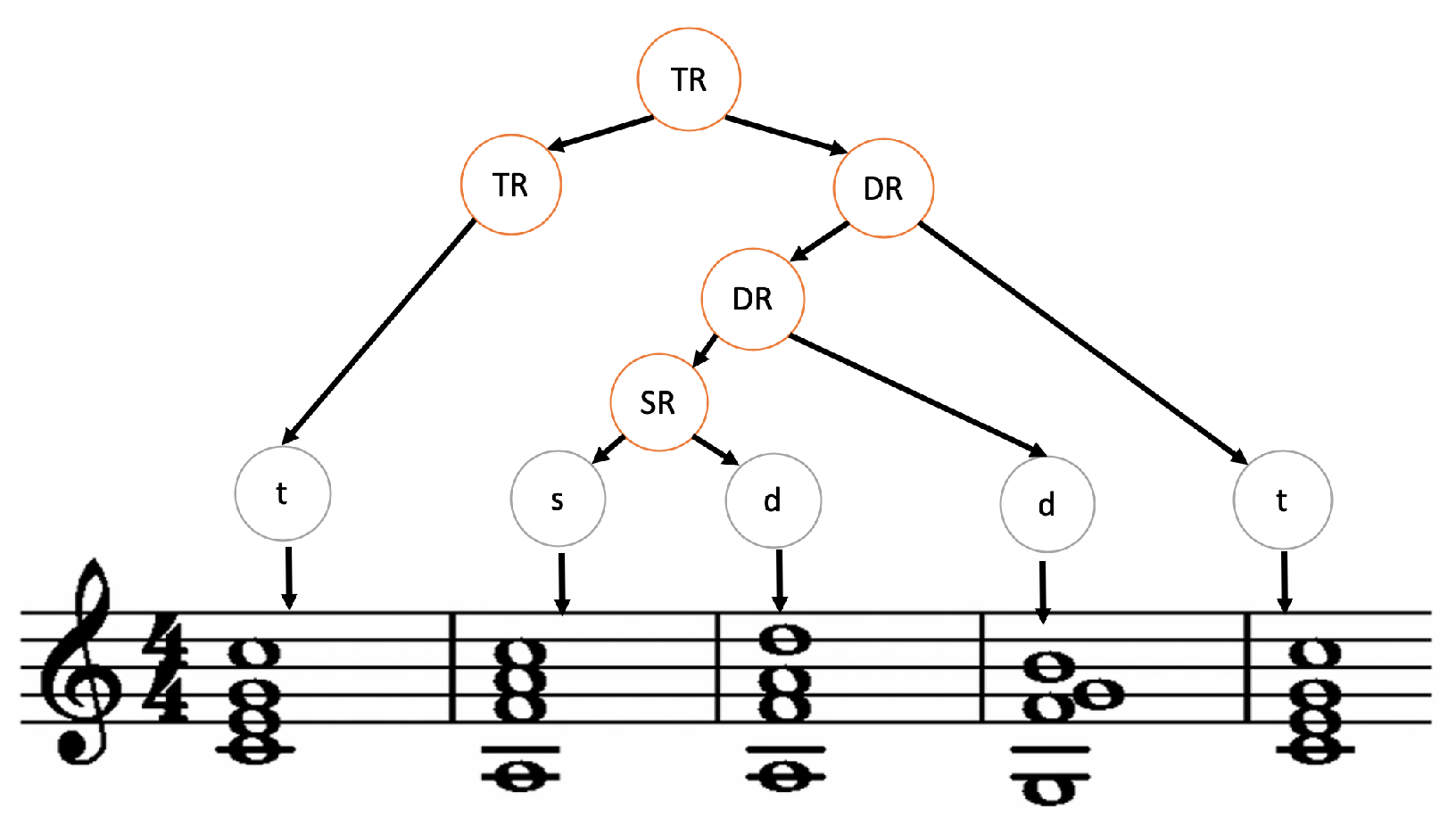
According to musical standards, a chord is a set of three or more notes that are played together. When you play several chords, you generate a chord progression. The structure of a chord progression is a hierarchy that can be represented with a tree. The idea of chord progression and how to encode the tree structure is illustrated in
Figure 1.
Firstly, the tree is constructed following some instructions that, in this work, are proposed by Rohrmeier’s theory. The first node in
Figure 1 is a tonic region
and it determines the key of the chord progression. Secondly, Rule (4b) is applied to get the nodes in level 2. Next,
derives into
t (Rule (4e)) and the second child employs Rule (4b). The last levels are obtained by applying Rules (4c), (4f) and (4g). Finally, each leaf node is replaced by a chord that complies with the same harmonic function (tonic, subdominant or dominant). Initially, in the algorithm, this replacement is made randomly.
In this work, we must construct chord progressions that follow a concrete tonal tension profile given by the user. The tonal tension profile can be represented with a curve and usually depends on the musical features of the chords and the tree structure associated with the chord progression. The difficulty lies in capturing such subjective properties through a mathematical model. To address this issue, the chords will be encoded as points in topological spaces such as TIS, capable of capturing musical properties [
13], and we apply some mathematical measures to capture all these musical properties. The four musical properties captured are: perceptual distance
, dissonance
, hierarchical tension
and
voice leading . All of them are linearly combined in an objective function
M. This function will give a score to each chord according to their musical properties. If you join the set of scores given by
M to the chords that are part of the progression, you can generate a curve that represents the tonal tension profile of a chord progression. To know if the tonal tension profile of a chord progression adapts to a curve given by the user, we calculate the regression
between both curves. Higher values of
will be translated into chord progressions that adapt to the tonal tension profile that the user is looking for. Therefore, we are looking for an optimization of
. Due to the wide amount of chord progressions that can be created manually, we need a heuristic algorithm to look for different optima according to the regression function, in this case, we used GP with some immune properties that improve its performance to create chord progressions.
Consequently, in our work the selection of the chord progressions can be considered as a search problem in a geometrical space (in this case TIS [
13]) and subjected to musical constraints. The regression
between the points
M and the initial curve drawn by the user will constitute the fitness function of our bioinspired algorithm.
The regression function
is the fitness of our bioinspired algorithm which, along with the constructed interface, constitutes a system that presents multiple options so that the user can choose among these chord progressions according to his/her preferences.
Figure 2 shows an overview of ChordAIS.
ChordAIS-Gen workflow is illustrated in
Figure 2. In a first step, the user sets some initial parameters, such as the key, the number of chords and the tonal tension profile of the chord progression. The tonal tension profile is a function that should be drawn by the user, and can have any shape. This information will be stored in ChordAIS-Gen for the subsequent iterations. The bioinspired algorithm generates a population of chord progressions. Each chord progression is represented as a tree, which captures its specific hierarchical structure, which has been created following the grammar proposed by [
35]. The leaf nodes will be the chords that are part of the chord progression. According to musical standards, a chord is a set of three or more notes that are played together. In this particular case, the chord is represented as a vector with
n elements, and each element is a number between 0 and 128, according to the MIDI standards. We use MIDI because the synthesizers used can understand this codification very easily. However, to measure the tonal tension of each MIDI chord, we encode them into the TIS and to get the tonal tension we apply our function
M. The result is a curve or profile whose points are the numbers that each chord has obtained according to
M. This curve is compared with the tonal tension profile that the user drew in the previous stage. The population of the chord progressions evolve to obtain individuals whose profile adapts best to the curve proposed by the user.
Finally, ChordAIS-Gen presents the best three minima (chord progressions) it could find to the user, who finally selects which chord progressions should be used according to his/her preferences and can play it through a simple synthesizer.
5. Genetic Programming and Immune Systems
Genetic programming (GP) is a heuristic algorithm that makes use of the chromosome evolution process to solve a problem [
40]. GP is specifically designed to evolve individuals which are traditionally represented as tree structures [
41]. The algorithm applies different operations to evolve the population and retrieve an optimal solution. Those operations are commonly crossover, mutation and selection. The crossover operation involves exchanging random branches of two trees to produce a new and different individual that is incorporated into the population in a future generation. Mutation involves modification of some properties in an individual. The selection consists of deciding which trees (individuals) will be preserved for the next generation.
GP has been applied to many applications such as robotics engineering, circuit design, art, financial engineering and so on. The nature of this algorithm makes it ideal to generate hierarchical structures that govern the chord progressions. Consequently, we decided to apply GP to optimize M and generate music. Although the traditional GP can only obtain a quasi-optimal solution, for this particular purpose the subjective criterion of the user plays an important role and cannot be predicted by our system. Therefore, it was strongly desired that ChordAIS-Gen searches for multiple solutions simultaneously, to give the user the opportunity to choose among different options.
To address this problem, we looked for similar algorithms that can be fused with GP to improve its behavior. We found that de Castro and Timmis [
42] developed an artificial immune system for multi-objective optimization called opt-aiNet. In opt-aiNet, each candidate solution (called antibody) is encoded as a vector whose quality is measured with an objective function. A population of antibodies, which represents a pool of candidate solutions, evolves following the immunological principles of clonal expansion, mutation and suppression. The evolution of the antibodies results in the optimization of the objective function because the objective value (or quality) of the solutions encoded by the antibodies increases. Initially, the antibodies are randomly initialized to explore the search space. Next, some antibodies are selected and cloned based on their quality. Each clone undergoes a mutation inversely proportional to its objective value. These mutated clones are subsequently re-evaluated with the objective function to determine if mutation increased their quality. Those mutated clones with higher quality values than before are introduced in the current population, while the ones whose quality decreased are discarded. In order to maintain diversity in the pool of candidate solutions, the algorithm eliminates those antibodies that are close together in the search space. The affinity between two antibodies is measured with the Euclidean distance between them, such that smaller distances mean greater affinity. Those antibodies whose affinity is higher than a given threshold are removed from the population while keeping the ones with the highest objective value. Finally, a number of newly generated antibodies are incorporated into the network. The algorithm converges when the quality of the current solutions cannot be further improved and no new solutions are found.
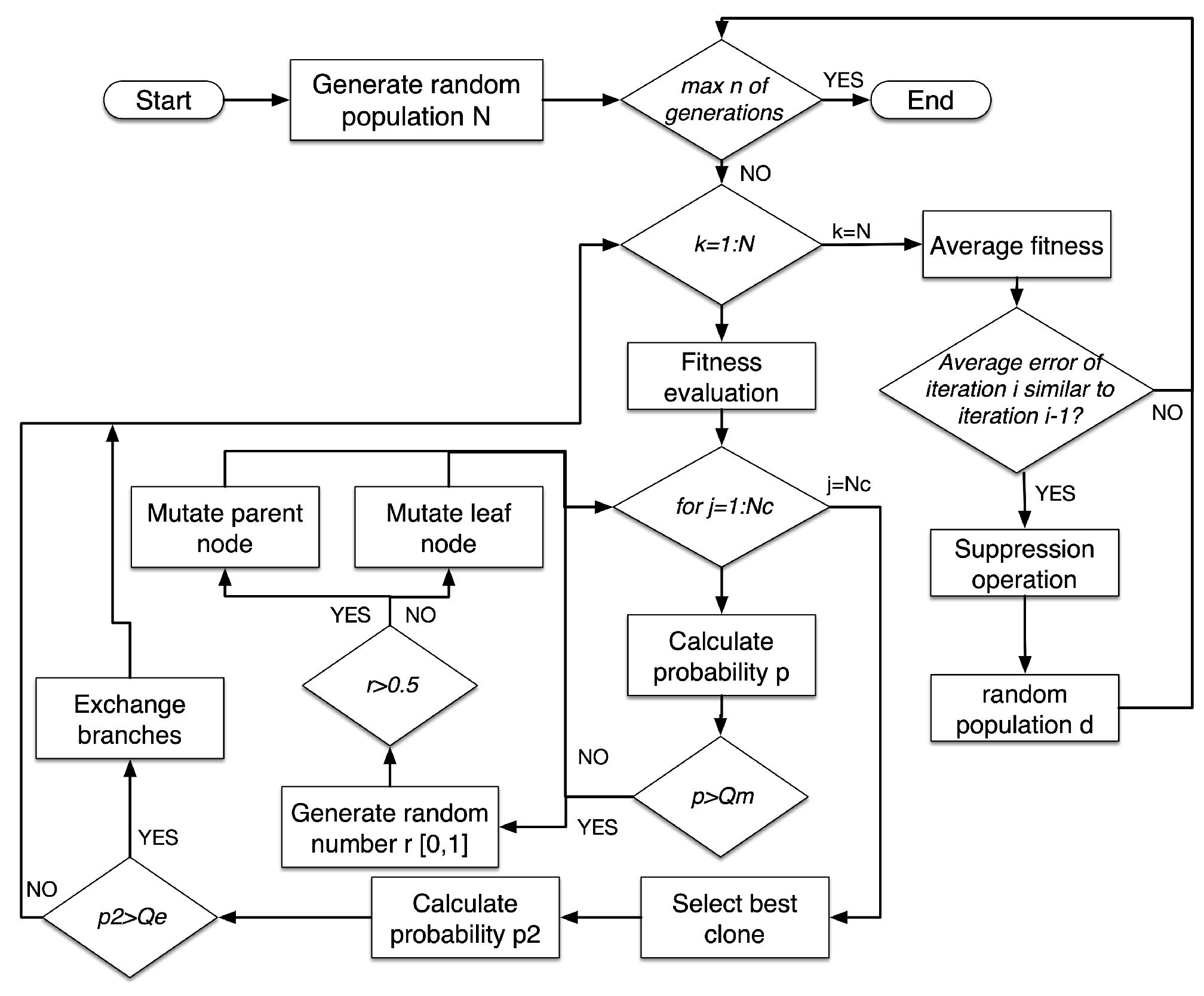
We developed a GP incorporating some of the operations proposed in opt-aiNet. The pseudo-code of the algorithm is shown in
Figure 3 and can be explained as follows:
- 1.
Randomly initialize a population of tree structures and chords.
- 2.
While the stopping criterion is not met do.
- (a)
Determine the fitness of each antibody (chord progression) according to M and normalize the matrix of profiles for the population.
- (b)
Generate a number of clones for each antibody (chord progression).
- (c)
Mutate each chord progression according to a probability . The mutation can follow two different procedures:
- (d)
Determine the fitness of all the clones.
- (e)
Select the clone with the highest fitness.
- (f)
Exchange two branches of different trees according to a probability . (cross-over operation). The node in which the new branch is inserted will depend on the fitness of the parent.
- (g)
Calculate the average fitness of the selected population.
- (h)
If the average error of the population is not significantly different from the previous iteration, then continue. Else, return to Step (a)
- (i)
Determine the affinity among all antibodies. Suppress all but the highest fitness of those antibodies whose affinities are less than the suppression threshold st and determine the number of antibodies, named memory cells, after suppression.
- (j)
Introduce a percentage d of randomly generated antibodies and return to Step 2.
- 3.
End While
The algorithm works as follows. One antibody represents a chord progression. Each progression consists of a tree, which is its representation of the hierarchical structure. Note that the leaf nodes will be the set of chords that will be played in the final step. This tree has been created following Rohrmeier’s grammar [
35]. The chord progressions are randomly initialized to explore the search space (Step 1) and evaluated to discover their fitness. The fitness is calculated as follows:
First, for each chord, we measure the tonal tension with M.
With the number obtained, we join the points to get the tonal tension profile.
The fitness will be the regression value between the tonal tension profile and the curve that the user has drawn.
Afterwards, some of them are selected and cloned according to the probability
(Step 2.b), which is empirically set. Each clone (chord progression) undergoes a mutation inversely proportional to their fitness (Step 2.c). As the chord progression is represented by a tree, we can mutate a leaf node or a parent node. If we mutate a leaf node (a chord), we have to mutate their individual notes. Note that a chord is represented as a vector, and each note is a number between 0 and 128 (according to the MIDI standards). To mutate a chord, we have to change one or several of these notes, which are simple numbers. To select the number of notes to be mutated, we framed the value of the chord according to
M between 0 and
n, where
n is the number of notes of the chord. The
i-note or
i-notes to be changed are randomly selected. The mutation value of each
i-note of the clone is calculated according to the value of
, represented in Equation (
10), where
is a random value between 0 and 12,
M is the evaluation function and
is a correction factor empirically set.
In this work, the trees have to be feasible, meaning that all have to follow the rules defined by the grammar. That means when we mutate a parent node, we have to re-structure all the leaf nodes of the branch. Therefore, the higher the position of the parent node, the higher the mutation will be. To select the node of the tree to be mutated, we sum the values of the chords according to M and we framed it between 0 and , where is the number of the parent nodes of the tree, decreasingly ordered according to their depth. From this node, we randomly apply new rules and generate new chords until we get the same number of nodes as before.
These mutated clones are subsequently re-evaluated with the objective function to determine if mutation increased their quality (Step 2.d). Those mutated clones with higher quality values than before are introduced in the current population, while the ones whose quality decreased are discarded (Step 2.e).
In the following step, some of the chord progressions exchange branches according to the probability (Step 2.b), which is empirically set. When a tree is selected, we randomly select a tree . To avoid unfeasible trees (which violated rules of the grammar), must have a branch with the same parent node than the tree . To select the node of the tree to be exchanged, we sum the values of the chords according to M and we framed it between 0 and , where is the number of the parent nodes of the tree which are the same, decreasingly ordered according to their depth. From this node, we exchange the branches of both trees.
In order to maintain diversity in the pool of candidate solutions, the algorithm eliminates those antibodies that are close together in the search space. The affinity between two antibodies is measured with the Euclidean distance between them, such that smaller distances mean greater affinity. Those antibodies whose affinity is higher than a given threshold are removed from the population while keeping the ones with the highest objective value (Step 2.g). Finally, a number of newly generated antibodies are incorporated into the network (Step 2.h). The algorithm converges when the quality of the current solutions cannot be further improved and no new solutions are found.
6. Evaluation
The aim of the evaluation is threefold. Firstly, we aim to validate the objective function M we designed as a good measure that captures the tonal tension profile. Secondly, we aim to validate the use of GP with immune properties in the overall system as a good solution, comparing it with other proposals. Finally, we aim to determine the usability of ChordAIS-Gen through the users’ experience.
Firstly, we developed a prototype of our algorithm by using MATLAB tool. MATLAB was selected because it can be successfully utilized for bioinspired and evolutionary computation and also because it can be run on multiple platforms. We created a basic interface where the user can draw a curve for the tonal tension. Our specific proposal of GP was implemented in MATLAB version 2019a using standard libraries for common operations such as creating random numbers, plotting curves and calculating the fitness with the correlation values. Due to the specific features of the algorithm (which include AIS and GP properties), it was programmed entirely without any external library specifically designed for genetic programming.
According to the theoretical description presented above, in our algorithm, the following parameters must be set:
: suppression threshold
N: initial population size
: number of clones per antibody
: range of the affinity proportional mutation
: Probability of mutation
: Probability of cross-over
d: percentage of random population.
Empirically, the parameters used were set as follows: = 0.001; N = 200; = 5; = 2.6; = 0.6; = 0.4; d = .
Note that the evaluation aims to demonstrate that
M reflects the tonal tension of the chord progression. Therefore, we need to evaluate
M in optimal conditions. That means we need to find the best values for weights
in Equation (
5) by applying cross-validation. A previous work, [
43] has demonstrated the independence of the hierarchical properties of the chord progressions, independently of the key. Additionally, we used cross-validation to calculate the weights
that best fit the scores resulting from a listening test with a total of 20 chord progressions. The final weights obtained were
,
,
,
.
The evaluation remains a challenge in music generation with expert systems because of the inherent subjectivity of the final product [
44]. Most works in the literature use a human expert [
12,
23,
45] or a group of human listeners [
11,
46,
47] to evaluate the results. They usually design a listening test and a comparative study between the present system and previous works, with successful results. Therefore, in this work, we will also perform a listening test, followed by statistical analysis and a comparative study between other proposals.
6.1. Evaluating the Objective Function
Firstly, we address the validation of the objective function M as a proxy for the perceptual evaluation of tonal tension profile in chord progressions. We expect the objective function to reflect the perceptual quality of the chord progressions independently of the tree structure associated.
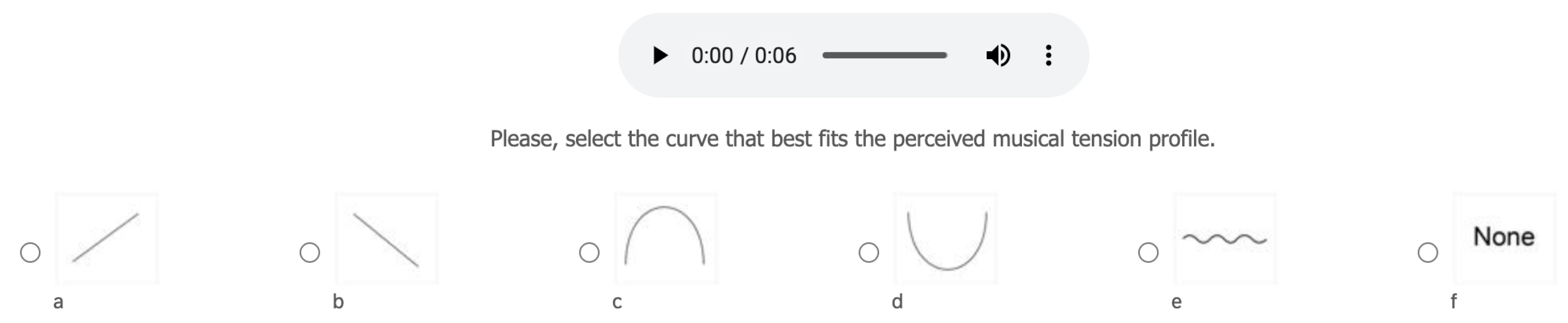
We designed a listening test that presents several chord progressions generated automatically. We created a total of 12 chord progressions with a total between 5 and 8 chords each one. Each chord progression had a different tree structure. All of them were in major or minor keys. We used a total of four different keys. The rhythm in which the chords are played was always regular to put the focus on the harmonic properties instead of in rhythmic features. The chord progressions were generated by our system and all of them follow some of the curves presented as options in
Figure 4. Each chord progression was presented with a reproduction bar, and they were synthesized with a standard piano. The presentation of each chord progression in the listening test is shown
Figure 4.
The listeners were presented the chord progressions in a random order. The progressions could be played as many times as they need. The listeners are given the options in
Figure 4, and they have to select which curve adapts best to the tonal tension profile of the chord progression. In total, 38 people took the test, among which 11 declared no musical training, 10 considered themselves amateurs, and 17 professional musicians.
We grouped the results according to the curves that the chord progressions represented. To analyze the results we calculated the hit rate of the subjective ratings versus the fitness values for the chord progressions included in the listening test. Note that the fitness value is the correlation between the curve expected by the system and the curve obtained evaluating M for all the chords. In general, chord progressions with higher fitness values have a higher hit rate for all curves tested.
We also aim to demonstrate that
M captures the tonal tension profile of any given chord progressions. Thus, we compared the fitness values of the chord progressions with all the curves given in the options. We calculated the correlation between the fitness of each curve and the hit rate that the users gave. As they were two datasets, we can apply the Pearson correlation. We present the Pearson correlation value
and the
p-value in
Table 1. The
p-value has been calculated by transforming the correlation to create a t-statistic measure to proof the null hypothesis. The null hypothesis states that there is no relation between the objective measure and the subjective values obtained from the participants of the listening test. Therefore, if one of the
p-values is lower than 0.05 the Pearson correlation is considered significant.
The first column gives the statistical measures corresponding to the tonal tension profile calculated by the measure M. The results suggest that the objective function captures the perceptual quality of the chords. The p-values are all much lower than for the null hypothesis and the Pearson correlation coefficients are above . This indicates that the subjective ratings of the users correlate strongly with the tonal tension profile that our model predicts.
To validate
M against other proposals, we use two works proposed previously: the Tonal Tension Model proposed by Lerdahl, which is one of the most prominent models in the community, was described in
Section 2 and captures hierarchical and linear properties following a different topological space, and ChordAIS, a previous work proposed in [
24], which captures only linear properties of chord progressions. ChordAIS captures the following properties: consonance, perceptual relatedness to the previous chord, perceptual relatedness to the key and the harmonic function it represents. In our present work, apart from these properties, we also included hierarchical properties, like the hierarchical tension, and also the voice leading.
Table 1 shows a comparison of the statistics resulting from organizing the subjective ratings obtained in the listening test as a function of distance measures from other chord representations. To clarify the statistical analysis, we only calculated the statistical analysis with the curve that correlates best with the subjective values, ignoring the other possibilities, that resulted in lower correlation values in all the cases, independently of the model applied.
M is the objective measure from Equation (
5). For the other columns,
L stands for the distance according to the Lerdahl’s model of tonal tension, and
C stands for the ChordAIS model, in which only linear properties of the music are considered.
The statistical analysis shows that M captures the tonal tension profile of the chords better than L and D. The high values obtained indicate the linear regression of the subjective ratings as a function of the objective values and the p-values are all below the 1% threshold for the null hypothesis, which suggests that the listeners’ ratings correlate with the fitness measure well. Note that Lerdahl’s measure L also correlates with the subjective ratings of the listening test, but obtaining slightly lower values for and p-value. Likewise, the and p-value in D are correlated, but below the rates obtained for M.
6.2. Evaluation of the Gp with Immune Properties
The proposed algorithm is capable of finding multiple local minima of the objective function while preserving diversity. The progressions with the highest fitness values would be considered most appropriate to be selected, as they comply with the specifications given by the users in the input. However, there are other chord progressions that can also comply with the rules. All these potential solutions can be local minima and can have different fitness values. We aim to evaluate if the chords selected by the algorithm are all considered better candidates than the chords that were discarded.
For this purpose, we performed a listening test to evaluate the perceptual quality of the chords proposed by the algorithm. We run the system 10 times with different curves and selected 2 candidate chords selected by the algorithm and 2 additional chords that were rejected, sampling the objective function regularly from lower to higher fitness values.
Finally, we designed a listening test that presents these 40 chord progressions ordered randomly with a picture of a curve that represents their tonal tension profile. As mentioned above, we included chords selected by the algorithm as well as chords rejected by it to validate the objective function. Each chord progression can be played multiple times before assessing it. This listening test also presents chord progressions with between 5 and 8 chords in each one. As in the previous listening test, each chord progression may have a different tree structure, with different keys. The rhythm in which the chords are played was always regular. Each chord progression was presented with a reproduction bar, and they were synthesized with a standard piano. The presentation of each chord progression in the listening test is shown
Figure 5.
The listeners were asked to rate how well the curve represents the tonal tension profile of the chord progression from 1 (Very bad) to 5 (Very good). In total, 35 people took the test, among which 8 declared no musical training, 10 considered themselves amateurs, and 17 professional musicians. We expect the chords selected by our algorithm to be rated positively by the listeners, while we expect the discarded chords to be rated negatively.
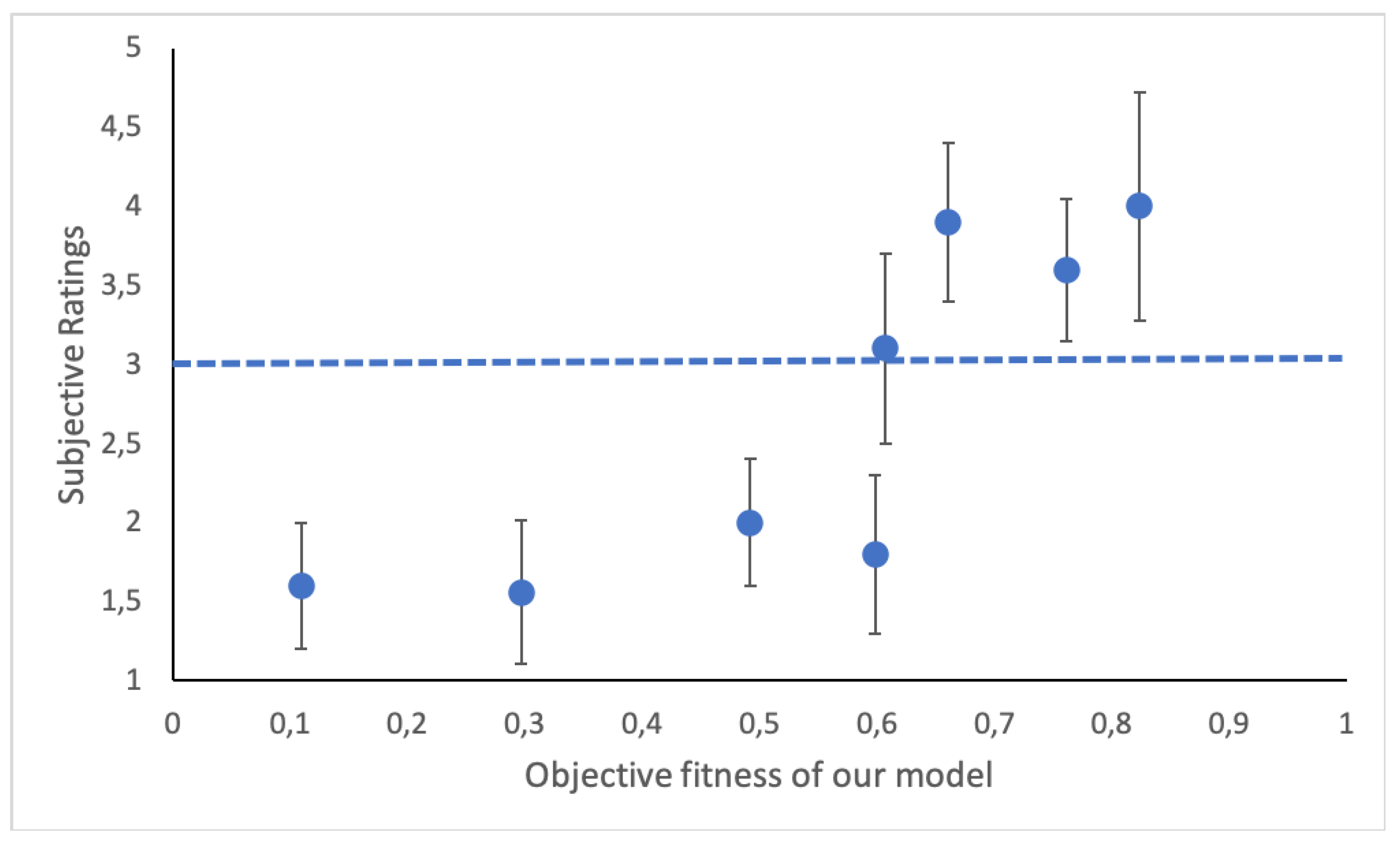
Figure 6 shows the values of the subjective ratings (represented in the vertical axis) versus the fitness values (in the horizontal axis) for the chord progressions included in the listening test. To simplify the analysis, we calculated the mean of the fitness values of the chord progressions that our algorithm ranked first, second, third, and successively until the eighth. We normalized these values between 0 and 1, and these mean fitness values were represented in the horizontal line. We also calculated the mean and standard deviation of the subjective ratings of the participants. The standard deviation is represented with the vertical lines, and the points are the cut points between the objective fitness of our model and the subjective ratings of the users for each chord progression. The first four points are chord progressions discarded by the algorithm, while the rest are progressions that our algorithm considers as good candidates. According to
Figure 6 all the progressions selected lie above the horizontal line that cuts through 3. This indicates that our algorithm selects chord progressions that follow the tonal tension profile presented, according to the listening participants. Most chords discarded lie below the fair rating. Therefore, according to our results, we can conclude that our algorithm is able to select options that adapt to their tonal tension profile. tension.
Our goal is to show that globally, our system can capture the tonal tension profile of a chord progression according to both musicians and non-musicians perceptions. As a future work, we will perform a deeper analysis to show how the results differ between people with and without musical training.
We aim to demonstrate that the proposed algorithm improves the performance of algorithms like AIS and GP. Therefore, we replace our algorithm with a standard version of GP and a standard version of AIS. We selected opt-aiNet, an optimization AIS proposed by [
42] which is quite similar to the present proposal and was used in previous work, and also selected a classical approach for GP. We configured the parameters of the algorithms to its best performance empirically.
Table 2 shows the values for the three algorithms.
There were two main reasons to create a new algorithm. The first one is that the different mutation patterns allowed to improve the performance of the algorithms. The second was to offer options with different properties. Therefore, we run the algorithms 50 times and calculated the mean and standard deviation of the fitness value of the best individual. All of them made use of the
M function. As we can see in
Table 2, the fitness value was better in our algorithm, although the GP and the AIS also performed positively.
Additionally, we aim to validate that our algorithm obtains candidates with different properties. For this purpose, we calculated the Euclidean distance between the three candidates proposed by our algorithms against the AIS, as GP only finds a single option. We also run the algorithms 50 times and calculated the mean and standard deviation of the normalized similarity measure of the three candidates in each run. The results in
Table 2 show that the similarity value is significantly better for the algorithm proposed.
According to the results, our algorithm proposes other candidate chord progressions that are different from the best candidate and are still rated positively according to the fitness value. Our algorithm keeps these candidate chords, which are less trivial to find with traditional methods, because of the maintenance of diversity feature.
One of the limitations of our work is that, as with most of the bioinspired algorithms mentioned, our algorithm is computationally intensive. We calculated a mean of the CPU consumed during the execution and the time it takes to output a complete chord progression. The CPU consumed was approximately 12.07% and the mean time was 9.85 min. In a future work, we would analyze how to improve the time of execution to get a more interactive tool capable of giving a response to the user in a shorter time.
6.3. Evaluating the Usability of Chordais-Gen as an Assistive Tool
In this third experiment, we aimed to evaluate the usability of ChordAIS-Gen from a user perspective. The system presented aims to help those users who might not have enough knowledge about tonal music to generate a good chord progression. The algorithm facilitates generating different but good options for candidate chords which can follow the progression, but we also want to validate if these chords are suitable selections for the user.
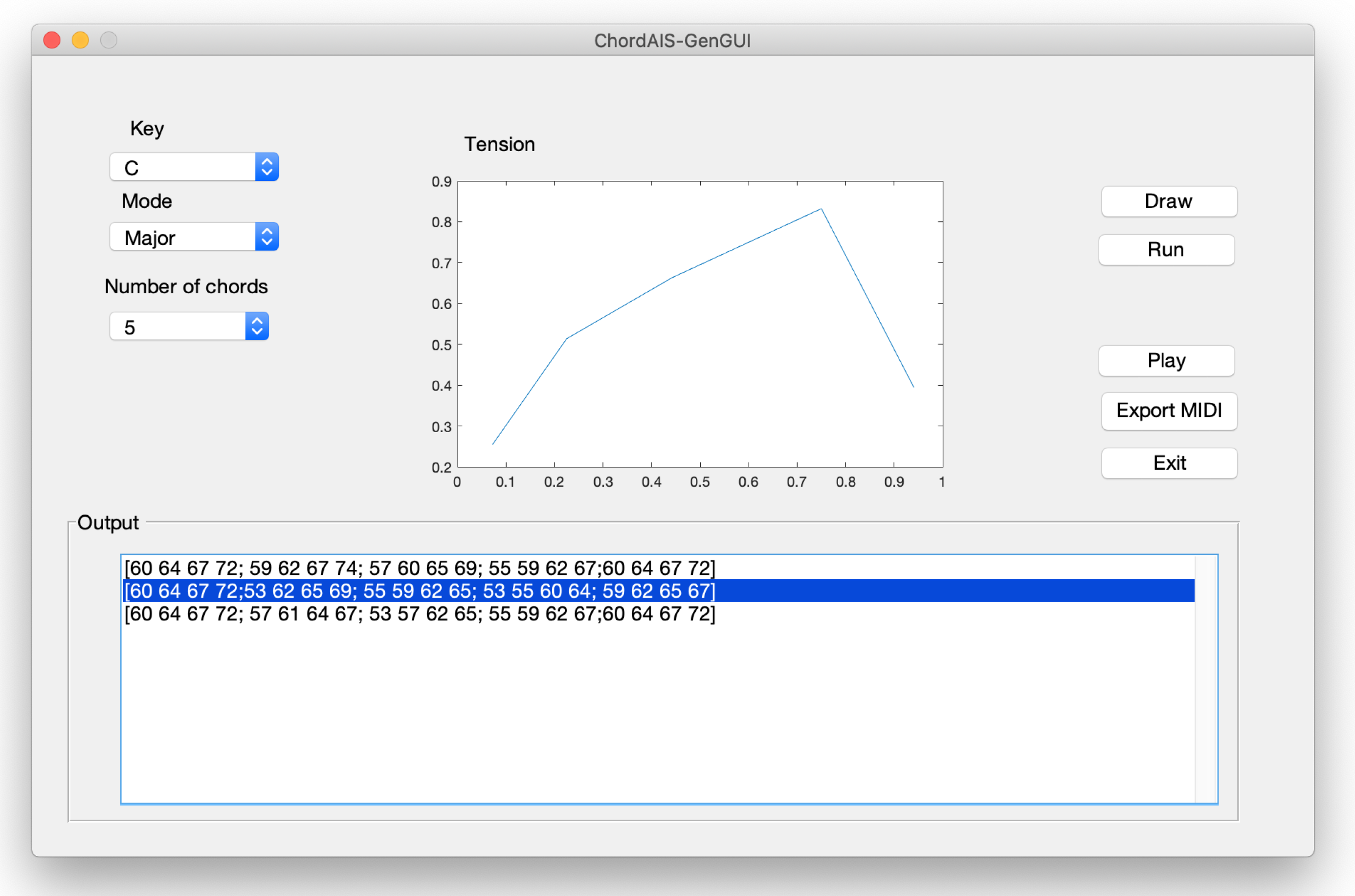
In total, 8 users without musical training were selected and asked about their experience with ChordAIS-Gen. Initially, they used the system to generate 5 chord progressions with any degree of freedom, to become familiar with ChordAIS-Gen. Then, they had to generate a total of 10 progressions. Each chord progression consists of a minimum of 5 chords and a maximum of 16 chords in a concrete key signature and with different curves. Initially, the users select the key, the number of chords and the tension profile. Then, ChordAIS-Gen proposes three-chord progressions. The user can play the progressions whenever they need to and select which one is more desirable according to their criterion. They can modify a concrete chord if they wish to. The interface constructed is shown in
Figure 7.
To also compare the ChordAIS-Gen system with our previous work, ChordAIS, we repeated the experiment with the same users. They used the ChordAIS system to generate 10 chord progressions, in the same conditions as in ChordAIS-Gen.
In every case, the chord progressions that both systems proposed are not ordered by their fitness, in order not to bias the selection of one particular progression. All the participants have used the tool for at least 10 min, and have generated a minimum of 8 progressions. With that experience, they had to respond to a questionnaire that aims to capture their opinion about the system. In particular, the users gave their opinion about three items:
The system complies with their expectation. The system is capable of giving good solutions that follow the initial parameters (tonal tension, key and number of chords).
The system can give nice chord progressions that the user could not otherwise have composed.
The system presents solutions that are different among them.
All the questions could be rated from 1 (“Completely unsatisfied”) to 5 (“Completely satisfied”).
Table 3 shows the mean ratings and the standard deviation of the experiment.
The table shows that, in general, ChordAIS-Gen satisfies users’ requirements (). The users are satisfied with the system, as it is capable of retrieving good and different candidate progressions that adapt to the tonal tension profile, with a mean of . Additionally, the users consider that amount of options to select chord progressions to be quite adequate (), meaning that ChordAIS-Gen can retrieve solutions which are different one from another. The authors consider that this feature can be improved in future work by adding a learning component to understand the users’ preferences and incorporate this to the selection of chord progressions.
The previous version, ChordAIS also obtained good results. The satisfaction degree and the usefulness of the ChordAIS also had high ratings, although slightly lower than in the new version. However, ChordAIS cannot retrieve information about the tonal tension profile, only about the key and number of chords. Additionally, the users gave a lower value when they were asked about the diversity of solutions (). Thus, the users think that both systems can assist them but ChordAIS generates more expected chord progressions than ChordAIS-Gen.
It is important to note that we also gave space to make some qualitative comments about our application and the experiments with the curves. Regarding the interface of our system, musicians would prefer to show the progressions with a musical score instead of a MIDI list. As the results can be exported to MIDI files, this shortcoming was partially addressed. In the experiments carried out, we obtained some comments in which they stated that they felt sometimes that the curves are too simple, and they would need a more complex curve to totally express the tonal tension profile of the chord progression.
On the contrary, the most common comment for non-musicians was that the extra description of the tonal tension was helpful to wholly understand the work. Additionally, as the curves represent general profiles, matching them with the chord progressions was easier than expected. However, in the usability test, the non-musicians needed deeper training to fully understand the tension profiles. Even though, some of them needed some help at some point while we were running the system to interpret the results and contrast them against the curve they depicted. In a future work, we will try to improve the interface. We also planned to create a new experiment in which the musical expert can draw their own curve instead of selecting among several standard curves.
7. Conclusions and Future Work
This present paper proposes a system that assists a user to generate tonal chord progressions, following a tonal tension profile. The tonal tension profile is a curve that modulates the path of the music played, and it depends on different musical properties. The system is able to search for different chord progressions that comply with musical constraints such as consonance, voice leading, hierarchical tension and perceptual distance. To capture all these musical properties, a function M, encoded in the Tonal Interval Space (TIS), has been designed. A Genetic Programming with artificial immune system properties has been developed and integrated into ChordAIS-Gen to find multiple solutions in parallel, resulting in multiple chord progressions that follow the tonal tension profile. This new algorithm can be applied to problems in very different contexts, including Healthcare, energy optimization or smart cities.
A listening test was carried out to demonstrate that the chord progressions proposed by ChordAIS-Gen adapt to the tonal tension profile. Most listeners appreciated the same curve that our model predicted with the function M. Additionally, most listeners also rated the chord progressions proposed by ChordAIS-Gen more positively than the progressions discarded. Statistical analysis showed that our algorithm is able to propose good candidates according to the subjective ratings. Additionally, we made a comparison to evaluate if the incorporation of AIS properties to a GP algorithm can improve the performance of those algorithms individually.
We would like to highlight the subjective nature of this task, the generation of music, is therefore hard to evaluate through mathematical measures. We developed the listening tests, which are subjective evaluations, and thus, whose results depend on factors such as culture, musical education or personal preferences. Those factors are not encoded in the objective function. Consequently, even when the participants involved were familiar with the Western tonal music, the results of the listening test can vary between individuals. For example, people with musical training may be more receptive to capture tonal tension due to wide exposure to Western tonal music, or can interpret dissonances as possibilities within the tonal music paradigm.
In this work, we focused on the long-term and hierarchical aspects of the automatic generation of chord progressions. Furthermore, we focused on the ability to provide multiple options that are considered good candidate solutions with variety among themselves. However, the system does not learn from previous experiences to understand the users’ preferences. Future work should investigate how to automatically incorporate this knowledge and combine it with the function constructed. Additionally, we will compare our results with other bioinspired algorithms and proposals based on artificial neural networks, which have demonstrated positive results in other areas [
48,
49].