Intelligent Control Based on a Neural Network for Aircraft Landing Gear with a Magnetorheological Damper in Different Landing Scenarios
Abstract
1. Introduction
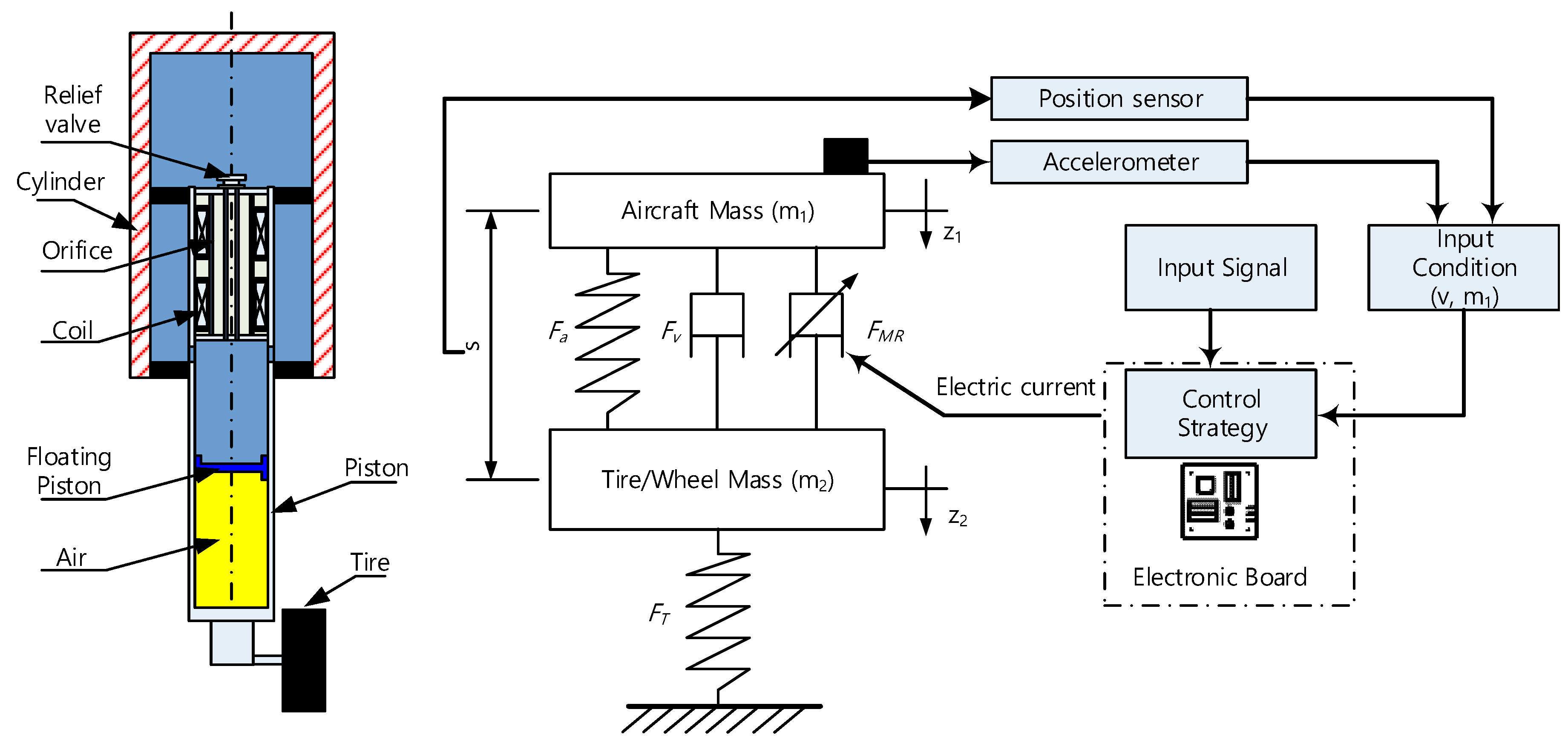
2. Landing Gear System
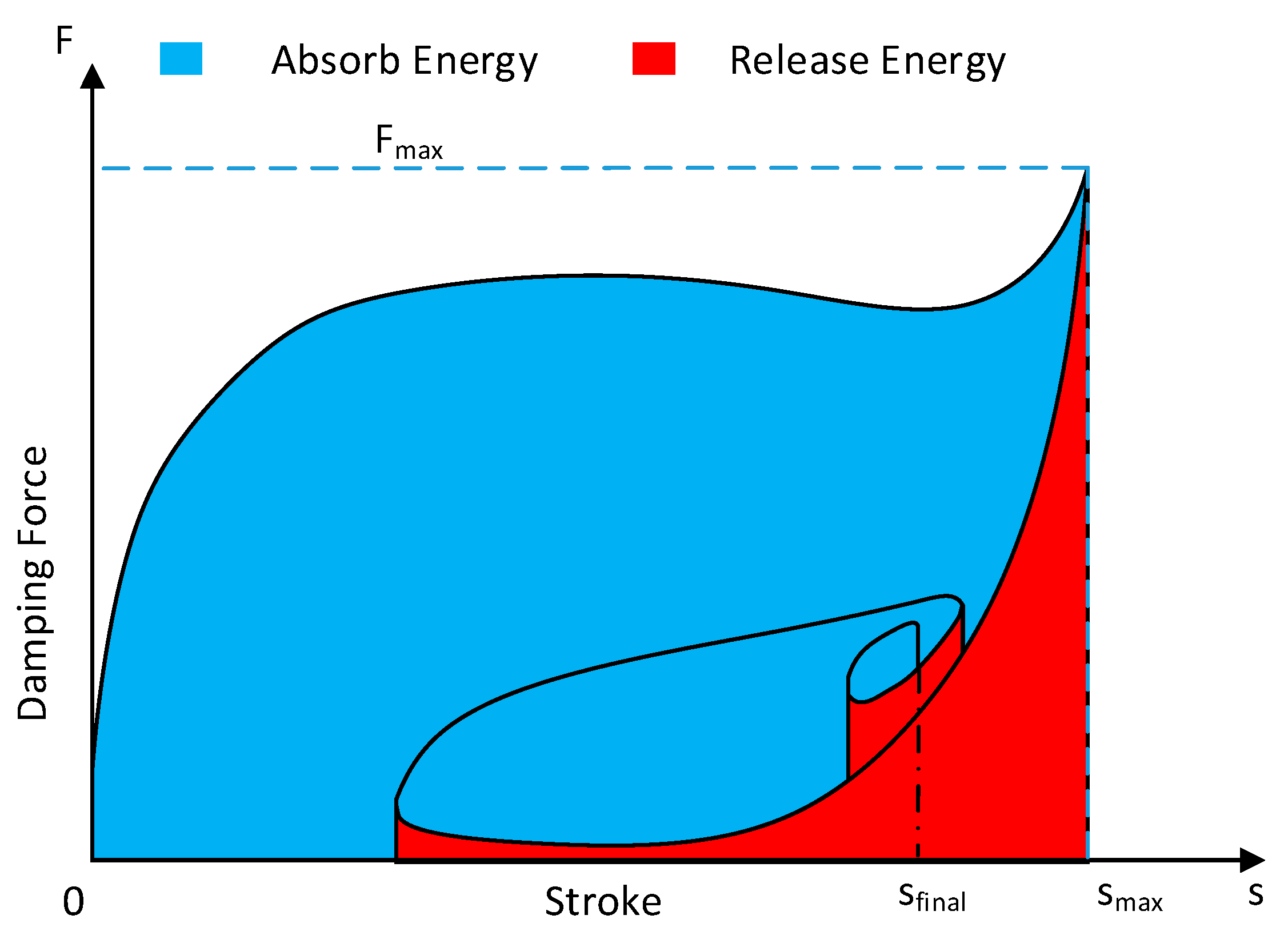
3. Control Target
4. Intelligent Controller Design
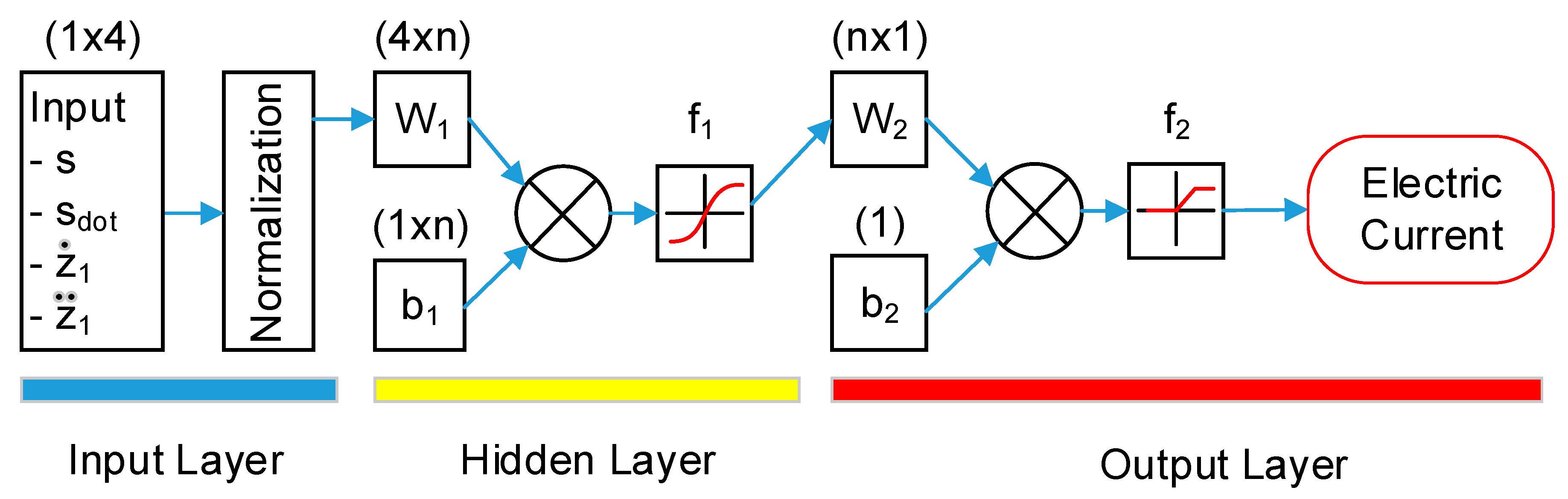
4.1. Neural Network Structure
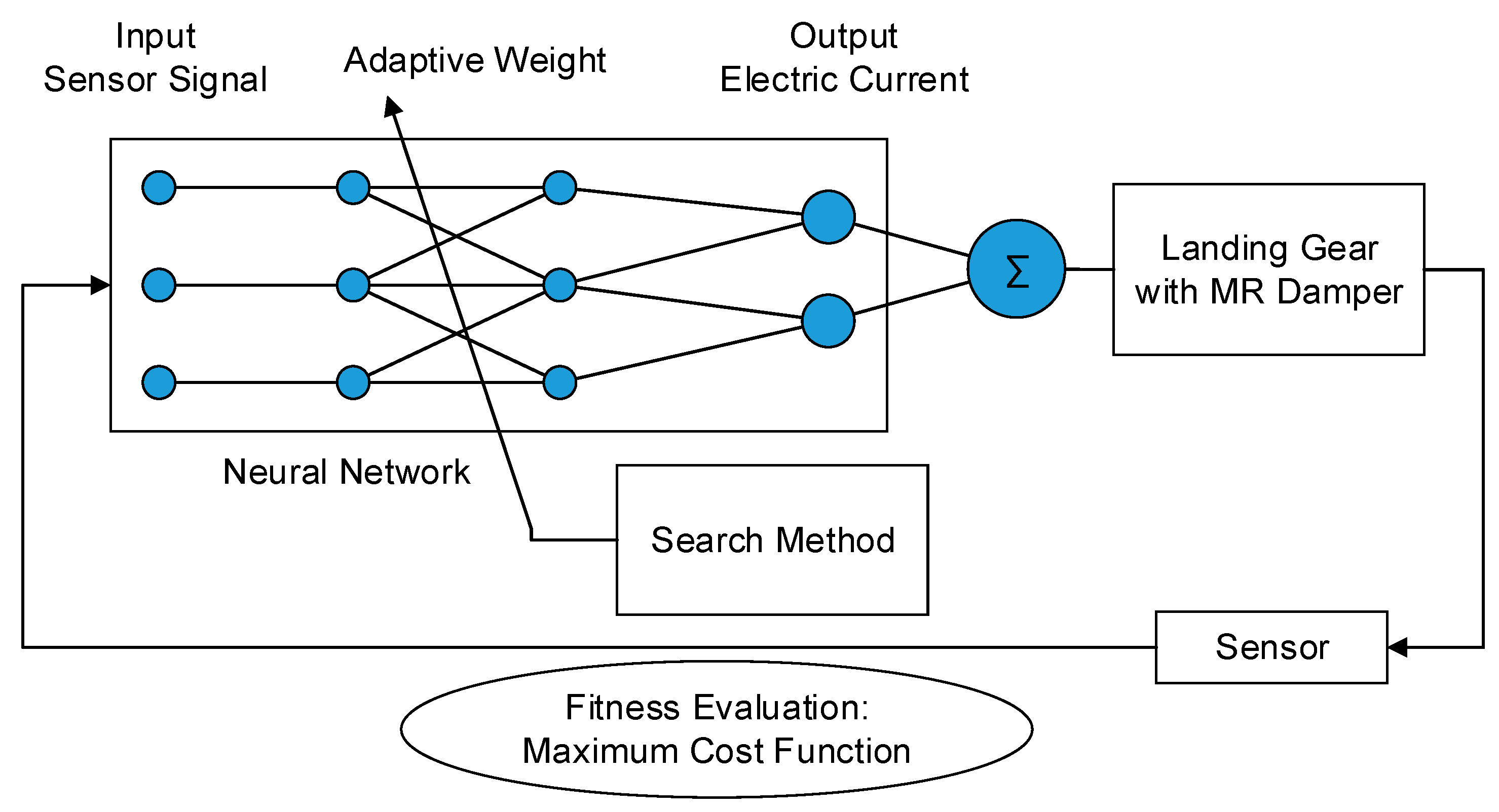
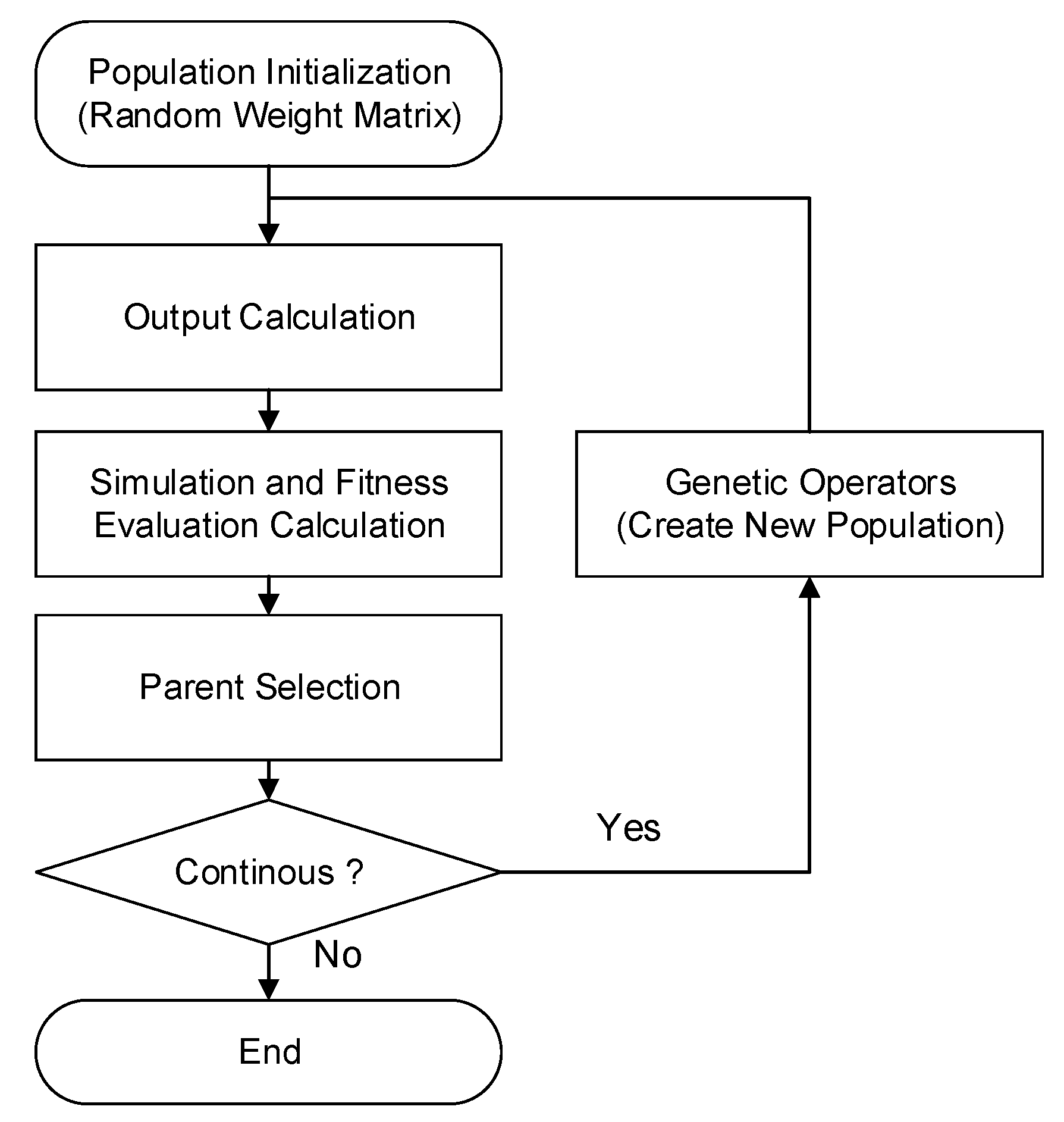
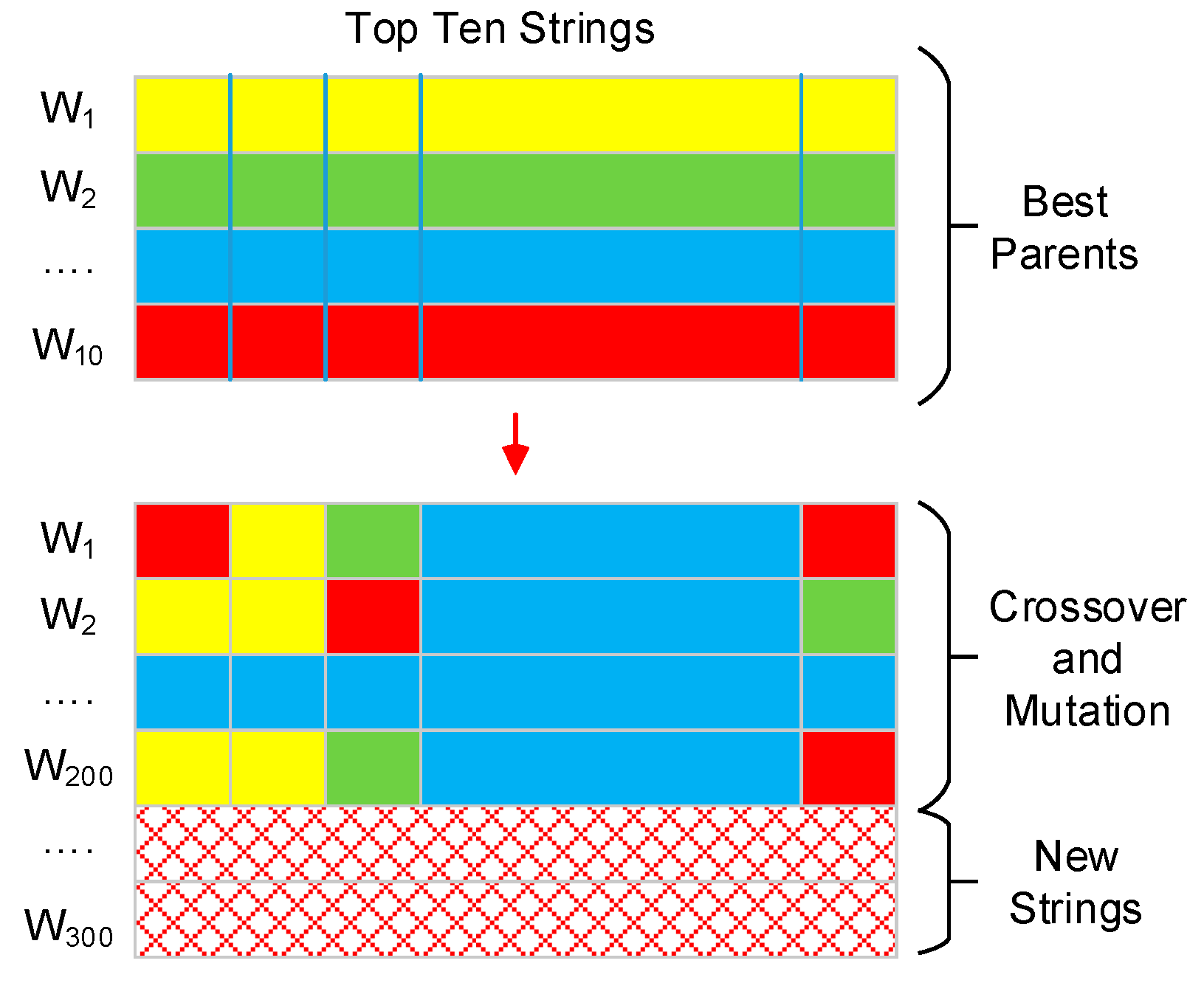
4.2. Genetic Algorithm
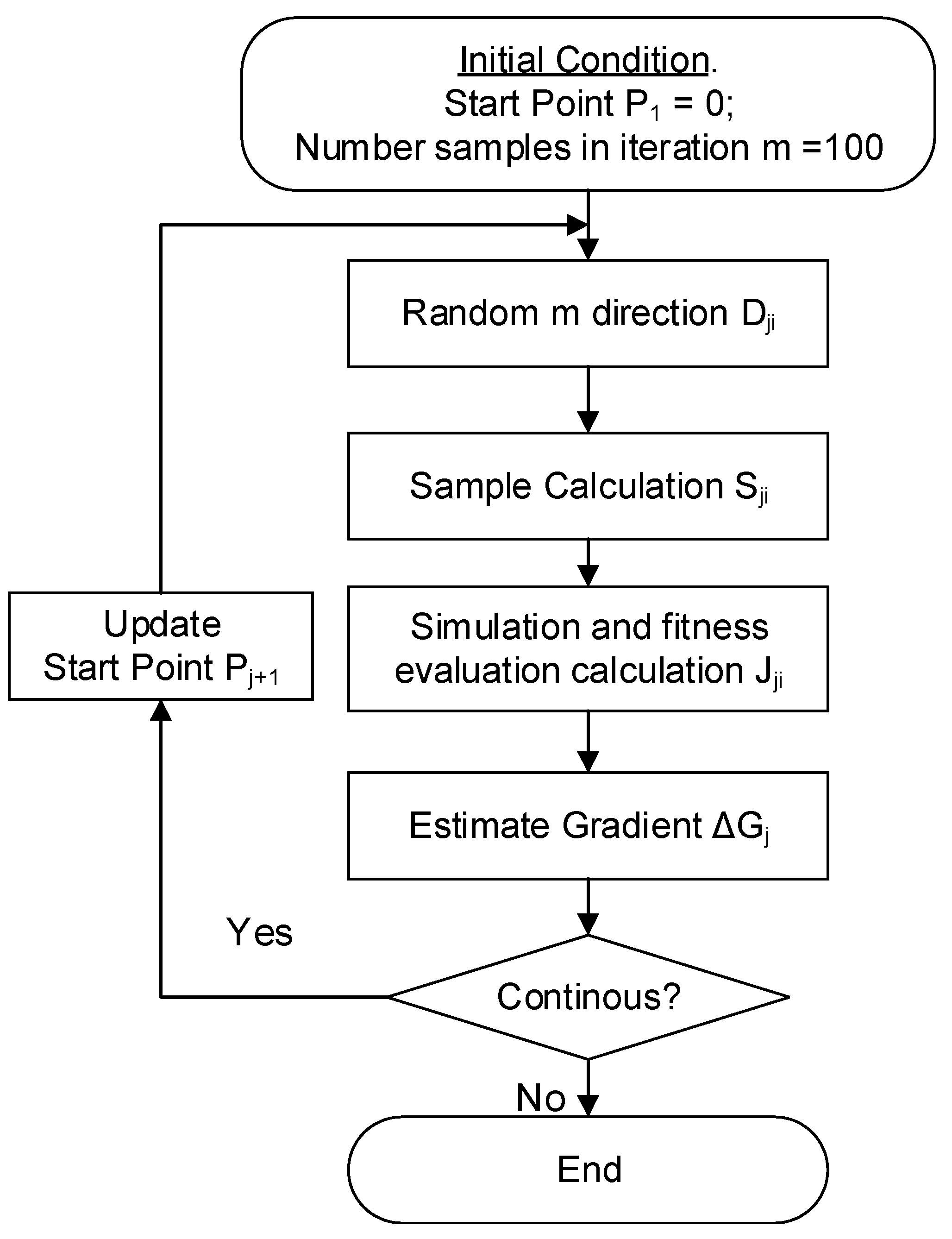
4.3. Policy Gradient Estimation
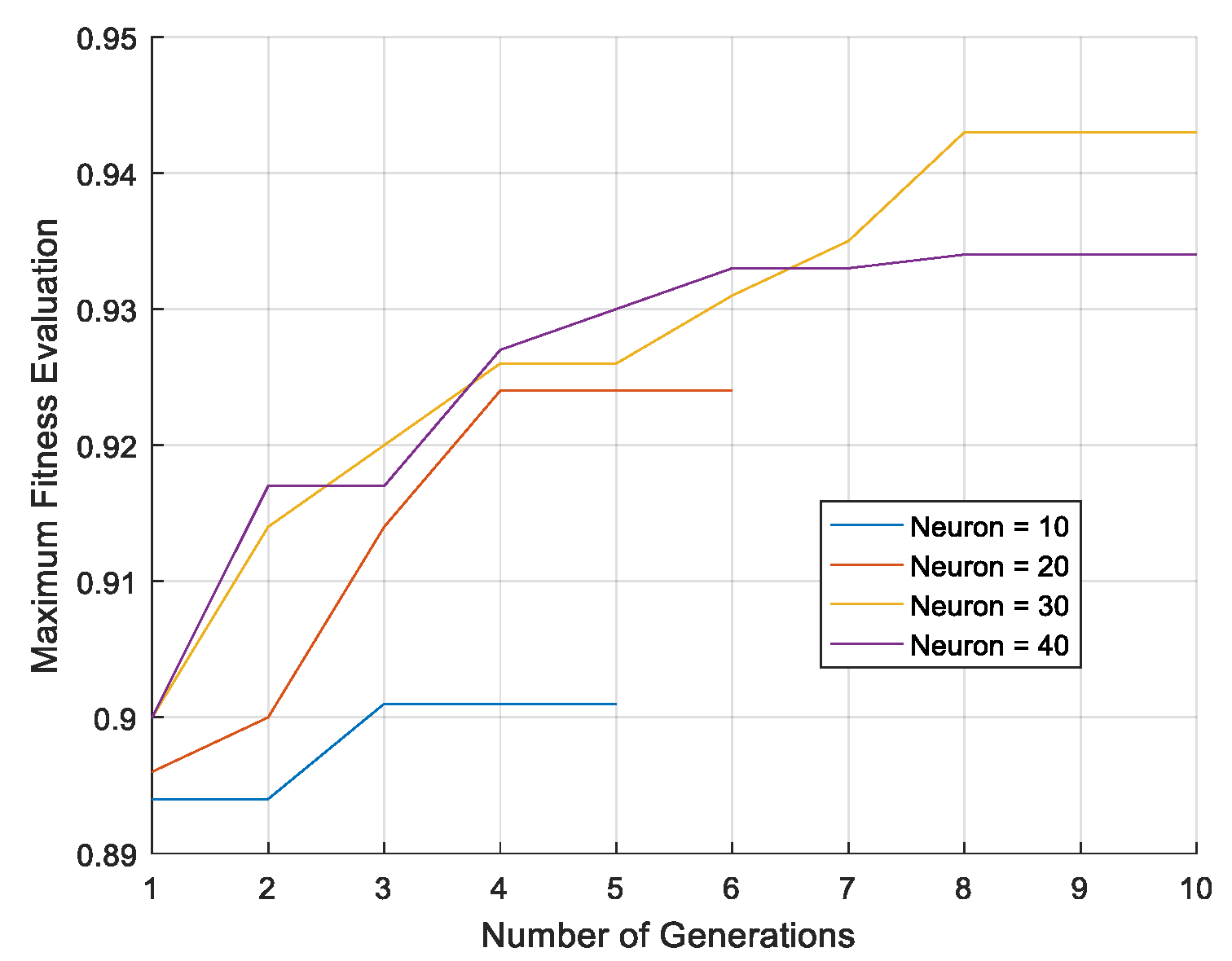
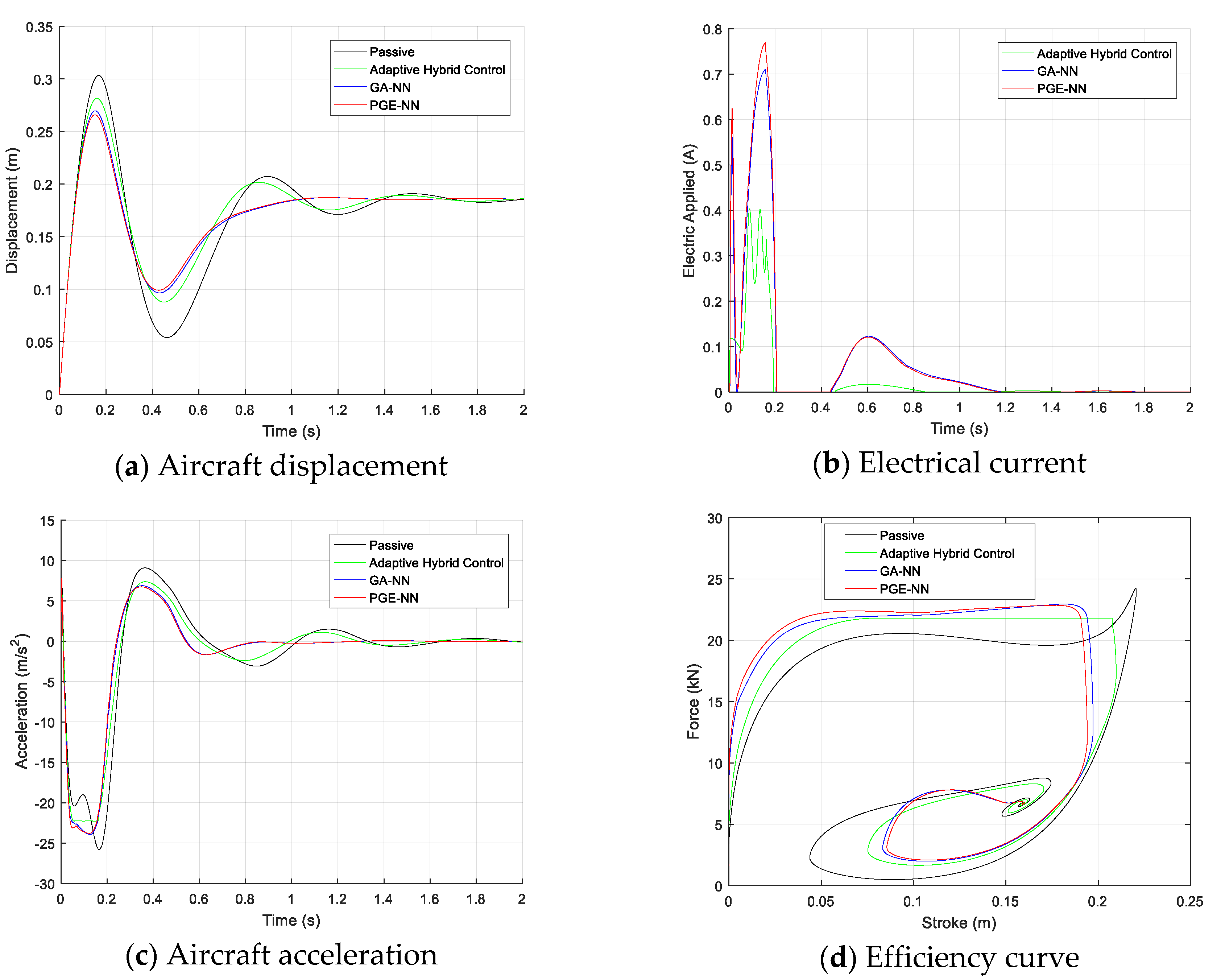
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Choi, S.-B.; Han, Y.-M. Magnetorheological Fluid Technology Applications in Vehicle Systems; CRC Press Taylor & Francis Group: Boca Raton, FL, USA, 2013; ISBN 978-1-4398-5674-1. [Google Scholar]
- Choi, Y.-T.; Wereley, N.M. Vibration Control of a Landing Gear System Featuring Electrorheological/Magnetorheological Fluids. J. Aircr. 2003, 40, 432–439. [Google Scholar] [CrossRef]
- Batterbee, D.C.; Sims, N.D.; Stanway, R.; Wolejsza, Z. Magnetorheological landing gear: 1. A design methodology. Smart Mater. Struct. 2007, 16, 2429–2440. [Google Scholar] [CrossRef][Green Version]
- Batterbee, D.C.; Sims, N.D.; Stanway, R.; Rennison, M. Magnetorheological landing gear: 2. Validation using experimental data. Smart Mater. Struct. 2007, 16, 2441–2452. [Google Scholar] [CrossRef]
- Fu, L.; Chen, S.; Bai, X.; Wang, J. Optimal control of aircraft landing gear state feedback based on magnetorheological damper. In Proceedings of the 2018 Chinese Control and Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 6673–6676. [Google Scholar]
- Balamurugan, L.; Jancirani, J.; Eltantawie, M.A. Generalized magnetorheological (MR) damper model and its application in semi-active control of vehicle suspension system. Int. J. Automot. Technol. 2014, 15, 419–427. [Google Scholar] [CrossRef]
- Kang, B.-H.; Han, C.; Choi, S.-B. A sky-ground hook controller for efficiency enhancement of aircraft landing gear with MR damper. In Proceedings of the SPIE 10967, Active and Passive Smart Structures and Integrated Systems XIII, Denver, CO, USA, 3–7 March 2019; pp. 1–8. [Google Scholar] [CrossRef]
- Dong, X.M.; Xiong, G.W. Vibration Attenuation of Magnetorheological Landing Gear System with Human Simulated Intelligent Control. Math. Probl. Eng. 2013, 2013, 242476 . [Google Scholar] [CrossRef]
- Gharapurkar, A.A. Robust Semi-active Control of Aircraft Landing Gear System Equipped with Magnetorheological Dampers. Master’s Thesis, Concordia University, Montreal, QC, Canada, 2014. [Google Scholar]
- Li, F.; Wei, G.; Qi, W.; Xinhe, X. Modeling and adaptive control of magneto-rheological buffer system for aircraft landing gear. Appl. Math. Model. 2015, 39, 2509–2517. [Google Scholar] [CrossRef]
- Choi, Y.-T.; Robinson, R.; Hu, W.; Wereley, N.M.; Birchette, T.S.; Bolukbasi, A.O.; Woodhouse, J. Analysis and Control of a Magnetorheological Landing Gear System for a Helicopter. J. Am. Helicopter. Soc. 2016, 61, 1–8. [Google Scholar] [CrossRef]
- Yoon, J.-Y.; Kang, B.-H.; Kim, J.-H.; Choi, S.-B. New control logic based on mechanical energy conservation for aircraft landing gear system with magnetorheological dampers. Smart Mater. Struct. 2020, 29, 084003. [Google Scholar] [CrossRef]
- Konar, A. Computational Intelligence: Principles, Techniques and Applications; Springer: Berlin/Heidelberg, Germany, 2005; ISBN 3-540-20898-4. [Google Scholar]
- Tian, Y.; Pei, K.; Jana, S.; Ray, B. DeepTest: Automated testing of deep-neural-network-driven autonomous cars. In Proceedings of the 40th International Conference on Software Engineering—ICSE’18, Gothenburg, Sweden, 27 May–3 June 2018; pp. 303–314. [Google Scholar]
- Mosavi, A.; Varkonyi, A. Learning in Robotics. Int. J. Comput. Appl. 2017, 157, 8–11. [Google Scholar] [CrossRef]
- Parker, G.; Zbeda, R. Learning Area Coverage for a Self-Sufficient Hexapod Robot Using a Cyclic Genetic Algorithm. IEEE Syst. J. 2014, 8, 778–790. [Google Scholar] [CrossRef]
- Zhu, S.X.; Han, Y.; Wang, B. Application of BP Neural Network PID Controller in Landing Gear Based on MRF Damper. Appl. Mech. Mater. 2015, 779, 226–232. [Google Scholar] [CrossRef]
- Holmes, G.; Sartor, P.; Reed, S.; Southern, P.; Worden, K.; Cross, E. Prediction of landing gear loads using machine learning techniques. Struct. Health Monit. 2016, 15, 568–582. [Google Scholar] [CrossRef]
- Luong, Q.V.; Jang, D.-S.; Hwang, J.-H. Robust Adaptive Control for an Aircraft Landing Gear Equipped with a Magnetorheological Damper. Appl. Sci. 2020, 10, 1459. [Google Scholar] [CrossRef]
- Han, C.; Kang, B.-H.; Choi, S.-B.; Tak, J.M.; Hwang, J.-H. Control of Landing Efficiency of an Aircraft Landing Gear System with Magnetorheological Dampers. J. Aircr. 2019, 56, 1980–1986. [Google Scholar] [CrossRef]
- Han, C.; Kim, B.-G.; Choi, S.-B. Design of a New Magnetorheological Damper Based on Passive Oleo-Pneumatic Landing Gear. J. Aircr. 2018, 55, 2510–2520. [Google Scholar] [CrossRef]
- Norman, S.C. Aircraft Landing Gear Design: Principles and Practices; AIAA Education; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1988; ISBN 0-930403-41-X. [Google Scholar]
- Li, Y.; Jiang, J.Z.; Neild, S.A.; Wang, H. Optimal Inerter-Based Shock–Strut Configurations for Landing-Gear Touchdown Performance. J. Aircr. 2017, 54, 1901–1909. [Google Scholar] [CrossRef]
- Hagan, M.T.; Demuth, H.B.; Beale, M.H.; De Jesús, O. Neural Network Design, 2nd ed.; Martin Hagan: Stillwater, OK, USA, 2014; ISBN 0-9717321-1-6. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction, 2nd ed.; A Bradford Book; The MIT Press: Cambridge, MA, USA; London, UK, 2018; ISBN 978-0-262-03924-6. [Google Scholar]
- Russell, S.; Norvig, P. Artificial Intelligence A Modern Approach, 3rd ed.; Pearson Education Limited: Essex, UK, 2016; ISBN 1-292-15396-2. [Google Scholar]
- Fazel, M.; Ge, R.; Kakade, S.M.; Mesbahi, M. Global Convergence of Policy Gradient Methods for the Linear Quadratic Regulator. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; p. 10. [Google Scholar]

| Symbol | Quantity | Value | Unit |
|---|---|---|---|
| Ap | cross-area of head piston | 2.5 × 10−3 | m2 |
| b | tire force index | 1.13 | |
| C | viscous damping coefficient | 6.58 | kNs/m |
| g | gravitational acceleration | 9.81 | m/s2 |
| m1 | sprung mass (aircraft mass) | 560–680 | kg |
| m2 | un-sprung mass | 18 | kg |
| n | polytropic process index | 1.3 | |
| p0 | initial air chamber charging pressure | 810 | kPa |
| pATM | atmospheric pressure | 101.3 | kPa |
| kT | tire force constant | 412 | kN/m |
| v | initial sink speed of aircraft at touchdown | 2–3 | m/s |
| V0 | initial air chamber volume | 6.37 × 10−4 | m3 |
| u | control input (electrical current) | 0–1 | A |
| Aircraft Mass(kg) | |||||
|---|---|---|---|---|---|
| 560 | 600 | 640 | 680 | ||
| Sink speed (m/s) | 2 | η1 | η2 | η3 | η4 |
| 2.5 | η5 | η6 | η7 | η8 | |
| 3 | η9 | η10 | η11 | η12 | |
| Parameter | Total Loops for Convergence | Number Simulation per Loop | Execution Time per Simulations (second) | Total Execution Time (hour) |
|---|---|---|---|---|
| GA-NN | 10 | 300 | 13.6 | 11.3 |
| PGE-NN | 11 | 100 | 12.9 | 3.9 |
| Maximum of Stroke smax (m) | Maximum of Damping Force Fmax (kN) | Total Energy Absorber Efficiency η (%) | |
|---|---|---|---|
| Passive Damper | 0.221 | 24.2 | 80.4 |
| Adaptive Hybrid Control | 0.210 | 21.8 | 94.0 |
| GA-NN | 0.197 | 22.9 | 94.6 |
| PGE-NN | 0.194 | 22.8 | 94.9 |
| Passive Damper | Adaptive Hybrid Control | |||||
|---|---|---|---|---|---|---|
| Fmax (kN) | smax (m) | η (%) | Fmax (kN) | smax (m) | η (%) | |
| m1 = 560 kg | ||||||
| v = 2 m/s | 14.3 | 0.177 | 79.4 | 14.3 | 0.146 | 96.5 |
| v = 2.5 m/s | 16.9 | 0.193 | 81.1 | 16.9 | 0.164 | 95.8 |
| v = 3 m/s | 19.7 | 0.207 | 84.9 | 19.7 | 0.186 | 94.6 |
| m1 = 600 kg | ||||||
| v = 2 m/s | 14.5 | 0.186 | 80.9 | 15.3 | 0.146 | 95.3 |
| v = 2.5 m/s | 17.2 | 0.200 | 83.3 | 18.2 | 0.160 | 98.8 |
| v = 3 m/s | 20.0 | 0.212 | 87.9 | 21.2 | 0.181 | 97.4 |
| m1 = 640 kg | ||||||
| v = 2 m/s | 14.7 | 0.194 | 82.7 | 15.6 | 0.157 | 96.4 |
| v = 2.5 m/s | 17.5 | 0.207 | 85.9 | 18.5 | 0.174 | 96.4 |
| v = 3 m/s | 21.5 | 0.217 | 86.1 | 21.5 | 0.195 | 95.8 |
| m1 = 680 kg | ||||||
| v = 2 m/s | 14.9 | 0.201 | 84.9 | 15.8 | 0.168 | 95.9 |
| v = 2.5 m/s | 18.6 | 0.212 | 84.7 | 18.8 | 0.189 | 94.1 |
| v = 3 m/s | 24.2 | 0.221 | 80.4 | 21.8 | 0.210 | 94.0 |
| m1 = 575 kg (Random Case 1) | ||||||
| v = 2.25 m/s | 15.7 | 0.188 | 80.6 | 15.7 | 0.158 | 96.0 |
| m2 = 625 kg (Random Case 2) | ||||||
| v = 2.75 m/s | 18.9 | 0.210 | 87.3 | 19.9 | 0.178 | 96.9 |
| m3 = 654 kg (Random Case 3) | ||||||
| v = 2.35 m/s | 16.8 | 0.205 | 85.7 | 17.7 | 0.173 | 96.0 |
| GA-NN | PGE-NN | |||||
|---|---|---|---|---|---|---|
| Fmax (kN) | smax (m) | η (%) | Fmax (kN) | smax (m) | η (%) | |
| m1 = 560 kg | ||||||
| v = 2 m/s | 14.8 | 0.144 | 94.4 | 14.7 | 0.144 | 94.7 |
| v = 2.5 m/s | 17.7 | 0.157 | 95.6 | 17.6 | 0.157 | 95.5 |
| v = 3 m/s | 20.6 | 0.177 | 94.0 | 20.6 | 0.177 | 94.8 |
| m1 = 600 kg | ||||||
| v = 2 m/s | 15.5 | 0.150 | 94.4 | 15.3 | 0.150 | 95.4 |
| v = 2.5 m/s | 18.1 | 0.164 | 96.8 | 18.1 | 0.164 | 97.3 |
| v = 3 m/s | 21.1 | 0.184 | 95.5 | 21.0 | 0.183 | 96.9 |
| m1 = 640 kg | ||||||
| v = 2 m/s | 16.2 | 0.155 | 94.2 | 16.1 | 0.155 | 94.8 |
| v = 2.5 m/s | 18.9 | 0.171 | 95.8 | 18.8 | 0.169 | 97.3 |
| v = 3 m/s | 21.7 | 0.191 | 96.1 | 21.7 | 0.189 | 97.6 |
| m1 = 680 kg | ||||||
| v = 2 m/s | 16.9 | 0.160 | 94.6 | 16.8 | 0.160 | 95.0 |
| v = 2.5 m/s | 19.7 | 0.178 | 94.9 | 19.6 | 0.175 | 95.0 |
| v = 3 m/s | 22.9 | 0.197 | 94.6 | 22.8 | 0.194 | 94.9 |
| m1 = 575 kg (Random Case 1) | ||||||
| v = 2.25 m/s | 16.4 | 0.149 | 97.8 | 16.1 | 0.152 | 97.2 |
| m2 = 625 kg (Random Case 2) | ||||||
| v = 2.75 m/s | 20.0 | 0.179 | 96.1 | 19.6 | 0.182 | 96.3 |
| m3 = 654 kg (Random Case 3) | ||||||
| v = 2.35 m/s | 18.4 | 0.167 | 95.8 | 18.2 | 0.182 | 95.8 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luong, Q.V.; Jang, D.-S.; Hwang, J.-H. Intelligent Control Based on a Neural Network for Aircraft Landing Gear with a Magnetorheological Damper in Different Landing Scenarios. Appl. Sci. 2020, 10, 5962. https://doi.org/10.3390/app10175962
Luong QV, Jang D-S, Hwang J-H. Intelligent Control Based on a Neural Network for Aircraft Landing Gear with a Magnetorheological Damper in Different Landing Scenarios. Applied Sciences. 2020; 10(17):5962. https://doi.org/10.3390/app10175962
Chicago/Turabian StyleLuong, Quoc Viet, Dae-Sung Jang, and Jai-Hyuk Hwang. 2020. "Intelligent Control Based on a Neural Network for Aircraft Landing Gear with a Magnetorheological Damper in Different Landing Scenarios" Applied Sciences 10, no. 17: 5962. https://doi.org/10.3390/app10175962
APA StyleLuong, Q. V., Jang, D.-S., & Hwang, J.-H. (2020). Intelligent Control Based on a Neural Network for Aircraft Landing Gear with a Magnetorheological Damper in Different Landing Scenarios. Applied Sciences, 10(17), 5962. https://doi.org/10.3390/app10175962





