Overview of Compressed Sensing: Sensing Model, Reconstruction Algorithm, and Its Applications
Abstract
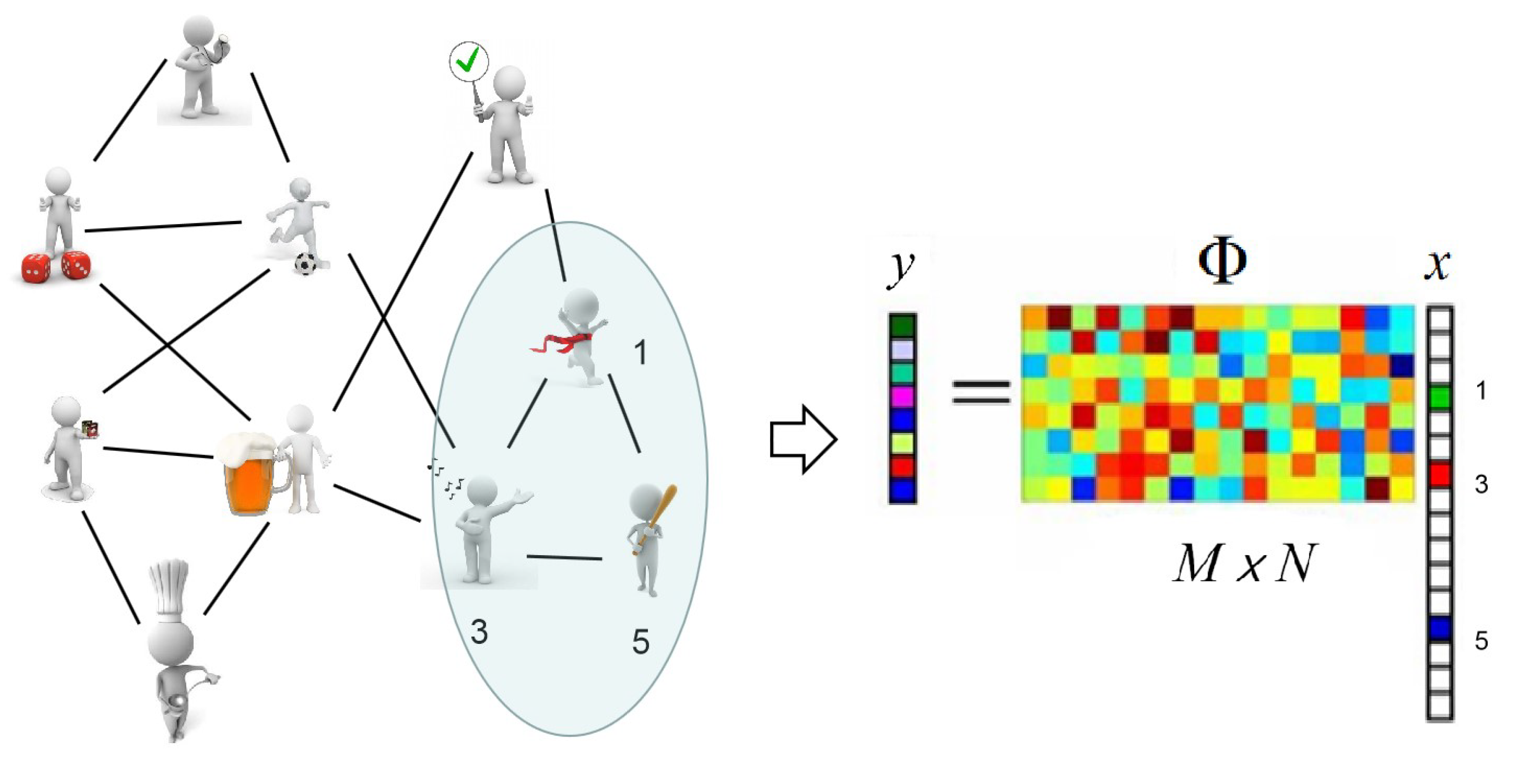
1. Introduction
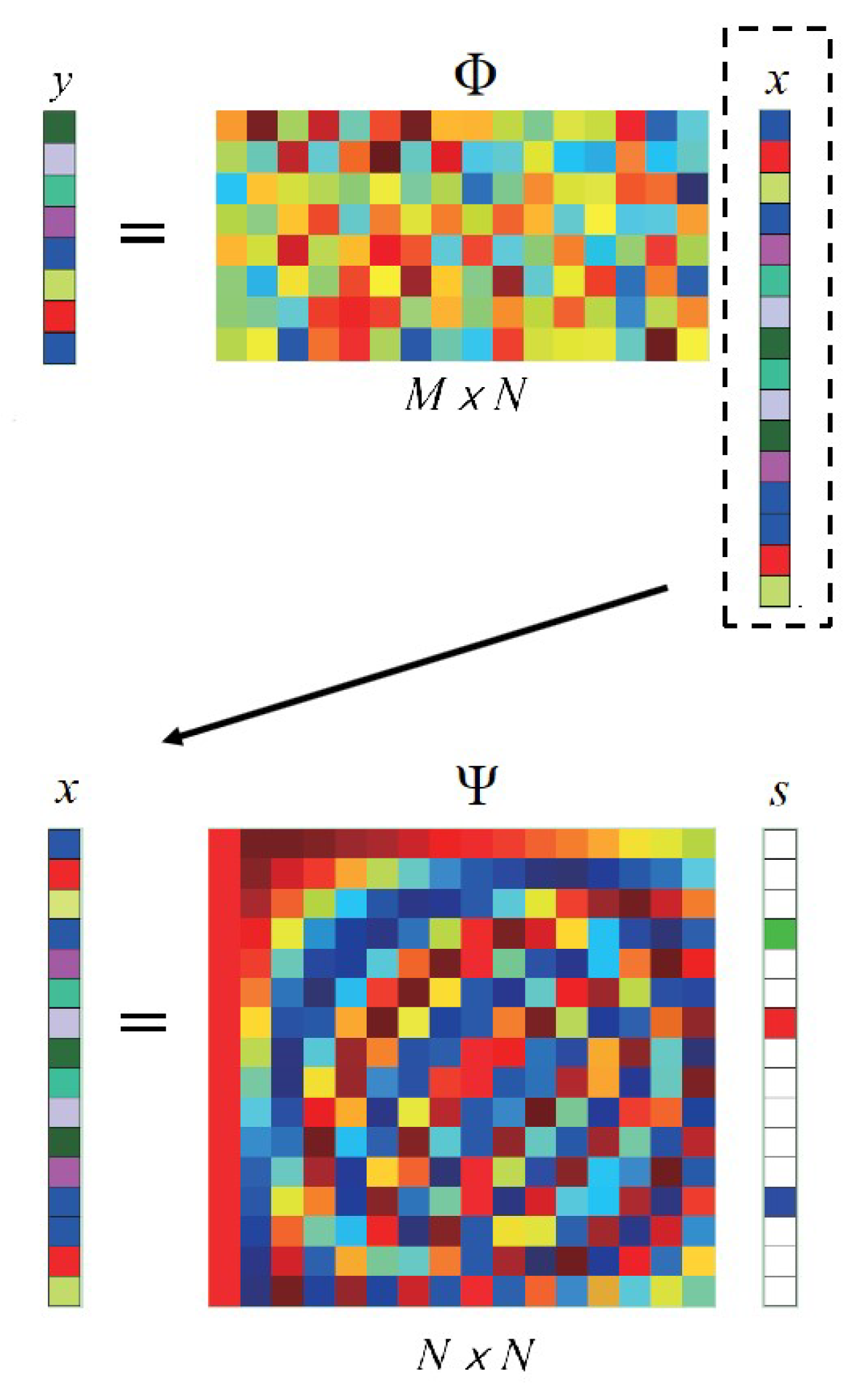
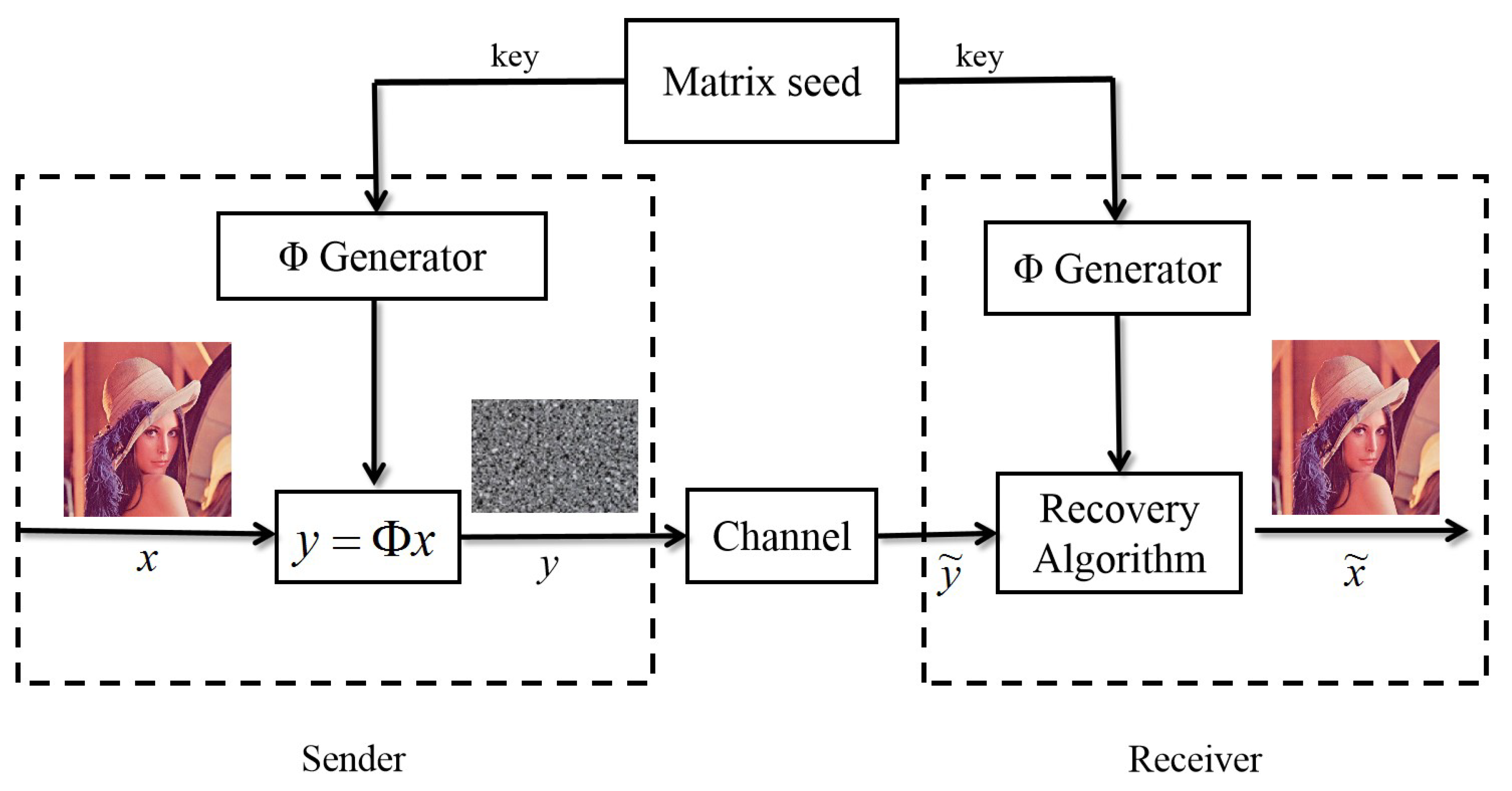
2. Sensing Methods
2.1. Sparse Dictionary Sensing
2.2. Block-Compressed Sensing
- Reshape 2D signal to a new 2D signal .
- We used an appropriate permutation matrix to process , and the process procedure was as follows:where is the permutated 2D sparse signal.
2.3. Chaotic Compressed Sensing
2.4. Deep-Learning Compressed Sensing
- input layer with nodes (B is block size);
- compressed-sensing layer, nodes, (its weights form the sensing matrix);
- reconstruction layers, nodes, each followed by a rectified linear unit (ReLU) [20] activation unit where is the redundancy factor; and
- output layer, nodes.
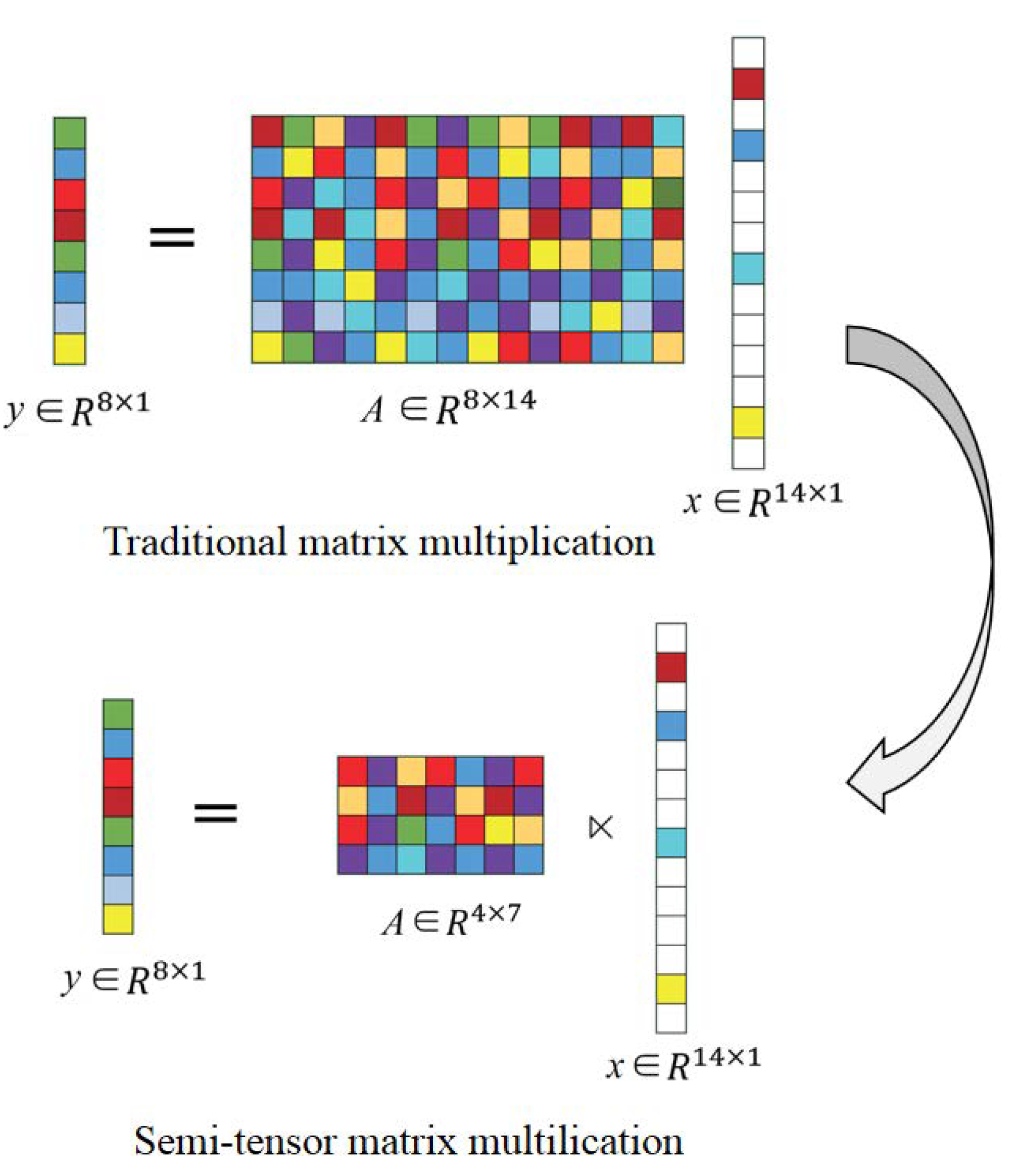
2.5. Semitensor-Product Compressed Sensing
2.6. Other Sensing Methods
3. Reconstruction Algorithm
3.1. Convex-Optimization Algorithm
3.2. Greedy Algorithm
3.3. Bayesian Algorithm
3.4. Noniterative Reconstruction Algorithm
3.5. Deep-Learning Algorithm
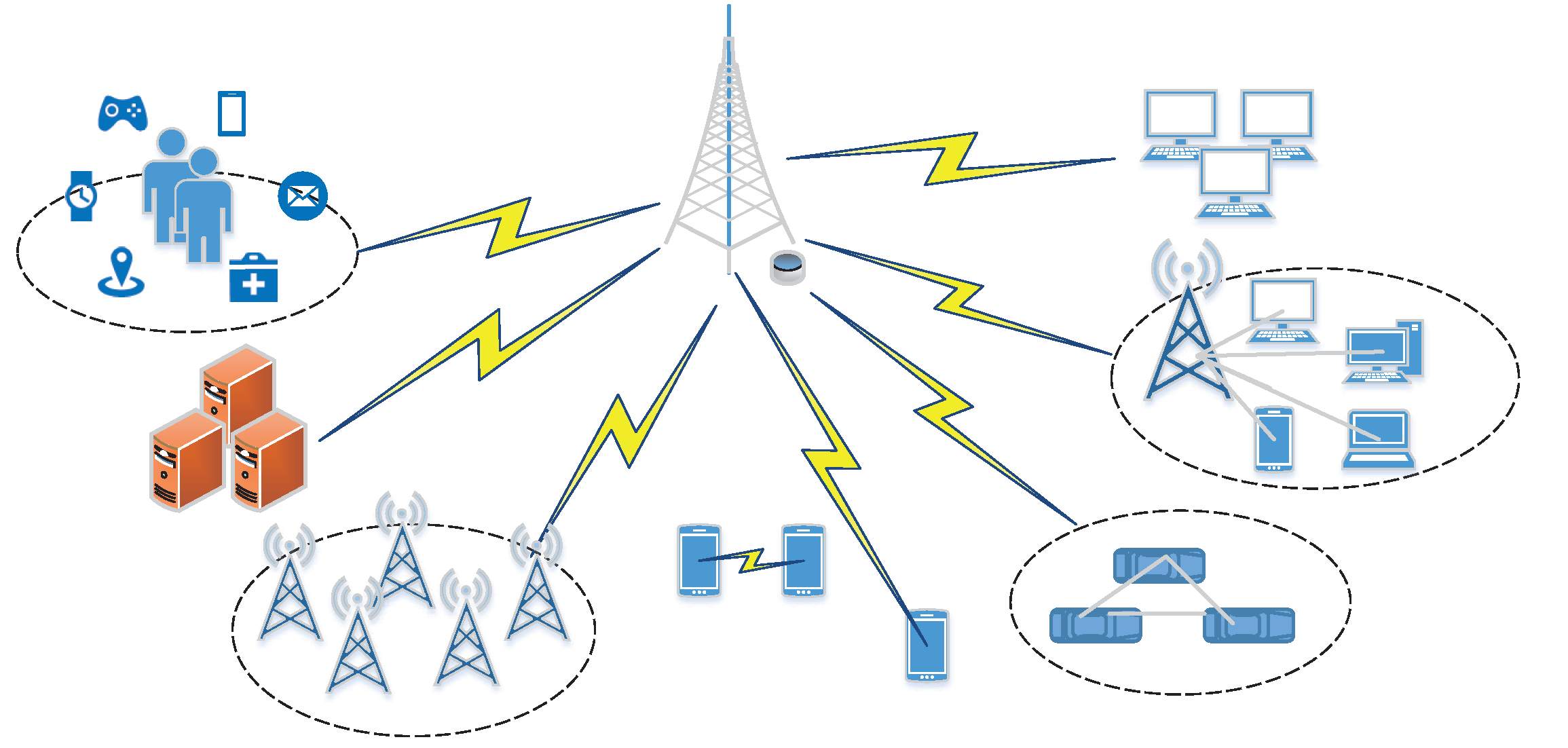
4. Compressed-Sensing Applications
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CS | compressed sensing |
| DFT | discrete Fourier transform |
| DWT | discrete wavelet transform |
| DCT | discrete cosine transform |
| RIP | restricted isometry property |
| DTI | diffusion tensor imaging |
| BCS | block-compressed sensing |
| PSNR | peak signal-to-noise ratio |
| CCS | chaotic compressed sensing |
| BCsM | Bernoulli chaotic sensing matrix |
| IRC | incoherence rotated chaotic |
| ReLU | rectified linear unit |
| BCSSPL-DDWT | block-compressed sensing smooth Landweber with dual-tree discrete wavelet transform |
| MS-BCS-SPL | multiscale block-compressed sensing smooth Landweber |
| MH-BCS-SPL | multihypothesis block-compressed sensing smooth Landweber |
| STP | semitensor product |
| STP-CS | semitensor product compressed sensing |
| WSNs | wireless sensor networks |
| IRLS | iteratively reweighted least-squares |
| PTP | P-tensor product |
| BP | basic pursuit |
| FOCUSS | focal underdetermined system solver |
| MP | matching pursuit |
| OMP | orthogonal matching pursuit |
| StOMP | stagewise orthogonal matching pursuit |
| ROMP | regularized orthogonal matching pursuit |
| CoSaOMP | compressive sampling matching pursuit |
| IHT | iterative hard thresholding |
| gOMP | generalized orthogonal matching pursuit |
| SBL | sparse Bayesian learning |
| MSBL | multiple sparse Bayesian learning |
| AMP | approximate message passing |
| VAMP | vector approximate message passing |
| LVAMP | learned vector approximate message passing |
| ISTA | iterative shrinkage-thresholding algorithm |
| ISTA-Net | iterative shrinkage-thresholding algorithm network |
| SCSNet | scalable convolutional network |
| IoT | Internet of Things |
| CML | coupled map lattice |
| DCML | diffusive coupled map lattice |
| GCML | global coupled map lattice |
| SCS | structured compressed sensing |
References
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Foucart, S. A note on guaranteed sparse recovery via l1-minimization. Appl. Comput. Harmon. A 2010, 29, 97–103. [Google Scholar] [CrossRef]
- Berardinelli, G. Generalized DFT-s-OFDM waveforms without Cyclic Prefix. IEEE Access 2017, 6, 4677–4689. [Google Scholar] [CrossRef]
- Faria, M.L.L.D.; Cugnasca, C.E.; Amazonas, J.R.A. Insights into IoT data and an innovative DWT-based technique to denoise sensor signals. IEEE Sens. J. 2017, 18, 237–247. [Google Scholar] [CrossRef]
- Lawgaly, A.; Khelifi, F. Sensor pattern noise estimation based on improved locally adaptive DCT filtering and weighted averaging for source camera identification and verification view document. IEEE Trans. Inf. Forensics Secur. 2017, 12, 392–404. [Google Scholar] [CrossRef]
- Candes, E.J.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
- Jia, T.; Chen, D.; Wang, J.; Xu, D. Single-pixel color imaging method with a compressive sensing measurement matrix. Appl. Sci. 2018, 8, 1293. [Google Scholar] [CrossRef]
- Sun, T.; Li, J.; Blondel, P. Direct under-sampling compressive sensing method for underwater echo signals and physical implementation. Appl. Sci. 2019, 9, 4596. [Google Scholar] [CrossRef]
- Bai, H.; Li, G.; Li, S.; Li, Q.; Jiang, Q.; Chang, L. Alternating optimization of sensing matrix and sparsifying dictionary for compressed sensing. IEEE Trans. Signal Process. 2015, 63, 1581–1594. [Google Scholar] [CrossRef]
- Duarte-Carvajalino, J.M.; Sapiro, G. Learning to sense sparse signals: Simultaneous sensing matrix and sparsifying dictionary optimization. IEEE Trans. Image Process. 2009, 18, 1395–1408. [Google Scholar] [CrossRef]
- Darryl, M.C.; Irvin, T.; Whittington, H.J.; Grau, V.; Schneider, J.E. Prospective acceleration of diffusion tensor imaging with compressed sensing using adaptive dictionaries. Magn. Reson. Med. 2016, 76, 248–258. [Google Scholar]
- Zhang, B.; Liu, Y.; Zhuang, J.; Yang, L. A novel block compressed sensing based on matrix permutation. In Proceedings of the IEEE Visual Communications and Image Processing, St. Petersburg, FL, USA, 10–13 December 2017; pp. 1–4. [Google Scholar]
- Bigot, J.; Boyer, C.; Weiss, P. An analysis of block sampling strategies in compressed sensing. IEEE Trans. Inf. Theory 2017, 62, 2125–2139. [Google Scholar] [CrossRef]
- Coluccia, G.; Diego, V.; Enrico, M. Smoothness-constrained image recovery from block-based random projections. In Proceedings of the IEEE 15th International Workshop on Multimedia Signal Processing, Pula, Italy, 30 September–2 October 2013; pp. 129–134. [Google Scholar]
- Li, X.; Bao, L.; Zhao, D.; Li, D.; He, W. The analyses of an improved 2-order Chebyshev chaotic sequence. In Proceedings of the IEEE 2012 2nd International Conference on Computer Science and Network Technology, Changchun, China, 29–31 December 2012; pp. 1381–1384. [Google Scholar]
- Gan, H.; Xiao, S.; Zhao, Y. A novel secure data transmission scheme using chaotic compressed sensing. IEEE Access 2018, 6, 4587–4598. [Google Scholar] [CrossRef]
- Peng, H.; Tian, Y.; Kurths, J.; Li, L.; Yang, Y.; Wang, D. Secure and energy-efficient data transmission system based on chaotic compressive sensing in body-to-body networks. IEEE Trans. Biomed. Circuits Syst. 2017, 11, 558–573. [Google Scholar] [CrossRef] [PubMed]
- Yao, S.; Wang, T.; Shen, W.; Pan, S.; Chong, Y. Research of incoherence rotated chaotic measurement matrix in compressed sensing. Multimed. Tools Appl. 2017, 76, 1–19. [Google Scholar] [CrossRef]
- Adler, A.; Boublil, D.; Elad, M.; Zibulevsky, M. A deep learning approach to block-based compressed sensing of images. arXiv 2016, arXiv:1609.01519. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Mun, S.; Fowler, J.E. Block compressed sensing of images using directional transforms. In Proceedings of the 2010 IEEE International Conference on Image Processing, Hong Kong, China, 26–29 September 2010; pp. 3021–3024. [Google Scholar]
- Fowler, J.E.; Mun, S.; Tramel, E.W. Multiscale block compressed sensing with smoothed projected Landweber reconstruction. In Proceedings of the 19th European Signal Processing Conference, Barcelona, Spain, 29 August–2 September 2011; pp. 564–568. [Google Scholar]
- Chen, C.; Tramel, E.W.; Fowler, J.E. Compressed-sensing recovery of images and video using multihypothesis predictions. In Proceedings of the IEEE 2012 46th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 4–7 November 2012; pp. 1193–1198. [Google Scholar]
- Cui, W.; Jiang, F.; Gao, X.; Tao, W.; Zhao, D. Deep neural network based sparse measurement matrix for image compressed sensing. arXiv 2018, arXiv:1806.07026. [Google Scholar]
- Sun, B.; Feng, H.; Chen, K.; Zhu, X. A deep learning framework of quantized compressed sensing for wireless neural recording. IEEE Access 2017, 4, 5169–5178. [Google Scholar] [CrossRef]
- Cheng, D. Semi-tensor product of matrices and its application to Morgen’s problem. Sci. China 2001, 44, 195–212. [Google Scholar]
- Cheng, D.; Zhang, L. On semi-tensor product of matrices and its applications. Acta Math. Appl. Sin. 2003, 19, 219–228. [Google Scholar] [CrossRef]
- Cheng, D.; Qi, H.; Xue, A. A survey on semi-tensor product of matrices. J. Syst. Sci. Complex. 2007, 20, 304–322. [Google Scholar] [CrossRef]
- Cheng, D.; Dong, Y. Semi-tensor product of matrices and its some applications to physics. New Dir. Appl. Control. Theory 2003, 10, 565–588. [Google Scholar] [CrossRef]
- Xie, D.; Peng, H.; Li, L.; Yang, Y. Semi-tensor compressed sensing. Digit. Signal Process. 2016, 58, 85–92. [Google Scholar] [CrossRef]
- Peng, H.; Tian, Y.; Kurths, J. Semitensor product compressive sensing for big data transmission in wireless sensor networks. Math. Probl. Eng. 2017, 2017, 8158465. [Google Scholar] [CrossRef]
- Wang, J.; Ye, S.; Ruan, Y.; Chen, C. Low storage space for compressive sensing: Semi-tensor product approach. Eurasip J. Image Video Process. 2017, 2017, 51. [Google Scholar] [CrossRef]
- Peng, H.; Mi, Y.; Li, L.; Stanley, H.E.; Yang, Y. P-tensor Product in Compressed Sensing. IEEE Internet Things J. 2019, 6, 3492–3511. [Google Scholar] [CrossRef]
- Nouasria, H.; Tolba, M.E. New sensing approach for compressive sensing using sparsity domain. In Proceedings of the 19th IEEE Mediterranean Electrotechnical Conference, Marrakech, Morocco, 2–7 May 2018; pp. 20–24. [Google Scholar]
- Boyer, C.; Bigot, J.; Weiss, P. Compressed sensing with structured sparsity and structured acquisition. Appl. Comput. Harmon. Anal. 2017, 46, 312–350. [Google Scholar] [CrossRef]
- Ishikawa, S.; Wu, W.; Lang, Y. A novel method for designing compressed sensing matrix. In Proceedings of the IEEE International Workshop on Advanced Image Technology, Chiang Mai, Thailand, 7–9 January 2018. [Google Scholar]
- Chen, S.S.; Donoho, D.L.; Saunders, M.A. Atomic decomposition by basis pursuit. SIAM Rev. 2001, 43, 129–159. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, J.; Chen, C.; Tian, F. Basic pursuit of an adaptive impulse dictionary for bearing fault diagnosis. In Proceedings of the 2014 IEEE International Conference on Mechatronics and Control, Jinzhou, China, 3–5 July 2014; pp. 2425–2430. [Google Scholar]
- Mohimani, H.; Babaie, M.; Jutten, C. A fast approach for overcomplete sparse decomposition based on smoothed l0-norm. IEEE Trans. Signal Process. 2009, 57, 289–301. [Google Scholar] [CrossRef]
- Yan, F.; Yang, P.; Yang, F.; Zhou, L.; Gao, M. Synthesis of pattern reconfigurable sparse arrays with multiple measurement vectors FOCUSS method. IEEE Trans. Antennas Propag. 2017, 65, 602–611. [Google Scholar] [CrossRef]
- Chen, J.; Ho, X. Theoretical results on sparse representations of multiple-measurement vectors. IEEE Trans. Signal Processs. 2006, 54, 4634–4643. [Google Scholar] [CrossRef]
- Majumdar, A.; Ward, R.K.; Aboulnasr, T. Algorithms to approximately solve NP hard row-sparse MMV recovery problem: Application to compressive color imaging. IEEE J. Emerg. Sel. Topic Circuits Syst. 2012, 2, 362–369. [Google Scholar] [CrossRef]
- Berg, E.; Friedlander, M.P. Theoretical and empirical results for recovery from multiple measurements. IEEE Trans. Inf. Theory 2010, 56, 2516–2527. [Google Scholar] [CrossRef]
- Figueiredo, M.A.T.; Nowak, R.D.; Wright, S.J. Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems. IEEE J. Sel. Top. Signal Process. 2008, 1, 586–597. [Google Scholar] [CrossRef]
- Wright, S.J.; Nowak, R.D.; Figueiredo, M.A.T. Sparse reconstruction by separable approximation. IEEE Trans. Signal Process. 2009, 57, 2479–2493. [Google Scholar] [CrossRef]
- Mallat, S.J.; Zhang, Z. Matching pursuits with time-frequency dictionaries. IEEE Trans. Signal Process. 1993, 41, 3397–3415. [Google Scholar] [CrossRef]
- Tropp, J.A.; Gilbert, A.C. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Donoho, D.L.; Tsaig, Y.; Drori, I.; Starck, J.L. Sparse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit. IEEE Trans. Inf. Theory 2012, 58, 1094–1121. [Google Scholar] [CrossRef]
- Needell, D.; Vershynin, R. Uniform uncertainty principle and signal recovery via regularized orthogonal matching pursuit. Found. Comput. Math. 2009, 9, 317–334. [Google Scholar] [CrossRef]
- Needell, D.; Tropp, J.A. Cosamp: Iterative signal recovery from incomplete and inaccurate samples. Appl. Comput. Harmon. Anal. 2009, 26, 301–321. [Google Scholar] [CrossRef]
- Blumensath, T.; Davies, M.E. Iterative hard thresholding for compressed sensing. Appl. Comput. Harmon. Anal. 2009, 27, 265–274. [Google Scholar] [CrossRef]
- Wen, J.; Zhou, Z.; Wang, J.; Tang, X.; Mo, Q. A sharp ocndition for exact support recovery with orthogonal matching pursuit. IEEE Trans. Signal Process. 2017, 65, 1370–1382. [Google Scholar] [CrossRef]
- Wang, J.; Kwon, S.; Shim, B. Generalized orthogonal matching pursuit. IEEE Trans. Signal Process. 2012, 60, 6202–6216. [Google Scholar] [CrossRef]
- Liu, E.; Temlyakov, V.N. The orthogonal super greedy algorithm and applications in compressed sensing. IEEE Trans Inf. Theory 2012, 58, 2040–2047. [Google Scholar] [CrossRef]
- Liu, E.; Temlyakov, V.N. Super greedy type algorithms. Adv. Comput. Math. 2012, 37, 493–504. [Google Scholar] [CrossRef]
- Wang, J.; Kwon, S.; Li, P.; Shim, B. Recovery of sparse signals via generalized orthogonal matching pursuit: A new analysis. IEEE Trans. Signal Process. 2016, 64, 1076–1089. [Google Scholar] [CrossRef]
- Zayyani, H.; Babaie, M.; Jutten, C. Decoding real-field codes by an iterative Expectation-Maximization (EM) algorithm. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing, Las Vegas, NV, USA, 31 March–4 April 2008; pp. 3169–3172. [Google Scholar]
- Ji, S.; Xue, Y.; Carin, L. Bayesian compressive sensing. IEEE Trans. Signal Process. 2008, 56, 2346–2356. [Google Scholar] [CrossRef]
- Wipf, D.P.; Rao, B.D. Sparse Bayesian learning for basis selection. IEEE Trans. Signal Process. 2004, 52, 2153–2164. [Google Scholar] [CrossRef]
- Wipf, D.P.; Rao, B.D. An empirical Bayesian strategy for solving the simultaneous sparse approximation problem. IEEE Trans. Signal Process. 2007, 55, 3704–3716. [Google Scholar] [CrossRef]
- Fang, J.; Shen, Y.; Li, H.; Wang, P. Pattern-coupled sparse Bayesian learning for recovery of block-sparse signals. IEEE Trans. Signal Process. 2015, 63, 360–372. [Google Scholar] [CrossRef]
- Tipping, M. Sparse Bayesian learning and the relevance vector machine. J. Mach. Learn. Res. 2001, 1, 211–244. [Google Scholar]
- Metzler, C.A.; Maleki, A.; Baraniuk, R.G. From denoising to compressed sensing. IEEE Trans. Inf. Theory 2016, 62, 5117–5144. [Google Scholar] [CrossRef]
- Mousavi, A.; Patel, A.B.; Baraniuk, R.G. A deep learning approach to structured signal recovery. In Proceedings of the 53rd Annual Allerton Conference on Communication, Control, and Computing, Monticello, IL, USA, 29 September–2 October 2015; pp. 1336–1343. [Google Scholar]
- Kulkarni, K.; Lohit, S.; Turaga, P.; Kerviche, R.; Ashok, A. ReconNet: Non-Iterative reconstruction of images from compressively sensed measurements. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 449–458. [Google Scholar]
- Mousavi, A.; Baraniuk, R.G. Learning to invert: Signal recovery via deep convolutional networks. In Proceedings of the IEEE IEEE International Conference on Acoustics, Speech and Signal Processing, New Orleans, LA, USA, 5–9 March 2017; pp. 2272–2276. [Google Scholar]
- Metzler, C.A.; Maleki, A.; Baraniuk, R.G. Learned DAMP: Principled neural-network-based compressive image recovery. arXiv 2017, arXiv:1704.06625. [Google Scholar]
- Borgerding, M.; Schniter, P.; Rangan, S. AMP-Inspired deep networks for sparse linear inverse problems. IEEE Trans. Signal Process. 2017, 65, 4293–4308. [Google Scholar] [CrossRef]
- Rangan, S.; Schniter, P.; Fletcher, A.K. Vector approximate message passing. arXiv 2016, arXiv:1610.03082. [Google Scholar]
- Yao, H.T.; Dai, F.; Zhang, D.M.; Ma, Y.; Zhang, S.L.; Zhang, Y.D.; Qi, T. DR2-Net:deep residual reconstruction network for image compressive sensing. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Bora, A.; Jalal, A.; Price, E. Compressed sensing using generative models. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 537–546. [Google Scholar]
- Zhang, J.; Ghanem, B. ISTA-Net: Interpretable Optimization-Inspired deep network for image compressive sensing. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Shi, W.; Jiang, F.; Liu, S.; Zhao, D. Scalable convolutional neural network for image compressed sensing. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Unde, A.S.; Malla, R.; Deepthi, P.P. Low complexity secure encoding and joint decoding for distributed compressive sensing WSNs. In Proceedings of the IEEE International Conference on Recent Advances in Information Technology, Dhanbad, India, 3–5 March 2016; pp. 89–94. [Google Scholar]
- Yi, C.; Wang, L.; Li, Y. Energy efficient transmission approach for WBAN based on threshold distance. IEEE Sens. J. 2015, 15, 5133–5141. [Google Scholar] [CrossRef]
- Xue, W.; Luo, C.; Lan, G.; Rana, R.; Hu, W.; Seneviratne, A. Kryptein: A compressive-sensing-based encryption scheme for the internet of things. In Proceedings of the ACM/IEEE International Conference on Information Processing in Sensor Networks, Pittsburgh, PA, USA, 18–21 April 2017. [Google Scholar]
- Orsdemir, A.; Altun, H.O.; Sharma, G. On the security and robustness of encryption via compressed sensing. In Proceedings of the IEEE Military Communications Conference, San Diego, CA, USA, 16–19 November 2008; pp. 1–7. [Google Scholar]
- Du, L.; Cao, X.; Zhang, W. Semi-fragile watermarking for image authentication based on compressive sensing. Sci. China Inf. Sci. 2016, 59, 1–3. [Google Scholar] [CrossRef]
- Hu, G.; Xiao, D.; Xiang, T. A compressive sensing based privacy preserving outsourcing of image storage and identity authentication service in cloud. Inf. Sci. 2017, 387, 132–145. [Google Scholar] [CrossRef]
- Xie, D.; Li, L.; Niu, X.; Yang, Y. Identification of coupled map lattice based on compressed sensing. Math. Probl. Eng. 2016, 2016, 6435320. [Google Scholar] [CrossRef]
- Li, L.; Xu, D.; Peng, H.; Kurths, J.; Yang, Y. Reconstruction of Complex Network based on the Noise via QR Decomposition and Compressed Sensing. Sci. Rep. 2017, 7, 15036. [Google Scholar] [CrossRef]
- Fang, Y.; Li, L.; Li, Y.; Peng, H.; Yang, Y. Low energy consumption compressed spectrum sensing based on channel energy reconstruction in cognitive radio network. Sensors 2020, 20, 1264. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Song, R.; Zhu, W.P. Pilot allocation for distributed-compressed-sensing-based sparse channel estimation in MIMO-OFDM systems. IEEE Trans. Veh. Technol. 2016, 65, 2990–3004. [Google Scholar] [CrossRef]
- Gao, Z.; Dai, L.; Dai, W.; Shim, B.; Wang, Z. Structured compressive sensing-based spatio-temporal joint channel estimation for FDD massive MIMO. IEEE Trans. Commun. 2016, 64, 601–617. [Google Scholar] [CrossRef]
- Pablo, A.V.; Ryan, G.M.; Yuriy, J.A. A compressed sensing framework for Monte Carlo transport simulations using random disjoint tallies. J. Comput. Theor. Trans. 2016, 45, 219–229. [Google Scholar]
- Pareschi, F.; Albertini, P.; Frattini, G.; Mangia, M.; Rovatti, R.; Setti, G. Hardware-algorithms co-design and implementation of an analog-to-information converter for biosignals based on compressed sensing. IEEE Trans. Biomed. Circuits Syst. 2016, 10, 149–162. [Google Scholar] [CrossRef]
- Chen, Z.; Hou, X.; Qian, X.; Gong, C. Efficient and robust image coding and transmission based on scrambled block compressive sensing. IEEE Trans. Multimedia 2018, 20, 1610–1621. [Google Scholar] [CrossRef]
- Bi, D.; Xie, Y.; Ma, L.; Li, X.; Yang, X.; Zheng, Y. Multifrequency compressed sensing for 2-D near-field synthetic aperture radar image reconstruction. IEEE Trans. Instrum. Meas. 2017, 66, 777–791. [Google Scholar] [CrossRef]
- Chen, F.; Lasaponara, R.; Masini, N. An overview of satellite synthetic aperture radar remote sensing in archaeology: From site detection to monitoring. J. Cult. Herit. 2017, 23, 5–11. [Google Scholar] [CrossRef]
- Li, T.; Shokr, M.; Liu, Y.; Cheng, X.; Li, T.; Wang, F.; Hui, F. Monitoring the tabular icebergs C28A and C28B calved from the Mertz Ice Tongue using radar remote sensing data. Remote Sens. Environ. 2018, 216, 615–625. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Fang, Y.; Liu, L.; Peng, H.; Kurths, J.; Yang, Y. Overview of Compressed Sensing: Sensing Model, Reconstruction Algorithm, and Its Applications. Appl. Sci. 2020, 10, 5909. https://doi.org/10.3390/app10175909
Li L, Fang Y, Liu L, Peng H, Kurths J, Yang Y. Overview of Compressed Sensing: Sensing Model, Reconstruction Algorithm, and Its Applications. Applied Sciences. 2020; 10(17):5909. https://doi.org/10.3390/app10175909
Chicago/Turabian StyleLi, Lixiang, Yuan Fang, Liwei Liu, Haipeng Peng, Jürgen Kurths, and Yixian Yang. 2020. "Overview of Compressed Sensing: Sensing Model, Reconstruction Algorithm, and Its Applications" Applied Sciences 10, no. 17: 5909. https://doi.org/10.3390/app10175909
APA StyleLi, L., Fang, Y., Liu, L., Peng, H., Kurths, J., & Yang, Y. (2020). Overview of Compressed Sensing: Sensing Model, Reconstruction Algorithm, and Its Applications. Applied Sciences, 10(17), 5909. https://doi.org/10.3390/app10175909





