A Novel Iterative Linear Matrix Inequality Design Procedure for Passive Inter-Substructure Vibration Control
Abstract
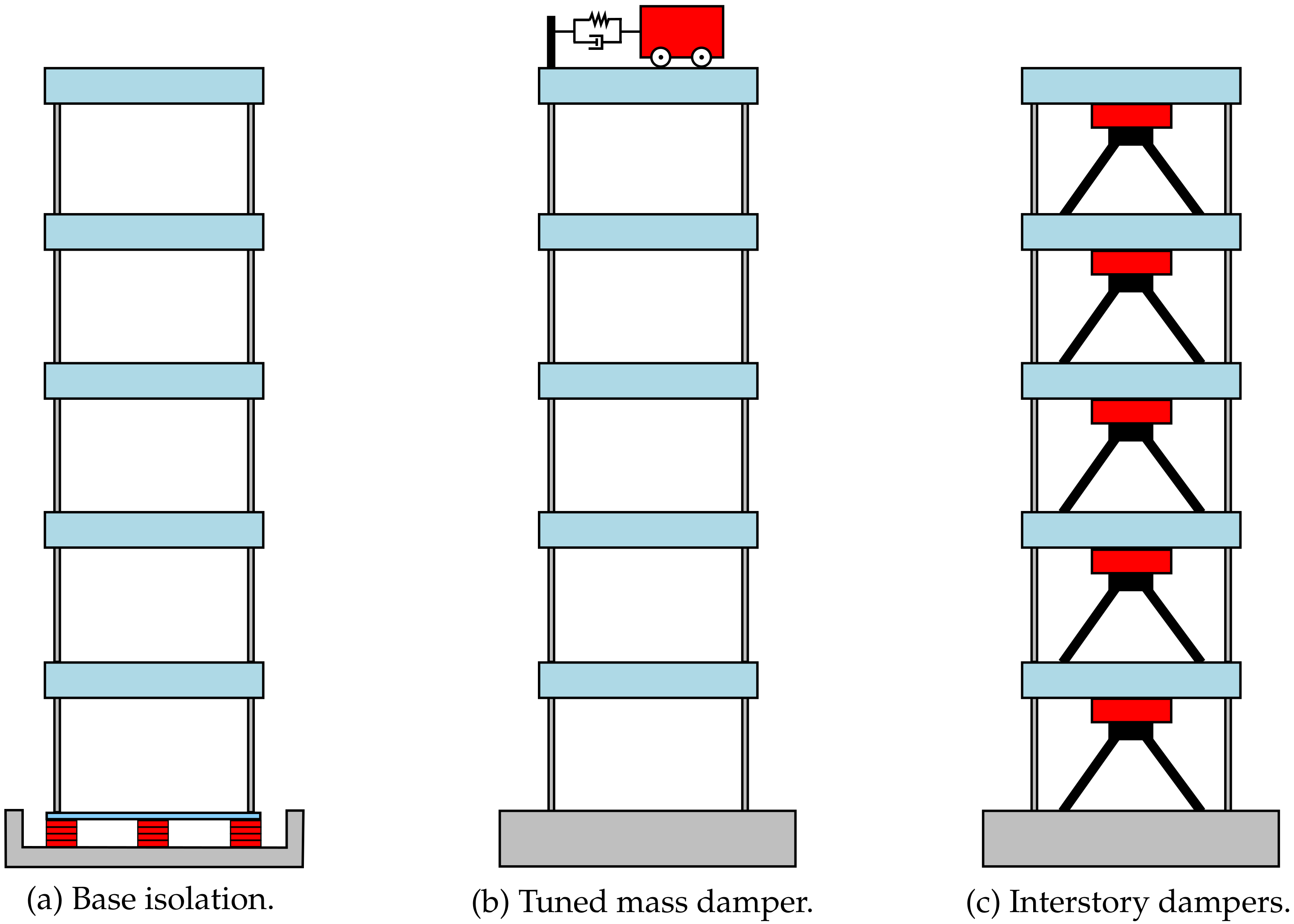
1. Introduction
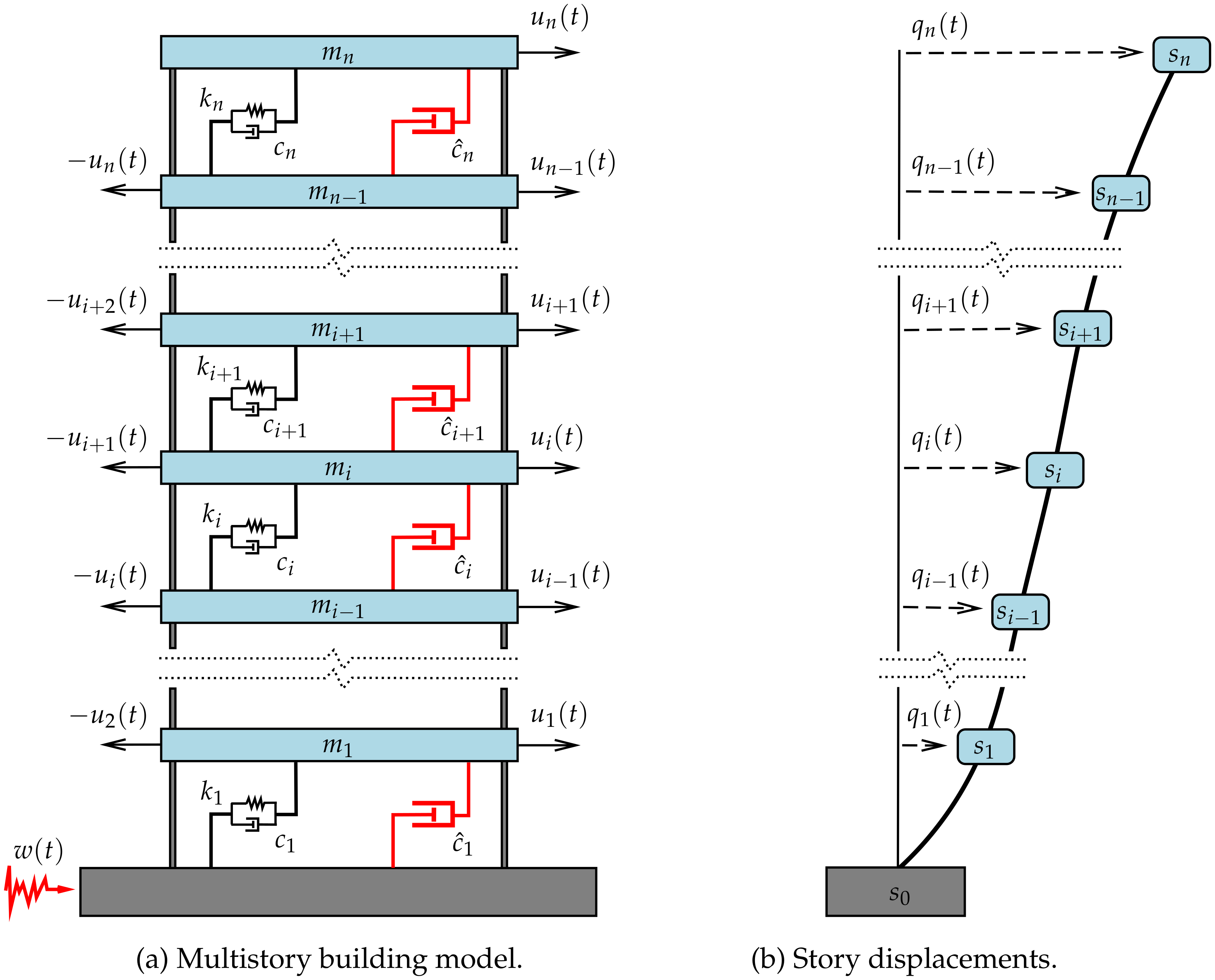
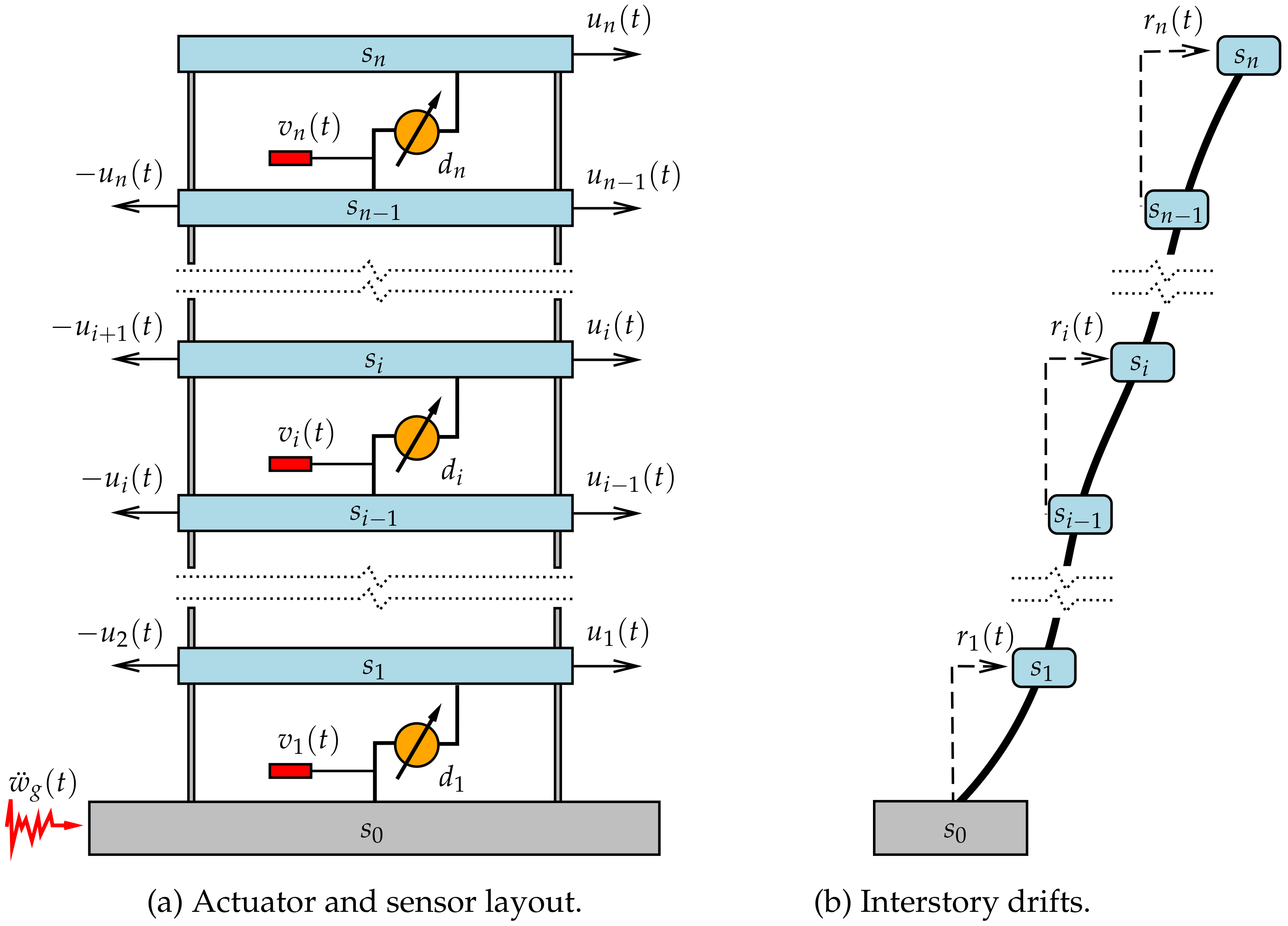
2. Connections between Interstory FVDs and Decentralized Velocity-Feedback Controllers
3. Design of Interstory FVD Systems Using a Decentralized SOF Approach
3.1. Decentralized SOF Controllers
3.2. ILMI Design Procedure
3.2.1. Initialization
3.2.2. Iterations
- Step i.a
- Solve the auxiliary LMI optimization problem with fixed matrices and to obtain an optimal triplet .
- Step i.b
- Solve the structured LMI optimization problem with fixed matrix to obtain an optimal quartet and a diagonal gain matrix with associated -value
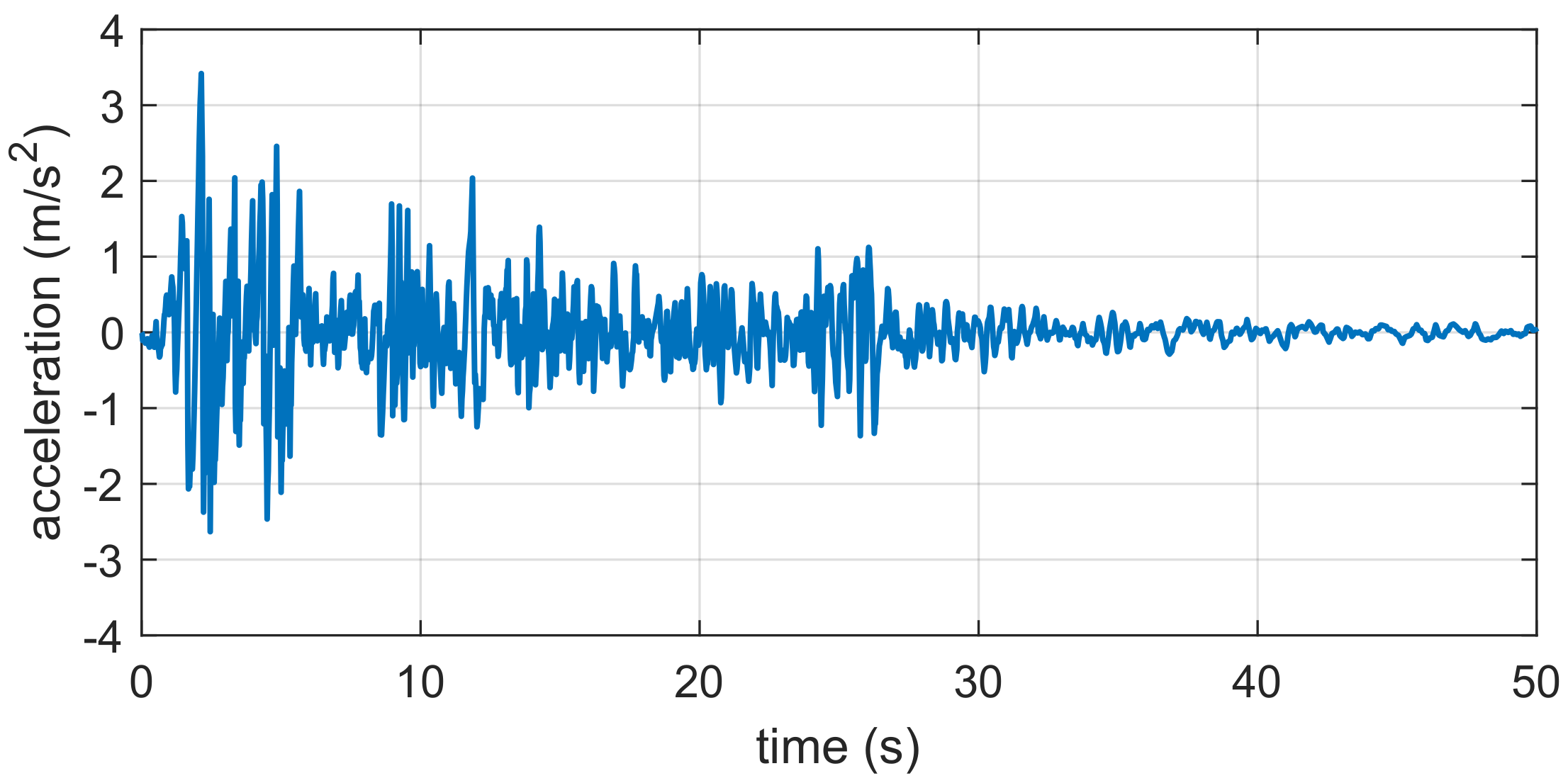
4. Numerical Results
4.1. FVD System Design
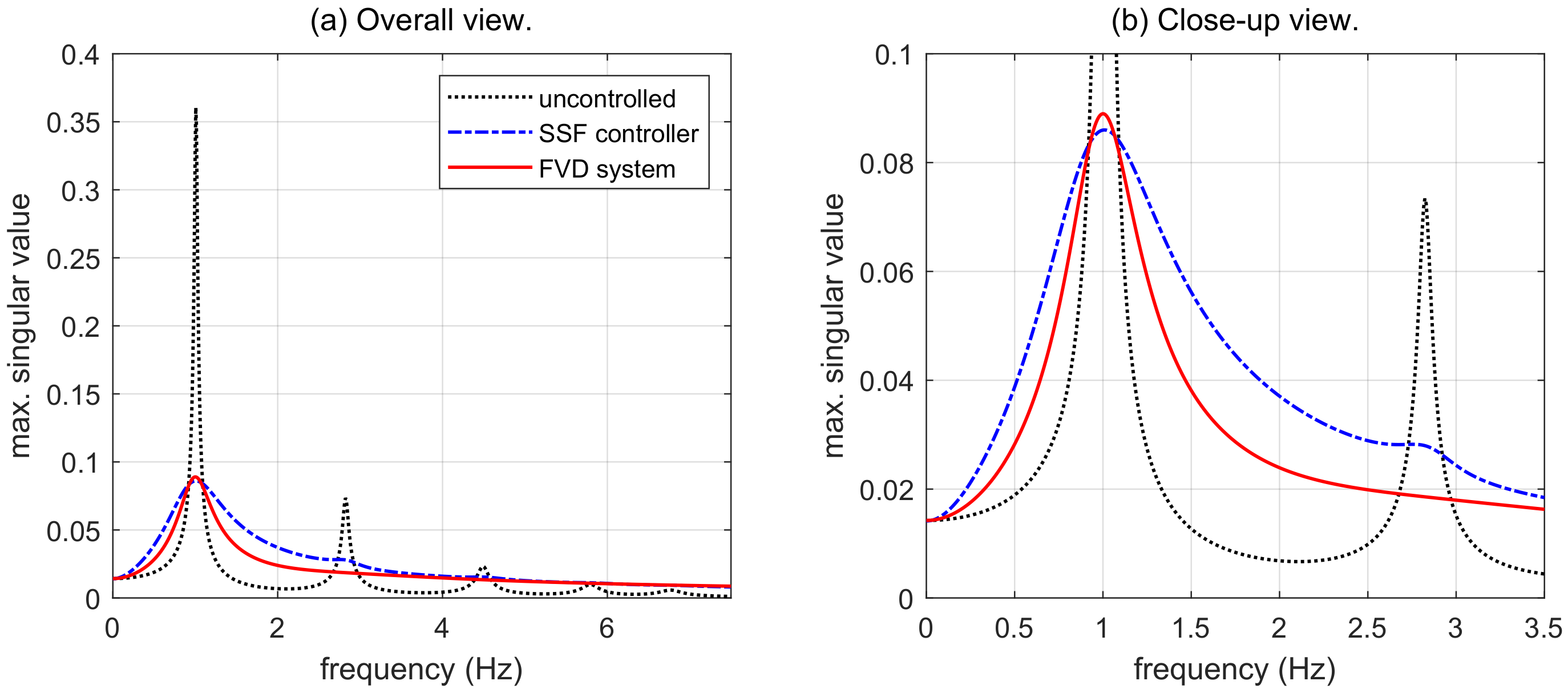
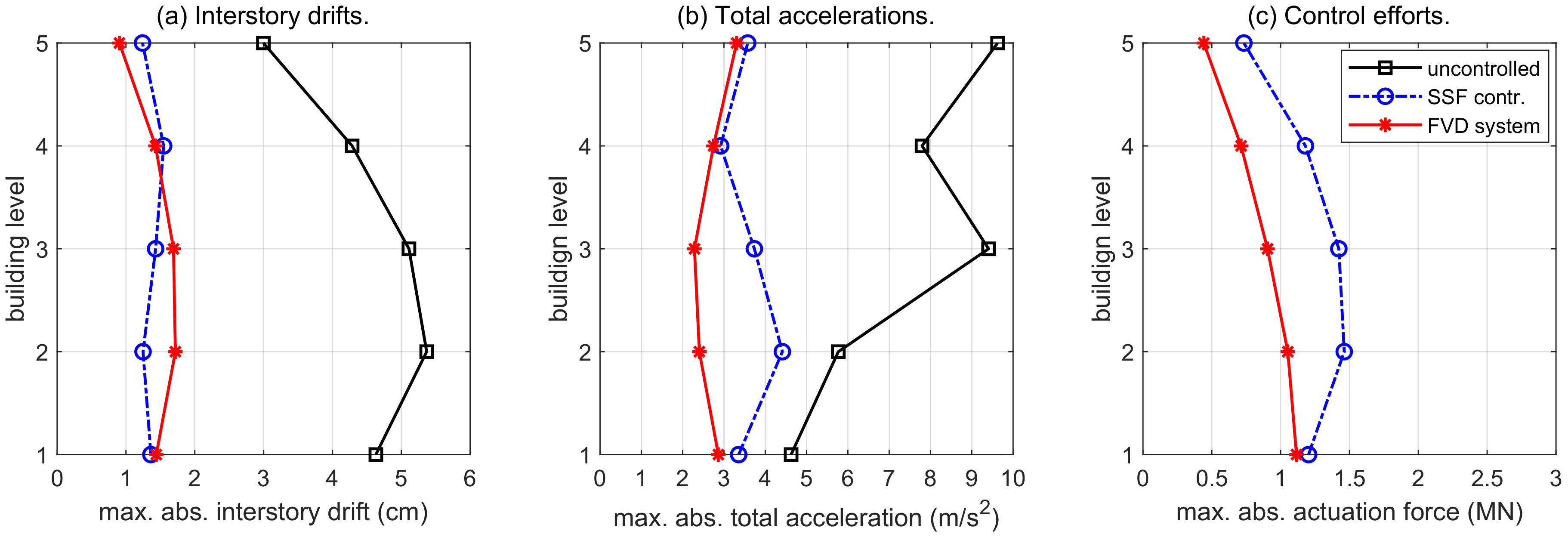
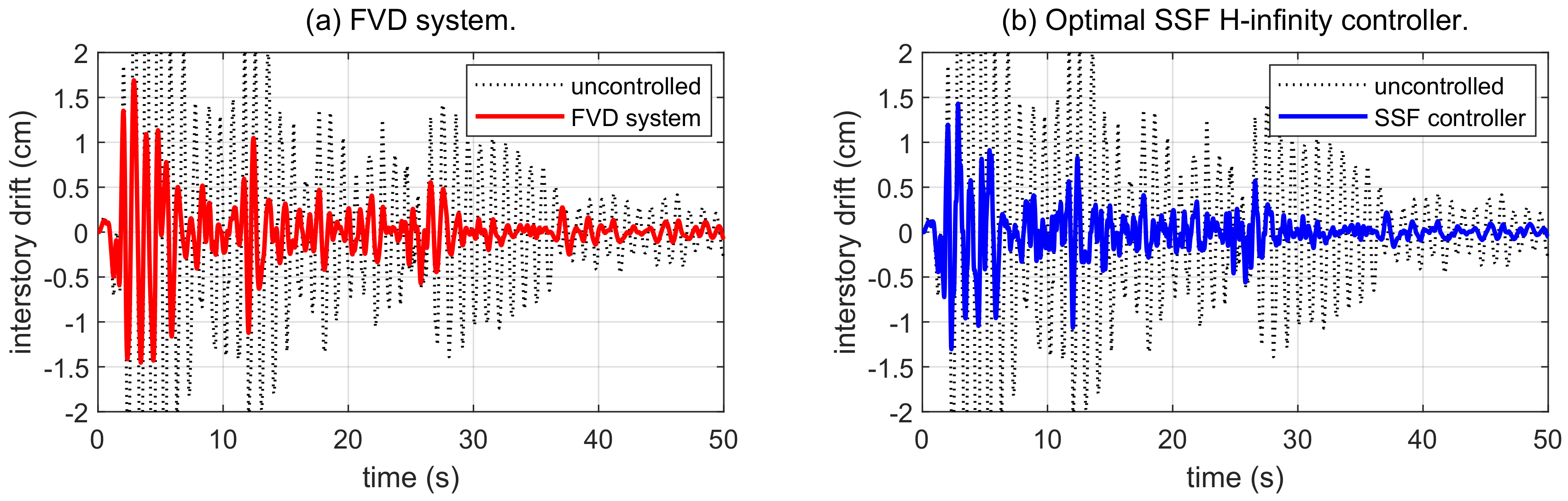
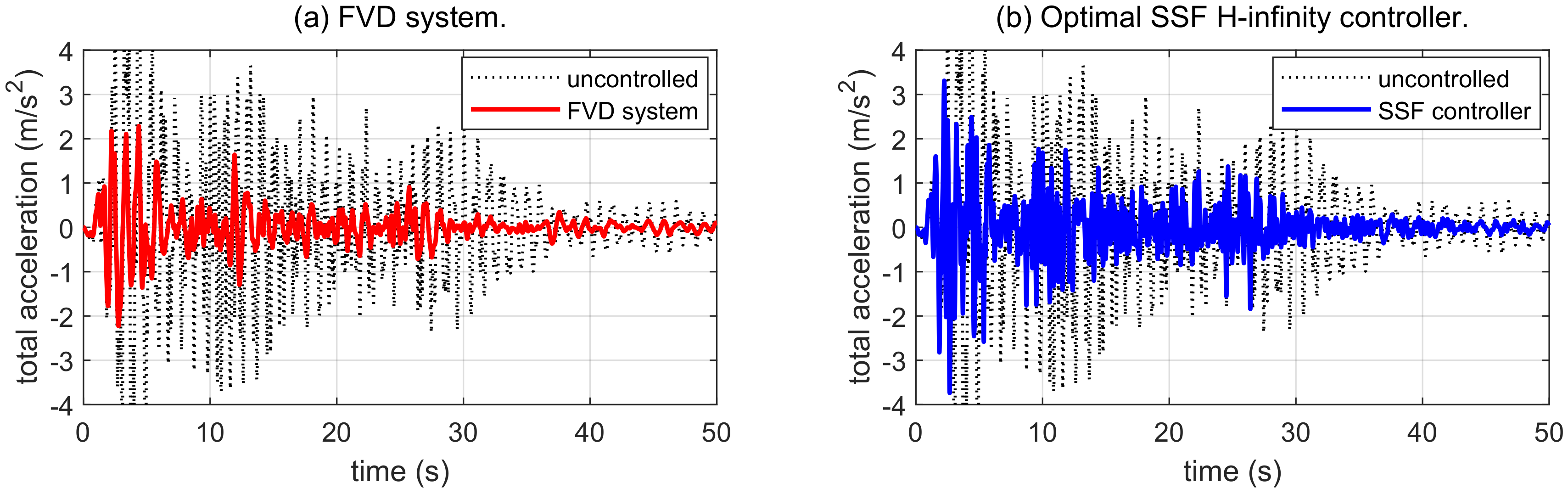
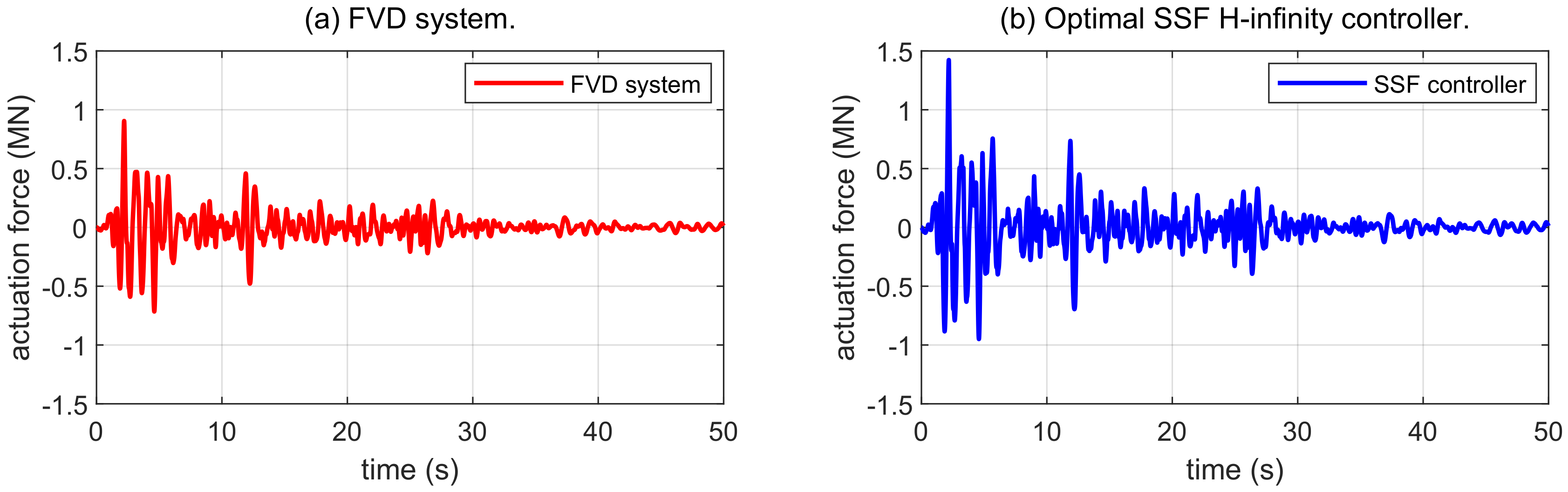
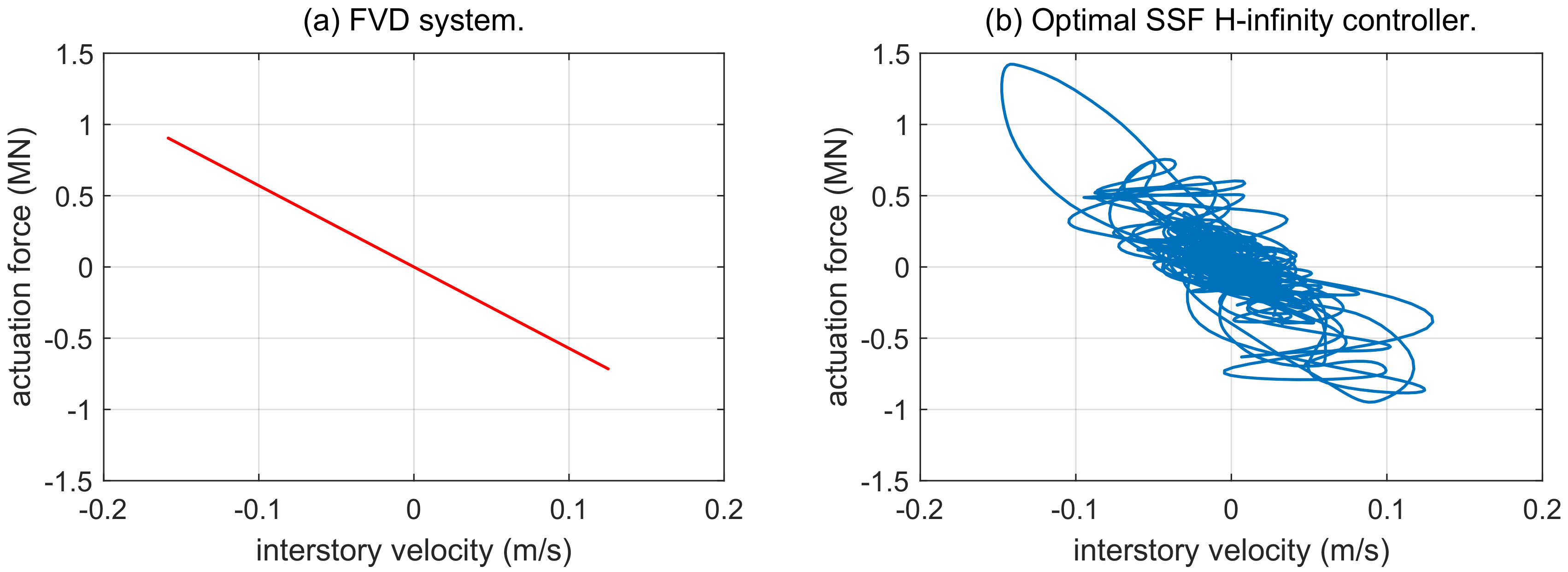
4.2. Seismic Response
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| BI | base isolation |
| BMI | bilinear matrix inequality |
| BRL | bounded real lemma |
| FRF | frequency response function |
| FVD | fluid viscous damper |
| ILMI | iterative linear matrix inequality |
| ISSD | inter-substructure damper |
| LMI | linear matrix inequaltiy |
| SOF | static output feedback |
| SSF | static state feedback |
| SVF | static velocity feedback |
| TD | tuned damper |
| TMD | tuned mass damper |
References
- Soong, T.T.; Spencer, B.F., Jr. Supplemental energy dissipation: State-of-the-art and state-of-the-practice. Eng. Struct. 2002, 24, 243–259. [Google Scholar] [CrossRef]
- Symans, M.D.; Charney, F.A.; Whittaker, A.S.; Constantinou, M.C.; Kircher, C.A.; Johnson, M.W.; McNamara, R.J. Energy dissipation systems for seismic applications: Current practice and recent developments. J. Struct. Eng. 2008, 134, 3–21. [Google Scholar] [CrossRef]
- Takewaki, I.; Fujita, K.; Yamamoto, K.; Takabatake, H. Smart passive damper control for greater building earthquake resilience in sustainable cities. Sustain. Cities Soc. 2011, 1, 3–15. [Google Scholar] [CrossRef]
- Ho, C.; Zhu, Y.; Lang, Z.Q.; Billings, S.A.; Kohiyama, M.; Wakayama, S. Nonlinear damping based semi-active building isolation system. J. Sound Vib. 2018, 424, 302–317. [Google Scholar] [CrossRef]
- De Domenico, D.; Impollonia, N.; Ricciardi, G. Soil-dependent optimum design of a new passive vibration control system combining seismic base isolation with tuned inerter damper. Soil Dyn. Earthq. Eng. 2018, 105, 37–53. [Google Scholar] [CrossRef]
- Peng, Y.; Ding, L.; Chen, J. Performance evaluation of base-isolated structures with sliding hydromagnetic bearings. Struct. Control Health Monit. 2019, 26, 1–21. [Google Scholar] [CrossRef]
- De Domenico, D.; Gandelli, E.; Quaglini, V. Adaptive isolation system combining low-friction sliding pendulum bearings and SMA-based gap dampers. Eng. Struct. 2020, 212, 1–25. [Google Scholar] [CrossRef]
- Elias, S.; Matsagar, V. Research developments in vibration control of structures using passive tuned mass dampers. Annu. Rev. Control 2017, 44, 129–156. [Google Scholar] [CrossRef]
- Love, J.S.; McNamara, K.P.; Tait, M.J.; Haskett, T.C. Series-type pendulum tuned mass damper-tuned sloshing damper. J. Vib. Acoust. 2020, 142, 1–8. [Google Scholar] [CrossRef]
- Pandey, D.K.; Sharma, M.K.; Mishra, S.K. A compliant tuned liquid damper for controlling seismic vibration of short period structures. Mech. Syst. Signal Process. 2019, 132, 405–428. [Google Scholar] [CrossRef]
- Lu, Z.; Li, K.; Ouyang, Y.; Shan, J. Performance-based optimal design of tuned impact damper for seismically excited nonlinear building. Eng. Struct. 2018, 160, 314–327. [Google Scholar] [CrossRef]
- Bathaei, A.; Zahrai, S.M.; Ramezani, M. Semi-active seismic control of an 11-DOF building model with TMD+MR damper using type-1 and -2 fuzzy algorithms. J. Vib. Control 2018, 24, 2938–2953. [Google Scholar] [CrossRef]
- Shih, M.H.; Sung, W.P. Structural control effect and performance of structure under control of impulse semi-active mass control mechanism. Iran. J. Sci. Technol. Trans. Civ. Eng. 2020. [Google Scholar] [CrossRef]
- De Domenico, D.; Ricciardi, G. Earthquake-resilient design of base isolated buildings with TMD at basement: Application to a case study. Soil Dyn. Earthq. Eng. 2018, 113, 503–521. [Google Scholar] [CrossRef]
- Li, Z.; Shu, G.; Huang, Z. Proper configuration of metallic energy dissipation system in shear-type building structures subject to seismic excitation. J. Constr. Steel Res. 2019, 154, 177–189. [Google Scholar] [CrossRef]
- Atam, E. Friction damper-based passive vibration control assessment for seismically-excited buildings through comparison with active control: A case study. IEEE Access 2019, 7, 4664–4675. [Google Scholar] [CrossRef]
- Tchamo, J.M.; Zhou, Y. An alternative practical design method for structures with viscoelastic dampers. Earthq. Eng. Eng. Vib. 2018, 17, 459–473. [Google Scholar] [CrossRef]
- De Domenico, D.; Ricciardi, G.; Takewaki, I. Design strategies of viscous dampers for seismic protection of building structures: A review. Soil Dyn. Earthq. Eng. 2019, 118, 144–165. [Google Scholar] [CrossRef]
- Palacios-Quiñonero, F.; Rubió-Massegú, J.; Rossell, J.M.; Karimi, H.R. Design of inerter-based multi-actuator systems for vibration control of adjacent structures. J. Frankl. Inst. 2019, 356, 7785–7809. [Google Scholar] [CrossRef]
- Palacios-Quiñonero, F.; Rubió-Massegú, J.; Rossell, J.M.; Karimi, H.R. Integrated design of hybrid interstory-interbuilding multi-actuation schemes for vibration control of adjacent buildings under seismic excitations. Appl. Sci. 2017, 7, 323. [Google Scholar] [CrossRef]
- Apostolakis, G. Optimal evolutionary seismic design of three-dimensional multistory structures with damping devices. J. Struct. Eng. 2020, 146, 1–16. [Google Scholar] [CrossRef]
- De Domenico, D.; Ricciardi, G. Earthquake protection of structures with nonlinear viscous dampers optimized through an energy-based stochastic approach. Eng. Struct. 2019, 179, 523–539. [Google Scholar] [CrossRef]
- Del Gobbo, G.M.; Williams, M.S.; Blakeborough, A. Comparing fluid viscous damper placement methods considering total-building seismic performance. Earthq. Eng. Struct. Dyn. 2018, 47, 2864–2886. [Google Scholar] [CrossRef]
- Li, Z.; Shu, G. Optimal placement of metallic dampers for seismic upgrading of multistory buildings based on a cost-effectiveness criterion using genetic algorithm. Struct. Des. Tall Spec. Build. 2019, 28, 1–18. [Google Scholar] [CrossRef]
- Altieri, D.; Tubaldi, E.; De Angelis, M.; Patelli, E.; Dall’Asta, A. Reliability-based optimal design of nonlinear viscous dampers for the seismic protection of structural systems. Bull. Earthq. Eng. 2018, 16, 963–982. [Google Scholar] [CrossRef]
- Sarcheshmehpour, M.; Estekanchi, H.E.; Ghannad, M.A. Optimum placement of supplementary viscous dampers for seismic rehabilitation of steel frames considering soil–structure interaction. Struct. Des. Tall Spec. Build. 2019, 29, 1–17. [Google Scholar] [CrossRef]
- Palacios-Quiñonero, F.; Rubió-Massegú, J.; Rossell, J.M.; Karimi, H.R. Distributed passive actuation schemes for seismic protection of multibuilding systems. Appl. Sci. 2020, 10, 2383. [Google Scholar] [CrossRef]
- De Domenico, D.; Qiao, H.; Wang, Q.; Zhu, Z.; Marano, G. Optimal design and seismic performance of Multi-Tuned Mass Damper Inerter (MTMDI) applied to adjacent high-rise buildings. Struct. Des. Tall Spec. Build. 2020. [Google Scholar] [CrossRef]
- Nabid, N.; Hajirasouliha, I.; Petkovski, M. Adaptive low computational cost optimisation method for performance-based seismic design of friction dampers. Eng. Struct. 2019, 198, 1–12. [Google Scholar] [CrossRef]
- Halperin, I.; Ribakov, Y.; Agranovich, G. Optimal viscous dampers gains for structures subjected to earthquakes. Struct. Control Health Monit. 2016, 23, 458–469. [Google Scholar] [CrossRef]
- Palacios-Quiñonero, F.; Rubió-Massegú, J.; Rossell, J.M.; Rodellar, J. Interstory-interbuilding actuation schemes for seismic protection of adjacent identical buildings. Smart Struct. Syst. 2019, 24, 67–81. [Google Scholar] [CrossRef]
- Akehashi, H.; Takewaki, I. Optimal viscous damper placement for elastic-plastic MDOF structures under critical double impulse. Front. Built Environ. 2019, 5, 1–17. [Google Scholar] [CrossRef]
- Pollini, N.; Lavan, O.; Amir, O. Towards realistic minimum-cost optimization of viscous fluid dampers for seismic retrofitting. Bull. Earthq. Eng. 2016, 14, 971–998. [Google Scholar] [CrossRef]
- Palermo, M.; Silvestri, S.; Landi, L.; Gasparini, G.; Trombetti, T. A direct five-step procedure for the preliminary seismic design of buildings with added viscous dampers. Eng. Struct. 2018, 173, 933–950. [Google Scholar] [CrossRef]
- Palacios-Quiñonero, F.; Rubio-Massegu, J.; Rossell, J.M.; Karimi, H.R. Optimal passive-damping design using a decentralized velocity-feedback H∞ approach. Model. Identif. Control 2012, 33, 87–97. [Google Scholar] [CrossRef]
- Rubió-Massegú, J.; Rossell, J.M.; Karimi, H.R.; Palacios-Quiñonero, F. Static output-feedback control under information structure constraints. Automatica 2013, 49, 313–316. [Google Scholar] [CrossRef]
- Rubió-Massegú, J.; Palacios-Quiñonero, F.; Rossell, J.M. Decentralized static output-feedback H∞ controller design for buildings under seismic excitation. Earthq. Eng. Struct. Dyn. 2012, 41, 1199–1205. [Google Scholar] [CrossRef]
- Palacios-Quiñonero, F.; Rubió-Massegú, J.; Rossell, J.M.; Karimi, H.R. Feasibility issues in static output-feedback controller design with application to structural vibration control. J. Frankl. Inst. 2014, 351, 139–155. [Google Scholar] [CrossRef]
- Chopra, A.K.; McKenna, F. Modeling viscous damping in nonlinear response history analysis of buildings for earthquake excitation. Earthq. Eng. Struct. Dyn. 2016, 45, 193–211. [Google Scholar] [CrossRef]
- Boyd, S.; Ghaoui, L.E.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; SIAM Studies in Applied Mathematics; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1994. [Google Scholar]
- Huo, L.; Qu, C.; Li, H. TLCD parametric optimization for the vibration control of building structures based on linear matrix inequality. J. Appl. Math. 2014, 2014, 1–10. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Wu, H.N. New insight into the simultaneous policy update algorithms related to H∞ state feedback control. Inf. Sci. 2019, 484, 84–94. [Google Scholar] [CrossRef]
- Kurata, N.; Kobori, T.; Takahashi, M.; Niwa, N.; Midorikawa, H. Actual seismic response controlled building with semi-active damper system. Earthq. Eng. Struct. Dyn. 1999, 28, 1427–1447. [Google Scholar] [CrossRef]
- Chopra, A.K. Dynamics of Structures. Theory and Applications to Earthquake Engineering, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2007. [Google Scholar]
- Balas, G.J.; Chiang, R.Y.; Packard, A.K.; Safonov, M.G. MATLAB Robust Control Toolbox User’s Guide, 2020a; The MathWorks, Inc.: Natick, MA, USA, 2020. [Google Scholar]
- Rubió-Massegú, J.; Rossell, J.M.; Palacios-Quiñonero, F.; Karimi, H.R. Static output-feedback controller design for vehicle suspensions: An effective two-step computational approach. IET Control Theory Appl. 2014, 8, 1566–1574. [Google Scholar] [CrossRef]
- Konstantinidis, D.; Makris, N.; Kelly, J.M. Health monitoring of fluid dampers for vibration control of structures: Experimental investigation. Earthq. Eng. Struct. Dyn. 2012, 41, 1813–1829. [Google Scholar] [CrossRef]
- Maizuar, M.; Zhang, L.; Miramini, S.; Mendis, P.; Thompson, R.G. Detecting structural damage to bridge girders using radar interferometry and computational modelling. Struct. Control Health Monit. 2017, 24, 1–6. [Google Scholar] [CrossRef]

| Mode | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| natural frequency (Hz) | 1.008 | 2.825 | 4.493 | 5.797 | 6.773 |
| Step | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| Upper bound | 0.0933 | 0.0911 | 0.0902 | 0.0900 | 0.0899 | 0.0898 | 0.0898 |
| Building Level | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Damping coefficient ( Ns/m) | 8.4144 | 6.6570 | 5.7092 | 5.1799 | 4.9493 |
| Building Level | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| FVD system | 68.89 | 68.01 | 66.93 | 66.65 | 69.81 |
| SSF controller | 70.58 | 76.76 | 72.00 | 63.89 | 58.61 |
| Building Level | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| FVD system | 38.09 | 58.32 | 75.70 | 64.78 | 65.65 |
| SSF controller | 27.43 | 23.48 | 60.28 | 62.54 | 62.85 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rubió-Massegú, J.; Palacios-Quiñonero, F.; Rossell, J.M.; Karimi, H.R. A Novel Iterative Linear Matrix Inequality Design Procedure for Passive Inter-Substructure Vibration Control. Appl. Sci. 2020, 10, 5859. https://doi.org/10.3390/app10175859
Rubió-Massegú J, Palacios-Quiñonero F, Rossell JM, Karimi HR. A Novel Iterative Linear Matrix Inequality Design Procedure for Passive Inter-Substructure Vibration Control. Applied Sciences. 2020; 10(17):5859. https://doi.org/10.3390/app10175859
Chicago/Turabian StyleRubió-Massegú, Josep, Francisco Palacios-Quiñonero, Josep M. Rossell, and Hamid Reza Karimi. 2020. "A Novel Iterative Linear Matrix Inequality Design Procedure for Passive Inter-Substructure Vibration Control" Applied Sciences 10, no. 17: 5859. https://doi.org/10.3390/app10175859
APA StyleRubió-Massegú, J., Palacios-Quiñonero, F., Rossell, J. M., & Karimi, H. R. (2020). A Novel Iterative Linear Matrix Inequality Design Procedure for Passive Inter-Substructure Vibration Control. Applied Sciences, 10(17), 5859. https://doi.org/10.3390/app10175859








