State-Constrained Sub-Optimal Tracking Controller for Continuous-Time Linear Time-Invariant (CT-LTI) Systems and Its Application for DC Motor Servo Systems
Abstract
1. Introduction
1.1. Solutions and Their Approximations of the Optimal Control Problems
1.2. Outline and Scope of the Paper
2. Analytic Solution of State-Constrained Optimal Tracking Problems
2.1. Model-Based Prediction
2.2. Inequality Constraints Using Prediction
2.3. Quadratic Penalty Function
2.4. Variational Approach
2.5. Analytical Solution of the Problem
3. State-Constrained Sub-Optimal Tracking Controller
3.1. State-Constrained Sub-Optimal Tracking Controller
- Identify using current state values and calculate .
- Calculate (24) and (35) using an algebraic Riccati equation solver with .
- Calculate (36)–(38) using the result of step 2 and applying .
- Calculate (9) using the result of step 3.
- Identify using the result of step 4.
- 6.
- Calculate using the result of step 5.
- 7.
- Calculate (24) and (35) using an algebraic Riccati equation solver with the result of step 6.
- 8.
- Calculate (36)–(38) using the result of step 7.
3.2. Stability of the Proposed Controller
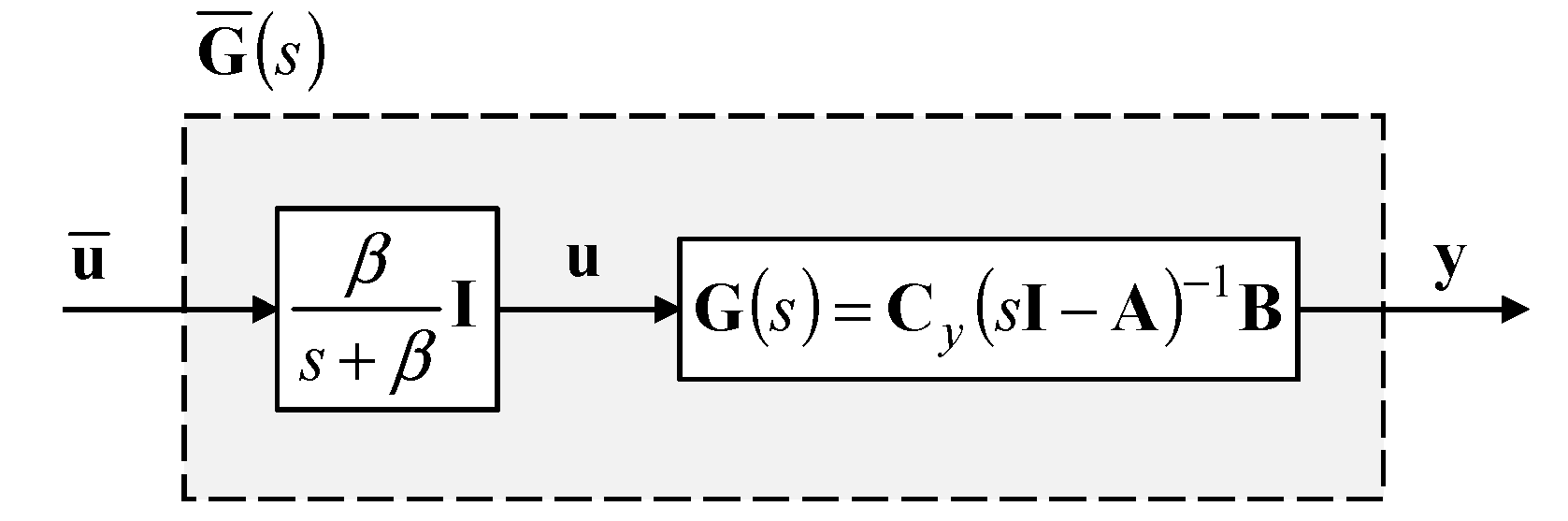
3.3. Model Modification for Input Smoothing
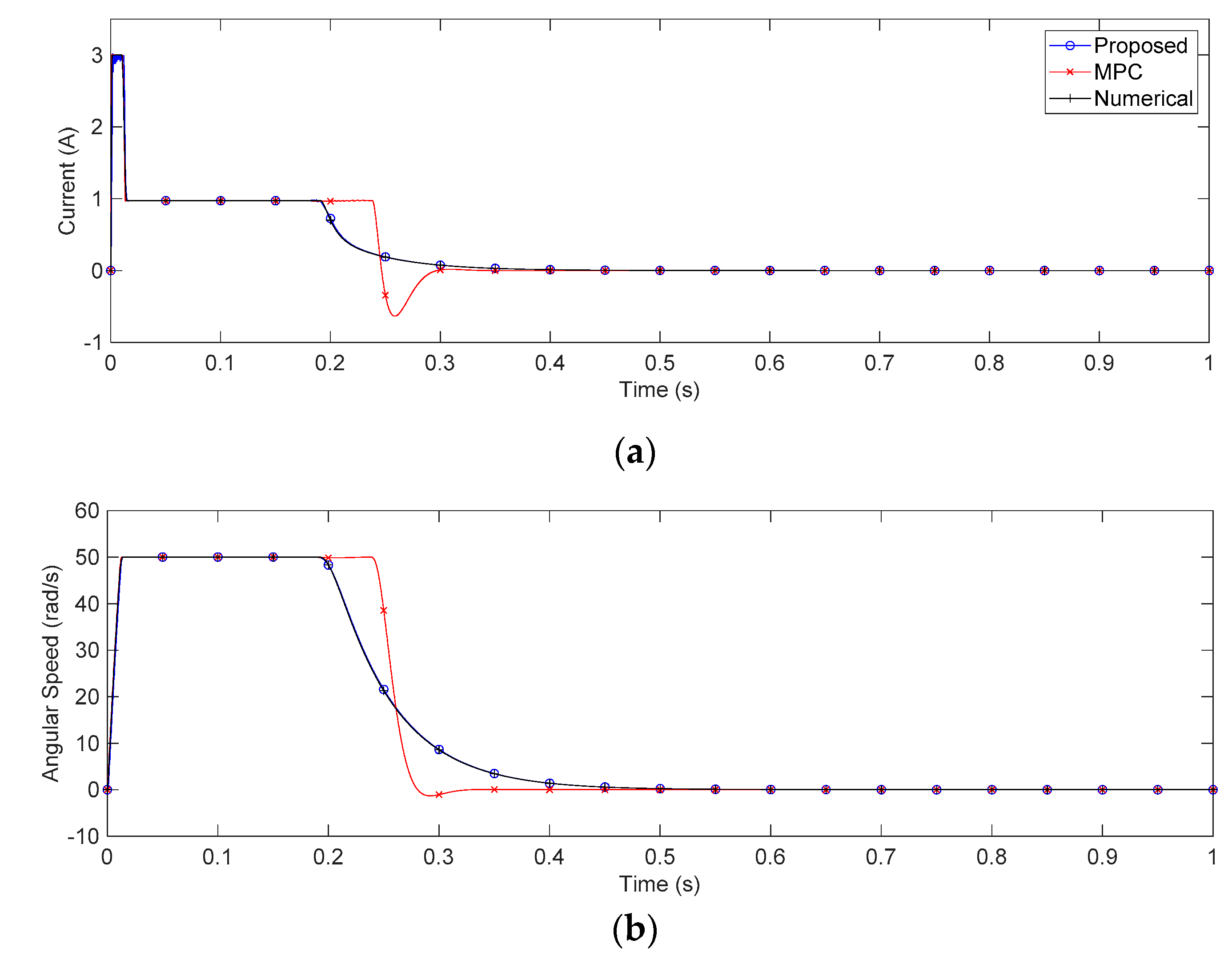
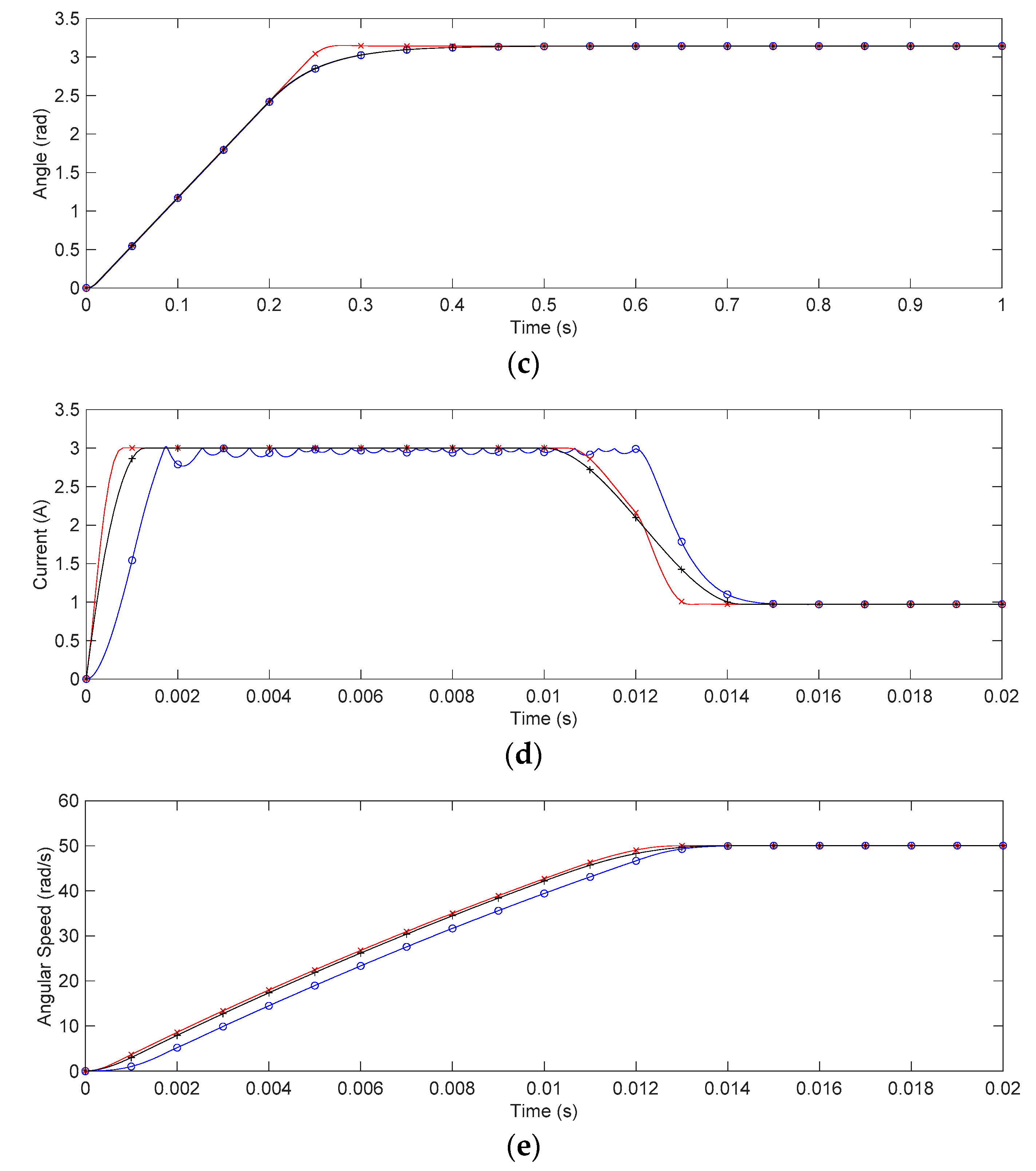
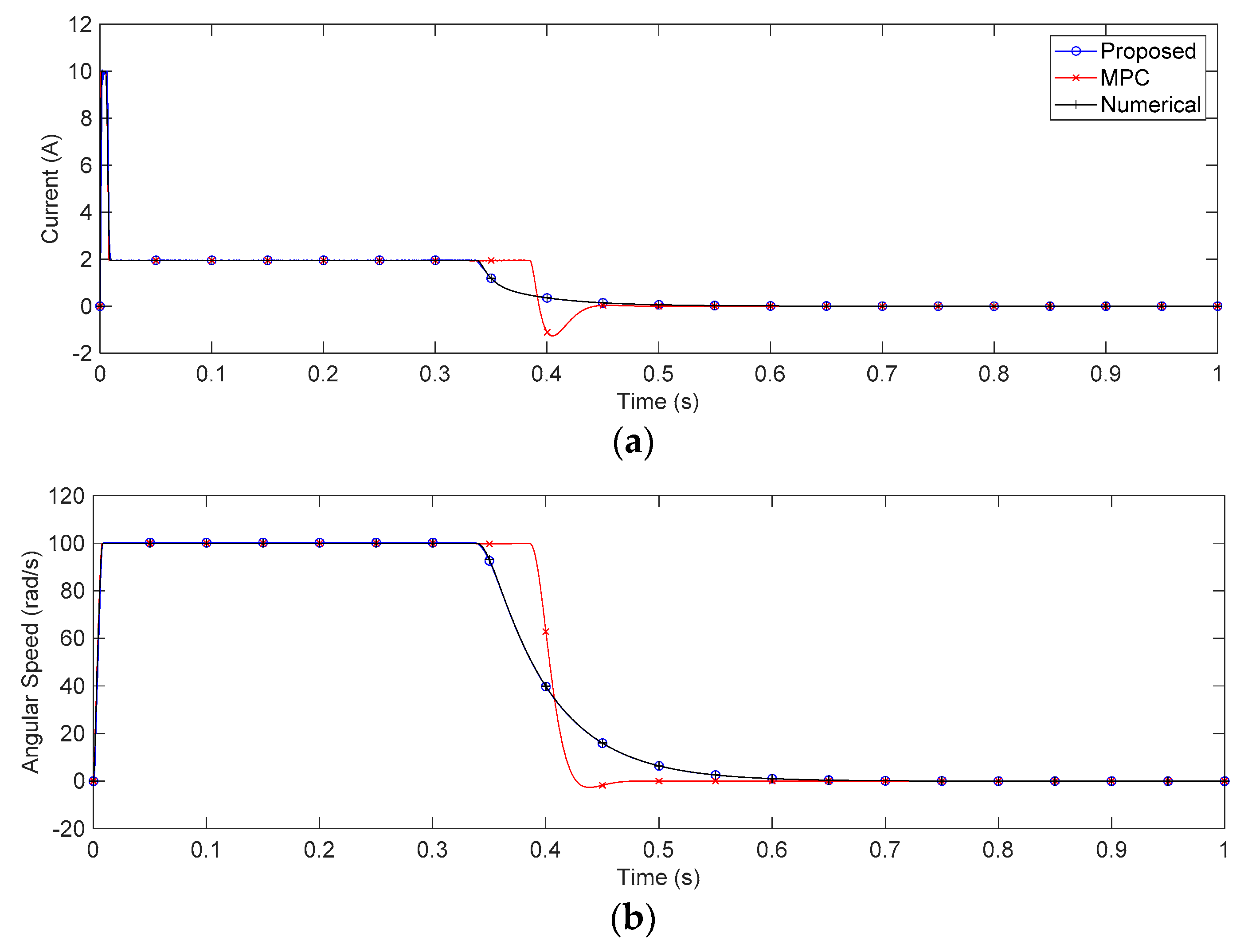
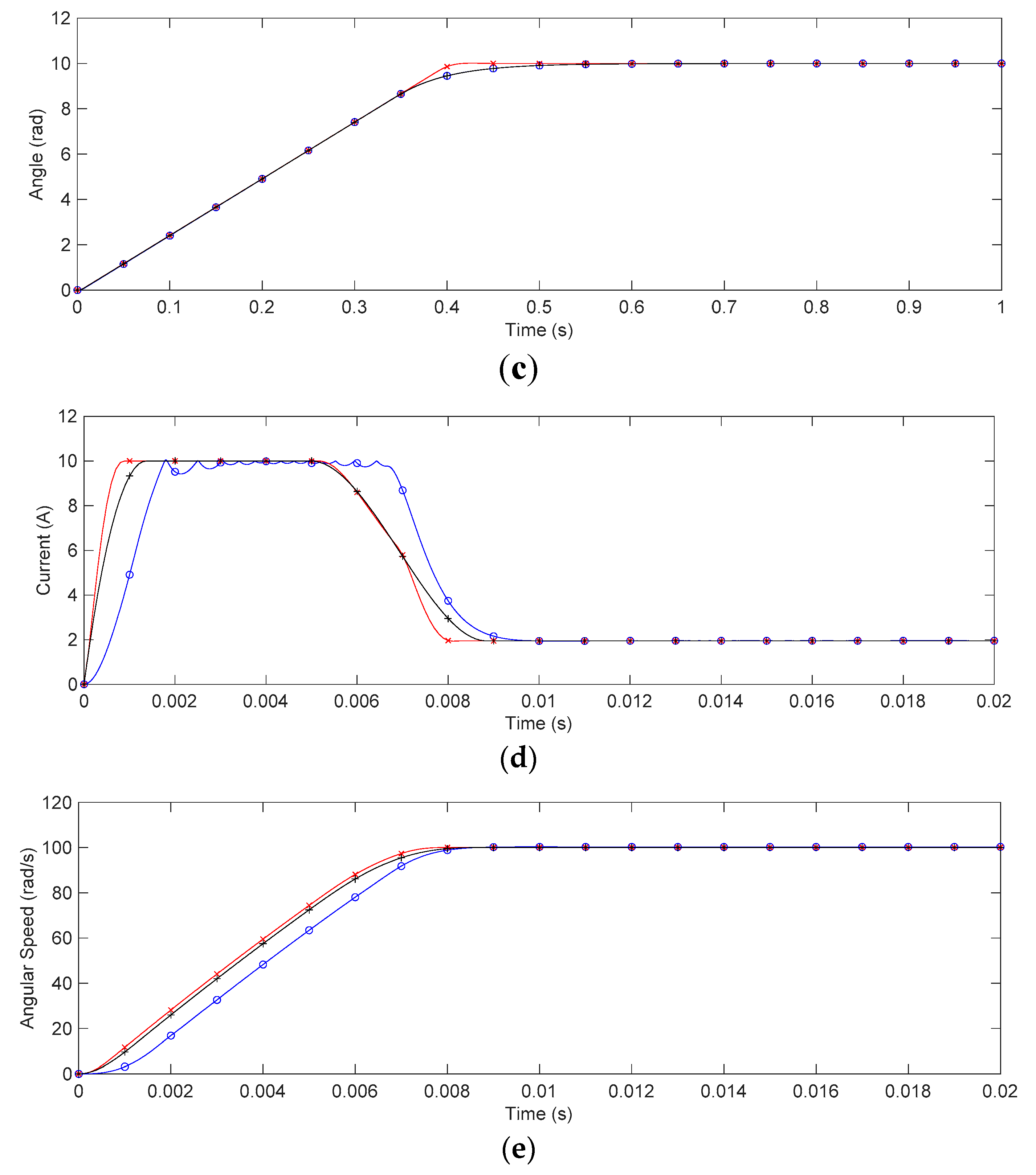
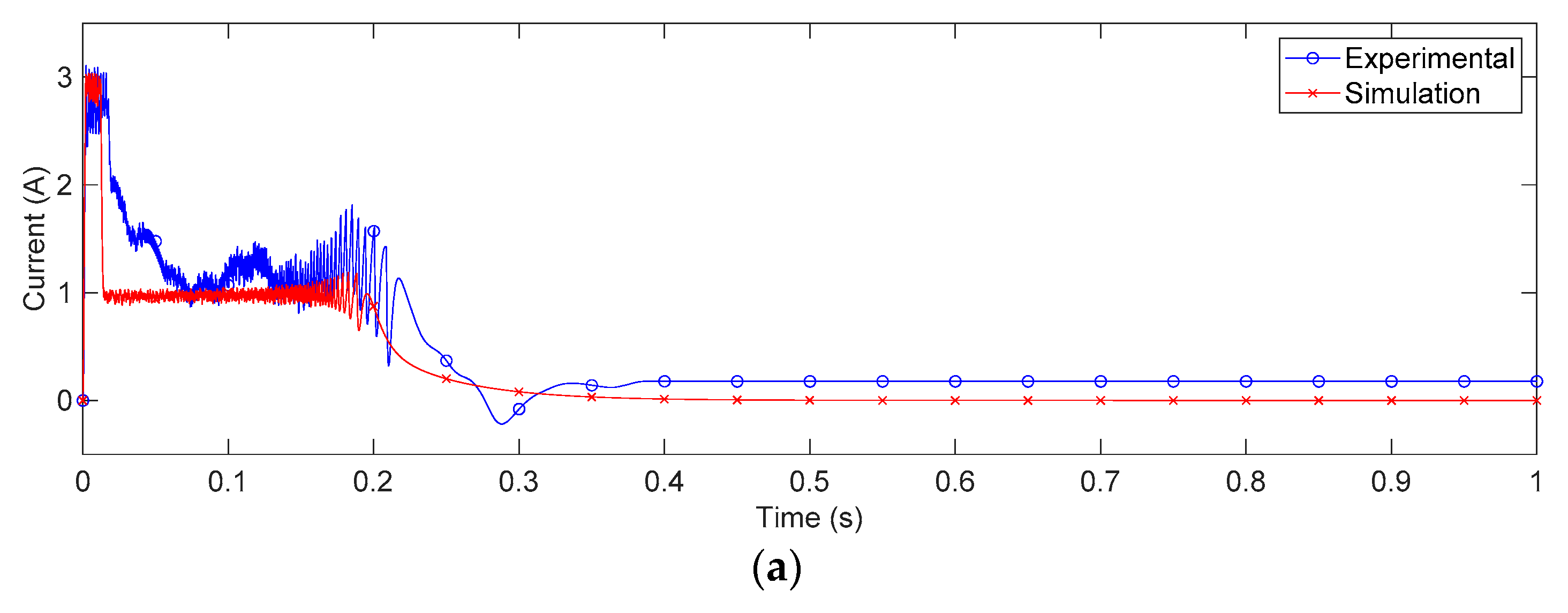
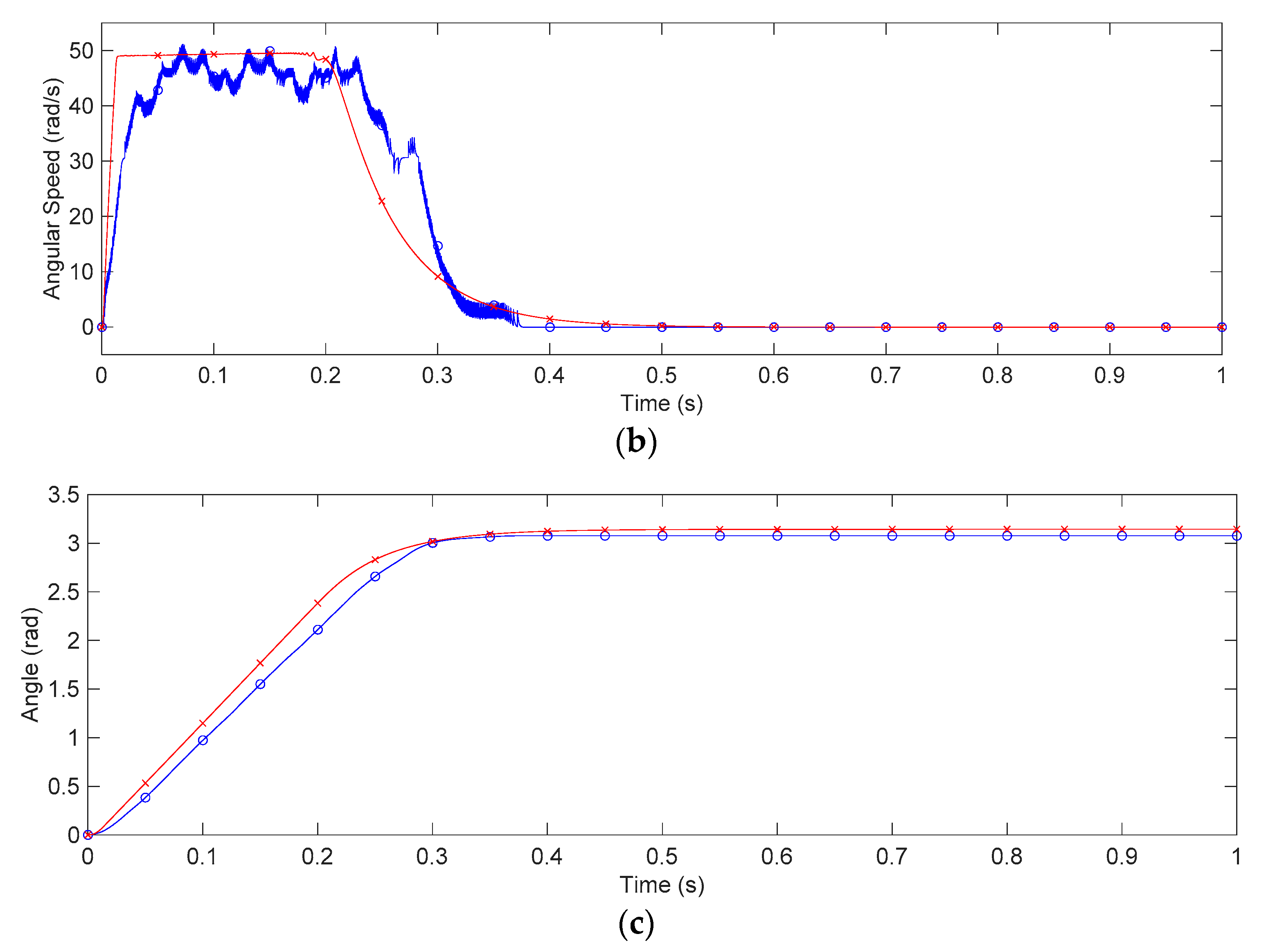
4. Case Study: Application for DC Motor Servo Systems
5. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Rubio, F.; Llopis-Albert, C.; Valero, F.; Suñer, J.L. Industrial robot efficient trajectory generation without collision through the evolution of the optimal trajectory. Robot. Auton. Syst. 2016, 86, 106–112. [Google Scholar] [CrossRef]
- Ragaglia, M.; Zanchettin, A.M.; Rocco, P. Trajectory generation algorithm for safe human-robot collaboration based on multiple depth sensor measurements. Mechatronics 2018, 55, 267–281. [Google Scholar] [CrossRef]
- Hung, C.W.; Vu, T.V.; Chen, C.K. The development of an optimal control strategy for a series hydraulic hybrid vehicle. Appl. Sci. 2016, 6, 93. [Google Scholar] [CrossRef]
- Guo, L.; Gao, B.; Gao, Y.; Chen, H. Optimal energy management for HEVs in eco-driving applications using bi-level MPC. IEEE Trans. Intell. Transp. Syst. 2016, 18, 2153–2162. [Google Scholar] [CrossRef]
- Chen, Z.; Hu, H.; Wu, Y.; Xiao, R.; Shen, J.; Liu, Y. Energy management for a power-split plug-in hybrid electric vehicle based on reinforcement learning. Appl. Sci. 2018, 8, 2494. [Google Scholar] [CrossRef]
- Kirk, D.E.; Donald, E. Optimal Control Theory: An Introduction; Dover Publications: Mineola, NY, USA, 2004; pp. 53–239. [Google Scholar]
- Athans, M.; Falb, P.L. Optimal Control: An Introduction to the Theory and Its Applications; Dover Publications: Mineola, NY, USA, 2007; pp. 221–812. [Google Scholar]
- Lewis, F.L.; Vrabie, D.; Syrmos, V.L. Optimal Control, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2012; pp. 110–212. [Google Scholar]
- Pontryagin, L.S. Mathematical Theory of Optimal Processes; John Wiley & Sons: Hoboken, NJ, USA, 1962; pp. 9–114. [Google Scholar]
- Elbert, P.; Ebbesen, S.; Guzzella, L. Implementation of dynamic programming for n-dimensional optimal control problems with final state constraints. IEEE Trans. Control Syst. Technol. 2012, 21, 924–931. [Google Scholar] [CrossRef]
- Böhme, T.J.; Frank, B.J.C. Hybrid Systems, Optimal Control and Hybrid Vehicles; Springer International: Cham, Switzerland, 2017; pp. 167–270. [Google Scholar]
- Betts, J.T. Survey of numerical methods for trajectory optimization. J. Guidance Control. Dyn. 1998, 21, 193–207. [Google Scholar] [CrossRef]
- Betts, J.T. Practical Methods for Optimal Control and Estimation Using Nonlinear Programming, 2nd ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2010; pp. 96–218. [Google Scholar]
- Mayne, D.Q.; Rawlings, J.B.; Rao, C.V.; Scokaert, P.O. Constrained model predictive control: Stability and optimality. Automatica 2000, 36, 789–814. [Google Scholar] [CrossRef]
- Qin, S.J.; Badgwell, T.A. A survey of industrial model predictive control technology. Control Eng. Pract. 2003, 11, 733–764. [Google Scholar] [CrossRef]
- Wang, L. Model Predictive Control System Design and Implementation Using MATLAB®; Springer-Verlag: London, UK, 2009; pp. 1–224. [Google Scholar]
- Aldaouab, I.; Daniels, M.; Ordóñez, R. MPC for optimized energy exchange between two renewable-energy prosumers. Appl. Sci. 2019, 9, 3709. [Google Scholar] [CrossRef]
- Bemporad, A.; Morari, M.; Dua, V.; Pistikopoulos, E.N. The explicit linear quadratic regulator for constrained systems. Automatica 2002, 38, 3–20. [Google Scholar] [CrossRef]
- Bemporad, A.; Borrelli, F.; Morari, M. Model predictive control based on linear programming—The explicit solution. IEEE Trans. Autom. Control. 2002, 47, 1974–1985. [Google Scholar] [CrossRef]
- Grancharova, A.; Johansen, T.A. Explicit Nonlinear Model Predictive Control: Theory and Applications; Springer-Verlag: London, UK, 2012; pp. 1–108. [Google Scholar]
- Bemporad, A.; Morari, M.; Dua, V.; Pistikopoulos, E.N. Corrigendum to: “The explicit linear quadratic regulator for constrained systems” [Automatica 38 (1)(2002) 3–20]. Automatica 2003, 39, 1845–1846. [Google Scholar] [CrossRef]
- Franklin, G.F.; Powell, J.D.; Workman, M. Digital Control of Dynamic Systems, 3rd ed.; Addison-Wesley: Menlo Park, CA, USA, 1998; pp. 96–118. [Google Scholar]
- Venkataraman, P. Applied Optimization with MATLAB Programming; John Wiley & Sons: Hoboken, NJ, USA, 2002; pp. 265–316. [Google Scholar]
- Bryson, A.E. Applied Optimal Control: Optimization, Estimation and Control; Hemisphere Publishing Corporation: Washington, DC, USA, 1975; pp. 212–245. [Google Scholar]
- Zhang, X.D. Matrix Analysis and Applications; Cambridge University Press: Cambridge, UK, 2017; pp. 60–61. [Google Scholar]
- Bernstein, D.S. Matrix Mathematics: Theory, Facts, and Formulas, 2nd ed.; Princeton university press: Princeton, NJ, USA, 2009; pp. 77–164. [Google Scholar]
- Khalil, H.K.; Grizzle, J.W. Nonlinear Systems, 3rd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 2002; pp. 111–194. [Google Scholar]
- Chen, C.T. Linear System Theory and Design, 3rd ed.; Oxford University Press: Oxford, UK, 1998; pp. 121–140. [Google Scholar]
- Lin, C.Y.; Liu, Y.C. Precision tracking control and constraint handling of mechatronic servo systems using model predictive control. IEEE/ASME Trans. Mechatron. 2011, 17, 593–605. [Google Scholar]
- Rădac, M.B.; Precup, R.E.; Petriu, E.M.; Preitl, S.; Dragoş, C.A. Data-driven reference trajectory tracking algorithm and experimental validation. IEEE Trans. Ind. Inf. 2012, 9, 2327–2336. [Google Scholar] [CrossRef]
- Premkumar, K.; Manikandan, B.V.; Kumar, C.A. Antlion algorithm optimized fuzzy PID supervised on-line recurrent fuzzy neural network based controller for brushless DC motor. Electr. Power Compon. Syst. 2017, 45, 2304–2317. [Google Scholar] [CrossRef]
- Hassan, A.K.; Saraya, M.S.; Elksasy, M.S.; Areed, F.F. Brushless DC motor speed control using PID controller, fuzzy controller, and neuro fuzzy controller. Int. J. Comput. Appl. 2018, 180, 47–52. [Google Scholar]
- Sun, Z.; Pritschow, G.; Zahn, P.; Lechler, A. A novel cascade control principle for feed drives of machine tools. CIRP Ann. 2018, 67, 389–392. [Google Scholar] [CrossRef]
- Guerra, R.H.; Quiza, R.; Villalonga, A.; Arenas, J.; Castaño, F. Digital twin-based optimization for ultraprecision motion systems with backlash and friction. IEEE Access 2019, 7, 93462–93472. [Google Scholar] [CrossRef]
- Andersson, J.A.; Gillis, J.; Horn, G.; Rawlings, J.B.; Diehl, M. CasADi: A software framework for nonlinear optimization and optimal control. Math. Program. Comput. 2019, 11, 1–36. [Google Scholar] [CrossRef]
- Anderson, B.D.; Moore, J.B. Optimal Control: Linear Quadratic Methods; Dover Publications: Mineola, NY, USA, 1990; pp. 68–100. [Google Scholar]
- Yao, Q.; Tian, Y. A model predictive controller with longitudinal speed compensation for autonomous vehicle path tracking. Appl. Sci. 2019, 9, 4739. [Google Scholar] [CrossRef]
- Wu, X.; Qiao, B.; Su, C. Trajectory planning with time-variant safety margin for autonomous vehicle lane change. Appl. Sci. 2020, 10, 1626. [Google Scholar] [CrossRef]

| Name | Unit | Value |
|---|---|---|
| Rotor inductance () | H | 0.0065 |
| Armature resistance () | Ω | 2.3 |
| Back EMF constant () | V·sec/rad | 0.09 |
| Torque constant () | Nm/A | 0.09 |
| Friction coefficient () | Nm·sec | 0.00175 |
| Rotor inertia () | Nm·rad | 0.0000525 |
| Gear ratio () | 0.25 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.; Jon, U.; Lee, H. State-Constrained Sub-Optimal Tracking Controller for Continuous-Time Linear Time-Invariant (CT-LTI) Systems and Its Application for DC Motor Servo Systems. Appl. Sci. 2020, 10, 5724. https://doi.org/10.3390/app10165724
Kim J, Jon U, Lee H. State-Constrained Sub-Optimal Tracking Controller for Continuous-Time Linear Time-Invariant (CT-LTI) Systems and Its Application for DC Motor Servo Systems. Applied Sciences. 2020; 10(16):5724. https://doi.org/10.3390/app10165724
Chicago/Turabian StyleKim, Jihwan, Ung Jon, and Hyeongcheol Lee. 2020. "State-Constrained Sub-Optimal Tracking Controller for Continuous-Time Linear Time-Invariant (CT-LTI) Systems and Its Application for DC Motor Servo Systems" Applied Sciences 10, no. 16: 5724. https://doi.org/10.3390/app10165724
APA StyleKim, J., Jon, U., & Lee, H. (2020). State-Constrained Sub-Optimal Tracking Controller for Continuous-Time Linear Time-Invariant (CT-LTI) Systems and Its Application for DC Motor Servo Systems. Applied Sciences, 10(16), 5724. https://doi.org/10.3390/app10165724






