Proximal Policy Optimization Through a Deep Reinforcement Learning Framework for Multiple Autonomous Vehicles at a Non-Signalized Intersection
Abstract
1. Introduction
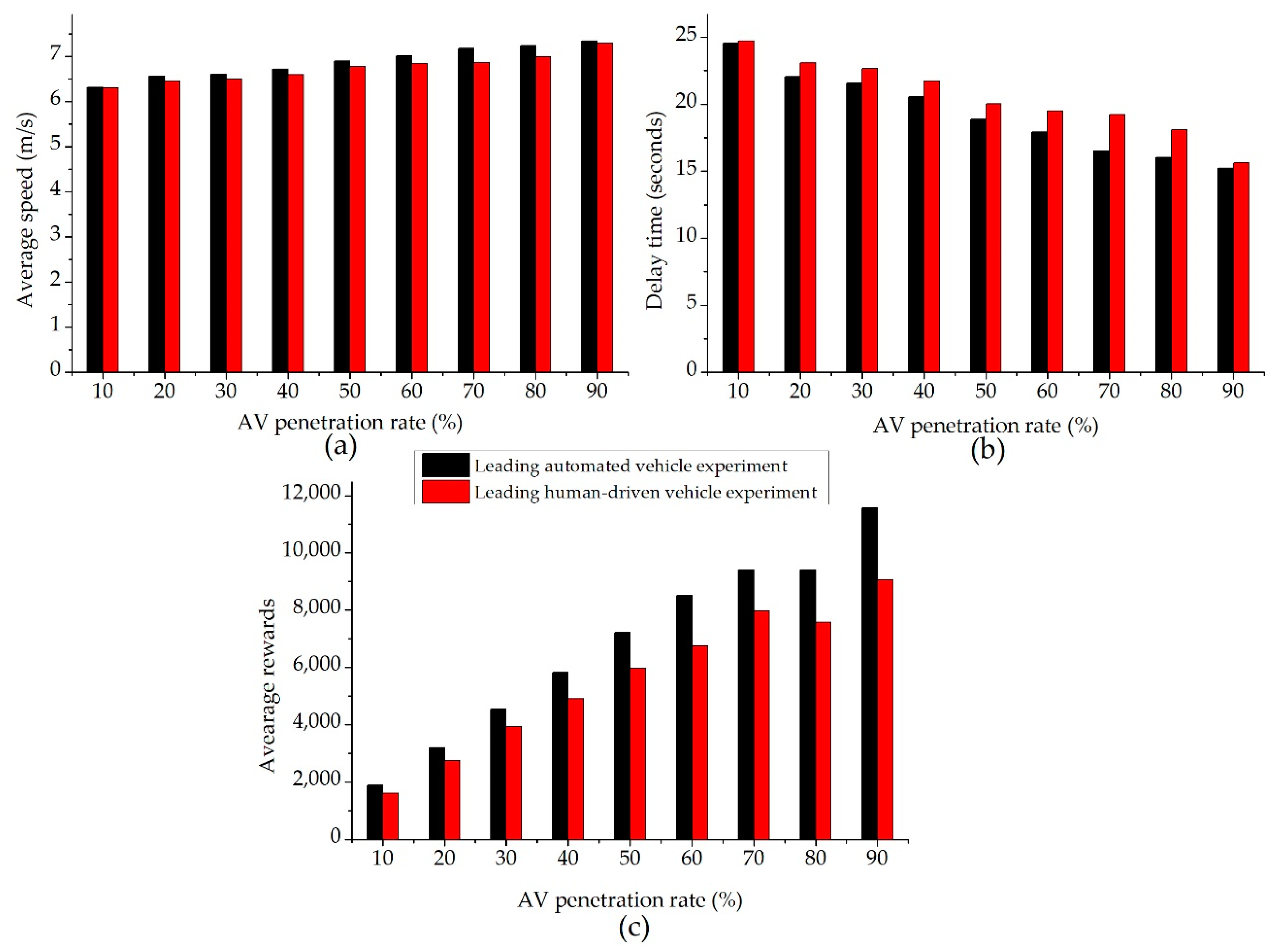
- An enhanced hybrid deep RL method is presented that uses a PPO algorithm through MLP and RL models in order to consider the effectiveness of the leading autonomous vehicle experiment at a non-signalized intersection based on an AV penetration rate that ranges from 10% to 100% in 10% increments. The leading autonomous vehicle experiment yields a significant improvement when compared with the leading human-driven vehicle and all human-driven vehicle experiments in terms of training policy, mobility, and energy efficiency.
- A set of PPO hyperparameters is proposed in order to explore the effect of the automated extraction feature on policy prediction and to obtain reliable simulation performance at a non-signalized intersection within the real traffic volume.
- The demonstration of a significant improvement in traffic perturbations at a non-signalized intersection is based on an AV penetration rate that ranges from 10% to 100% in 10% increments.
2. Methods
2.1. Deep Reinforcement Learning (Deep RL)
2.2. Longitudinal Dynamic Models
2.3. Policy Optimization
| Algorithm 1 PPO with an Adaptive KL Penalty Algorithm |
| 1: Initial policy parameters θ0, weight control β0, target KL-divergence δtag 2: For k = 0, 1, 2…do 3: Gather set of trajectories on policy 4: Optimize the KL penalized using minibatch SGD 5: Compute KL divergence between the new and old policy 6: If δ > 1.5 δtag then βk+1 = 2βk 7: Else if δ < δtag/1.5 then βk+1 = βk/2 8: Else pass 9: End if 10: End for |
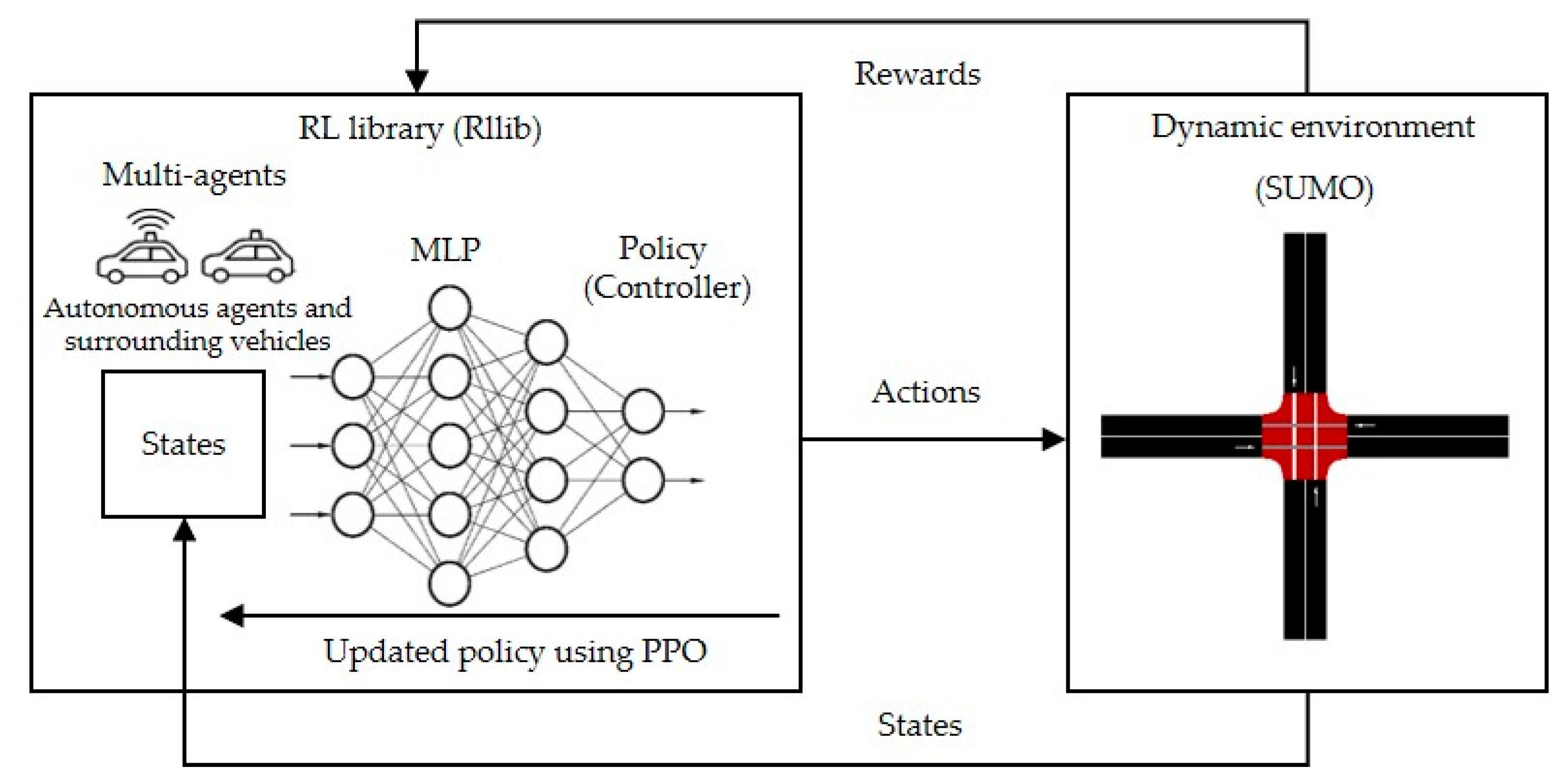
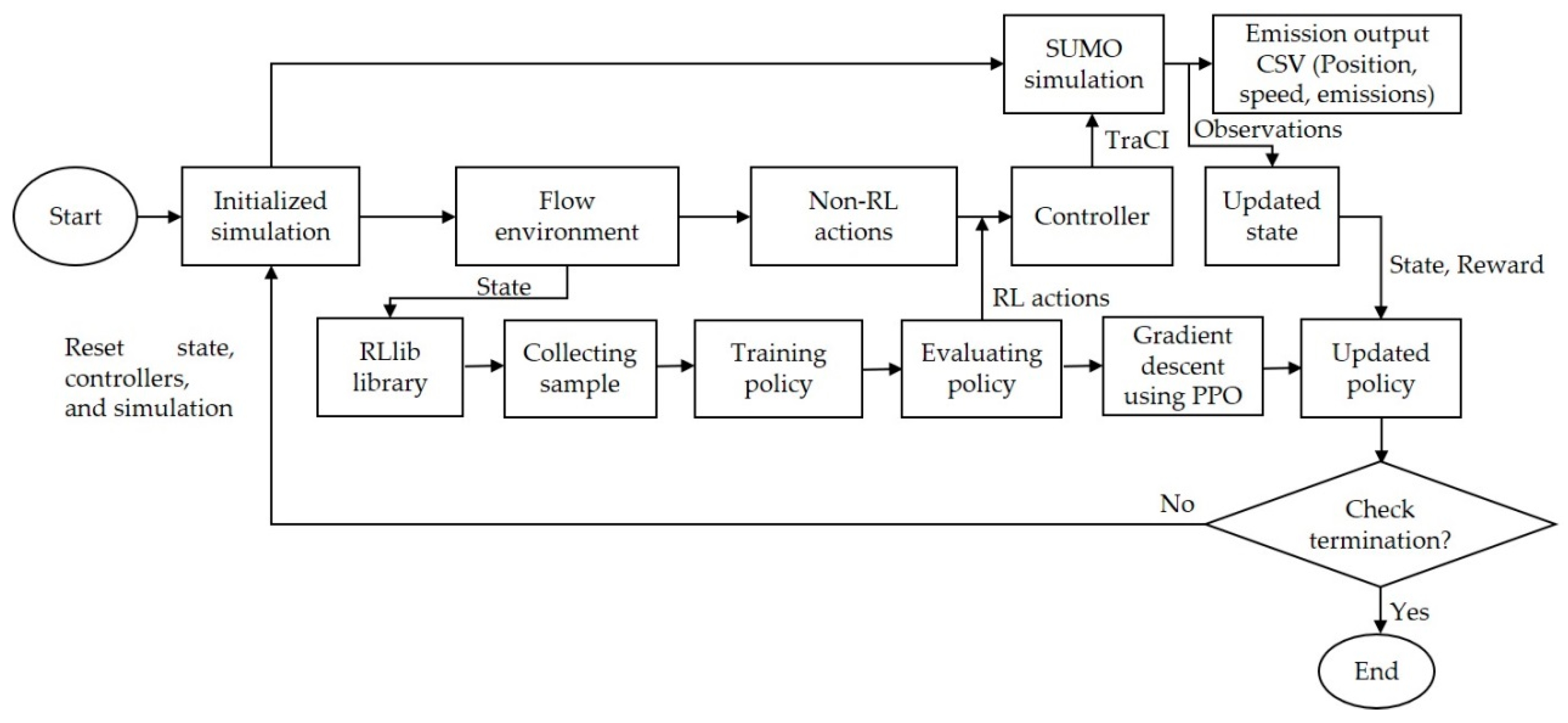
2.4. Proposed Method’s Architecture
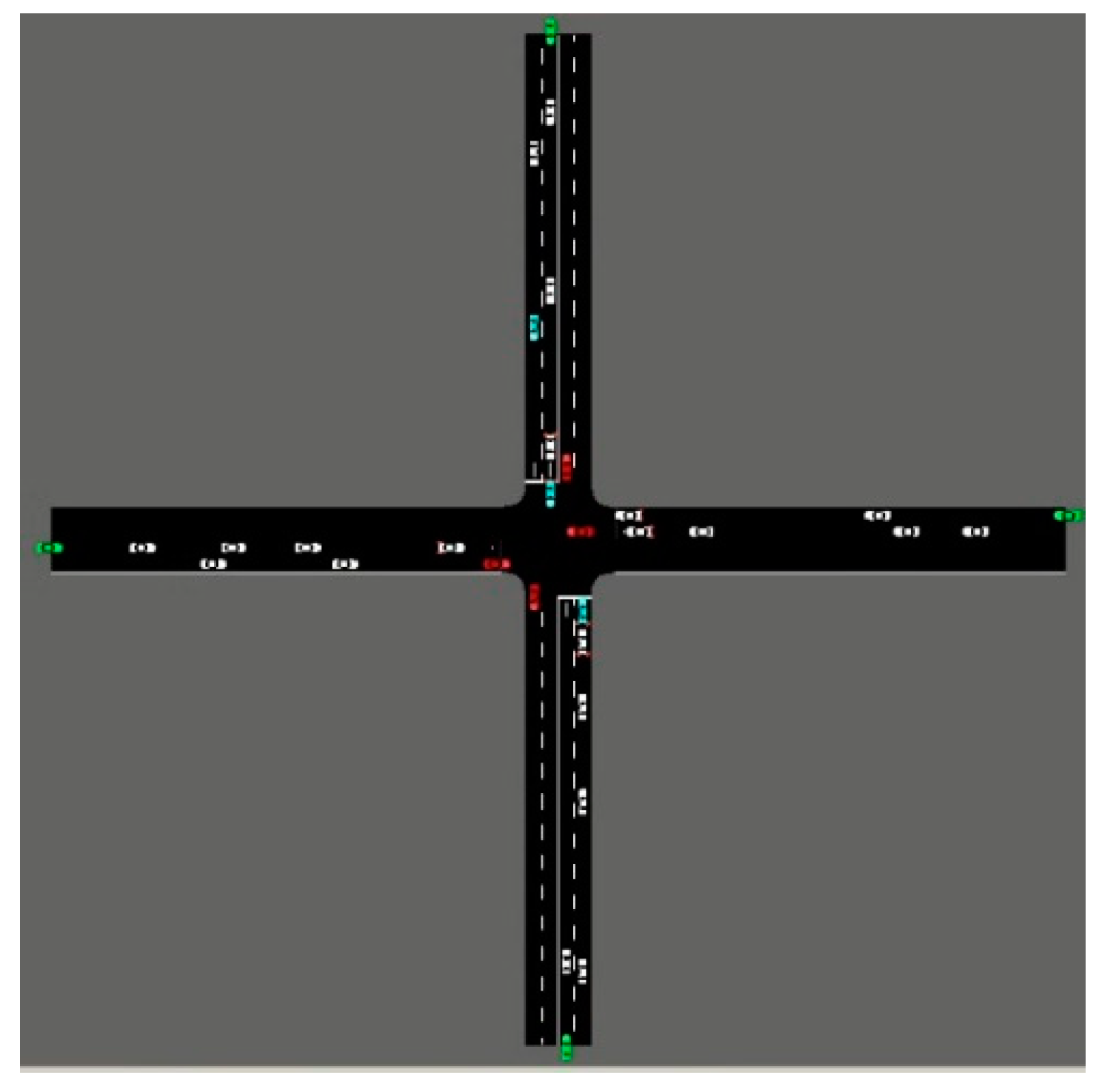
2.4.1. Initialized Simulation
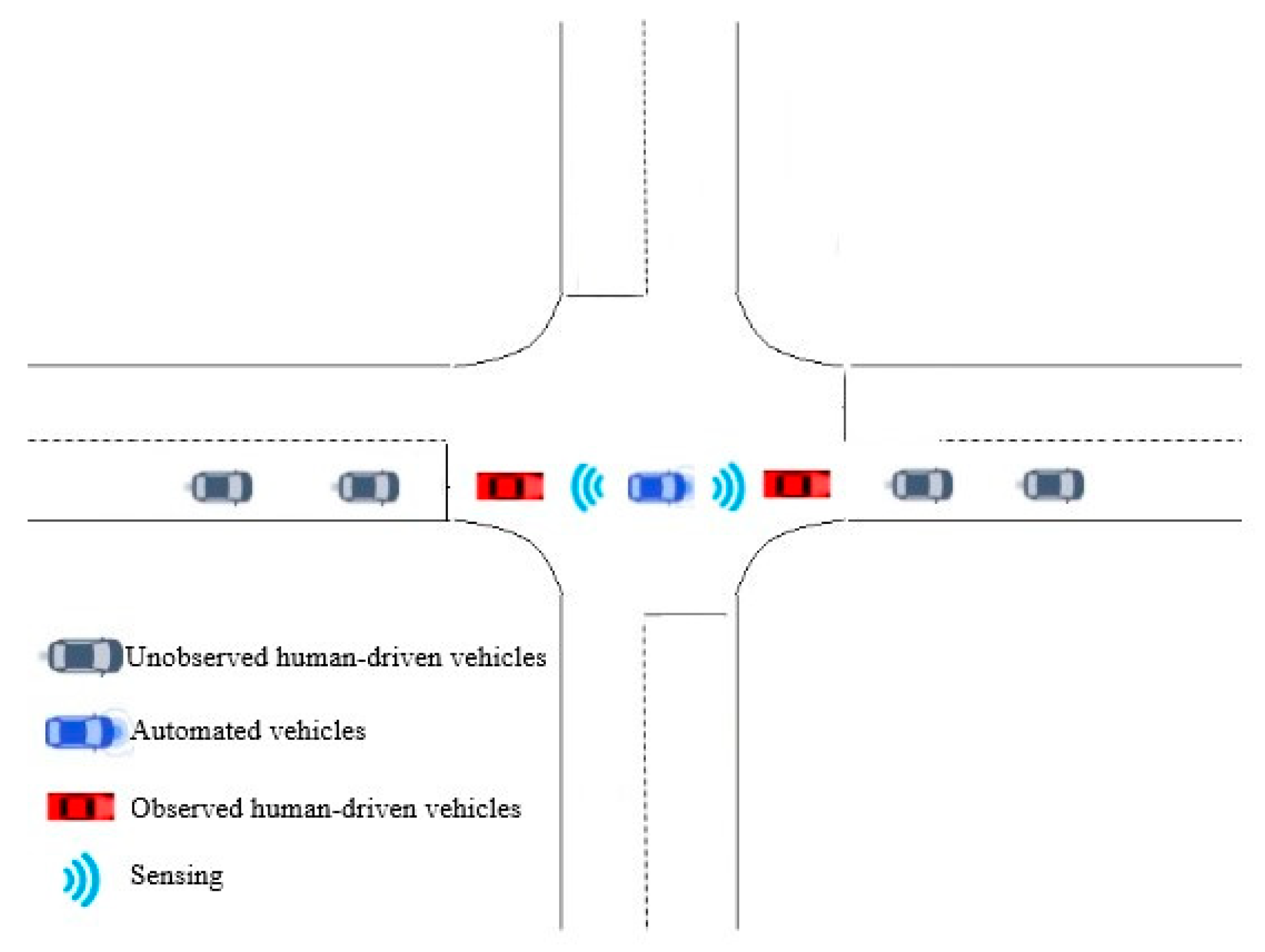
2.4.2. Observation Space
2.4.3. State Space
2.4.4. Action Space
2.4.5. Controller
2.4.6. Reward Function
2.4.7. Termination
3. Experimental Results and Analysis
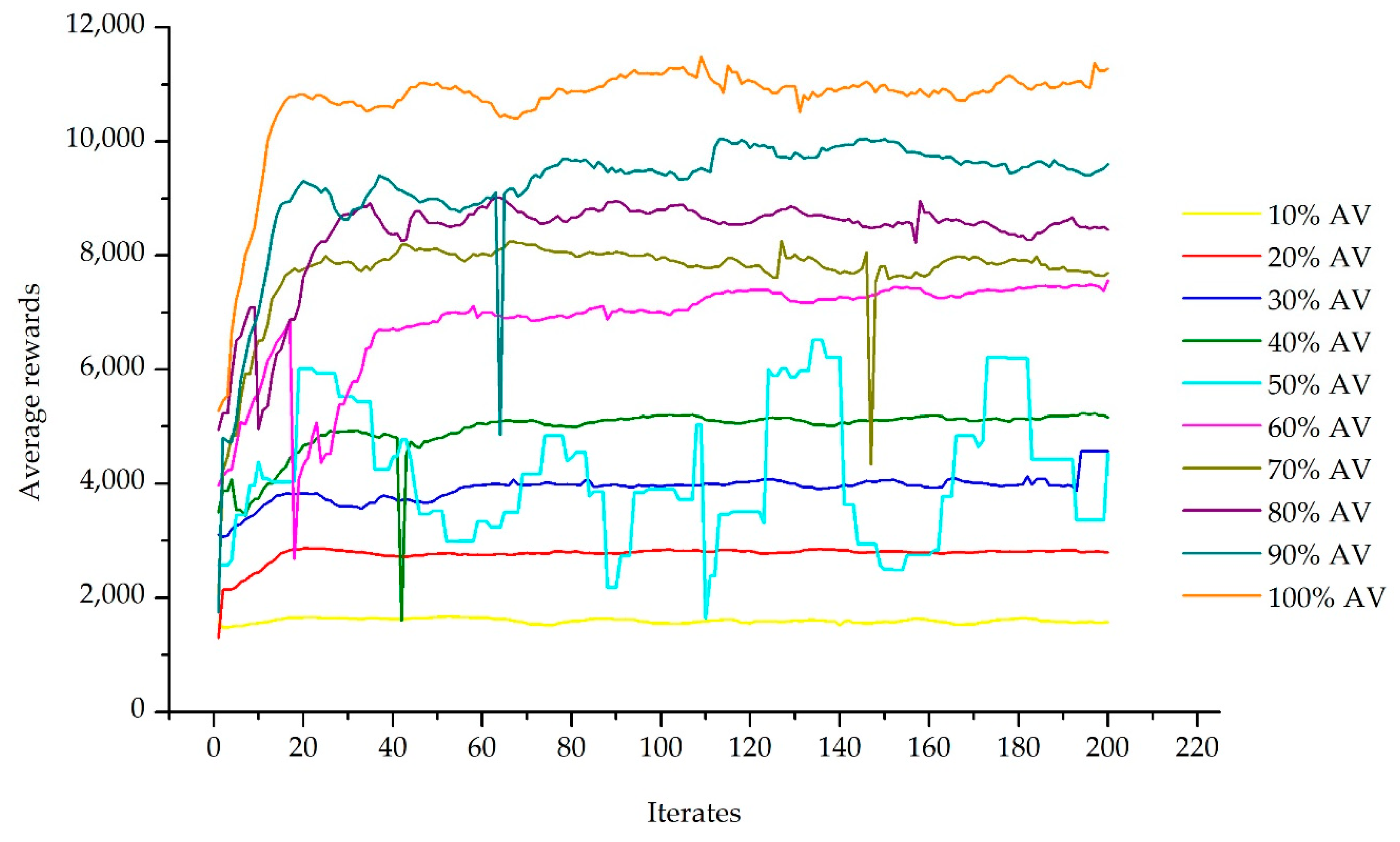
3.1. Hyperparameter Setting and Evaluation Metrics
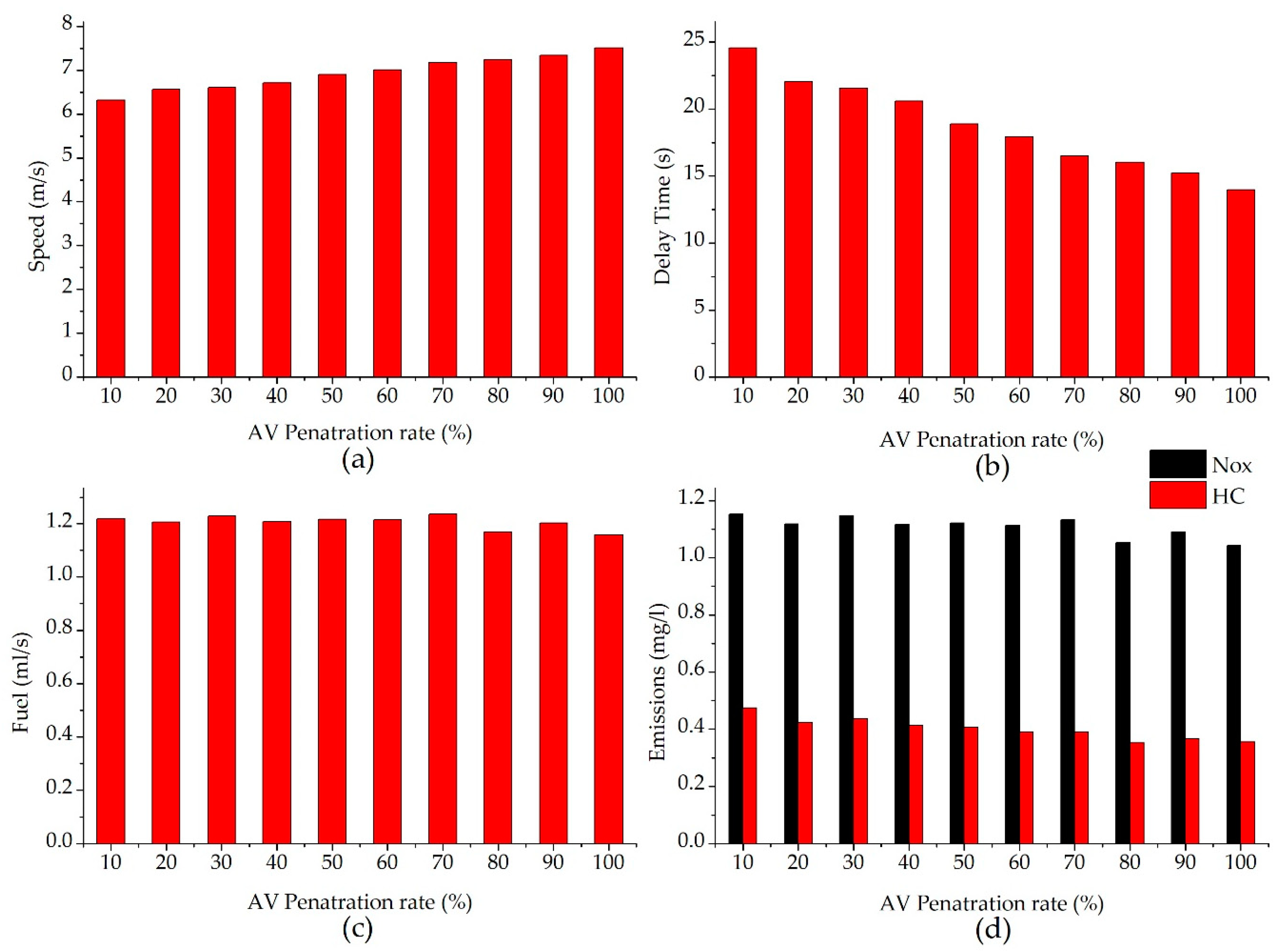
- Mean speed: the average speed of all vehicles at a non-signalized intersection.
- Delay time: the time difference between real and free-flow travel times of all vehicles.
- Fuel consumption: the average fuel consumption value of all vehicles.
- Emissions: the average emission values of all vehicles, including nitrogen oxide (NOx) and hydrocarbons (HC).
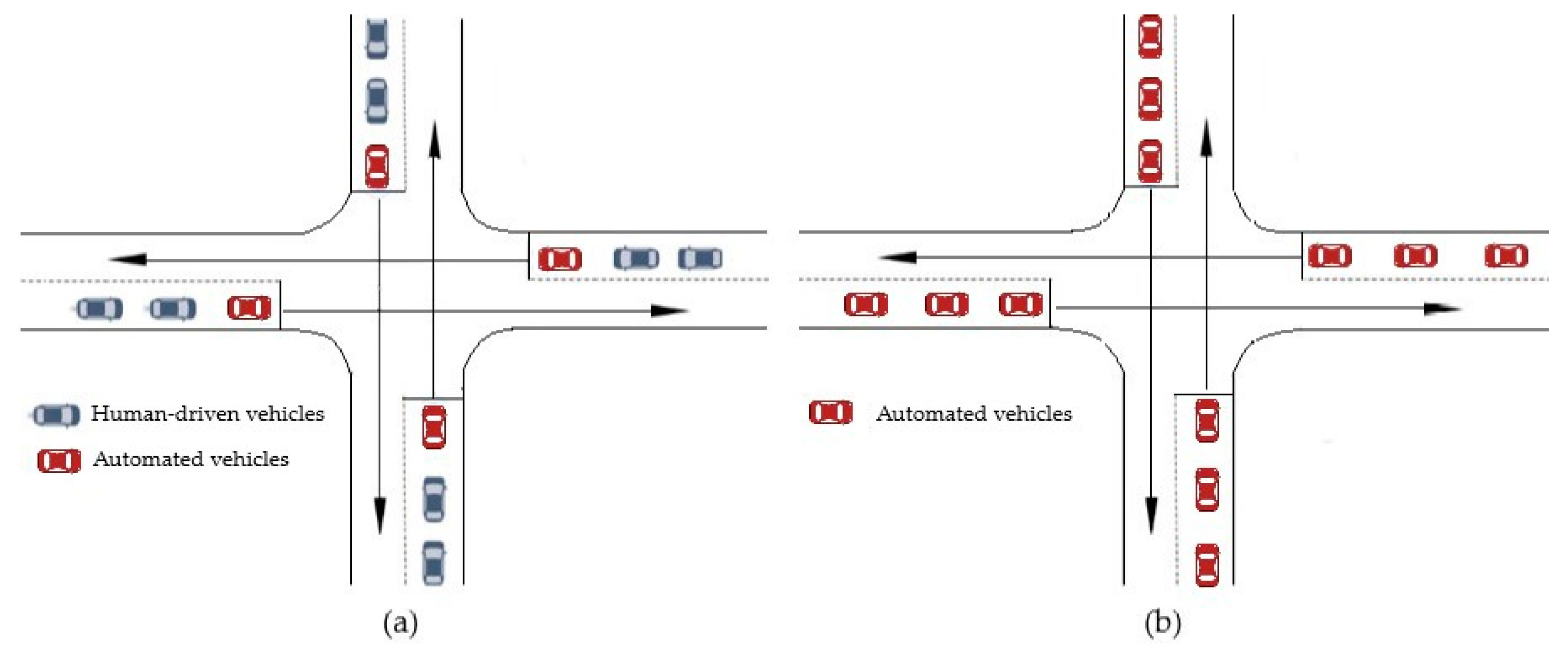
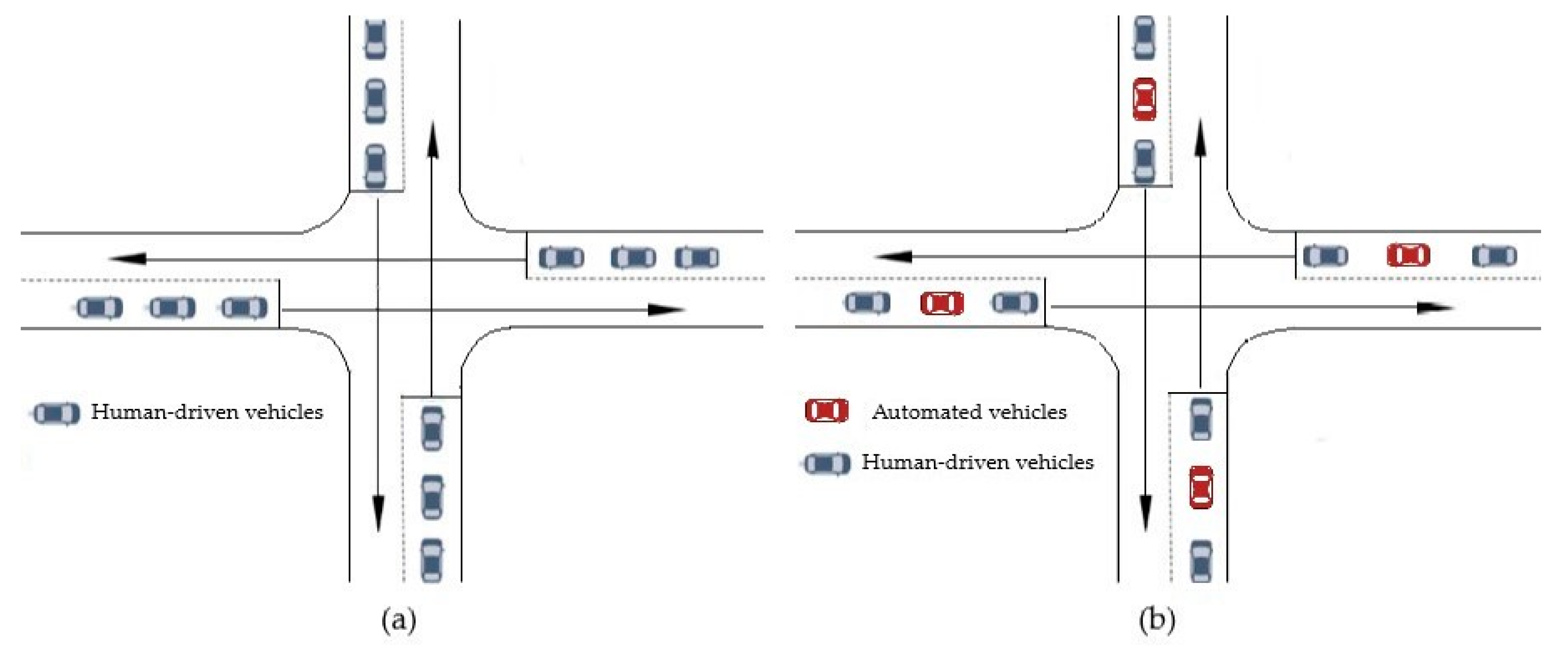
3.2. Experimental Scenarios
3.3. Experimental Results and Analysis
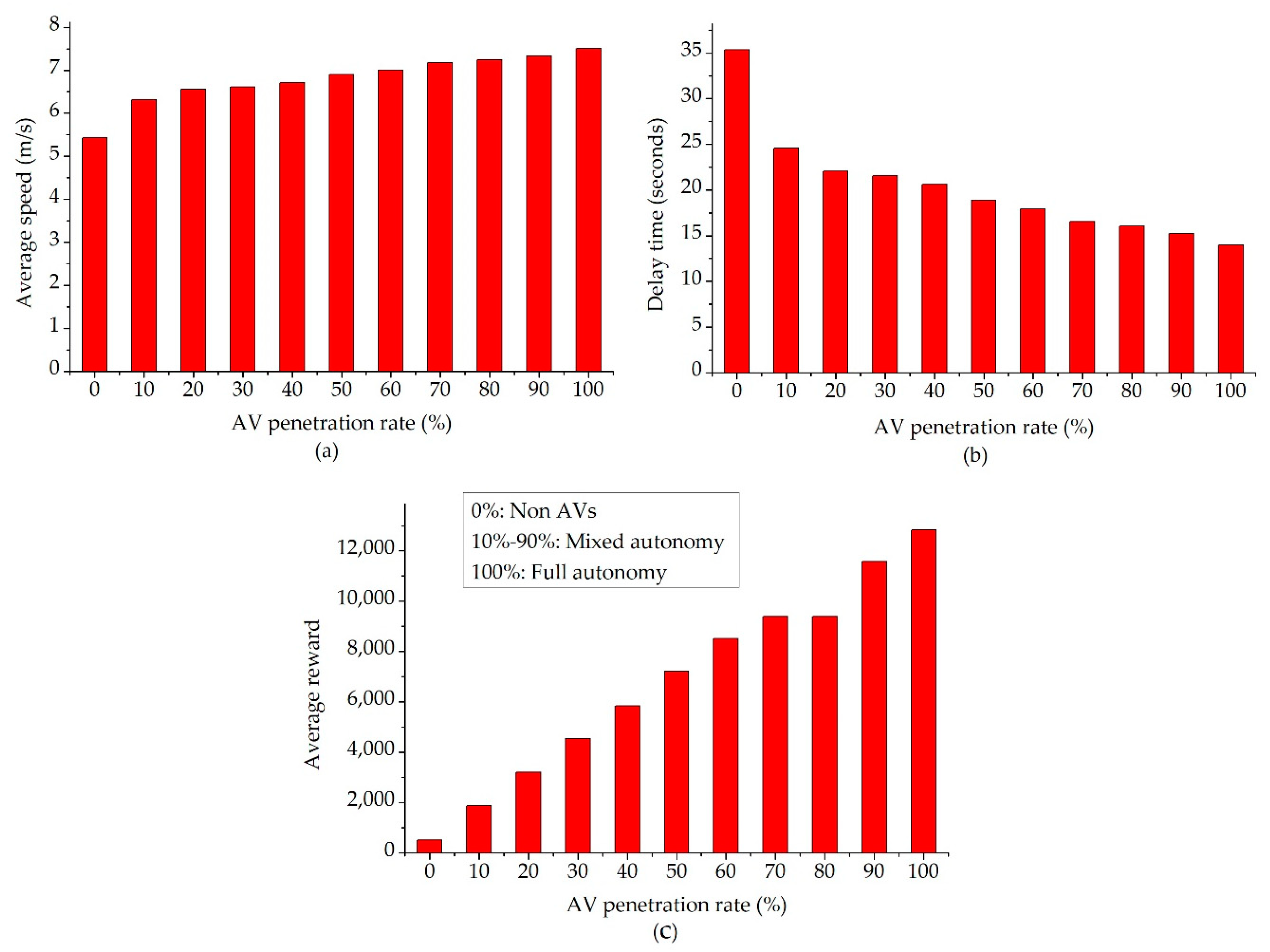
3.3.1. Training Policy’s Performance
3.3.2. Effect of the Leading Automated Vehicle on the Smoothing Velocity
3.3.3. Effect of the Leading Automated Vehicle on Mobility and Energy Efficiency
3.3.4. Performance Comparison
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- National Highway Traffic Safety Administration. Traffic Safety Facts 2015: A Compilation of Motor Vehicle Crash Data from the Fatality Analysis Reporting System and the General Estimates System. The Fact Sheets and Annual Traffic Safety Facts Reports, USA. 2017. Available online: https://crashstats.nhtsa.dot.gov/Api/Public/ViewPublication/812384 (accessed on 26 April 2017).
- Wadud, Z.; MacKenzie, D.; Leiby, P.N. Help or hindrance? The travel, energy and carbon impacts of highly automated vehicles. Transp. Res. Part A Policy Pract. 2016, 86, 1–18. [Google Scholar] [CrossRef]
- Fagnant, D.; Kockelman, K. Preparing a nation for automated vehicles: Opportunities, barriers and policy recommendations. Transp. Res. Part A Policy Pract. 2015, 77, 167–181. [Google Scholar] [CrossRef]
- Rajamani, R.; Zhu, C. Semi-autonomous adaptive cruise control systems. IEEE Trans. Veh. Technol. 2002, 51, 1186–1192. [Google Scholar] [CrossRef]
- Davis, L. Effect of adaptive cruise control systems on mixed traffic flow near an on-ramp. Phys. A Stat. Mech. Appl. 2007, 379, 274–290. [Google Scholar] [CrossRef]
- Milanes, V.; Shladover, S.E. Modeling cooperative and autonomous adaptive cruise control dynamic responses using experimental data. Transp. Res. Part C Emerg. Technol. 2014, 48, 285–300. [Google Scholar] [CrossRef]
- Treiber, M.; Hennecke, A.; Helbing, D. Congested traffic states in empirical observations and microscopic simulations. Phys. Rev. E 2000, 62, 1805–1824. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, X.; Gong, J.; Liu, J. The Research of Car-Following Model Based on Real-Time Maximum Deceleration. Math. Probl. Eng. 2015, 2015, 1–9. [Google Scholar] [CrossRef]
- Bellman, R. A Markovian Decision Process. J. Math. Mech. 1957, 6, 679–684. [Google Scholar] [CrossRef]
- Howard, R.A. Dynamic Programming and Markov Processes; The M.I.T. Press: Cambridge, UK, 1960. [Google Scholar]
- Sutton, R.; Barto, A. Reinforcement Learning: An Introduction. IEEE Trans. Neural Netw. 1998, 9, 1054. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing atari with deep reinforcement learning. arXiv 2013, arXiv:1312.5602. [Google Scholar]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; Driessche, G.V.D.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef] [PubMed]
- Duan, Y.; Chen, X.; Houthooft, R.; Schulman, J.; Abbeel, P. Benchmarking deep reinforcement learning for continuous control. arXiv 2016, arXiv:1604.06778. [Google Scholar]
- Bellemare, M.G.; Naddaf, Y.; Veness, J.; Bowling, M. The Arcade Learning Environment: An Evaluation Platform for General Agents. J. Artif. Intell. Res. 2013, 47, 253–279. [Google Scholar] [CrossRef]
- Todorov, E.; Erez, T.; Tassa, Y. MuJoCo: A Physics Engine for Model-Based Control. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems; Institute of Electrical and Electronics Engineers (IEEE): Vilamoura, Portugal, 7–12 October 2012; pp. 5026–5033. [Google Scholar]
- Levine, S.; Finn, C.; Darrell, T.; Abbeel, P. End-to-end training of deep visuomotor policies. J. Mach. Learn. Res. 2016, 17, 1–40. [Google Scholar]
- Tan, K.L.; Poddar, S.; Sarkar, S.; Sharma, A. Deep Reinforcement Learning for Adaptive Traffic Signal Control. In Proceedings of the Volume 3, Rapid Fire Interactive Presentations: Advances in Control Systems; Advances in Robotics and Mechatronics; Automotive and Transportation Systems; Motion Planning and Trajectory Tracking; Soft Mechatronic Actuators and Sensors; Unmanned Ground and Aerial Vehicles; ASME International: Park City, UT, USA, 9–11 October 2019. [Google Scholar]
- Gu, J.; Fang, Y.; Sheng, Z.; Wen, P. Double Deep Q-Network with a Dual-Agent for Traffic Signal Control. Appl. Sci. 2020, 10, 1622. [Google Scholar] [CrossRef]
- Gregurić, M.; Vujić, M.; Alexopoulos, C.; Miletić, M. Application of Deep Reinforcement Learning in Traffic Signal Control: An Overview and Impact of Open Traffic Data. Appl. Sci. 2020, 10, 4011. [Google Scholar] [CrossRef]
- Tan, T.; Bao, F.; Deng, Y.; Jin, A.; Dai, Q.; Wang, J. Cooperative Deep Reinforcement Learning for Large-Scale Traffic Grid Signal Control. IEEE Trans. Cybern. 2019, 50, 2687–2700. [Google Scholar] [CrossRef]
- Bakker, B.; Whiteson, S.; Kester, L.; Groen, F. Traffic Light Control by Multiagent Reinforcement Learning Systems. ITIL 2010, 281, 475–510. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nat. 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Lillicrap, T.P.; Harley, T.; Silver, D.; Kavukcuoglu, K. Asynchronous methods for deep reinforcement learning. arXiv 2016, arXiv:1602.01783. [Google Scholar]
- Schulman, J.; Levine, S.; Moritz, P.; Jordan, M.I.; Abbeel, P. Trust region policy optimization. arXiv 2015, arXiv:1502.05477. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Ye, F.; Cheng, X.; Wang, P.; Chan, C.-Y. Automated Lane Change Strategy using Proximal Policy Optimization-based Deep Reinforcement Learning. arXiv 2020, arXiv:2002.02667. [Google Scholar]
- Wei, H.; Liu, X.; Mashayekhy, L.; Decker, K. Mixed-Autonomy Traffic Control with Proximal Policy Optimization. In Proceedings of the 2019 IEEE Vehicular Networking Conference (VNC); Institute of Electrical and Electronics Engineers (IEEE): Los Angeles, CA, USA, 4–6 December 2019; pp. 1–8. [Google Scholar]
- Pomerleau, D.A. An autonomous land vehicle in a neural network. Adv. Neural Inf. Process. Syst. 1988, 1. [Google Scholar]
- Wymann, B.; Espi’e, E.; Guionneau, C.; Dimitrakakis, C.; Coulom, R.; Sumner, A. TORCS, the Open Racing Car Simulator, v1.3.5. Available online: http://www.torcs.org (accessed on 1 January 2013).
- Dosovitskiy, A.; Ros, G.; Codevilla, F.; Lopez, A.; Koltun, V. CARLA: An Open Urban Driving Simulator. arXiv 2017, arXiv:1711.03938. [Google Scholar]
- Behrisch, M.; Bieker, L.; Erdmann, J.; Krajzewicz, D. SUMO—Simulation of Urban MObility: An Overview. In Proceedings of the Third International Conference on Advances in System Simulation, Barcelona, Spain, 23–28 October 2011. [Google Scholar]
- Krajzewicz, D.; Hertkorn, G.; Feld, C.; Wagner, P. SUMO (Simulation of Urban MObility): An open-source traffic simulation. In Proceedings of the 4th Middle East Symposium on Simulation and Modelling, Dubai, UAE, 2–4 September 2002; pp. 183–187. [Google Scholar]
- Krajzewicz, D.; Erdmann, J.; Behrisch, M.; Bieker, L. Recent development and applications of sumo-simulation of urban mobility. Int. J. Adv. Syst. Meas. 2012, 5, 128–138. [Google Scholar]
- Wegener, A.; Piórkowski, M.; Raya, M.; Hellbrück, H.; Fischer, S.; Hubaux, J. TraCI: An Interface for Coupling Road Traffic and Network Simulators. In Proceedings of the 11th Communications and Networking Simulation Symposium, New York, NY, USA, 14–17 April 2008. [Google Scholar]
- Wu, C.; Parvate, K.; Kheterpal, N.; Dickstein, L.; Mehta, A.; Vinitsky, E.; Bayen, A.M. Framework for Control and Deep Reinforcement Learning in Traffic. In Proceedings of the 2017 IEEE 20th International Conference on Intelligent Transportation Systems (ITSC); Institute of Electrical and Electronics Engineers (IEEE): Yokohama, Japan, 2017; pp. 1–8. [Google Scholar]
- Vinitsky, E.; Kreidieh, A.; Le Flem, L.; Kheterpal, N.; Jang, K.; Wu, F.; Liaw, R.; Liang, E.; Bayen, A.M. Benchmarks for Reinforcement Learning in Mixed-Autonomy Traffic. In Proceedings of the Conference on Robot Learning, Zürich, Switzerland, 29–31 October 2018. [Google Scholar]
- Wu, C.; Kreidieh, A.; Parvate, K.; Vinitsky, E.; Bayen, A.M. Flow: Architecture and Benchmarking for Reinforcement Learning in Traffic Control. arXiv 2017, arXiv:1710.05465. [Google Scholar]
- Wu, C.; Kreidieh, A.; Vinitsky, E.; Bayen, A.M. Emergent behaviors in mixed-autonomy traffic. In Proceedings of the 1st Annual Conference on Robot Learning, Mountain View, CA, USA, 13–15 November 2017; Volume 78, pp. 398–407. [Google Scholar]
- Kreidieh, A.R.; Wu, C.; Bayen, A.M. Dissipating Stop-and-Go Waves in Closed and Open Networks Via Deep Reinforcement Learning. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC); Institute of Electrical and Electronics Engineers (IEEE): Maui, Hawaii, USA, 2018; pp. 1475–1480. [Google Scholar]
- Treiber, M.; Kesting, A. Traffic Flow Dynamics. Traffic Flow Dynamics: Data, Models and Simulation; Springer Berlin Heidelberg: Berlin, Heidelberg, 2013. [Google Scholar] [CrossRef]
- Graesser, L.; Keng, W.L. Foundations of Deep Reinforcement Learning: Theory and Practice in Python; Addison-Wesley Professional: Boston, MA, USA, 2019; Chapter 7. [Google Scholar]
- Wu, C.; Kreidieh, A.; Parvate, K.; Vinitsky, E.; Bayen, A.M. Flow: A Modular Learning Framework for Autonomy in Traffic. arXiv 2017, arXiv:1710.05465v2. [Google Scholar]
- Liang, E.; Liaw, R.; Nishihara, R.; Moritz, P.; Fox, R.; Gonzalez, J.; Goldberg, K.; Stoica, I. Ray RLlib: A composable and scalable reinforcement learning library. arXiv 2017, arXiv:1712.09381. [Google Scholar]
- Brockman, G.; Cheung, V.; Pettersson, L.; Schneider, J.; Schulman, J.; Tang, J.; Zaremba, W. OpenAI Gym. arXiv 2016, arXiv:1606.01540. [Google Scholar]
| Parameters | Value |
|---|---|
| Desired speed (m/s) | 15 |
| Time gap (s) | 1.0 |
| Minimum gap (m) | 2.0 |
| Acceleration exponent | 4.0 |
| Acceleration (m/s2) | 1.0 |
| Comfortable acceleration (m/s2) | 1.5 |
| Parameters | Value |
|---|---|
| Number of training iterations | 200 |
| Time horizon per training iteration | 6000 |
| Gamma | 0.99 |
| Hidden layers | 256 × 256 × 256 |
| Lamda | 0.95 |
| Kullback–Leibler (KL) target | 0.01 |
| Number of SGD iterations | 10 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quang Tran, D.; Bae, S.-H. Proximal Policy Optimization Through a Deep Reinforcement Learning Framework for Multiple Autonomous Vehicles at a Non-Signalized Intersection. Appl. Sci. 2020, 10, 5722. https://doi.org/10.3390/app10165722
Quang Tran D, Bae S-H. Proximal Policy Optimization Through a Deep Reinforcement Learning Framework for Multiple Autonomous Vehicles at a Non-Signalized Intersection. Applied Sciences. 2020; 10(16):5722. https://doi.org/10.3390/app10165722
Chicago/Turabian StyleQuang Tran, Duy, and Sang-Hoon Bae. 2020. "Proximal Policy Optimization Through a Deep Reinforcement Learning Framework for Multiple Autonomous Vehicles at a Non-Signalized Intersection" Applied Sciences 10, no. 16: 5722. https://doi.org/10.3390/app10165722
APA StyleQuang Tran, D., & Bae, S.-H. (2020). Proximal Policy Optimization Through a Deep Reinforcement Learning Framework for Multiple Autonomous Vehicles at a Non-Signalized Intersection. Applied Sciences, 10(16), 5722. https://doi.org/10.3390/app10165722





