1. Introduction
The equilibrium traffic assignment problem has been widely studied since the early 1950s [
1], both with respect to theoretical properties and proposing solution methods and algorithms. The Method of Successive Averages (MSA) is one of the most commonly used algorithms for solving the problem; it was proposed by References [
2,
3], and its convergence was stated by Reference [
4]. The MSA proposed by References [
2,
3] operates on link flows (MSA-FA). On the other hand, Reference [
5] proposed the MSA-CA which operates on link costs; while, Reference [
6] devised the MSA-ACO based on Ant Colony Optimisation. Solution algorithms in the case of elastic demand were proposed and analysed by References [
5,
7,
8].
The MSA algorithm at each iteration,
k, averages the traffic flows calculated by stochastic uncongested network loading, with weight 1/
k, with the results of the previous iteration, with weight (
k–1)/
k. Alternative step sequences (or weighting methods) were proposed, among others, by References [
9,
10,
11]. More recently, Reference [
12] proposed three revised versions of the traditional MSA method, namely: (i) Restarting MSA (RMSA), where the iteration counter is re-initialised after a specific number of iterations; (ii) Double RMSA (R2MSA), where the iteration counter is re-initialised to a variable value; (iii) Weighted MSA (WMSA), based on the self-regulated averaging method proposed by Reference [
13] for solving the stochastic user equilibrium problem. The above-mentioned MSA schemes have been adopted by Reference [
14] for solving a stochastic frequency-based assignment considering pre-trip/en-route path choice behaviour. Similarly, Reference [
15], which extended the approach proposed in Reference [
16], compared different MSA-based resolution techniques in the case of a stochastic assignment with multi-vehicle types (i.e., connected, automated, and autonomous vehicles, as well as traditional ones).
A generalisation of the averaging procedure, not limited to the traffic assignment problem, was provided by Reference [
17]; while, Reference [
18] proposed a refresh memory method for solving the combined assignment-control problem.
With the computing capabilities of modern PCs, the solution time of the traffic assignment problem is fairly short, also for large-size networks, if the problem has to be solved only once or a few times. Network Design Problems (NDPs) are usually solved by adopting procedures that use assignment algorithms as subroutines (bi-level approach); some reviews on NDPs can be found in References [
19,
20,
21,
22]. Indeed, for evaluating the objective function corresponding to a solution to the NDP, it is necessary to estimate traffic flows on the network. In this case, in most approaches, the assignment problem has to be solved a number of times equal to the solutions examined by the NDP algorithm; hence, several thousands of times in real-scale applications. Therefore, reducing the computing time of assignment algorithms is an important target since it may lead to a significant reduction in computing times for solving NDPs. In this context, Reference [
23] proposed an MSA-based algorithm acting on the traffic flows adopted in the initialisation phases for reducing calculation times of NDPs when the topology of the network configuration remains unchanged.
With respect to the previous literature, in this paper we propose a new method that adopts a variant to the MSA algorithm: It is based on a parameter that can be set for each network to minimise the computing time. Moreover, in order to show its promising performance, it has been compared to other methods proposed in the literature. Finally, after the setting phase, the algorithm can be included within the NDP algorithm, minimising the whole computing time for solving the problem.
The remaining part of the paper is organised as follows:
Section 2 introduces the model formulation; the proposed algorithm is analysed in
Section 3, and
Section 4 summarises the numerical results;
Section 5 concludes the paper and outlines the research prospects. In
Appendix A the convergence of the proposed algorithm is stated, and
Appendix B presents a comparison with some MSA-based algorithms is provide. In
Appendix C and
Appendix D, the Network Design Problem and the algorithm used for its solution in the numerical test are illustrated.
2. Model Formulation
The traffic assignment problem consists of estimating traffic flows on a transportation network. In order to solve this problem, we need three elements: the travel demand (summarised in an Origin-Destination matrix), the transportation supply (modelled with a supply model) and the user path choice behaviour (modelled with a path choice model). Several models can be used for solving the problem depending on the transportation system (road network, mass-transit network, multimodal transportation network, etc.), the assumptions on the travel demand (fixed or variable), the approach to studying the interactions between demand and supply (user equilibrium or dynamic approach), the dependence or otherwise of link costs on flows (uncongested or congested), the assumption on the route choice model (deterministic or stochastic), and so forth. An in-depth analysis of traffic assignment models can be found elsewhere (see, for instance, Reference [
24]). Even if the proposed algorithm can also be used to solve other assignment problems, in this paper, we consider the congested road network, fixed demand, user equilibrium approach and stochastic route choice model.
On a road network, the link flow vector,
f, once the transport demand has been fixed, depends on link costs, and hence, on the link cost vector,
c:
with:
where
A is the link-path incidence matrix, whose components,
alp, are equal to 1 if link
l belongs to path
p and 0 otherwise;
P is the path choice probability matrix, with a column for each
od pair and a row for each path
p; the generic element,
Pp,od, of this matrix represents the probability that a user will use path
p from origin
o to destination
d (if path
p does not connect the
od pair,
Pp,od is equal to 0);
d is the demand vector, whose components are the demand values
dod for each
od pair.
The generic cost, cl, of link l can be assumed dependent only on the flow on the same link, fl.
Substituting (2) in (1), we obtain the following:
which relates flows,
f, and costs,
c. Equation (3) is a fixed-point problem; the solution is represented by the equilibrium traffic flows,
f*, which is congruent with the corresponding link costs,
c =
χ(
f*).
In this case, it may be stated, under some assumptions, that the solution to the fixed-point problem (4) exists and is unique [
5] and that the MSA algorithm converges to it [
4].
3. Solution Algorithm
In order to solve the fixed-point problems (4) we propose an algorithm based on the MSA general framework. The first formulation of MSA [
2] generates a succession of feasible link flow vectors,
f k, starting from an initial solution (usually
f 0 =
0). At each iteration
k, the solution
fk is generated by combining traffic flows obtained by a Stochastic Uncongested Network (SUN) assignment,
fSUNk =
φSUN(
ck), with the previous solution,
f k−1At each iteration
k, in order to generate the solution
fk, the results of the SUN assignment,
fSUNk, are averaged, with weight 1/
k, with the results of the previous iteration,
f k−1, with weight (
k − 1)/
k:
that is:
Since the algorithm works directly on flows, it is also known as MSA-FA (Flow Averaging). Algorithm 1 reports the code of the traditional MSA-FA algorithm, where
ε represents the stop threshold.
| Algorithm 1 Traditional MSA-FA algorithm |
- 1:
k = 0 - 2:
f0 = 0 - 3:
do while |fSUNk − f k−1|/f k−1 ≥ ε - 4:
k = k + 1 - 5:
ck = χ(f k−1) - 6:
fSUNk = φSUN(ck) - 7:
fk = f k−1 + 1/k · (fSUNk − f k−1) - 8:
loop - 9:
f * = fk - 10:
end
|
It is worth noting that the averages applied to the flows belonging to successive iterations have to be considered an algorithmic trick and should not be confused with the weights that simulate the learning process in the dynamic assignment models. Indeed, the MSA algorithms apply to stationary models, while the simulation of learning processes (comparison between expected and experienced performances) are typical of day-to-day dynamics models [
24,
25].
Since, as shown in
Appendix B, most of the MSA-based algorithms proposed in the literature for solving the traffic assignment problem are based on a modification of the weight formulation (i.e., term 1/
k in the traditional MSA algorithm), our proposal consists in providing a further variant of the MSA-FA algorithm substituting the term
k in Equation (5) or (6) with the following function:
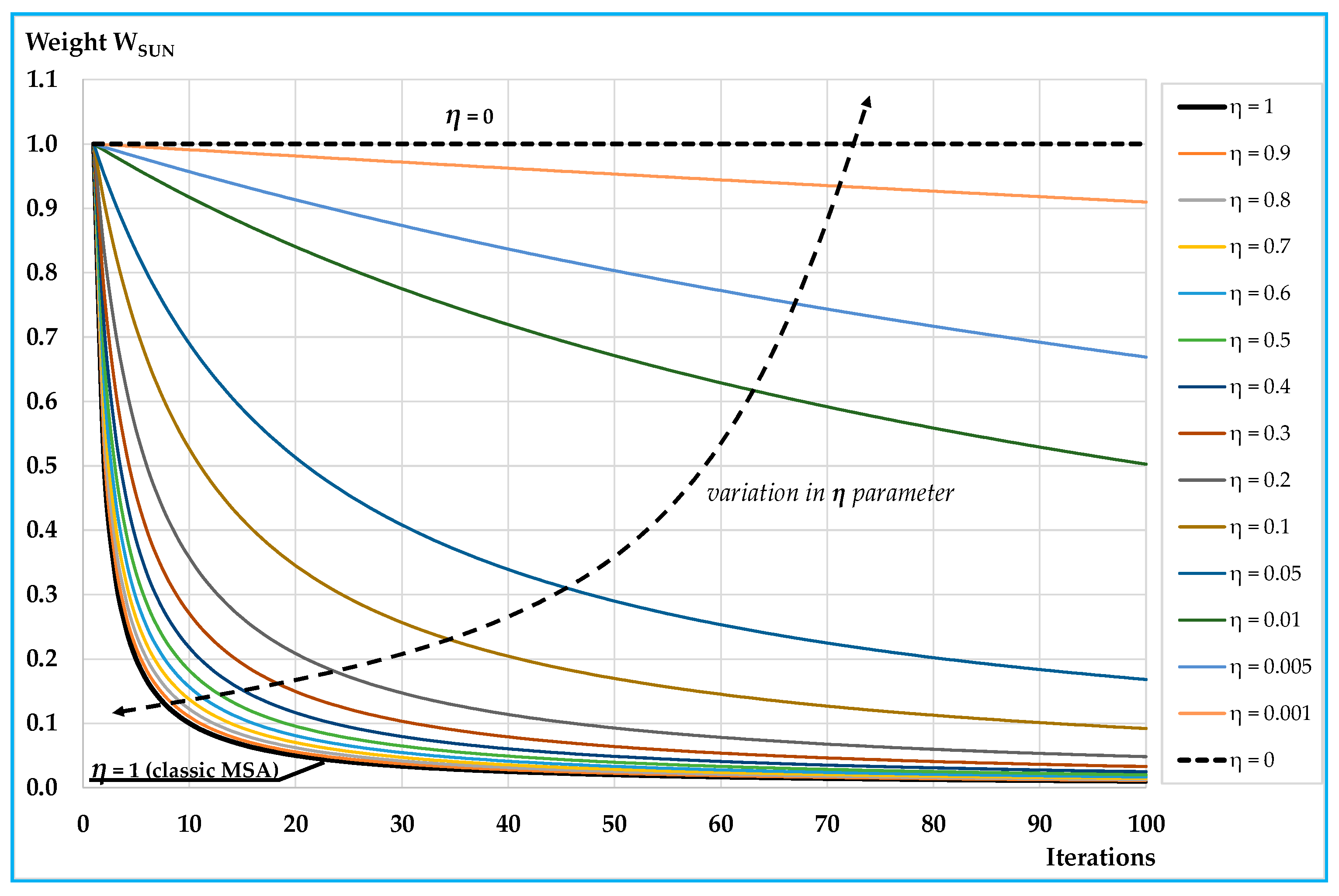
where
η is a parameter between 0 and 1; for
η = 1 we obtain the classic MSA algorithm, and for
η = 0 we obtain that
fk =
fSUNk (in this case the algorithm does not consider at each iteration the results of the previous ones). This method tends to muffle the weight given to
f k−1 (with
η < 1) with respect to the corresponding weight given with the classic MSA algorithm. The weights of
f k−1,
w−1, and
fSUNk,
wSUN, at each iteration
k become:
In Algorithm 2 the code of the generalised MSA-FA algorithm (i.e., GMSA-FA) is reported.
Figure 1 reports the values at each iteration
k of
wSUN (equal to 1 −
w−1) for values of
η between 1 (classic MSA) and 0 and for the first 100 iterations.
| Algorithm 2 Generalised MSA-FA algorithm |
- 1:
k = 0 - 2:
f0 = 0 - 3:
do while |fSUNk − f k−1|/f k−1 ≥ ε - 4:
k = k + 1 - 5:
ck = χ(f k−1) - 6:
fSUNk = φSUN(ck) - 7:
fk = f k−1 + 1/ξ(k) · (fSUNk − f k−1) - 8:
loop - 9:
f * = fk - 10:
end
|
It can be noted that the weight of
fSUNk decreases less rapidly for lower values of parameter
η. Convergence of the proposed algorithm is stated in
Appendix A, where the algorithm is shown to converge for each value of
η > 0.
5. Conclusions and Research Prospects
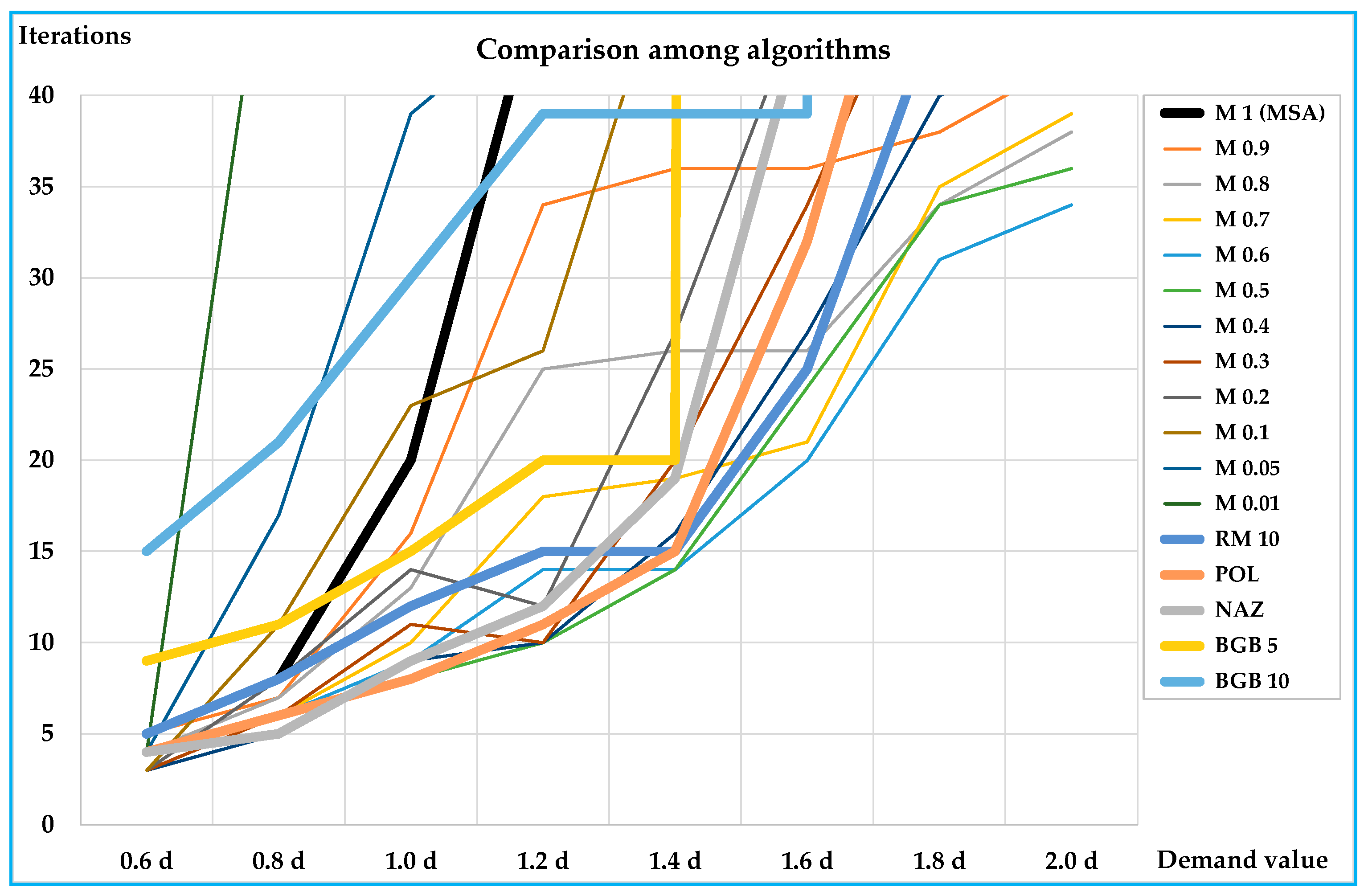
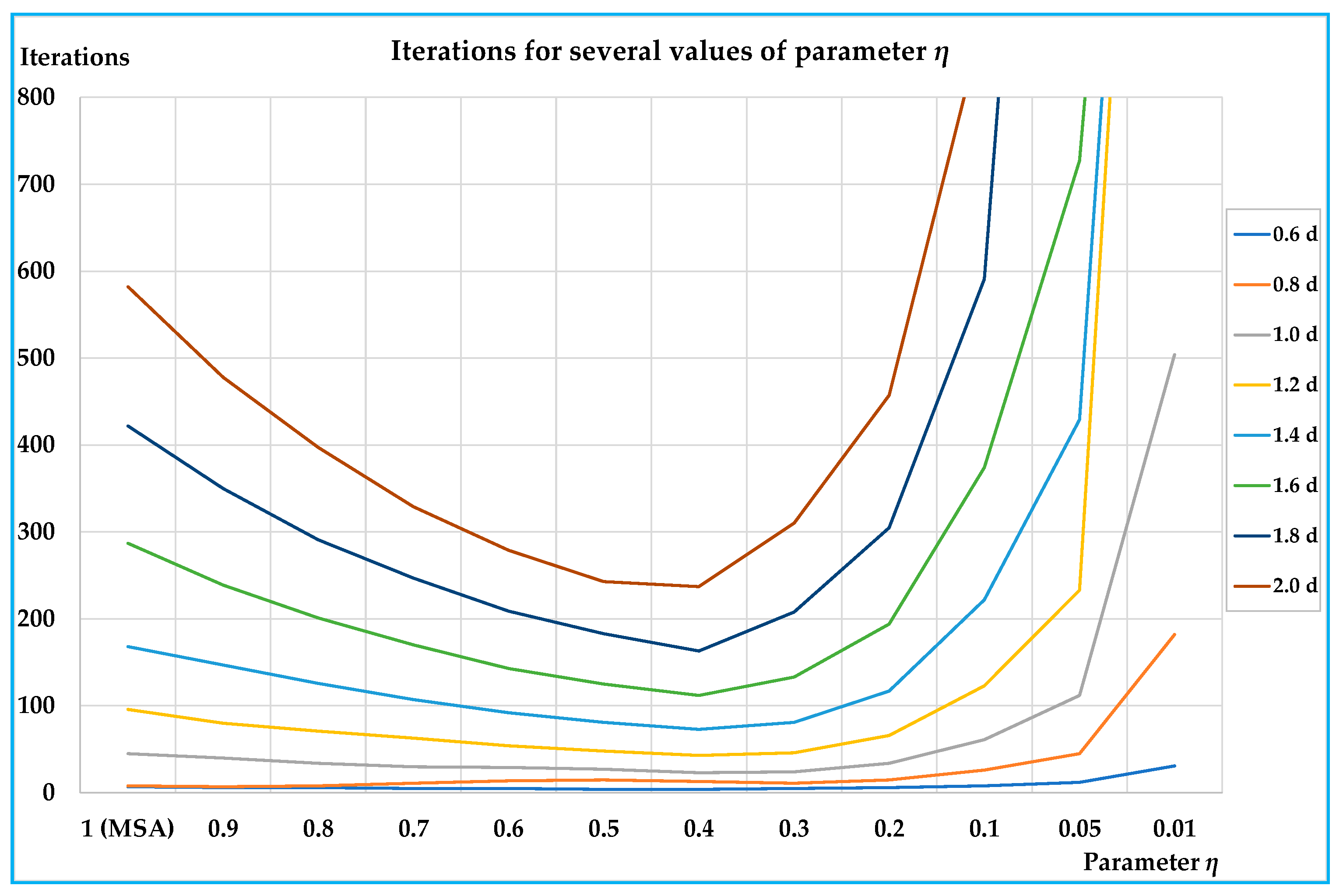
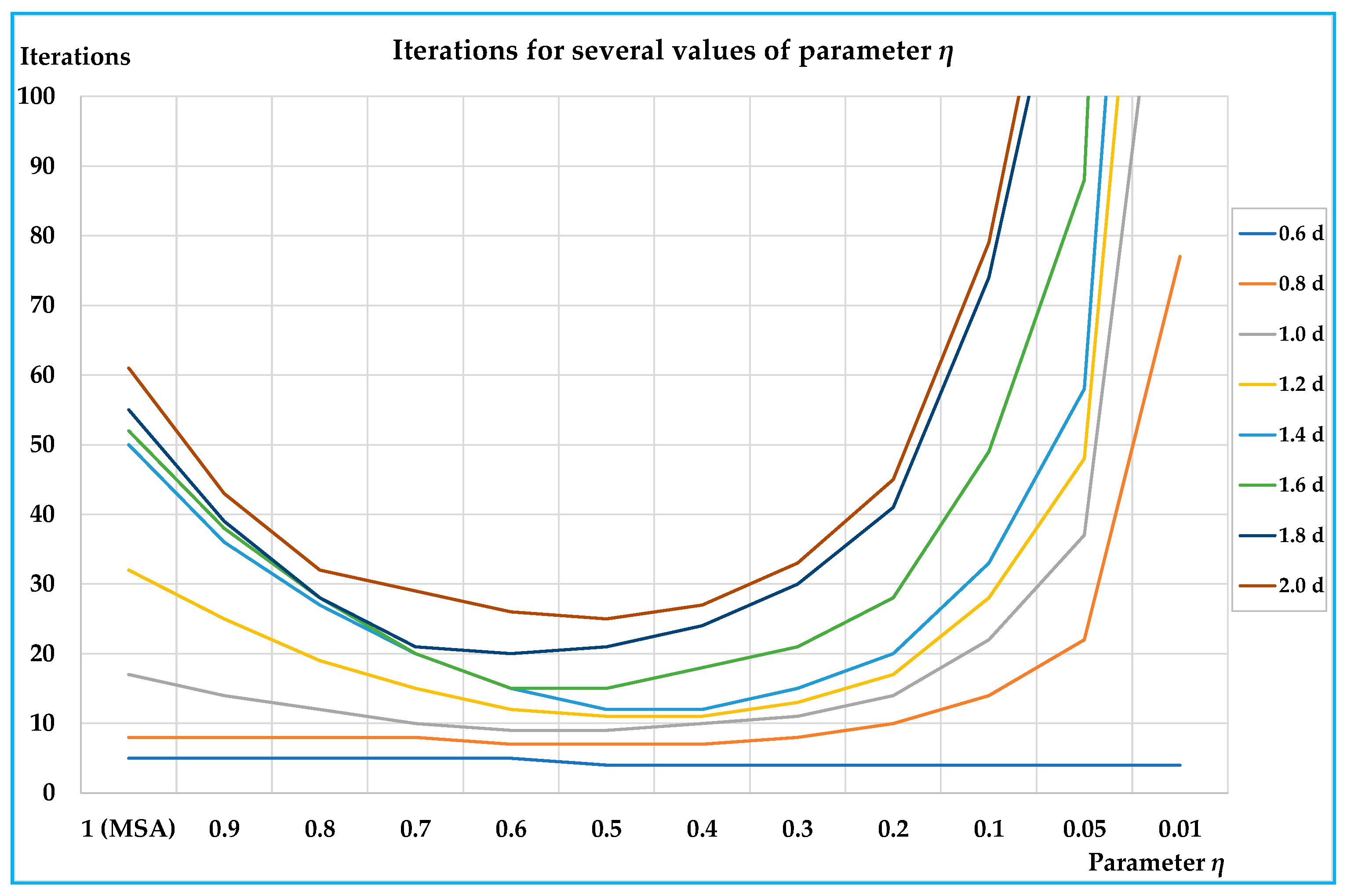
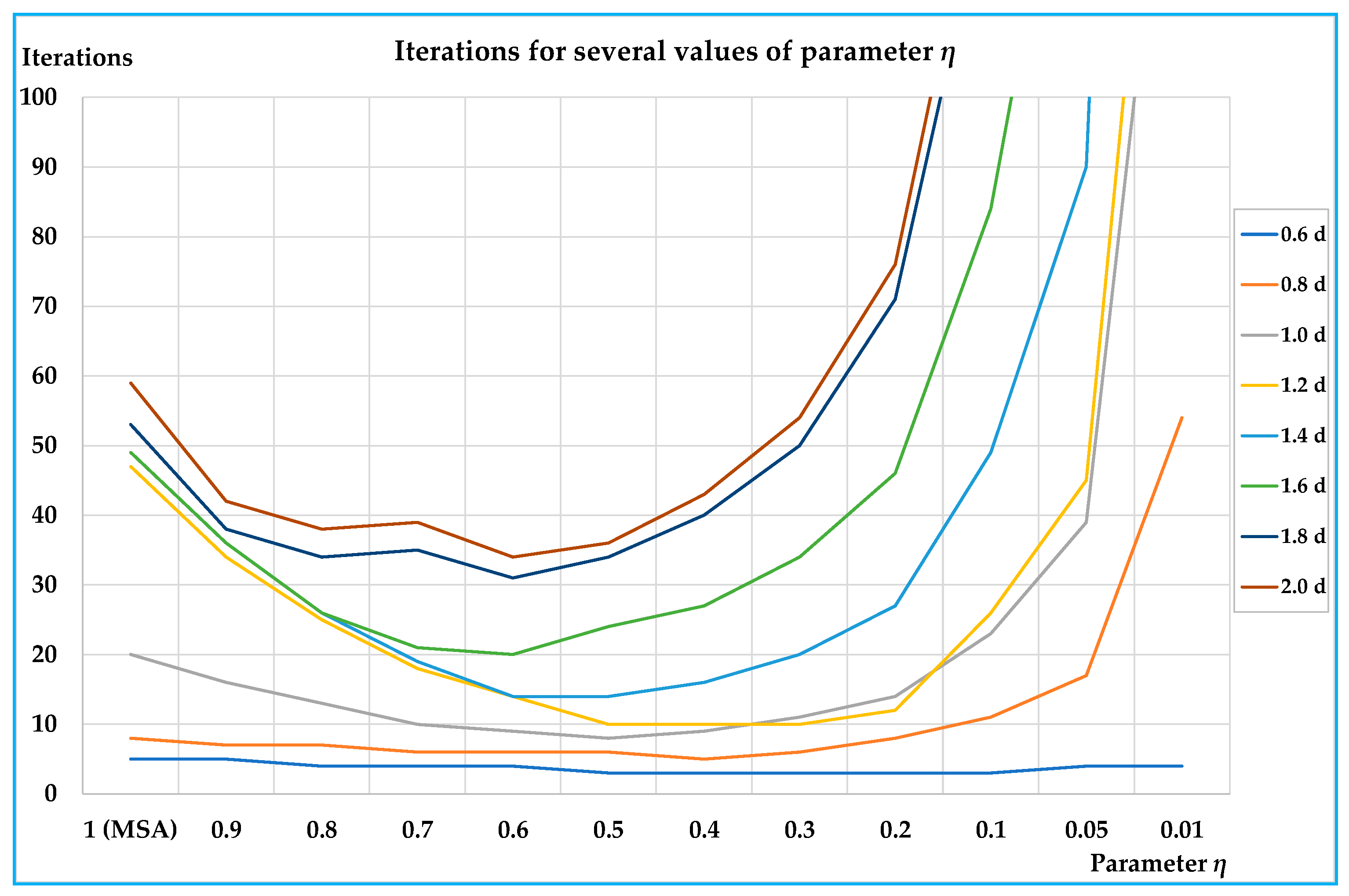
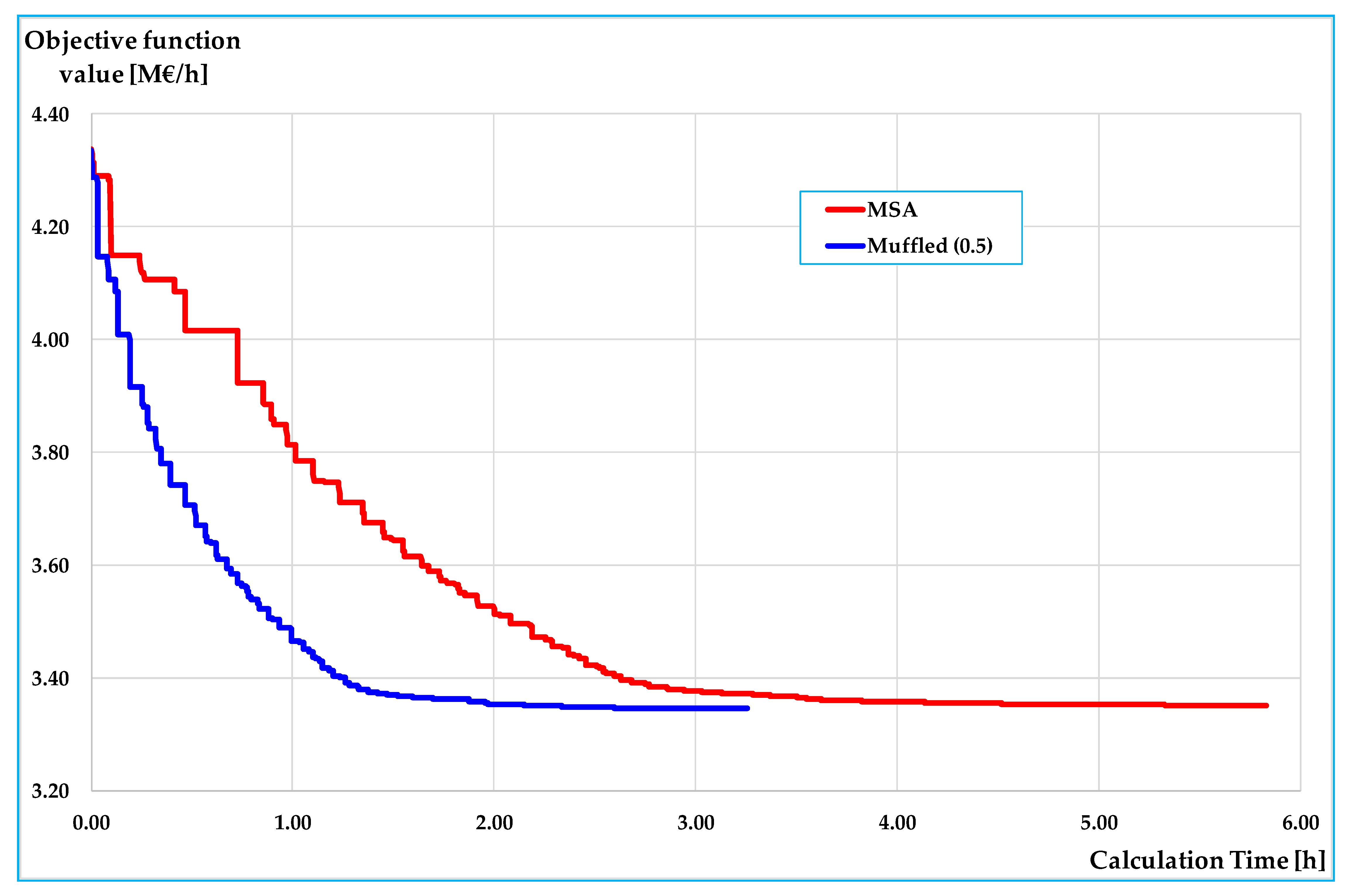
The results obtained on the small and on the real-scale networks show that the proposed algorithm is able to reduce the number of iterations for convergence, and hence, computing times compared with the classic MSA approach; in particular, the reductions arrive in percentage up to –79% with respect to the classic MSA for the best value of the parameter. On all networks the results are similar, showing that the benefits of the proposed algorithm are significant for medium-high congested demand levels (average saturation degrees over about 0.4); less significant, but not negligible, are the benefits for lower demand levels.
In all tests, the best values of parameter
η lie between 0.3 and 0.6. An important characteristic of the proposed algorithm is that there is a parameter that can be opportunely chosen, so to optimise the performances before starting with network design procedure; moreover, examining
Figure 3,
Figure 5,
Figure 6 and
Figure 8 it is evident that, especially for medium-high levels of demand, a minimum can be found. In our test, we adopt a 0.1 step, but the parameter
η can assume any value between 1 (MSA) and 0 (0 excluded), and therefore, other values can be tested in order to find the one that minimises the computing times.
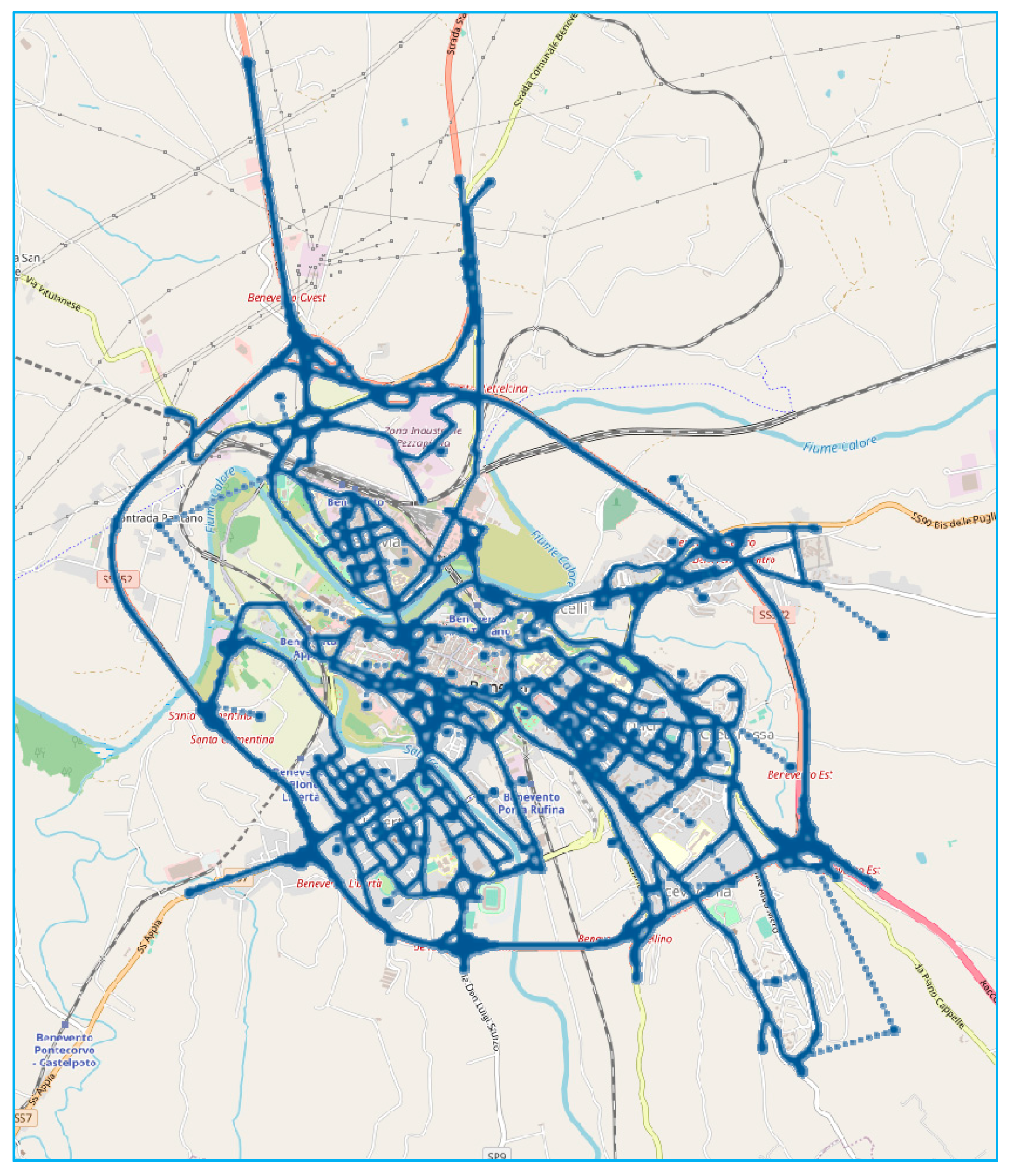
The reduction in computing times can be not important if the assignment procedure is performed only once or a few times: with current computing capabilities, the savings are lower than a minute on the real-scale network. By contrast, if the assignment is a subroutine of the Network Design Problem, that requires the calculation of the equilibrium traffic flows many thousands of times, the reduction in computing time of an assignment is transferred to the computing time of the network design algorithm, allowing as much as several days to be saved in the calculation. In our test on the rural road network, the proposed algorithm is able to save about 44% of computing time, equivalent to about 2.5 h for a single NSA procedure.
Future research will focus on testing other real-scale networks, testing the algorithm on multimodal networks and under the assumption of elastic demand and proposing a similar algorithm for solving the combined assignment-control problem. Moreover, testing the proposed algorithm within other real-scale network design procedures will be the subject of future studies.