Adaptive Trajectory Tracking Safety Control of Air Cushion Vehicle with Unknown Input Effective Parameters
Abstract
1. Introduction
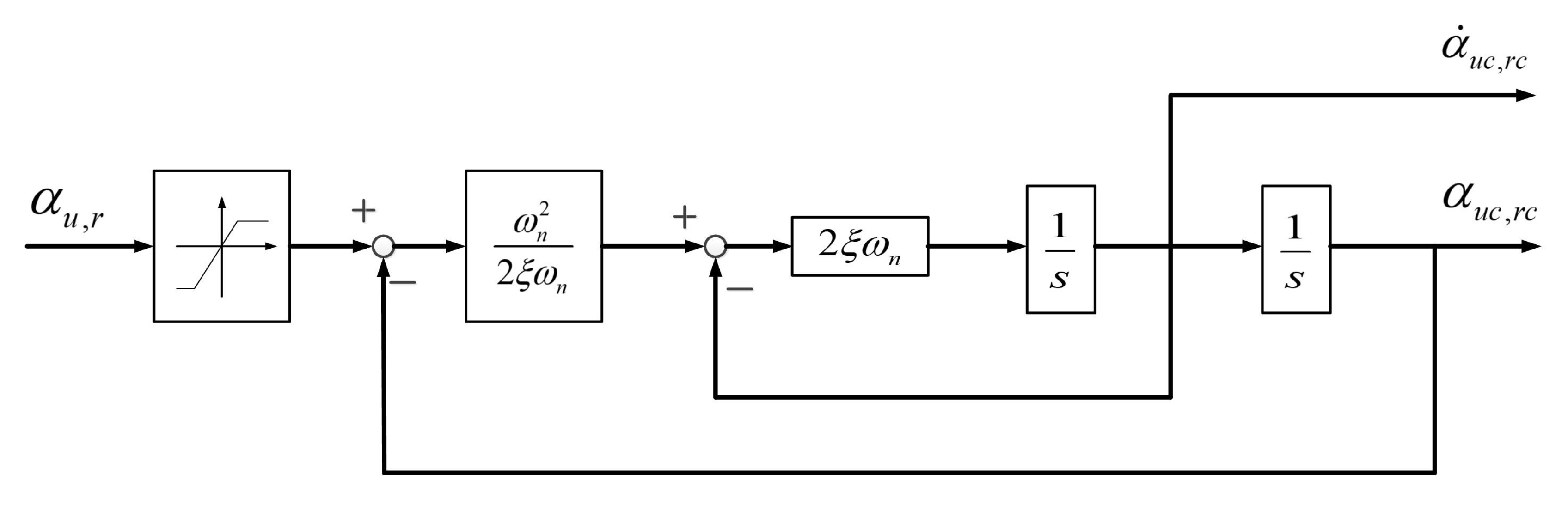
- A four-DOF vector mathematical model of an ACV is proposed to simplify the controller design. Based on the vector model, RBFNN is adopted to provide the estimation of the model uncertainties and external wind disturbance. Command filters and auxiliary systems are integrated with the control law such that the complicated computation of the virtual control derivative can be avoided.
- A Nussbaum function is first introduced into the study on the ACV to solve the unknown nonlinear relationships between the actuator’s input and output.
- The yaw rate error constraint of the ACV is approached by introducing a BLF in combination with an adaptive Nussbaum function to prevent the tail swing phenomenon caused by the large yaw rate.
- The stability analysis shows that the proposed control algorithm can accurately track the set trajectory and ensure that the yaw rate error and the roll angle are within a safe range. All the error signals of the whole closed-loop control system can converge into a small neighbourhood around zero. The comparative simulation results illustrate the effectiveness and superiority of the proposed trajectory tracking control scheme.
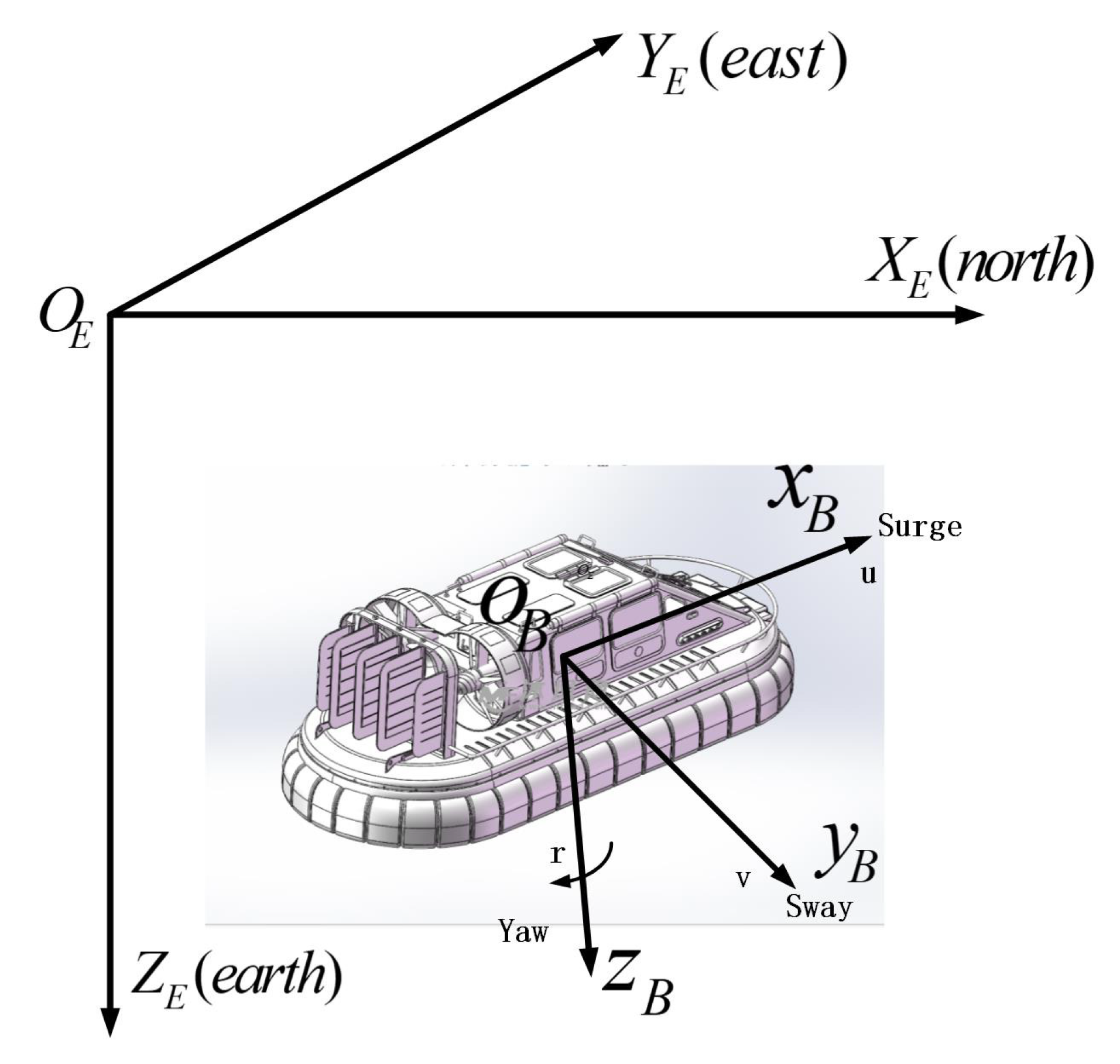
2. System Description and Analysis
2.1. Preliminaries
2.2. ACV Model
2.2.1. Hydrodynamics
2.2.2. Aerodynamics
2.2.3. Air Momentum
2.2.4. Roll Restoring Moment
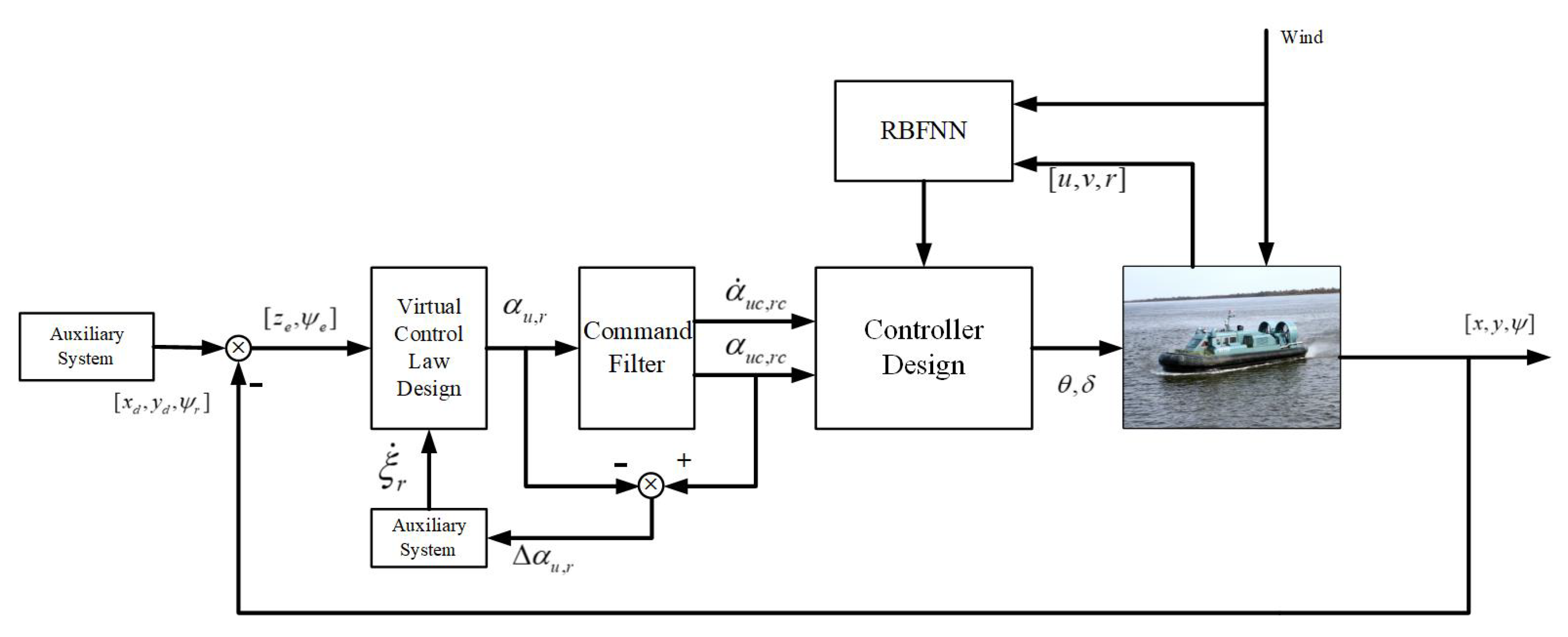
3. Controller Design and Stability Analysis
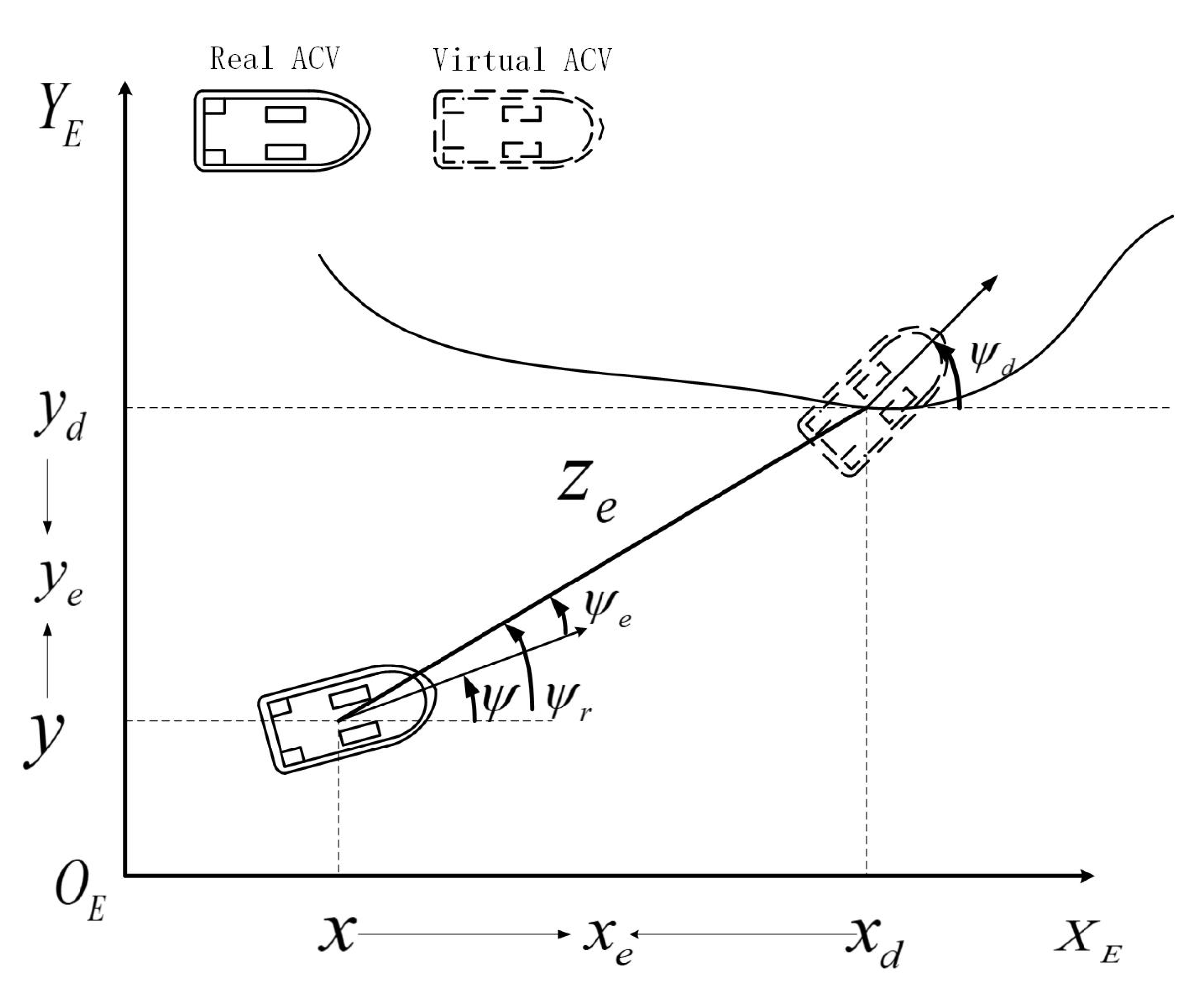
3.1. Position Controller Design
3.2. Yaw Controller Design
3.3. Stability Analysis
- The tracking errors of the ACV can converge to small neighbourhoods around zero.
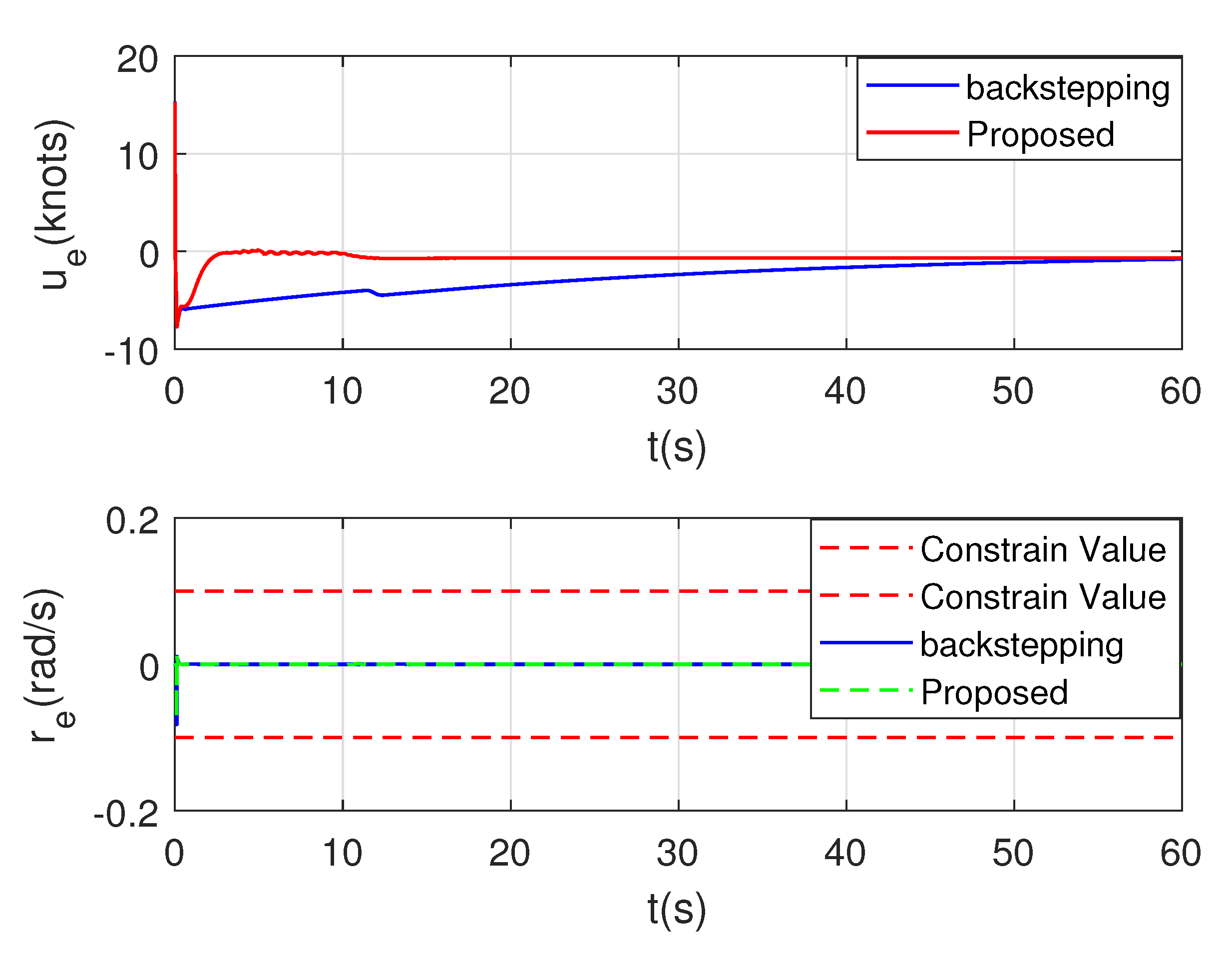
- The yaw rate r is constrained tofor.
- All the signals in the closed-loop system are bounded.
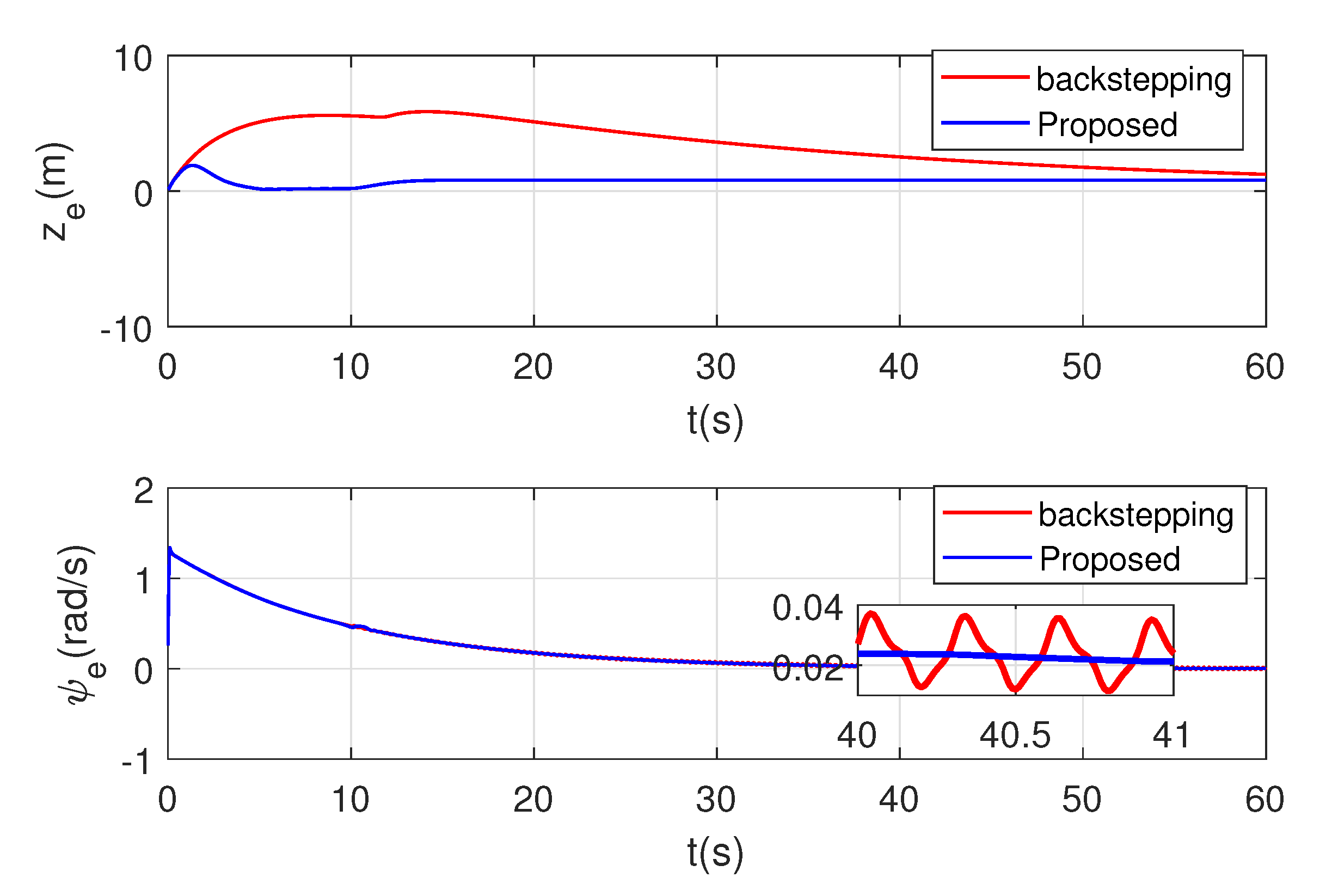
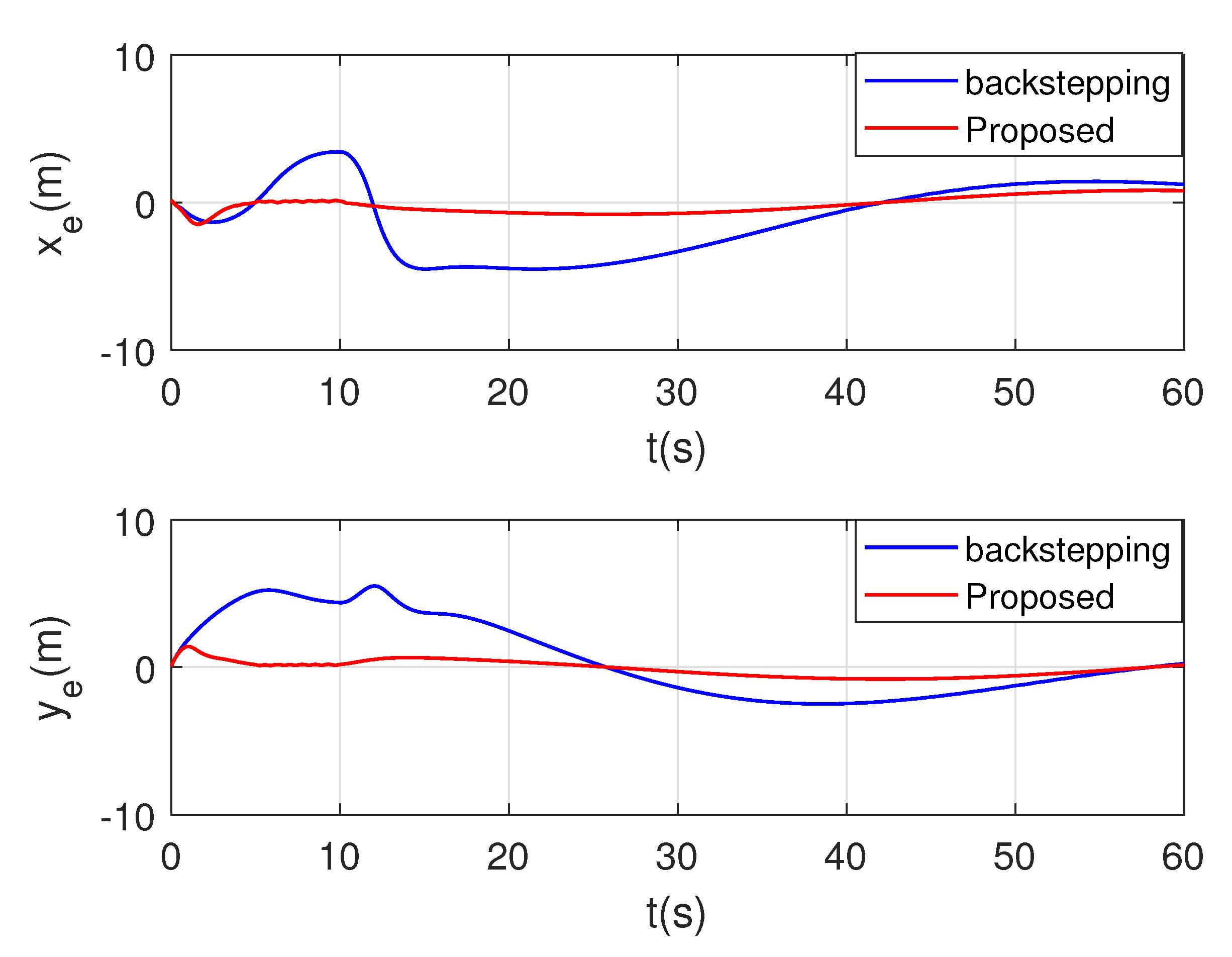
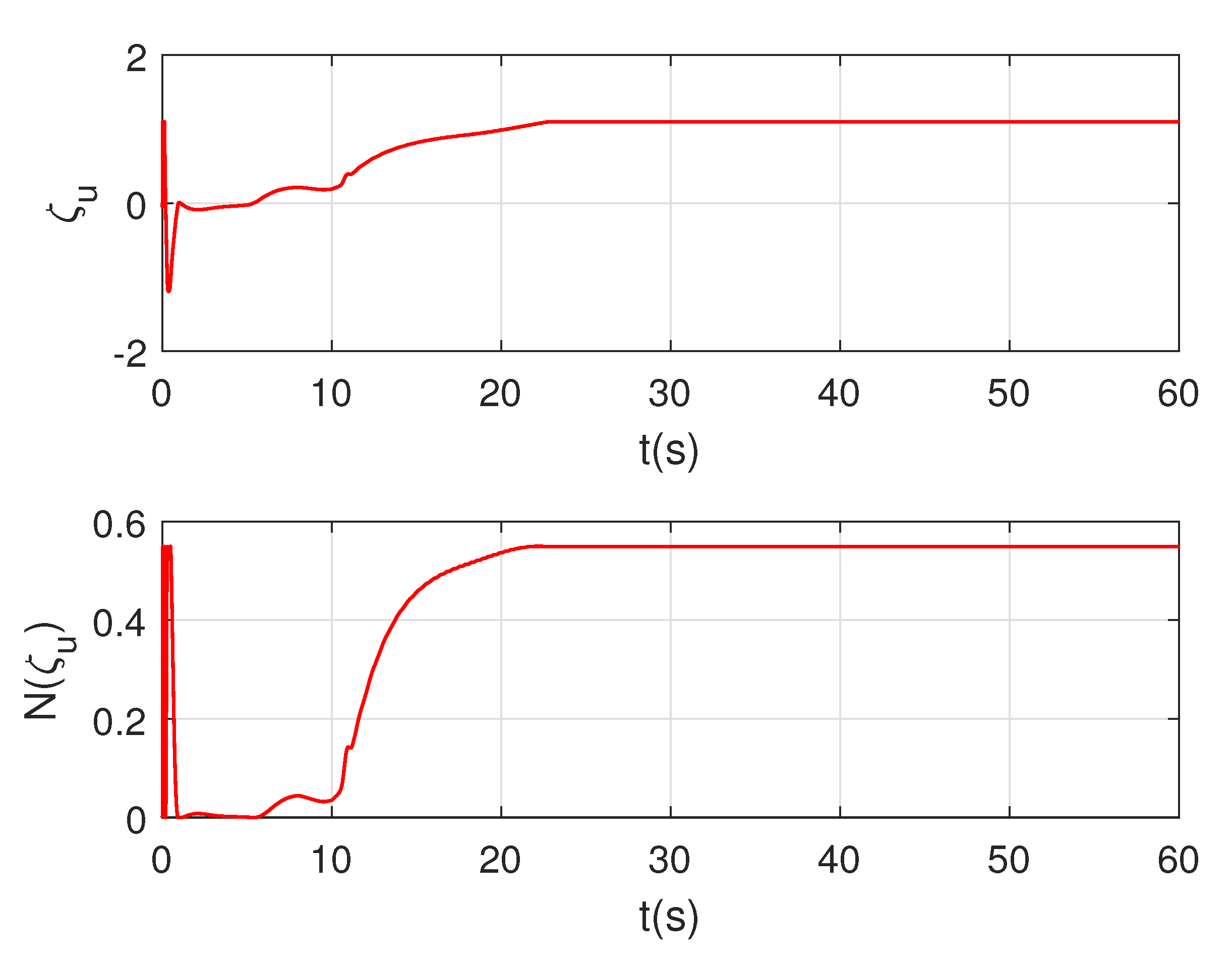
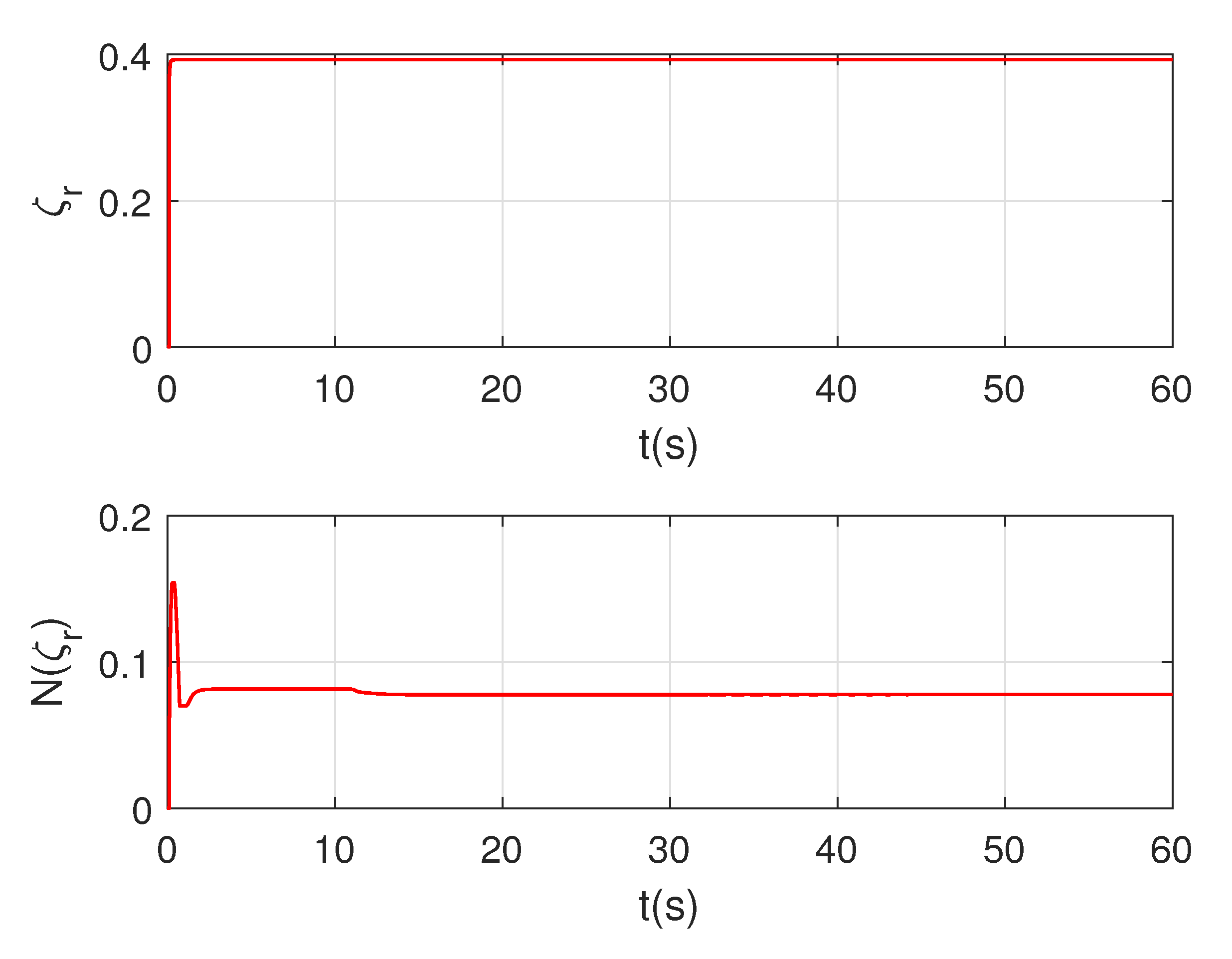
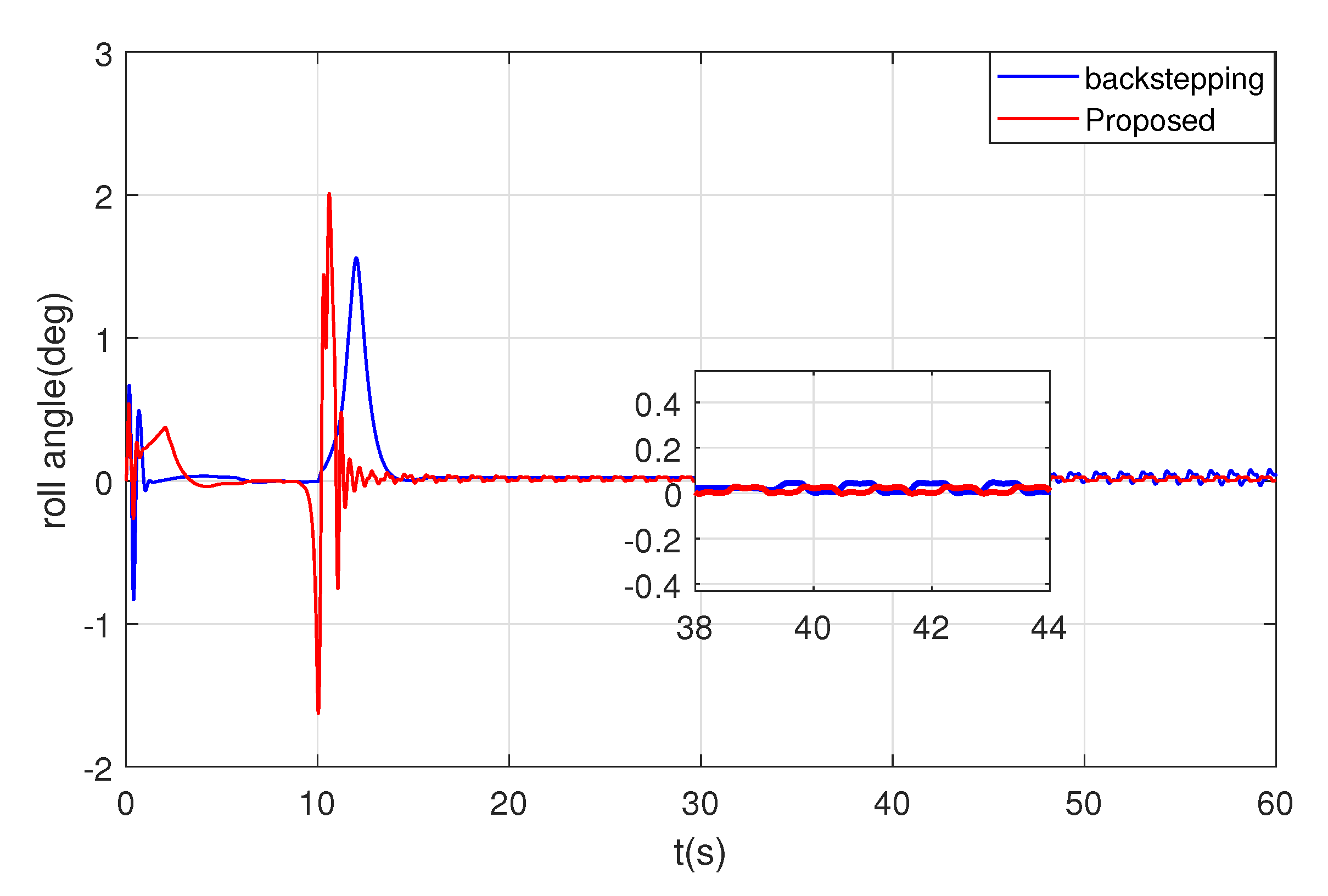
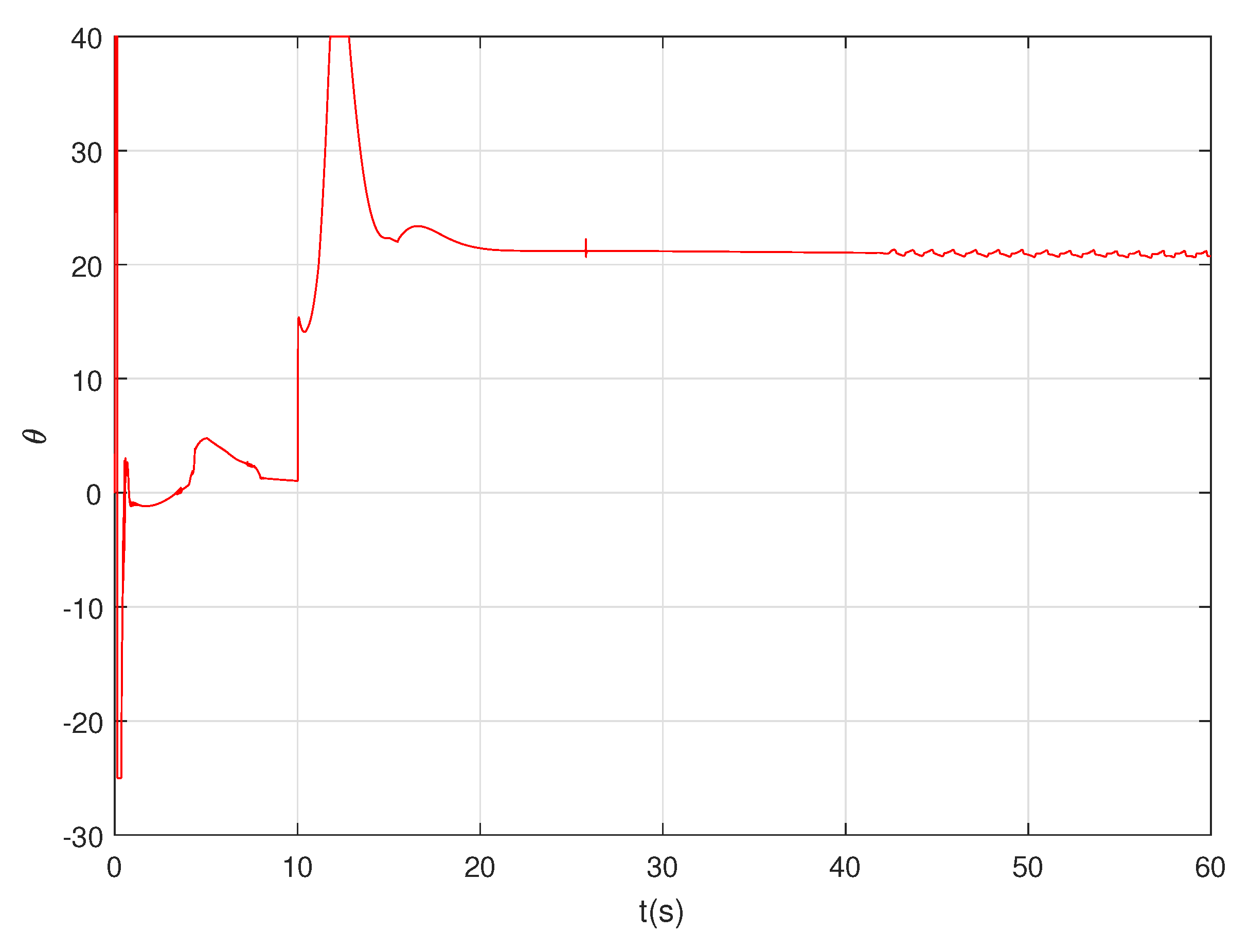
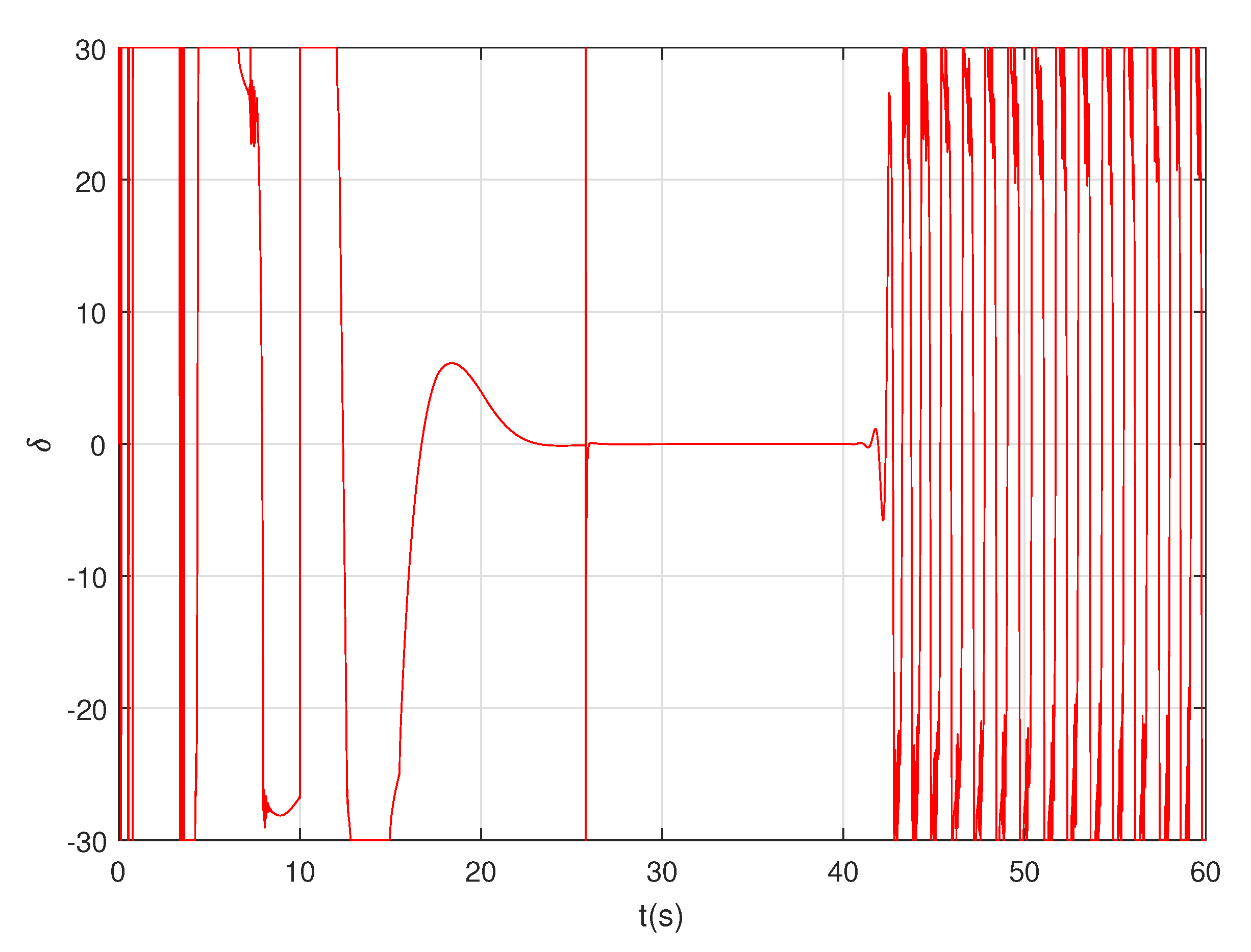
4. Simulations
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ACV | air Cushion vehicle |
| DOF | degrees of freedom |
| RBFNN | radial basis function neural network |
| BLF | barrier Lyapunov function |
References
- Yifan, Y.; Jun, L.; Zhou, X.L. A review of research on the control of fully-lift hovercraft. Ship Sci. Technol. 2012, 34, 11–15. [Google Scholar]
- Pagotti, A.P.; Rafikova, E.; Rafikov, M. SDRE Trajectory Tracking Control for a Hovercraft Autonomous Vehicle: Selected Papers of the XVII International Symposium on Dynamic Problems of Mechanics. In Proceedings of DINAME 2017; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Yun, L.; Bliault, A. Theory Design of Air Cushion Craft; Butterworth-Heinemann: Oxford, UK, 2000. [Google Scholar]
- Shojaei, K. Neural adaptive robust control of underactuated marine surface vehicles with input saturation. Appl. Ocean Res. 2015, 53, 267–278. [Google Scholar] [CrossRef]
- Aranda, J.; Chaos, D.; Dormido-Canto, S.; Muñoz, R.; Diaz, J.M. Benchmark control problems for a non-linear underactuated hovercraft:a simulation laboratory for control testing. IFAC Proc. Vol. 2006, 39, 463–468. [Google Scholar] [CrossRef]
- Rigatos, G.G.; Raffo, G.V. Input-output linearizing control of the underactuated hovercraft using the derivative-free nonlinear Kalman filter. Unmanned Syst. 2015, 39, 127–142. [Google Scholar] [CrossRef]
- Morales, R.; Sira-Ramírez, H.; Somolinos, J.A. Linear active disturbance rejection control of the hovercraft vessel model. Ocean Eng. 2015, 39, 100–108. [Google Scholar] [CrossRef]
- Zhao, J.; Pang, J. Trajectory control of underactuated hovercraft. In Proceedings of the IEEE 2010 8th World Congress on Intelligent Control and Automation, Jinan, China, 7–9 July 2010; pp. 3904–3907. [Google Scholar]
- Aranda, J.A.; García, D.C.; Canto, S.D.; Mansilla, R.M.; Martínez, J.M.D. A control for tracking and stabilization o faunderactuated non-linear RC hovercraft. In Proceedings of the 7th IFAC Conference Manoeuvring Control Marine Crafts (MCM), Lisbon, Portugal, 20–22 September 2006. [Google Scholar]
- Sira-Ramirez, H. Dynamic second-order sliding mode control of the hovercraft vessel. IEEE Trans. Control Syst. Technol. 2002, 10, 860–865. [Google Scholar] [CrossRef]
- Hua, F. Analysis and Consideration on Safety of All-Lift Hovercraft; SHIP & BOAT: Shanghai, China, 2008. [Google Scholar]
- Fu, M.Y.; Gao, S. Human-Centered Automatic Tracking System for Underactuated Hovercraft Based on Adaptive Chattering-Free Full-Order Terminal Sliding Mode Control. IEEE Access 2018, 6, 37883–37892. [Google Scholar] [CrossRef]
- Fu, M.Y.; Gao, S. Design of driver assistance system for air cushion vehicle with uncertainty based on model knowledge neural network. Ocean. Eng. 2019, 172, 296–307. [Google Scholar] [CrossRef]
- Bechlioulis, C.P.; Karras, G.C.; Heshmati-Alamdari, S.; Kyriakopoulos, K.J. Trajectory Tracking With Prescribed Performance for Underactuated Underwater Vehicles Under Model Uncertainties and External Disturbances. IEEE Trans. Control. Syst. Technol. 2017, 25, 429–440. [Google Scholar] [CrossRef]
- Garcia, G.; Keshmiri, S. Nonlinear Model Predictive Controller for Navigation, Guidance and Control of a Fixed-Wing UAV. In Proceedings of the Aiaa Guidance, Navigation, &Control Conference, Portland, OR, USA, 8–11 August 2013. [Google Scholar]
- He, W.; Yin, Z.; Sun, C. Adaptive Neural Network Control of a Marine Vessel With Constraints Using the Asymmetric Barrier Lyapunov Function. IEEE Trans. Cybern. 2017, 47, 1641–1651. [Google Scholar] [CrossRef]
- Kogiso, K.; Hirata, K. Reference Governor for Constrained Systems with Time-Varying References; North-Holland Publishing Co.: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Herrmann, G.; Turner, M.C.; Postlethwaite, I. A robust override scheme enforcing strict output constraints for a class of strictly proper systems. IFAC Proc. Vol. 2005, 38, 49–54. [Google Scholar] [CrossRef]
- Hatanaka, T.; Takaba, K. Computations of probabilistic output admissible set for uncertain constrained systems. Automatica 2008, 44, 479–487. [Google Scholar] [CrossRef]
- Liu, Z.; Geng, C.; Zhang, J. Model predictive controller design with disturbance observer for path following of unmanned surface vessel. In Proceedings of the IEEE International Conference on Mechatronics & Automation, Takamatsu, Japan, 6–9 August 2017. [Google Scholar]
- Kostarigka, A.K.; Rovithakis, G.A. Prescribed Performance Output Feedback/Observer-Free Robust Adaptive Control of Uncertain Systems Using Neural Networks. IEEE Trans. Syst. Man Cybern. Part Cybern. Publ. IEEE Syst. Man Cybern. Soc. 2011, 41, 1483–1494. [Google Scholar] [CrossRef] [PubMed]
- Kostarigka, A.K.; Rovithakis, G.A. Adaptive dynamic output feedback neural network control of uncertain MIMO nonlinear systems with prescribed performance. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 138–149. [Google Scholar] [CrossRef]
- Yin, Z.; He, W.; Yang, C. Tracking control of a marine surface vessel with full-state constraints. Int. J. Syst. Sci. 2017, 48, 535–546. [Google Scholar] [CrossRef]
- Zheng, Z.; Huang, Y.; Xie, L.; Zhu, B. Adaptive Trajectory Tracking Control of a Fully Actuated Surface Vessel With Asymmetrically Constrained Input and Output. IEEE Trans. Control Syst. Technol. 2017, 26, 1851–1859. [Google Scholar] [CrossRef]
- Zheng, Z.; Feroskhan, M. Path Following of a Surface Vessel With Prescribed Performance in the Presence of Input Saturation and External Disturbances. IEEE/ASME Trans. Mechatron. 2017, 22, 2564–2575. [Google Scholar] [CrossRef]
- Zhang, G.Q.; Huang, C.F.; Wu, X.X.; Zhang, X.K. Adaptive finite-time control of ship dynamic positioning considering uncertain gain of servo system. Acta Autom. Sin. 2018, 44, 1907–1912. [Google Scholar]
- Morse, A.S. Recent problems in parameter adaptive control. Model. Autom. 1982, 3, 733–740. [Google Scholar]
- Chen, C.; Liu, Z.; Xie, K.; Liu, Y.; Zhang, Y.; Chen, C.P. Adaptive Fuzzy Asymptotic Control of MIMO Systems with Unknown Input Coefficients Via a Robust Nussbaum Gain based Approach. IEEE Trans. Fuzzy Syst. 2016, 25, 1252–1263. [Google Scholar] [CrossRef]
- Zhang, J.; Mu, X.W. Nussbaum function and its application in system stabilization. Math. Pract. Theory 2017, 20, 239–245. [Google Scholar]
- Chen, C.; Liu, Z.; Zhang, Y.; Chen, C.P.; Xie, S.L. Adaptive control of MIMO mechanical systems with unknown actuator nonlinearities based on the Nussbaum gain approach. IEEE/CAA J. Autom. Sin. 2016. [Google Scholar] [CrossRef]
- Wang, D.; Fu, M.; Ge, S.S.; Li, D. Velocity Free Platoon Formation Control for Unmanned Surface Vehicles with Output Constraints and Model Uncertainties. Appl. Sci. 2020, 10, 1118. [Google Scholar] [CrossRef]
- Fossen, T.I.; Strand, J.P. Passive nonlinear observer design for ships using Lyapunov methods: Full-scale experiments with a supply vessel. Automatica 1999, 35, 3–16. [Google Scholar] [CrossRef]
- Krstic, M.; Kokotovic, P.V.; Kanellakopoulos, I. Nonlinear and Adaptive Control Design; Wiley: Hoboken, NJ, USA, 1995. [Google Scholar]
- Sepulchre, R.; Jankovic, M.; Kokotovic, P.V. Constructive Nonlinear Control; Springer: New York, NY, USA, 2012. [Google Scholar]

| Variable | Value | Variable | Value |
|---|---|---|---|
| 40,000 | |||
| 45 | |||
| 93 | 260 | ||
| 140.8 | 212 | ||
| 65 | 8.9 | ||
| 2.4 | 23.6 | ||
| 1 | 5.9 | ||
| 5 | 45 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, M.; Dong, L.; Xu, Y.; Wang, C. Adaptive Trajectory Tracking Safety Control of Air Cushion Vehicle with Unknown Input Effective Parameters. Appl. Sci. 2020, 10, 5695. https://doi.org/10.3390/app10165695
Fu M, Dong L, Xu Y, Wang C. Adaptive Trajectory Tracking Safety Control of Air Cushion Vehicle with Unknown Input Effective Parameters. Applied Sciences. 2020; 10(16):5695. https://doi.org/10.3390/app10165695
Chicago/Turabian StyleFu, Mingyu, Lijing Dong, Yujie Xu, and Chenglong Wang. 2020. "Adaptive Trajectory Tracking Safety Control of Air Cushion Vehicle with Unknown Input Effective Parameters" Applied Sciences 10, no. 16: 5695. https://doi.org/10.3390/app10165695
APA StyleFu, M., Dong, L., Xu, Y., & Wang, C. (2020). Adaptive Trajectory Tracking Safety Control of Air Cushion Vehicle with Unknown Input Effective Parameters. Applied Sciences, 10(16), 5695. https://doi.org/10.3390/app10165695





