Abstract
This paper solved the problem of transmitting quantum bits (qubits) in a multi-hop and bidirectional way. Considering that the Greenberger–Horne–Zeilinger (GHZ) states are less prone to the decoherence effects caused by the surrounding environment, we proposed a bidirectional quantum communication scheme based on quantum teleportation and the composite GHZ-GHZ states. On a multi-hop quantum path, different types of GHZ states are previously shared between the adjacent intermediate nodes. To implement qubit transmission, the sender and intermediate nodes perform quantum measurements in parallel, and then send their measurement results and the types of previously shared GHZ states to the receiver independently. Based on the received information, the receiver performs unitary operations on the local particle, thus retrieving the original qubit. Our scheme can avoid information leakage at the intermediate nodes and can reduce the end-to-end communication delay, in contrast to the hop-by-hop qubit transmission scheme.
1. Introduction
Quantum teleportation is a process of transmitting unknown quantum states between two distant nodes based on entanglement and some auxiliary classical communication. Since Bennett proposed the concept of quantum teleportation [1], where Einstein–Podolsky–Rosen (EPR) pairs are used as an entanglement channel, quantum teleportation has been paid extensive attention in recent years. Some quantum teleportation schemes have been proposed by using Greenberger–Horne–Zeilinger (GHZ) states, mixed W states, and other entangled states as quantum channels [2,3,4,5].
To realize qubit transmission in a quantum communication network, Wang et al. [6] proposed the idea of quantum wireless multi-hop communication based on arbitrary EPR pairs and teleportation, where simultaneous entanglement swapping is utilized to reduce the end-to-end quantum communication delay. To overcome the decoherence effects caused by the surrounding environments and take advantage of partially entangled EPR pairs efficiently, Yu et al. [7] proposed a wireless quantum communication scheme. However, hop-by-hop qubit transmission introduces great communication delay and information leakage at the intermediate nodes. After that, Chen et al. [8] proposed a wide area quantum communication network via partially entangled EPR states, where sequential entanglement swapping is exploited. In this scheme, the security of qubit transmission is improved, while end-to-end quantum communication delay is not reduced to a great extent. Compared to two-particle entanglement, multi-particle entangled states are equipped with better entanglement properties, and are more powerful in revealing the nonlocality of quantum physics [9,10]. Zhan and Zou et al. proposed multi-hop quantum teleportation schemes based on W states and GHZ–Bell channels [11,12]. Considering that duplex quantum communication between two arbitrary nodes is crucial to the future quantum networks, Li et al. [13] first proposed the bidirectional controlled quantum transmission scheme using a five-qubit entangled state. Since then, some schemes for bidirectional quantum communication have been proposed [14,15,16,17,18,19,20,21].
To address all the issues mentioned above, such as quantum communication delay, information leakage, and duplex quantum communication, in this paper we investigate multi-hop bidirectional quantum communication based on GHZ states, considering that GHZ states are less prone to the decoherence effects caused by the surrounding environment [22]. The main contribution of this work is as follows.
We propose a scheme for multi-hop bidirectional quantum communication using the composite GHZ-GHZ channel, where all the nodes perform quantum measurements in parallel. After that, they send the measurement results and the types of previously shared GHZ-GHZ states to the sender and receiver through the classical channel independently. Based on the received information, the sender and receiver perform appropriate unitary operations to recover the original qubit. Our scheme has a shorter delay for the end-to-end quantum communication and avoids information leakage at the intermediate nodes.
The rest of this paper is organized as follows. In Section 2, one-hop bidirectional quantum communication based on a GHZ-GHZ entangled channel is discussed. In Section 3, we investigate two-hop directional quantum communication. In Section 4, a scheme for multi-hop bidirectional quantum communication is proposed. Finally, some discussions and conclusions are given in Section 5.
2. One-Hop Bidirectional Quantum Communication
In this section, we investigate one-hop bidirectional quantum communication through the composite GHZ-GHZ states. Eight types of GHZ states used in quantum communication are given by
These GHZ states can be transformed into each other through unitary operations, such as
where , are Pauli matrices, and is the identity matrix.
Assume that Alice intends to transmit an arbitrary qubit to Bob, while Bob intends to transmit to Alice at the same time, and are given by
where , , and are complex probability amplitudes satisfying , .
Without loss of generality, Alice and Bob previously share a six-particle GHZ-GHZ state, given by
where the particles , and belong to Alice and particles , and belong to Bob, as shown in Figure 1.
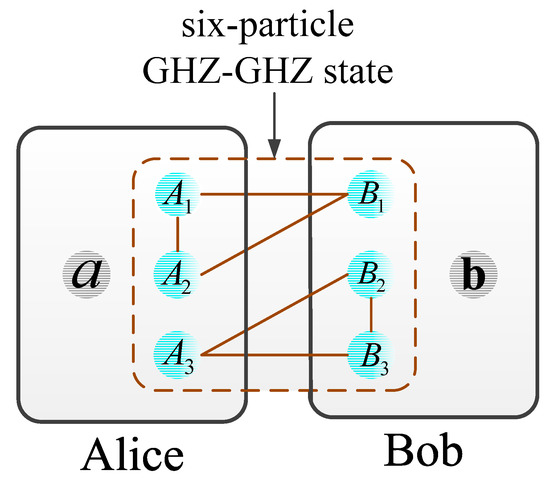
Figure 1.
The composite Greenberger–Horne–Zeilinger (GHZ)-GHZ state previously shared between Alice and Bob.
The state of the initial eight-particle system is given by
As shown in Figure 2, to achieve bidirectional qubit transmission, Alice and Bob perform Control-NOT (CNOT) gates and Hadamard gates in parallel, and the state of the entire system becomes
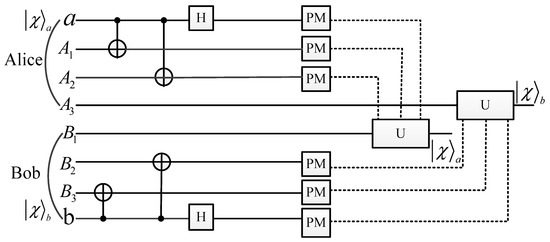
Figure 2.
Quantum circuit for one-hop bidirectional quantum communication, where the dashed lines represent classical channels and the solid lines represent quantum channels.
After that, Alice and Bob perform quantum measurements (denoted as PM in Figure 2) on the particles , , and , , under the basis , and then inform each other of their measurement results through classical channel. According to the received measurement results, Alice and Bob perform appropriate unitary operations on the particle and particle to recover the original qubit. For example, when Alice’s measurement result is and Bob’s measurement result is , from Equation (6) we can see that the quantum state of the particles and would be . Alice can retrieve the original qubit by performing the identity operation I on particle and Bob can retrieve the original qubit by performing the Pauli-X operation on particle , respectively. Table 1 lists Alice’s and Bob’s unitary operations corresponding to the received measurement results.

Table 1.
The relations between Alice’s and Bob’s measurement results and unitary operations.
Similarly, when other types of GHZ-GHZ states are previously shared between Alice and Bob, the unitary operations corresponding to Alice’s and Bob’s measurement results are listed in Table 2. The first row shows the GHZ-GHZ states shared between Alice and Bob, while the first column shows Alice’s and Bob’s measurement results.

Table 2.
The unitary operations to realize one-hop bidirectional quantum communication.
3. Two-Hop Directional Quantum Communication
Assume that Alice intends to send an arbitrary qubit to Bob; at the same time, Bob intends to send to Alice, where and , while there is no GHZ state shared directly between Alice and Bob. Suppose that Candy previously shared a six-particle GHZ-GHZ state with Alice and Bob, respectively, as shown in Figure 3.
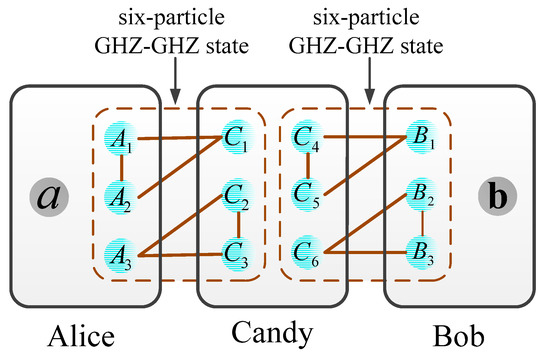
Figure 3.
The composite GHZ-GHZ entanglement channel in a two-hop quantum communication case.
Without loss of generality, assume that was previously shared between Alice and Candy, while was previously shared between Candy and Bob. The state of the initial fourteen-particle system is given by
As shown in Figure 4, to achieve bidirectional two-hop qubit transmission, Alice, Bob, and Candy perform CNOT, Hadamard operations, and quantum measurements in parallel. After that, the measurement results of Alice and Candy and the type of the composite GHZ-GHZ channel between Alice and Candy are transmitted to Bob. Similarly, the measurement results of Bob and Candy and the type of the composite GHZ-GHZ channel between Bob and Candy are transmitted to Alice. Based on the received information, Alice and Bob perform appropriate unitary operations on the particles and to recover the original qubit.
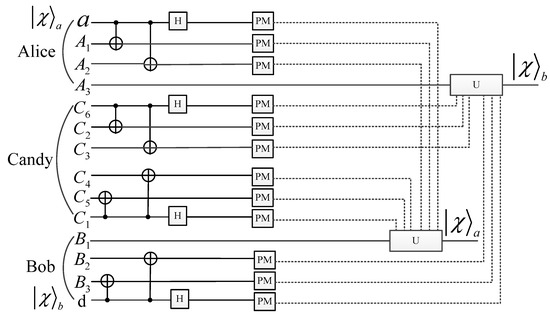
Figure 4.
Quantum circuit for two-hop bidirectional quantum communication.
For example, if Bob receives measurement results and , and Alice receives measurement results and , the quantum state of the particles and would be . Alice can retrieve the original qubit by performing the Pauli-XZ operation on particle , and Bob can retrieve the original qubit by performing the Pauli-Z operation on particle .
If the above two-hop qubit transmission is realized hop-by-hop, after Alice performs CNOT, Hadamard operations, and the projective measurement, the quantum state of Candy’s particle would be when she was informed of Alice’s measurement result of , according to Table 2. After Candy performs CNOT, Hadamard operations, and the projective measurement, the quantum state of Bob’s particle would be when he was informed of Candy’s measurement result of . Similarly, in the other direction, when Bob’s measurement result is , the quantum state of Candy’s particle would be . If Candy’s measurement result is , the quantum state of Alice’s particle would be , which is compatible with Equation (8).
4. Multi-Hop Bidirectional Quantum Communication
In this section, we generalize two-hop bidirectional quantum communication to the multi-hop case.
4.1. N-Hop Bidirectional Quantum Communication
Specifically, in the n-hop case, the entanglement channel between the node and the nodes is shown in Figure 5. Assume that the node intends to transmit an arbitrary qubit to the node , while the node intends to transmit to the node at the same time, where and .
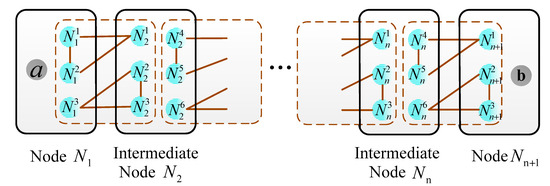
Figure 5.
The composite GHZ-GHZ entanglement channel in the n-hop quantum communication case.
To achieve bidirectional n-hop qubit transmission, each node on the quantum path performs quantum measurements simultaneously. After that, the node and all intermediate nodes send their measurement results together with the types of the composite GHZ-GHZ states shared between themselves and the next-hop nodes to the node through classical channels independently. Similarly, the node and all intermediate nodes send their measurement results together with the types of the GHZ-GHZ states to the node independently. Based on the received information, the node and the node perform appropriate unitary operations locally to recover the original qubit.
According to the analysis in Section 3, the unitary operations of and can be determined in a hop-by-hop manner. We take the qubit transmission from the node to the node as an example. Given that node intends to transmit to the node , after ’s CNOT, Hadamard operations, and quantum projective measurement, the quantum state of ’s particle would be , where is a unitary matrix. After performs CNOT, Hadamard operations, and quantum projective measurement, the quantum state of ’s particle would be . Similarly, after all the intermediate nodes perform CNOT, Hadamard operations, and quantum projective measurements, the quantum state of the node ’s particle would be .
To recover the original qubit locally, the node needs to perform the unitary operation on his particle , given by
where is determined according to Table 2, based on the measurement results of the node and the composite GHZ-GHZ state previously shared between the node and .
Similarly, for the other direction of qubit transmission, the node can perform the unitary operation on its particle to recover the original qubit ,
where is determined according to Table 2, based on the measurement results of the node and the composite GHZ-GHZ state previously shared between the node and .
4.2. Example of Multi-Hop Bidirectional Quantum Communication
An example is presented to better illustrate the whole process of multi-hop bidirectional quantum communication. Assume that two nodes named and intend to transmit two qubits and to each other. We might as well suppose that three intermediate nodes , and are involved in the quantum path ‘’, as shown in Figure 6.

Figure 6.
An example of multi-hop bidirectional quantum communication.
Assume that the composite GHZ-GHZ states , , , and were previously shared on the quantum path. To implement the qubit transmission from to , and all the intermediate nodes perform quantum measurements simultaneously, then they send their measurement results and the type of the composite GHZ-GHZ states previously shared between themselves and the next-hop nodes to the node through classical channels. Assume the node receives a group of measurement results , , , and from , , , respectively; the unitary operation required for recovering the original qubit locally is given by
where , , , and are determined according to Table 2.
When it comes to the qubit transmission from to , and all the intermediate nodes perform quantum measurements simultaneously, then they send their measurement results and the type of the composite GHZ-GHZ state previously shared between themselves and the next-hop node to the node through classical channels. Assume the node receives a group of measurement results , , , and from , , , and respectively; the unitary operation required for recovering the original qubit locally is given by
where , , , and are determined according to Table 2.
5. Discussions and Conclusions
5.1. Discussions
In the process of multi-hop quantum communication, the quantum communication delay is introduced mostly by quantum measurements, unitary operations, and transmission of classical information. Due to the limited decoherence time in the quantum memory and the demand for QOS (Quality of Service), a short delay is expected in quantum communication. Assume that each quantum measurement takes milliseconds, unitary operation takes milliseconds, and one-hop transmission of classic information through classical channel takes milliseconds.
In our scheme, as shown in Figure 7, quantum measurements (CNOT, Hadamard operations, and projective measurements are included) are performed simultaneously, and classical information is sent to the destination node independently. Taking to denote the hop count of the classical information transmitted from the i-th node to the destination node, therefore the total end-to-end quantum communication delay in the n-hop case is given by
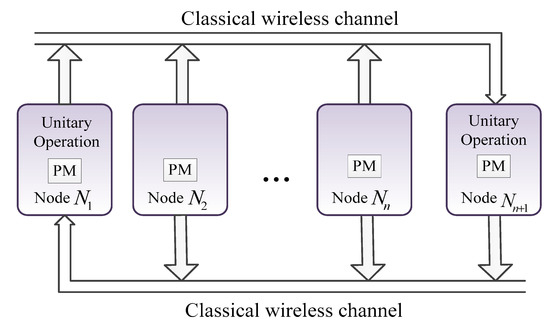
Figure 7.
The proposed scheme in this paper.
For hop-by-hop qubit transmission [7], as shown in Figure 8, the total end-to-end quantum communication delay is given by
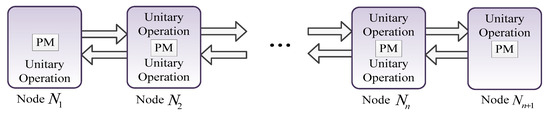
Figure 8.
Hop-by-hop qubit transmission.
Given that , the end-to-end quantum communication delay in our scheme and hop-by-hop qubit transmission scheme is demonstrated by Figure 9.
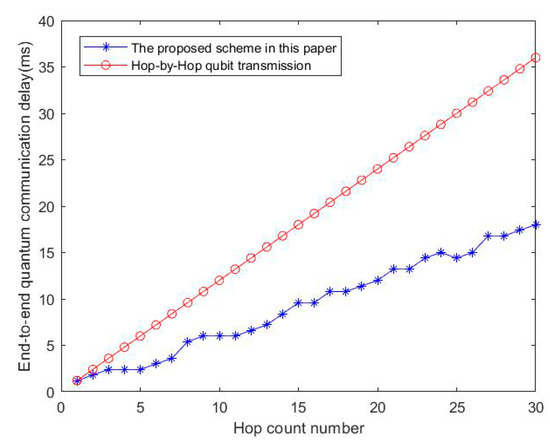
Figure 9.
The comparison of two schemes in terms of communication delay.
From Figure 9, it is obvious that our scheme has a shorter end-to-end quantum communication delay. In a wide-area quantum communication network where the hop count number n is large, our scheme shows obvious advantage in the end-to-end quantum communication delay.
In addition to the shorter quantum communication delay, our scheme shows other notable advantages, such as: (i) Duplex quantum communication is available for two arbitrary nodes compared with other quantum network schemes [6,7,8,11,12]. (ii) The composite GHZ-GHZ states are used as the quantum channel, which is less prone to the decoherence effects caused by the surrounding environment [22]. (iii) Only quantum projective measurements and unitary operations are needed to implement qubit transmission. Auxiliary qubits are not required, in contrast to the bidirectional quantum communication scheme based on GHZ-Bell states [20]. (iv) In our scheme, for an intermediate node, it is not necessary to recover the original qubit locally and then teleport it to its next-hop node. Therefore, information leakage can be avoided compared with the hop-by-hop qubit transmission scheme [7].
5.2. Conclusions
In summary, we propose a bidirectional quantum communication protocol using the composite GHZ-GHZ state as quantum channel. Two arbitrary nodes in a quantum communication network can transmit qubits to each other based on quantum measurements performed in parallel by all the nodes involved. The original qubits can be retrieved locally at the destination site based on the measurement results and the types of GHZ channel. Information leakage is avoided in our scheme, and it has a shorter delay for the end-to-end quantum communication, in contrast to the hop-by-hop qubit transmission scheme.
There are many avenues for future work and extensions. One aspect is the imperfection of quantum channel, which is crucial for the efficiency and fidelity of qubit transmission. Another important aspect is the extension to multi-user quantum communication, which is a realistic scenario for future quantum networks.
Author Contributions
Data curation, S.S. and N.C.; methodology, S.S. and N.C.; supervision, B.Y.; validation, S.S.and N.C.; visualization, B.Y.; writing—original draft, S.S.; writing—review and editing, N.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (Grant No. 61701285).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and einstein-podolsky-rosen channels. Phys. Rev. Lett. 1993, 70, 1895–1899. [Google Scholar] [CrossRef] [PubMed]
- Espoukeh, P.; Pedram, P. Quantum teleportation through noisy channels with multi-qubit GHZ states. Quant. Inf. Process. 2014, 13, 1789–1811. [Google Scholar] [CrossRef]
- Joo, J.; Park, Y.J.; Oh, S.; Kim, J. Quantum teleportation via a W state. New J. Phys. 2003, 5, 136. [Google Scholar] [CrossRef]
- Karlsson, A.; Bourennane, M. Quantum teleportation using three-particle entanglement. Phys. Rev. A 2002, 58, 4394–4400. [Google Scholar] [CrossRef]
- Cao, Z.L.; Song, W. Teleportation of a two-particle entangled state via W class states. Physica A 2005, 347, 177–183. [Google Scholar] [CrossRef]
- Wang, K.; Yu, X.T.; Lu, S.L.; Gong, Y.X. Quantum wireless multihop communication based on arbitrary Bell pairs and teleportation. Phys. Rev. A 2014, 89, 022329. [Google Scholar] [CrossRef]
- Yu, X.T.; Zhang, Z.C.; Xu, J. Distributed wireless quantum communication networks with partially entangled pairs. Chin. Phys. B 2014, 23, 010303. [Google Scholar] [CrossRef]
- Chen, N.; Quan, D.X.; Pei, C.X.; Yang, H. Quantum communication for satellite-to-ground networks with partially entangled states. Chin. Phys. B 2015, 24, 020304. [Google Scholar] [CrossRef][Green Version]
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865–942. [Google Scholar] [CrossRef]
- Tashima, T.; Tame, M.S.; Őzdemir, Ş.K.; Nori, F.; Koashi, M.; Weinfurter, H. Photonic multipartite entanglement conversion using nonlocal operations. Phys. Rev. A 2016, 94, 052309. [Google Scholar] [CrossRef]
- Zhan, H.T.; Yu, X.T.; Xiong, P.Y.; Zhang, Z.C. Multi-hop teleportation based on W state and EPR pairs. Chin. Phys. B 2016, 25, 050305. [Google Scholar] [CrossRef]
- Zou, Z.Z.; Yu, X.T.; Gong, Y.X.; Zhang, Z.C. Multihop teleportation of two-qubit state via the composite GHZ–Bell channel. Phys. Lett. A 2017, 381, 76–81. [Google Scholar] [CrossRef]
- Li, Y.H.; Li, X.L.; Sang, M.H.; Nie, Y.Y.; Wang, Z.S. Bidirectional controlled quantum teleportation and secure direct communication using five-qubit entangled state. Quant. Inf. Process. 2013, 12, 3835–3844. [Google Scholar] [CrossRef]
- Hassanpour, S.; Houshmand, M. Bidirectional teleportation of a pure EPR state by using GHZ states. Quant. Inf. Process. 2016, 15, 905–912. [Google Scholar] [CrossRef]
- Duan, Y.J.; Zha, X.W. Bidirectional quantum controlled teleportation via a six-qubit entangled state. Int. J. Theor. Phys. 2014, 53, 3780–3786. [Google Scholar] [CrossRef]
- Zhang, D.; Zha, X.W.; Li, W.; Yu, Y. Bidirectional and asymmetric quantum controlled teleportation via maximally eight-qubit entangled state. Quant. Inf. Process. 2015, 14, 3835–3844. [Google Scholar] [CrossRef]
- Sang, M.H. Bidirectional quantum teleportation by using five-qubit cluster state. Int. J. Theor. Phys. 2016, 55, 1333–1335. [Google Scholar] [CrossRef]
- Fang, S.H.; Jiang, M. A novel scheme for bidirectional and hybrid quantum information transmission via a seven-qubit state. Int. J. Theor. Phys. 2017, 57, 523–532. [Google Scholar] [CrossRef]
- Fang, S.H.; Jiang, M. Bidirectional and asymmetric controlled quantum information transmission via five-qubit brown state. Int. J. Theor. Phys. 2017, 56, 1530–1536. [Google Scholar] [CrossRef]
- Cai, R.; Yu, X.T.; Zhang, Z.C. Bidirectional teleportation protocol in quantum wireless multi-hop network. Int. J. Theor. Phys. 2018, 57, 1723–1732. [Google Scholar] [CrossRef]
- Zhou, R.G.; Xu, R.; Lan, H. Bidirectional quantum teleportation by using six-qubit cluster state. IEEE Access 2019, 7, 44269–44275. [Google Scholar] [CrossRef]
- Saha, D.; Panigrahi, P.K. N-qubit quantum teleportation, information splitting and superdense coding through the composite GHZ–Bell channel. Quant. Inf. Process. 2011, 11, 615–628. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).