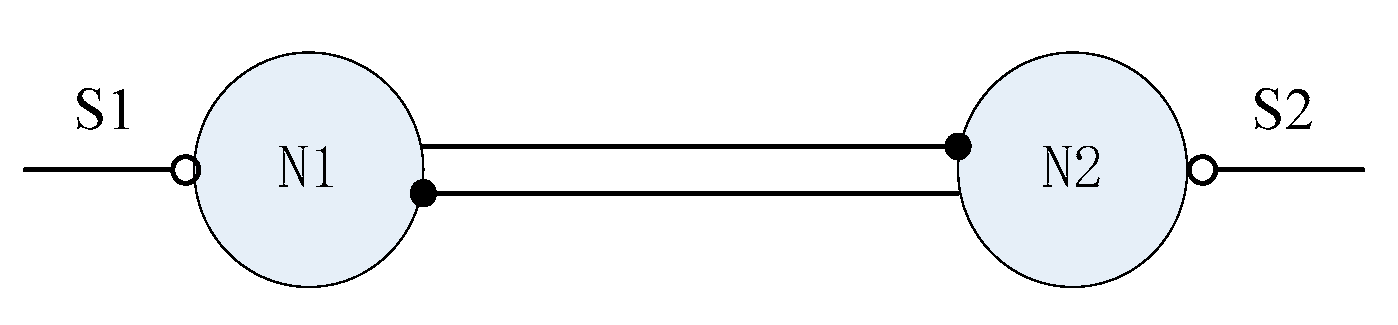1. Introduction
Compared with traditional control methods, Central Pattern Generator (CPG) network control has been widely used for the motion control of bionic robots because it can significantly reduce the dimension of control variables without losing the complexity of its output motion mode; the method also has some other advantages [
1,
2,
3]. However, the study of CPG control network to date has been polarized: one direction has focused on the control function [
4,
5,
6] and ignored the biology rationality. In this direction, a control network is designed only for certain fixed situations, which leads to the poor functional adaptability of the control network. Once there are new control requirements, it is difficult for the control network to be developed into a new, qualified one according to the previous research; instead, it has to be researched again from the basic link. Especially when applied to the motion control of a bionic robot, the above-mentioned CPG control network will have the following disadvantages: with excessive prior knowledge and excessive factors given by humans in each link of the control system, which includes the design of the CPG network, the setting method of network parameters and the establishment of the neuron model in the control network, the control function of the CPG network has lower complexity, worse adaptability and worse inheritance capabilities in future research.
Another direction has focused on biological rationality, but not the function of CPG control, which means that the control network is only similar to a real neural network in form but of no practical use [
7,
8,
9]. Dehmamy et al. [
10] modeled axon growth with driven diffusion. Their simulation showed that with background potential derived from the concentration guiders, even coupled random walkers can generate realistic paths for axons. Marinov et al. [
11] proposed an ad-hoc growth model built upon the diffusion principle to reproduce the shape of Micro-Tissue Engineered Neural Networks (Micro-TENNs). The proposed model imposed various rules for individual neuronal growth to a 3D diffusion equation. Fard et al. [
12] proposed a generative growth model to investigate growth rules for axonal branching patterns in cat area 17. The model achieves better statistical accuracy both locally and globally than the commonly used Galton–Watson model. Gafarov et al. [
13] proposed a closed-loop growth model in which neural activity affects neurite outgrowth in an interactive way. Experiments showed that the model can be potentially used to form large-scale neural networks by self-organization. However, it is very difficult to study how the scattered neurons in different parts of the growth region form the whole network through interactive behaviors with biological methods, because the growth environment of cells is complex, and so it is difficult to precisely control their growth conditions to verify the specific growth mechanism. Therefore, the study of the growth process of a neural network by numerical simulation is very effective. In a simulation environment, researchers can set strict growth conditions and analyze the growth result of the network in a variety of ways and then compare it with a real biological neural network to verify the validity of the designed model [
9,
14,
15,
16].
However, the numerical simulation of the growth of a biological neural network has often been unable to simulate the control function of the network, and it can only compare the simulation model with the real biological network in terms of morphology and statistics. At the same time, in the control based on a neural network, it is precisely the complexity of the formation process of the biological neural network and the simplifications and assumptions made for the simulation model that make the network control model unrealistic and not universally applicable [
17]. Therefore, it is necessary to combine the growth process with the control function in the control of bionic robots based on the CPG network to allow the two to develop in a coordinated way in the long term.
Therefore, we propose some physical characteristics (including axon resistance, capacitance, length and diameter, etc.) that can determine the corresponding parameters of the control model to combine the growth process and the function of the CPG control network. By coordinating the two, we aim to realize the control function of the CPG network under the condition of biological reality as far as possible. In this way, the complexity of the developed control model will be closer to that of a biological neural network, and the control network will have more control functions.
2. Establishment of Self-Growing Model of Neurons
In the formation process of a neural network, the position of each neuron is fixed, axons and dendrites grow from the neuron, and the axon of the former neuron and the dendrite of the latter neuron form a synaptic contact and finally realize the connection of the whole network. Studies have shown that, with the continuous elongation and swerving of the axon, the growth of the tail end of the neuron will not change the shape of the other part [
9]. Therefore, the process of growing and eventually forming synaptic connections with another neuron in the neuron model can be simplified into the following model:
where
k is the number of neurons in the gravitational field,
dj is the distance from the growth cone to the
jth neuron and
is the direction vector of gravitation on the growth cone generated by the
jth neuron.
In Equation (1), the growth cone can be regarded as a particle with a mass of
m. Regard the neuron as a sphere with a mass
M concentrated in the center; the distribution range of dendrites is understood as a sphere with radius
r because the dendrites are numerous and dense. The guiding effect of the chemical molecules on the growth cone can be equivalent to the gravitational effect on particle
m in the gravitational field generated by mass
M, and the motion trajectory of the particle in the gravitational field can be regarded as the axon. The position of growth cone particle in the gravitational field is
Pi(
xi,
yi,
zi) at a certain time, with a growth rate of
Vi(
vxi,
vyi,
vzi), and the gravitation on the growth cone can be determined from Newton’s law of gravitation. Thus, the acceleration is
After a short period of time ∆
t (∆
t is defined as 0.01 s in this paper), the displacement of the growth cone is
Thus, the new position
Pi+1(
xi+1,
yi+1,
zi+1) of the growth cone is
and the new growth rate
Vi+1 (
vxi+1,
vyi+1,
vzi+1) is
Pi+1(
xi+1,
yi+1,
zi+1) and
Vi+1 (
vxi+1,
vyi+1,
vzi+1) can be used for the next iteration. In this way, the continuous growth process of axons is discretized into a programmable iterative process.
Although it is reasonable to use the gravitational field model to describe the chemotaxis of growth cones, the growth of the model’s axon is quite different from that in the actual situation. Experiments show that the overall deflection of the axon does not become more obvious as the concentration gradient increases gradually, because the axon grows faster on the side of the inverse gradient than the side along the gradient (growth rate regulation), which counteracts the chemotaxis. The results show that when the concentration gradient is large, the chemotactic deflection plays a leading role [
8]. In addition, the guiding effect of chemical factors on the growth cone is either attraction or repulsion, but we only consider the case of attraction when modeling, because the mathematical model of the repulsion case is the same as that of the attraction case except with the opposite direction of force.
In fact, the growth direction of the growth cone depends on many intracellular and extracellular signals, which may lead to large fluctuations in the growth direction [
9]. For example, the noise gradient in the chemoattractant orientation perception stage mentioned in [
18,
19] is one of the factors making the deflection direction of the growth cone uncertain when proceeding. In order to describe the uncertain component of the deflection direction of the growth cone, many studies on the mathematical modeling of the axon growing process introduce a random motion component based on the deterministic motion generated by gravity [
20,
21], as shown in
Figure 1.
In
Figure 1,
Pi is the position of the growth cone after the
i-1th growing process.
Pi+1 is the position of the growth cone after the
ith growing process without the effect of a random motion component. ∆
xi, ∆
yi and ∆
zi are the projected length of the
ith growth length of the growth cone on the
x,
y, and
z axes, and
is the real position of the growth cone after the
ith growing process under the effect of random motion component.
As can be seen from
Figure 1, we can calculate the angle between the
ith growth segment and the coordinate axis, (
θxi,
θyi,
θzi) using the following formula:
Furthermore, we add a random motion component to this growing process:
where ∆
θx, ∆
θy and ∆
θz meet uniform distribution in the interval (−
cδ,
cδ).
δ > 0, which ensures that the random motions lead to the largest deflection angle,
c ∈ (0, 1) implies the intensity of random motion, and (
,
,
) is the real deflection angle of this growing process considering the random motion. Then, we can calculate the real displacement of the growth cone in this process, (∆
, ∆
, ∆
), using the following formula:
where
li is the length of the axon segment of the
ith growing process; the random motion only changes the deflection of each growing process, but not the step size. Finally, we calculate the real position of the growth cone after the
ith growing process,
(
,
,
), using the following formula:
Then, we use (, , ) and Vi+1 (vxi+1, vyi+1, vzi+1) calculated from Equations (2) to (5) for the next iteration.
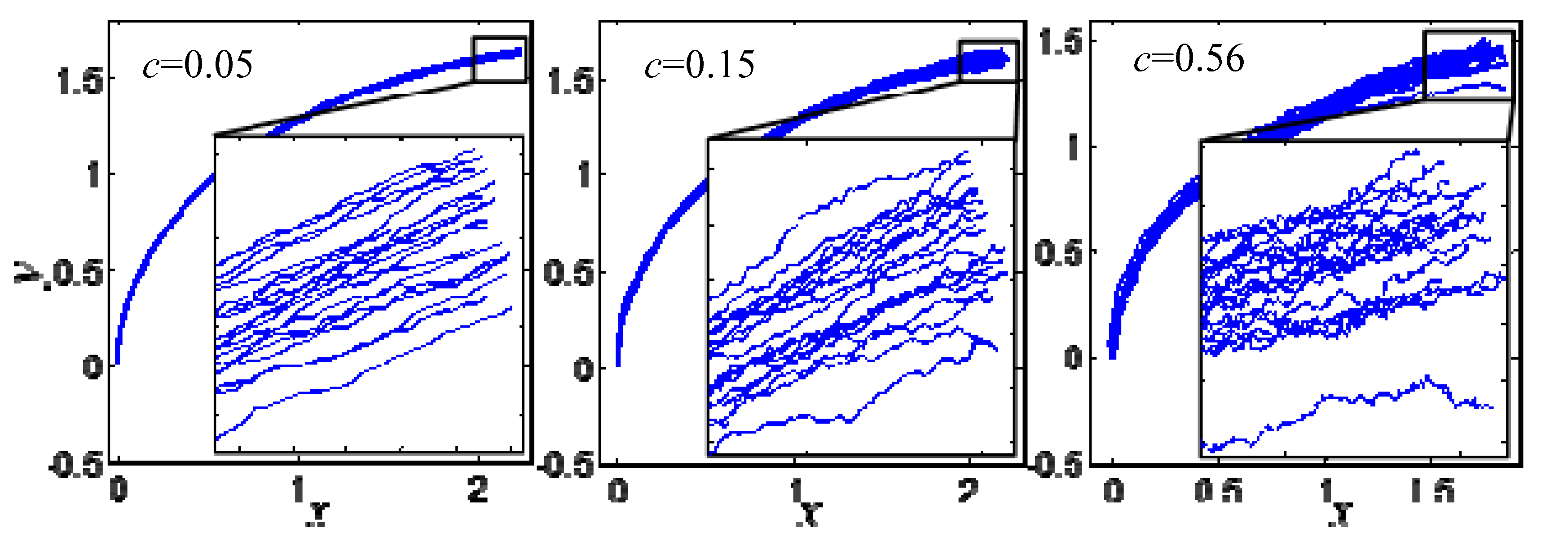
Three intensities of random motion values are selected as
c = 0.05,
c = 0.15 and
c = 0.56, and 20 of the corresponding 200 axons are selected to draw the growing diagram of the growth cone under the effect of random motion of different intensities, as shown in
Figure 2.
According to the growth details that can be seen in
Figure 2, the growth of the growth cone is relatively smooth around
c = 0.05 with small random fluctuations. The random fluctuations increases gradually around
c = 0.15, but the deflection angle of the growth cone does not change extremely, and the growth of the growth cone is still in order. However, when
c = 0.56, the trajectory of the growth cone changes abruptly and the partial shape of the growth cone is obviously out-of-order. Therefore, the randomness of the growing process of the growth cone increases gradually with the increase of the effect intensity of random motion.
3. Establishment of Neuronal Axonal Signal Transmission Model
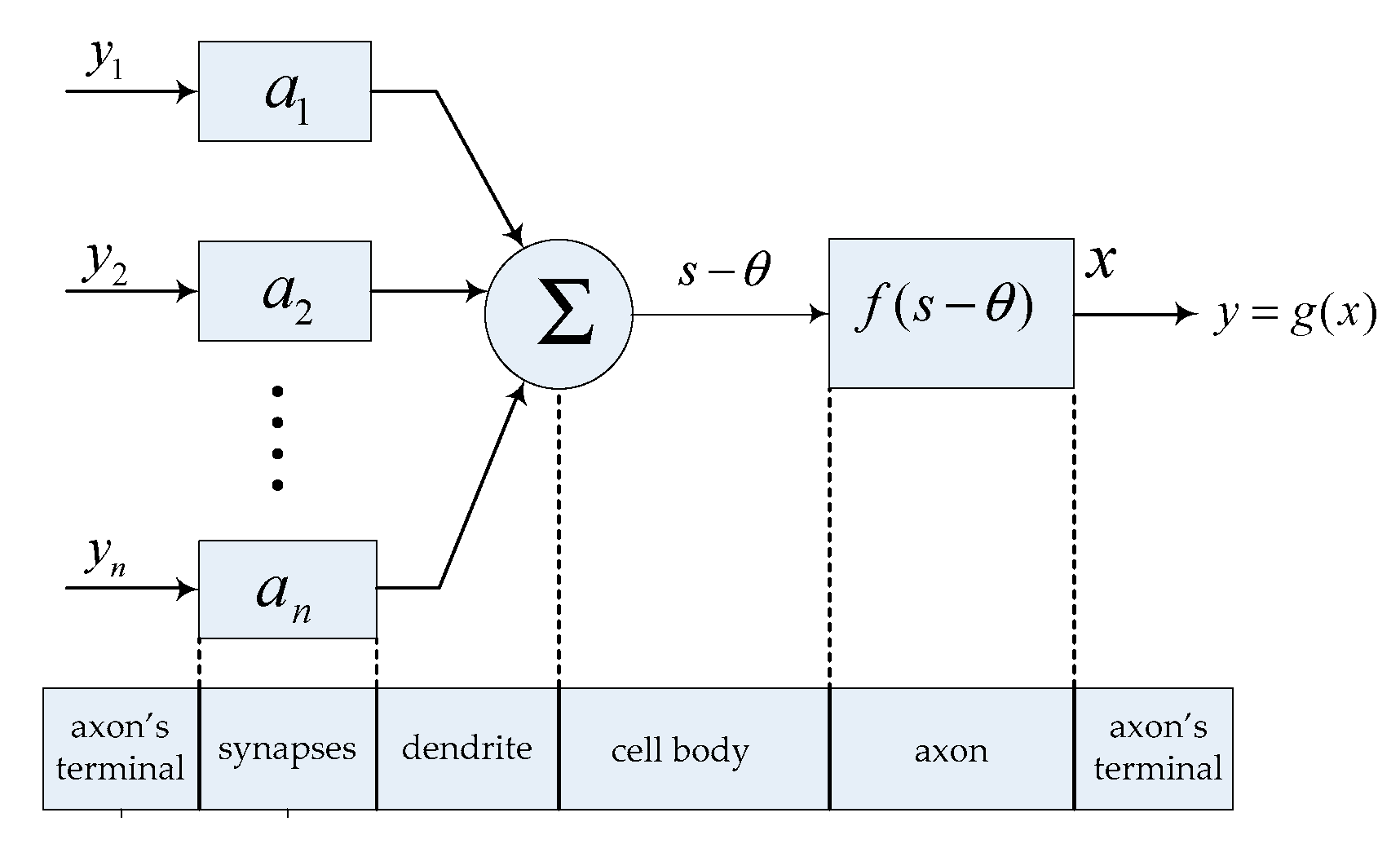
In order to describe the signal transmission process of the neurons listed above, a simplified model of neuron signal transmission, as shown in
Figure 3, is established in this paper.
If there are n neurons on a neuron’s dendrite to form synaptic connections with it, the output signals of these n neurons are
y1,
y2,
…,
yn,, the connection weights of synapses are a
1, a
2,
…,
an, the change of membrane potential caused by the input is
s and the excitation threshold is
θ; the membrane potential is
x when reaching the axon’s terminal after being transmitted through the whole axon, and the neuron output signal is
y. Then, the signal transmission process of the neuron is
where
f(.) represents the function of an axon on membrane potential and
g(.) represents the nonlinear output function of neurons, which is different for different biological neurons. In this paper, the commonly used threshold function is taken; i.e.,
g(
x) = max(0,
x).
In 1957, W. Rall proposed the equivalent cable model of an axon during signal transmission [
22], which regarded the cable as composed of many identical resistance capacitance circuits, considered the current flow in extracellular fluid and the distribution of extracellular potential and finally obtained the distribution of membrane potential in time space
λ2(
∂2V/
∂x2) =
τ(
∂V/
∂t)+
V, where
V is the potential of the membrane and
λ and
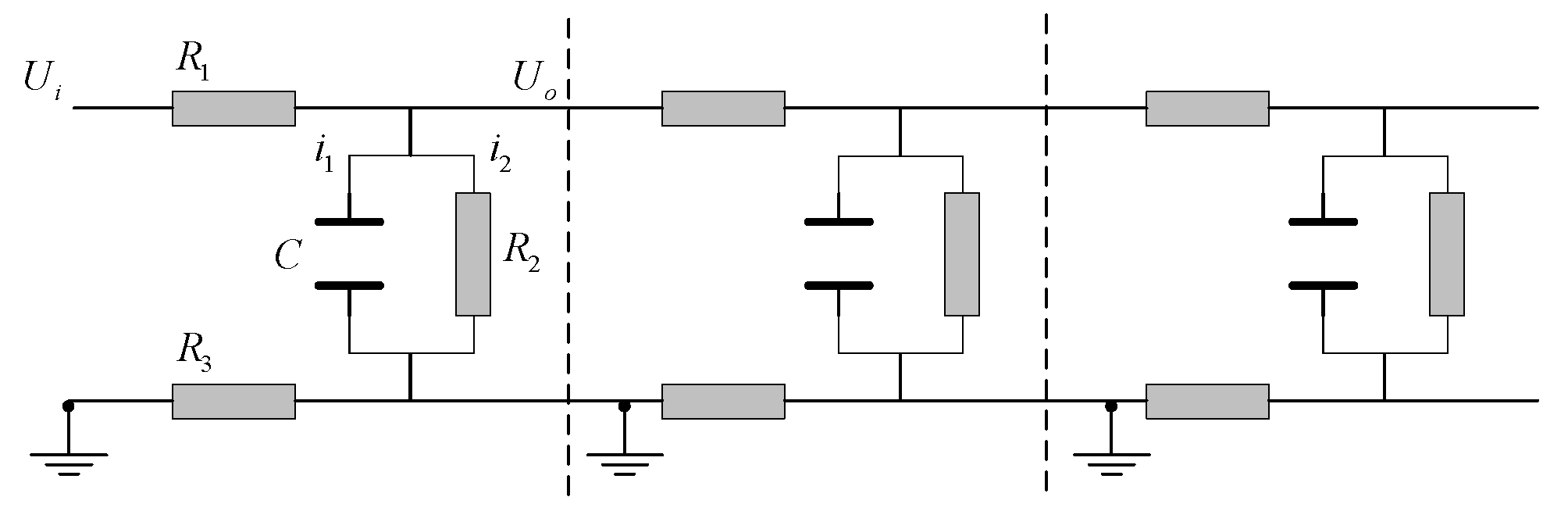
τ are the time constant and length constant of the thin film of the cable joint. This model is a second-order partial differential equation, and the solution is relatively complex. In this paper, we only consider the input and output characteristics of the neuron as a signal processing unit instead of the distribution of membrane potential on the whole axon, so we assume that the extracellular potential along the whole axon is always 0—equivalent to grounding—as can be seen in
Figure 4. Thus,
U is equal to the membrane potential. Given the output change of an input signal after the membrane potential is transmitted through the whole axon, we can calculate
f(.) as shown in Formula (10).
First, we analyze the basic resistance capacitance circuit in
Figure 4 separately and calculate the transfer function between the output
U0 and the input
Ui of each section. In
Figure 4,
i is the current,
R is the resistance and
C is the capacitance [
18]. The following equation can be obtained from Kirchhoff’s law and Ohm’s law.
Equations (11) and (12) are substituted into Equation (13):
The Laplace transform of Equation (14) is
Finally, we obtian the transfer function between
U0 and
Ui:
Assume
τ and b as Equation (17):
As can be seen from
Figure 4, the total transfer function of the axon to the membrane potential is
F(
S) =
GN(
S).
N is the number of basic links on the whole axon. Thus far, the signal transmission model of the neuron has been determined. Finally, the amplitude–frequency and phase–frequency characteristics of
G(
S) are analyzed to determine the physical characteristics of the neuron self-growing model:
where
ω is the angular frequency.
The amplitude–frequency characteristic of Equation (19) is
The phase–frequency characteristic of Equation (19) is
(1) Influence of axon length on amplitude and phase lag
Suppose an axon cable is composed of
N basic links as shown in
Figure 4; then, the amplitude of the input signal is attenuated to (1/
)
N after being transmitted through the axon, and the phase lag is –
Narctan(
τω/
b). The longer the axon is, the more basic links in the corresponding cable model there should be; in other words, the larger
N is. We can see that
b > 1 from Equation (17), and so the longer the axon is, the larger
N is and the larger the amplitude attenuation and phase lag are. The length of the axon can be obtained by the iteration in Equation (8). If the length of the axon corresponding to the basic link of a resistance capacitance loop is
l1 and the total length of the axon is
L [
23], then the amplitude of the signal will decay to (1/
)
L/l1 and the phase lag will be –
Narctan(
τω/
b) after passing through the whole axon.
(2) Diameter of the axon
As can be seen from Equations (20) and (21), the amplitude–frequency and phase–frequency characteristics of the neuron signal transmission are determined by the two parameters
τ and
b. In Equations (16) and (17),
R2 is the electrical leakage resistance between the inside and outside of the cell within a basic link, whose resistance value is much higher than
R1 and
R3, which is equivalent to the myelin sheath of the outer layer of the axon of biological neurons and plays an insulating role.
C is the leakage capacitance between the inside and outside of the cell within a basic link.
R3 is the conductive resistance of the extracellular fluid within a basic link.
R2,
R3 and C are the same for every neuron and do not change with the gradual growth of axons.
R1 represents the resistance of the axon core within a basic link, which can be obtained according to the resistance law:
where
ρ is the resistivity of the inner core of the axon,
s is the cross-sectional area of the axon—
s =
π2d/4 since the cable model is cylindrical—and
d is the diameter of the axon. The axon diameters of different neurons determine the amplitude–frequency and phase–frequency characteristics of the basic link in the cable model.
(3) Connection weight to the postsynaptic neuron
Since |
G(
jω)| < 1, the cable model shown in
Figure 4 must cause the attenuation of signal amplitude during signal transmission. However, we occasionally want a single neuron to transmit the signal without changing its amplitude when controlling, only changing its phase. For example, in the CPG control network of the joint of a legged robot, each joint is controlled by a motor neuron with joint angular displacement output, and the output signals of the motor neuron in the symmetrical position of the body need to have the same amplitude, because the joint angle of these joints has the same range. If all the intermediate neurons in the network do not change the amplitude of the signal during signal transmission, the output of each joint with the same amplitude can be obtained from the input with the same amplitude. In this paper, a proportional amplification link is artificially added after each basic link to prevent the change of signal transmission amplitude, as shown in
Figure 5.
According to Equation (20), we can obtain
K in
Figure 5:
As can be seen from Equation (23), the amplitude of the output signal from the original single basic link remains constant after passing the proportional amplification link. The output signal of the whole axon is equivalent to multiplying the original output by
KN. According to the definition of connection weight, this is equivalent to the connection weight between the neuron and the postsynaptic neuron:
If the input signal of the neuron is an ideal impulse signal or step signal, then we can say that
ω = 0. According to Equation (17), Equation (24) is
Because R2 is much larger than R1 and R3, we know that b tends to 1. According to N = L/l1, we can select l1 reasonably so that the order of magnitude of N will not be too large, and this will mean that the connection weights between all the neurons in the network meet a ∈ (1, 2).
In Equation (18), the transition time of the first-order system’s response to the impulse signal and the step signal—called the delay—is proportional to the time constant
τ, which is assumed to be
kτ, where k is a constant coefficient related to the allowable error value of the response. If there are
N basic links on the whole axon, as shown in
Figure 5, the total delay of the output signal relative to the input signal will be
Nkτ =
Lkτ/
l1, which is equivalent to the delay of the output of a basic link with a time constant of
Lτ/
l1 to the input:
Therefore, when the input signal is an impulse signal or a step signal, the self-growing model of a neuron with multiple physical properties can be simplified as follows: the whole neuron is regarded as a basic link, and the length of the axon obtained from the self-growing is used as the total time constant Tr of the neuron to the input signal. A random number from (1, 2) is selected as the connection weight value a between the neuron and the postsynaptic neuron. In addition, the ends of the axons of biological neurons diverge and form synaptic connections with dendrites of many other neurons; thus, multiple axons of the neurons are made to grow directly from the cell body without considering the choice of branching points to simplify the model.
4. Structure of Local CPG Network
(1) Study of neuron model
In 1987, Matsuoka proposed a mathematical neuron monomer model and studied the “oscillator” network output with different numbers of neurons and different connection structures based on it [
24]. The mathematical model of the neuron monomer is
where
x represents the membrane potential of the neuron;
s stands for neuron input;
y is the output of the neuron;
f is the quantity reflecting the fatigue effect of neurons;
b is a constant coefficient representing the size of fatigue effect;
θ presents the membrane potential threshold that activates the neuron, and without losing generality, we can take
θ = 0;
g(
x) is the nonlinear output function; and
Tr represents the time constant of the rise of the membrane potential caused by the input signal.
Ta represents the time constant of the neuronal fatigue effect. Since the physical characteristics of neurons of the model were not taken into account, there is no concept of the axon, and thus the membrane potential will not change after axon transmission. We continue to regard
x as the membrane potential at the end of the axon, and so this model differs from the model established in Equation (10) by only one fatigue characteristic characterized by
f and
Ta. Set
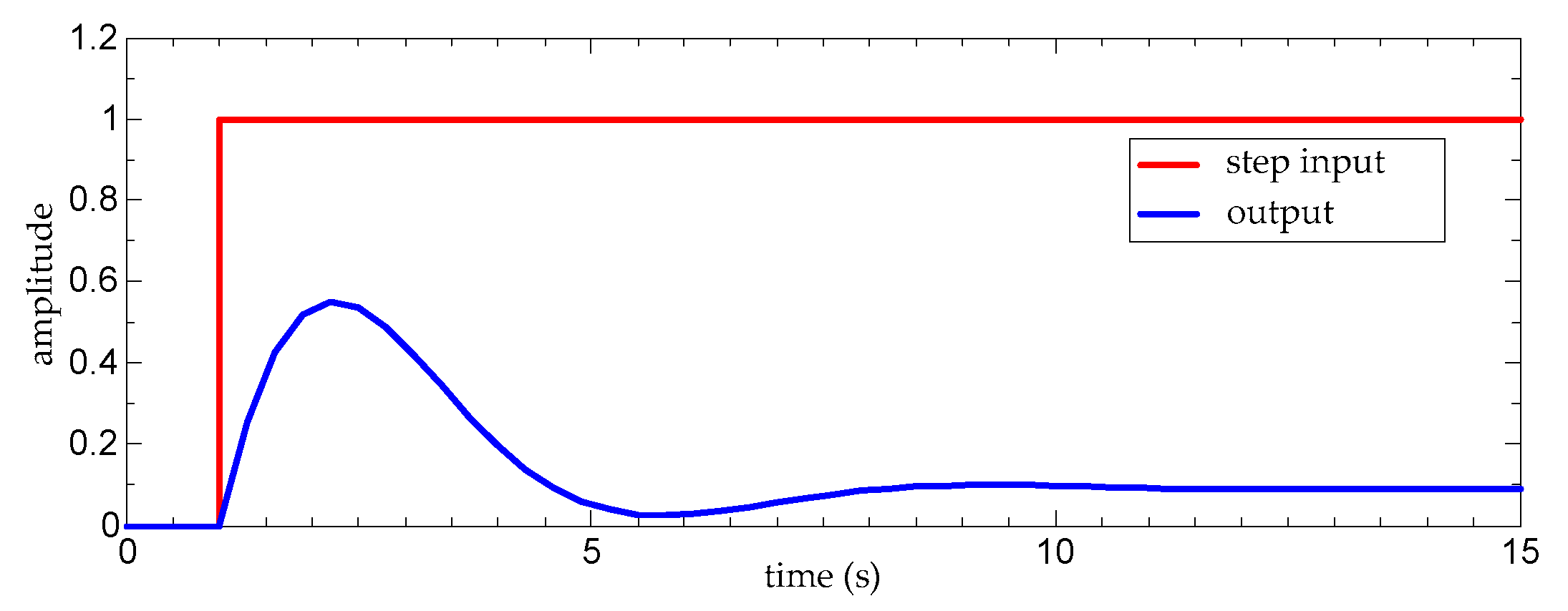
s as the step input signal with n amplitude of 1,
Tr = 1,
b = 10,
Ta = 10, and calculate the change of the output signal of the neuron monomer model over time; the results are shown in
Figure 6.
As can be seen from
Figure 6, first, the neuron is activated and the membrane potential rises; then, the membrane potential declines slowly due to the fatigue effect and remains at a low level. Although the step signal continues, the neuron will not be activated again. We can see that, under appropriate parameters, the mathematical model of the neuron monomer conforms to the signal transmission characteristics of biological neurons.
(2) Double neural oscillator model
Connect two neuron monomer models and make the two inhibit each other as shown in
Figure 7. If N1 and N2 are the neurons, the hollow endpoint connection presents the excitatory connection and the solid endpoint connection presents the inhibitory connection; S1 and S2 are the step input signals with an amplitude of 1 with slightly different step times. If S1 and S2 have the same step time, the two neurons will have the same output and will not produce an oscillation because of the symmetrical structure of the network.
The mathematical model of each neuron monomer is
where ∑
ajiyj are the inputs from other neurons. If the input is excitatory, the operator preceding it has a plus sign, with a minus sign for the inhibitory input.
Assume
Tr1 =
Tr2 = 1,
b1 =
b2 = 2.5,
a21 =
a12 = 1.5 and
Ta1 =
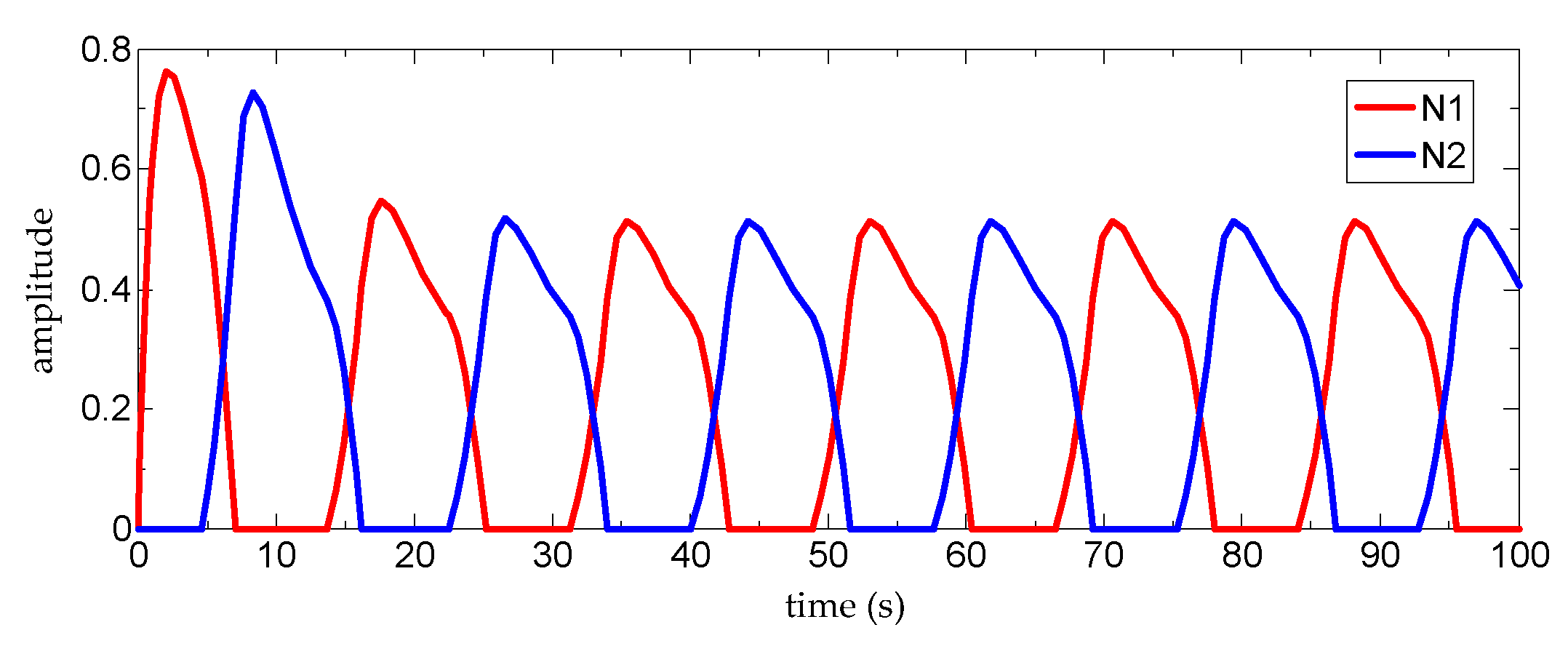
Ta2 = 12 and calculate the variation of the output signal of the oscillator model with time. The results are shown in
Figure 8.
In the spinal CPG network of mammals, the interactivity of neurons responsible for the coordination of the left and right sides of the body and the coordination of the extensor and flexor muscles of each joint inhibits the output [
25]. It can be seen in
Figure 5 that the reciprocal inhibition outputs of the two neurons have the same form as the reciprocal inhibition outputs of the neurons in the biological CPG network, indicating that the neuron monomer model in Equation (26) can reflect the characteristics of the reciprocal inhibition output caused by the reciprocal inhibition structure in the biological CPG network.
(3) Connection structure of local CPG network
As can be seen from the analysis above, as long as the neuron model represented by Equation (27) is composed of inhibitory connections among the neurons and appropriate parameters are taken, the interactive inhibitory output between the neurons will be obtained. Since each neuron monomer in the neuron model represented in Equation (27) has two time constants,
Tr and
Ta, and each neuron in the simplified model of self-growing neurons established in
Section 3 has only one time constant,
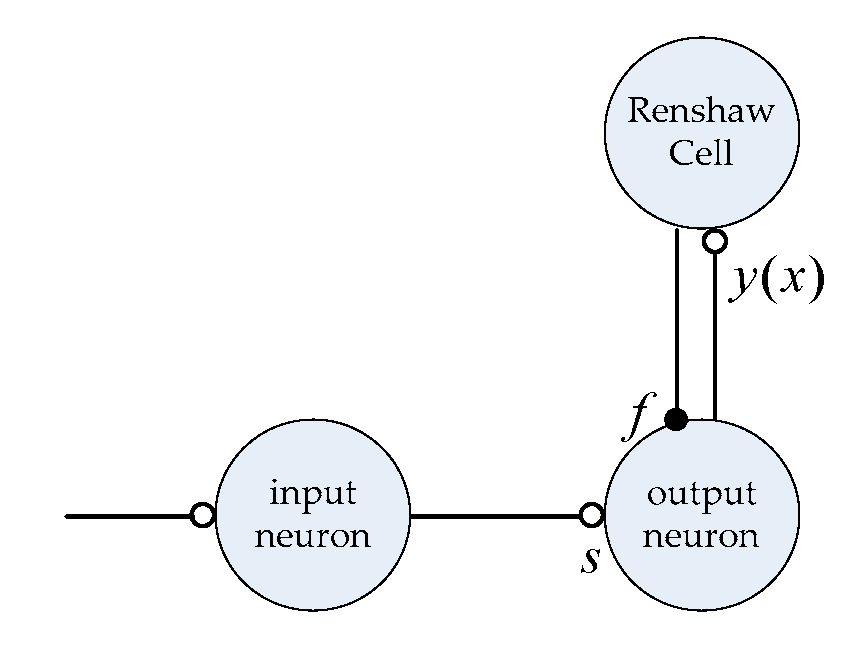
Tr, we cannot make the growth algorithm of single neuron grow into a local CPG network which has the function of controlling a robot joint. In order to solve this contradiction, we modify the original neuron monomer model, as shown in Equation (29), according to the characteristics of the neuron connections in a biological CPG network.
The original neuron monomer model is described with the structure shown in
Figure 6. We can see that the excitatory connection from the input neurons to the output neurons in
Figure 9 is equivalent to the input signal
S of the original model. The inhibition from the Renshaw Cell to the output neurons is equivalent to the fatigue characteristic in the original model; thus, the input and output characteristics of signal transmission of the structure shown in
Figure 9 are essentially the same as those in the Matsuoka neuron monomer model.
According to Equation (29), the modified neuron monomer model only contains one time constant,
Tr, and each axon contains a connection weight
a to the postsynaptic neuron, which is consistent with the simplified model of self-growing neurons established in
Section 3. Moreover, the connection structure shown in
Figure 6 has the anatomical basis of the biological CPG network. Known as an inhibitory intermediate neuron directly connected to motor neurons, the Renshaw Cell is involved in the coordination of most extensor and flexor muscles as part of the ipsilateral inhibitory network [
14,
25]. Moreover, the structure in
Figure 6 can be seen in many models of spinal motor nerve circuits [
26,
27].
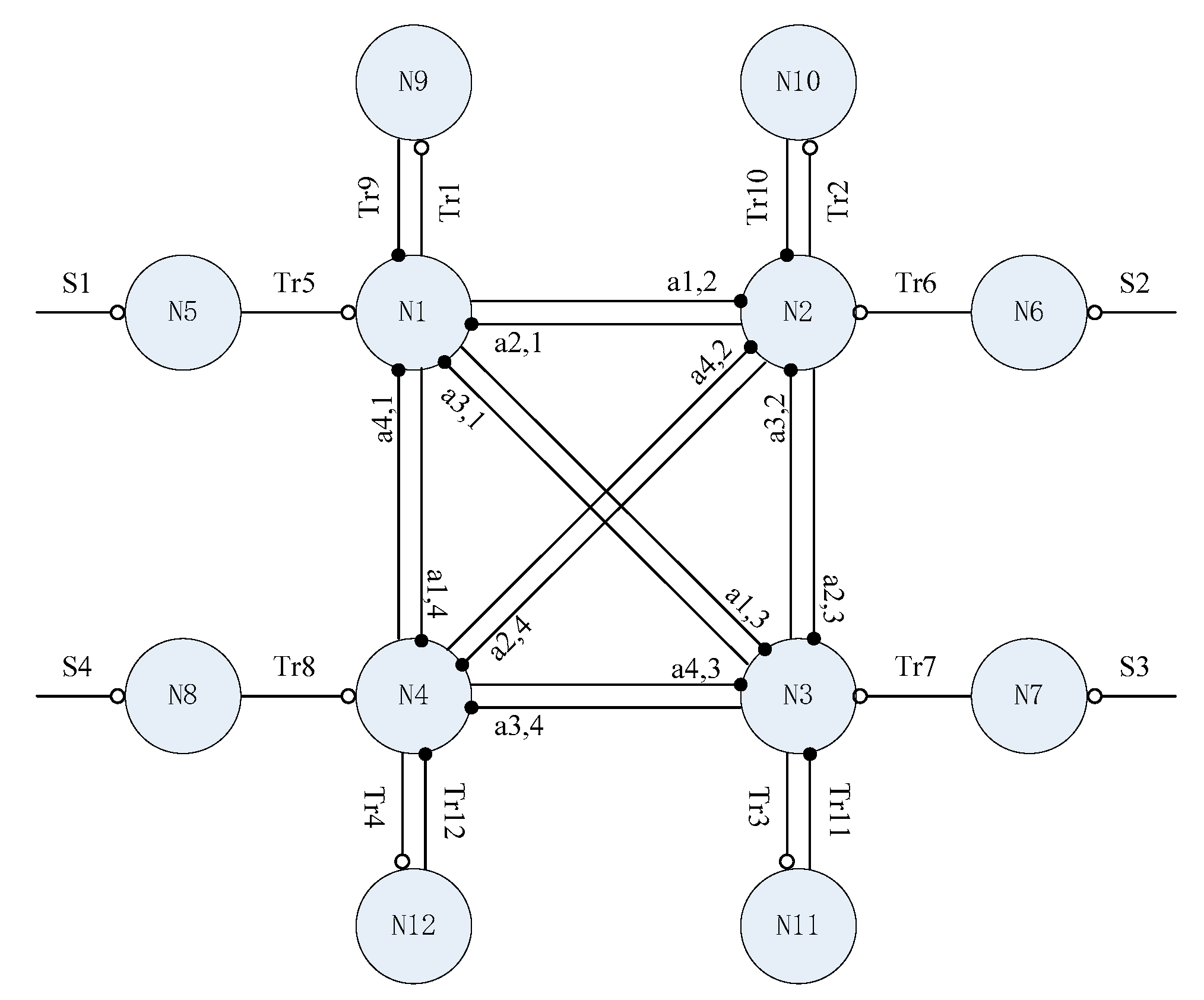
A local CPG network for the control of a quadruped robot’s hip joint can be formed with four identical structures, as shown in
Figure 10. In
Figure 10, N1, N2, N3 and N4 are the output neurons, respectively corresponding to the four hips of the quadruped robot. N5, N6, N7 and N8 are input neurons, and S1, S2, S3 and S4 are step input signals of the same amplitude. N9, N10, N11 and N12 are four output neurons connected with Renshaw Cells,
Tri is the time constant of each neuron and
ai,j is the connection weight of the synapse between the axon of neuron
i and the neuron
j; the connection weights between peripheral neurons are not shown in
Figure 10. The network structure is the growth target of the local CPG network self-growing algorithm.
(4) Output of local CPG network
One of the basic features of a biological CPG network is that it can obtain a periodic output signal with a certain rhythm from a simple non-rhythmic input signal. In order to verify that the network growth model proposed in this paper can obtain growth results with biological CPG network characteristics, a CPG network growth experiment was carried out and is presented in this section. Assume that the radius
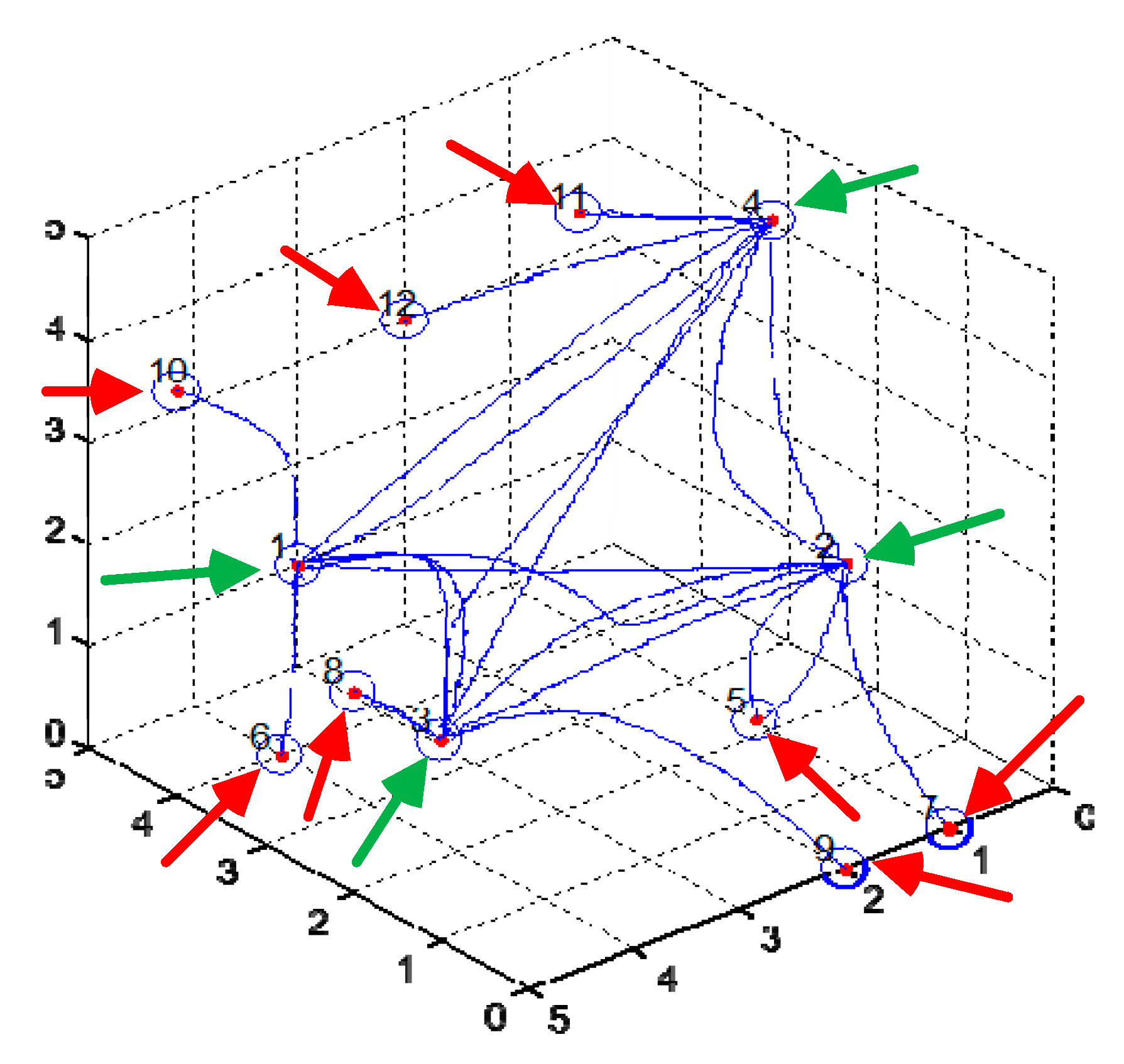
r of a single neuron in the growth model is 0.1 units of length and the growth space is a cube with a side length of 5; 12 neurons were randomly distributed in the growth space as shown in
Figure 11.
In
Figure 11, a circle represents a neuron, and the number (1, 2, …, 12) next to it shows the number of neurons. The neurons numbered 1, 2, 3 and 4 are the output neurons, represented by N1, N2, N3 and N4 (as shown by the green arrow in
Figure 11); the neurons numbered 5–12 are peripheral neurons, represented by N5–N12. Numbers N5, N6, N7 and N8 are input neurons (as shown by the red arrow in
Figure 11). The solid blue lines are the growing connections, as shown in
Figure 11.
For simplicity, take
l1 =
r = 0.1,
τ = 10. Putting the length of the blue solid line in
Figure 11 into Equation (26), the value of Tr can be obtained as shown in
Table 1.
Step input signals with amplitude of 1 were input to the four input neurons. Observe the output signals of the network; a representative growth result was taken for discussion. The connection structure of the network growth is shown in
Figure 11. In
Figure 11, each neuron axon contains two parameters: the time constant Tr and the connection weight a. Since there are 24 axons in the network, there are 48 parameters with 24 time constants and 24 connection weights in the network. Such a large number of parameters in the network is not conducive to the study of the rule between the output and growth results of the network. In order to facilitate the analysis, the axons in the network are divided into two categories: in the first category are the axons that inhibit the connection between the output neurons, with a total of 12; the second category are the axons connected with the peripheral neuron (the input neuron and the Renshaw Cell) between the output neuron, with a total of 12. For the first type of axons, only the connection weights in the growth results are used, and the time constants are all set to 0. For the second type of axon, only the time constant in the growth result is used, and the connection weights are all fixed values. This halves the network’s parameter variables. The time constants of the axons of each neuron after a certain growing process are shown in
Table 1.
According to Equation (25), the connection weight
a ∈ (1, 2) can be obtained. In order to simplify the calculation, a random number between (1, 2) is taken as the value of
a. The connection weights obtained are shown in
Table 2, and the connection weights between the output neuron and the peripheral neuron are set to 1 and 2, which meet
a ∈ [1, 2]. The output result of the entire network is calculated according to Equation (29), as shown in
Figure 12.
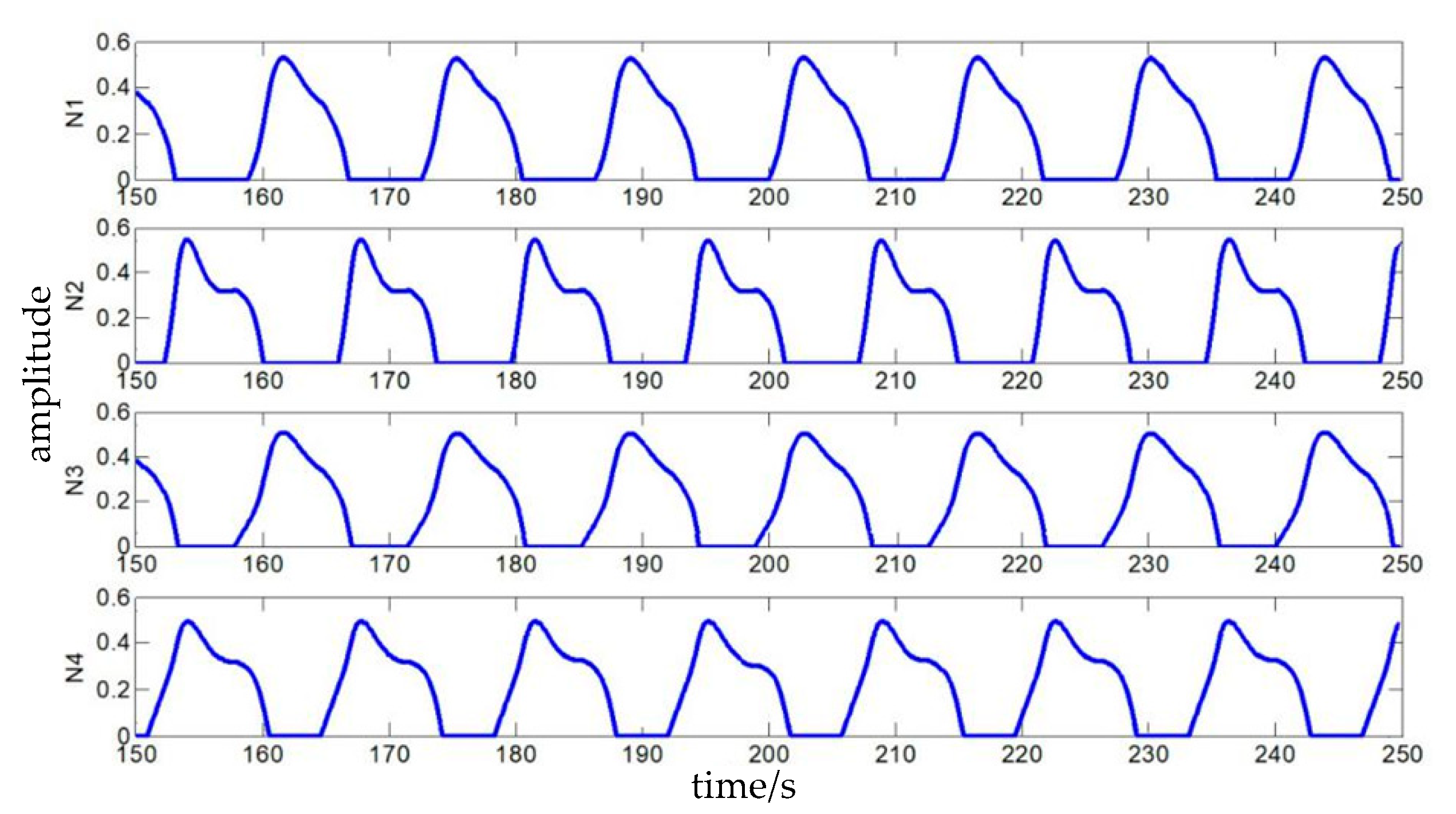
As can be seen from
Figure 12, the output signals of the four output neurons have the same period and phase difference and a similar range of amplitude after a period of stability. Furthermore, it is verified that the self-growing network model established in this paper can obtain a local CPG network which can satisfy the biological CPG network input and output characteristics, and the output of the network can be used for the control of the hip joint of quadruped robot. If the output signal of neuron N1 is used as the basis to calculate the phase difference, it can be determined that the output phase difference between N2 and N1 is 168.0°, the output phase difference between N3 and N1 is 33.6° and the output phase difference between N4 and N1 is 264.0°. The ideal phase differences of the corresponding hip joints of the quadruped robot at the walk gait are 180°, 90° and 270°. We can see that the phase difference between N3 and N1 is large, but the other two phase differences are very close, which shows that the local CPG network obtained by self-growing can output the corresponding control signals for the hip joint to the quadruped robot at a walking gait.
5. Experiment and Analysis
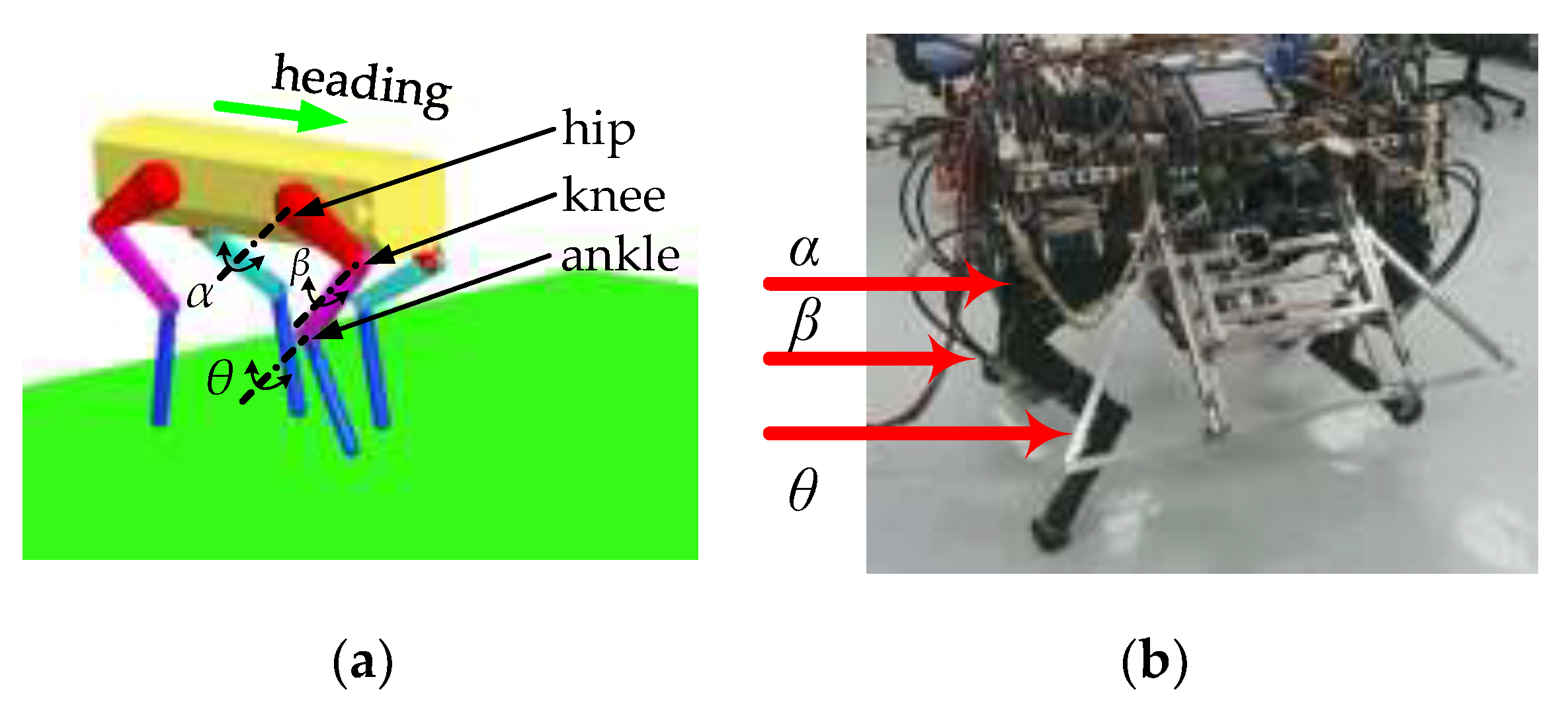
(1) Quadruped robot prototype
The experimental platform of the quadruped robot is shown in
Figure 13. There are three joints on each leg: the hip joint
α, knee joint
β and ankle joint
θ. The size of the platform is 1.2 m × 0.5 m × 1.4 m, and the weight is 150 kg.
Figure 13a is the simulation prototype of the quadruped robot, and
Figure 13b is the experiment of the quadruped robot.
(2) Foot trajectory and joint trajectory planning
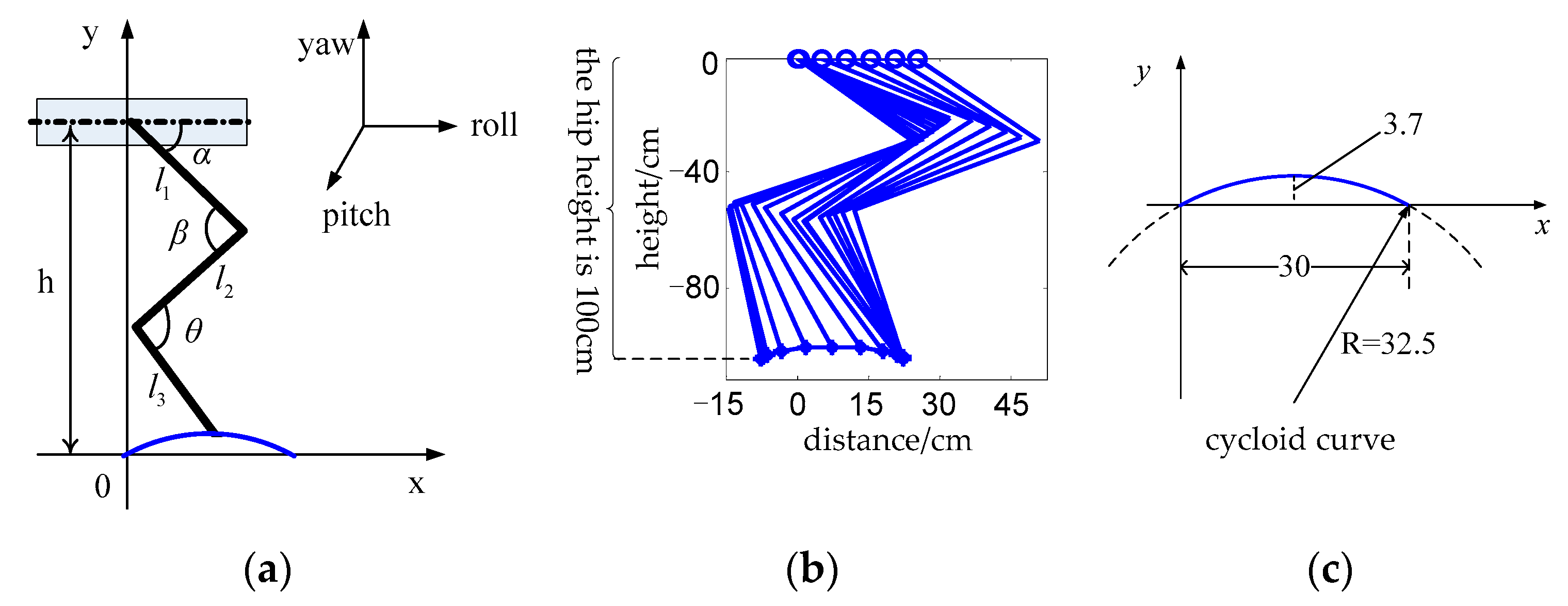
Since the ideal angular displacement of the hip joint can be approximated as a cosine function [
14], we assume that the control signal of the hip joint is
α = 3cos(2
πt/
T). The trajectory of the foot is a cycloid, as shown in
Figure 14b. The height of the robot’s hip joint is
h = 100 cm from the ground, and the step length of each stride is 30 cm. The former leg is taken as an example to calculate the joint angular displacement and that of the knee and ankle joints, as shown in
Figure 14a; thus, we obtain the following formula:
where
l1 = 45 cm,
l2 = 60 cm and
l3 = 50 are the lengths of the robot’s thigh, middle leg and calf;
x and
y are the analytic coordinates of the foot trajectory, as shown in
Figure 14c, where
α and
h are known. Thus, Equation (30) is a system of two equations with two unknowns,
β and
θ, whose solution is unique. The calculated relationship between
β,
θ and
α is shown in
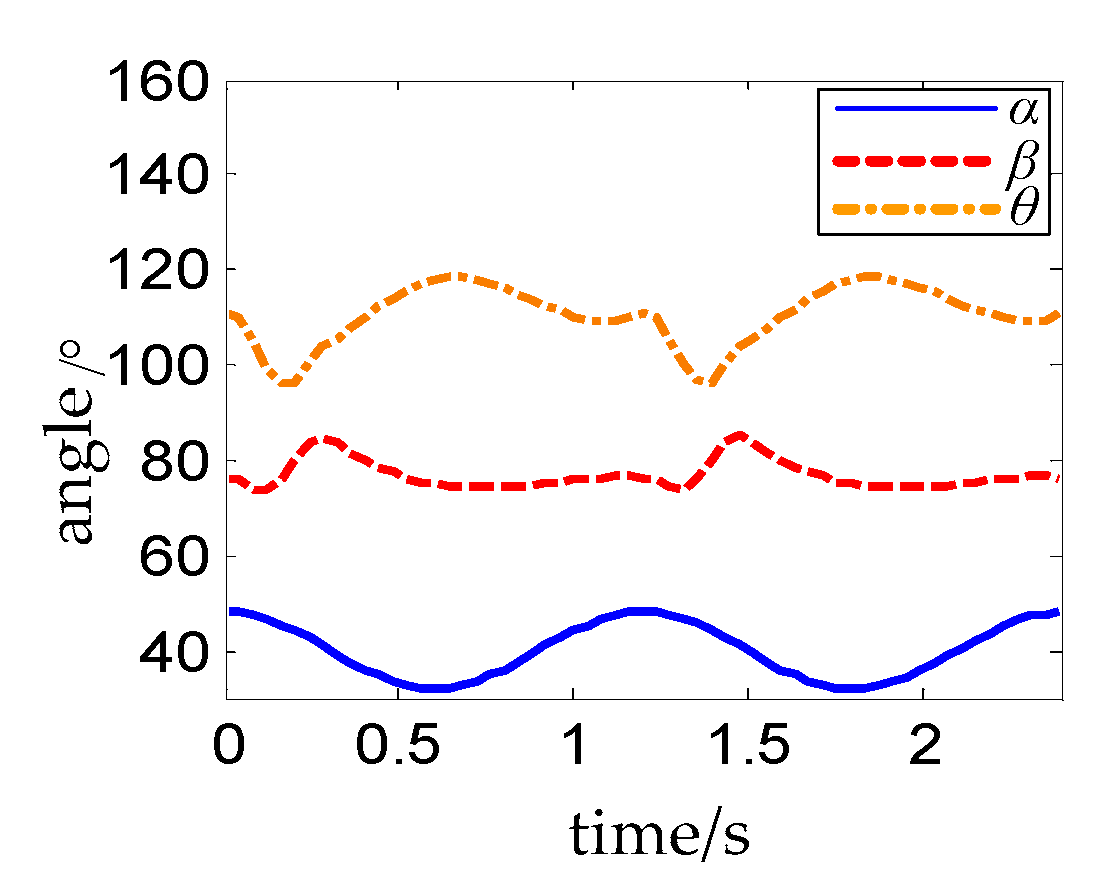
Figure 15.
α ranges from 30° to 50°, which can be seen from the solid blue line in
Figure 15, in order to make sure that the quadruped robot has a large stability margin when walking. The joint trajectory planning process of the hind leg of the robot is the same as that of the foreleg except for the different range of joint angles and the different shape of the curve.
Thus, the experimental prototype of the quadruped robot used for local CPG network gait control has been completed. It is only necessary to input periodic control signals corresponding to the angular displacements of the four hip joints into the prototype, and then the control signals of the knee and ankle joints of each leg will be obtained according to the corresponding relations in
Figure 15; thus, we can drive the robot prototype to walk.
(3) Experiment on simulation prototype and experimental prototype
The random selected parameters
a ∈ [1, 2] of the self-growing network are shown in
Table 3. The time constant
Tr is shown in
Table 1. After calculating the output of the network and cosine to fit the output signal according to Equation (29), the result is shown in
Figure 16. We can see that the output of the network is definitely the interaction oscillations between N1, N3, N2, and N4. N1 and N3 are input to the left front and the right hind hip joint of the simulation prototype, while N2 and N4 are input to the right front and the left hind hip joint of simulation prototype; then, the trot gait of the robot is implemented, and the simulation decompositions are shown in
Figure 17a. As can be seen from
Figure 17a, from
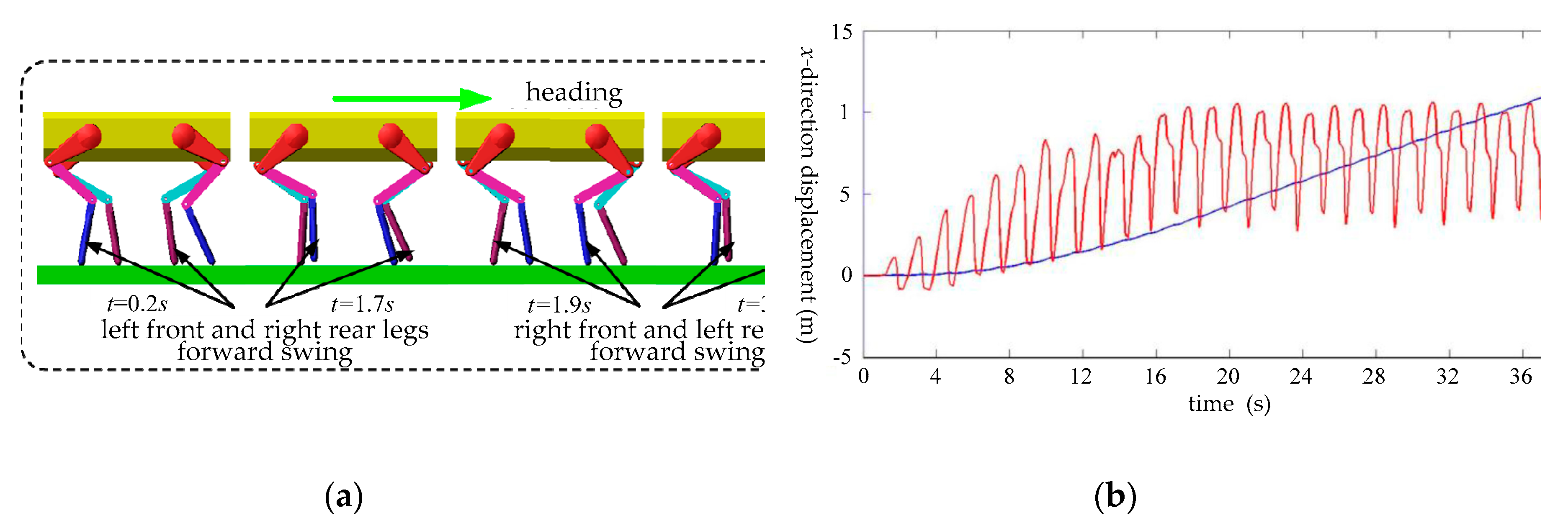
t = 0.2 s to
t = 1.7 s, the left front leg and the right hind leg are in the swing phase and swing forward; from
t = 1.9 s to
t = 3.4 s, the right front leg and the left hind leg are in the swing phase and swing forward. Each swing time is about 1.6 s.
The y-direction velocity and x-direction displacement of the simulation prototype are shown in
Figure 17b, where the red solid line is the y-direction velocity curve and the blue solid line is the
x-direction displacement curve. It can be seen from
Figure 17b that the simulation prototype enters a stable walking state gradually, and the y-direction velocity and
x-direction displacement reach a stable change when
t = 16 s.
In
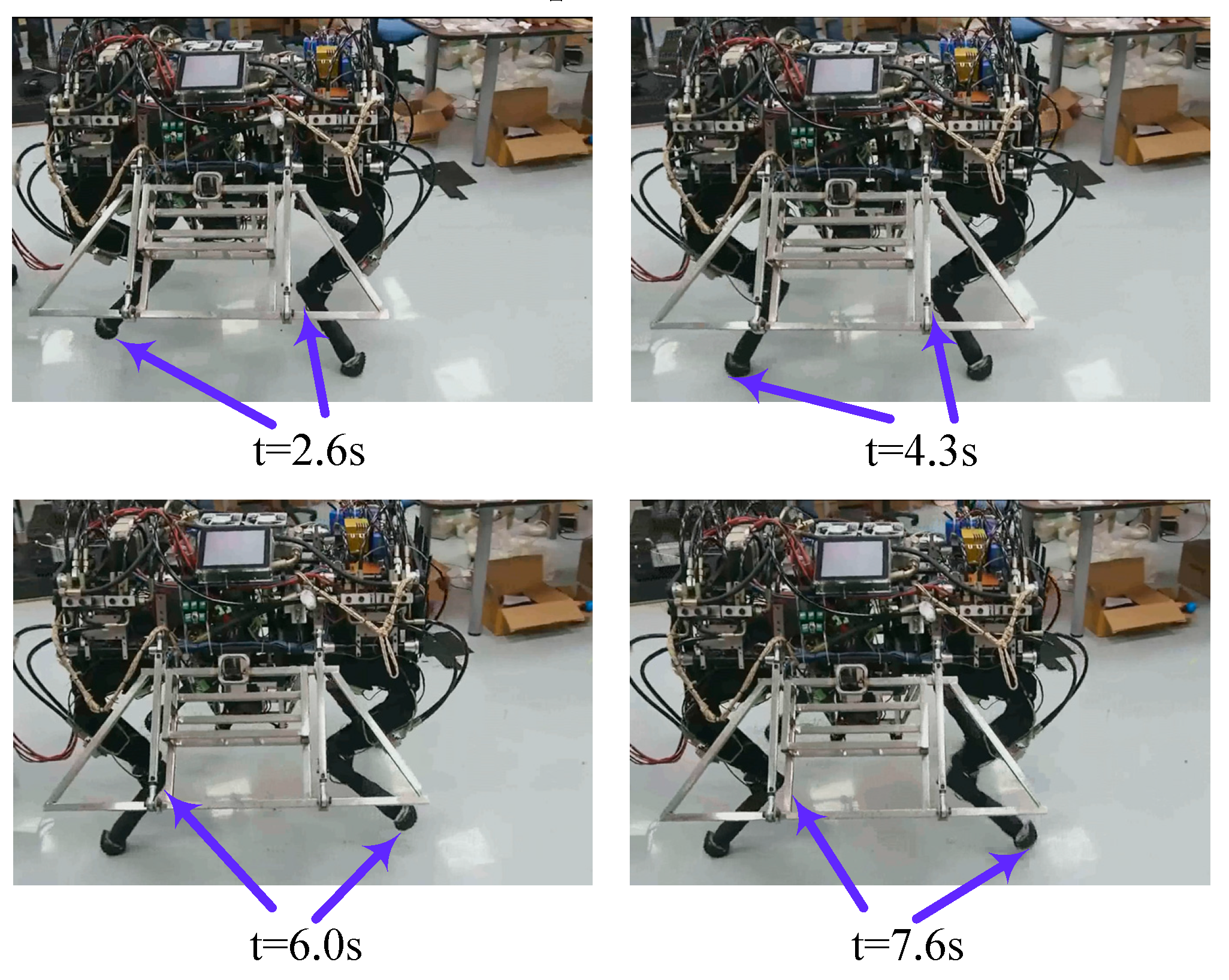
Figure 16, N1 and N3 in the output of the self-growing network are input to the left front and the right hind hip joint of the experimental prototype, respectively, while N2 and N4 are input to the right front and the left hind hip joint of the experimental prototype respectively. The trot gait decompositions of the experimental prototype obtained are shown in
Figure 18. Combining
Figure 17a and
Figure 18, we can see that the experimental prototype and the simulation prototype have the same gait cycle (about
T = 1.7 s) under the control of the same self-growing network, and the self-growing network can achieve stable control of the trot gait of the simulation prototype and the experimental prototype.
The experiment above shows that the quadruped robot control system based on a CPG neural network self-growing algorithm can accomplish the growth of the network, the signal output of the network and the control of a robot’s joint, and then realize the rhythmic movement of a quadruped robot. This shows that the CPG neural network self-growing algorithm can be well applied to the rhythm control of a robot. The experiment preliminarily simulated the process from growth to mastery of a certain rhythmic movement of the CPG neural network and verifies the feasibility of the idea of realizing robot rhythmic movement control by combining the microscopic mechanism of the growth and the macro characteristics of the output of the neural network.
6. Conclusions
In this paper, the biological neuron axon could continuously elongate and turn, and the growth of the back part did not change the shape of the previously used grown part. Combined with the law of gravitation, random motion, the Rall cable model and the Matsuoka oscillator model, a local CPG self-growing network with multiple physical characteristics was established. The fusion of a self-growing network and CPG has been realized, the control ability of self-growing network was presented, and the motion control of a quadruped robot was completed. Our conclusions are as follows.
(1) An axon self-growing algorithm based on universal gravitation and random motion was established, the Rall Cable Model for studying the potential distribution of an axon membrane was analyzed and simplified, and multiple physical properties of the synapse (including resistance, capacitance, axon length and diameter, etc.) were combined with the Rall Cable Model to establish a simplified model of single neuron signal transmission, as shown in Equation (19). The multi-physical properties obtained by the neuron self-growth model (such as the synapse length calculated by Equation (9) and the resistance R1 calculated by Equation (22)) were added to Equation (17) to calculate parameters τ and b of Equation (19). On this basis, the entire synapse system of the neuron’s self-growth is taken as a whole, as well as the key parameters in the control model: the delay time constant Tr and the synapse, as shown in Equations (25) and (26). The connection weight corresponds to the axon length and axon diameter in the growth model, which allows the combination of the growth and development process of the neuron and the control function.
(2) By analyzing the Matsuoka oscillator model (shown in Equation (27)) and comparing the difference between the mathematical model of its neuron monomer and the model built in this article, a local CPG network topology is proposed as shown in
Figure 10. This topology is regarded as the goal of network self-growth. A neural network growth model based on gravitational field control is established, meaning that the network can grow the target topology from any initial position of the neuron, as shown in
Figure 11, to obtain the rhythm output signal corresponding to the angular displacement of the hip joint of the quadruped robot, as shown in
Figure 12.
(3) The quadruped robot motion control simulation prototype and experimental prototype are used as shown in
Figure 13: the output signal of the local CPG network (as shown in
Figure 16) is used as the hip joint control signal of the simulation prototype and the experimental prototype to control the quadruped robot simulation. The prototype and the experimental prototype realized walking with a trot gait, as shown in
Figure 17 and
Figure 18, which verified the feasibility of the local CPG network self-growth model with multi-physical characteristics proposed in this paper for the gait control of a quadruped robot.
Since the gait control of the quadruped robot by the CPG network in this article is still an open-loop control system, it was not possible to change the gait of the robot through environmental feedback information or to adapt to the complex road conditions and change the rhythm and mode of the network output accordingly. Therefore, in order to give the self-growth-based network model higher practical value when applied to the motion control of a footed robot, the research work that needs to be done in the next stage is as follows:
(1) Continue to improve the self-growth model of neurons, considering more physical characteristics that can be linked to the control model parameters, so that the built model can be constantly close to the complexity of the biological neural network in terms of its microstructure and control function. For example, in this paper, the diameter of the neuron axon is constant. The fundamental reason for this is that only a one-dimensional size of the axon can be obtained by using the trajectory of the particle in the gravitational field as the axon model. The biological mechanism that determines the diameter must be introduced into the self-growth model to obtain a biologically reasonable diameter, so that the control model does not lose its general applicability.
(2) Study how many parameters obtained by network self-growth affect the network output. In the simulation experiment, we found that the time constant only affects the shape, amplitude and period of the output signal and does not affect the mutual inhibition mode, which is mainly affected by the connection weight. Moreover, not every time the network grows can the interactive inhibition output between output neurons be obtained. On occasion, individual or all output neurons will output a constant value signal after reaching stability; that is, the acquisition of the interactive inhibition output is important for the network growth parameters. This is conditional, but we still do not know the necessary condition.
(3) Study the micro-mechanism of interaction with the environment and the adjustment of the upper central system during the development of the CPG network and construct feedforward and feedback pathways for network development, so that the growth and development of the network can change the connection weights between synapses in biological neural networks by learning. Based on the research of (2), weight change is carried out in the direction in which the desired network output can be obtained to realize closed-loop control.