Abstract
Establishing high-rate secure communications is a potential application of continuous-variable quantum key distribution (CVQKD) but still challenging for the long-distance transmission technology compatible with modern optical communication systems. Here, we propose a photon subtraction-induced plug-and-play scheme for enhancing CVQKD with discrete-modulation (DM), avoiding the traditional loopholes opened by the transmission of local oscillator. A photon subtraction operation is involved in the plug-and-play scheme for detection while resisting the extra untrusted source noise of the DM-CVQKD system. We analyze the relationship between secret key rate, channel losses, and untrusted source noise. The simulation result shows that the photon-subtracted scheme enhances the performance in terms of the maximal transmission distance and make up for the deficiency of the original system effectively. Furthermore, we demonstrate the influence of finite-size effect on the secret key rate which is close to the practical implementation.
1. Introduction
Quantum key distribution (QKD) [1,2,3] is a primary application of quantum cryptography, which enables two remote legitimate communication parties, Alice and Bob, to share random secret key sequences [4,5,6] in public channel preventing the eavesdropper Eve by physical laws [7,8,9,10]. There are two research fields for QKD, i.e., discrete-variable QKD(DVQKD) and continuous-variable QKD (CVQKD) [11,12,13,14]. In DVQKD, information is encoded on properties of single photon, and it uses single-photon detector at the receiver side. In CVQKD, information is encoded in two quadratures of the optical field [15,16], and relies on coherent detection including homodyne and heterodyne detectors [16,17,18].
In recent decades, CVQKD has become a hot issue due to its simplicity of implementation [19,20], compatibility with modern fiber networks [21] and high detection efficiency that can realize higher secret key rate in short distances [22]. Unfortunately, the reconciliation efficiency of Gaussian modulated CVQKD (GM-CVQKD), whose secret keys are modulated following Gaussian distribution, is sensitive to channel losses [23], so that this scheme is unsuitable in long distance situations. To solve this problem, CVQKD with discrete modulation (DM-CVQKD) has been proposed by A. Leverrier and P. Grangier [24]. In DM-CVQKD, such as four-state and eight-state modulation protocol, quantum states are nonorthogonal and information is represented by the sign of quadrature [25,26,27,28], which is Gaussian random value in GM-CVQKD [29]. The maximum transmission distance of DM-CVQKD is greater than that of GM-CVQKD, and its unconditional security against collective attack have been proved [25] under the condition of low modulation variance. Actually, most studies of DM-CVQKD focus on one-way schemes that a local oscillator (LO) will be sent together with signal pulses to simplify the detection [30,31]. However, the transfer of LO will open some loopholes for eavesdroppers. The loopholes can be exploited to conduct some attacks such as wavelength attacks, saturation attacks, and LO fluctuation attack [32,33,34].
An improved scheme called real local oscillator in which the LO is generated on the receiver’s side without transmitting through the quantum channel has been proposed [35,36,37,38]. In this scheme, the loopholes resulted by the transmission of LO are closed, but its performance would be poor because of the incidental frequency out-sync between two independent laser sources. Subsequently, plug-and-play (PP) dual-phase-modulated coherent-states (DPMCS) CVQKD have been proposed to solve the above-mentioned problems in experiments by Huang et al. [39] and Valivarthi et al. [40]. In the PP DPMCS scheme, LO is generated by Alice without transmitting through the quantum channel, whereas quantum state is modulated by Bob based on the classical light sent from the source of Alice [39]. Therefore, the loophole resulting from transmitting LO is closed, and the polarization drift of the fiber channel would be compensated automatically [41,42]. However, the transmission of the classical light from Alice to Bob still results in extra excess noise [43] that would reduce the maximum transmission distance. Moreover, the PP protocol suffers Trojan-horse attack [44,45] and the secure distance is limited by the Rayleigh scattering [46].
Fortunately, some non-Gaussian operations can be used for performance improvement of the CVQKD system because of the fact that this operation will strengthen the entanglement degree of the yielded system [47,48,49,50]. Motivated by the characteristics of photon subtraction (PS) operation, which is a mature technology in implementation, in this paper, we propose an approach for enhancing the PP DM-CVQKD protocol with photon subtraction implemented at Bob’s side. Compared with the original protocol, our scheme significantly improved system performance, and the deficiency of the original scheme is made up to a certain extent, which provides a greater reference value for the experiment and practical application. Moreover, in order to get closer to the practical case [51], we consider the finite-size effect on the secret key rate and the simulation result shows that the PS-based scheme has better performance in a finite-size scenario.
This paper is structured as follows. In Section 2, we suggest a PS-induced plug-and-play scheme for CVQKD with discrete modulation. In Section 3, numerical simulations demonstrate the performance improvement of the PS-induced CVQKD with with discrete modulation. Finally, we conclude this paper in Section 4.
2. Photon-Subtracted Plug-and-Play DM-CVQKD
2.1. Plug-and-Play DM-CVQKD Protocol
In the prepare-and-measure (PM) version of DM-CVQKD, Bob randomly chooses one of the coherent states [24] for four-state modulation or [52] for eight-state modulation, as shown in Figure 1, with the modulation variance and sends it to Alice through an untrusted channel. To simplify the security proof, we choose the entanglement-based (EB) scheme which is equivalent to the PM scheme in security [53], and the detailed description of the PM version of PP CVQKD is shown in [39,40]. In the EB scheme of original DM-CVQKD, Bob prepares an entanglement state, namely Einstein–Podolsky–Rosen (EPR) state, and sends one mode to Alice where another mode B is kept by Bob for measurement.
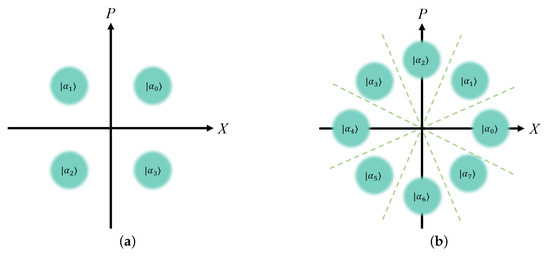
Figure 1.
Phase space representations of coherent states with (a) four-state modulation and (b) eight-state modulation.
The EB scheme of PP DM-CVQKD is shown in Figure 2a and its steps are as follows.
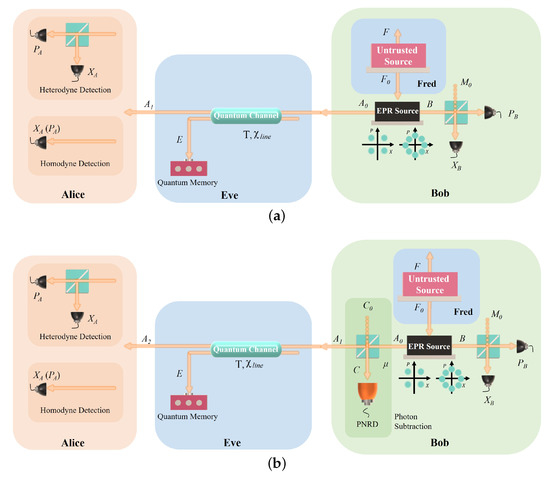
Figure 2.
(a) the EB scheme of PP DM-CVQKD protocol. Here, Fred is assumed to controlled by Eve, and he will introduce an untrusted source noise; (b) the corresponding PS-based PP DM-CVQKD scheme. PNRD, photon number resolving detector.
- Fred prepares a EPR state . Fred can be a neutral party; however, to derive the tight security bound, Fred is assumed to be controlled by Eve, that is to say, Fred would introduce the untrusted source noise. Notice that the state is utilized to simulate the coherent state with extra untrusted noise , which characterized by a phase insensitive amplifier (PIA) with a gain g in the PM scheme. Namely, the state is virtually a two-mode state [43] and the calculation method of two-mode entanglement state is still suitable. The quadratures and of Bob and Alice respectively can be expressed aswhere ( with the shot noise variance 1) and . Here, is the variance of vacuum noise.
- Alice sends the mode to Bob through an untrusted channel. We assume that Eve performs the collective Gaussian attack strategy, which is proved to be an optimal attack on reverse reconciliation protocols. The transmittance of the channel represented by T and the channel-added noise is .
- Alice randomly measures one quadrature of the mode using homodyne detection or two quadratures with heterodyne detection, while Bob measures mode B with heterodyne detection. After that, Alice and Bob share two strings of correlated data as raw keys.
- Alice and Bob apply post-processing procedure, e.g., reverse reconciliation and privacy amplification to acquire secure secret key sequences.
2.2. Photon-Subtracted Plug-and-Play DM-CVQKD
In what follows, we suggest a PS-based PP DM-CVQKD scheme. As shown in Figure 2b, different from the above scheme, after the Step 1 in PP DM-CVQKD scheme, the mode would intersect with a vacuum state at beamsplitter with transmittance . Afterwards, the state is split into two modes C and . The yielded triparite state can be expressed as
The positive operator-valued measurement (POVM) is applied to the photon number resolving detector (PNRD) so that the PNRD can be used to measure mode C [49]. The subtracted photon number m depends on and the operation succeeds only when the POVM element clicks. After the PS the state reads
where represents the partial trace of the multi-mode state and is the success probability of subtracting m photons, as shown in Appendix A. By applying the photon subtraction operation, the covariance matrix of state reads
where , , and are calculated in Appendix A. The subsequent quantum state transfer, detection, and post-processing procedure is the same as the PP DM-CVQKD scheme. After passing through the unsafe channel, the covariance matrix of state can be represented as
where , and represents the excess noise of channel.
We can derive from [54] that, after photon subtraction operation with a given , the of the two-mode squeezed vacuum (TMSV) state is the same for four-state and eight-state modulation. Namely, the four-state and eight-state modulation protocols demonstrate the similar performance after photon subtraction, so that we take the four-state modulation protocol into account without loss of generality while performing the PS-based PP scheme in the DM-CVQKD. Notice that, after the PS operation, the entanglement degree of the coherent state is strengthened [13].
Finally, the asymptotic secret key rate of reverse reconciliation against collective attacks can be calculated as
where is the reconciliation efficiency, is the Holevo bound of the mutual information between Eve and Alice, and is the Shannon mutual information between Alice and Bob following the photon subtraction.
3. Security Analysis
The transmittance of the photon subtraction beamsplitter may have an influence on the success probability of subtracting m photons which plays a significant role in the security analysis. As shown in Figure 3, the success probability is reduced as the increasing photon-subtracted number m. Note that, although is highest when , all the signals received by PNRD are reflected from quantum state through a beamsplitter and state cannot be sent to Alice, which means that the scheme cannot work. Figure 4 shows the secret key rate as a function of channel losses. We find that the PS-based PP scheme demonstrates better performance in the case of high channel losses but worse in low channel losses range because of the low success rate of photon subtraction operation. The 1-photon subtraction (1-PS) scenario is best-performing; in other words, more channel losses can be tolerated for compared with that of number . Moreover, we can also perceive that the source noise evaluated by g (dash line in Figure 4 where ) will reduce the secret key rate as well as have an influence on the tolerance of channel losses.
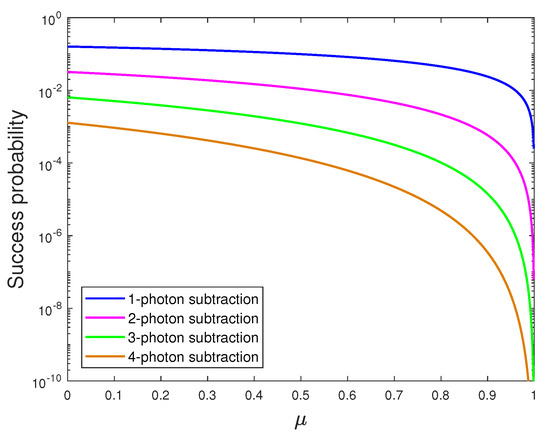
Figure 3.
The success probability of photon subtraction as a function of transmittance for the modulation variance .
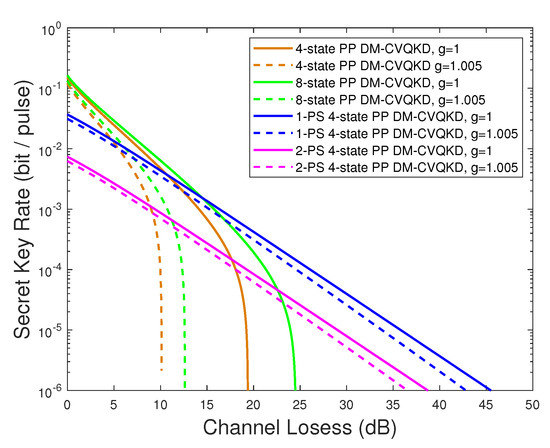
Figure 4.
The secret key rate as a function of channel losses. The solid line corresponds to the case that and the dash line corresponds to . The modulation variance , the channel excess noise , and the reconciliation efficiency .
Figure 5 shows the secret key rate of the plug-and-play DM-CVQKD as a function of channel losses for the tunable g. Figure 5a,b are the four-state and eight-state PP DM-CVQKD protocols, respectively. Figure 5c,d are the protocols with 1-PS and 2-PS operations, respectively. The insecure area shown in the chart signifies that the secret key rate is zero or negative, which means that Alice and Bob cannot acquire the secret key sequence. Compared with the four-state PP DM-CVQKD, the eight-state PP DM-CVQKD could tolerate more untrusted source noise for the same channel losses. Furthermore, after applying 1-PS operation, the four-state PP DM-CVQKD could demonstrate the longer transmission distance for the same value of g, whereas it tolerates more untrusted source noise at the same channel losses owing to the enhancement of entanglement degree.
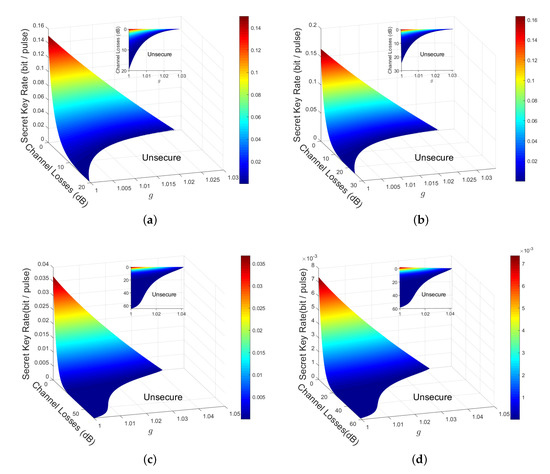
Figure 5.
The secret key rate of plug-and-play DM-CVQKD of (a) PP 4-state DM-CVQKD protocol, (b) PP 8-state DM-CVQKD protocol, (c) 1-PS PP 4-state DM-CVQKD protocol and (d) 2-PS PP 4-state DM-CVQKD protocol. The modulation variance , the channel excess noise , and the reconciliation effiency .
In the asymptotic case, the number of communication signals is deemed to be infinite [55]; in other words, the channel is totally known. In practice, it is impossible for the number of exchanged signals to be infinite so we have to take the finite-size effect into account. Figure 6 shows the secret key rate as a function of channel losses in the finite-size scenario. Figure 6a,b are the four-state and eight-state DM-CVQKD, respectively, while Figure 6c,d correspond to the schemes involved the 1-PS and 2-PS operations, respectively. We find that the secret key rate of DM-CVQKD in a finite-size scenario is lower than that of the asymptotic case whether it performs the PS operation or not. The finite-size secret key rate is closer to the asymptotic case with the increasing block size N of transmitted photons due to the fact that more signals could be utilized for parameter estimation and the quantum channel would be closer to being entirely known. Generally, the channel characters will not be estimated perfectly because of the finitude of signals so we need to consider the worst case. The analysis of finite-size effect and the calculation of the secret key rate of the PS-based PP DM-CVQKD system for the finite-size scenario is shown in Appendix B.
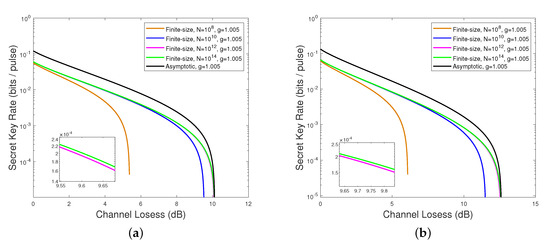
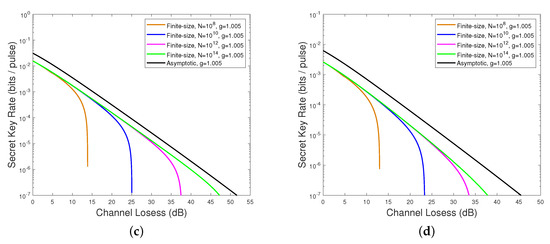
Figure 6.
The secret key rate as a function of channel losses for PP DM-CVQKD protocol in the
finite-size scenario. (a) PP four-state protocol; (b) PP eight-state protocol; (c) 1-PS PP four-state protocol; (d) 2-PS PP four-state protocol. The parameters are as follows: the modulation variance , the channel excess noise , the reconciliation efficiency and the gain g = 1.005.
4. Conclusions
We have proposed a PS-based PP scheme for performance improvement of the DM-CVKQD system by using PS operation on Bob’s side. The proposed scheme can tolerate more channel losses compared with the original scheme so that it extends the maximal transmission distances. The secret key rate of the eight-state PP DM-CVQKD system is slightly higher than that of the four-state system for the same parameters in numerical simulation. We demonstrate the relation between secret key rate, channel losses and untrusted source noise (characterized by g), and find that the PS-based scheme can tolerate more untrusted source noise. In addition, we take the finite-size effect into account and show its influence on the secret key rate with the tunable numbers of subtracted photons and exchanged signals. This research provides a feasible method to improve the performance of PP CVQKD, which has a certain reference value for experiment and application.
Author Contributions
Conceptualization, writing—original draft preparation, C.Y.; software, Y.M.; validation and formal analysis, Y.G.; supervision, S.Z.; All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (Grant Nos. 61572529, 61871407).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| QKD | Quantum Key Distribution |
| CVQKD | Continuous-Variable Quantum Key Distribution |
| DVQKD | Discrete-Variable Quantum Key Distribution |
| EPR | Einstein–Podolsky–Rosen |
| PP | Plug-and-Play |
| PS | Photon Subtraction |
| EB | Entanglement-Based |
| PM | Prepare-and-Measurement |
| TMSV | Two-Mode Squeezed Vacuum |
Appendix A. Derivation of the Asymptotic Secret Key Rate
In this section, we consider the characteristics of the transmitted states in the PS-based PP DM-CVQKD scheme and derive the asymptotic secret key rate of it. Here, we take the asymptotic secret key rate of the four-state PP DM-CVQKD protocol into account without loss of generality. We assume that Bob and Alice perform heterodyne detection and homodyne detection, respectively. In the EB scheme of original DM-CVQKD, Bob prepares a two-mode entangled state given by
where for four-state protocol and for eight-state protocol with
and
In four-state protocol, can be calculated as
whereas, in eight-state protocol, it can be expressed as
The covariance matrix of state can be expressed as
where , and
Here, , and are the annihilation and creation operators, respectively, on Alice’s and Bob’s mode. The success probability of subtracting m photons can be calculated as
where is a combination number and . After the m-photon subtraction operation, the covariance matrix is given in Equation (4), and the parameters are given by
The mutual information can be expreseed as
with and . Meanwhile, the Holevo bound can be calculated as
where is the Von Neumann entropy that is given by
and are the symplectic eigenvalues derived from covariance matrices calculated by
with
and
Combining with Equation (6), we can obtain the asymptotic secret key rate.
Appendix B. Derivation of Finite-Size Secret Key Rate
We assume that the detection methods of Alice and Bob are the same as the asymptotic case and the photon subtraction operation is performed on Bob’s side. In this scenario, N is the number of entire transmitted signals and n is the number of signals used for secret key extraction. The rest of the signals are utilized for estimating the parameters of insecure channels that can be implemented by sampling of s couples of correlated variables . The finite-size secret key rate can be expressed as
where , and are defined the same as above, and is the failure probability of parameter estimation and is in connection with privacy amplification that is given by
Here, the parameter denotes the failure probability of privacy amplification and demonstrates the smoothing parameter. The symbol represents the Hilbert space corresponding to Alice’s raw key which usually employs binary encoding so we set . Because of the unknown channel, we have to estimate some arguments to derive which would minimize the secret key rate. The s couples of samples can be related as
where and z follow a centered normal distribution with variance . Moreover, we can find the covariance matrix that minimizes the secret key rate with a probability of at least 1- that is given by
where and are the minimized t and maximized of the samples, respectively. For this normal linear model, the maximum-likelihood estimators and can be expressed as
Futhermore, and follow the distribution that
where t and are the authentic values of the parameters. Therefore, and can be calculated as
where satisfies and erf is the error function given by
The value of the above-mentioned error probabilities can be assigned as
Finally, the secret key rate of finite-size scenario can be calculated using the derived bound and .
References
- Grosshans, F.; Grangier, P. Continuous variable quantum cryptography using coherent states. Phys. Rev. Lett. 2002, 88, 057902. [Google Scholar] [CrossRef] [PubMed]
- Grosshans, F.; Van Assche, G.; Wenger, J.; Brouri, R.; Cerf, N.J.; Grangier, P. Quantum key distribution using gaussian-modulated coherent states. Nature 2003, 421, 238–241. [Google Scholar] [CrossRef] [PubMed]
- Weedbrook, C.; Lance, A.M.; Bowen, W.P.; Symul, T.; Ralph, T.C.; Lam, P.K. Quantum cryptography without switching. Phys. Rev. Lett. 2004, 93, 170504. [Google Scholar] [CrossRef] [PubMed]
- Cerf, N.J.; Levy, M.; Van Assche, G. Quantum distribution of Gaussian keys using squeezed states. Phys. Rev. A 2001, 63, 052311. [Google Scholar] [CrossRef]
- Zhou, J.; Huang, D.; Guo, Y. Long-distance continuous-variable quantum key distribution using separable Gaussian states. Phys. Rev. A 2018, 98, 042303. [Google Scholar] [CrossRef]
- Lo, H.K.; Curty, M.; Tamaki, K. Secure quantum key distribution. Nat. Photonics 2014, 8, 595. [Google Scholar] [CrossRef]
- Vazirani, U.; Vidick, T. Fully device independent quantum key distribution. Commun. ACM 2019, 62, 133. [Google Scholar] [CrossRef]
- Li, X.H.; Deng, F.G.; Zhou, H.Y. Efficient quantum key distribution over a collective noise channel. Phys. Rev. A 2008, 78, 022321. [Google Scholar] [CrossRef]
- Pljonkin, A.; Singh, P.K. The Review of the Commercial Quantum Key Distribution System. In Proceedings of the 2018 Fifth International Conference on Parallel, Distributed and Grid Computing (PDGC), Solan, Himachal Pradesh, India, 20–22 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 795–799. [Google Scholar]
- Pljonkin, A. Vulnerability of the Synchronization Process in the Quantum Key Distribution System. Int. J. Cloud Appl. Comput. (IJCAC) 2019, 9, 50–58. [Google Scholar] [CrossRef]
- Zhao, W.; Liao, Q.; Huang, D.; Guo, Y. Performance analysis of the satellite-to-ground continuous-variable quantum key distribution with orthogonal frequency division multiplexed modulation. Quantum Inf. Process. 2019, 18, 39. [Google Scholar] [CrossRef]
- Liao, Q.; Guo, Y.; Xie, C.; Huang, D.; Huang, P.; Zeng, G. Composable security of unidimensional continuous-variable quantum key distribution. Quantum Inf. Process. 2018, 17, 113. [Google Scholar] [CrossRef]
- Huang, P.; He, G.; Fang, J.; Zeng, G. Performance improvement of continuous-variable quantum key distribution via photon subtraction. Phys. Rev. A 2013, 87, 012317. [Google Scholar] [CrossRef]
- Wang, X.; Cao, Y.; Wang, P.; Li, Y. Advantages of the coherent state compared with squeezed state in unidimensional continuous variable quantum key distribution. Quantum Inf. Process. 2018, 17, 344. [Google Scholar] [CrossRef]
- Gong, L.H.; Song, H.C.; He, C.S.; Liu, Y.; Zhou, N.R. A continuous variable quantum deterministic key distribution based on two-mode squeezed states. Phys. Scr. 2014, 89, 035101. [Google Scholar] [CrossRef]
- Jouguet, P.; Kunz-Jacques, S.; Diamanti, E. Preventing calibration attacks on the local oscillator in continuous-variable quantum key distribution. Phys. Rev. A 2013, 87, 062313. [Google Scholar] [CrossRef]
- Liang, K.; Cao, Z.; Liu, W.; Wang, J.; Chai, G.; Zhang, T. Security analysis of continuous-variable quantum key distribution with imperfect Faraday mirror. Laser Phys. Lett. 2019, 16, 115202. [Google Scholar] [CrossRef]
- Ye, W.; Zhong, H.; Liao, Q.; Huang, D.; Hu, L.; Guo, Y. Improvement of self-referenced continuous-variable quantum key distribution with quantum photon catalysis. Opt. Express 2019, 27, 17186–17198. [Google Scholar] [CrossRef]
- Li, M.; Cvijetic, M. Continuous-variable quantum key distribution with self-reference detection and discrete modulation. IEEE J. Quantum Electron. 2018, 54, 1–8. [Google Scholar] [CrossRef]
- Gyongyosi, L.; Imre, S. Adaptive multicarrier quadrature division modulation for long-distance continuous-variable quantum key distribution. In Quantum Information and Computation XII; International Society for Optics and Photonics: Bellingham, WA, USA, 2014; Volume 9123, p. 912307. [Google Scholar]
- Zhao, W.; Guo, Y.; Zhang, L.; Huang, D. Phase noise estimation using Bayesian inference for continuous-variable quantum key distribution. Opt. Express 2019, 27, 1838–1853. [Google Scholar] [CrossRef]
- Li, Y.M.; Wang, X.Y.; Bai, Z.L.; Liu, W.Y.; Yang, S.S.; Peng, K.C. Continuous variable quantum key distribution. Chin. Phys. B 2017, 26, 040303. [Google Scholar] [CrossRef]
- Jouguet, P.; Kunz-Jacques, S.; Leverrier, A. Long-distance continuous-variable quantum key distribution with a Gaussian modulation. Phys. Rev. A 2011, 84, 062317. [Google Scholar] [CrossRef]
- Leverrier, A.; Grangier, P. Unconditional security proof of long-distance continuous-variable quantum key distribution with discrete modulation. Phys. Rev. Lett. 2009, 102, 180504. [Google Scholar] [CrossRef]
- Leverrier, A.; Grangier, P. Continuous-variable quantum key distribution protocols with a discrete modulation. arXiv 2010, arXiv:1002.4083. [Google Scholar]
- Ghorai, S.; Grangier, P.; Diamanti, E.; Leverrier, A. Asymptotic security of continuous-variable quantum key distribution with a discrete modulation. Phys. Rev. X 2019, 9, 021059. [Google Scholar] [CrossRef]
- Becir, A.; El-Orany, F.; Wahiddin, M. Continuous-variable quantum key distribution protocols with eight-state discrete modulation. Int. J. Quantum Inf. 2012, 10, 1250004. [Google Scholar] [CrossRef]
- Wang, X.-Y.; Bai, Z.-L.; Wang, S.-F.; Li, Y.-M.; Peng, K.C. Four-state modulation continuous variable quantum key distribution over a 30-km fiber and analysis of excess noise. Chin. Phys. Lett. 2013, 30, 010305. [Google Scholar] [CrossRef]
- Huang, P.; Fang, J.; Zeng, G. State-discrimination attack on discretely modulated continuous-variable quantum key distribution. Phys. Rev. A 2014, 89, 042330. [Google Scholar] [CrossRef]
- Wang, T.; Huang, P.; Zhou, Y.; Liu, W.; Zeng, G. Pilot-multiplexed continuous-variable quantum key distribution with a real local oscillator. Phys. Rev. A 2018, 97, 012310. [Google Scholar] [CrossRef]
- Huang, B.; Huang, Y.; Peng, Z. Practical security of the continuous-variable quantum key distribution with real local oscillators under phase attack. Opt. Express 2019, 27, 20621–20631. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.C.; Sun, S.H.; Jiang, M.S.; Liang, L.M. Local oscillator fluctuation opens a loophole for Eve in practical continuous-variable quantum-key-distribution systems. Phys. Rev. A 2013, 88, 022339. [Google Scholar] [CrossRef]
- Huang, P.; Huang, J.; Wang, T.; Li, H.; Huang, D.; Zeng, G. Robust continuous-variable quantum key distribution against practical attacks. Phys. Rev. A 2017, 95, 052302. [Google Scholar] [CrossRef]
- Wu, X.D.; Wang, Y.J.; Huang, D.; Guo, Y. Simultaneous measurement-device-independent continuous variable quantum key distribution with realistic detector compensation. Front. Phys. 2020, 15, 1–12. [Google Scholar] [CrossRef]
- Huang, D.; Huang, P.; Lin, D.; Wang, C.; Zeng, G. High-speed continuous-variable quantum key distribution without sending a local oscillator. Opt. Lett. 2015, 40, 3695–3698. [Google Scholar] [CrossRef] [PubMed]
- Soh, D.B.; Brif, C.; Coles, P.J.; Lütkenhaus, N.; Camacho, R.M.; Urayama, J.; Sarovar, M. Self-referenced continuous-variable quantum key distribution protocol. Phys. Rev. X 2015, 5, 041010. [Google Scholar] [CrossRef]
- Kleis, S.; Rueckmann, M.; Schaeffer, C.G. Continuous variable quantum key distribution with a real local oscillator using simultaneous pilot signals. Opt. Lett. 2017, 42, 1588–1591. [Google Scholar] [CrossRef]
- Wang, T.; Huang, P.; Zhou, Y.; Liu, W.; Ma, H.; Wang, S.; Zeng, G. High key rate continuous-variable quantum key distribution with a real local oscillator. Opt. Express 2018, 26, 2794–2806. [Google Scholar] [CrossRef]
- Huang, D.; Huang, P.; Wang, T.; Li, H.; Zhou, Y.; Zeng, G. Continuous-variable quantum key distribution based on a plug-and-play dual-phase-modulated coherent-states protocol. Phys. Rev. A 2016, 94, 032305. [Google Scholar] [CrossRef]
- Valivarthi, R.; Etcheverry, S.; Aldama, J.; Zwiehoff, F.; Pruneri, V. Plug-and-play continuous-variable quantum key distribution for metropolitan networks. Opt. Express 2020, 28, 14547–14559. [Google Scholar] [CrossRef]
- Liao, Q.; Wang, Y.; Huang, D.; Guo, Y. Dual-phase-modulated plug-and-play measurement-device-independent continuous-variable quantum key distribution. Opt. Express 2018, 26, 19907–19920. [Google Scholar] [CrossRef]
- Zhang, H.; Ruan, X.; Wu, X.; Zhang, L.; Guo, Y.; Huang, D. Plug-and-play unidimensional continuous-variable quantum key distribution. Quantum Inf. Process. 2019, 18, 128. [Google Scholar] [CrossRef]
- Wu, X.D.; Wang, Y.J.; Zhong, H.; Liao, Q.; Guo, Y. Plug-and-play dual-phase-modulated continuous-variable quantum key distribution with photon subtraction. Front. Phys. 2019, 14, 41501. [Google Scholar] [CrossRef]
- Jain, N.; Anisimova, E.; Khan, I.; Makarov, V.; Marquardt, C.; Leuchs, G. Trojan-horse attacks threaten the security of practical quantum cryptography. New J. Phys. 2014, 16, 123030. [Google Scholar] [CrossRef]
- Gisin, N.; Fasel, S.; Kraus, B.; Zbinden, H.; Ribordy, G. Trojan-horse attacks on quantum-key-distribution systems. Phys. Rev. A 2006, 73, 022320. [Google Scholar] [CrossRef]
- Subacius, D.; Zavriyev, A.; Trifonov, A. Backscattering limitation for fiber-optic quantum key distribution systems. Appl. Phys. Lett. 2005, 86, 011103. [Google Scholar] [CrossRef]
- Guo, Y.; Ye, W.; Zhong, H.; Liao, Q. Continuous-variable quantum key distribution with non-Gaussian quantum catalysis. Phys. Rev. A 2019, 99, 032327. [Google Scholar] [CrossRef]
- Guo, Y.; Liao, Q.; Wang, Y.; Huang, D.; Huang, P.; Zeng, G. Performance improvement of continuous-variable quantum key distribution with an entangled source in the middle via photon subtraction. Phys. Rev. A 2017, 95, 032304. [Google Scholar] [CrossRef]
- Ma, H.X.; Huang, P.; Bai, D.Y.; Wang, S.Y.; Bao, W.S.; Zeng, G.H. Continuous-variable measurement-device-independent quantum key distribution with photon subtraction. Phys. Rev. A 2018, 97, 042329. [Google Scholar] [CrossRef]
- Liao, Q.; Guo, Y.; Huang, D.; Huang, P.; Zeng, G. Long-distance continuous-variable quantum key distribution using non-Gaussian state-discrimination detection. New J. Phys. 2018, 20, 023015. [Google Scholar] [CrossRef]
- Jouguet, P.; Kunz-Jacques, S.; Leverrier, A.; Grangier, P.; Diamanti, E. Experimental demonstration of long-distance continuous-variable quantum key distribution. Nat. Photonics 2013, 7, 378–381. [Google Scholar] [CrossRef]
- Guo, Y.; Ding, J.; Mao, Y.; Ye, W.; Liao, Q.; Huang, D. Quantum catalysis-based discrete modulation continuous variable quantum key distribution with eight states. Phys. Lett. A 2020, 384, 126340. [Google Scholar] [CrossRef]
- Wu, X.D.; Chen, F.; Wu, X.H.; Guo, Y. Controlling continuous-variable quantum key distribution with entanglement in the middle using tunable linear optics cloning machines. Int. J. Theor. Phys. 2017, 56, 415–426. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Y.; Wang, X.; Xu, B.; Peng, X.; Guo, H. Non-Gaussian postselection and virtual photon subtraction in continuous-variable quantum key distribution. Phys. Rev. A 2016, 93, 012310. [Google Scholar] [CrossRef]
- Leverrier, A.; Grosshans, F.; Grangier, P. Finite-size analysis of a continuous-variable quantum key distribution. Phys. Rev. A 2010, 81, 062343. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).