Numerical Verification of Interaction between Masonry with Precast Reinforced Lintel Made of AAC and Reinforced Concrete Confining Elements
Abstract
Featured Application
Abstract
1. Introduction
2. Laboratory Tests
3. Material and Numerical Models
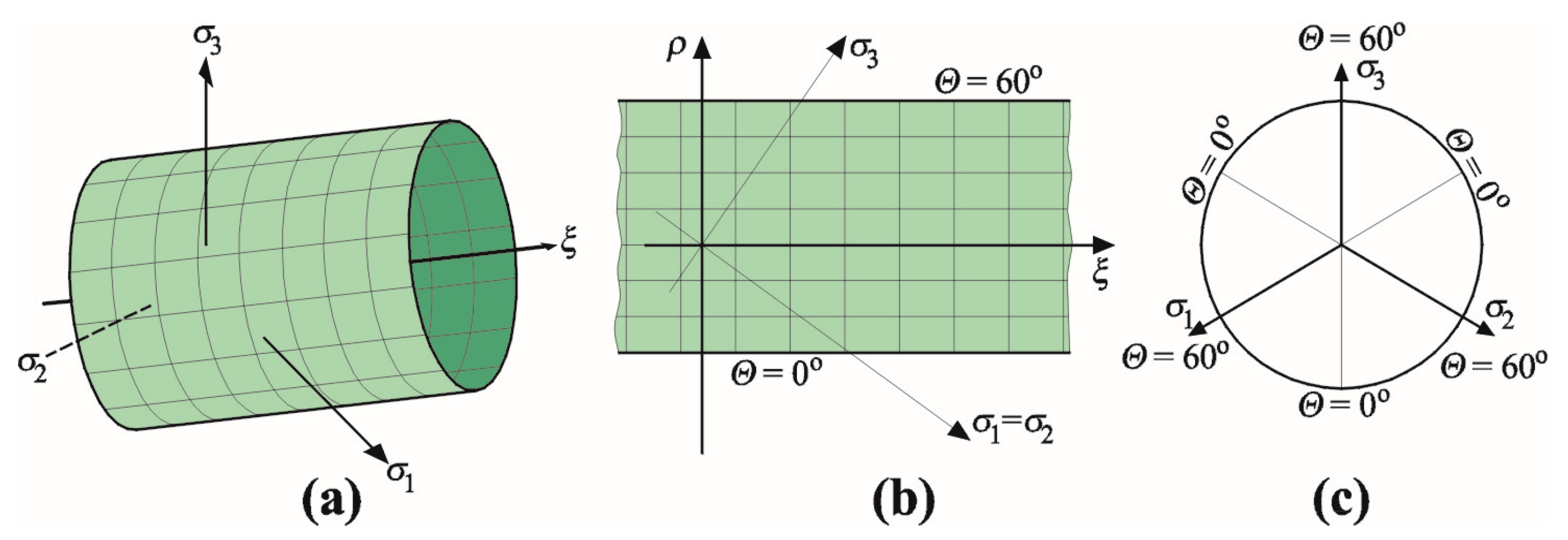
3.1. General Comments and Strategy Employed for Masonry Modelling
- (a)
- (b)
- The mezzo-model—a variant of the macro-model that is similar to the periodic micro-structure, which includes non-linear relations between mean stresses and mean deformations of the element, composed of masonry units and mortar layers equivalent to a given medium (of the same dimensions). Its basic element (representative volume element [35]) contains the required geometrical and physical information about any type of component for the masonry elements [36,37];
- (c)
- The micro-model, which identifies the masonry structure as a heterogeneous material. Classification into finite elements is made for each material (mortar, masonry unit). Different non-linear behaviour is assumed for bricks and mortar, including potential interaction forces between them. This type of model is usually used to analyse small constructions or to perform in-depth analysis. Its description requires information about the characteristics of components and the contact between them [22,32,33,34,35,36,38,39,40].
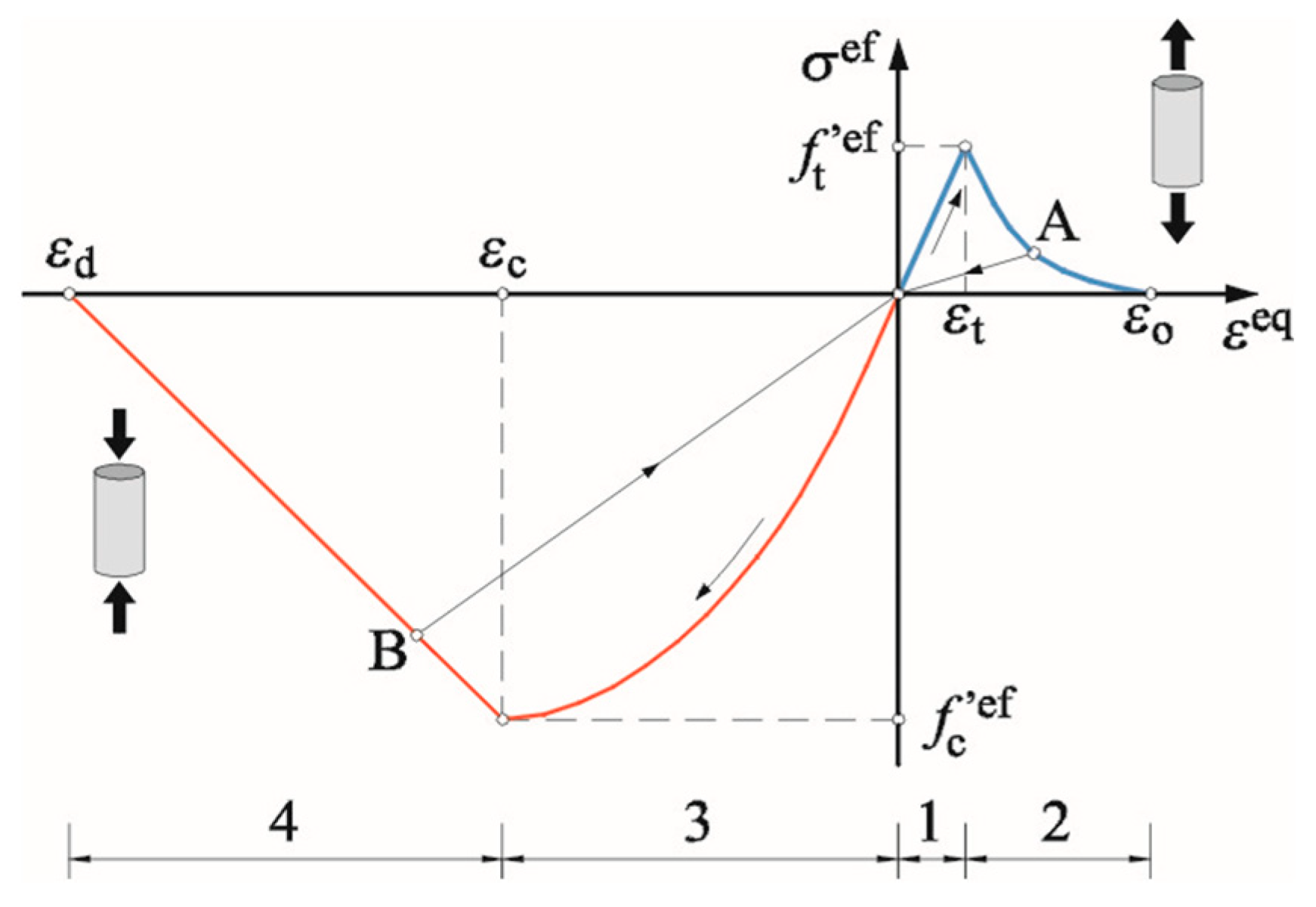
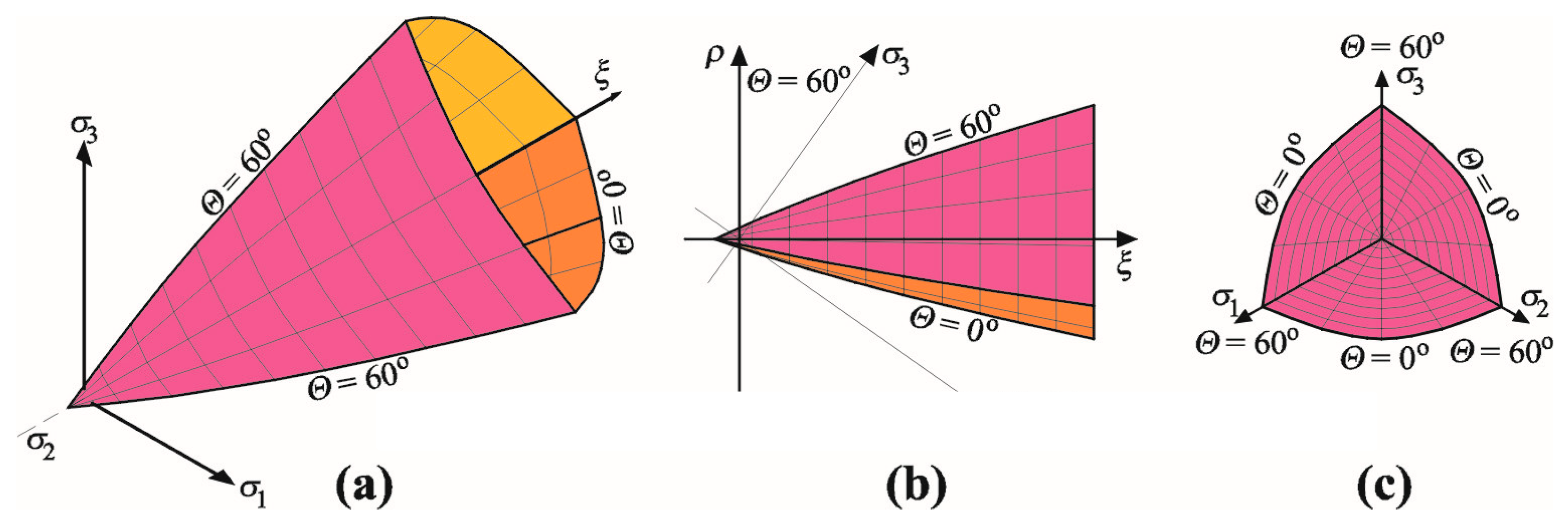
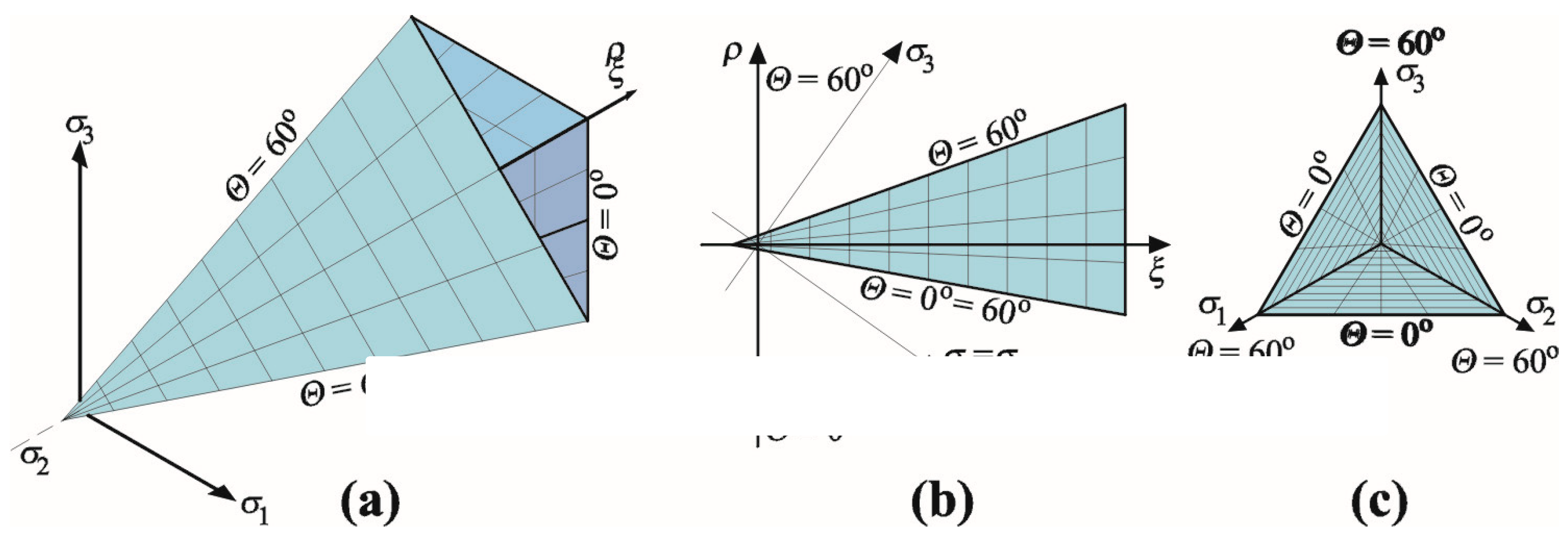
3.2. Material Models
- Non-linear behaviour under compression, including hardening and softening
- Material cracking resulting from tension, based on non-linear mechanics of cracking
- Defined failure criterion for the material exposed to biaxial compression
- Softening of the material due to tension
- Reduced stiffness of the wall after cracking
- Possible modelling of cracks with set or changeable direction
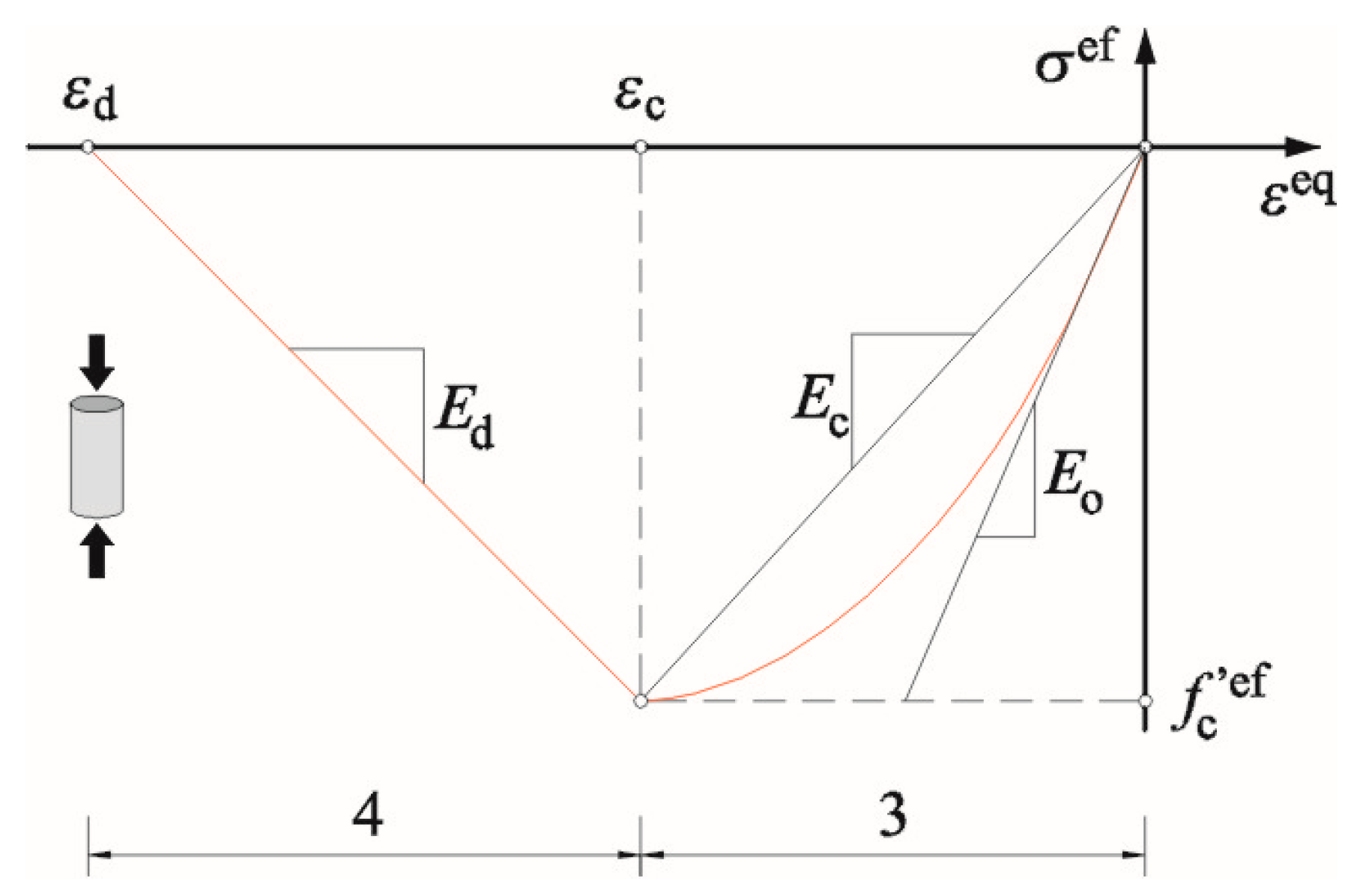
3.2.1. Model of Concrete in Confining Elements—Elastic-Based Degradation Model
- The model of fictitious cracks resulting from the cracking mechanics and the accepted rule for crack width,
- The model of local deformations of a material point.
3.2.2. Model of the Wall and Lintels—Elastic–Plastic-Based Degradation Model
3.2.3. Model of Contact (Interface) Elements
3.2.4. Model of Reinforcement
3.2.5. Numerical Models of Whole Walls and Their Parts
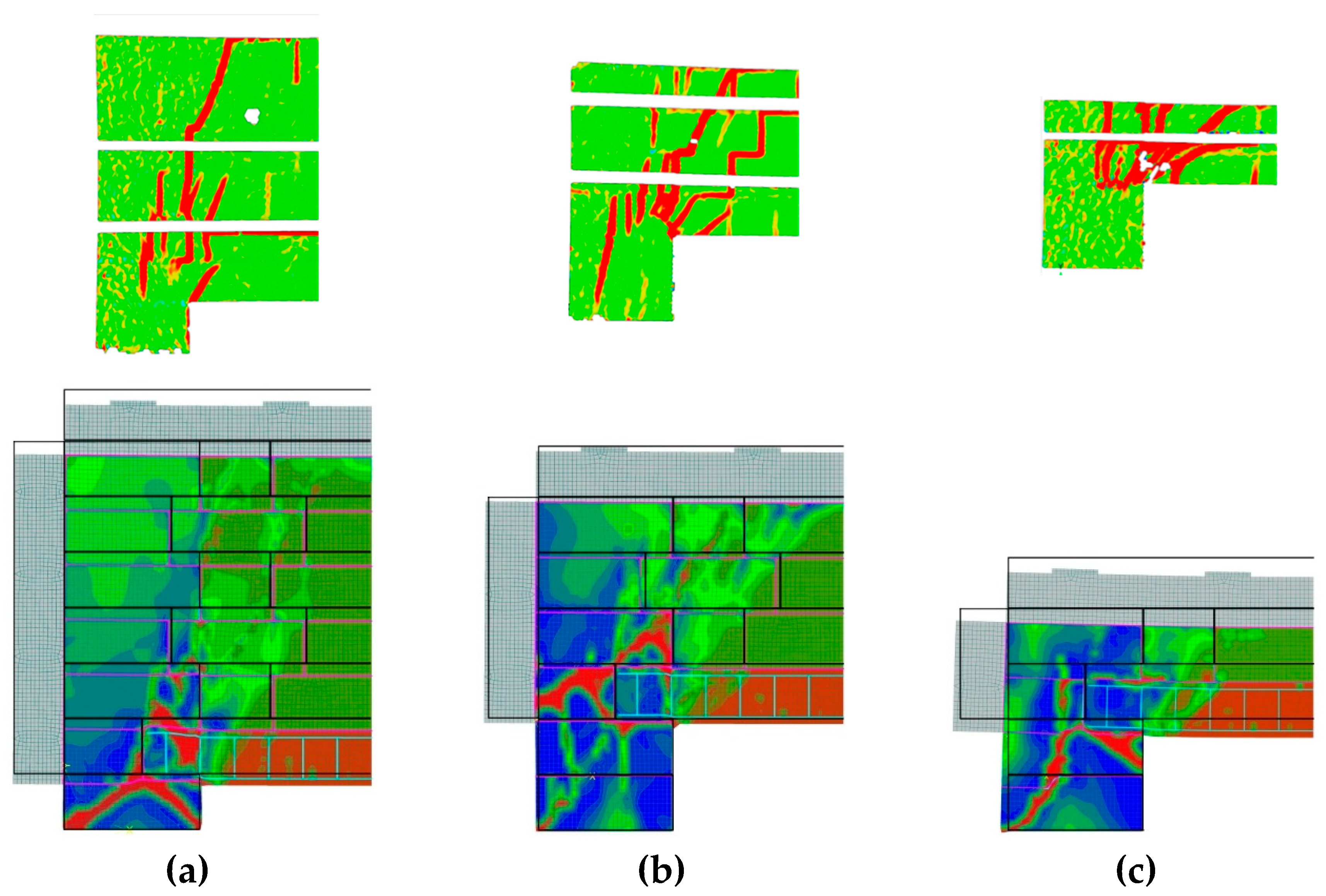
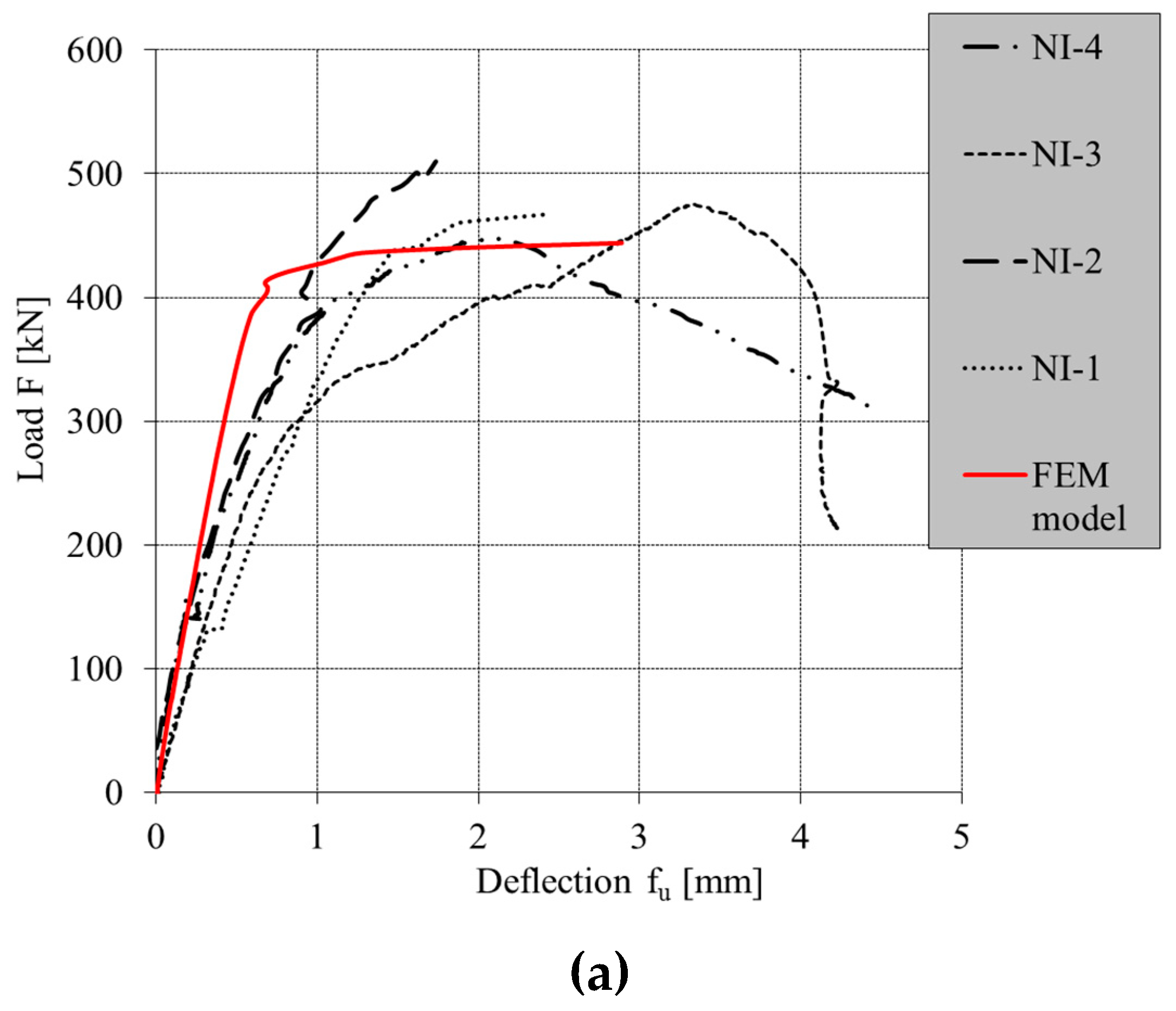
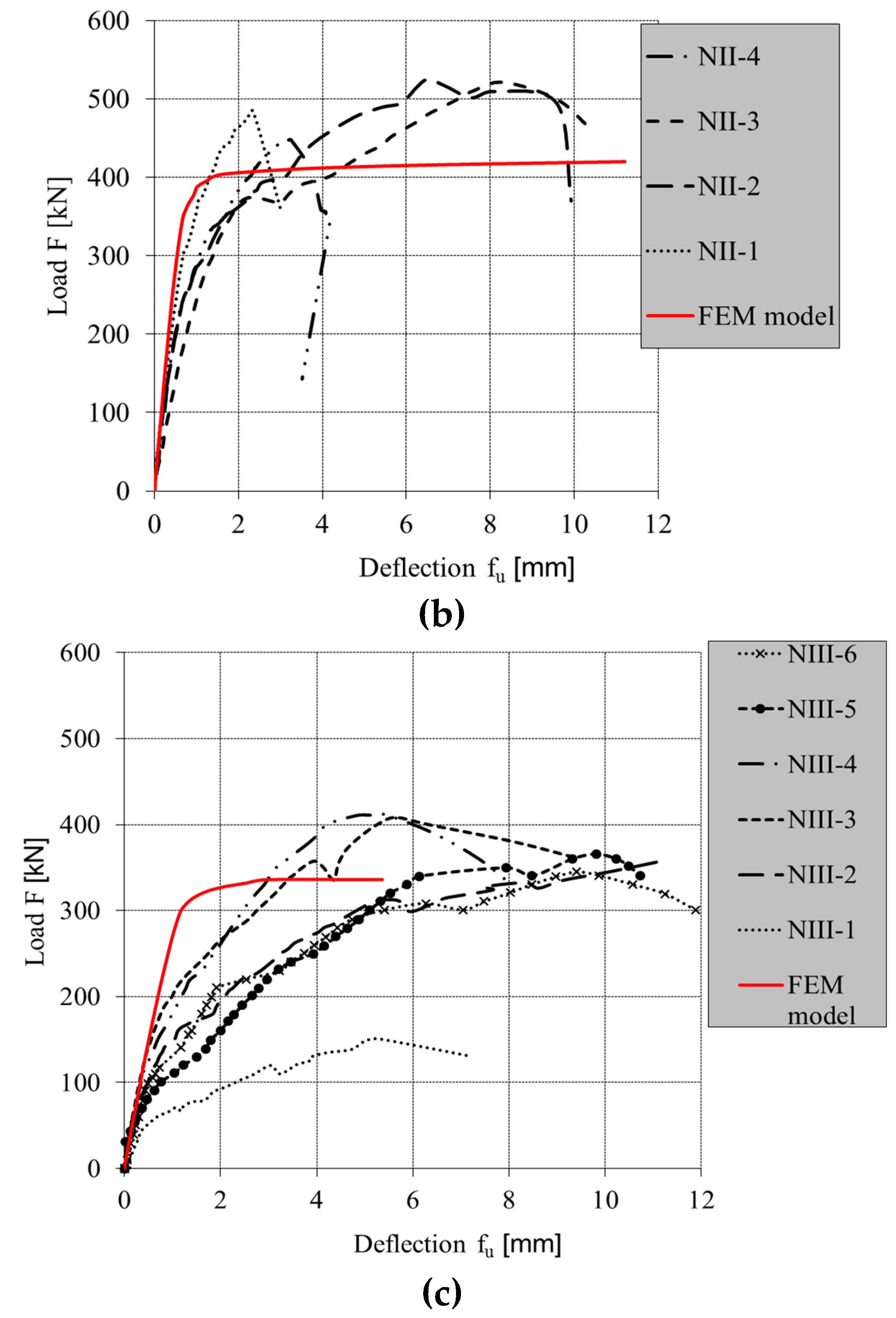
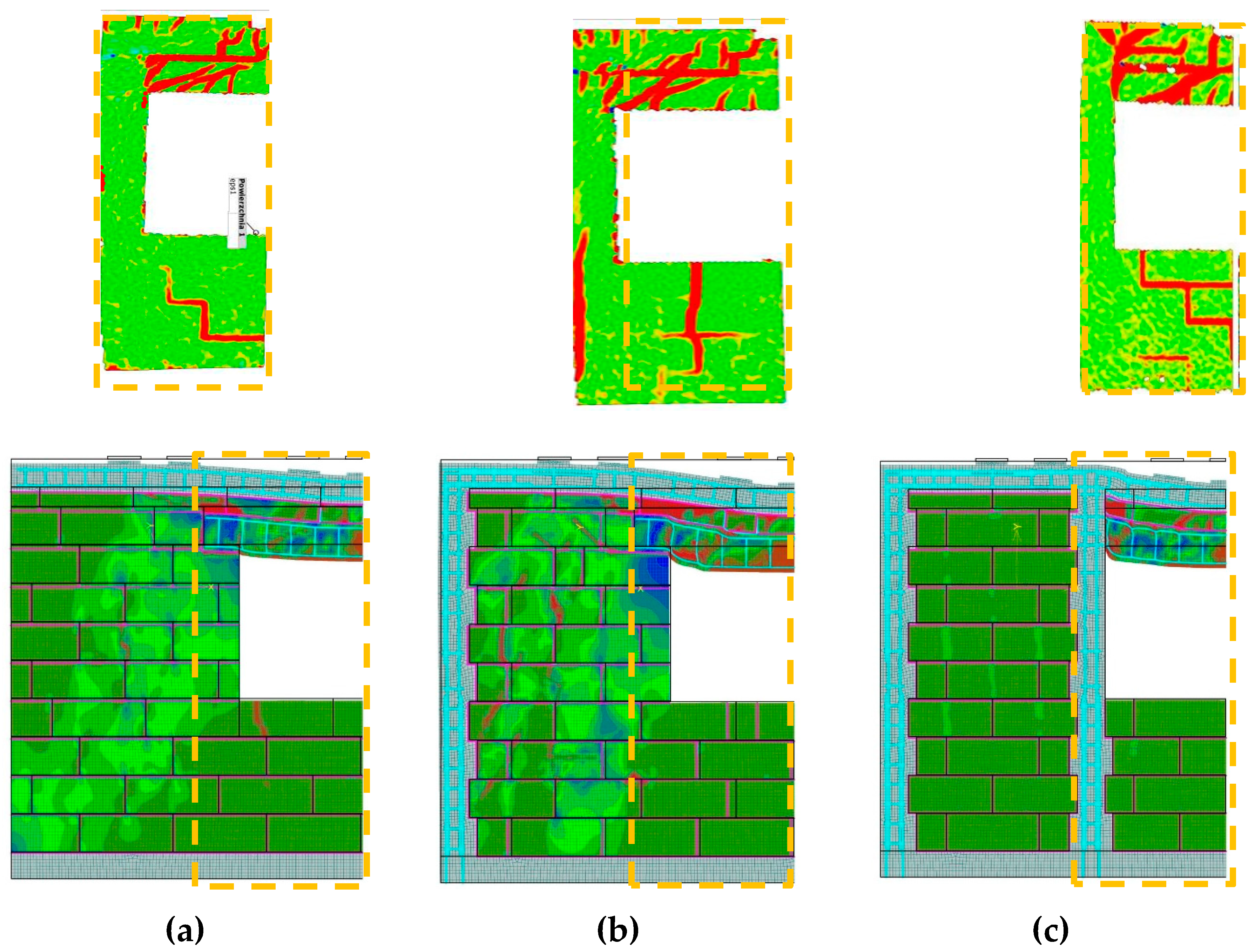
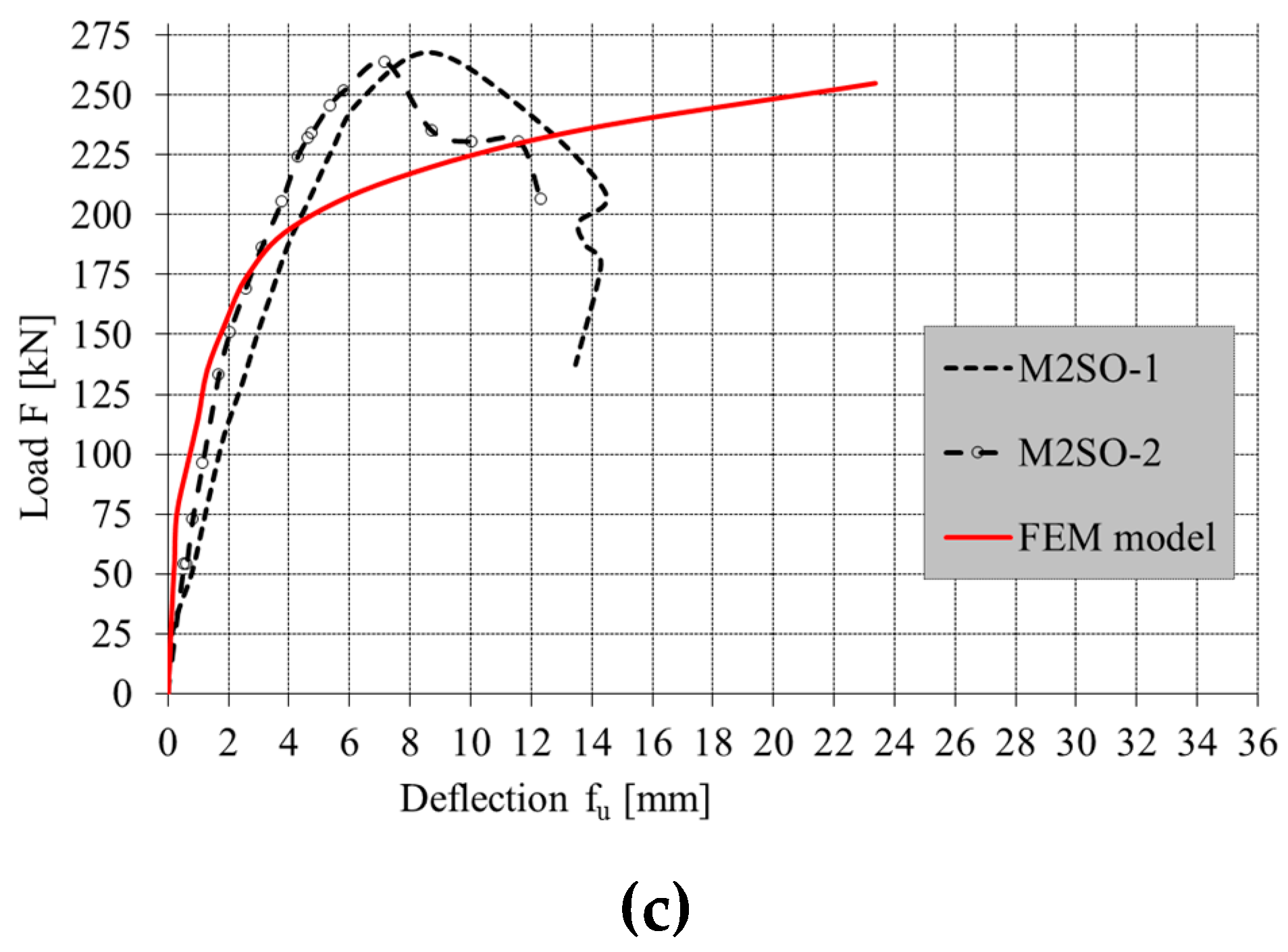
4. Results of Numerical Analysis
4.1. Parts of Walls
4.2. Full-Scale Walls
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zienkiewicz, O.C.; Taylor, R.L. The Finite Element Method; MacGraw-Hill Book Company: New York, NY, USA, 1977. [Google Scholar]
- Chen, W.F. Plasticity for Reinforced Concrete; McGraw-Hill Book Company: New York, NY, USA, 1982. [Google Scholar]
- Jirásek, M.; Bazant, Z.P. Inelastic Analysis of Structures; John Wiley & Sons: Hoboken, NJ, USA, 2002. [Google Scholar]
- Nasiri, E.; Liu, Y. Development of a detailed 3D FE model for analysis of the in-plane behaviour of masonry infilled concrete frames. Eng. Struct. 2017, 143, 603–616. [Google Scholar] [CrossRef]
- Wendner, R.; Vorel, J.; Smith, J.; Hoover, C.G.; Bažant, Z.P.; Cusatis, G. Characterization of concrete failure behavior: A comprehensive experimental database for the calibration and validation of concrete models. Mater. A. Struct. 2015, 48, 3603–3626. [Google Scholar] [CrossRef]
- Lemos, J.V. Discrete Element Modeling of the Seismic Behavior of Masonry Construction. Buildings 2019, 9, 43. [Google Scholar] [CrossRef]
- Rasulo, A.; Pelle, A.; Lavorato, D.; Fiorentino, G.; Nuti, C.; Briseghella, B. Finite Element Analysis of Reinforced Concrete Bridge Piers Including a Flexure-Shear Interaction Model. Appl. Sci. 2020, 10, 2209. [Google Scholar] [CrossRef]
- Drobiec, Ł. FEM model of the masonry made of hollow calcium silicate units. Proc. Eng. 2017, 193, 462–469. [Google Scholar] [CrossRef]
- Drobiec, Ł. Limitation of cracking in AAC masonry under the window zone. Mauerwerk 2017, 21, 332–342. [Google Scholar] [CrossRef]
- Drobiec, Ł. Analyse von Spannungen und Verformungen im Brüstungsbereich von Wandmodellen aus Porenbeton und Kalksandstein. Mauerwerk 2020, 24, 2–16. [Google Scholar] [CrossRef]
- Marcon, M.; Vorel, J.; Ninšcević, K.; Wan-Wendner, R. Modeling Adhesive Anchors in a Discrete Element Framework. Materials 2017, 10, 917. [Google Scholar] [CrossRef]
- Ceroni, F.; Darban, H.; Luciano, R. Analysis of bond behavior of injected anchors in masonry elements by means of Finite Element Modeling. Comp. Struct. 2020, 241, 112099. [Google Scholar] [CrossRef]
- Christou, G.; Ungermann, J.; Wolters, K.; Hegger, J.; Claßen, M. Ermüdung von Verbunddübelleisten: Analyse und Modellentwicklung. Beton- und Stahlbetonbau. 2020, 115, 355–363. [Google Scholar] [CrossRef]
- Deng, M.; Yang, S. Experimental and numerical evaluation of confined masonry walls retrofitted with engineered cementitious composites. Eng. Struct. 2020, 207, 110249. [Google Scholar] [CrossRef]
- Nowak, R.; Orłowicz, R. Selected problems of failures and repairs of historic masonry vaults. MATEC Web Conf. 2019, 284, 05008. [Google Scholar] [CrossRef]
- Abdellatef, M.; Alnaggar, M.; Boumakis, G.; Cusatis, G.; Di-Luzio, G.; Wendner, R. Lattice Discrete Particle Modeling for coupled concrete creep and shrinkage using Solidification Microprestress Theory. CONCREEP 2015, 10, 184–193. [Google Scholar]
- Rita, M.; Fairbairn, E.; Ribeiro, F.; Andrade, H.; Barbosa, H. Optimization of Mass Concrete Construction Using a Twofold Parallel Genetic Algorithm. Appl. Sci. 2018, 8, 399. [Google Scholar] [CrossRef]
- Ponikiewski, T.; Steidl, T.; Krause, P. Moisture transport in cellular concrete walls with the connector for thermal insulation. Period. Polytech. Civ. Eng. 2018, 62, 986–991. [Google Scholar] [CrossRef]
- Drobiec, Ł.; Wyczółkowski, R.; Kisiołek, A. Numerical Modelling of Thermal Insulation of Reinforced Concrete Ceilings with Complex Cross-Sections. Appl. Sci. 2020, 10, 2642. [Google Scholar] [CrossRef]
- Podroužek, J.; Marcon, M.; Ninšcević, K.; Wan-Wendner, R. Bio-Inspired 3D Infill Patterns for Additive Manufacturing and Structural Applications. Materials. 2019, 12, 499. [Google Scholar] [CrossRef]
- Drobiec, Ł. FEM Micro-Model for Masonry Reinforced in Bed Joints. Proc. Brit. Mason. Soc. 2006, 5, 2005. [Google Scholar]
- Jasiński, R. Numerical Analysis of the Strains and Stress States Reinforced Clay Brick Masonry Walls Horizontally Sheared. Int. J. Eng. Technol. Manag. 2018, 8, 20–37. [Google Scholar] [CrossRef]
- Drobiec, Ł.; Jasiński, R. Adoption of the Willam-Warnke failure criterion for describing behavior of Ca-Si hollow blocks. Procedia Engin. 2017, 193, 470–477. [Google Scholar] [CrossRef]
- Jasiński, R. Identification of the Parameters of Menetrey -Willam Failure Surface of Calcium Silicate Units. IOP Conference Series. Mat. Sci. Eng. 2017, 245, 032045. [Google Scholar] [CrossRef]
- D’Altri, A.M.; Messali, F.; Rots, J.; Castellazzi, G.; De Miranda, S. A damaging block-based model for the analysis of the cyclic behaviour of full-scale masonry structures. Eng. Fr. Mech. 2019, 209, 423–448. [Google Scholar] [CrossRef]
- D’Altri, A.M.; Sarhosis, V.; Milani, G.; Rots, J.; Cattari, S.; Lagomarsino, S.; Sacco, E.; Tralli, A.; Castellazzi, G.; de Miranda, S. Modeling Strategies for the Computational Analysis of Unreinforced Masonry Structures: Review and Classification. Arch. Comput. Methods Eng. 2019, 1–33. [Google Scholar] [CrossRef]
- Mazur, W.; Drobiec, L.; Jasiński, R. Research of Light Concrete Precast Lintels. Proc. Engin. 2016, 161, 611–617. [Google Scholar] [CrossRef]
- Mazur, W.; Drobiec, Ł.; Jasiński, R. Research and numerical investigation of masonry—AAC precast lintels interaction. Procedia Eng. 2017, 193, 385–392. [Google Scholar] [CrossRef]
- Drobiec, Ł.; Jasiński, R.; Mazur, W. Precast lintels made of autoclaved aerated concrete—Test and theoretical analyses. Cement Wapno Beton 2017, 5, 339–413. [Google Scholar]
- Chu, T.C.; Ranson, W.F.; Sutton, M.A.; Peters, W.H. Application of digital-image-correlation techniques to experimental mechanics. Experiment. Mech. 1985, 25, 232–244. [Google Scholar] [CrossRef]
- Lourenço, P.B. Computational Strategies for Masonry Structures. Ph.D. Thesis, Delft University, Delft, The Netherland, 1996. [Google Scholar]
- Lourenço, P.B.; Rots, J.G.; Blaauwendraad, J. Two Approaches for the Analysis of Masonry Structures. Micro Macro-Modeling. Heron. 1995, 4, 313–340. [Google Scholar]
- Gambrotta, L.; Logomarsino, S. Damage models for the seismic response of trick masonry shear walls. Part I. The mortar joint model and its applications. Earthq. Eng. Struct. Dynam. 1997, 26, 423–439. [Google Scholar] [CrossRef]
- Gambrotta, L.; Logomarsino, S. Damage models for the seismic response of trick masonry shear walls. Part II. The continuum model and its applications. Earthq. Eng. Struct. Dynam. 1997, 26, 441–462. [Google Scholar] [CrossRef]
- Lopez, J.; Oller, S.; Onnte, E.; Lubliner, J. A Homogeneous Constitutive Model for Masonry. Int. J. Num. Meth. Eng. 1999, 46, 149–156. [Google Scholar] [CrossRef]
- Lourenço, P.B.; Rots, J.G.; Blaauwendraad, J. Continuum Model for Masonry: Parameter Estimation and Validation. ASCE J. Struct. Eng. 1998, 124, 642–652. [Google Scholar] [CrossRef]
- Lourenço, P.B. On the Use of Homogenization Techniques for the Analysis of Masonry Structures. Mason. Int. 1997, 1, 26–32. [Google Scholar]
- Lourenço, P.B. Two Aspect Related to the Analysis of Masonry Structures: Size Effect and Parameter Sensibility; Technische Universiteit Delft: Delft, The Netherland, 1997. [Google Scholar]
- Lotfi, H.R.; Shing, P.B. Interface Model Applied to Fracture of Masonry Structures. ASCE J. Struct. Eng. 1994, 1, 63–80. [Google Scholar] [CrossRef]
- Jasiński, R. Research and Modelling of Masonry Shear Walls. Ph.D. Thesis, Silesian University of Technology, Gliwice, Poland, 2017. [Google Scholar]
- Alfaiate, J.; de Almeida, J.R. Modelling Discrete Cracking on Masonry Walls. Masonry International. J. Brit. Mason. Soc. 2004, 2, 83–93. [Google Scholar]
- Jasiński, R. Validation of elastic-brittle, and elastic-plastic FEM model of the wall made of calcium silicate and AAC masonry units. IOP Conference Series. Mat. Sci. Eng. 2019, 603, 1757–8981. [Google Scholar] [CrossRef]
- Červenka, J.; Papanikolaou, V.K. Three dimensional combined fracture-plastic material model for concrete. Int. J. Plasticity. 2008, 24, 2192–2220. [Google Scholar] [CrossRef]
- Hordijk, D.A. ocal Approach to Fatigue of Concrete. Ph.D. Thesis, Delft University, Delft, The Netherland, 1991. [Google Scholar]
- Code, M. Fib Model Code for Concrete Structures; Ernst & Sohn: Berlin, Germany, 2010. [Google Scholar]
- Kupfer, H.; Hilsdorf, H.K.; Rüsch, H. Behavior of Concrete under Biaxial Stress. J. Am. Concr. Inst. Proc. 1969, 8, 656–666. [Google Scholar]
- Menétrey, P.; Willam, K.J. Triaxial failure criterion for concrete and its generalization. Aci Struct. J. 1995, 92, 311–318. [Google Scholar] [CrossRef]
- Hoek, E.; Brown, E.T. Empirical Criterion for Rock Masses. J. Geotech. Eng. Div. 1980, 106, 1575. [Google Scholar]
- Weihe, S. Implicit Integration Schemes for Multi-Surface Yeld Criteria Subjected to Hardening/Softening Behavior. Master’s Thesis, University of Colorado-Boulder, Boulder, Colorado, 1989. [Google Scholar]
- Červenka, V.; Červenka, J. ATENA Program Documentation. Copyright 2000–2015 Červenka Consulting s.r.o. Prague, 2015. Available online: https://www.cervenka.cz/assets/files/atena-pdf/ATENA-Engineering-2D_Tutorial.pdf (accessed on 6 August 2020).
- Červenka, V. Constitutive model for cracked reinforced concrete. J. Proc. 1985, 82, 877–882. [Google Scholar] [CrossRef]
- Bruehwiler, E.; Wittman, F.H. The Wedge Splitting Test, A New Method of Performing Stable Fracture-Mechanics Tests. Eng. Fract. Mech. 1990, 35, 117–125. [Google Scholar] [CrossRef]
- Drobiec, Ł.; Jasiński, R.; Rybarczyk, T. The influence of the type of mortar on the compressive behaviour of walls made of Autoclaved Aerated Concrete (AAC). In Brick and Block Masonry—Trends, Innovations and Challenges; Taylor & Francis Group: London, UK, 2016; pp. 1531–1538. [Google Scholar]
- Jasiński, R. Research on the Influence of Bed Joint Reinforcement on Strength and Deformability of Masonry Shear Walls. Materials 2019, 12, 2543. [Google Scholar] [CrossRef] [PubMed]
- Drobiec, Ł. Analysis of AAC walls subjected to vertical load. Mauerwerk 2019, 23, 387–403. [Google Scholar] [CrossRef]








| Element Name | Model Drawing | Model during Tests | Number of Models |
|---|---|---|---|
| 1 | 2 | 3 | 4 |
| N1 | 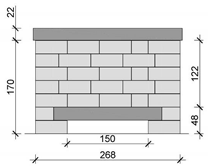 |  | 4 |
| N2 |  |  | 4 |
| N3 | 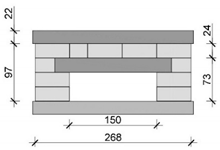 |  | 6 |
| Element Name | Model Drawing | Model during Tests | Number of Models |
|---|---|---|---|
| 1 | 2 | 3 | 4 |
| MNSO | 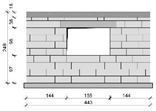 |  | 2 |
| MSO | 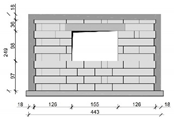 |  | 2 |
| M2SO | 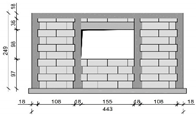 |  | 2 |
| Parameter | Test Formula or Results | Concrete in Confining Elements and Tie Beams |
|---|---|---|
| Uniaxial compressive strength , N/mm2 | Obtained from tests on cylindrical specimens ø150 × 300 mm | 25.5 |
| Deformations corresponding to uniaxial compressive strength of concrete εc | 1.682 × 10−3 | |
| Uniaxial tensile strength , N/mm2 | Obtained from “Brasilian Test” for cylindrical specimens ø 150 × 300 mm | 2.32 |
| Initial modulus of elasticity , N/mm2 | Obtained from tests on cylindrical specimens ø 150 × 300 mm | 3032 |
| Poisson’s ratio | 0.2 | |
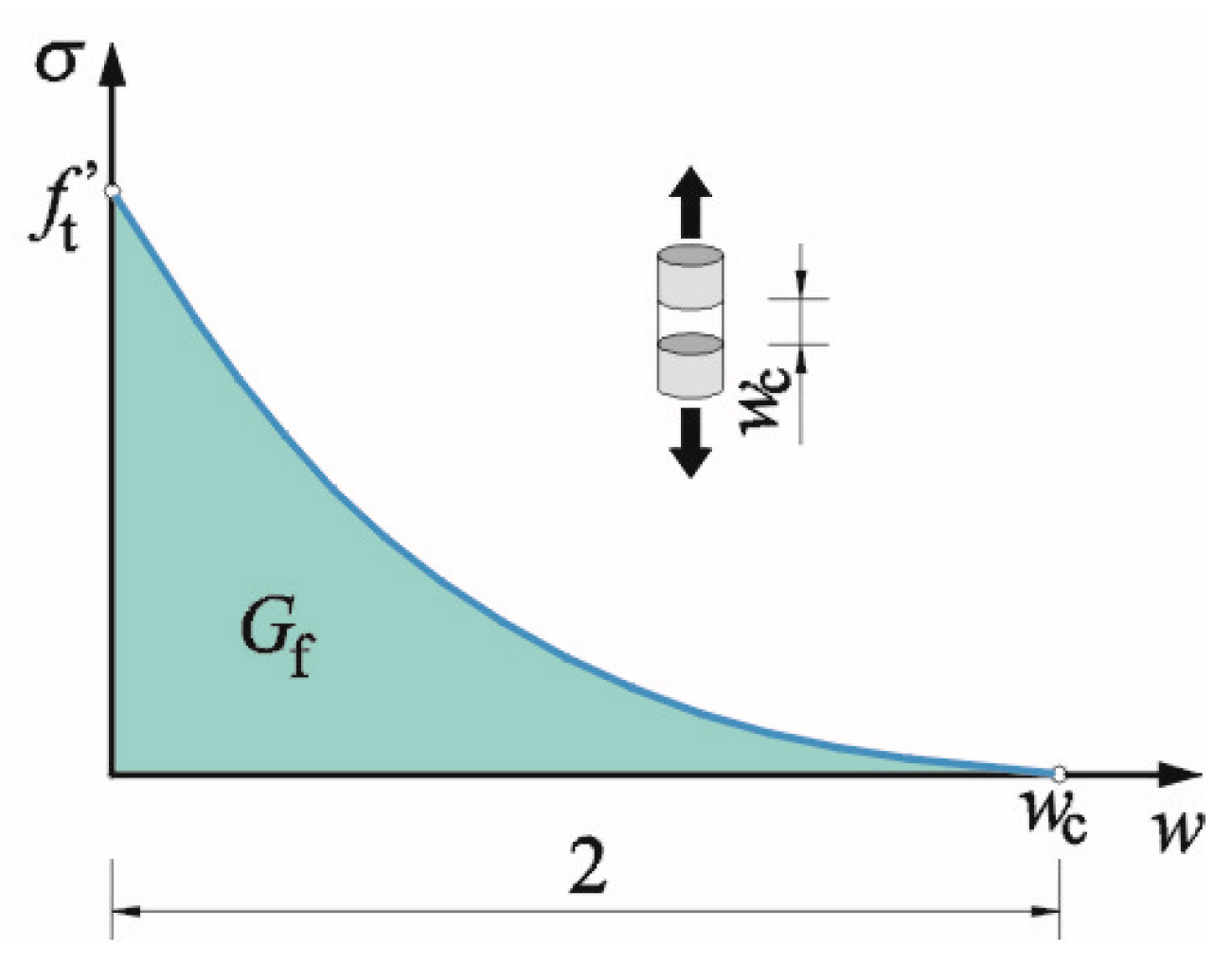
| Fracture energy Gf, MN/m | Calculated from the relationship | 5.793 × 10−5 |
| Weakening function at tension | Assumed softening described by the exponential function | exponential |
| Displacement wc under tension, m | Displacements were calculated from the equation | −5.0 × 10−4 |
| Model of cracks | developing in uniform directions | fixed |
| Weakening under compression | Assumed default value of displacement | 0.05 mm |
| Reduced compressive strength in the direction parallel to cracks | Assumed default value of coefficient c | 0.8 |
| Parameter | Test Formula or Results | Masonry | Lintel |
|---|---|---|---|
| Uniaxial compressive strength fb, N/mm2 | Assumed from the tests | 4.04 | 3.71 |
| Plastic strain under compression εcp | Assumed from the tests | 3.33 × 10−4 | 3.771 |
| Uniaxial tensile strength fbt, N/mm2 | Assumed from the tests | 0.61 | 0.61 |
| Initial modulus of elasticity Ec, N/mm2 | Assumed from the tests | 2204 | 2198 |
| Poisson’s ratio ν | Assumed from the tests | 0.200 | 0.179 |
| Fracture energy Gf, MN/m | Assumed from the tests | 1.07 × 10−5 | 1.602 × 10−5 |
| Weakening function at tension | Assumed softening described by the exponential function | -- | -- |
| Displacement wc under tension [m] | Displacements were calculated from the equation | 4.36 × 10−4 | -- |
| Crack spacing smax [m] | Assumed constant value | 0.5 | 0.5 |
| Coefficient of tensile strength reduction at the softening phase cts | Assumed constant value for unreinforced material | 0 | 0 |
| Model of cracks | developing in uniform directions | -- | -- |
| Critical displacement under compression, m | −5.0 × 10−4 | −5.0 × 10−4 | |
| Reduction of compressive strength caused by cracking fc-lim | 0.8 | 0.8 | |
| Compressive stiffness of cracks sF | 20.0 | 20.0 | |
| Size of aggregate particles [m] | Determined on the basis of macroscopic observations of the masonry units | 0.02 | 0.02 |
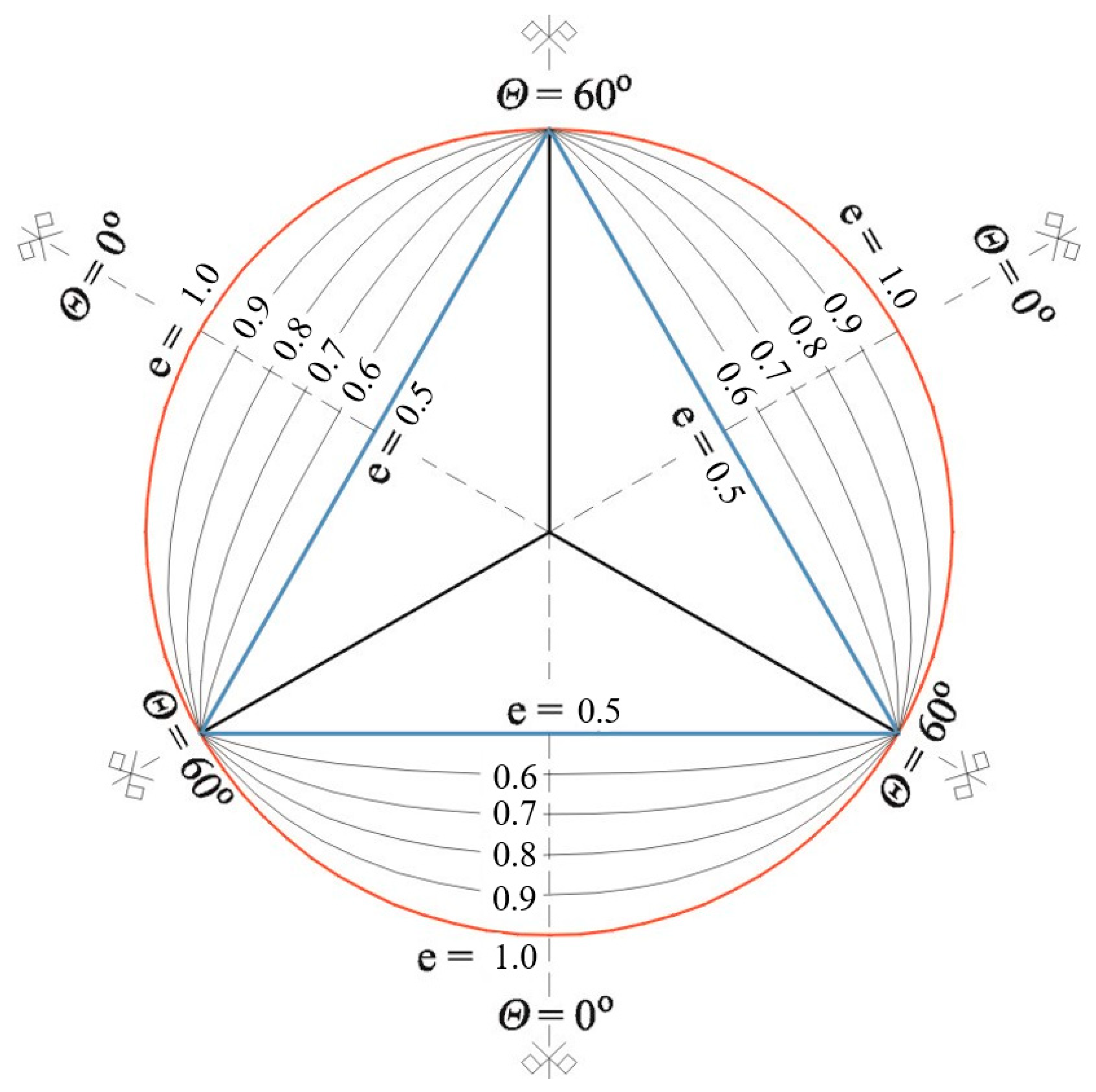
| Eccentricity of elliptical function e | Determined from the tests | 0.5 | 0.5 |
| Direction of plastic flow | Assumed as for incompressible material | β = 0 | β = 0 |
| Parameter | Test Formula or Results | Bed Joint | Head Joint |
|---|---|---|---|
| 1 | 2 | 3 | 4 |
| Normal stiffness Knn, MN/m | Calculated from the equation: E—the greater of the elasticity moduli of adjacent materials; a—dimension of finite element | 1.02 × 106 | 1.02 × 106 |
| Shear stiffness Ktt, MN/m | Calculated from the equation: E—the greater of the shear moduli of adjacent materials; a—dimension of finite element | 4.51 × 105 | 4.51 × 105 |
| Tensile strength fbt, N/mm2 | Determined from tests | 0.29 | 0 |
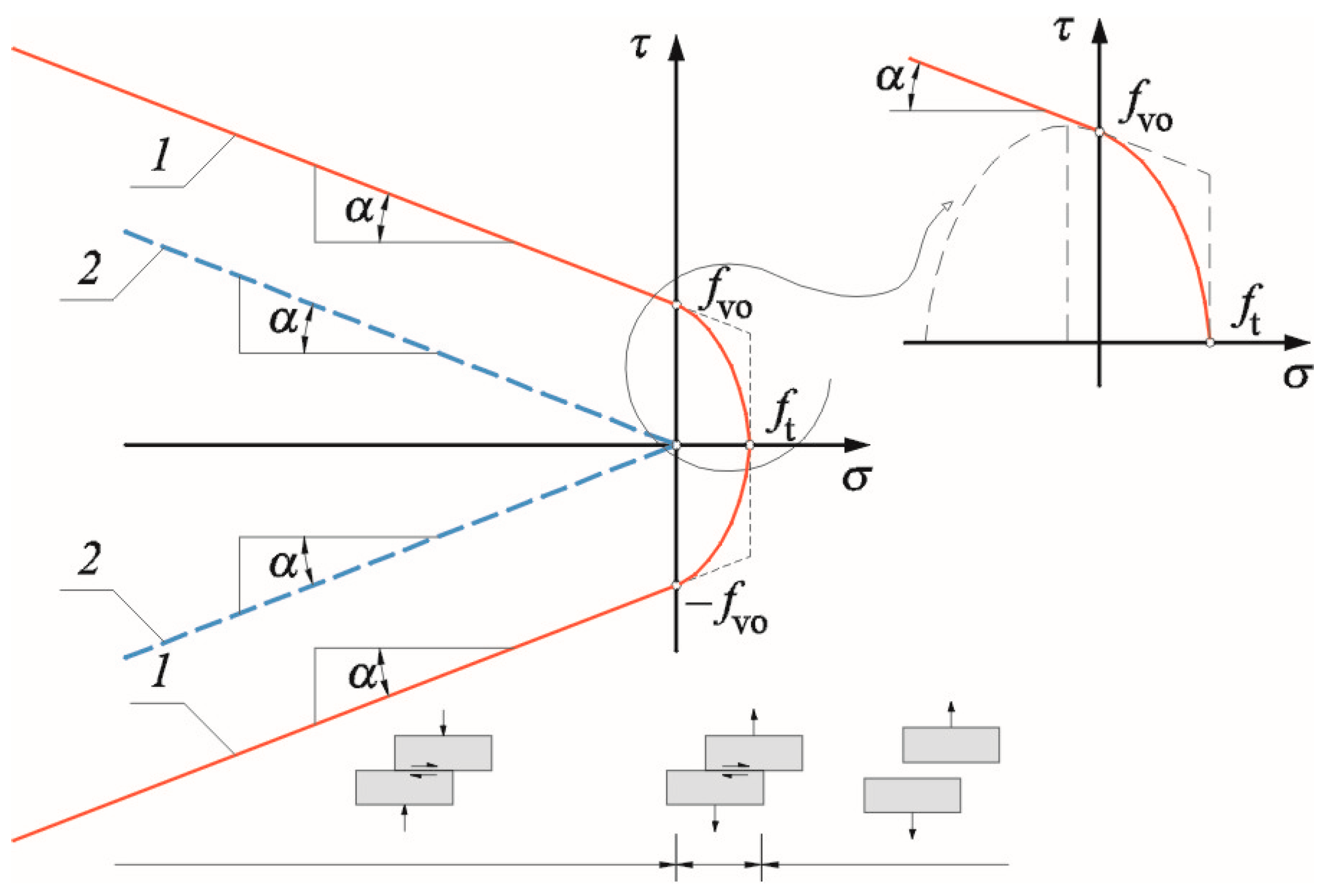
| Cohesion fv0 | Determined from tests | 0.31 | -- |
| Friction coefficient tgα | Determined from tests | 0.626 | 0.92 |
| Normal stiffness Knn,min, MN/m | Calculated as 0.01 Knn | 1.02 × 104 | 1.02 × 104 |
| Shear stiffness Ktt,min, MN/m | Calculated as 0.01 Ktt | 4.51 × 103 | 4.51 × 103 |
| Fracture energy under shearing , MN/m | Determined from tests | 2.37 × 104 | -- |
| Displacement u1c, mm | Calculated from the equation: | −6.13 × 104 | -- |
| Equivalent displacement , mm | Calculated from the equation: | 4.09 × 104 | -- |
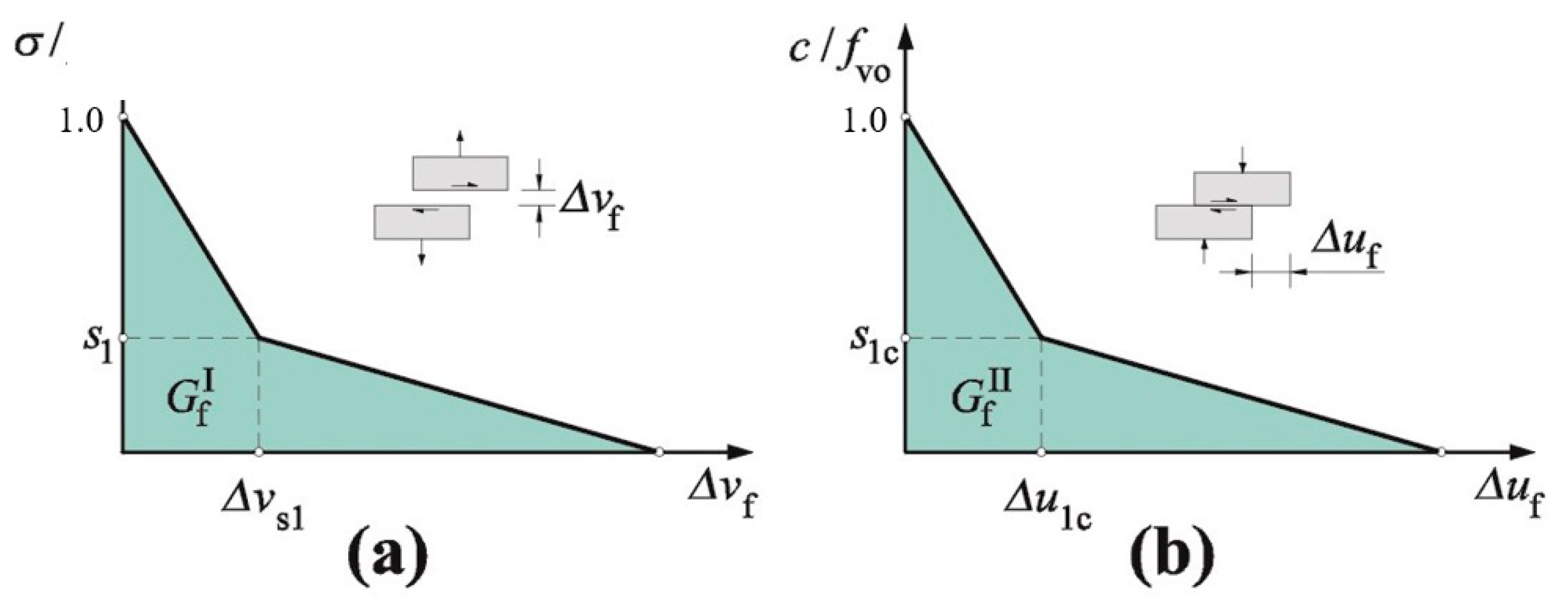
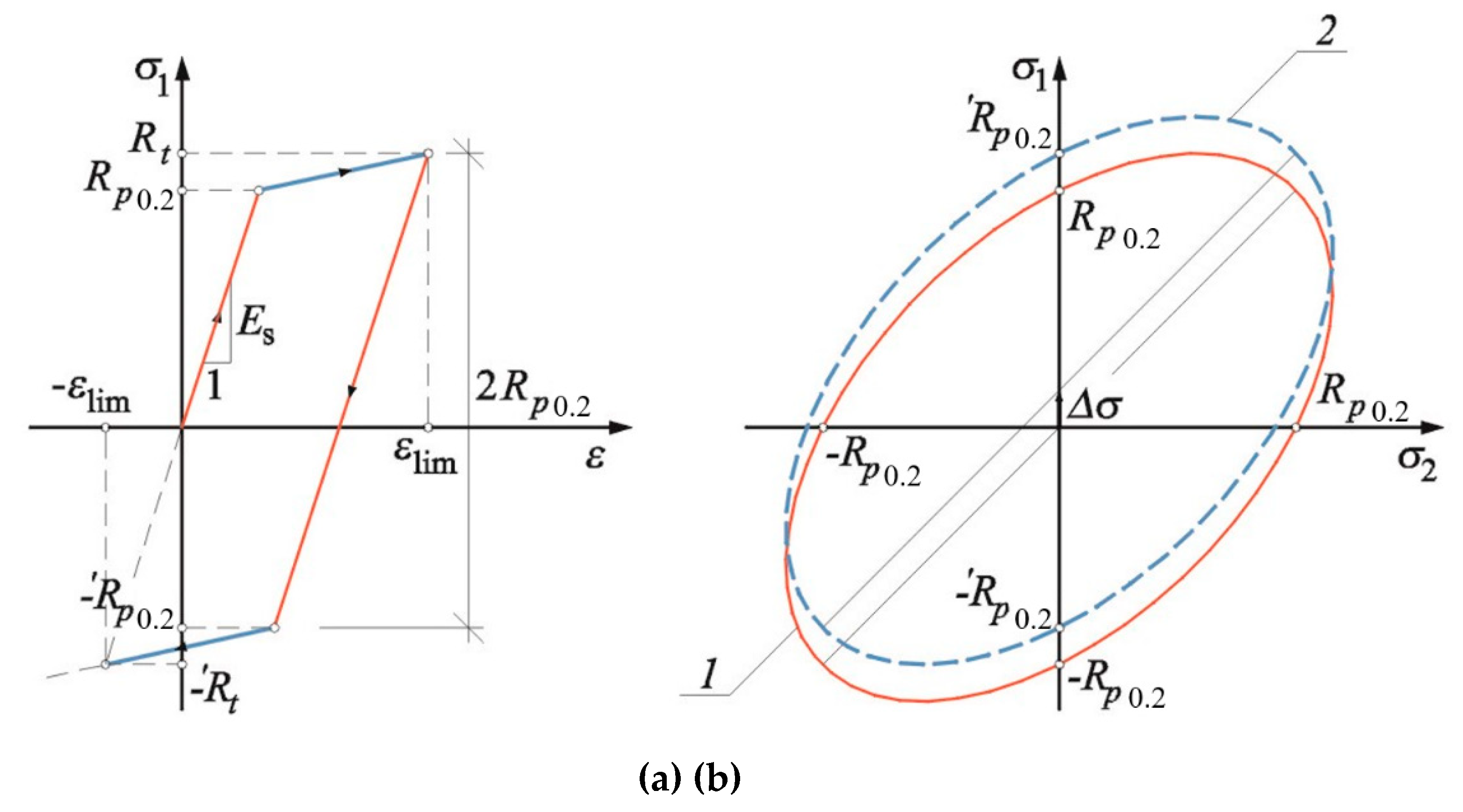
| Weakening function at tension | -- | Assumed default relationship acc. to Figure 3b | |
| Softening function at tension | Assumed as for incompressible material | Assumed two-section relationship acc. to Figure 3a | Assumed default relationship acc. to Figure 3b |
| Parameter | Test Formula or Results | Bed Joint | Head Joint |
|---|---|---|---|
| 1 | 2 | 3 | 4 |
| Normal stiffness Knn, MN/m | Calculated from the equation: | 3.92 × 106 | 1.02 × 106 |
| Shear stiffness Ktt, MN/m | Calculated from the equation: | 1.67 × 105 | 4.51 × 105 |
| Tensile strength fbt, N/mm2 | Assumed value as for the wall | 1.5 | 1.5 |
| Cohesion fv0 | ∞ | ∞ | |
| Friction coefficient tgα | ∞ | ∞ | |
| Normal stiffness Knn,min, MN/m | Calculated as 0.01 Knn | 3.92 × 104 | 1.02 × 104 |
| Shear stiffness Ktt,min, MN/m | Calculated as 0.01 Ktt | 1.67 × 103 | 4.51 × 103 |
| Type of Reinforcement and Dimensions of Rebar Cross-Section, mm | Parameter | |||||
|---|---|---|---|---|---|---|
| Es N/mm2 | ν | Rp0,2 N/mm2 | ET N/mm2 | Rt N/mm2 | εlim % | |
| Longitudinal reinforcement in lintels (round rebars with a diameter of 8 mm) | 198,000 | 0.3 | 520 | 245 | 544 | 9.9 |
| Transverse reinforcement in lintels (round rebars with a diameter of 4.5 mm) | 201,000 | 479 | 233 | 501 | 9.6 | |
| Longitudinal reinforcement in confining elements and tie beams (round rebars with a diameter of 12 mm) | 179,330 | 616 | 242 | 644 | 11.9 | |
| Transverse reinforcement in lintels (round rebars with a diameter of 10 mm) | 178,500 | 685 | 261 | 716 | 12.3 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Drobiec, Ł.; Jasiński, R.; Mazur, W.; Rybraczyk, T. Numerical Verification of Interaction between Masonry with Precast Reinforced Lintel Made of AAC and Reinforced Concrete Confining Elements. Appl. Sci. 2020, 10, 5446. https://doi.org/10.3390/app10165446
Drobiec Ł, Jasiński R, Mazur W, Rybraczyk T. Numerical Verification of Interaction between Masonry with Precast Reinforced Lintel Made of AAC and Reinforced Concrete Confining Elements. Applied Sciences. 2020; 10(16):5446. https://doi.org/10.3390/app10165446
Chicago/Turabian StyleDrobiec, Łukasz, Radosław Jasiński, Wojciech Mazur, and Tomasz Rybraczyk. 2020. "Numerical Verification of Interaction between Masonry with Precast Reinforced Lintel Made of AAC and Reinforced Concrete Confining Elements" Applied Sciences 10, no. 16: 5446. https://doi.org/10.3390/app10165446
APA StyleDrobiec, Ł., Jasiński, R., Mazur, W., & Rybraczyk, T. (2020). Numerical Verification of Interaction between Masonry with Precast Reinforced Lintel Made of AAC and Reinforced Concrete Confining Elements. Applied Sciences, 10(16), 5446. https://doi.org/10.3390/app10165446







