Free Vibrations of Tapered Horseshoe Circular Arch with Constant Volume
Abstract
1. Introduction
2. Problem Formulation
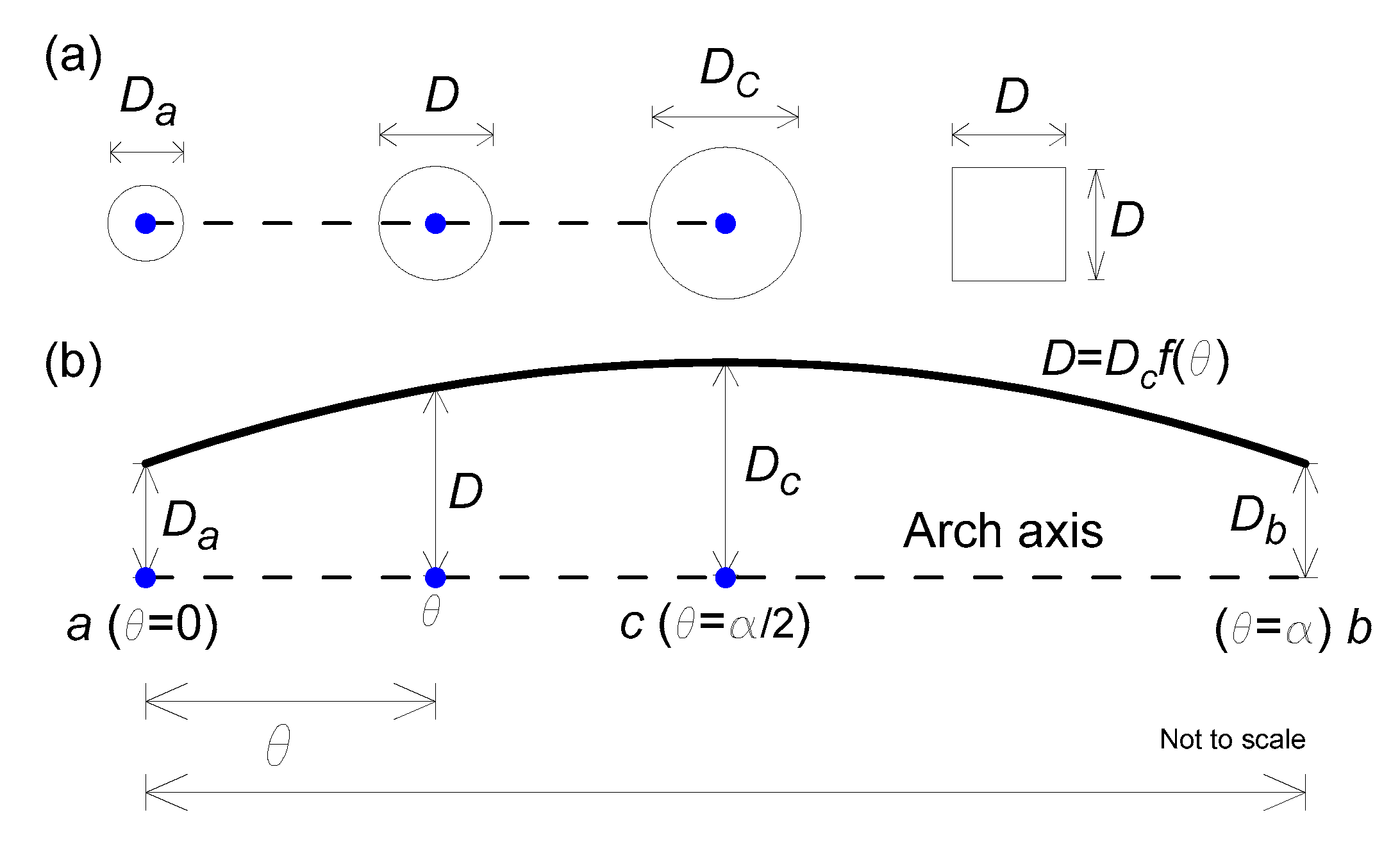
2.1. Geometry of Arch
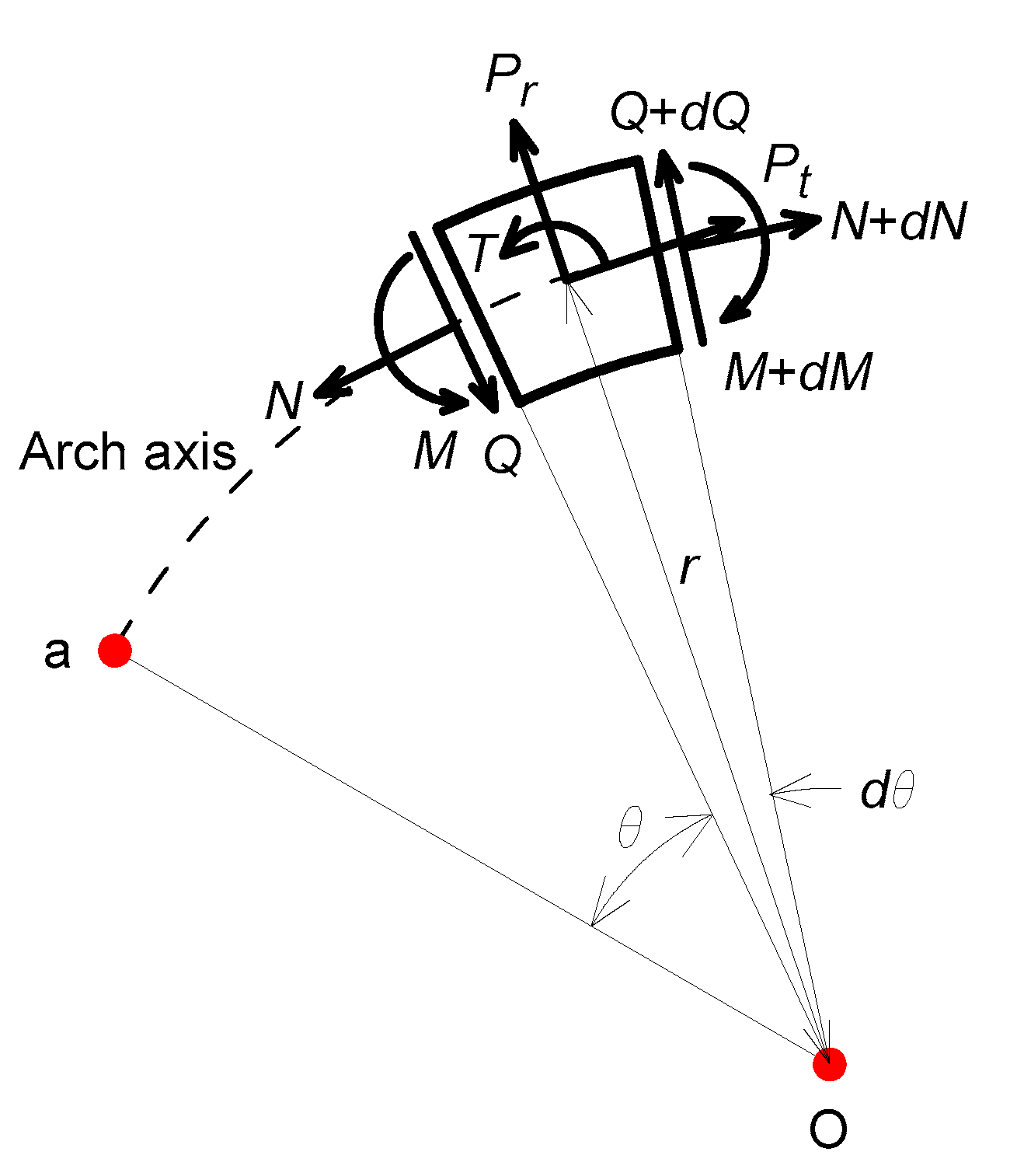
2.2. Governing Differential Equations
2.3. Boundary Conditions
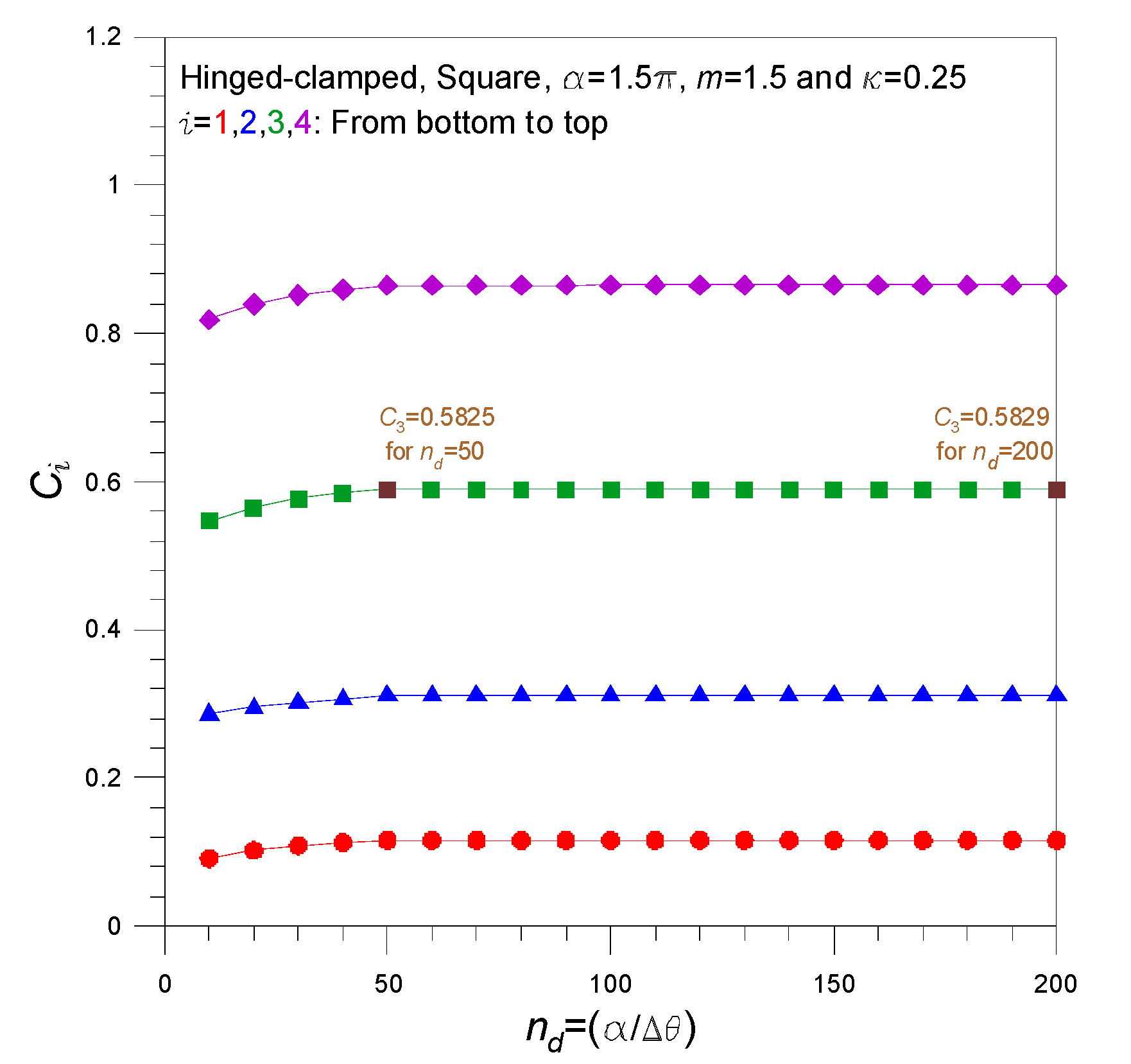
3. Solution Methods and Validation
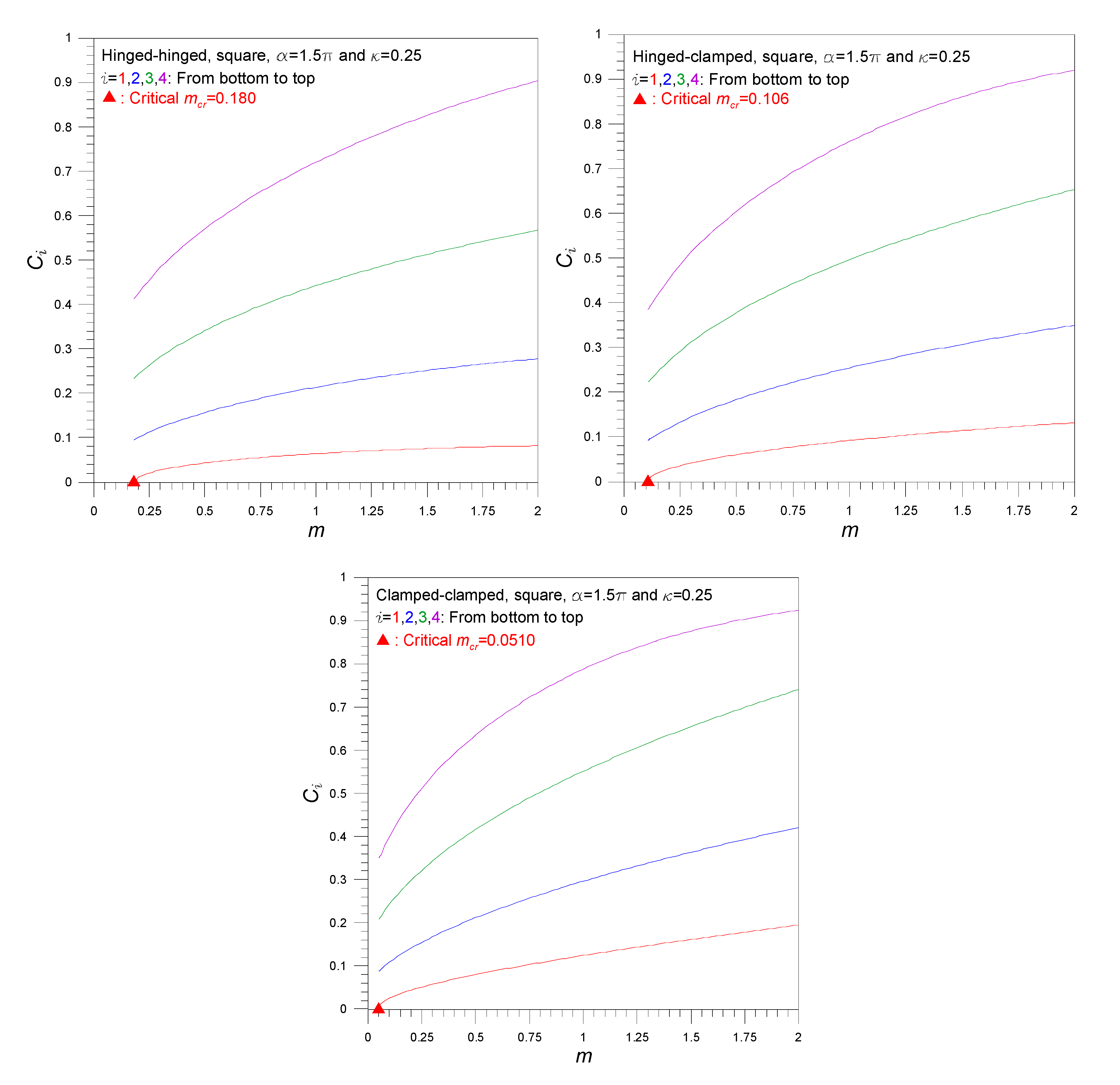
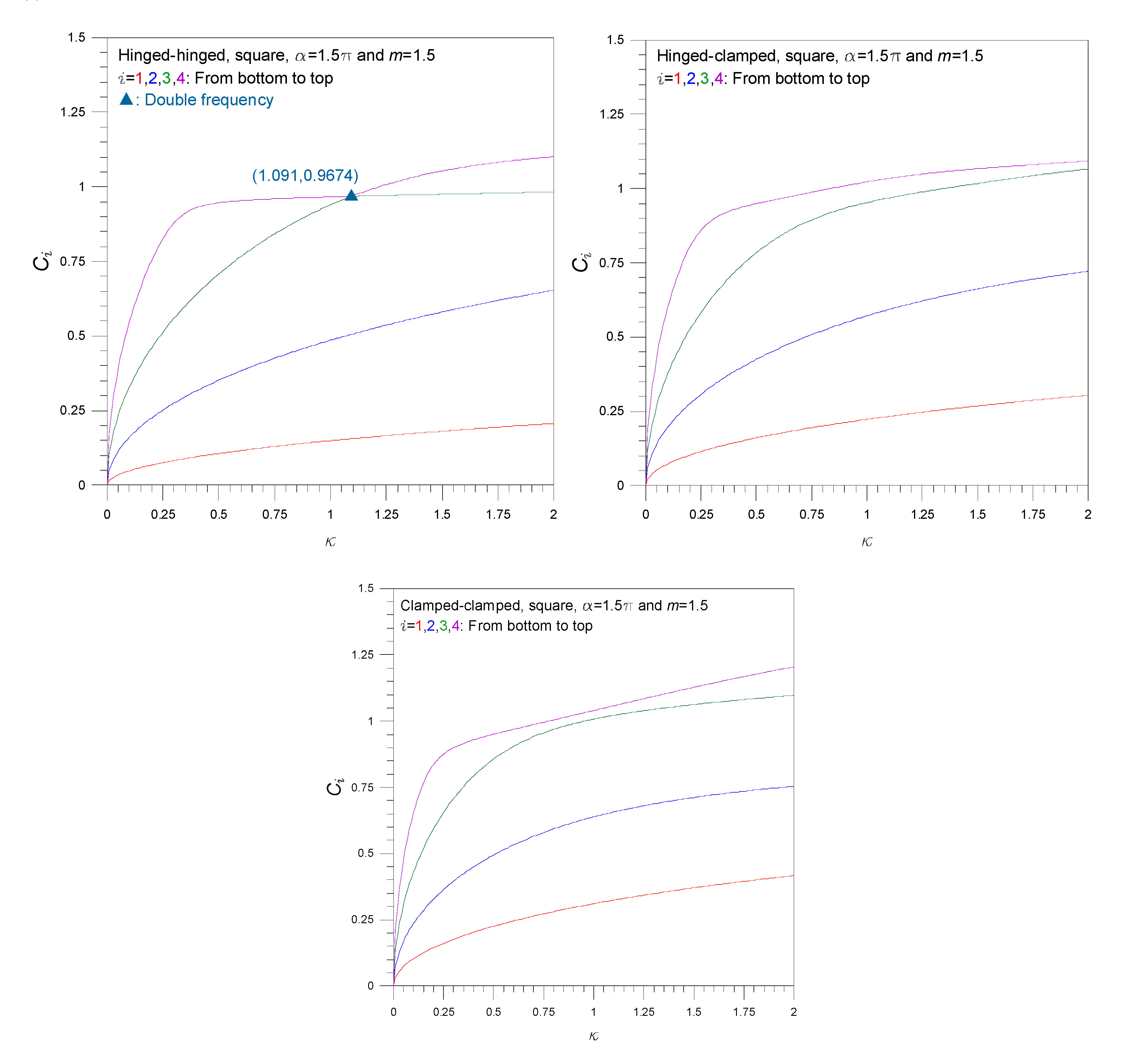
4. Numerical Examples and Discussions
5. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Lee, B.K.; Oh, S.J.; Lee, T.E. In-plane free vibrations of horseshoe circular arch. J. Korean Soc. Civ. Eng. 2014, 34, 1043–1052. [Google Scholar] [CrossRef]
- Lee, B.K.; Park, K.K.; Oh, S.J.; Lee, T.E. Planar free vibrations of horseshoe elliptic arch. KSCE J. Civil. Eng. 2016, 20, 1411–1418. [Google Scholar] [CrossRef]
- Lee, J.K.; Lee, B.K. Free vibration and buckling of tapered columns made of axially functionally graded materials. Appl. Math. Model. 2019, 75, 73–87. [Google Scholar] [CrossRef]
- Rao, S.S. Vibration of Continuous System; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007. [Google Scholar]
- Timoshenko, S.P. Vibration Problem in Engineering; D. Van Nostrand Company, Inc.: New York, NY, USA, 1937. [Google Scholar]
- Henrych, J. The Dynamics of Arches and Frames; Elsevier Science Publishing Company: Amsterdam, The Netherlands, 1981. [Google Scholar]
- Chidamparam, P.; Leissa, A.W. Vibrations and planar curved beams, rings and arches. Appl. Mech. Rev. 1993, 56, 467–483. [Google Scholar] [CrossRef]
- Tufekci, E.; Ozdemir, O. Exact solution of free in-plane vibration of a stepped circular arch. J. Sound Vib. 2016, 295, 725–738. [Google Scholar] [CrossRef]
- Lü, Q.; Lü, C.F. Exact two-dimensional solutions for in-plane natural frequencies of laminated circular arches. J. Sound Vib. 2009, 318, 920–982. [Google Scholar] [CrossRef]
- Joo, S.M.; Park, K.K.; Lee, B.K.; Hwang, H.J. Free vibration analysis of fixed ended parabolic arches. J. Korean Soc. Civ. Eng. 1985, 5, 31–38. [Google Scholar]
- Nieh, K.Y.; Huang, C.S.; Tseng, Y.P. An analytical solution for in-plane free vibration and stability of loaded elliptic arches. Comput. Struct. 2003, 81, 1311–1327. [Google Scholar] [CrossRef]
- Malekzadeh, P.; Setoodeh, A.R.; Barmshouri, E. A hybrid layerwise and differential quadrature method for in-plane free vibration of laminated thick circular arches. J. Sound Vib. 2008, 315, 212–225. [Google Scholar] [CrossRef]
- Shin, Y.J.; Kwon, K.M.; Yun, J.H. Vibration analysis of a circular arch with variable cross-section using differential transformation and generalized differential quadrature. J. Sound Vib. 2008, 309, 9–19. [Google Scholar] [CrossRef]
- Noori, A.R.; Aslan, T.A.; Temel, B. An efficient approach for in-plane free and forced vibrations of axially functionally graded parabolic arches with nonuniform cross section. Compos. Struct. 2018, 200, 701–710. [Google Scholar] [CrossRef]
- Lee, J.K.; Lee, B.K. Free vibration of AFG circular arch with symmetric and anti-symmetric boundary conditions at mid-arc. Symmetry 2020, 12, 417. [Google Scholar] [CrossRef]
- Wilson, J.F.; Lee, B.K. In-plane free vibrations of catenary arches with unsymmetric axes. Struct. Eng. Mech. 1995, 3, 511–525. [Google Scholar] [CrossRef]
- Perkins, N.C. Planar vibration of an elastica arch: Theory and Practice. J. Vib. Acoust. 1990, 112, 374–379. [Google Scholar] [CrossRef]
- Riedel, C.H.; Kang, B.S. Free vibration of elastically coupled dual-span curved beams. J. Sound Vib. 2016, 290, 820–838. [Google Scholar] [CrossRef]
- Oh, S.J.; Lee, B.K.; Lee, I.W. Natural frequencies of non-circular arches with rotatory inertia and shear deformation. J. Sound Vib. 1999, 219, 23–33. [Google Scholar] [CrossRef]
- Lee, B.K.; Lee, T.E.; Choi, J.M. Dynamic optimal arches with constant volume. Int. J. Struct. Stab. Dyn. 2012, 12, 1250044. [Google Scholar] [CrossRef]
- Oh, S.J.; Lee, B.K.; Lee, I.W. Free vibrations of non-circular arches with non-uniform cross-section. Int. J. Solids Struct. 2000, 37, 4871–4891. [Google Scholar] [CrossRef]
- Borg, S.F.; Gennaro, J.J. Advanced Structural Analysis; Van Nostrand Reinhold Company: New York, NY, USA, 1959. [Google Scholar]
- Weaver, W.; Timoshenko, S.P.; Young, D.H. Vibration Problems in Engineering; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1990. [Google Scholar]
- Burden, R.L.; Faires, D.J.; Burden, A.M. Numerical Analysis; Cengage Learning: Boston, MA, USA, 2016. [Google Scholar]
- Lee, J.K.; Lee, B.K. In-plane free vibration of uniform circular arches made of axially functionally graded materials. Int. J. Struct. Stab. Dyn. 2019, 19, 1950084. [Google Scholar] [CrossRef]




| End Condition | Geometry of Arch with Non-Dimensional Parameters | Angular Frequency (rad/s) | ||
|---|---|---|---|---|
| ADINA | This Study | |||
| Hinged-hinged | 443.2 | 441.0 | ||
| 1428.0 | 1434.5 | |||
| 2932.3 | 2968.5 | |||
| 4147.6 | 4259.5 | |||
| Hinged-clamped | Uniform cross-section | 595.0 | 591.0 | |
| 1574.3 | 1584.6 | |||
| 3040.8 | 3045.5 | |||
| 4323.9 | 4363.9 | |||
| Clamped-clamped | 375.8 | 382.4 | ||
| 841.1 | 852.0 | |||
| 1513.8 | 1534.7 | |||
| 2313.0 | 2375.0 | |||
| End Condition | Index * | Frequency Parameter | ||||
|---|---|---|---|---|---|---|
| Hinged-hinged | 0.03 | 0 | 0.02628 | 0.08804 | 0.18147 | 0.30340 |
| 1 | 0.02628 | 0.08799 | 0.18124 | 0.30272 | ||
| 0.1 | 0 | 0.04794 | 0.16045 | 0.33027 | 0.54985 | |
| 1 | 0.04791 | 0.16014 | 0.32886 | 0.54594 | ||
| Hinged-clamped | 0.1 | 0 | 0.07270 | 0.19714 | 0.37902 | 0.60448 |
| 1 | 0.07265 | 0.19674 | 0.37736 | 0.60025 | ||
| 0.3 | 0 | 0.12521 | 0.33693 | 0.64030 | 0.90027 | |
| 1 | 0.12497 | 0.33502 | 0.63295 | 0.89397 | ||
| Clamped-clamped | 0.3 | 0 | 0.17660 | 0.39766 | 0.71535 | 0.90445 |
| 1 | 0.17626 | 0.39542 | 0.70764 | 0.89934 | ||
| 0.9 | 0 | 0.29736 | 0.62380 | 1.00197 | 1.03688 | |
| 1 | 0.29611 | 0.61738 | 0.99030 | 1.02230 | ||
| End Condition | Cross-Section | Frequency Paramete | |||
|---|---|---|---|---|---|
| Hinged-hinged | Square | 0.07555 | 0.25147 | 0.51290 | 0.82607 |
| Circular | 0.07384 | 0.24586 | 0.50174 | 0.81136 | |
| Hinged-clamped | Square | 0.11427 | 0.30716 | 0.58290 | 0.86026 |
| Circular | 0.11171 | 0.30045 | 0.57070 | 0.84994 | |
| Clamped-clamped | Square | 0.16130 | 0.36368 | 0.65471 | 0.87560 |
| Circular | 0.15771 | 0.35597 | 0.64163 | 0.86855 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, B.K.; Kim, G.S.; Oh, S.J.; Lee, T.E. Free Vibrations of Tapered Horseshoe Circular Arch with Constant Volume. Appl. Sci. 2020, 10, 5431. https://doi.org/10.3390/app10165431
Lee BK, Kim GS, Oh SJ, Lee TE. Free Vibrations of Tapered Horseshoe Circular Arch with Constant Volume. Applied Sciences. 2020; 10(16):5431. https://doi.org/10.3390/app10165431
Chicago/Turabian StyleLee, Byoung Koo, Gweon Sik Kim, Sang Jin Oh, and Tae Eun Lee. 2020. "Free Vibrations of Tapered Horseshoe Circular Arch with Constant Volume" Applied Sciences 10, no. 16: 5431. https://doi.org/10.3390/app10165431
APA StyleLee, B. K., Kim, G. S., Oh, S. J., & Lee, T. E. (2020). Free Vibrations of Tapered Horseshoe Circular Arch with Constant Volume. Applied Sciences, 10(16), 5431. https://doi.org/10.3390/app10165431




