Temporal Variability in the Response of a Linear Time-Invariant Catchment System to a Non-Stationary Inflow Concentration Field
Abstract
1. Introduction
2. Materials and Methods
2.1. Formulation of the Model
2.2. Variance of Inflow and Outflow Concentrations
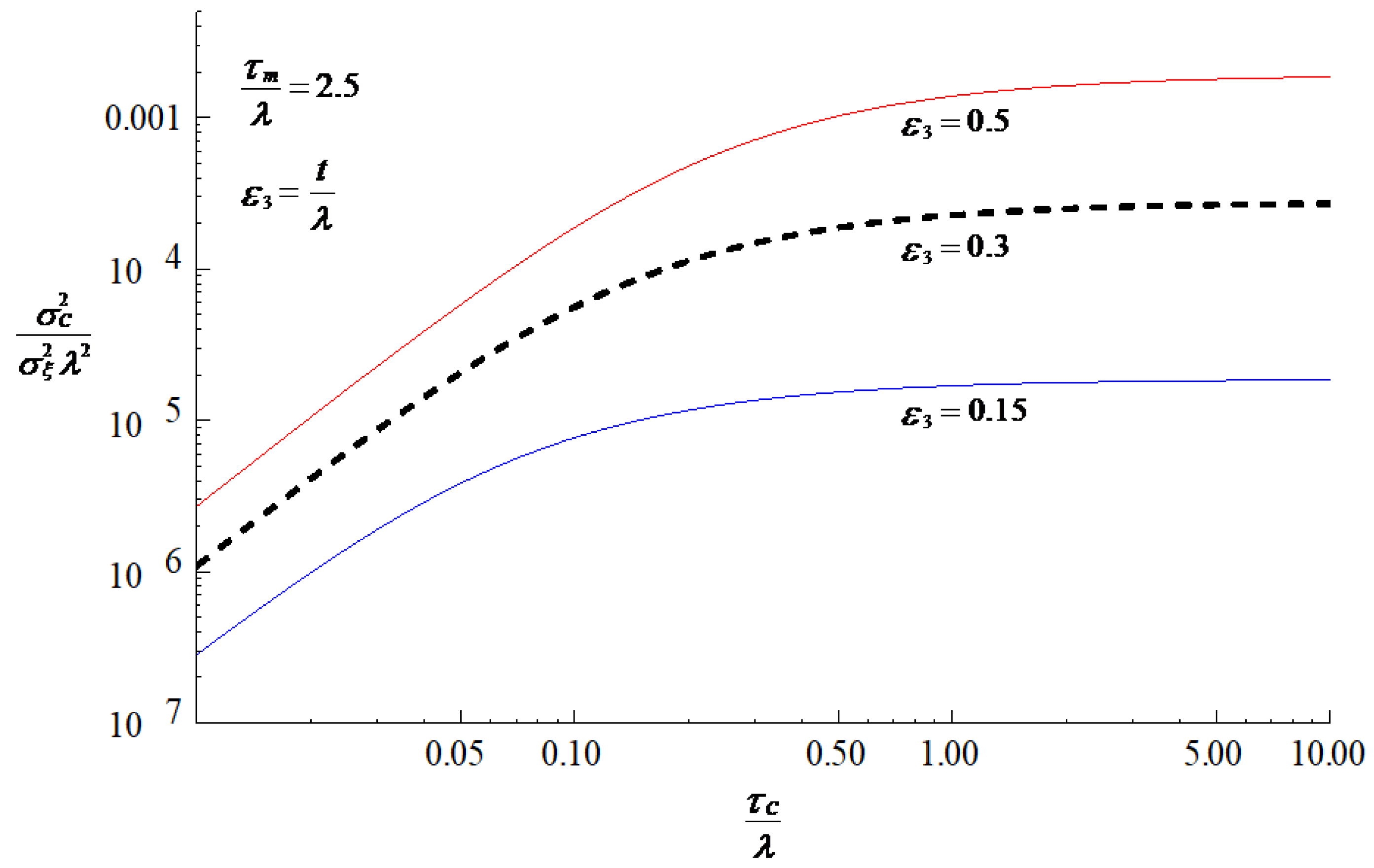
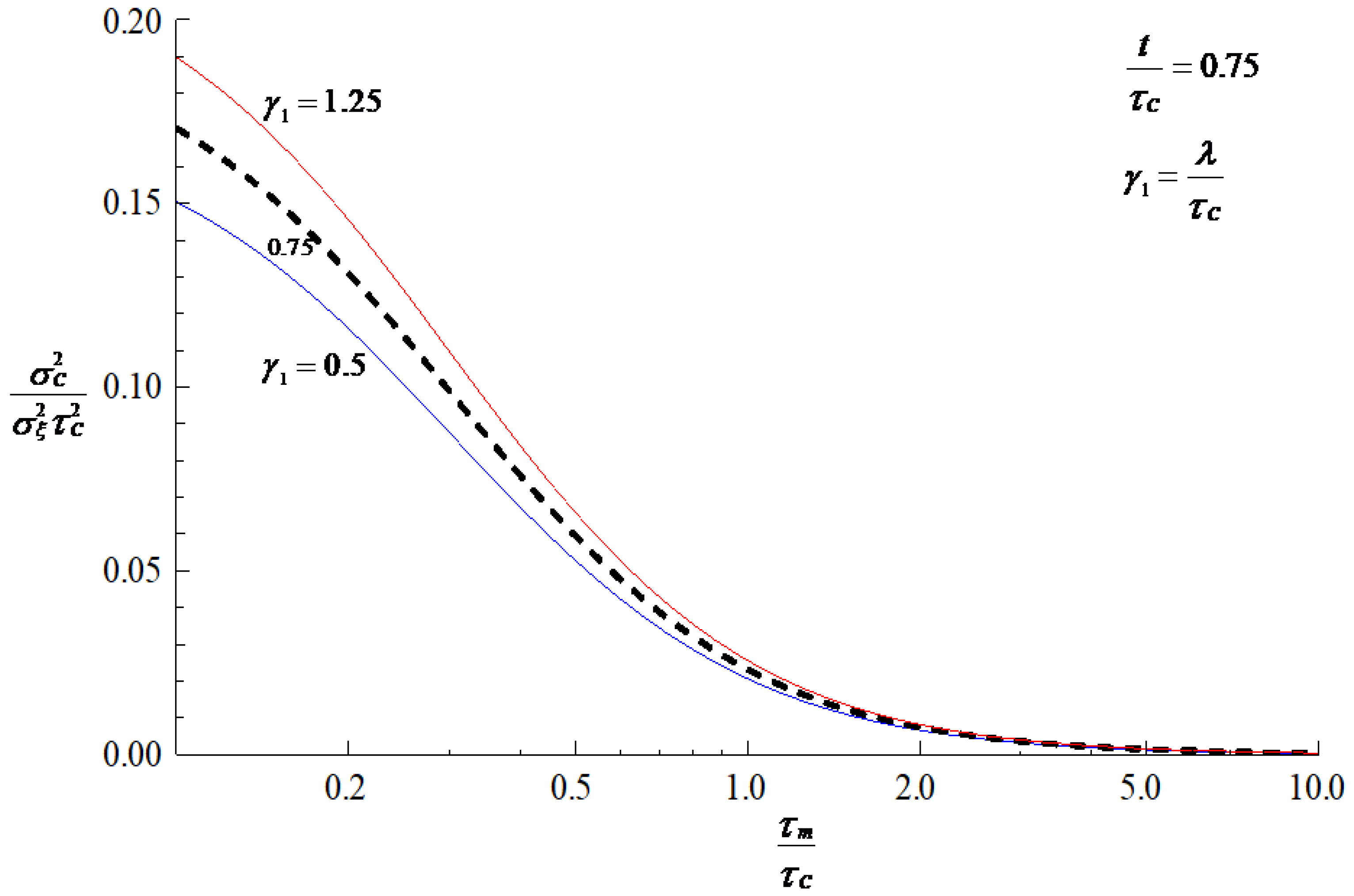
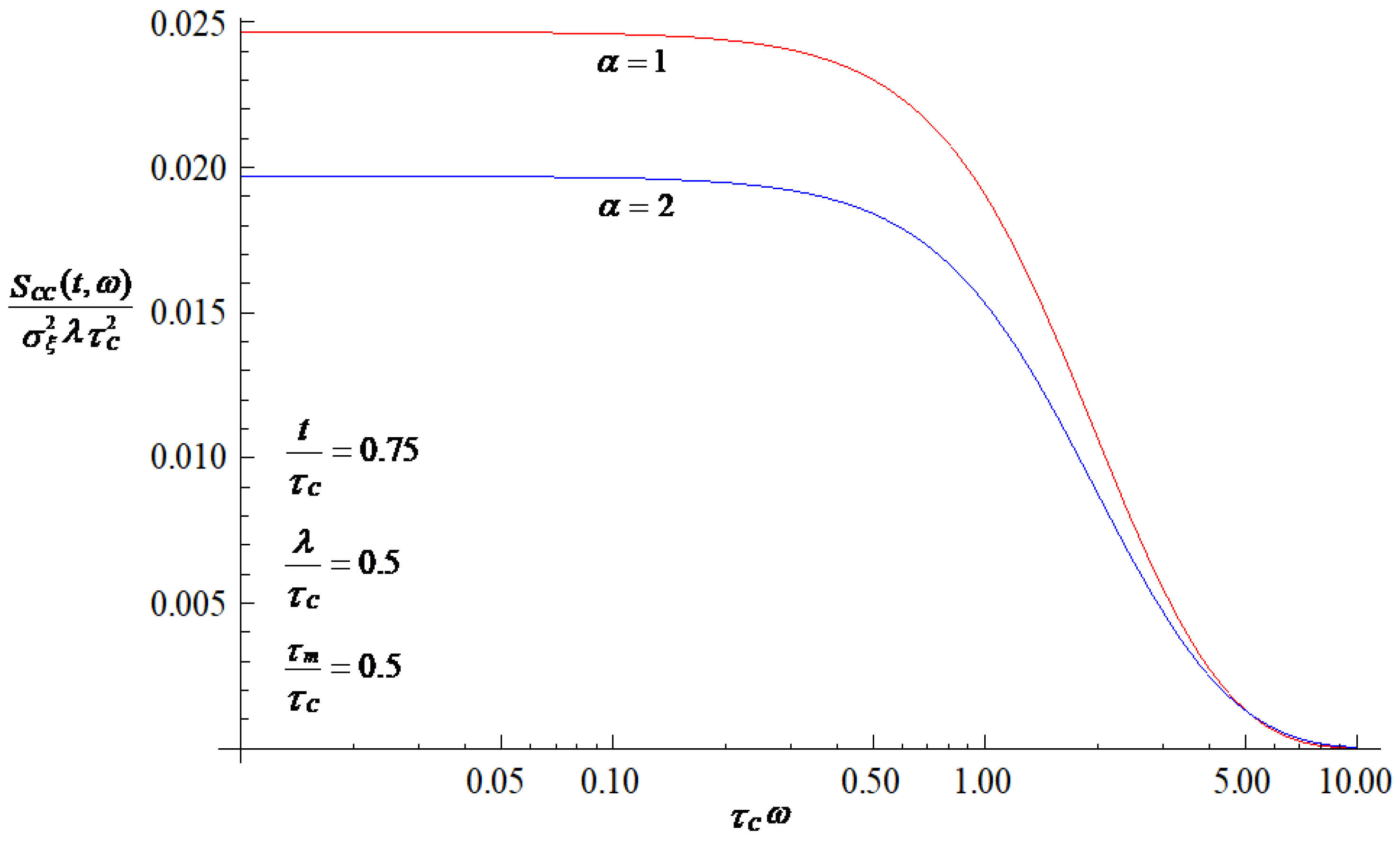
3. Results and Discussion
4. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- McGrath, G.; Hinz, C.; Sivapalan, M. Assessing the impact of regional rainfall variability on rapid pesticide leaching potential. J. Contam. Hydrol. 2010, 113, 56–65. [Google Scholar] [CrossRef] [PubMed]
- Kaufmann, V.; Pinheiro, A.; Castro, N.M. Simulating transport of nitrogen and phosphorus in a Cambisol after natural and simulated intense rainfall. J. Contam. Hydrol. 2014, 160, 53–64. [Google Scholar] [CrossRef] [PubMed]
- Dufilho, A.C.; Falco, S. Preferential flow modelling of chlorpyrifos leaching in two arid soils of irrigated agricultural production areas in Argentine Patagonia. J. Contam. Hydrol. 2019, 229, 103584. [Google Scholar] [CrossRef] [PubMed]
- Sivakumar, B. Chaos in Hydrology: Bridging Determinism and Stochasticity; Springer: Berlin, Germany, 2016. [Google Scholar]
- Rinaldo, A.; Marani, A. Basin scale model of solute transport. Water Resour. Res. 1987, 23, 2107–2118. [Google Scholar] [CrossRef]
- Loague, K.; Green, R.E.; Giambelluca, T.W.; Liang, T.C.; Yost, R.S. Impact of uncertainty in soil, climatic, and chemical information in a pesticide leaching assessment. J. Contam. Hydrol. 1990, 5, 171–194. [Google Scholar] [CrossRef]
- Kirchner, J.W.; Feng, X.; Neal, C. Fractal stream chemistry and its implications for contaminant transport in catchments. Nature 2000, 403, 524–527. [Google Scholar] [CrossRef]
- Kirchner, J.W.; Feng, X.; Neal, C. Catchment-scale advection and dispersion as a mechanism for fractal scaling in stream tracer concentrations. J. Hydrol. 2001, 254, 82–101. [Google Scholar] [CrossRef]
- Botter, G.; Bertuzzo, E.; Rinaldo, A. Transport in the hydrologic response: Travel time distributions, soil moisture dynamics, and the old water paradox. Water Resour. Res. 2010, 46, W03514. [Google Scholar] [CrossRef]
- Sousa, M.R.; Frind, E.O.; Rudolph, D.L. An integrated approach for addressing uncertainty in the delineation of groundwater management areas. J. Contam. Hydrol. 2013, 148, 12–24. [Google Scholar] [CrossRef]
- Baroni, G.; Zink, M.; Kumar, R.; Samaniego, L.; Attinger, S. Effects of uncertainty in soil properties on simulated hydrological states and fluxes at different spatio-temporal scales. Hydrol. Earth Syst. Sc. 2017, 21, 2301–2320. [Google Scholar] [CrossRef]
- Dagan, G. Flow and Transport in Porous Formations; Springer: New York, NY, USA, 1989. [Google Scholar]
- Gelhar, L.W. Stochastic Subsurface Hydrology; Prentice Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Zhang, D. Stochastic Methods for Flow in Porous Media: Coping with Uncertainties; Academic Press: San Diego, CA, USA, 2002. [Google Scholar]
- Rubin, Y. Applied Stochastic Hydrogeology; Oxford University Press: New York, NY, USA, 2003. [Google Scholar]
- Domenico, P.A. Concepts and Models in Groundwater Hydrology; McGraw-Hill: New York, NY, USA, 1972. [Google Scholar]
- Małoszewski, P.; Zuber, A. Determining the turnover time of groundwater systems with the aid of environmental tracers. J. Hydrol. 1982, 57, 207–231. [Google Scholar] [CrossRef]
- Molénat, J.; Davy, P.; Gascuel-Odoux, C.; Durand, P. Study of three subsurface hydrological systems based on spectral and cross-spectral analysis of time series. J. Hydrol. 1999, 222, 152–164. [Google Scholar] [CrossRef]
- Jiménez-Martínez, J.; Longuevergne, L.; Le Borgne, T.; Davy, P.; Russian, A.; Bour, O. Temporal and spatial scaling of hydraulic response to recharge in fractured aquifers: Insights from a frequency domain analysis. Water Resour. Res. 2013, 49, 3007–3023. [Google Scholar] [CrossRef]
- Pedretti, D.; Russian, A.; Sanchez-Vila, X.; Dentz, M. Scale dependence of the hydraulic properties of a fractured aquifer estimated using transfer functions. Water Resour. Res. 2016, 52, 5008–5024. [Google Scholar] [CrossRef]
- Olsthoorn, T.N. Do a bit more with convolution. Groundwater 2007, 46, 13–22. [Google Scholar] [CrossRef] [PubMed]
- Palanisamy, B.; Workman, S.R. Observed hydrographs: On their ability to infer a time-invariant hydrological transfer function for flow prediction in ungauged basins. Hydrol. Process. 2012, 28, 401–413. [Google Scholar] [CrossRef]
- Dooge, J.C.I. A general theory of the unit hydrograph. J. Geophys. Res. 1959, 64, 241–256. [Google Scholar] [CrossRef]
- Lumley, J.L.; Panofsky, H.A. The Structure of Atmospheric Turbulence; John Wiley: New York, NY, USA, 1964. [Google Scholar]
- Priestley, M.B. Spectral Analysis and Time Series; Academic Press: Cambridge, MA, USA, 1981. [Google Scholar]
- Luo, J.; Cirpka, O.A.; Fienen, M.N.; Wu, W.; Mehlhorn, T.L.; Carley, J.; Jardine, P.M.; Criddle, C.S.; Kitanidis, P.K. A parametric transfer function methodology for analyzing reactive transport in nonuniform flow. J. Contam. Hydrol. 2006, 83, 27–41. [Google Scholar] [CrossRef]
- Butera, I.; Tanda, M.G.; Zanini, A. Simultaneous identification of the pollutant release history and the source location in groundwater by means of a geostatistical approach. Stoch. Environ. Res. Risk Assess. 2012, 27, 1269–1280. [Google Scholar] [CrossRef]
- Zhao, Y.; Rathore, S.S.; Liu, M.; Luo, J. Joint Bayesian inversion for analyzing conservative and reactive breakthrough curves. J. Hydrol. 2018, 567, 446–456. [Google Scholar] [CrossRef]
- McGuire, K.J.; McDonnell, J.J. A review and evaluation of catchment transit time modeling. J. Hydrol. 2006, 330, 543–563. [Google Scholar] [CrossRef]
- Godsey, S.E.; Aas, W.; Clair, T.A.; de Wit, H.A.; Fernandez, I.J.; Kahl, J.S.; Malcolm, I.A.; Neal, C.; Neal, M.; Nelson, S.J.; et al. Generality of fractal 1/f scaling in catchment tracer time series, and its implications for catchment travel time distributions. Hydrol. Process. 2010, 24, 1660–1671. [Google Scholar] [CrossRef]
- Jury, W.A.; Sposito, G.; White, R.E. A transfer function model of solute transport through soil: 1. Fundamental concepts. Water Resour. Res. 1986, 22, 243–247. [Google Scholar] [CrossRef]
- Dagan, G.; Nguyen, V. A comparison of travel time and concentration approaches to modeling transport by groundwater. J. Contam. Hydrol. 1989, 4, 79–91. [Google Scholar] [CrossRef]
- Duffy, C.J.; Gelhar, L.W. A frequency domain approach to water quality modeling in groundwater: Theory. Water Resour. Res. 1985, 21, 1175–1184. [Google Scholar] [CrossRef]
- Reeks, M.W. On a kinetic equation for the transport of particles in turbulent flows. Phys. Fluids A Fluid Dyn. 1991, 3, 446–456. [Google Scholar] [CrossRef]
- Gillespie, D.T. Fluctuation and dissipation in Brownian motion. J. Phys. 1993, 61, 1077–1083. [Google Scholar] [CrossRef]
- Korošak, D.; Cvikl, B.; Kramer, J.; Jecl, R.; Prapotnik, A. Fractional calculus applied to the analysis of spectral electrical conductivity of clay-water system. J. Contam. Hydrol. 2007, 92, 1–9. [Google Scholar] [CrossRef]
- Mann, M.E.; Lees, J.M. Robust estimation of background noise and signal detection in climatic time series. Clim. Change 1996, 33, 409–445. [Google Scholar] [CrossRef]
- Schulz, M.; Mudelsee, M. REDFIT: Estimating red-noise spectra directly from unevenly spaced paleoclimatic time series. Comput. Geosci. 2002, 28, 421–426. [Google Scholar] [CrossRef]
- Langevin, P. Sur la théorie du mouvement brownien. C. R. Acad. Sci. (Paris) 1908, 146, 530–533. [Google Scholar]
- Priestley, M.B. Evolutionary spectra and non-stationary processes. J. R. Stat. Soc. B 1965, 27, 204–237. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, C.-M.; Ma, K.-C.; Chuang, M.-H. Temporal Variability in the Response of a Linear Time-Invariant Catchment System to a Non-Stationary Inflow Concentration Field. Appl. Sci. 2020, 10, 5356. https://doi.org/10.3390/app10155356
Chang C-M, Ma K-C, Chuang M-H. Temporal Variability in the Response of a Linear Time-Invariant Catchment System to a Non-Stationary Inflow Concentration Field. Applied Sciences. 2020; 10(15):5356. https://doi.org/10.3390/app10155356
Chicago/Turabian StyleChang, Ching-Min, Kuo-Chen Ma, and Mo-Hsiung Chuang. 2020. "Temporal Variability in the Response of a Linear Time-Invariant Catchment System to a Non-Stationary Inflow Concentration Field" Applied Sciences 10, no. 15: 5356. https://doi.org/10.3390/app10155356
APA StyleChang, C.-M., Ma, K.-C., & Chuang, M.-H. (2020). Temporal Variability in the Response of a Linear Time-Invariant Catchment System to a Non-Stationary Inflow Concentration Field. Applied Sciences, 10(15), 5356. https://doi.org/10.3390/app10155356




