Compound Heuristic Information Guided Policy Improvement for Robot Motor Skill Acquisition
Abstract
:1. Introduction
2. Dynamic Movement Primitives
3. Path Integral Policy Improvement with Covariance Matrix Adaption
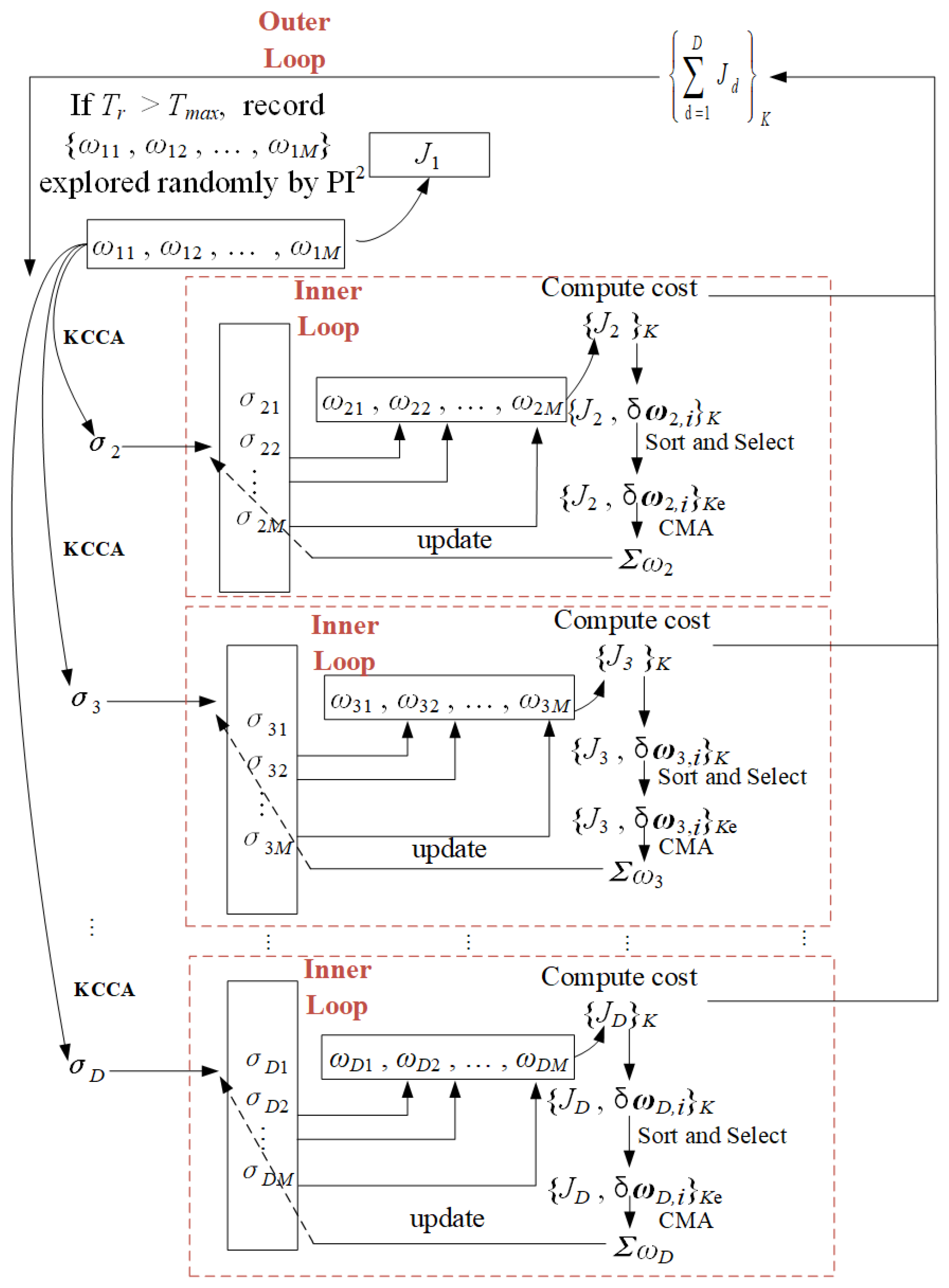
4. PI2-CMA with Kernel Canonical Correlation Analysis
4.1. Nonlinear Correlation Heuristic Information
4.2. Robot Intelligent Trajectory Inference with KCCA
4.3. The Combination of KCCA and CMA
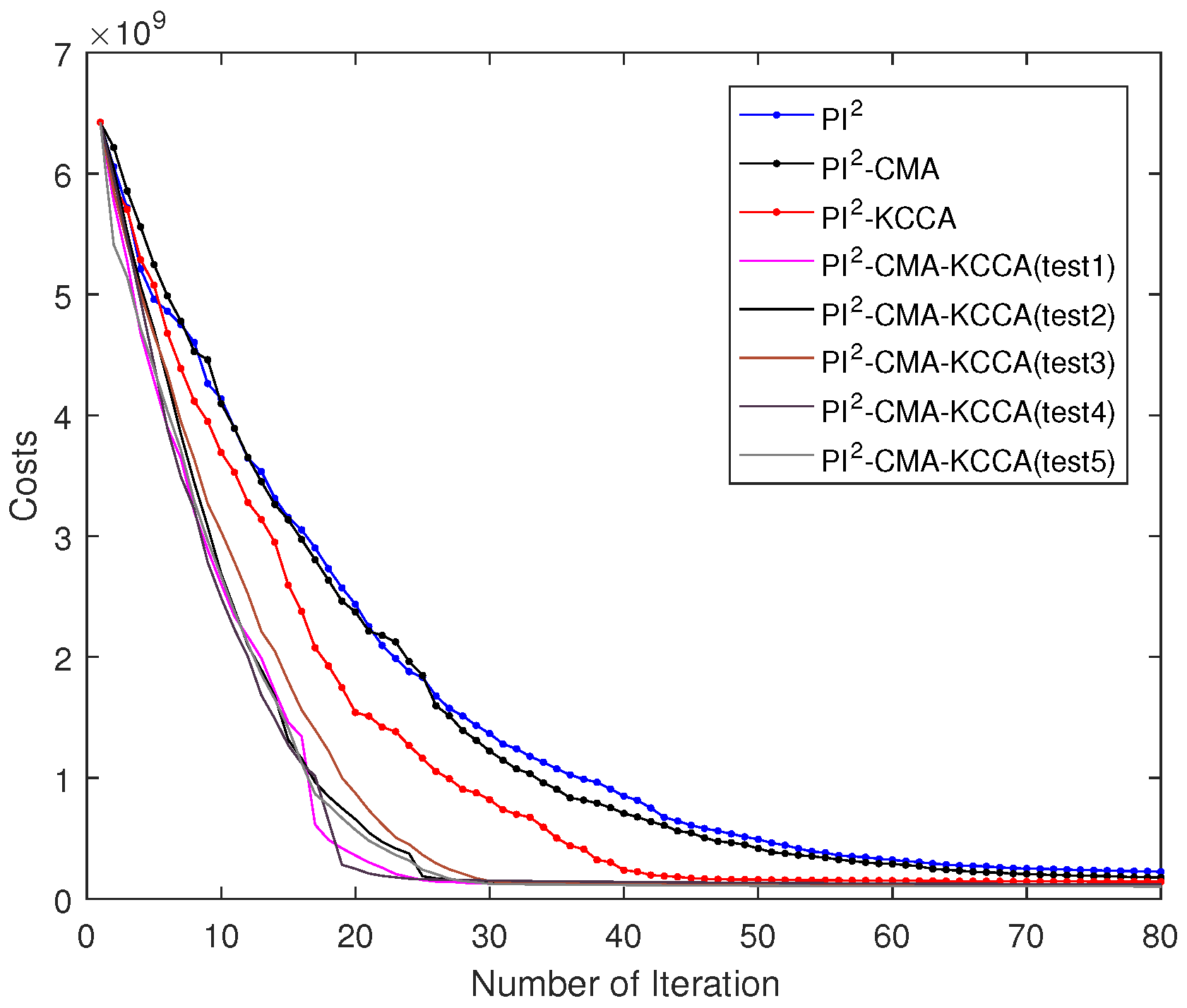
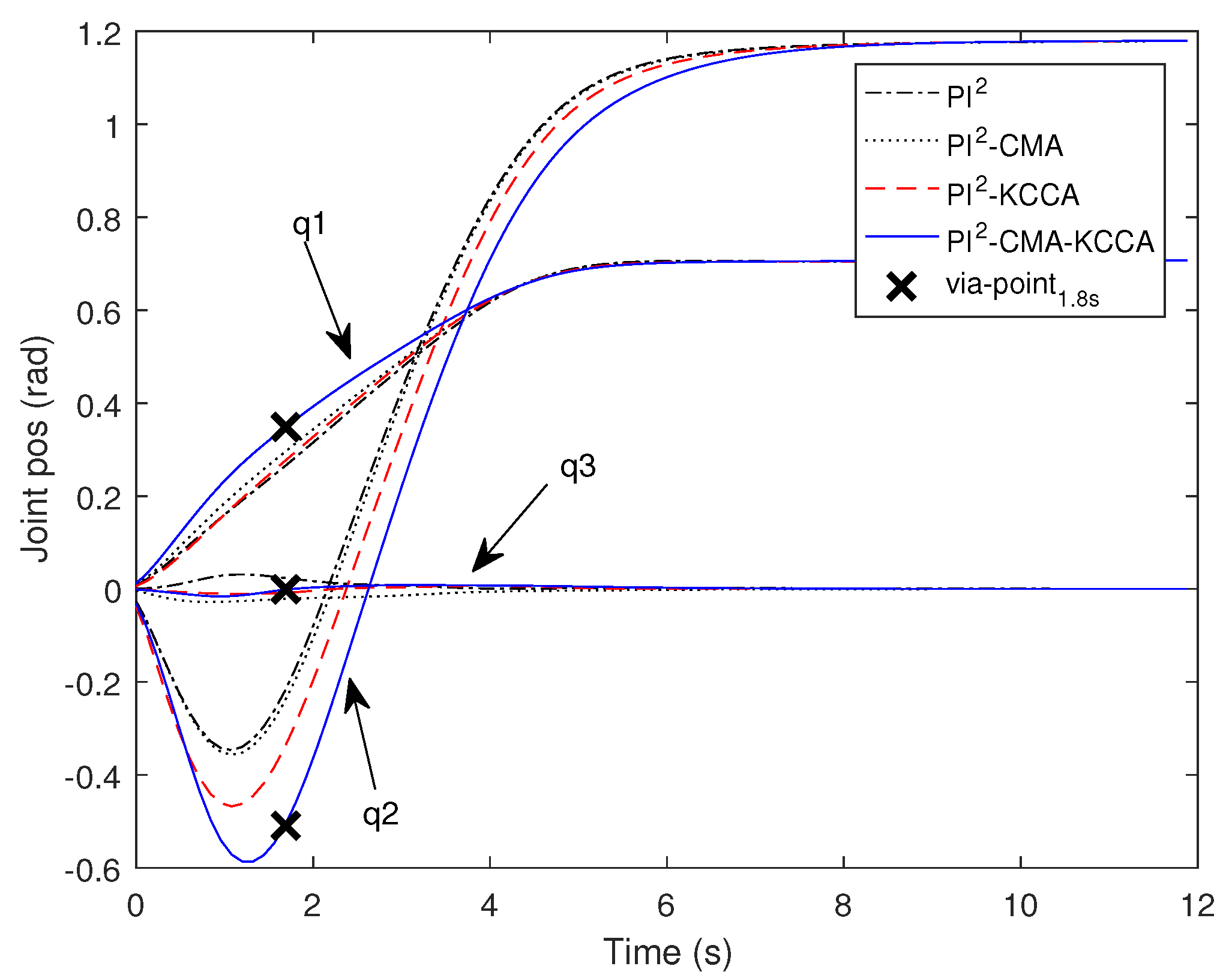
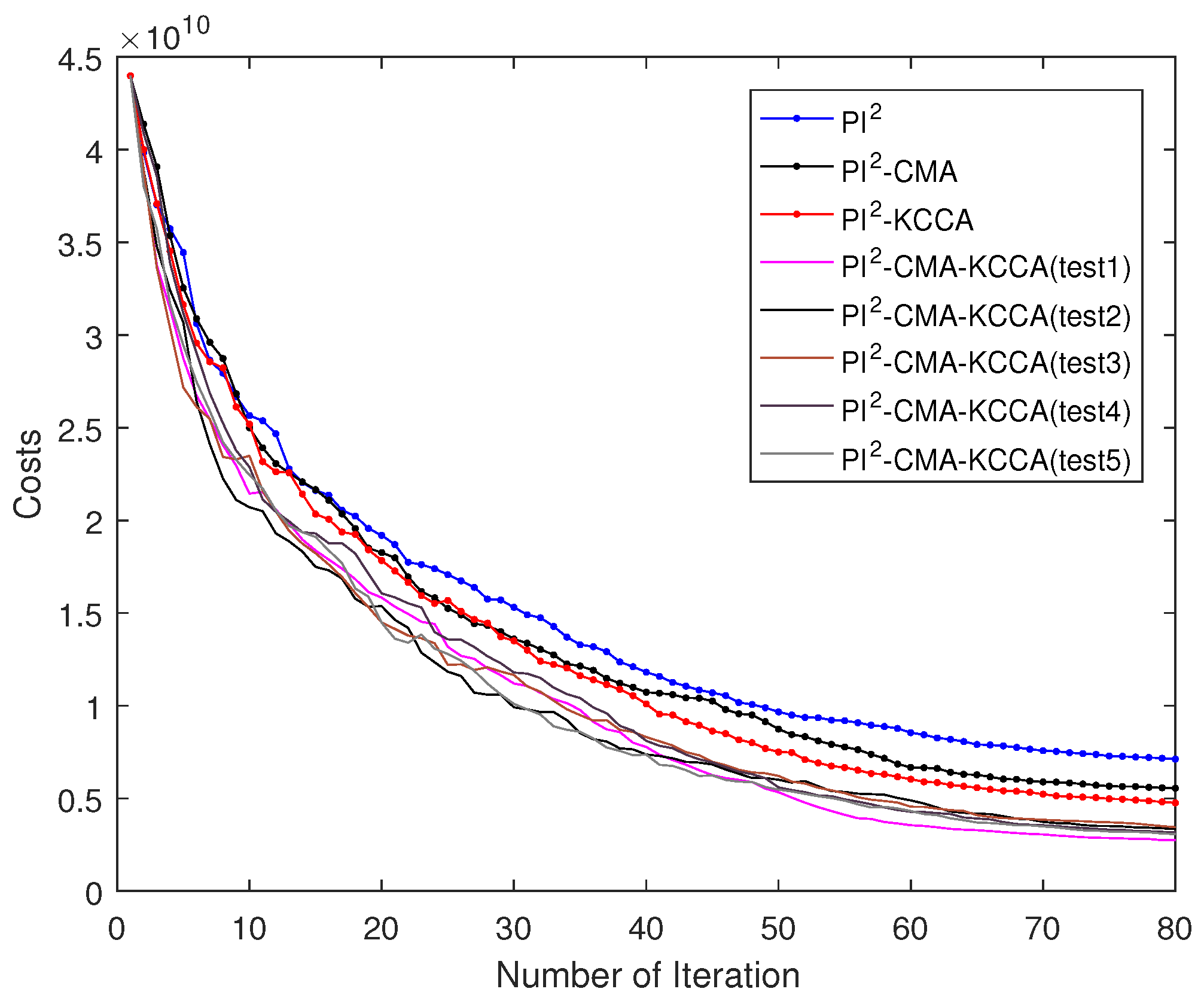
5. Evaluations
5.1. Passing through One Via-Point with SCARA
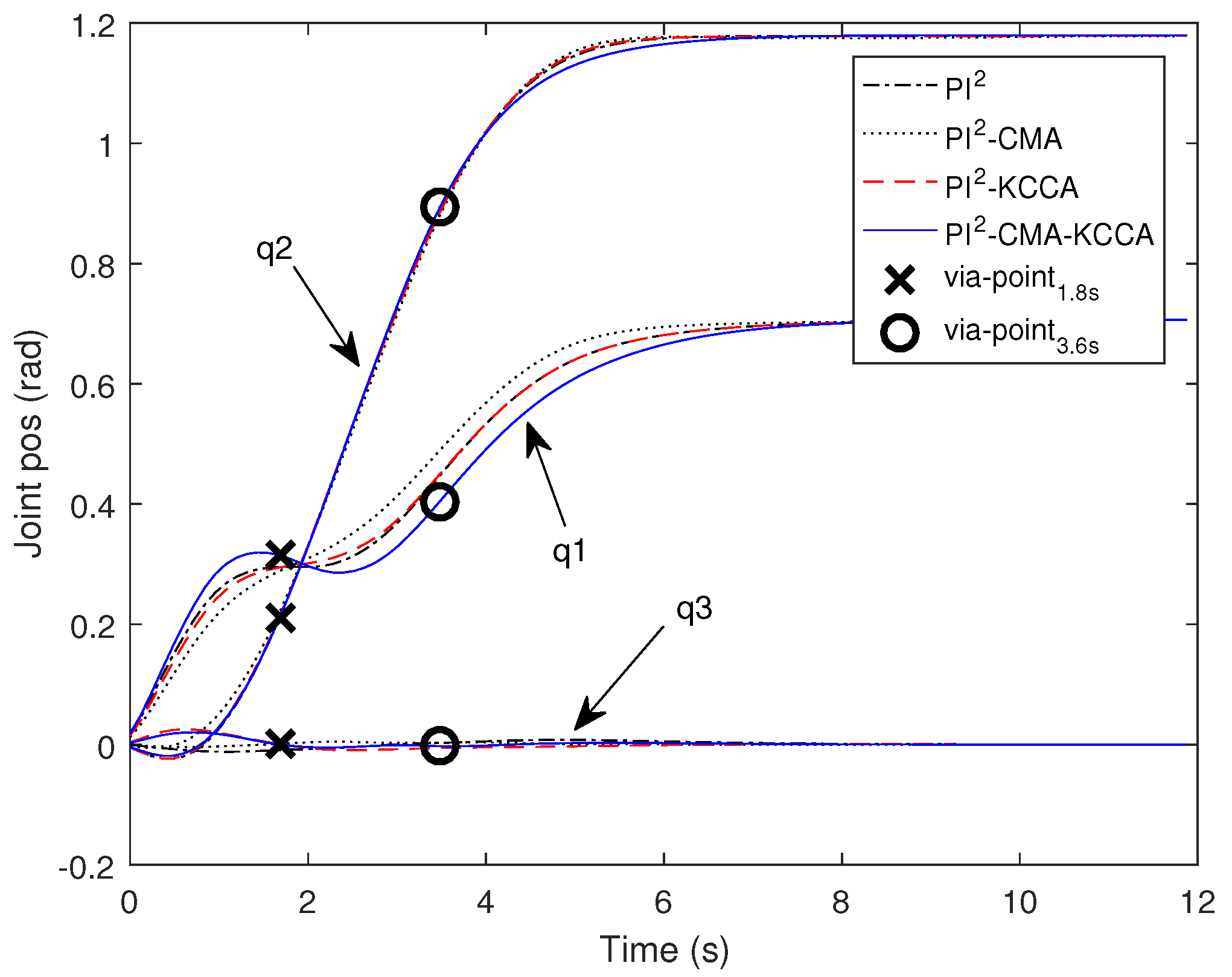
5.2. Passing through Two Via-Point with SCARA
5.3. Passing Through One Via-Point with Swayer
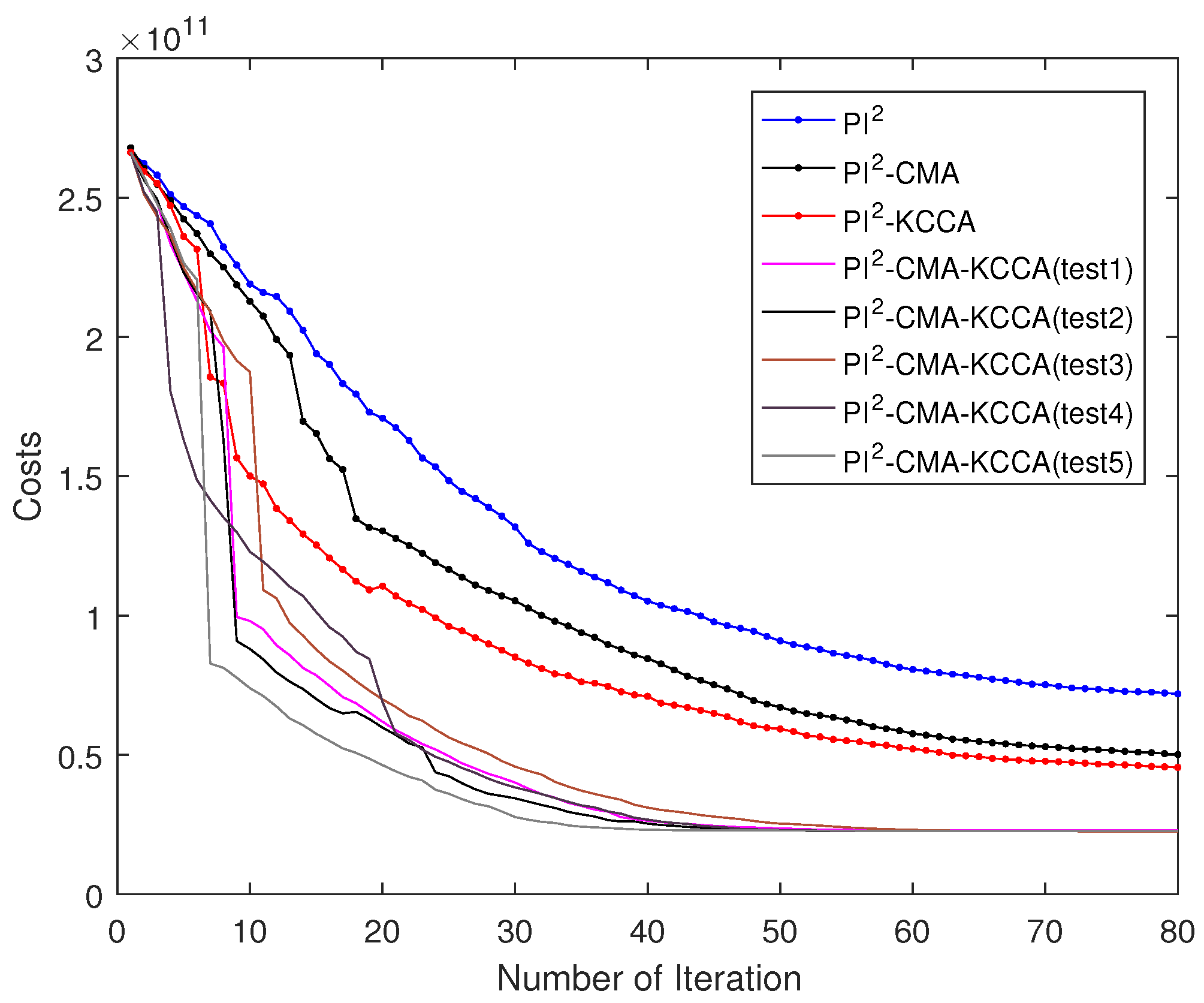
5.4. Performance Comparison of Four Algorithms
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Siciliano, B.; Khatib, O. Springer Handbook of Robotics; Springer: Berlin/Heidelberg, Germany, 2016; pp. 987–1008. [Google Scholar]
- Takano, W.; Nakamura, Y. Statistical mutual conversion between whole body motion primitives and linguistic sentences for human motions. Int. J. Robot. Res. 2015, 34, 1314–1328. [Google Scholar]
- Paraschos, A.; Daniel, C.; Peters, J.; Neumann, G. Probabilistic movement primitives. In Proceedings of the 27th Annual Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 5–10 December 2013; pp. 2616–2624. [Google Scholar]
- Khansari-Zadeh, S.M.; Billard, A. BM: An iterative algorithm to learn stable nonlinear dynamical systems with Gaussian mixture models. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 2381–2388. [Google Scholar]
- Ratliff, N.D.; Bagnell, J.A.; Zinkevich, M.A. Maximum margin planning. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, 25–29 June 2006; pp. 729–736. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning; A Bradford Book; The MIT Press: Cambridge, MA, USA; London, UK, 1998; pp. 665–685. [Google Scholar]
- Peters, J.; Schaal, S. Natural Actor-Critic. Neurocomputing 2008, 71, 1180–1190. [Google Scholar]
- Kober, J.; Peters, J. Learning motor primitives for robotics. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 2112–2118. [Google Scholar]
- Peters, J.; Altun, Y. Relative entropy policy search. In Proceedings of the Twenty-Fourth AAAI Conference on Artificial Intelligence, Atlanta, GA, USA, 11–15 July 2010; pp. 1607–1612. [Google Scholar]
- Theodorou, E.; Buchli, J.; Schaal, S. A Generalized Path Integral Control Approach to Reinforcement Learning. J. Mach. Learn. Res. 2010, 11, 3137–3181. [Google Scholar]
- Stulp, F.; Sigaud, O. Path integral policy improvement with covariance matrix adaptation. In Proceedings of the 29 th International Conference on Machine Learning, Edinburgh, UK, 26 June–1 July 2012; pp. 281–288. [Google Scholar]
- Fu, J.; Teng, X.; Cao, C.; Lou, P. Intelligent trajectory planning based on reinforcement learning with KCCA inference for robot. J. Huazhong Univ. Sci. Technol. (Nat. Sci. Ed.) 2019, 47, 96–102. [Google Scholar]
- Ijspeert, A.J.; Nakanishi, J.; Hoffmann, H.; Pastor, P.; Schaal, S. Dynamical Movement Primitives: Learning Attractor Models for Motor Behaviors. Neural Comput. 2013, 25, 328–373. [Google Scholar]
- Melzer, T.; Reiter, M.; Bischof, H. Appearance models based on kernel canonical correlation analysis. Pattern Recognit. 2003, 36, 1961–1971. [Google Scholar]

| Symbol | Definition |
|---|---|
| The desired acceleration, velocity, position of the joint | |
| Fitting function. is a phase variable | |
| The probability-weighted value of the kth trajectory of the dth DOF at time i | |
| The dth joint’s correction weight vector at time i | |
| Average value of over time | |
| The dth joint’s weight vector | |
| The dth joint’s weight vector with perturbation | |
| Mapping function. Mapping a variable to V-dimensional space | |
| The weight perturbation sample of the dth joint, i.e., | |
| The dth joint’s cost for given task | |
| The total cost of D joints at the pth iteration | |
| Kernel matrix | |
| Decline rate of cost between and | |
| and which are calculated from K roll-outs | |
| and which are calculated from elite roll-outs, and elite roll-outs are obtained by sorting K roll-outs according to the cost |
| Algorithm | Final Cost |
|---|---|
| PI2 | |
| PI2-CMA | |
| PI2-KCCA | |
| PI2-CMA-KCCA(test1) | |
| PI2-CMA-KCCA(test2) | |
| PI2-CMA-KCCA(test3) | |
| PI2-CMA-KCCA(test4) | |
| PI2-CMA-KCCA(test5) |
| Algorithm | Final Cost |
|---|---|
| PI2 | |
| PI2-CMA | |
| PI2-KCCA | |
| PI2-CMA-KCCA(test1) | |
| PI2-CMA-KCCA(test2) | |
| PI2-CMA-KCCA(test3) | |
| PI2-CMA-KCCA(test4) | |
| PI2-CMA-KCCA(test5) |
| Algorithm | Final Cost |
|---|---|
| PI2 | |
| PI2-CMA | |
| PI2-KCCA | |
| PI2-CMA-KCCA(test1) | |
| PI2-CMA-KCCA(test2) | |
| PI2-CMA-KCCA(test3) | |
| PI2-CMA-KCCA(test4) | |
| PI2-CMA-KCCA(test5) |
| Task | PI2 | PI2-CMA | PI2-KCCA | PI2-CMA-KCCA |
|---|---|---|---|---|
| One Via-Point Task with SCARA | 96.5% | 97.2% | 97.8% | 98.5% |
| Two Via-Point Task with SCARA | 84.0% | 87.4% | 89.7% | 92.8% |
| One Via-Point Task with Swayer | 73.0% | 81.3% | 83.0% | 91.5% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, J.; Li, C.; Teng, X.; Luo, F.; Li, B. Compound Heuristic Information Guided Policy Improvement for Robot Motor Skill Acquisition. Appl. Sci. 2020, 10, 5346. https://doi.org/10.3390/app10155346
Fu J, Li C, Teng X, Luo F, Li B. Compound Heuristic Information Guided Policy Improvement for Robot Motor Skill Acquisition. Applied Sciences. 2020; 10(15):5346. https://doi.org/10.3390/app10155346
Chicago/Turabian StyleFu, Jian, Cong Li, Xiang Teng, Fan Luo, and Boqun Li. 2020. "Compound Heuristic Information Guided Policy Improvement for Robot Motor Skill Acquisition" Applied Sciences 10, no. 15: 5346. https://doi.org/10.3390/app10155346
APA StyleFu, J., Li, C., Teng, X., Luo, F., & Li, B. (2020). Compound Heuristic Information Guided Policy Improvement for Robot Motor Skill Acquisition. Applied Sciences, 10(15), 5346. https://doi.org/10.3390/app10155346






