1. Introduction
By defining what robustness means in the context of this research, we can focus on the engineering applications of the proposed method. We refer to robustness as the “relative insensitivity of the solution to errors of some sort” [
1]; also, we refer to numerical stability to denote robustness against round-off errors [
2].
The design of the Kalman filter (KF) usually aims to “ensure that the covariance matrix of estimation uncertainty (the dependent variable of the matrix Riccati equation) remains symmetric and positive definite” [
1,
3]. The main problem to be solved in this research is the numerical robustness of KF. The proposed algorithm is useful in applications where the influence of round-off errors reduces the accuracy of the numerical solution of the associated Riccati equation. The fidelity of the solution may degrade to the point that it corrupts the Kalman gain when the Riccati equation does not stay symmetric and positive definite, and it can corrupt the estimate [
1]. Verhaegen and Van Dooren have shown that the asymmetry of
is one of the factors contributing to the numerical instability of the Riccati equation [
4].
The problem was circumvented by Bierman [
5] using unit triangular matrix diagonal (UD) factorization, which was one of several alternatives available to those in need of computationally efficient and stable algorithms. This decomposition of the covariance matrix is of the form:
where
denotes the diagonal matrix and
is the upper triangular matrix with ones along its main diagonal. One of the individual characteristics of UD factorization and the Cholesky method is that there is no need to solve simultaneous Equations [
6]. Additionally, UD factorization does not use a square root numerical operation [
6], but more recently square root filtering using standard matrix decomposition has found greater acceptance [
7]. In this matrix,
S is obtained in a triangular matrix from the well-known Cholesky decomposition [
8,
9], a drawback of which is that it cannot be used if the covariance matrix is singular [
6]. Both the square root and Bierman methods can be used only if one has single-dimensional measurements with uncorrelated measurement noise. Generally, one does not have this in practice [
8,
9]. To overcome the limitation, another method can be used—which is one of the topics of this research—that will facilitate the solution of this type of problem, as the computation can be performed in parallel because it is formulated in the form of matrix and matrix-vector operations without the need for additional transformations [
10], where the solution also is able to deal with ill-conditioned matrices. This method is singular value decomposition (SVD).
The singular values (which are positive by definition) or principal standard deviation
are the square roots of the diagonal elements. For the discrete time linear problem, which is evaluated in this research, the first KF based on SVD was researched by Wang, Libert, and Manneback [
8,
9]. In this paper, the algorithm is further improved by making the filter adaptable to changes in sensor quality.
The Riccati equation of the Kalman filter is an important tool for designing navigation systems, particularly those that incorporate sensors with diverse error characteristics, such as the Global Navigation Satellite System (GNSS) and the inertial navigation system (INS). The Riccati equation permits us to predict the performance of a given system design as a function of the subsystem and component error characteristics [
2]. Designers can then search for the mixture of components that will reach a predefined set of performance endpoints at the lowest framework cost. The design of the Kalman filter is aimed at making sure the estimation uncertainty of the covariance matrix (the dependent variable of the matrix Riccati equation) remains symmetric and positive definite [
1]. In this research, we design an adaptive Kalman filter implementation based on SVD, provide its derivation, and discuss the stability issues numerically. The filter is derived by substituting the SVD of the covariance matrix into the conventional discrete Kalman filter equations after its initial propagation and adaptive estimation of the covariance measurement matrix
.
One application of SVD in navigation is to apply it in calculating position errors to decompose the geometric matrix G, where error analysis with SVD is used to construct the pseudo inverse of G, making the solution numerically stable. While the linear least squares (LLS) is somewhat susceptible to round-up errors, where the normal equation is sometimes close to singular, SVD fixes the round-up problem and produces a solution that is the best approximation in the least-squares sense [
11].
Different applications in the area of ionospheric tomography, as the problem to be solved, encounter the same ill-conditioned issue for the design matrix, which is composed of contributions of unknown parameters containing the ionospheric electron density (IED) in the total electron content (STEC) measurements, which is often not square, ill-posed, and ill-conditioned. Many methods have been employed to circumvent the problem of ill-posedness in the GNSS tomographic equation [
12]. Those algorithms are iterative and include the Kalman filter, singular value decomposition, and algebraic reconstruction [
7,
9].
In the field of industrial electronic applications where numerical stability is necessary, an example is sensorless motor control, where the advantages of estimating the speed/position of the rotor include reduced hardware complexity, lower cost, reduced machine drive size, the elimination of the sensor cable, noise immunity, and increased reliability [
13]; for example, a motor without a position sensor is suitable for harsh environments (such as submerged pumps). Other applications include diagnostics, the fault-tolerant control of AC drives, distributed generation and storage systems, robotics, vision and sensor fusion technologies, signal processing and instrumentation applications, and the real-time implementation of the Kalman filter for industrial control systems [
13]. We briefly discuss the numerical stability of the Kalman filter related to industrial control systems and sensor fusion for cardiorespiratory signal extraction, but focus on numerical examples in aerospace applications like GNSS navigation.
The safe and efficient operation of control systems requires computer-based failure detection algorithms [
13], where diagnosis may be used to provide fault-tolerant control. Several failures can occur in electrical systems, and redundant design is one of the solutions to assure the continuity and, therefore, the reliability of operations. Kalman filters can be used in fault-tolerant controls, for example, in aircraft control, home and municipal appliances (gas turbines, cooling systems, and heat pumps), and electric vehicles.
A challenge in the real-time implementation of Kalman filters is the high computational complexity, and among the main difficulties is numerical stability when computing the covariance matrices as well the computational load and execution time. There are three possible solutions to circumvent these issues, and one solution is to modify the algorithm, which is the scope of this paper. In addition, an efficient digital architecture to implement the estimator [
13], and parallel computing can be used. The observability problem physically means that one or more state variables (or linear combinations) are hidden from the view of the observer (i.e., the measurements) [
6]. This is a challenge in the sensorless control of AC drives, which can be accentuated when the stator frequency is close to zero and the rotor voltage carries small values. In addition, under continuous excitation conditions, when the stator frequency is close to zero and when the inductor rotor voltage carries small values, an estimation of the speed of an induction motor (IM) is not likely to be obtainable. In practice, compared with extended Luenberger observers and slipping modes, the Kalman filter appears to function well in these conditions with no divergence [
13]. With this trade-off, the complexity of the Kalman filter is higher.
Other important applications of the KF are in the signal extraction and fusion of sensors, self-driving cars, GNSS/INS integration, and biomedical sensors; for example, when extracting cardiorespiratory signals from noninvasive and noncontacting sensor arrangements, such as magnetic induction sensors. In those applications, the signals are separated for monitoring purposes; by using the KF, it is possible to measure the heart and breathing rates in real time [
14], improving the estimation of results, whereas other filtering techniques fail to extract relevant information due to the mixing of respiratory and cardiac signals and disturbance by measurement noise [
14].
The second objective of this paper is to promote the use of continuous adaptation changes in the measurement error covariance matrix
. The Kalman gain
weights the innovation for the measurement error covariance matrix
(the estimation error covariance matrix
is influenced by
), where higher values of
make the measurement update step differ a little from the predicted value when the Kalman gain
becomes very small [
15]. On the contrary, high values of
engender more trust in the estimation of the state; Zhang et al. [
16] showed that inappropriate tuning parameters may lead to low convergence by introducing adaptive technology consisting of adjustments to the noise covariance matrices to improve the estimation accuracy. Muñoz-Bañon et al. [
17] showed that the Kalman filter can be used to integrate high-level localization subsystems, where the covariance information plays an essential role as new observations become available. This approach will be used in this research.
The proper selection of
and
is vital for optimal filter performance, as the system model should describe as closely as possible the time evolution of the measured data, and the choices should reflect the system model error and measurement noise [
15]. This research only explores changes in the measurement error covariance matrix
. Zhang et al. [
18] showed that when the system being considered has a stronger nonlinear action, the accuracy of the mode estimation will be poor. In order to address the shortcomings of the KF-based algorithm (K-SVD) and enhance the estimation precision, the adaptive filtering algorithm (K-SVD adaptive) was investigated, consisting of the adaptive estimation of
, which is a function of the standard deviation.
4. SVD of Kalman Filter
In practical terms, if
is positive definite, then Equation (13) can be compacted to:
where
is an
×
diagonal matrix. Specifically, if
is itself positive definite, then it will have an asymmetric singular decomposition (which is also an eigendecomposition):
where the principal standard deviations
are the square roots of the diagonal elements of A. Assuming that the covariance of the Kalman filter has been propagated and updated for everything from the filter algorithm, the singular value decomposition of the equation of
. is:
Equation (6) can then be written as:
The idea is to find the factors
and
from Equation (18), such that:
We define the following
matrix:
Then, we compute its singular value decomposition:
Multiplying each term on the left by its transpose, we get:
Comparing the result of Equation (23) with Equations (18) and (19), it is easy to associate
and
with
and
. In the orthodox Kalman measurement update, substituting Equation (8) into (9) yields:
Lemma 1. Using the matrix inversion lemma in the case where the inverse of a positive definite matrix A adds a rank-one matrix yields: where the superscript T denotes the complex conjugate transpose (or Hermitian) operation. It is well known in the literature that this formula is handy to develop a recursive least-squares algorithm for the recursive identification or design of an adaptive filter [21]. The lemma on Equations (24) and (25) yields: Implementing the singular value decomposition of a symmetric positive definite matrix into
and
yields:
To make the system adaptable to changes in sensor quality, the measurement noise is also estimated, which leads to a time-variant matrix. When the signal comes from different sensors, at each discrete time step
the noise covariance matrix is updated by appraising the standard deviation (std) of an arithmetically differentiated (diff) small-signal segment [
14]:
The adaptive computation of the KF and SVD-based (K-SVD) algorithm can be added independent of the SVD portion, as for some applications the measurement covariance matrix is known and can be pre-computed at the algorithm initiation.
After computing Equations (29) and (30), let
be the Cholesky decomposition of the inverse of the covariance matrix. If covariance matrix
is known, but not the inverse, then the reverse Cholesky decomposition
,
[
8] upper triangular can be identified. It then follows that
is the necessary Cholesky decomposition [
20] in Equation (31).
Now, we consider the
×
n matrix:
and compute its singular value decomposition:
Multiplying each term on the left by its transpose produces:
Then, Equation (28) can be written as follows:
Comparing both sides of Equation (36):
The update measurement formulation is obtained, which requires calculating the singular value decomposition of the nonsymmetrical matrix without specifically defining its left orthogonal component that has a larger dimension. The Kalman gain term can be derived as:
Inserting
and
will not alter the gain. Thus, the Kalman filter gain can be written as:
where
denotes the identity matrix. Next, from Equation (26), for
we get:
The Kalman gain
is fully defined, and the state vector measurement is given by:
| Algorithm 1. Singular value decomposition-based Kalman filtering: |
|
Input:
|
|
Initialization (k = 0). Perform SVD on
to determine the initial
and
. The initial
, where
and
are orthogonal and diagonal matrices, respectively. Matrix
contains the singular values of
.
|
Steps (k = 1 to n): Update
and
by constructing the
matrix using a pre-array (32). Use only the right SVD factor V. Compute the Kalman gain
from Equation (43). Update the estimate
from Equation (44). Notice that
is triangular, and the computation of
can be obtained from step 2. Compute the extrapolation
; from Equation (3),
and
can be obtained by the SVD from the Equation (21) pre-array matrix
without forming the left orthogonal factor (the one associated with Equation (13) of the SVD). Compute the measured noise time-variant matrix using Equations (29) and (30).
|
|
Return: Compute
using Equation (31) as
.
|
The Algorithm 1 requires the Cholesky decomposition of noise covariance matrices ; for time-invariant matrices, the Cholesky decomposition is performed once during the initial step—i.e., before the KF recursion. Note that the algorithm also requires the m × m matrix inversion for the terms and in Equation (31). Again, if the process noise covariance is constant over time, the matrix calculation is pre-computed while the filter is initialized.
5. Numerical Experiments: Applications in Navigation
The computer round-off for floating-point arithmetic is always demarcated by a single parameter , called the unit round-off error, which is demarcated as 1 in machine precision.
In MATLAB, the parameter “eps” satisfies the definition above [
2].
Round-off errors are a side effect of computer arithmetic using fixed or floating-point data words with a fixed number of bits [
2]. The next example demonstrates that round-off can still be a problem when implementing KF in MATLAB environments and how a problem that is well-conditioned can be made ill-conditioned by the filter implementation [
2]. The problem is taken from Grewal and Andrews, and it is significant, as it shows the filter’s observational behavior. The example does not make use of the Algorithm 1 adaptive computation from Equations (29) and (30), and the resulting algorithm is called K-SVD.
Example 1. Let denote the n × n identity matrix. Considering the filtering problem with the measurement sensitivity matrix: and covariance matrices. and ; to simulate round-off, it is assumed that:
but .
In this case, although
has rank = 2 in machine precision, the product
with round-off will equal:
which is singular, and the results remain unchanged when
R is added to
.
All the KF tests were carried out with the same precision (64-bit floating-point) in MATLAB running on a standard personal computer with an Intel(R) Core(TM) processor, i5-4200U CPU @ 1.60 GHz 2.30 GHz, 8.0 GB RAM, where the unit round-off error is
. The MATLAB eps function is twice the unit round-off error [
2,
22]. Hereafter, the set of numerical experiments is repeated for various values of the ill-conditioned parameter
; as such, delta tends toward the machine precision limit
. This example does not prove the robustness of the solution of the UD, square root Kalman (SQRK), and K-SVD methods. Full implementation would require temporal updates; however, observational updates have created difficulties with traditional implementation [
2].
Figure 1 illustrates how the conventional KF and a few other choice implementation methods work on various ill-conditioned experiments as the conditioned parameter
.
For this particular example, the square root-based (SQRK-based Carlson), Cholesky-based (UD-based Bierman), and K-SVD-based methods appear to degrade more gracefully than the others. The SQRK, UD decomposition, and K-SVD solutions also retain nine digits (
of accuracy at
, while the other methods have no bits of accuracy in the calculated solution [
1]. The other methods worth mentioning in this research are conventional KF, Potter square root filter, and Joseph stabilization.
The problem analyzed corresponds to an ill-conditioned intermediate result where
for inversion in the Kalman gain formula in Equation (8). In this case, although
has rank = 2 in machine precision, the product
is not invertible, and the observational filter updates fail. The results are provided graphically in
Figure 1, showing that the K-SVD-based method performs as well as the UD-based and SQRK-based Kalman filter methods.
Examples 2 and 3 as outlined were run one time—i.e., the research team performed a simulation. In each run, the dynamic state real trajectory was
; the estimated dynamic state path was
; and the root mean square error (RMSE) of the state vector for each component is given as follows [
22]:
Examples 2 and 3 use a GPS configuration loaded as Yuma ephemeris data from a GPS satellite from March 2014, downloaded from the US Coast Guard site YUMA Almanac [
2].
Example 2. The following example shows a navigation simulation with a dual-frequency GPS receiver on a 100 km-long figure-8 track for 1 h with signal outages of 1 min each. The problem is taken from Grewal and Andrews, and it is significant as it shows the filter’s observational behavior [2]. The state vector corresponds to nine host vehicle model dynamic variables and two receiver clock error variables. The nine host vehicle variables are: east error (m), north error (m), altitude error (m), east velocity error (m/s), north velocity error (m/s), altitude rate error (m/s), east acceleration error (m), north acceleration error (m), and upward acceleration error (m). The MATLAB m-file solves the Riccati equation with a dynamic coefficient matrix structure [2], where the 9 × 9 matrix corresponds to the host vehicle dynamics and the 2 × 2 to the clock error. Table 1 summarizes the outcome for a simulation using real ephemeris GPS data and an ill-conditioned intermediate result where
for inversion in the Kalman gain formula in Equation (8). The example does not make use of the Algorithm 1 adaptive computation from Equations (29) and (30), and the resulting algorithm is called K-SVD.
The results in
Table 1 show that the conventional KF is not suitable to gracefully handle round-off errors, and other filter methods can be used to better handle the round-off issue. A large
corresponds to a well-conditioned state. Once degradation happens, some of the filters decay faster than the K-SVD. The filter robustness can then be obtained by comparing the outcomes shown in
Table 1 against those with the worst performance. The threshold where the filter can handle the error is reached when the algorithm produces “NaN,” or not a number, and this happens when the conventional KF is at
. A comparison of the K-SVD with SQR-KF and UD-KF shows that the K-SVD algorithm is superior in handling round-off errors. UD-KF is slightly better than SQR-KF, and the conventional KF performs as well as the other two. Regarding the execution time, K-SVD and conventional KF are slower than SQRT and UD, and this is because SVD is computationally more costly than Cholesky decomposition [
22]. However, SVD is suitable for parallel computing and has a better numerical stability.
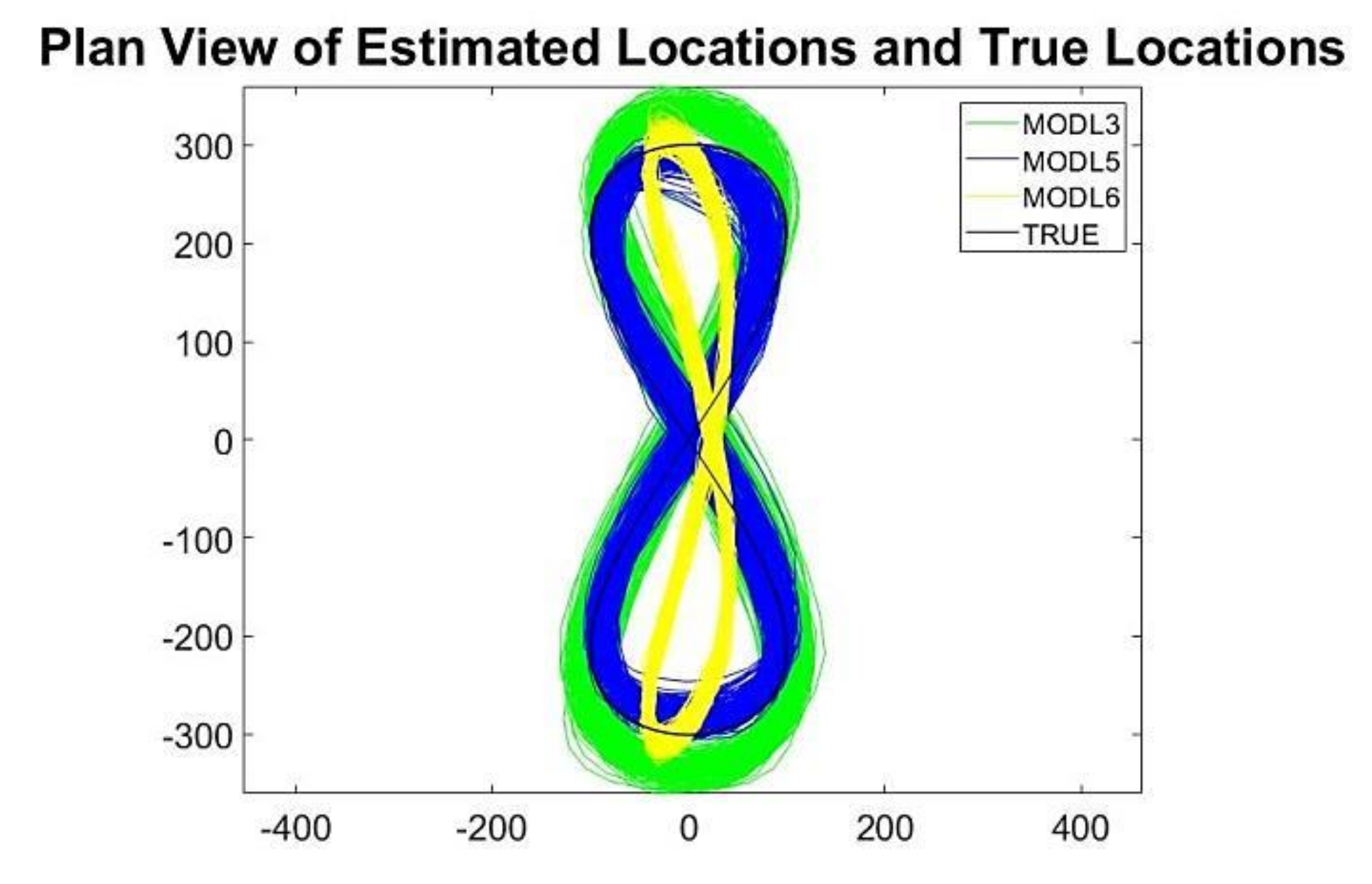
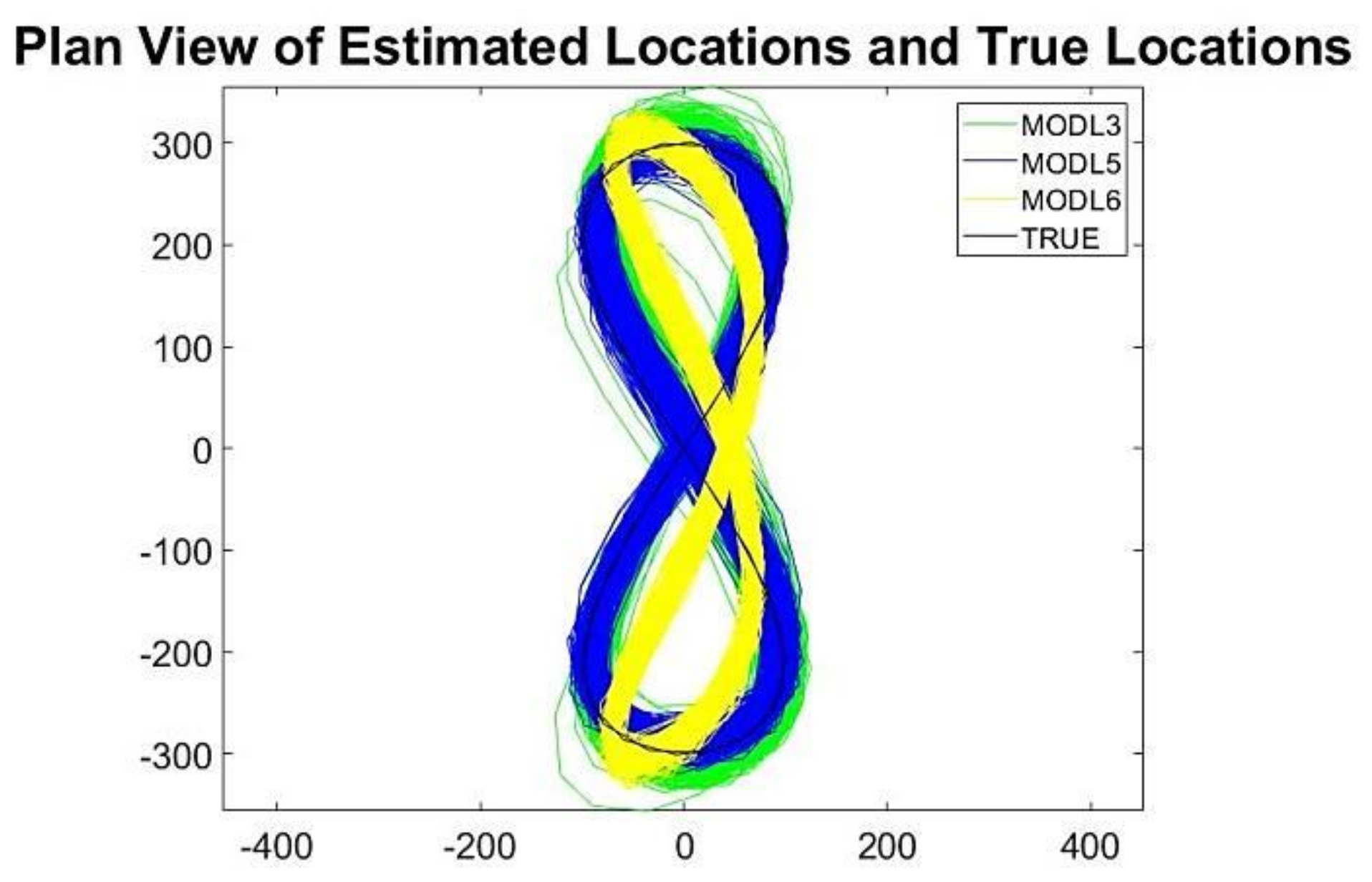
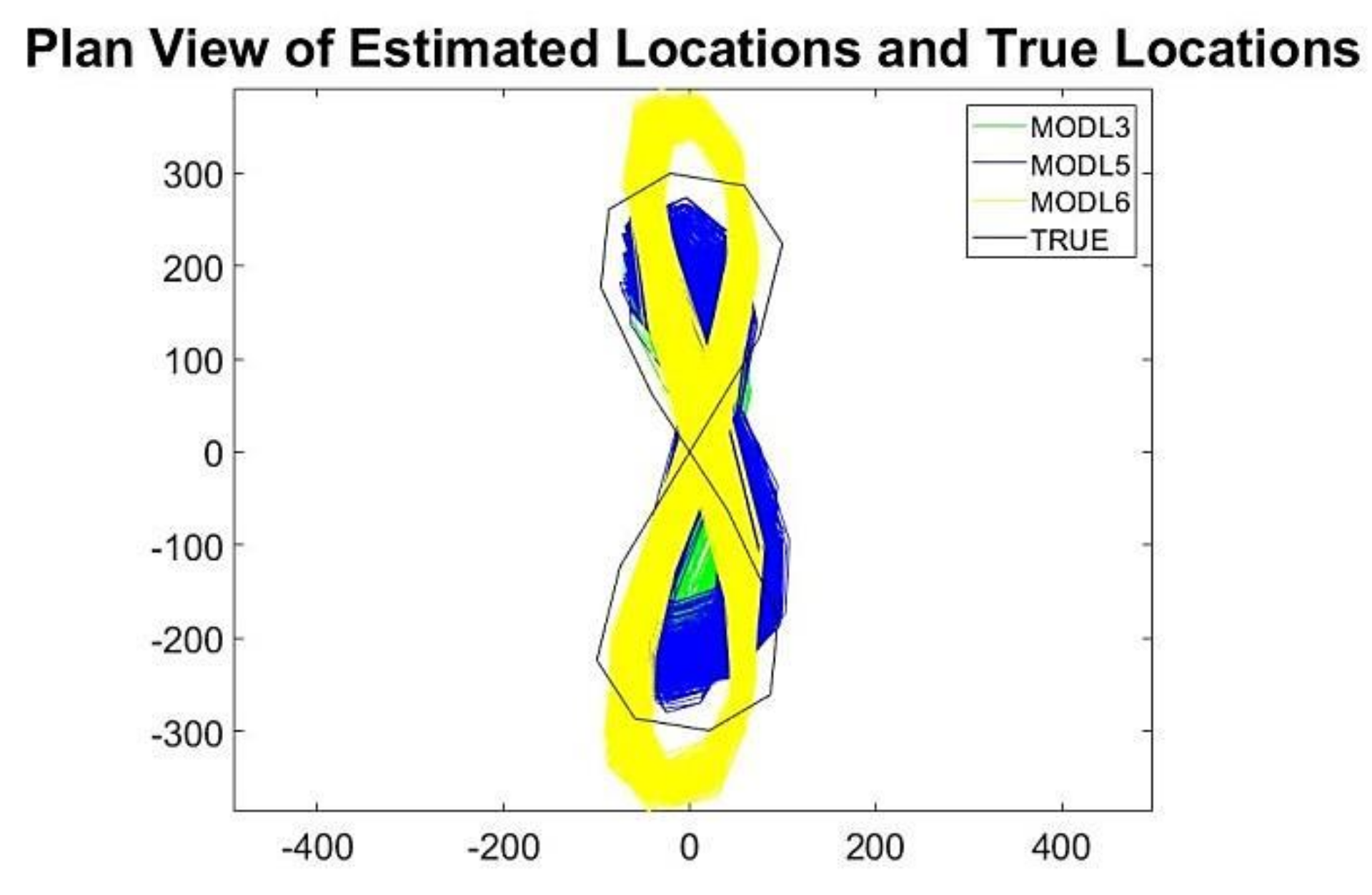
Example 3. To compare and evaluate the performance of the new algorithm with conventional KF implementations, we include example 3, which is taken from [2]. The example is a comparison of the GNSS navigation performance with four vehicle tracking models, using a simulated racetrack with a 1.5 km figure-8 track at 90, 140, 240, and 360 kph average speed and a nominal low-cost clock, with a relative stability of part/part over 1 s. The number of states in the KF model varies as satellites come into and fall from view. The vehicle states (position, velocity, and acceleration) are as follows: position north, position east, position up (vertical), velocity north, velocity east, velocity vertical, acceleration north, acceleration east, acceleration vertical. Models 3 and 5 do not include the three acceleration states (north, east, vertical). Table 2 lists the number of state variables and the minimum and maximum number of visible satellites.
Table 3 lists the parametric models used in this research to model a single component of the motion of a host vehicle. The model parameters mentioned in
Table 3 include the standard deviation
and the correlation time constant
of position, velocity, acceleration, and jerk (derivative of acceleration) [
2]. The example 3 makes use of the Algorithm 1 adaptive computation from Equations (29) and (30), and the resulting algorithm is called K-SVD adaptive.
Regarding the host vehicle dynamic models in
Table 3, the third model is a navigation model that is often used to track the GNSS receiver phase and frequency error, and to track the vehicle position and velocity. The fifth model is restricted root mean square (RMS) speed and acceleration, and is a further refinement of a vehicle with bounded velocity and acceleration. These also perform better when the signals are lost, because the model takes the true vehicle limitations into consideration. Model 6 is the bounded RMS location, and may be suitable for ships and land vehicles with restricted altitude excursions, including vehicles operating within tightly confined areas [
2]. Each model was tuned to the simulated vehicle dynamics by putting its autonomous model parameters to fit the values described in [
2].
The results from the experiment in Example 3 are shown in
Table 4 and
Figure 2,
Figure 3,
Figure 4,
Figure 5,
Figure 6,
Figure 7,
Figure 8,
Figure 9,
Figure 10,
Figure 11,
Figure 12 and
Figure 13. The experiment was designed to have a side-by-side comparison between the conventional KF and its novel factored form, K-SVD and K-SVD adaptive.
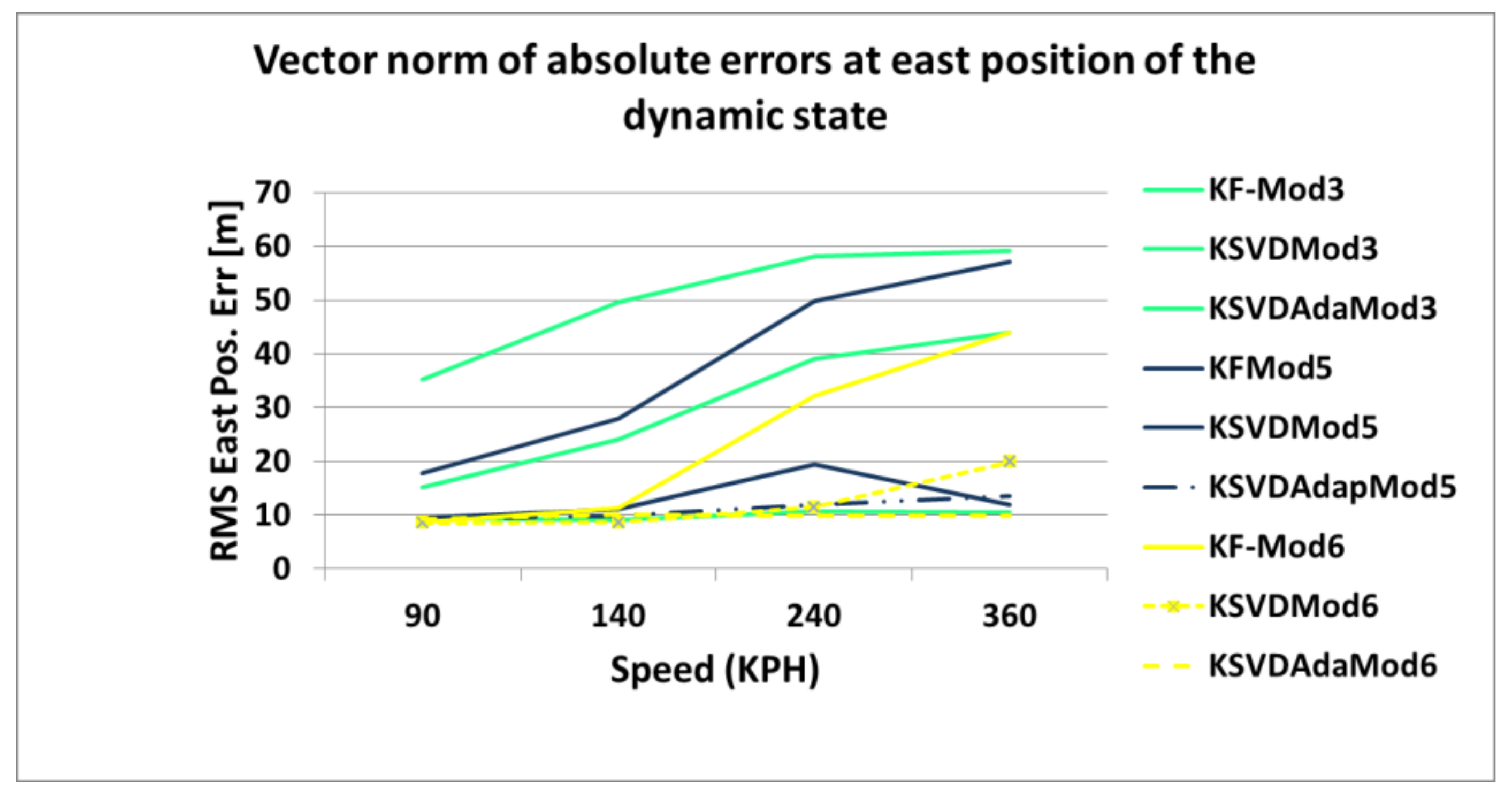
Comparing the values for each model in
Table 4 at different velocities, it is clear that when the velocity is increased (e.g., from 90 to 360 kph), the conventional KF always increases the RMS error absolute value well above the K-SVD by about 172%. At the model level, the best performer in all cases is model 5. From the figures above, it can be inferred that with all things being equal (the only difference in the MATLAB source code is the algorithm to compute the Kalman filter), K-SVD adaptive has a better prediction accuracy than the conventional KF and traditional factored KFs. This means that K-SVD adaptive is more robust than the current known factor-based algorithms, at the same time providing a better filtering capability when it performs the same operations. The algorithm captures the information that matters, which is the N-dimensional subspace of
spanned by the first columns of V or the right orthogonal factor [
8,
9]. By performing a matrix multiplication, the algorithm realizes a low dimensionality reduction that captures much of the variability and corresponds with the selection of the eigenvectors with the largest eigenvalues (since SVD orders them from the largest to smallest). Additionally, by adapting to variations in the covariance measurement error, the algorithm has a higher accuracy.
Figure 14,
Figure 15,
Figure 16,
Figure 17,
Figure 18 and
Figure 19 represent the results of
Table 4. By observing
Figure 14, it is easy to see that K-SVD adaptive model 6 performs better for the north position. K-SVD model 5 also performs relatively well compared with the conventional KF. Similar results can be inferred from
Figure 15; K-SVD adaptive model 6 is the best performer, followed by K-SVD adaptive models 3 and 5. Conclusive results can also be seen for the downward position RMS error in
Figure 16. Model 5 performs better, independent of the filter type. Model 6 is also a good performer for downward velocity, and the worst is model 3.
Figure 17 illustrates the results for the north velocity RMS. From this figure, K-SVD adaptive model 6 is the best performer, followed closely by K-SVD model 5. From
Figure 18, the best performer is K-SVD adaptive model 5, and finally, regarding the downward speed velocity RMS from
Figure 19, K-SVD models 3 and 6 perform relatively well.
Example 4. Distance measuring equipment (DME) operations will continue to expand as a different navigation source in space-based navigational systems such as GPS and Galileo [23]. In the 21st century, airborne navigation has become increasingly reliant on satellite guidance; nonetheless, satellite signals are extremely low, can be spoofed, and are not necessarily available. There are mandates from the US and European Union that require maintaining and upgrading ground-based navigation aids. The following example simulates a simplified model of an electronic DME-to-DME position and velocity navigation system, where the noise measurement of a slant range (distance) is the underlying observable. The airborne distance measuring equipment transmits a pulse that is received and returned by the ground station, while the aircraft equipment triangulates the transit time in terms of distance based on the propagation delay. The aircraft flies along a fixed path at a cruising speed of 583 kph [
6]. The duration of the flight is 3000 s, the initial coordinates at t = 0 are appropriately defined as normal random variables,
,
, sample time T = 2 s,
m/s, and the maximum deviation in the acceleration for the aircraft is
= 0.001
.
Suppose that two DME stations are found on the x-axis, as shown in
Figure 20. The positions of the DME stations are identified. The aircraft follows a circular path at the end of the trajectory, at a constant speed with the same velocity as the linear motion, turning for 270° with a gyro of 20 km. The trajectory is depicted in
Figure 21 and assumed to be level, with constant velocity plus small perturbations caused by small random accelerations. This model is only practical for short intervals.
For navigation based on estimation, it is necessary to extrapolate the position or initial state of the airplane, which is supposedly known, to a posterior time step using the dynamic equation of the process and knowing the excitation that disturbs the system.
To obtain distance
, it is necessary to have the following geometric relations for both DMEs; the measurements in terms of
and
are then:
To estimate the aircraft position using the above mathematical expressions, it is necessary to clear x and y as a function of trigonometric functions, and the equations are solved using linearization by expansion:
Writing Equations (50) and (51) in matrix form, we have:
Thus, the evaluation of the partial derivatives leads to:
Substituting in (53), we have:
Finally, we notice that the equation above can be generalized further because the cosine and sine terms represent the line of sight into the two DME channels, along with direction cosine between the y- and x-axes [
6]. Please note the connection between the observables,
, and the estimated quantity,
is not linear. Therefore,
Matrix
is sometimes called the linearized matrix. Applying the inverse matrix method, we have:
Figure 21 depicts the results after running Equations (47)–(61) in MATLAB code:
As seen in
Figure 21, the error does not go to infinity when the nominal trajectory goes through the origin, because the assumed aircraft dynamics (i.e., random walk) gives the filter some memory, and all the weight is not placed on the current measurement. From the figure, it can be seen that the aircraft reaches the origin in about 1063 s. What it is illustrated here is the classical error dilution of precision (DOP) when the line of sight is 180° apart relative to the aircraft. The detected peak is the greatest in the y-axis, and the error occurs due to the mathematical effect of navigating the DME geometry on the position measurement. After that, the position is calculated using conventional KF and K-SVD, and the general formulation is:
The covariance of is and that of is , then .
The state equations are then:
where
and
denote the incremental position in the horizontal and vertical plane, respectively.
Let
be the error in the process, and the matrix maintains the values of
from Equation (6):
denotes the measurement error:
The results from calculating the position using conventional KF and Algorithm 1 without the adaptive computation (K-SVD) from Equations (29) and (30) are shown in
Figure 22.
From
Figure 22, is it easy to see that at about 333 m from the origin, the DME presents singularity in the calculation due to DOP, and at that critical point the KF and K-SVD perform fine; however, the KF does not perform as well as K-SVD at the cusp of the circular return. Additionally, the results show how far the RMS is above the KF compared with the K-SVD in this DME example (see
Figure 23).
The results from
Figure 23 indicate that the RMS is lower for the K-SVD filter compared with the conventional KF. When solving the observation equation to obtain the calculated position, it is likely that the error of the observables is manifested by producing erratic oscillations in the position. This makes the computed trajectory uneven, making the motion of the airplane very unstable. By using a prediction system that minimizes that noise, it is possible to produce estimates of unknown or known variables that tend to be more precise than those based on the measurement alone (see Equation (61)). It is demonstrated that advantages can be obtained when combining the position of the airplane based on observables and predictions. Given that the DME was left in place to circumvent the reliability problem of GPS and to increase reliability, the best filter to deal with the singularities at the origin is K-SVD.
7. Conclusions and Future Scope
The computation of the novel Kalman-SVD algorithm is based on the computation of the singular value decomposition of an unsymmetrical matrix without explicitly forming its left orthogonal factor that has a high dimension [
19]. K-SVD does a truncation that keeps only the top
n right singular vectors by setting
(where superscript T denotes the transpose of a matrix and n denotes the number of rows), equal to the n rows of
(n × n matrix). That is equivalent to removing or zeroing out m number of singular values from the original matrix (m + n) by –n, where (m + n) denotes the rows, therefore reducing the dimension, which is far less than the original dimension, thus filtering out the noise.
The other conclusion of this research is related to the robustness of the adaptive algorithm. Compared with other KF-based decomposition algorithms, K-SVD adaptive can handle round-off errors, which makes the algorithm useful in critical applications, making it possible to deal with singular systems that are ill-conditioned.
From the analysis of example 3, we can conclude that the accuracy of position and speed can be improved by choosing the model that performs the best for the worst-case scenario, which in this case is the highly dynamic conditions of maneuvering a vehicle. The tracking capabilities can also be increased by adding to the K-SVD algorithm the adaptive computation of the measurement noise matrix as a time-variant matrix. From the analysis of example 4, we can conclude that K-SVD is suitable to deal with real dynamic conditions for ground navigation systems. From the analysis of the literature, it seems that one of the drawbacks of using K-SVD and KF in general is their high computational load. In that sense, K-SVD can be used in applications where the KF is currently used with the advantages of robustness and accuracy.
The algorithm developed in this research also has superior accuracy compared with regular decomposition-based KF algorithms by adapting the measurement matrix at each step and at the same time using the simplest form to update the error of the covariance matrix P, which is the most common equation to compute the algorithm. Additionally, the proposed Algorithm 1 does not require matrix inverting, and the system of interest does not need to have a square shape.
Our effort in this paper is guided by the increasing utilization of Kalman filtering in operations that demand high reliability, where the robustness of the algorithm is a necessary condition to perform critical operations. More work can be done in future K-SVD adaptive applications by including the Joseph stabilized form instead of the conventional form of the Riccati equation to avoid the propagation of antisymmetric problems and fine-tuning the process noise covariance matrix
. We believe that the key points and principles derived here will find their way to applications in high-speed signal processing by combining K-SVD, K-SVD adaptive and SVD compressive sensing [
25]. For future research, we intend to explore particular technology uses.