Prediction Capability of Cartesian Cut-Cell Method with a Wall-Stress Model Applied to High Reynolds Number Flows
Abstract
1. Introduction
2. Governing Equation and Simulation Method
2.1. Governing Equation
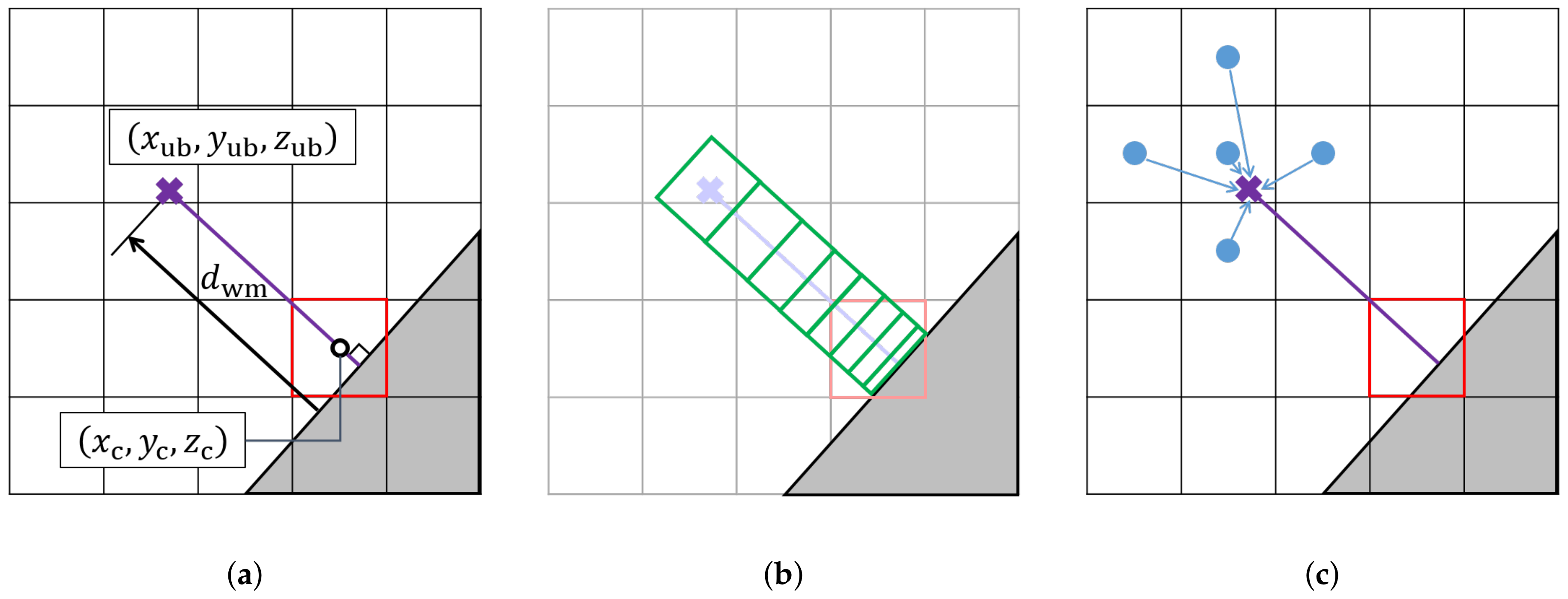
2.2. Wall-Stress Model
- The upper bound of the wall-stress model mesh is set on the wall-normal line passing through a CFD cell center that includes the cut-plane by the object. The upper bound is placed at distance from the wall. The distance corresponds to . The location of the upper bound of the wall-stress model in the CFD domain is decided as follows:where denotes the distance from the wall to the CFD cell center .
- The one-dimensional non-uniform mesh for the wall-stress model is generated from the wall to the upper bound. The wall-stress model mesh is generated using the following formula:where denotes the cell number from the wall; denotes the rate of the increment of the grid distancing between neighboring grid points. The grid distancing increases by between neighboring grid points. Constants and is decided to satisfy the following conditions:
- The upper boundary values and T are decided by inverse distance weighted interpolation using instantaneous values of the neighbor cell-center of the Cartesian cut-cell simulation as follows:The wall boundary condition of the wall-stress model equations is the non-slip and adiabatic wall in the present study.
- The obtained wall-stress is provided to the CFD cell at , which includes the cut-plane by the object.
3. Flow around a Triangular Column
3.1. Simulation Conditions
3.2. Simulation Results
4. Flow around the 30P30N Three-Element High-Lift Airfoil Configuration
4.1. Simulation Conditions
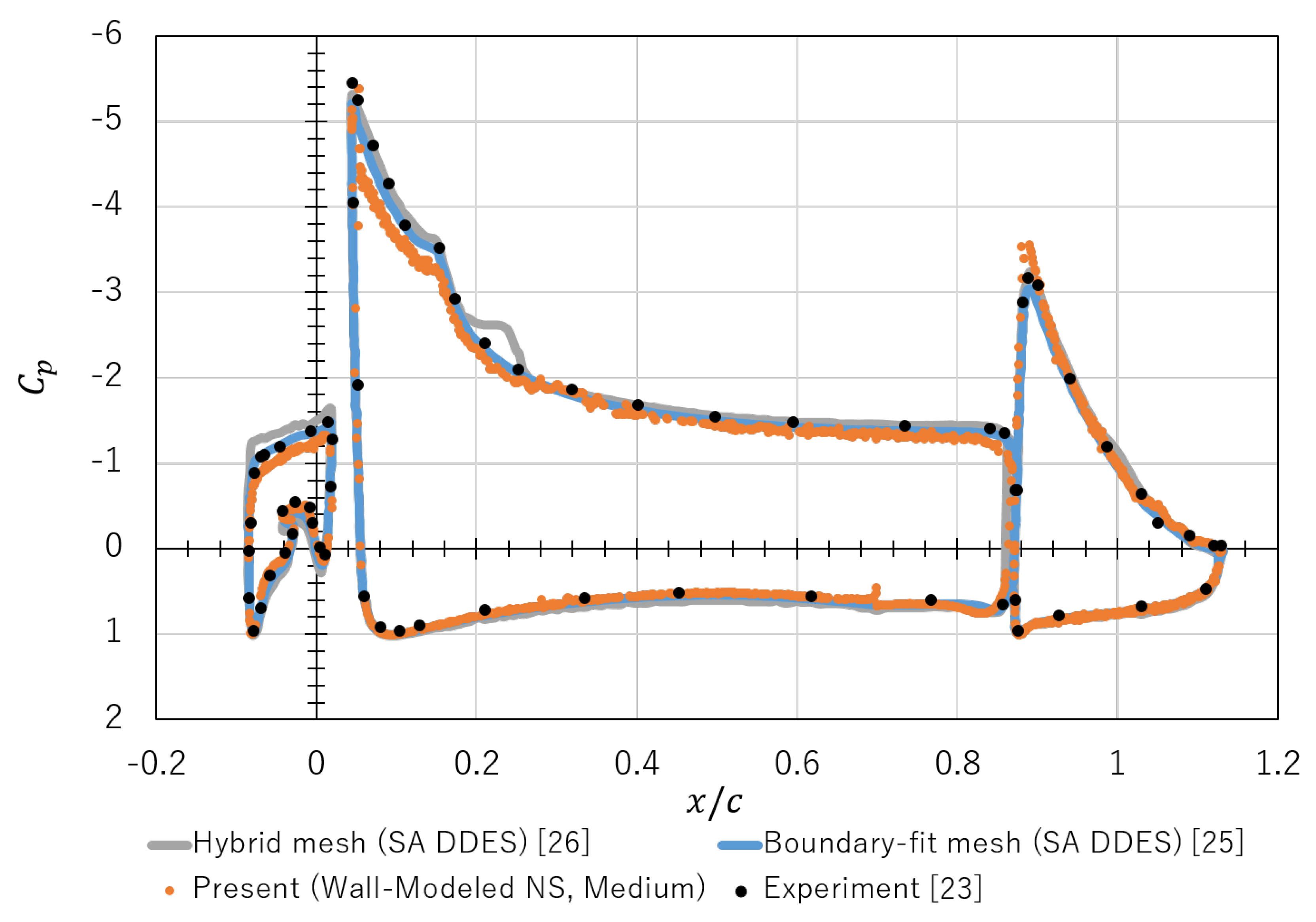
4.2. Simulation Result by Wall-Modelled Navier–Stokes Simulation
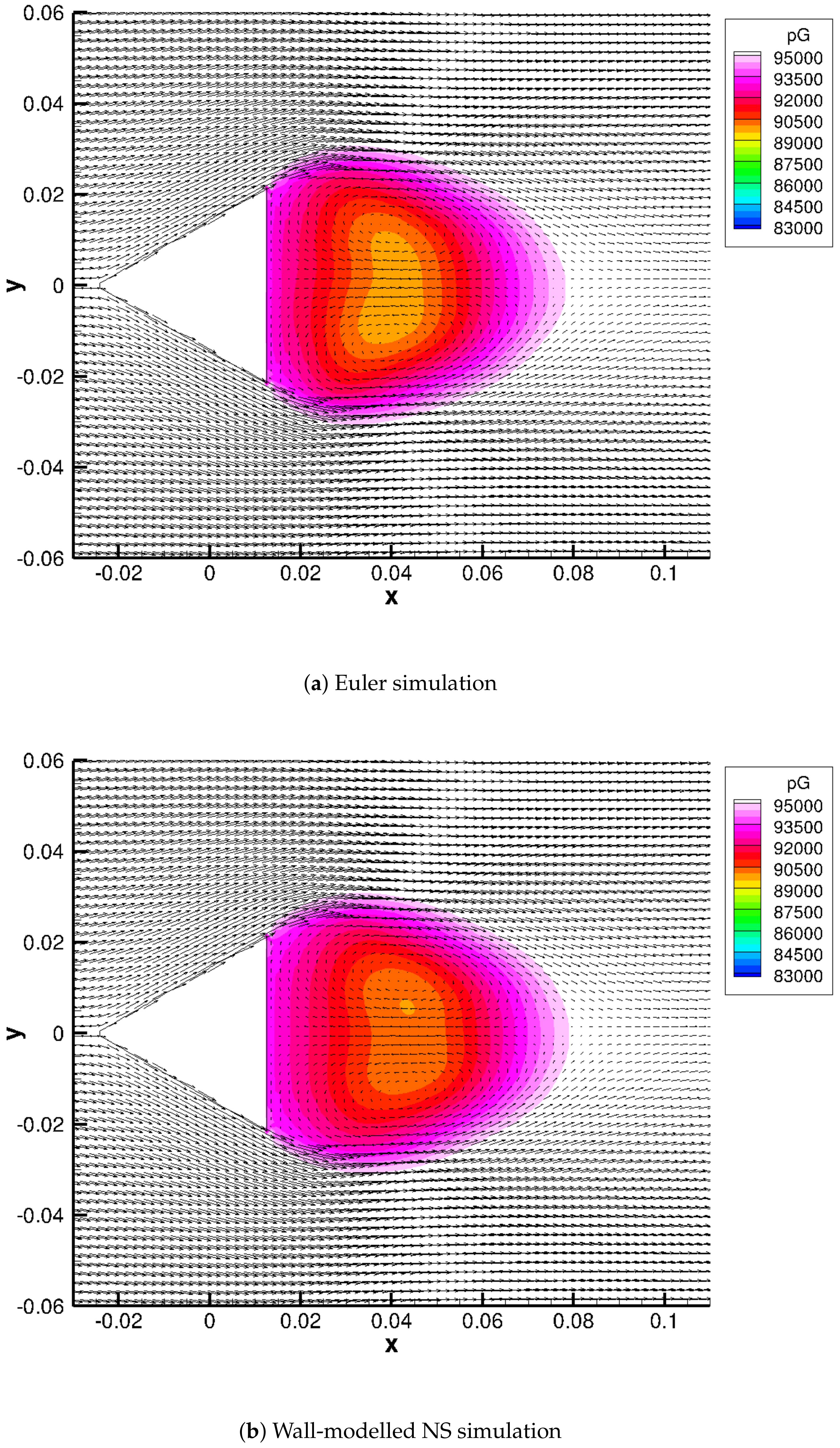
4.3. Simulation Result with the Euler Equation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Choi, H.; Moin, P. Grid-point requirements for large eddy simulation: Chapman’s estimates revisited. Phys. Fluids 2012, 24, 1–6. [Google Scholar] [CrossRef]
- Baurle, R.A.; Tam, C.J.; Edwards, J.R.; Hassan, H.A. Erratum: Hybrid Simulation Approach for Cavity Flows: Blending, Algorithm, and Boundary Treatment Issues. AIAA J. 2003, 41, 1463–1480. [Google Scholar] [CrossRef]
- Nikitin, N.V.; Nicoud, F.; Wasistho, B.; Squires, K.D.; Spalart, P.R. An approach to wall modeling in large-eddy simulations. Phys. Fluids 2000, 12, 1629–1632. [Google Scholar] [CrossRef]
- Nicoud, F.; Baggett, J.S.; Moin, P.; Cabot, W. Large eddy simulation wall-modelling based on suboptimal control theory and linear stochastic estimation. Phys. Fluids 2001, 13, 2968–2984. [Google Scholar] [CrossRef]
- Kawai, S.; Larsson, J. Wall-modeling in large eddy simulation: Length scales, grid resolution, and accuracy. Phys. Fluids 2012, 24, 1–10. [Google Scholar] [CrossRef]
- Bose, S.T.; Moin, P. A dynamic slip boundary condition for wall-modeled large-eddy simulation. Phys. Fluids 2014, 26. [Google Scholar] [CrossRef]
- Larsson, J.; Kawai, S.; Bodart, J.; Bermejo-Moreno, I. Large eddy simulation with modeled wall-stress: Recent progress and future directions. Mech. Eng. Rev. 2016, 3, 15-00418. [Google Scholar] [CrossRef]
- Fukushima, Y.; Kawai, S. Wall-modeled large-eddy simulation of transonic airfoil buffet at high reynolds number. AIAA J. 2018, 56, 2372–2388. [Google Scholar] [CrossRef]
- Clarke, D.K.; Salas, M.D.; Hassan, H.A. Euler calculations for multielement airfoils using Cartesian grids. AIAA J. 1986, 24, 353–358. [Google Scholar] [CrossRef]
- Yang, G.; Causon, D.M.; Ingram, D.M. Calculation of compressible flows about complex moving geometries using a three-dimensional Cartesian cut cell method. Int. J. Numer. Methods Fluids 2000, 33, 1121–1151. [Google Scholar] [CrossRef]
- Harada, M.; Imamura, T. Comparison of Immersed Boundary Method and Cut-Cell Method on Cartesian Grids—Validation of Pressure and Shear Stress Distributions on Near-Wall Region. J. Jpn. Soc. Aeronaut. S. 2016, 64, 200–207. (In Japanese) [Google Scholar] [CrossRef]
- Ueno, K.; Natsume, Y.; Shimasaki, S.I.; Iwai, K.; Ohsasa, K. Numerical Study of Oscillating Melt Flows and Its Solute Transport Driven by Electromagnetic Force around Dendrite. Tetsu-to-Hagane 2016, 102, 141–150. (In Japanese) [Google Scholar] [CrossRef]
- Takeda, Y.; Ueno, K.; Matsuyama, S.; Tanno, H. Coupled Numerical Analysis of Three-Dimensional Unsteady Flow with Pitching Motion of Reentry Capsule. Trans. Jpn. Soc. Aeronaut. Space Sci. 2020, in press. [Google Scholar]
- Peskin, C.S. Numerical analysis of blood flow in the heart. J. Comput. Phys. 1977, 25, 220–252. [Google Scholar] [CrossRef]
- Iaccarino, G.; Verzicco, R. Immersed boundary technique for turbulent flow simulations. Appl. Mech. Rev. 2003, 56, 331. [Google Scholar] [CrossRef]
- Mittal, R.; Iaccarino, G. Immersed Boundary Methods. Annu. Rev. Fluid Mech. 2005, 37, 239–261. [Google Scholar] [CrossRef]
- Shima, E.; Kitamura, K. On New Simple Low-Dissipation Scheme of AUSM-Family for All Speeds. In Proceedings of the 47th AIAA Aerospace Science Meeting Including New Horizons Forum Aerospace Exposition, Reston, VA, USA, 5–8 January 2009; pp. 1272–2010. [Google Scholar] [CrossRef]
- Kim, K.H.; Kim, C. Accurate, efficient and monotonic numerical methods for multi-dimensional compressible flows. Part II: Multi-dimensional limiting process. J. Comput. Phys. 2005, 208, 570–615. [Google Scholar] [CrossRef]
- Thornber, B.; Mosedale, A.; Drikakis, D.; Youngs, D.; Williams, R.J. An improved reconstruction method for compressible flows with low Mach number features. J. Comput. Phys. 2008, 227, 4873–4894. [Google Scholar] [CrossRef]
- Shu, C.W.; Osher, S. Efficient implementation of essentially non-oscillatory shock-capturing schemes. J. Comput. Phys. 1988, 77, 439–471. [Google Scholar] [CrossRef]
- Jameson, A.; Baker, T. Solution of the Euler equations for complex configurations. In Proceedings of the 6th Computational Fluid Dynamics Conference Danvers, Danvers, MA, USA, 13–15 July 1983. [Google Scholar] [CrossRef]
- Lindsey, W.F. Drag of Cylinders of Simple Shapes; NACA Report 619; NACA Langley Aeronautical Lab.: Langley Field, VA, USA, 1937. [Google Scholar]
- Murayama, M.; Yokokawa, Y.; Ura, H.; Nakakita, K.; Yamamoto, K.; Ito, Y.; Takaishi, T.; Sakai, R.; Shimoda, K.; Kato, T.; et al. Experimental Study of Slat Noise from 30P30N Three-Element High-Lift Airfoil in JAXA Kevlar-Wall Low-Speed Wind Tunnel. In Proceedings of the 2018 AIAA/CEAS Aeroacoustics Conference, Reston, VA, USA, 25–29 June 2018. [Google Scholar] [CrossRef]
- Pascioni, K.; Cattafesta, L.N.; Choudhari, M.M. An Experimental Investigation of the 30P30N Multi-Element High-Lift Airfoil. In Proceedings of the 20th AIAA/CEAS Aeroacoustics Conference, Reston, VA, USA, 16–20 June 2014. [Google Scholar] [CrossRef]
- Sakai, R.; Ihida, T.; Murayama, M.; Ito, Y.; Yamamoto, K. Aerodynamic Simulation of 30P30N Airfoil using Second-Order Low-Dissipation Scheme on Cartesian Hybrid Grid. In Proceedings of the Fifth Aerodynamics Prediction Challenge, Tokyo, Japan, 1 July 2019; pp. 83–89. [Google Scholar]
- Ueno, Y. Validation of Aerodynamic Noise from 3-Element High-Lift Airfoil Configulation using Cflow. In Proceedings of the Fifth Aerodynamics Prediction Challenge, Tokyo, Japan, 1 July 2019; pp. 103–116. [Google Scholar]








| (Wall-Modeled NS) | ||
|---|---|---|
| , |
| Coarse | Fine | |
|---|---|---|
| Euler | ||
| Wall-Modelled NS | ||
| Experiment [22] | ||
| (Wall-Modeled NS) | |||||
|---|---|---|---|---|---|
| Coarse | Medium | Fine | |||
| Total Number of Cells | Lift Coefficient | ||
|---|---|---|---|
| Present Wall-Modelled NS | Coarse | 15,972,528 | |
| Medium | 93,515,136 | ||
| Fine | 612,392,768 | ||
| Boundary-fitted mesh (SA DDES) [25] | 70,445,430 | ||
| Hybrid mesh (SA DDES) [26] | 242,000,000 | ||
| Experiment [23] | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takeda, Y.; Ueno, K.; Ishikawa, T.; Takahashi, Y. Prediction Capability of Cartesian Cut-Cell Method with a Wall-Stress Model Applied to High Reynolds Number Flows. Appl. Sci. 2020, 10, 5050. https://doi.org/10.3390/app10155050
Takeda Y, Ueno K, Ishikawa T, Takahashi Y. Prediction Capability of Cartesian Cut-Cell Method with a Wall-Stress Model Applied to High Reynolds Number Flows. Applied Sciences. 2020; 10(15):5050. https://doi.org/10.3390/app10155050
Chicago/Turabian StyleTakeda, Yuki, Kazuyuki Ueno, Tatsuya Ishikawa, and Yuta Takahashi. 2020. "Prediction Capability of Cartesian Cut-Cell Method with a Wall-Stress Model Applied to High Reynolds Number Flows" Applied Sciences 10, no. 15: 5050. https://doi.org/10.3390/app10155050
APA StyleTakeda, Y., Ueno, K., Ishikawa, T., & Takahashi, Y. (2020). Prediction Capability of Cartesian Cut-Cell Method with a Wall-Stress Model Applied to High Reynolds Number Flows. Applied Sciences, 10(15), 5050. https://doi.org/10.3390/app10155050





