Automatic Tortuosity Estimation of Nerve Fibers and Retinal Vessels in Ophthalmic Images
Abstract
1. Introduction
- We propose an automatic curvilinear tortuosity measurement method with the exponential curvature estimation, which measures the tortuosity value from the original image directly with few complex pre-processing steps of the traditional methods.
- Our proposed method is robust, which has been validated quantitatively using one retinal blood vessel tortuosity dataset and two corneal nerve tortuosity datasets. As a complementary output, we have made all the tortuosity datasets available online.
2. Methods
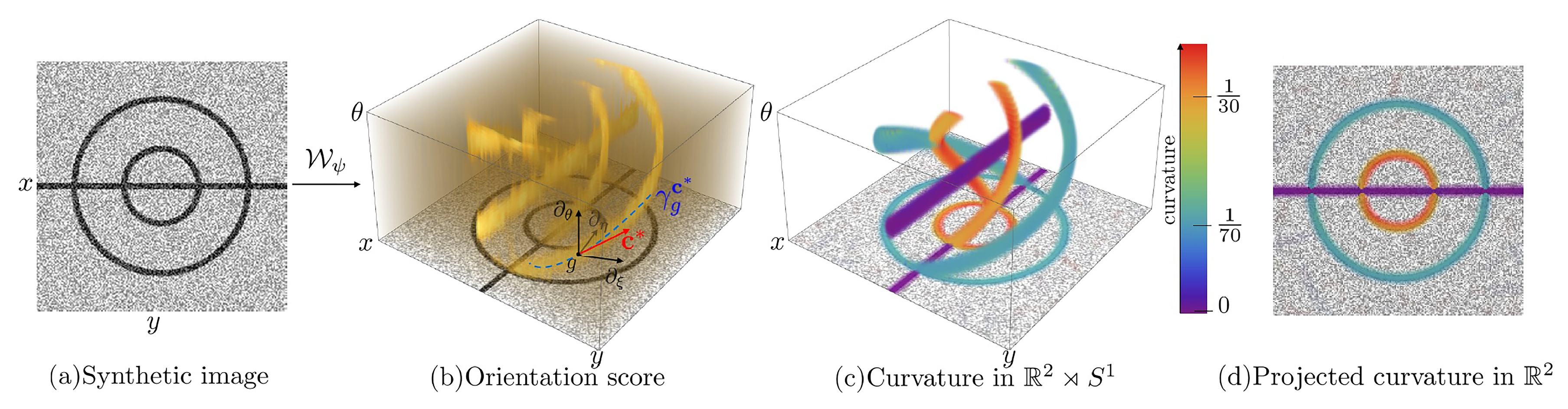
2.1. Curvilinear Structure Enhancement
2.2. Curvilinear Structure Tortuosity Representation
2.2.1. Representation of the Curvature Orientation
2.2.2. Exponential Curvature Estimation
3. Datasets and Metrics
4. Experimental Results
4.1. Tortuosity Classification
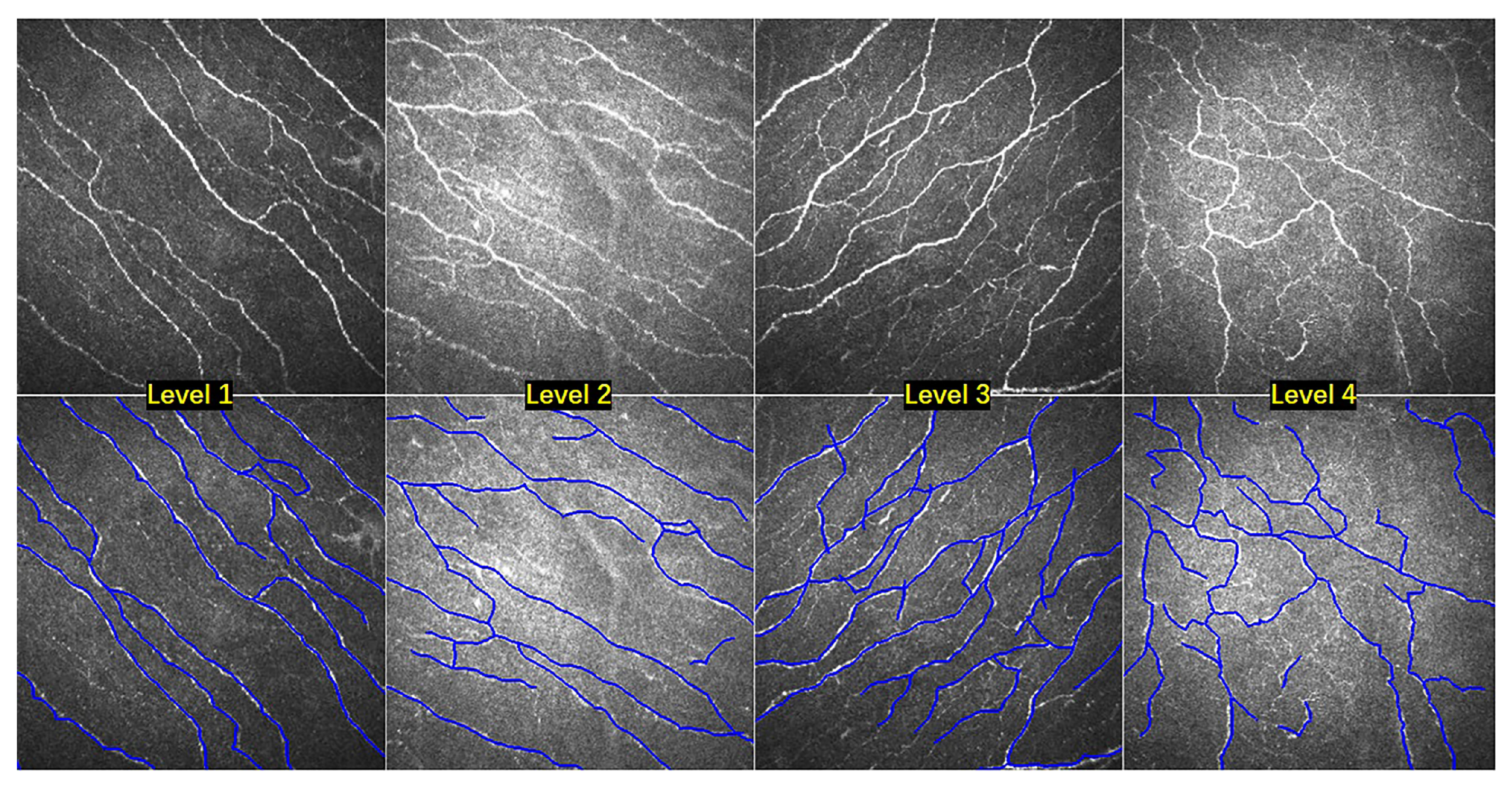
4.2. Nerve Fibers Tortuosity Grading
4.3. Retinal Vessels Tortuosity Grading
4.4. Clinical Evaluation
4.5. The Effectiveness of Curvilinear Structure Enhancement for Tortuosity Grading
4.6. The Effectiveness of Curvilinear Structure Enhancement for Fiber Segmentation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Annunziata, R.; Kheirkhah, A.; Aggarwal, S.; Hamrah, P.; Trucco, E. A fully automated tortuosity quantification system with application to corneal nerve fibres in confocal microscopy images. Med. Image Anal. 2016, 32, 216–232. [Google Scholar] [CrossRef] [PubMed]
- Scarpa, F.; Zheng, X.; Ohashi, Y.; Ruggeri, A. Automatic evaluation of corneal nerve tortuosity in images from in vivo confocal microscopy. Invest. Ophthal. Vis. Sci. 2011, 52, 6404–6408. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Drexler, W. Optical coherence tomography angiography and photoacoustic imaging in dermatology. Photochem. Photobiol. Sci. 2019, 18, 945–962. [Google Scholar] [CrossRef] [PubMed]
- van Sloun, R.J.; Demi, L.; Schalk, S.G.; Caresio, C.; Mannaerts, C.; Postema, A.W.; Molinari, F.; van der Linden, H.C.; Huang, P.; Wijkstra, H.; et al. Contrast-enhanced ultrasound tractography for 3D vascular imaging of the prostate. Sci. Rep. 2018, 8, 1–8. [Google Scholar] [CrossRef]
- Edwards, K.; Pritchard, N.; Vagenas, D.; Russell, A.; Malik, R.A.; Efron, N. Standardizing corneal nerve fibre length for nerve tortuosity increases its association with measures of diabetic neuropathy. Diabet. Med. 2014, 31, 1205–1209. [Google Scholar] [CrossRef]
- Kim, J.; Markoulli, M. Automatic analysis of corneal nerves imaged using in vivo confocal microscopy. Clin. Exp. Optom. 2018, 101, 147–161. [Google Scholar] [CrossRef]
- Grisan, E.; Foracchia, M.; Ruggeri, A. A Novel Method for the Automatic Grading of Retinal Vessel Tortuosity. IEEE Trans. Med. Imaging 2008, 27, 310–319. [Google Scholar] [CrossRef]
- Frangi, A.; Niessen, W.; Vincken, K.; Viergever, M. Multiscale vessel enhancement filtering. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention, Cambridge, MA, USA, 11–13 October 1998; pp. 130–137. [Google Scholar]
- Bankhead, P.; Scholfield, C.N.; McGeown, J.G.; Curtis, T.M. Fast retinal vessel detection and measurement using wavelets and edge location refinement. PLoS ONE 2012, 7, e32435. [Google Scholar] [CrossRef]
- Läthén, G.; Jonasson, J.; Borga, M. Blood vessel segmentation using multi-scale quadrature filtering. Patter. Recogn. Lett. 2010, 31, 762–767. [Google Scholar] [CrossRef]
- Zhang, J.; Dashtbozorg, B.; Bekkers, E.; Pluim, J.; Duits, R.; ter Haar Romeny, B.M. Robust Retinal Vessel Segmentation via Locally Adaptive Derivative Frames in Orientation Scores. IEEE Trans. Med. Imaging 2016, 35, 2631–2644. [Google Scholar] [CrossRef]
- Zhao, Y.; Zheng, Y.; Liu, Y.; Zhao, Y.; Luo, L.; Yang, S.; Na, T.; Wang, Y.; Liu, J. Automatic 2D/3D Vessel Enhancement in Multiple Modality Images Using a Weighted Symmetry Filter. IEEE Trans. Med. Imaging 2017, 37, 438–450. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Rada, L.; Chen, K.; Harding, S.; Zheng, Y. Automated Vessel Segmentation Using Infinite Perimeter Active Contour Model with Hybrid Region Information with Application to Retinal Images. IEEE Trans. Med. Imaging 2015, 34, 1797–1807. [Google Scholar] [CrossRef] [PubMed]
- Hart, W.E.; Goldbaum, M.H.; Kube, P.; Nelson, M. Measurement and classification of retinal vascular tortuosity. Int. J. Med. Inform. 1999, 53, 239–252. [Google Scholar] [CrossRef]
- Holmes, T.; Pellegrini, M.; Miller, C.; Epplin-Zapf, T.; Larkin, S.; Luccarelli, S.; Staurenghi, G. Automated software analysis of corneal micrographs for peripheral neuropathy. Investig. Ophthalmol. Vis. Sci. 2010, 51, 4480–4491. [Google Scholar] [CrossRef] [PubMed]
- Goh, K.; Hsu, W.; Lee, M.; Wang, H. ADRIS: An Automatic Diabetic Retinal Image Screening System; Medical Data Mining and Knowledge Discovery; Physica-Verlag: Heidelberg, Germany, 2001; pp. 181–210. [Google Scholar]
- Heneghan, C.; Flynn, J.; O’Keefe, M.; Cahill, M. Characterization of changes in blood vessel width and tortuosity in retinopathy of prematurity using image analysis. Med. Image Anal. 2002, 6, 407–429. [Google Scholar] [CrossRef]
- Bracher, D. Changes in peripapillary tortuosity of the central retinal arteries in newborns. Graefe’s Arch. Clin. Exp. Ophthalmol. 1982, 218, 211–217. [Google Scholar] [CrossRef]
- Patašius, M.; Marozas, V.; Lukoševičius, A.; Jegelevičius, D. Evaluation of tortuosity of eye blood vessels using the integral of square of derivative of curvature [elektroninis išteklius]. In Proceedings of the 3rd European Medical & Biological Engineering Conference, IFMBE European Conference on Biomedical Engineering EMBEC’05, Prague, Czech Republic, 20–25 November 2005; Volume 11. [Google Scholar]
- Bullitt, E.; Gerig, G.; Pizer, S.M.; Lin, W.; Aylward, S.R. Measuring tortuosity of the intracerebral vasculature from MRA images. IEEE Trans. Med. Imaging 2003, 22, 1163–1171. [Google Scholar] [CrossRef]
- Chandrinos, K.; Pilu, M.; Fisher, R.; Trahanias, P. Image Processing Techniques for the Quantification of Atherosclerotic Changes. In Proceedings of the VIII Mediterranean Conference on Medical and Biological Engineering and Computing, Limassol, Cyprus, 14–17 June 1998. [Google Scholar]
- Bribiesca, E.; Bribiescacontreras, G. 2D tree object representation via the slope chain code. Patter. Recogn. 2014, 47, 3242–3253. [Google Scholar] [CrossRef]
- Kallinikos, P.; Berhanu, M.; O’Donnell, C.; Boulton, A.; Efron, N.; Malik, R. Corneal nerve tortuosity in diabetic patients with neuropathy. Investig. Ophthal. Vis. Sci. 2004, 45 2, 418–422. [Google Scholar] [CrossRef]
- Smedby, O.; Högman, N.; Nilsson, S.; Erikson, U.; Olsson, A.; Walldius, G. Two-dimensional tortuosity of the superficial femoral artery in early atherosclerosis. J. Vasc. Res. 1993, 30, 181–191. [Google Scholar] [CrossRef]
- Bribiesca, E. A measure of tortuosity based on chain coding. Patter. Recogn. 2013, 46, 716–724. [Google Scholar] [CrossRef]
- Annunziata, R.; Kheirkhah, A.; Aggarwal, S.; Cavalcanti, B.; Hamrah, P.; Trucco, E. Tortuosity classification of corneal nerves images using a multiple-scale-multiple-window approach. In Proceedings of the MICCAI Workshop OMIA, Boston, MA, USA, 14 September 2014; pp. 113–120. [Google Scholar]
- Mehrgardt, P.; Zandavi, S.M.; Poon, S.K.; Kim, J.; Markoulli, M.; Khushi, M. U-Net Segmented Adjacent Angle Detection (USAAD) for Automatic Analysis of Corneal Nerve Structures. Data 2020, 5, 37. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, J.; Pereira, E.; Zheng, Y.; Su, P.; Xie, J.; Zhao, Y.; Shi, Y.; Qi, H.; Liu, J.; et al. Automated Tortuosity Analysis of Nerve Fibers in Corneal Confocal Microscopy. IEEE Trans. Med. Imaging 2020. [Google Scholar] [CrossRef] [PubMed]
- Scarpa, F.; Ruggeri, A. Development of Clinically Based Corneal Nerves Tortuosity Indexes. In Proceedings of the MICCAI Workshop OMIA, Québec City, QC, Canada, 14 September 2017; pp. 219–226. [Google Scholar]
- Felsberg, M.; Sommer, G. The monogenic signal. IEEE Trans. Signal Process. 2001, 49, 3136–3144. [Google Scholar] [CrossRef]
- Hacihaliloglu, I.; Rasoulian, A.; Abolmaesumi, P.; Rohling, R. Local Phase Tensor Features for 3D Ultrasound to Statistical Shape+Pose Spine Model Registration. IEEE Trans. Med. Imaging 2014, 33, 2167–2179. [Google Scholar] [CrossRef]
- Bekkers, E.; Duits, R.; Berendschot, T.; ter Haar Romeny, B. A multi-orientation analysis approach to retinal vessel tracking. J. Math. Imaging Vis. 2014, 49, 583–610. [Google Scholar] [CrossRef]
- Franken, E.; Duits, R. Crossing-preserving coherence-enhancing diffusion on invertible orientation scores. Int. J. Comput. Vis. 2009, 85, 253–278. [Google Scholar] [CrossRef]
- Bekkers, E.; Zhang, J.; Duits, R.; ter Haar Romeny, B.M. Curvature Based Biomarkers for Diabetic Retinopathy via Exponential Curve Fits in SE(2). In Proceedings of the MICCAI: International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; pp. 113–120. [Google Scholar]
- Oliveira-Soto, L.; Efron, N. Morphology of corneal nerves using confocal microscopy. Cornea 2001, 20, 374–384. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the MICCAI: International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015. [Google Scholar]





| Tortuosity Metrics | Symbols | |
|---|---|---|
| 1 | Tortuosity Density [7] | TD |
| 2 | Absolute Curvature [14] | AC |
| 3 | Squared Curvature [14] | SQC |
| 4 | Weighted Absolute Curvature [15] | WAC |
| 5 | Absolute Direction Angle Change [16] | AAC |
| 6 | Arc-Chord Length Ratio [17] | ACR |
| 7 | Chord Length [18] | CHD |
| 8 | Curve Length [18] | CUR |
| 9 | Directional Change of a Line [19] | DCI |
| 10 | Inflection Count Metric [20] | ICM |
| 11 | Mean Direction Angle Change [21] | MAC |
| 12 | Slope Chain Coding [22] | SCC |
| 13 | Tortuosity Coefficient [23] | TC |
| CCM-A Dataset | CCM-B Dataset | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Level-1 | Level-2 | Level-3 | Level-4 | Overall | Low | Mid | High | Overall | ||
| Annunziata [1] | Sen | 0.718 | 0.644 | 0.660 | 0.707 | 0.663 | 0.783 | 0.743 | 0.761 | 0.766 |
| Spec | 0.867 | 0.790 | 0.783 | 0.857 | 0.806 | 0.904 | 0.860 | 0.864 | 0.912 | |
| Acc | 0.858 | 0.780 | 0.759 | 0.843 | 0.790 | 0.877 | 0.826 | 0.847 | 0.848 | |
| Kexp based SVM | Sen | 0.731 | 0.654 | 0.669 | 0.713 | 0.675 | 0.811 | 0.758 | 0.786 | 0.784 |
| Spec | 0.878 | 0.802 | 0.794 | 0.865 | 0.816 | 0.914 | 0.865 | 0.887 | 0.921 | |
| Acc | 0.865 | 0.788 | 0.775 | 0.853 | 0.797 | 0.909 | 0.833 | 0.870 | 0.868 | |
| Kexp+ based SVM | Sen | 0.742 | 0.674 | 0.683 | 0.734 | 0.715 | 0.824 | 0.765 | 0.790 | 0.810 |
| Spec | 0.898 | 0.819 | 0.811 | 0.881 | 0.852 | 0.929 | 0.873 | 0.891 | 0.929 | |
| Acc | 0.881 | 0.799 | 0.793 | 0.864 | 0.820 | 0.914 | 0.841 | 0.883 | 0.882 | |
| Manual Segmentation | Automated Segmentation | Error (%) | |||
|---|---|---|---|---|---|
| Arteries | Veins | Arteries | Veins | ||
| WAC | 0.919 | 0.814 | 0.877 | 0.768 | 8.8 |
| DCI | 0.787 | 0.589 | 0.734 | 0.621 | 8.4 |
| TC | 0.949 | 0.853 | 0.919 | 0.812 | 7.1 |
| CHD | 0.801 | 0.662 | 0.756 | 0.638 | 6.9 |
| AC | 0.922 | 0.837 | 0.893 | 0.801 | 6.5 |
| ICM | 0.684 | 0.575 | 0.661 | 0.542 | 5.6 |
| CUR | 0.813 | 0.701 | 0.784 | 0.677 | 5.3 |
| SCC | 0.850 | 0.770 | 0.827 | 0.745 | 4.8 |
| SQC | 0.925 | 0.826 | 0.901 | 0.812 | 3.8 |
| MAC | 0.820 | 0.814 | 0.801 | 0.795 | 3.8 |
| ACR | 0.792 | 0.656 | 0.812 | 0.629 | 3.4 |
| TD | 0.890 | 0.760 | 0.912 | 0.753 | 2.9 |
| AAC | 0.838 | 0.695 | 0.841 | 0.677 | 2.1 |
| Kexp | 0.945 | 0.868 | 0.928 | 0.857 | 1.9 |
| Metrics | Healthy | Dry Eye | Diabetes | Dry Eye and Diabetes |
|---|---|---|---|---|
| AC | 5.73 ± 4.89 | 5.56 ± 3.43 | 4.12 ± 2.23 | 4.72 ± 3.69 |
| WAC () | 0.47 ± 0.18 | 0.48 ± 0.17 | 0.50 ± 0.20 | 0.52 ± 0.26 |
| AAC | 14.93 ± 10.18 | 12.74 ± 7.95 | 13.51 ± 8.23 | 13.36 ± 9.75 |
| ACR | 0.98 ± 0.01 | 0.97 ± 0.01 | 0.97 ± 0.01 | 0.97 ± 0.01 |
| CHD | 73.31 ± 20.63 | 69.16 ± 19.06 | 62.02 ± 16.80 | 63.74 ± 21.72 |
| CUR | 74.85 ± 21.03 | 70.92 ± 19.48 | 64.11 ± 17.09 | 65.47 ± 21.63 |
| DCI () | 0.33 ± 0.26 | 0.37 ± 0.35 | 0.44 ± 0.42 | 0.42 ± 0.32 |
| ICM | 5.82 ± 1.64 | 5.60 ± 1.60 | 5.13 ± 1.50 | 5.23 ± 1.68 |
| MAC | 0.64 ± 4.16 | 0.80 ± 3.29 | 0.05 ± 3.67 | 0.36 ± 3.90 |
| SQC () | 0.30 ± 0.14 | 0.32 ± 0.14 | 0.36 ± 0.15 | 0.36 ± 0.17 |
| SCC () | 0.36 ± 0.09 | 0.36 ± 0.07 | 0.35 ± 0.08 | 0.34 ± 0.07 |
| TC () | 0.42 ± 0.22 | 0.41 ± 0.13 | 0.43 ± 0.17 | 0.45 ± 0.22 |
| TD | 0.09 ± 0.03 | 0.10 ± 0.01 | 0.10 ± 0.01 | 0.10 ± 0.01 |
| Kexp | 0.17 ± 0.06 | 0.21 ± 0.04 | 0.24 ± 0.07 | 0.25 ± 0.05 |
| Enhancement | IPACHR | U-Net | ||
|---|---|---|---|---|
| FDR | Sen | FDR | Sen | |
| Raw | 0.394 ± 0.007 | 0.738 ± 0.010 | 0.428 ± 0.008 | 0.749 ± 0.013 |
| Vesselness filtering [8] | 0.375 ± 0.006 | 0.753 ± 0.004 | 0.367 ± 0.010 | 0.552 ± 0.019 |
| WSF [13] | 0.363 ± 0.007 | 0.759 ± 0.004 | 0.353 ± 0.009 | 0.788 ± 0.004 |
| Ours | 0.357 ± 0.010 | 0.760 ± 0.005 | 0.338 ± 0.007 | 0.807 ± 0.005 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Chen, B.; Zhang, D.; Zhang, J.; Liu, J.; Zhao, Y. Automatic Tortuosity Estimation of Nerve Fibers and Retinal Vessels in Ophthalmic Images. Appl. Sci. 2020, 10, 4788. https://doi.org/10.3390/app10144788
Chen H, Chen B, Zhang D, Zhang J, Liu J, Zhao Y. Automatic Tortuosity Estimation of Nerve Fibers and Retinal Vessels in Ophthalmic Images. Applied Sciences. 2020; 10(14):4788. https://doi.org/10.3390/app10144788
Chicago/Turabian StyleChen, Honghan, Bang Chen, Dan Zhang, Jiong Zhang, Jiang Liu, and Yitian Zhao. 2020. "Automatic Tortuosity Estimation of Nerve Fibers and Retinal Vessels in Ophthalmic Images" Applied Sciences 10, no. 14: 4788. https://doi.org/10.3390/app10144788
APA StyleChen, H., Chen, B., Zhang, D., Zhang, J., Liu, J., & Zhao, Y. (2020). Automatic Tortuosity Estimation of Nerve Fibers and Retinal Vessels in Ophthalmic Images. Applied Sciences, 10(14), 4788. https://doi.org/10.3390/app10144788





