Next Article in Journal
Effect of Daily Intake of a Saffron Infusion on Blood Cholesterol Levels
Next Article in Special Issue
Probabilistic Resilience Analysis of the Icelandic Power System under Extreme Weather
Previous Article in Journal
Effect of the Soft and Hard Interbedded Layers of Bedrock on the Mechanical Characteristics of Stabilizing Piles
Previous Article in Special Issue
Evidence-Based Analysis of Cyber Attacks to Security Monitored Distributed Energy Resources
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 10
Issue 14
10.3390/app10144761
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A Risk-Based Approach to Assess the Operational Resilience of Transmission Grids

by
Milorad Papic
1,
Svetlana Ekisheva
2 and
Eduardo Cotilla-Sanchez
3,*
1
Independent Consultant, Boise, ID 83702, USA
2
North American Electric Reliability Corporation, Atlanta, GA 30326, USA
3
School of Electrical Engineering & Computer Science, Oregon State University, Corvallis, OR 97331, USA
*
Author to whom correspondence should be addressed.
Appl. Sci. 2020, 10(14), 4761; https://doi.org/10.3390/app10144761
Submission received: 1 June 2020 / Revised: 19 June 2020 / Accepted: 7 July 2020 / Published: 10 July 2020
(This article belongs to the Special Issue Probabilistic Methods for Power System Resilience Assessment)
Browse Figures
Versions Notes

Abstract

:
Modern risk analysis studies of the power system increasingly rely on big datasets, either synthesized, simulated, or real utility data. Particularly in the transmission system, outage events have a strong influence on the reliability, resilience, and security of the overall energy delivery infrastructure. In this paper we analyze historical outage data for transmission system components and discuss the implications of nearby overlapping outages with respect to resilience of the power system. We carry out a risk-based assessment using North American Electric Reliability Corporation (NERC) Transmission Availability Data System (TADS) for the North American bulk power system (BPS). We found that the quantification of nearby unscheduled outage clusters would improve the response times for operators to readjust the system and provide better resilience still under the standard definition of N-1 security. Finally, we propose future steps to investigate the relationship between clusters of outages and their electrical proximity, in order to improve operator actions in the operation horizon.

1. Introduction

Maintaining an adequate level of reliability and resilience in the planning and operation of the power grid is a challenging problem that operating entities face today due to frequent extreme events (e.g., failure of multiple physical components, natural disasters, cyber-attacks) and the increasing complexity of energy system infrastructure. Major catastrophic events, often called high-impact and low-probability (HILP) events, led to a large number of cascading events and blackouts. The major catastrophic events, in most cases, result in interruptions to customers and inconvenience to residents in affected areas due to loss of not just electricity, but also water, and communication. Therefore, power system resilience today is receiving more attention by regulators and the utility industry as a key factor of the defense against HILP events that have significant economical and societal impact. The reliability and resilience are two critical factors of electric grids, as highlighted by some relevant publications and policy guidelines [1,2,3,4,5,6,7]. Grid reliability as a fundamental objective of electric utilities covers two distinct attributes: adequacy and security, which are usually studied under HILP events. North American Electric Reliability Corporation (NERC) standards require entities to perform planning studies for their systems under extreme contingencies but extreme disaster events are not considered [8]. On the other hand, grid resilience studies are dealing primarily with catastrophic HILP events and are focusing on a diverse range of issues, such as flexibility, hardening, security, and recovery. Standards for resilience studies in planning and operation of power systems have not been developed yet.
According to a new study by scientists at the National Oceanic and Atmospheric Administration (NOAA), in the last decade the number and cost of natural and other types of catastrophic disaster events has risen significantly. The trend of stronger, deadlier, and more frequent natural disasters will continue in the years to come [9]. The events of the last decade have resulted in several large-area power outages, which impacted daily activities of power customers and communities. Examples include Hurricane Ivan in Florida (2004), Hurricane Katrina in Louisiana (2005), Hurricane Irene in Puerto Rico (2011), Fukushima Earthquake in Japan (2011), Superstorm Sandy in New York (2012), the terrorist attack at Metcalf substation in California (2013), the large flooding event in Michigan (2014), the polar vortex event in North America (2014), Typhoon Soudelor in the Philippines (2015), Hurricanes Harvey in Texas and Irma in Florida (2017), Hurricane Michael in Florida (2018), the Mississippi River flooding (2019), and Hurricane Dorian in North Carolina (2019) [9]. These catastrophic events have shown the vulnerability of the electric grid and the lack of adequate methodologies for evaluating resilience under these HILP events. Understanding comprehensive risks associated with extreme events is important because it affects the ability of companies and individuals to plan for resilience such as prevention, adaption, and recovering from these events. Resilience analysis has to consider both the impact and probability of an event.
An effort to develop methodologies and tools to mitigate or minimize the risk from HILP events and to improve electric grid resilience in areas of planning and operation continues but by far does not provide comprehensive solution. Enhancing the resilience of a power system needs to be coordinated for all segments (generation, transmission, distribution, customers), and solutions are required for physical- and cyber-types of extreme contingencies. We review next works on resilience issues in areas of generation, transmission, distribution, and cyber-part of the power system.
Resilience assessment of a generation functional zone of bulk power system (BPS) based on various methods for adequacy calculations is presented in [10,11,12,13,14]. Venu and Verma [10] propose the concept of adequacy resilience which is an indicator of adaptability of power system to ensure the required reliability level. Ly et al. [11] examine the extent of resource adequacy and the North American power system’s resilience to extreme weather events. Van Harte et al. [12] discuss how the proposed framework with new management structures within Eskom integrate risk management across various functions of a power system (generation, transmission, distribution, customer services, communication, etc.). The authors of [13] propose a security-constrained redispatching approach to predict potential critical scenarios, satisfy additional N-1 security criteria, and increase the system resilience under wet snowstorms. The authors of [14] propose and formulate a resilience-constrained unit commitment model which ensures a resilient supply of loads of the system with microgrid in case of multiple outages.
Resilience assessment and its attributes (prevention, adaptation, and recovery) for a distribution system was a focus of many recent works [15,16,17,18,19,20,21,22,23,24,25,26,27] as they present resilience and risk analysis of distribution systems under extreme weather events. The authors of [18] present an extensive literature review on power system restoration issues. References [19,20,21,22] present the use of microgrids as local resources and blackstart reserves to enhance the power system resilience. Fan et al. [23] present a mixed integer programming approach for optimal power grid intentional islanding. Sun et al. [24] present optimal generator startup strategy for power system restoration. Qiu and Li [25] present an integrated approach for power system restoration planning. Ton and Wang [26] emphasize the need for more research to enhance resilience of distribution systems to climate change and extreme weather. Arab et al. [27] present a proactive approach to cope with emergencies caused by extreme weather events, improve resilience, and minimize the restoration cost of power systems.
In the planning horizon, various models to improve power system resilience are proposed in [28,29,30,31,32,33]. Romero et al. [28,29] propose a two-stage stochastic model to optimize investments that improve the resilience against earthquakes and to make the appropriate resilient decision making. Lagos et al. [30] propose a resilience centered simulation-based approach to identify the network investments that offer the solution for risks caused by natural hazards. A transmission expansion decision approach—based on a multi-level mixed integer programming (MIP)—to make investment decisions against terrorist threats is proposed in [31]. The authors od [32,33] demonstrate that hardening is one of the most effective ways to increase the power system resilience under extreme weather events.
Various methods on resilience assessment of the power system under cyber-attacks are presented in [34,35,36,37,38]. Guo et al. [34] present a reliability assessment of a cyber-physical power system considering cyber-attacks against monitoring functions. Al-Ammar and Fisher [35] perform resilience assessment of the power system to cyber and physical attacks, and they consider the degree of vulnerability to be a measure of the resilience of power system to attacks via cyber means or through physical means. The results of a survey of Information and Communication Technologies (ICT) vulnerabilities of a power system and relevant defense methodologies are presented in [36]. Huang et al. [37] present an integrated resilience response framework that links the situation awareness with resilience enhancement and provides effective and efficient responses in preventive and emergency states. A probabilistic risk-based methodology for security assessment of a power system by taking into account vulnerabilities of ICT systems that involve control and protection is presented in [38].
Different methodologies for assessing power system resilience are presented in [39,40,41,42,43,44,45,46]. Yan et al. [39] analyze the grid resilience to False Data Injection (FDI) attacks with different magnitudes and number of false data inputs. Van Harte et al. [40] propose an approach to prioritize power system resilience capabilities in order to contain the impact and restore the network quickly with a framework for assessing different disaster scenarios. Panteli et al. [41] propose a sequential-simulation based time-series model for evaluating the effect of wind on transmission lines and entire power infrastructure. Zhang et al. [42] propose a toughness approach to quantify the robustness of a power system against potential disasters. Ciapesoni at al. [43,44] present a risk-based resilience assessment methodology in operation-planning mode to predict the riskiest contingencies including threat intensity and component vulnerability that will affect the power system resilience. Chi et al. [45] present a literature survey on power distribution system resilience assessment.
A variety of studies have addressed the resilience solutions based on recovery and restoration to minimize the impact of extreme and catastrophic events [46,47,48,49,50]. Wang et al. [46] present and review the research towards methods and tools of forecasting natural disaster related power system disturbances, hardening and pre-storm operations, and restoration models. Arab et al. [47] present a significant change in power grid response and recovery schemes by developing a framework for proactive recovery of power assets to enhance the resilience. Van Harte et al. [48] present the different blackout recovery mechanisms available to the System Operator to respond to and recover from such an extreme event. Perrings et al. [49] propose the use of price functions to estimate people’s willingness to pay for more resilience in the power supply. Ju et al. [50] present a reconfiguration model for load restoration in radial distributed systems that includes multiple energy services, including local combined heat and power (CHP) plants, to meet the demand of critical loads during post-disaster horizons.
Outage data obtained from bulk transmission equipment play an important role in BPS planning, operations, and maintenance practices. Outage data statistics are considered essential when evaluating past, present, and future grid resilience. NERC has been collecting continent-wide transmission outage and inventory data in Transmission Availability Data System (TADS) since 2008 [51,52]. TADS has been used to (a) assess the root cause of outages on major BPS elements; (b) to calculate typical reliability indices; and to (c) identify reliability risks due to independent, common mode, and dependent outages [53,54,55,56,57,58]. The fundamental aspects of common mode and dependent outages in the power systems are presented and reviewed in [59,60,61,62,63]. Another major mechanism of failure in the power grid is a cascading outage. A cascading outage is a defined as a sequence of dependent outages that successively weaken or degrade the power transmission system [64]. The work in [65,66,67,68,69,70,71] shows how to assess cascading via a sequence of dependent outages, how to benchmark the proposed analysis methodologies, and how to evaluate the cascading from historical outage data. The authors of [72,73,74,75,76,77,78,79,80] present a variety of methodologies for assessment of BPS resilience using historical outage data for major BPS components such as lines and transformers. Eskandarpour et al. [72] present a multi-dimensional machine learning model to improve power grid resilience through predictive outage estimation. Kelly-Gorham et al. [73] present an approach to compute overall transmission grid resilience using historical utility outage data. Thomson et al. [74] evaluate transformer historical failure data to assess the facility resilience and reliability. Campbell [75] suggests solutions for reducing impacts from weather-related outages that include improved tree-trimming schedules to keep rights-of-way clear, placing distribution and some transmission lines underground, implementing Smart Grid improvements to enhance power system operations and control, inclusion of more distributed generation, and changing utility maintenance practices and metrics to focus on power system reliability. Eskandarpour and Khodaei [76] present a machine learning based prediction method to determine the potential outage of power grid components in response to hurricanes. Dagle [77] indicates that power system operators now have an unprecedented wealth of data, coming from a variety of sources, such as demand response, synchrophasors, supervisory control and data acquisition (SCADA) systems, which, if managed properly, can provide opportunities for the efficiency, reliability, and resilience of the power system. Duchesne et al. [78] propose an approach combining Monte Carlo simulation, machine learning, and variance reduction techniques in the context of operation planning to assess the expected performance of the system over a certain look-ahead horizon that can guide the operation planner in decision-making.
Quantifying and analyzing the impact of cascading outages is an important part of grid resilience assessment. The NERC State of Reliability (SOR) report [79] reviews past reliability performance of the BPS, examines the state of system design, planning, and operations, and the ongoing efforts by NERC and the industry to continually improve system reliability and resiliency. This independent report is based on an analysis of data and metrics, which enables NERC to examine trends, identify potential risks to reliability, establish priorities, and develop effective mitigation strategies. The state of reliability also provides guidance to industry asset owners and operators in the form of recommendations to enhance the resilience of the BPS.
In this paper, we discuss the power system resilience concept in operation planning by evaluating the historical cluster outages of multiple transmission elements (e.g., lines, transformers) recorded within a 2-min time interval. This type of an outage is a threat to operating a single-contingency reliability criterion to each utility Transmission Operator (TOP). The paper further develops the methodology proposed in [80] that, for the first time, used the TADS data for assessing the resilience of BPS under these nearby overlapping outages. To gain a better understanding of how clusters of nearby outages can impact the system resilience in the future, this study examines both sustained and momentary outages. We perform a comprehensive analysis of the North American combined inventory and cluster outage data for both automatic sustained and momentary outages within a 2-min window. The analysis aims to identify the actionable information from outage data statistics that could be helpful in preventing or mitigating the consequences of newly studied overlapping outage clusters. In addition, this paper presents a methodology to evaluate a likelihood of clusters of different sizes and the overall cluster for a Transmission Owner (TO) based on its transmission inventory.

Operational Grid Resilience: Background and Definitions

The U.S. National Academies define resilience as “the ability to anticipate, prepare for, and adapt to changing conditions and withstand, respond to, and recover rapidly from disruptions” [6]. NERC defines power grid resilience as “the ability to reduce the magnitude and/or duration of disruptive events” [3]. Complementary definitions and power system resiliency metrics are presented in [81,82]: the power system is resilient if it operates reliably over range of operating conditions and has the capability to deliver power and absorb and to adapt to events of low probability and high consequence. The CIGRE C4.47 Power System Resilience Working Group defines power system resilience as the ability to limit the extent, severity, and duration of system degradation following an extreme event [83].
Robust and resilient operation of a power grid requires anticipation of unplanned outages that could lead to cascading and blackouts. Planning and operation standards are designed so the power grid shall always be operated such that instability, uncontrolled separation, cascading, or voltage collapse will not occur because of any single contingency or two sequential N-1 contingencies (N-1, time for readjustment, and another N-1). On the other hand, planning standards cover credible N-2 contingencies, such as double-circuit outages, circuits on common structures, or stuck breaker conditions. The specific NERC reliability standards that relate to the BPS capability to withstand events in anticipation of potential outages, manage the system after an event, and prepare to restore or rebound after an event are TPL-001-4, TOP-002, EOP-004-3, EOP-005-2, EOP-006-2, EOP-011-1, CIP-014-2, PRC-006-3, PRC-016-1, and TPL-007-1 [39]. While these criteria fulfill for example the NERC requirements to meet performance standards and operate securely under the N-1 contingency criterion, this is not a guarantee that the system is immune to multiple N-k outages. Detecting and preventing multiple outages is critical to maintaining power system reliability and resilience. Operation planning engineers, as well as control room operators, face complex situations resulting from these multiple events. When power grids have high volume of renewable energy sources or they are heavily stressed with high power transfers it becomes an increasingly challenging task to make electricity grids most efficient, reliable, and resilient.
A growing body of publications in recent years presents the concept of resilience by assessing the impact and mitigation measures to major disturbances as result of adverse weather, natural disasters, hurricanes, earthquakes, and cyberattacks [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50]. Reference [3] emphasizes, “To increase system resilience requires an understanding of a wide range of preparatory, preventive, and remedial actions, as well as how these impact planning, operation and restoration over the entire life cycle of different kinds of grid failures”.

2. Materials and Methods

2.1. Risk-Based Methodology

A large body of work on power systems follows the classic definition of risk by Lowrance [84] whereby risk is defined as the impact of an event times the probability of occurrence for this event. Similarly, to the data-driven approach in this paper, other works have used large datasets and statistical or probabilistic approaches to the analysis of power system events in terms of quantifying risk [44,84,85,86,87]. With enough data available, one can also use these datasets as a source of features and train modern machine learning approaches to predicting and quantifying risk [78,86]. Machine learning and artificial intelligence approaches also can provide timely recommendations to the operator in charge of remedial actions [76,78]. Common sources of data that recent research increasingly incorporates to risk and reliability studies are those characterizing renewable resources [88,89].
There is not a unique definition for resilience today, but the majority of published definitions focus on the power system ability to anticipate, absorb, and rapidly recover from an external, high-impact, low-probability event. A conceptual framework of power system resilience covers the following steps [46,86]:
  • Step 1: Threat/Event characterization,
  • Step 2: Vulnerability of system’s components,
  • Step 3: System response, and
  • Step 4: System restoration.
The key attributes of a resilient power system are robustness, resistance, resourcefulness, and redundancy. Due to the limitations mentioned above our study does not cover all these attributes and results are primarily related to step 1. To measure for example the robustness of a power system a comprehensive study needs to be performed to establish a threshold value of the consequence beyond which the performance of the system is considered to be unacceptable.
It is important to note the similarities and differences on risk studies versus resilience studies. Reference [90] provides the definition for resilience of an infrastructure as “the ability to anticipate, prepare for, and adapt to changing conditions and withstand, respond to, and recover rapidly from disruption”. It also states that resilience management goes beyond risk management to address the complexities of a power grid and the uncertainty of future treats, as it includes risk analysis as a central component. Risk analysis depends on characterization of the threats, vulnerabilities, and consequences of adverse events to determine the expected loss of critical functionality [90]. Due to the scope of this paper and the datasets we are leveraging, the authors are not applying the traditional risk-based methodology presented in [91] but focusing on the risk factors that come from the outages included in the analysis. Therefore, authors have used the results on cluster statistics to evaluate an aggregated risk at operating entity level that could be helpful to TOs to identify mitigation measures to prevent or minimize the impacts of those outages.
CIGRE WG C4.47 proposed the reliability framework under a broader perspective to cover three components: adequacy, security, and resilience. A system that is resilient is not necessarily reliable. However, a reliable system must be resilient to extreme events, otherwise it would not satisfy the general definition of reliability. This perspective is supported also by FERC—Federal Energy Regulatory Commission—which indicates in [92] that “resilience is a component of reliability in relation to an event”, and by NERC which states in [79] that “a bulk power system that provides an adequate level of reliability is a resilient one”.

2.2. Transmission Availability Data System (TADS)

2.2.1. Overview

NERC has been collecting North American automatic outage data for transmission elements of 200 kilovolts (kV) and above since 1 January 2008. An automatic outage is defined as an outage that results from the automatic operation of a switching device, causing an element to change from an in-service state to a not in-service state. Single-pole tripping followed by successful AC single-pole (phase) reclosing is not an automatic outage [51]. Transmission elements of BPS reportable in TADS are (1) alternating current (AC) circuits (overhead and underground), (2) transformers (no generator step-up units), (3) direct current (DC) circuits (a DC circuit element is a complete line, not just a single pole), and (4) AC/DC back-to-back converters [51]. In 2015, TADS’ reporting changed to align with the implementation of the Federal Energy Regulation Commission (FERC)-approved bulk electric system (BES) definition [87]. Two additional voltage classes were added—namely, less than 100 kV and 100–199 kV. Sustained automatic outages are the only outages collected at voltage classes below 200 kV.

2.2.2. Analysis Dataset and Definitions

For this analysis, TADS automatic (momentary and sustained) outages of TADS elements of 200 kV and above for years 2013–2019 were grouped by Transmission Owner (TO). These outages were sorted in chronological order, then examined to select groups of outages inside a TO with starting times of two consecutive outages separated by at most 2 min. This process resulted in 4246 groups that contained 10,501 outages (or 32.6% of all TADS automatic outages over the 7 years). Next, these groups were examined to detect outages that do not overlap in time with at least one other outage in the group. (Overlapping outages are defined here as outages that overlap in time, for any period of time. Namely, if two outages start at the same time, they overlap; if one of the outages starts earlier, the second outage should start before the first one ends for them to overlap.) These outages were removed from the study, and groups were redefined to contain only outages that overlap with one or more outages in the group. The resulted sets of outages are called clusters. Namely, a cluster is a set of automatic outages of transmission elements in the same company that satisfies the following conditions: (a) when sorted by their start time, a difference between start time of any two consecutive outages does not exceed 2 min; (b) each outage in a cluster overlaps in time with at least one other outage in a cluster. Condition (b) implies that outages in each cluster are “continuous,” i.e., at any moment from the earliest start of all outages in the cluster to the latest end of all outages at least one outage continues. The size of a cluster is defined as the number of outages it contains. For any cluster of size 2 and greater, the operator has at least one N-2 contingency, but depending on the cluster size may have multiple N-2, N-3, N-4… contingencies.
The final data set processed for this study consists of 2918 clusters comprised of 6942 automatic outages (or 21.6% of all 32,198 automatic outages of TADS elements 200 kV and above from 2013 to 2019). Table 1 illustrates a breakdown of the outages in clusters by transmission element type and by voltage class as reported in TADS. For transformers, the voltage class is the high-side voltage. Voltages are operating voltages.

3. Results

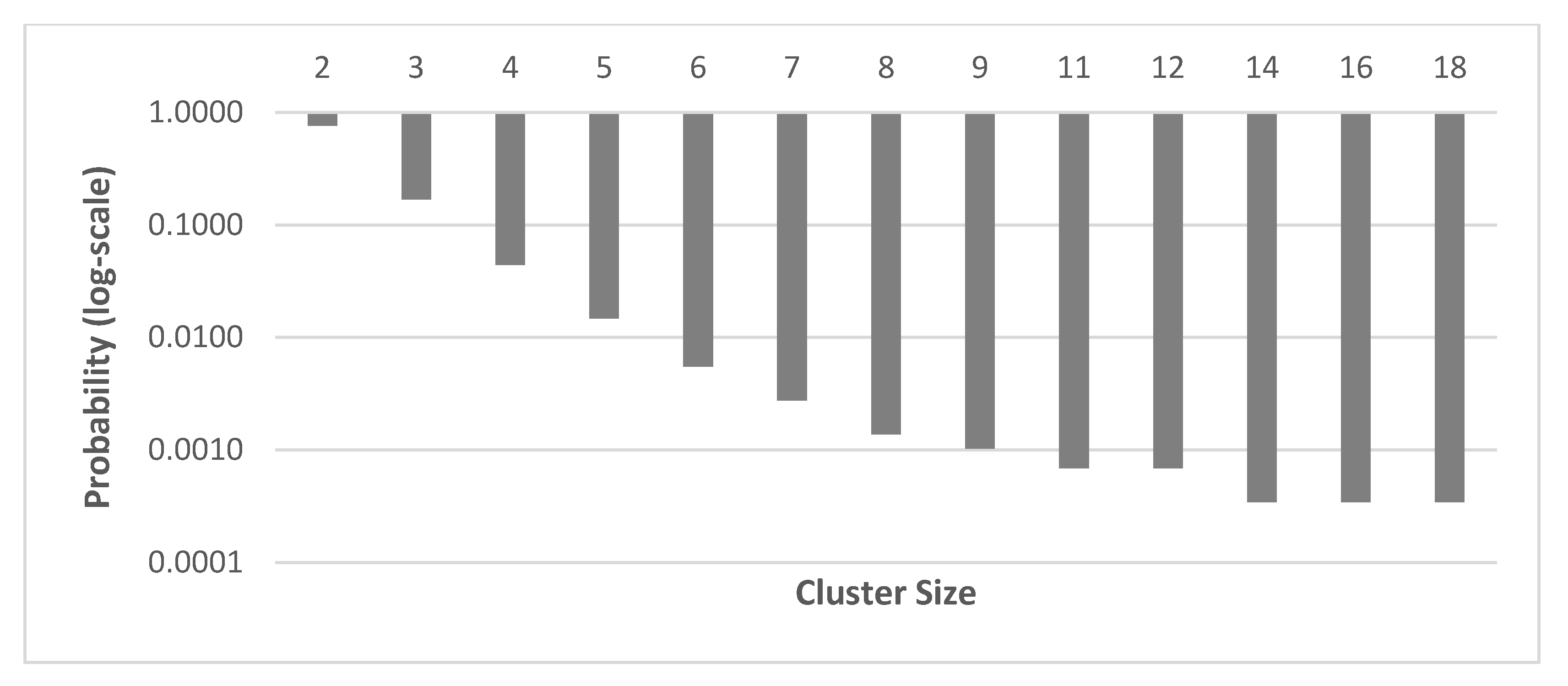
3.1. Analysis of Clusters

3.1.1. Clusters by Year and Size Distribution

The outages listed in Table 1 are grouped together into clusters as summarized in Table 2. The inclusion of automatic outages for all TADS elements allows the capture of more nearby overlapping outages and a better evaluation of their risks to dynamic stability and resilience of the transmission system. As mentioned in Section 2.2.2, the clusters contain 21.6% of all automatic outages, indicating how common this type of outage and their clusters are for the North American BPS.
Table 2 indicates that with an exception of the year 2014, the number of clusters in North America stayed consistent during the study period. In 2014 the number was significantly lower, and the largest cluster contained only seven outages. Overall, most clusters (76%) consist of two outages, with several outliers (clusters with sizes between 11 and 18). The average size of a cluster equals 2.4 outages. An empirical distribution of the cluster size is illustrated in Figure 1.

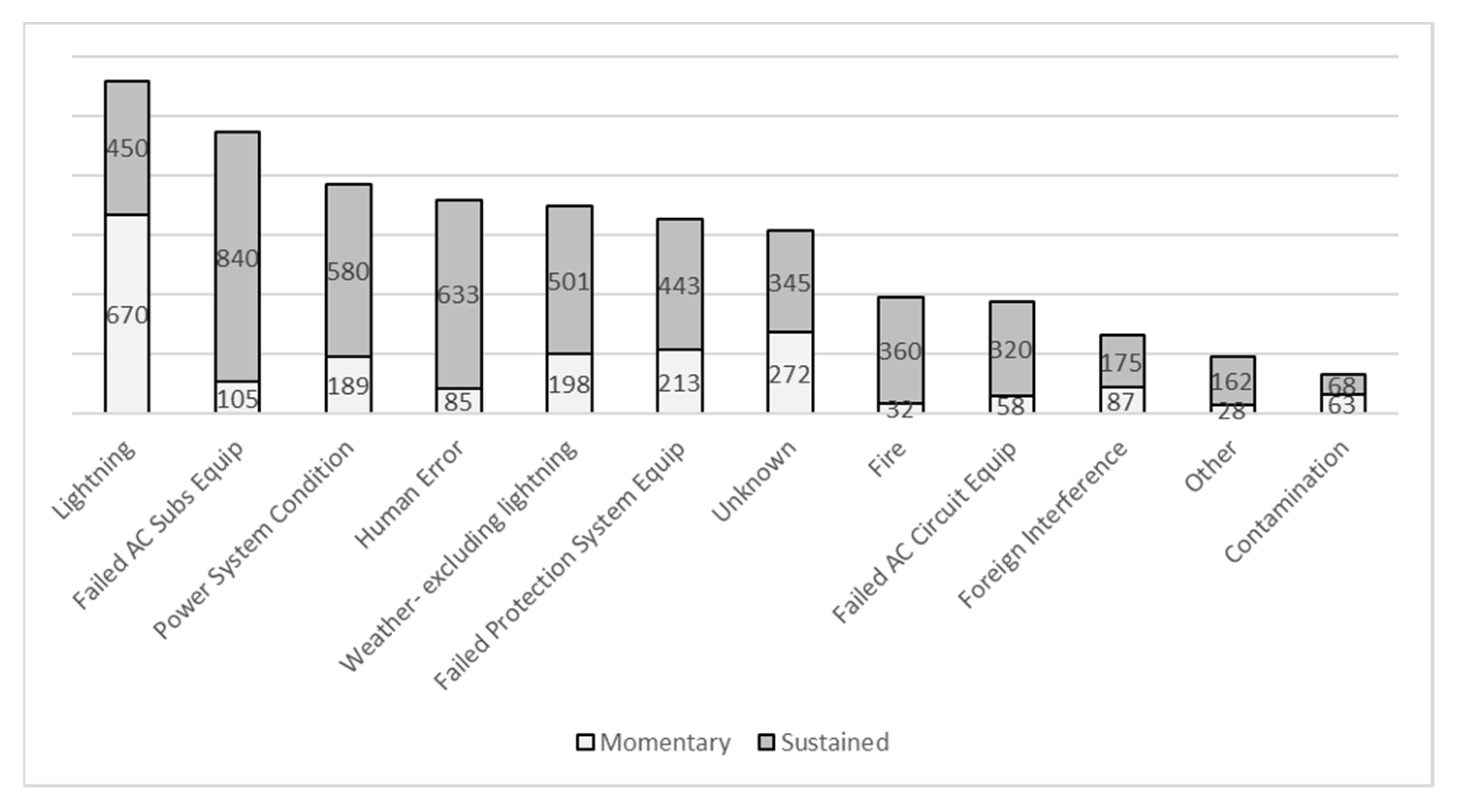
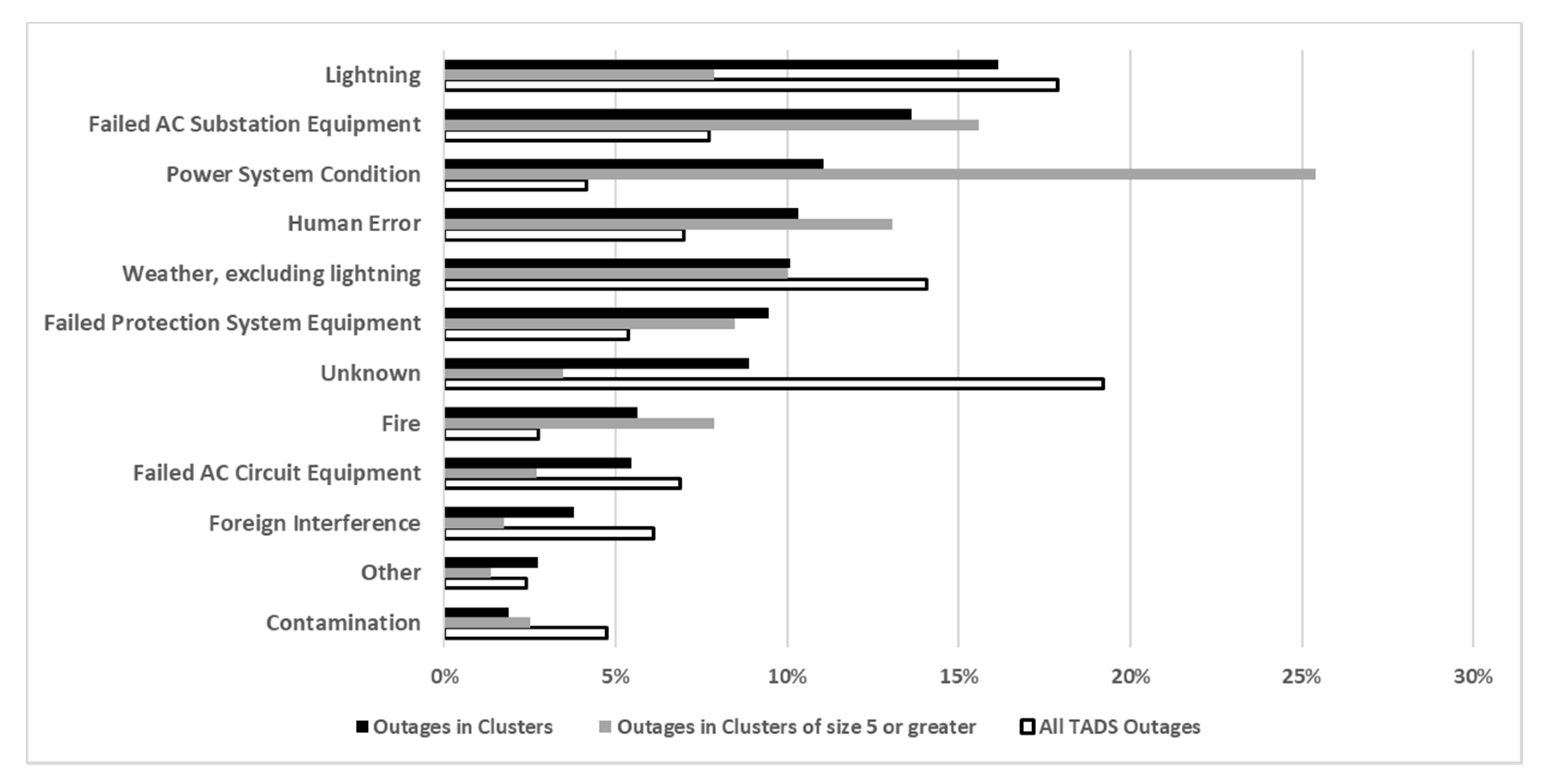
3.1.2. Initiating Causes of Outages

The 6942 outages in clusters are divided into 2007 momentary outages and 4945 sustained outages (i.e., outages lasting at least 1 min). The percentage of sustained outages in clusters is significantly higher than in the total population of automatic outages for years 2013–2019 (71% versus 58%). Figure 2 lists the outages by TADS initiating cause. Several of the smallest groups are not shown (together they contain less than 1% of outages in clusters).
Lightning initiates the largest number of outages in clusters, but the majority of them are momentary. In contrast, Failed AC substation equipment is the leading cause of sustained outages in clusters, but it initiates a relatively small number of momentary outages. Power system condition is the third largest group. Next, we compare rankings of causes for outages in all clusters, in the largest clusters (size five and above), and for all TADS outages for the 7 years (Figure 3).
Lightning, the top cause of outages in clusters, is the second leading cause of all automatic outages in TADS, but it initiates only 8% of outages in large clusters. Unknown, the leading cause of TADS outages, ranks relatively low for clusters: it initiates 9% of outages in clusters and only 3% of outages in large clusters, because causes of larger transmission events tend to be better investigated and reported.
Prominently, Power system condition causes 25% of outages in large clusters while in TADS it ranks low (4% of TADS outages). This cause is reported for automatic outages caused by power system conditions such as instability, overload trip, out-of-step, abnormal voltage, abnormal frequency, or unique system configurations (e.g., an abnormal terminal configuration due to existing condition with one breaker already out of service) [9].
A variety of malicious attacks included Vandalism, Terrorism, or Malicious Acts, which caused only five outages in the clusters for the 7 years and no outages within large clusters—that being the reason why this cause is not shown in Figure 3.

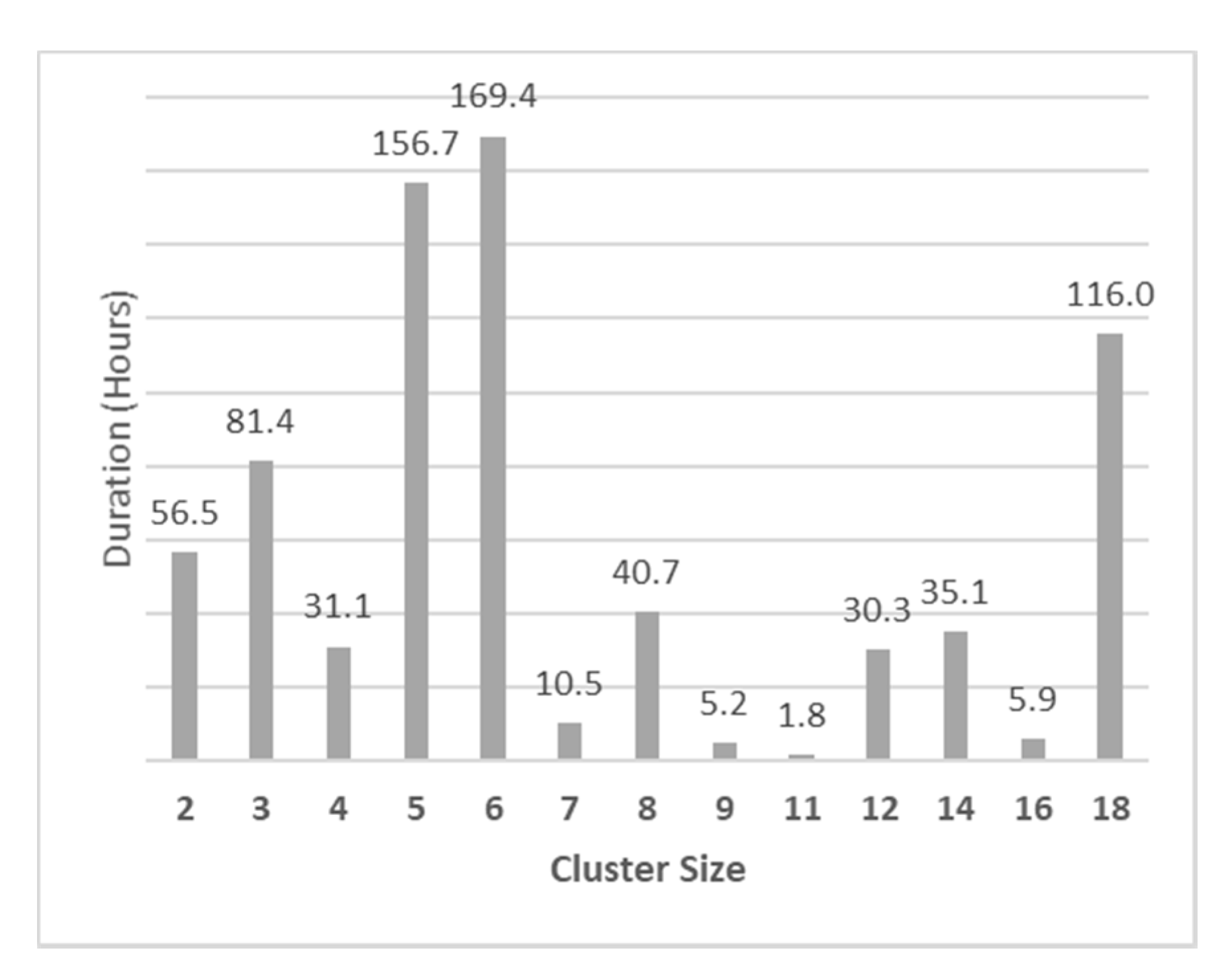
3.1.3. Cluster Duration

Next, we define a cluster duration as the time elapsed between the earliest start time and the latest end time of all outages in the cluster and find that the average cluster duration is 61.4 h. The average cluster duration by cluster size is shown in Figure 4.
Figure 4 confirms that there is no observable correlation between cluster size and duration (note that there are few data points for clusters of largest sizes). Further analysis reveals that sustained outages in clusters tend to be longer than the overall sustained outages (the average outage duration is 51 h versus 40 h). The longest outages in clusters are initiated by Environmental, Failed AC/DC Terminal Equipment, and Failed AC circuit equipment (the average durations are 435, 169, and 153 h, respectively). Overall, a cluster duration depends more on causes of the outages rather than on the cluster size.

3.1.4. Analysis of Largest Clusters

Next, we investigate in more detail the largest clusters from 2013 to 2019. Table 3 provides a summary of the 10 largest clusters, their sizes are nine and greater.
Table 3 informs that majority of outages in largest clusters are outages of ac circuits with two exceptions: both clusters of size 11 had seven transformers and four ac circuit outages each. One of these clusters (2017) was initiated by human error and the second one (2018) by lightning, but all remaining outages in these clusters were caused by power system conditions. These findings confirm the expectation that reported violations such as overloads and voltage problems usually trigger the operation of protection systems that trip out additional system elements such as lines, transformers, generators, load, etc.
Overall, Power system condition appears as an initiating cause in the six largest clusters out of 10. Additionally, six clusters contain weather-related outages (Weather, Lightning, Fire).
Another interesting observation is that all outages in each cluster with size 9–12 started simultaneously, and 11 outages in a cluster of size 14 started simultaneously and 1 min after the first three outages. This observation helps explain an absence of correlation between cluster size and cluster duration. All clusters of size 9–16 are shorter than the average cluster duration of 61 h, and some of them are very short.

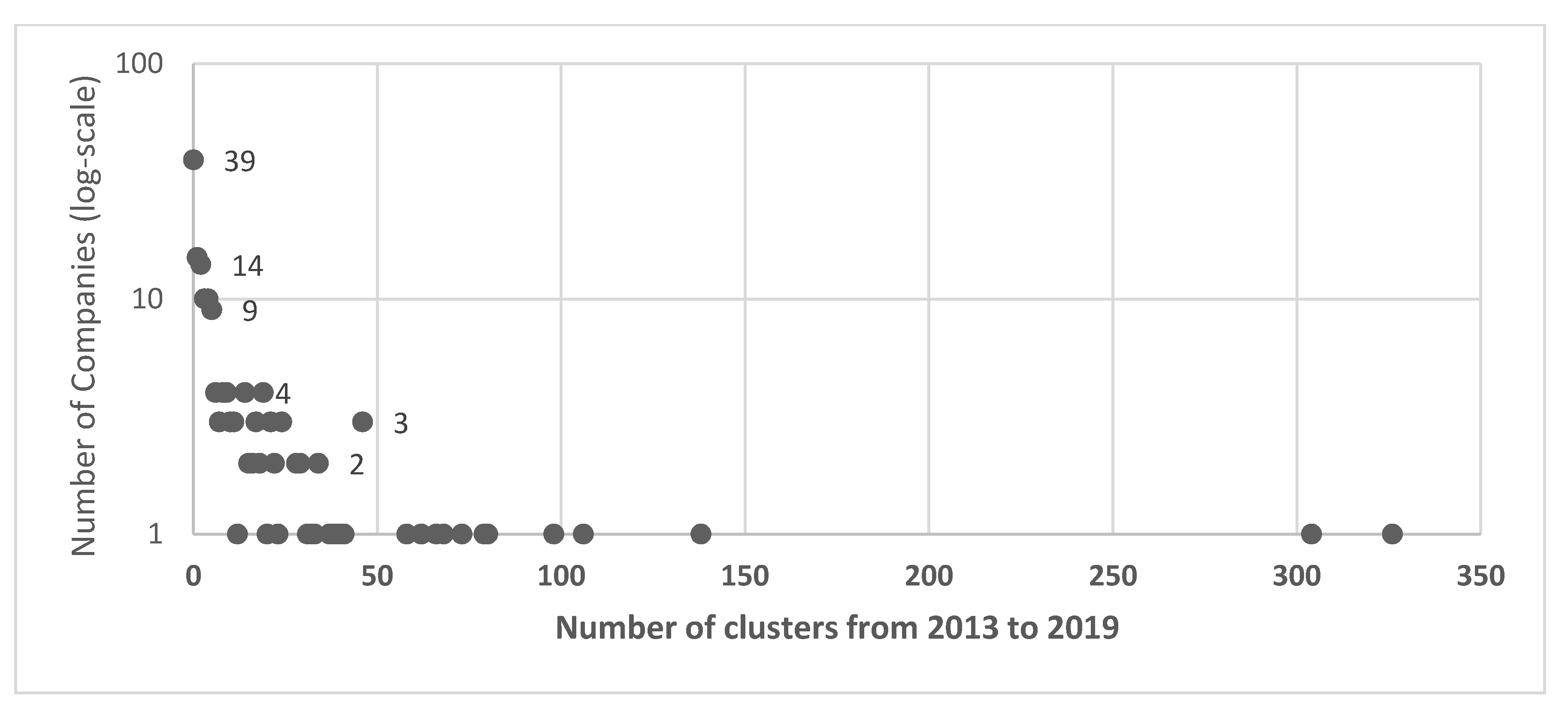
3.2. Cluster Risk to Transmission Owner (TO)

3.2.1. Distribution of Clusters by TO

The average annual number of clusters per company (TO) with TADS inventory above 200 kV was 2.4 from 2013 to 2019. It did not change significantly from year to year—similarly to the number of clusters. However, there is a large variability in the number of clusters by TO; this variability primarily reflects a company size. Figure 5 illustrates the distribution of number of clusters per TO for 7 years.
The 39 entities (about 22% of companies with TADS elements of 200 kV and above) have not experienced a cluster from 2013–2019. The 39 TOs had at least 20 clusters each. Out of these, four companies have more than 100 clusters each (with two more than 300 clusters each) over the 7 years. These outliers are the TOs with large inventory of TADS elements above 200 kV.

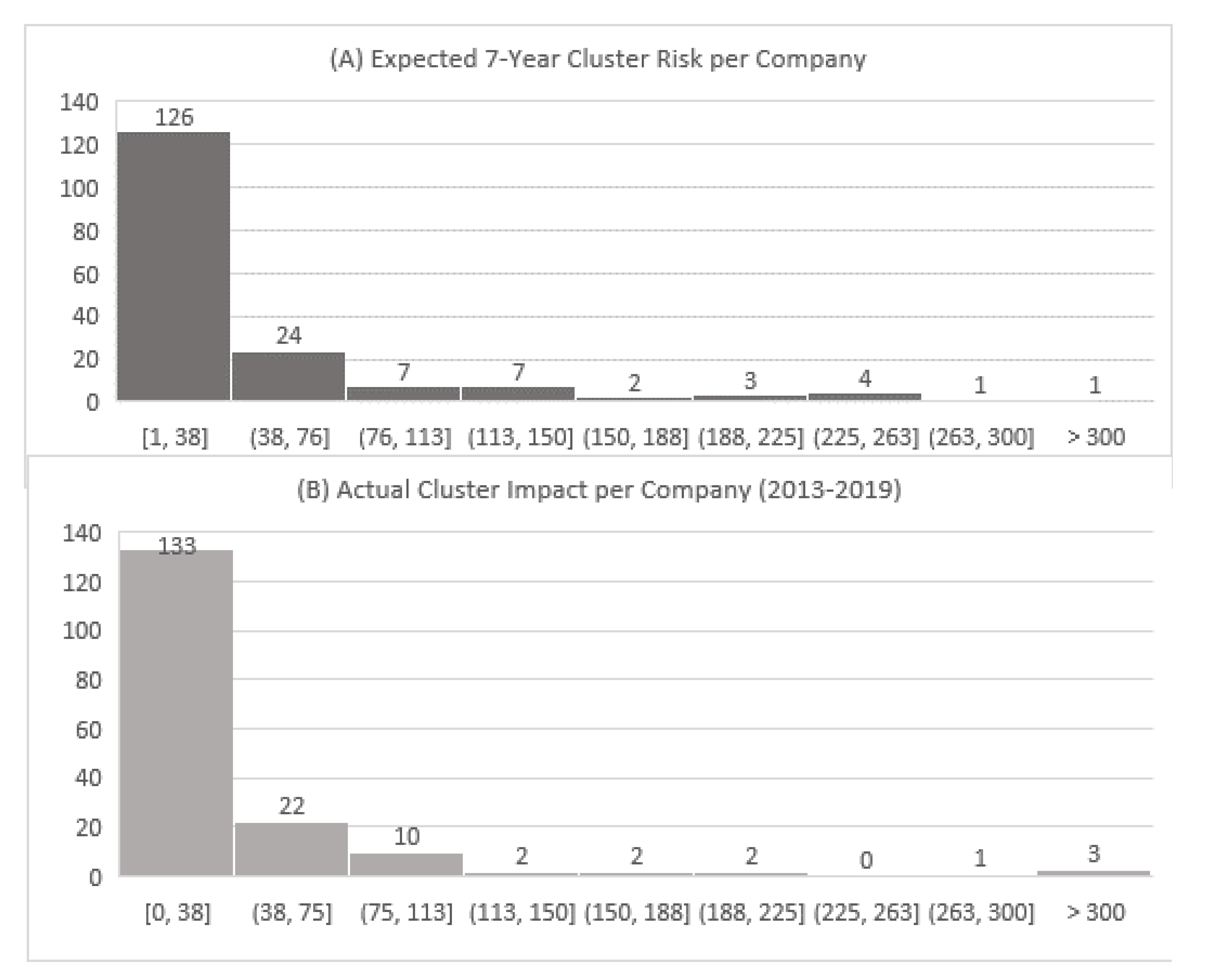
3.2.2. Company Risk Assessment

The cluster statistics presented in the previous sections can be used to evaluate a company risk caused by clusters of overlapping outages. The impact I of a cluster can be defined, for example, as its size or, in more sophisticated way, as the sum of equivalent MVA values of transmission elements involved in this cluster. The likelihood of a cluster can be estimated as follows. The expected number nk(7) of clusters of size k over 7 years for a company A is estimated by:
nk(7) = Nk(7)*Inv(A)/Inv(TADS)
where Nk(7) is the number of clusters of size k in the TADS data from 2013 to 2019, listed in the last column of Table 2, Inv(A) is the company A inventory of transmission elements of the 200 kV and above reportable in TADS, and Inv(TADS) = 8910 is the average annual TADS inventory of the 200 kV+ from 2013 to 2019 (for k ≤ Inv(A)). Finally, the number nk(1) of clusters of size k for a given year can be estimated by nk(7)/7 (again under the assumption of stationarity of the number of clusters). Finally, the estimates nk(1) are plugged into formula (2) for the company cluster risk R(1 year):
R(1 year) = Σk Ik * nk(1),
where k is the size of a cluster and Ik is the impact of a cluster of size k. Estimates nk(1) can be further used to calculate likelihood of a cluster of a given size for an hour, a day etc. The company risk, as defined by (2), is proportional to a company inventory and the time period for which the risk is estimated.
For example, assuming that a cluster impact is defined as the cluster size (Ik = k), for a company X with the transmission inventory of 62 elements with voltages above 200 kV, the 1-year cluster risk R(1 year) = 6.9 is calculated from 1-year estimates of number of clusters listed in Table 4.
For two actual TOs that report to TADS, anonymized companies A and B with similar inventory of about 62 elements a year, the numbers of observed clusters from 2013 to 2019 were as follows: company A experienced three clusters of size 2; company B had 13 clusters of size 2, six clusters of size 3, and two clusters of size 4 (the total of 20 clusters).
These empirical data show that for company B the suggested methodology provides good estimates of the number of clusters based on the combined inventory alone; however, it is not the case for company A. More general evaluation of the cluster risk estimates is illustrated in Figure 6. Figure 6A shows a histogram of the expected 7-year cluster risk for all TOs that reported in TADS from 2013–2019 and had at least one transmission element above 200 kV, with the cluster risk for each company calculated by formula (2) adjusted for 7 years. Figure 6B shows a histogram of actual cluster impact for the same set of TOs; for these calculations a likelihood of a cluster of a given size is replaced with the number of the clusters the TO had in 2013–2019. The histograms (A) and (B) are reasonably close in the middle parts of the corresponding distributions. The predictable differences between them are as follows. The distribution (A) starts with a small positive value, as even a TO with one reportable element has a positive expected cluster risk defined by formula (2), while the distribution (B) starts with value 0 since some TOs with few elements had no clusters over the years 2013–2019. A more prominent difference between (A) and (B) is observable in their right-hand tails. Distribution (B) has as outliers the companies that experienced multiple and/or large clusters caused, for example, by wildfires and hurricanes during the years 2013–2019 while distribution (A) of the expected cluster risk by definition consists of the sample mean values for the companies of the same size and outliers tend to be “absorbed”. If a time frame of the analysis increases, the histograms (A) and (B) are expected to become closer and closer.
Another way to get more precise cluster risk estimates is to use the detailed analysis by element type, which would require a derivation of count tables similar to Table 2 for all possible combinations of elements in a cluster of a given size. For example, for cluster of size 2, there would be six possible combinations (ac circuit, ac circuit), (ac circuit, dc circuit), (ac circuit, ac/dc back-to-back converter), etc. Moreover, if the equivalent MVA is chosen as a cluster impact I, further breakdown of element types by voltage classes should be done. This analysis is beyond the scope of this paper.
It is important to remember that due to a filtering procedure applied to the complete set of the 2013–2019 TADS automatic outages as a first step of data processing (described in Section 2.2.2), many overlapping outages are eliminated from the study (longer outages with starting times separated by greater than 2 min). Therefore, the presented statistics on clusters are intended to provide a lower estimate of the frequency of such transmission events on the system and inside a TO.

4. Discussion

In addition to time clustered outages, future work is needed to identify which of the time clustered outages are also electrically close to each other. For example, a good step in this direction is to examine each outage within the time cluster using existing Generation Shift Distribution Factor technology (Gen DFAX). TADS data identify each line by a unique line name identifier, including each terminal’s from and to substation name identifier. Such TADS information could be defined and improved to map to existing monitored transformers/line to each Gen DFAX table row.
TADS substation identifiers could also be mapped to generation shift columns in the Gen DFAX table. The Gen DFAX table columns would need to include every 230 kV and above bus within each TO boundary. Otherwise, some transformer/line buses in TADS could be missing in the Gen DFAX table. An analysis of such distribution factors could be used to identify which of the time clustered outages are electrically close.
Overlapping electrically close forced outages are much more likely to challenge grid resiliency. Overlapping unplanned N-2 (or N-3, etc.) outages that are electrically close outages are more likely to challenge the response time of TOP or generation operators to readjust the system prior to the final N-1 event in the cluster.

5. Conclusions

The study reported in this paper provides insights on the quantification of power system resilience using historical outage data in TADS. We also discussed multiple challenges to grid resilience under overlapping nearby outages. The assessment of nearby outages in the operation horizon of the BPS goes beyond standard requirements. The comprehensive historical data analysis of cluster outages provides an operating entity with a quantitative method to identify the outages with the highest risks. The knowledge gained from this study shall help companies to understand potential risks and to identify mitigation measures to prevent or minimize the impacts of those outages. The approach presented here can be helpful to the industry in the process of monitoring risks to such time clustered outages.
In addition to the TADS data analysis in this paper, other NERC required event reports that analyze multiple outages should be cross referenced to TADS reported outages and noted in TADS. Based on these more in-depth after the fact event reports, the associated TADS data should be updated as needed. Similarly, further analysis could include non-automatic outages at lower voltages—including manual switching errors—to quantify their contribution to overall risk.
Future research to identify better alternative methods, beyond the discussed above Gen DFAX method, is needed to identify electrically close outages. In addition, future research around outage prediction based on machine learning algorithms is needed to proactively cope with overlapping electrically close outages and to improve grid resilience.

Author Contributions

Conceptualization, M.P. and S.E.; methodology, S.E.; software, S.E.; validation, M.P., S.E., and E.C.-S.; formal analysis, S.E.; writing—original draft preparation, M.P., S.E., and E.C.-S.; writing—review and editing, M.P., S.E., and E.C.-S. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Acknowledgments

The authors are grateful to NERC’s TADS Working Group and NERC staff for their support and materials. The definition of clusters in this paper was suggested by Jim Robinson.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. National Infrastructure Advisory Council. A Framework for Establishing Critical Infrastructure Resilience Goals; National Infrastructure Advisory Council: Washington D.C., USA, 2010.
  2. North American Electric Reliability Corporation. Severe Impact Resilience: Considerations and Recommendations; North American Electric Reliability Corporation: Atlanta, GA, USA, 2012. [Google Scholar]
  3. National Academy of Sciences. Terrorism and the Electric Power Delivery System. 2012. Available online: https://www.nap.edu/login.php?record_id=12050&page=https%3A%2F%2Fwww.nap.edu%2Fdownload%2F12050 (accessed on 2 May 2020).
  4. Executive Office of the President of the United States. Economic Benefits of Increasing Electric Grid Resilience to Weather Outages. 2013. Available online: http://energy.gov/sites/prod/files/2013/08/f2/Grid%20Resiliency%20Report_FINAL.pdf (accessed on 2 May 2020).
  5. National Research Council. The Resilience of the Electric Power Delivery System in Response to Terrorism and Natural Disasters: Summary of a Workshop; The National Academies Press: Washington, DC, USA, 2013.
  6. National Academies of Sciences. Engineering, and Medicine. Enhancing the Resilience of the Nation’s Electricity System; The National Academies Press: Washington, DC, USA, 2017. [Google Scholar] [CrossRef]
  7. Resilient Electricity Networks for Great Britain, (RESNET). Available online: https://www.tyndall.ac.uk/projects/resnet-resilient-electricity-networks-great-britain (accessed on 2 May 2020).
  8. North American Electric Reliability Corporation. Reliability Standards for the Bulk Electric Systems of North America. 2020. Available online: https://www.nerc.com/pa/Stand/Pages/AllReliabilityStandards.aspx (accessed on 2 May 2020).
  9. National Oceanic and Atmospheric Administration. National Centers for Environmental Information. U.S. Billion-Dollar Weather and Climate Disasters: Overview. 2019. Available online: https://www.ncdc.noaa.gov/billions/ (accessed on 2 May 2020).
  10. Venu, V.V.; Verma, A.K. A Novel Adequacy Resiliency Paradigm for Power System Reliability Measures. In Proceedings of the IEEE Power and Energy Society General Meeting, Minneapolis, MN, USA, 25–29 July 2010. [Google Scholar]
  11. Ly, T.C.; Moura, J.N.; Velummylum, G. Assessing the Bulk System’s Resource Resilience to Future Extreme Winter Weather Events. In Proceedings of the IEEE PES General Meeting, Denver, CO, USA, 26–30 July 2015. [Google Scholar]
  12. Van Harte, M.; Koch, R.; Mike, N.; Havford, G.; Bala, M. Integrated risk management and system adequacy assessment: Implementation of the ISO 31000:2009 standard. In Proceedings of the South African power system CIGRE Conference, Recife, Brazil, 3–6 April 2011. [Google Scholar]
  13. Ciapesoni, E.; Cirio, D.; Pitto, A.; Masucco, S.; Sforna, M.P. Security-Constrained Redispatching to enhance power system resilience in case of wet snow events. In Proceedings of the Power System Computation Conference (PSCC), Genoa, Italy, 11–15 June 2018. [Google Scholar]
  14. Eskandarpour, R.; Edwards, G.; Khodaei, A. Resilience-Constrained Unit Commitment Considering the Impact of Microgrid. In Proceedings of the North American Power Symposium, Denver, CO, USA, 18–20 September 2016. [Google Scholar]
  15. Li, G.; Zhang, P.; Luh, P.B.; Li, W.; Bie, Z.; Serna, C.; Zhao, Z. Risk Analysis for Distribution Systems in the Northeast U.S. Under Wind Storms. IEEE Trans. Power Syst. 2013, 29, 889–898. [Google Scholar] [CrossRef]
  16. Yuan, W.; Wang, J.; Qiu, F.; Chen, C.; Kang, C.; Zeng, B. Robust optimization-based resilient distribution network planning against natural disasters. IEEE Trans. Smart Grid 2016, 7, 2817–2826. [Google Scholar] [CrossRef]
  17. Chen, C.; Wang, J.; Ton, D. Modernizing Distribution System Restoration to Achieve Grid Resiliency Against Extreme Weather Events: An Integrated Solution. Proc. IEEE 2017, 105, 1267–1288. [Google Scholar] [CrossRef]
  18. Liu, Y.; Fan, R.; Terzija, V. Power system restoration: A literature review from 2006 to 2016. J. Mod. Power Syst. Clean Energy 2016, 4, 332–341. [Google Scholar] [CrossRef] [Green Version]
  19. Hongda, R.; Schulz, N. A Clustering-based Microgrid Planning for Resilient Restoration in Power Distribution System. IEEE T & D. 2020. Available online: https://www.ieeet-d.org/IEEE20/Public/SessionDetails.aspx?FromPage=Sessions.aspx&SessionID=1191&SessionDateID=17 (accessed on 10 July 2020).
  20. Li, Z.; Shahidehpour, M.; Aminifar, F.; AlAbdulwahab, A.; Al-Turki, Y. Networked Microgrids for Enhancing the Power System Resilience. Proc. IEEE 2017, 105, 1289–1310. [Google Scholar] [CrossRef]
  21. Lassetter, C.; Cotilla-Sanchez, E.; Kim, J. A Learning Scheme for Microgrid Reconnection. IEEE Trans. Power Syst. 2018, 33, 691–700. [Google Scholar] [CrossRef]
  22. Schneider, K.P.; Tuffner, F.K.; Elizondo, M.A.; Liu, C.C.; Xu, Y.; Ton, D. Evaluating the feasibility to use microgrids as a resiliency resource. IEEE Trans. Smart Grid 2017, 8, 687–696. [Google Scholar]
  23. Fan, N.; Izraelevitz, D.; Pan, F.; Pardalos, P.M.; Wang, J. A mixed integer programming approach for optimal power grid intentional islanding. Energy Syst. 2012, 3, 77–93. [Google Scholar] [CrossRef]
  24. Sun, W.; Liu, C.-C.; Zhang, L. Optimal generator start-up strategy for bulk power system restoration. IEEE Trans. Power Syst. 2011, 26, 1357–1366. [Google Scholar] [CrossRef]
  25. Qiu, F.; Li, P. An integrated approach for power system restoration planning. Proc. IEEE 2017, 105, 1234–1252. [Google Scholar] [CrossRef]
  26. Ton, D.T.; Wang, P.W.-T. A more Resilient Grid. IEEE Power Energy Mag. 2015, 13, 26–34. [Google Scholar] [CrossRef]
  27. Arab, A.; Khodaei, A.; Khator, S.K.; Ding, K.; Emesih, V.A.; Han, Z. Stochastic Pre-Hurricane Restoration Planning for Electric Power Systems Infrastructure. IEEE Trans. Smart Grid 2015, 6, 1046–1054. [Google Scholar] [CrossRef]
  28. Romero, N.R.; Nozick, L.K.; Dobson, I.D.; Xu, N.; Jones, D. Transmission and Generation Expansion to Mitigate Seismic Risk. IEEE Trans. Power Syst. 2013, 28, 3692–3701. [Google Scholar] [CrossRef]
  29. Romero, N.; Xu, N.; Nozick, L.K.; Dobson, I.; Jones, D. Investment Planning for Electric Power Systems Under Terrorist Threat. IEEE Trans. Power Syst. 2011, 27, 108–116. [Google Scholar] [CrossRef]
  30. Lagos, T.; Moreno, R.; Espinosa, A.N.; Panteli, M.; Sacaan, R.; Ordonez, F.; Rudnick, H.; Mancarella, P.; Navarro, A. Identifying Optimal Portfolios of Resilient Network Investments Against Natural Hazards, With Applications to Earthquakes. IEEE Trans. Power Syst. 2020, 35, 1411–1421. [Google Scholar] [CrossRef] [Green Version]
  31. Nagarajan, H.; Yamangil, E.; Bent, R.; Van Hententyck, P.; Backhaus, S. Optimal resilient transmission grid design. In Proceedings of the Power System Computation Conference (PSCC), Genoa, Italy, 1–8 June 2016. [Google Scholar]
  32. U.S. Department of Energy. Hardening and Resiliency: U.S. Energy Industry Response to Recent Hurricane Seasons. 2010. Available online: http://www.oe.netl.doe.gov/docs/HR-Re-port-final-081710.pdf (accessed on 2 May 2020).
  33. Panteli, M.; Trakas, D.N.; Mancarella, P.; Hatziargyriou, N.D. Boosting the Power Grid Resilience to Extreme Weather Events Using Defensive Islanding. IEEE Trans. Smart Grid 2016, 7, 2913–2922. [Google Scholar] [CrossRef]
  34. Guo, J.; Wang, Y.; Guo, C.; Dong, S.; Wen, B. Cyber-Physical Power System (CPPS) Reliability Assessment Considering Cyber Attacks against Monitoring Functions. In Proceedings of the IEEE Power and Energy Society General Meeting, Boston, MA, USA, 17–21 July 2016. [Google Scholar]
  35. Al-Ammar, E.; Fisher, J. Resiliency Assessment of the Power System Network to Cyber and Physical Attacks. In Proceedings of the IEEE Power and Energy Society General Meeting, Montreal, QC, Canada, 18–22 June 2006. [Google Scholar]
  36. Gardner, R.M.; Grid Consortium. A Survey of ICT Vulnerabilities of Power Systems and Relevant Defense Methodologies. In Proceedings of the IEEE PES General Meeting, Tampa, FL, USA, 24–28 June 2007. [Google Scholar]
  37. Huang, G.; Wang, J.; Chen, C.; Qi, J.; Guo, C. Integration of Preventive and Emergency Responses for Power Grid Resilience Enhancement. IEEE Trans. Power Syst. 2017, 32, 1. [Google Scholar] [CrossRef]
  38. Ciapesoni, E.; Cirio, D.; Pitto, A.; Sforma, M. An Integrated Framework for Power and ICT System Risk-Based Security Assessment. Int. J. Eng. Res. Appl. 2014, 4, 42–51. [Google Scholar]
  39. Yan, J.; Tang, Y.; Tang, B.; He, H.; Sun, Y. Power Grid Resilience Against False ta Injection Attacks. In Proceedings of the IEEE Power and Energy Society General Meeting, Boston, MA, USA, 17–21 July 2016. [Google Scholar]
  40. Van Harte, M.; Panteli, M.; Koch, R.; Mahomed, S.; Jordaan, A. Resiliency of critical infrastructure: Power system resilience capabilities and assessment framework. In Proceedings of the DMISA Conference, Eastern Cape Province, South Africa, 27–28 September 2017. [Google Scholar]
  41. Panteli, M. Assessment of the Resilience of Transmission Networks to Extreme Wind Events. In Proceedings of the 52nd Hawaii International Conference on System Sciences, Maui, HI, USA, 8–11 January 2019. [Google Scholar]
  42. Zhang, H.; Yuan, H.; Li, G.; Lin, Y. Quantitative Resilience Assessment under a Tri-Stage Framework for Power Systems. Energies 2018, 11, 1427. [Google Scholar] [CrossRef] [Green Version]
  43. Ciapesoni, E.; Cirio, D.; Pitto, A.; Masucco, S.; Sforna, M.; Marcacci, P. Model based resilience assessment and threats mitigation: A sensitivity based approach. In Proceedings of the 2018 AEIT International Annual Conference, Bari, Italy, 3–5 October 2018. [Google Scholar]
  44. Ciapessoni, E.; Cirio, D.; Kjølle, G.; Massucco, S.; Pitto, A.; Sforna, M. Probabilistic Risk-Based Security Assessment of Power Systems Considering Incumbent Threats and Uncertainties. IEEE Trans. Smart Grid 2016, 7, 2890–2903. [Google Scholar] [CrossRef]
  45. Chi, Y.; Xu, Y.; Hu, C.; Feng, S. A State-of-the Art Literature Survey of Power Distribution System Resilience Assessment. In Proceedings of the IEEE Power and Energy Society General Meeting, Portland, OR, USA, 5–9 August 2018. [Google Scholar]
  46. Wang, Y.; Chen, C.; Wang, J.; Baldick, R. Research on Resilience of Power Systems Under Natural DisastersA Review. IEEE Trans. Power Syst. 2015, 31, 1–10. [Google Scholar] [CrossRef]
  47. Arab, A.; Khodaei, A.; Han, Z.; Khator, S.K. Proactive Recovery of Electric Power Assets for Resiliency Enhancement. IEEE Access 2015, 3, 99–109. [Google Scholar] [CrossRef]
  48. Van Harte, M.A.; Koch, R.; Nambiar, A.; Joseph, S.; Tshwagong, I.; Naidoo, L.; Heideman, U. Power system resilience—Enablers supporting an effective Blackout response. In Proceedings of the CIGRE 8th Southern Africa Regional Conference, Somerset West Cape, South Africa, 14–17 November 2017. [Google Scholar]
  49. Perrings, C.; Larson, E.K.; Maliszewski, P.J. Valuing the resilience of the electrical power infrastructure. In Proceedings of the IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011. [Google Scholar]
  50. Ju, C.; Yao, S.; Wang, P. Resilient Post-Disaster System Reconfiguration for Multiple Energy Service Restoration. In Proceedings of the IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 26–28 November 2017. [Google Scholar]
  51. North American Electric Reliability Corporation. Transmission Availability Data System (TADS) Definitions. 2016. Available online: https://www.nerc.com/pa/RAPA/tads/Pages/default.aspx (accessed on 2 May 2020).
  52. Papic, M.; Clemons, M.; Ekisheva, S.; Langthorn, J.; Ly, T.; Pakeltis, M.; Quest, R.; Schaller, J.; Till, D.; Weisman, K. Transmission Availability Data System (TADS) Reporting and Data Analysis. In Proceedings of the 12th International Conference Probabilistic Methods Applied to Power Systems, PMAPS, Beijing, China, 16–20 October 2016. [Google Scholar]
  53. Bian, J.; Ekisheva, S.; Slone, A. Top Risks to Transmission Outages. In Proceedings of the IEEE PES General Meeting, Washington, DC, USA, 27–31 July 2014. [Google Scholar]
  54. Ekisheva, S.; Gugel, H. North American AC Circuit Outage Rates and Durations in Assessment of Transmission System Reliability and Availability. In Proceedings of the IEEE PES General Meeting, Denver, CO, USA, 26–30 July 2015. [Google Scholar]
  55. Ekisheva, S.; Gugel, H. North American Transformer Outage Rates and Durations in Assessment of Transmission System Reliability and Availability. In Proceedings of the IEEE PES General Meeting, Denver, CO, USA, 26–30 July 2015. [Google Scholar]
  56. Ekisheva, S.; Lauby, M.G.; Gugel, H. North American Transformer Outages Initiated by Transmission Equipment Failures and Human Error. In Proceedings of the IEEE PES General Meeting, Boston, MA, USA, 17–21 July 2016. [Google Scholar]
  57. Schaller, J.; Ekisheva, S. Leading Causes of Outages for Transmission Elements of the North American Bulk Power System. In Proceedings of the PES General Meeting, Boston, MA, USA, 17–21 July 2016. [Google Scholar]
  58. Ekisheva, S.; Papic, M.; Clemons, M.S.; Quest, R.; Pakeltis, M.J.; Weisman, K. Outage Statistics, Reliability and Availability of DC Circuits in North American Bulk Power System. In Proceedings of the IEEE PES General Meeting, Chicago, IL, USA, 16–20 July 2017. [Google Scholar]
  59. Billinton, R. Basic models and methodologies for common mode and dependent transmission outage events. In Proceedings of the IEEE PES General Meeting, San Diego, CA, USA, 22–26 July 2012. [Google Scholar]
  60. Papic, M.; Awodele, K.; Billinton, R.; Dent, C.; Eager, D.; Hamoud, G.; Jirutitijaroen, C.P.; Kumbale, M.; Mitra, J.; Samaan, N.A.; et al. Overview of common mode outages in power systems. In Proceedings of the IEEE PES General Meeting, San Diego, CA, USA, 22–26 July 2012. [Google Scholar]
  61. Papic, M.; Agarwal, S.; Bian, J.; Billinton, R.; Dent, C.; Dobson, I.; Jirutitijaroen, P.; Li, W.; Menten, T.; Mitra, J.; et al. Effects of Dependent and Common Mode Outages on the Reliability of Bulk Electric System—Part I: Basic Concepts. In Proceedings of the IEEE PES General Meeting, Washington, DC, USA, 27–31 July 2014. [Google Scholar]
  62. Papic, M.; Agarwal, S.; Bian, J.; Billinton, R.; Dent, C.; Dobson, I.; Jirutitijaroen, P.; Li, W.; Menten, T.; Mitra, J.; et al. Effects of Dependent and Common Mode Outages on the Reliability of Bulk Electric System—Part II: Outage Data Analysis. In Proceedings of the IEEE PES General Meeting, Washington, DC, USA, 27–31 July 2014. [Google Scholar]
  63. Papic, M.; Agarwal, S.; Allan, R.N.; Billinton, R.; Dent, C.; Ekisheva, S.; Gent, D.; Jiang, K.; Li, W.; Mitra, J.; et al. Research on Common-Mode and Dependent (CMD) Outage Events in Power Systems—A Review. IEEE Trans. Power Syst. 2016, 32, 1. [Google Scholar] [CrossRef] [Green Version]
  64. IEEE PES Task Force on Cascading Failure. Initial review of methods for cascading failure analysis in electric power transmission systems. In Proceedings of the IEEE PES General Meeting, Pittsburgh, PA, USA, 20–24 July 2008. [Google Scholar]
  65. Vaiman; Bell, K.; Chen; Chowdhury; Dobson, I.; Hines; Papic; Miller; Zhang. Risk Assessment of Cascading Outages: Methodologies and Challenges. IEEE Trans. Power Syst. 2011, 27, 631–641. [Google Scholar] [CrossRef]
  66. Bialek, J.; Ciapessoni, E.; Cirio, D.; Cotilla-Sanchez, E.; Dent, C.; Dobson, I.; Henneaux, P.; Hines, P.; Jardim, J.; Miller, S.; et al. Benchmarking and Validation of Cascading Failure Analysis Tools. IEEE Trans. Power Syst. 2016, 31, 4887–4900. [Google Scholar] [CrossRef] [Green Version]
  67. Henneaux, P.; Ciapessoni, E.; Cirio, D.; Cotilla-Sanchez, E.; Diao, R.; Dobson, I.; Gaikwad, A.; Miller, S.; Papic, M.; Pitto, A.; et al. Benchmarking Quasi-Steady State Cascading Outage Analysis Methodologies. In Proceedings of the International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Boise, ID, USA, 24–28 June 2018. [Google Scholar]
  68. Carreras, B.A.; Newman, D.E.; Dobson, I.; Degala, N.S. Validating OPA with WECC data. In Proceedings of the Hawaii International Conference on System Sciences, Maui, HI, USA, 7–10 January 2013. [Google Scholar]
  69. Dobson, I. Estimating the Propagation and Extent of Cascading Line Outages From Utility Data With a Branching Process. IEEE Trans. Power Syst. 2012, 27, 2146–2155. [Google Scholar] [CrossRef]
  70. Papic, M.; Dobson, I. Comparing a Transmission Planning Study of Cascading with Historical Line Outage Data. In Proceedings of the PMAPS International Conference, Beijing, China, 16–20 October 2016. [Google Scholar]
  71. Dobson, I.; Carrington, N.; Zhou, K.; Wang, Z.; Carreras, B.A.; Reynolds-Barredo, J.M. Exploring Cascading Outages and Weather via Processing Historic Data. In Proceedings of the 51st Hawaii International Conference on System Sciences, Hilton Waikoloa Village, HI, USA, 3–6 January 2018. [Google Scholar]
  72. Eskandarpour, R.; Khodaei, A.; Arab, A. Improving Power Grid Resilience through Predictive Outage Estimation. In Proceedings of the North American Power Symposium, Morgantown, WV, USA, 17–19 September 2017. [Google Scholar]
  73. Kelly-Gorham, M.R.; Hines, P.; Dobson, I. Using historical utility outage data to compute overall transmission grid resilience. In Proceedings of the IEEE PES General Meeting, Atlanta, GA, USA, 6–8 August 2019. [Google Scholar]
  74. Thompson, C.C.; Stringer, A.D.; Barriga, C.I. An Evaluation of Transformer Historical Failure Data for Facility Resiliency and Reliability. In Proceedings of the IEEE Power and Energy Society General Meeting, Atlanta, GA, USA, 4–8 August 2019. [Google Scholar]
  75. Campbell, R.J. Weather-Related Outages and Electric System Resiliency; Congressional Research Service: Washington D.C., USA, 2012.
  76. Eskandarpour, R.; Khodaei, A. Machine Learning Based Power Grid Outage Prediction in Response to Extreme Events. IEEE Trans. Power Syst. 2017, 32, 3315–3316. [Google Scholar] [CrossRef]
  77. Dagle, J. Resilient Networks Minitrack. In Proceedings of the 52nd Hawaii International Conference on System Sciences, Grand Wailea, Maui, HI, USA, 8–11 January 2019. [Google Scholar]
  78. Duchesne, L.; Karangelos, E.; Wehenkel, L. Using Machine Learning to Enable Probabilistic Reliability Assessment in Operation Planning. In Proceedings of the Power System Computation Conference (PSCC), Dublin, Ireland, 11–15 June 2018. [Google Scholar]
  79. North American Electric Reliability. Corporation State of Reliability. 2019. Available online: www.nerc.com/pa/RAPA/PA/Performance%20Analysis%20DL/NERC_SOR_2019.pdf (accessed on 2 May 2020).
  80. Papic, M.; Ekisheva, S.; Robinson, J.; Cummings, R. Multiple Outage Challenges to Transmission Grid Resilience. In Proceedings of the IEEE PES General Meeting, Atlanta, GA, USA, 4–8 August 2019. [Google Scholar]
  81. Gholami, A.; Shiekari, T.; Amirioun, M.H.; Aminifar, F.; Amini, M.H.; Sargolzaei, A. Toward a Consensus on the Definition and Taxomony of Power System Resilience. IEEE Access 2018, 6, 32035–32053. [Google Scholar] [CrossRef]
  82. Venkata, S.S.; Hatziargyriou, N. Grid Resilience. IEEE Power Energy Mag. 2015, 13, 16–23. [Google Scholar] [CrossRef]
  83. International Council on Large Electric Systems. C4.47 PSR Working Group; Power System Resilience Definition; International Council on Large Electric Systems: Paris, France, 2018. [Google Scholar]
  84. Lowrance, W.W. Of acceptable risk. Science and the determination of safety. J. Chem. Educ. 1977, 54, A345. [Google Scholar] [CrossRef]
  85. Piacenza, J.R.; Faller, K.J.; Bozorgirad, M.A.; Cotilla-Sanchez, E.; Hoyle, C.; Tumer, I. Understanding the Impact of Decision Making on Robustness During Complex System Design: More Resilient Power Systems. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part B Mech. Eng. 2019, 6. [Google Scholar] [CrossRef]
  86. Espinoza, S.; Poulos, A.; Rudnick, H.; De La Llera, J.C.; Panteli, M.; Mancarella, P. Risk and Resilience Assessment With Component Criticality Ranking of Electric Power Systems Subject to Earthquakes. IEEE Syst. J. 2020, 14, 2837–2848. [Google Scholar] [CrossRef]
  87. Natural Environment Research Council. Bulk Electric System (BES) Definition, Notification, and Exception Process. Available online: http://www.nerc.com/pa/RAPA/Pages/BES.aspx (accessed on 2 May 2020).
  88. Karki, R.; Dhungana, D.; Billinton, R. An Appropriate Wind Model for Wind Integrated Power Systems Reliability Evaluation Considering Wind Speed Correlations. Appl. Sci. 2013, 3, 107–121. [Google Scholar] [CrossRef]
  89. Johnson, B.; Cotilla-Sanchez, E. Estimating the impact of ocean wave energy on power system reliability with a well-being approach. IET Renew. Power Gener. 2020, 14, 608–615. [Google Scholar] [CrossRef]
  90. Linkov, I.; Bridges, T.; Creutzig, F.; Decker, J.; Fox-Lent, C.; Kröger, W.; Lambert, J.H.; Levermann, A.; Montreuil, B.; Nathwani, J.; et al. Changing the resilience paradigm. Nat. Clim. Chang. 2014, 4, 407–409. [Google Scholar] [CrossRef]
  91. Papic, M.; Ciniglio, O. Prevention of NERC C3 Category Outages in Idaho Power’s Network: Risk Based Methodology and Practical Application. In Proceedings of the IEEE PES General Meeting, Vancouver, BC, Canada, 21–25 July 2013; pp. 1–6. [Google Scholar]
  92. Federal Energy Regulatory Commission. Comments of the North American Electric Reliability Corporation; Federal Energy Regulatory Commission: Washington D.C., USA, 2018.
Applsci 10 04761 g001 550
Figure 1. Distribution of cluster sizes (2013–2019).
Figure 1. Distribution of cluster sizes (2013–2019).
Applsci 10 04761 g001
Applsci 10 04761 g002 550
Figure 2. Outages in clusters by initiating cause (2013–2019).
Figure 2. Outages in clusters by initiating cause (2013–2019).
Applsci 10 04761 g002
Applsci 10 04761 g003 550
Figure 3. Comparative breakdown of outages by initiating cause (2013–2019).
Figure 3. Comparative breakdown of outages by initiating cause (2013–2019).
Applsci 10 04761 g003
Applsci 10 04761 g004 550
Figure 4. Average cluster duration by cluster size (2013–2019).
Figure 4. Average cluster duration by cluster size (2013–2019).
Applsci 10 04761 g004
Applsci 10 04761 g005 550
Figure 5. Distribution of number of clusters by Transmission Owner (TO) for 7 years (2013–2019).
Figure 5. Distribution of number of clusters by Transmission Owner (TO) for 7 years (2013–2019).
Applsci 10 04761 g005
Applsci 10 04761 g006 550
Figure 6. Evaluation of cluster risk estimates.
Figure 6. Evaluation of cluster risk estimates.
Applsci 10 04761 g006
Table
Table 1. Transmission Availability Data System (TADS) automatic outages in clusters by element type and voltage class.
Table 1. Transmission Availability Data System (TADS) automatic outages in clusters by element type and voltage class.
Voltage ClassAC CircuitAC/DC BTB ConverterDC CircuitTransformer
200–299 kV30341217604
300–399 kV162126 403
400–499 kV * 37
400–599 kV594 389
500–599 kV * 39
600–799 kV123 43
Grand Total537238931439
* Voltage class for DC circuits only.
Table
Table 2. TADS automatic outages in clusters by element type and voltage class.
Table 2. TADS automatic outages in clusters by element type and voltage class.
Cluster Size20132014201520162017201820192013–2019
22902493403203363343492218
386546792745364490
423142014212512129
5973629743
6035211416
711002228
810100114
910011003
1100001102
1210000102
1400000011
1600000011
1810000001
All sizes4133284364354384274412918
Table
Table 3. Ten largest clusters (2013–2019).
Table 3. Ten largest clusters (2013–2019).
Cluster SizeYearDuration (Hours)TADS ElementsInitiating Causes of Outages
920132.39 acLightning
9201711.68 ac, 1 transPower system condition, Human error, Unknown
920161.69 acFailed AC substation equipment
1120172.04 ac, 7 transHuman error, Power system condition
1120181.64 ac, 7 transLightning, Power system condition
12201811.912 acHuman error, Fire, Power system condition
12201348.712 acContamination
14201935.113 ac, 1 transFire, Power system condition
1620195.913 ac, 3 transFire, Power system condition (wildfires in California)
182013116.018 acWeather-initiated (extreme rainfall)
Table
Table 4. Estimated frequencies of clusters for Company X.
Table 4. Estimated frequencies of clusters for Company X.
Expected Number of ClustersCluster Size
234567891112141618All Sizes
7 years15.4333.4090.8980.2990.1110.0560.0280.0210.0140.0140.0070.0070.00720.304
1 year2.2050.4870.1280.0430.0160.0080.0040.0030.0020.0020.0010.0010.0012.901

Share and Cite

MDPI and ACS Style

Papic, M.; Ekisheva, S.; Cotilla-Sanchez, E. A Risk-Based Approach to Assess the Operational Resilience of Transmission Grids. Appl. Sci. 2020, 10, 4761. https://doi.org/10.3390/app10144761

AMA Style

Papic M, Ekisheva S, Cotilla-Sanchez E. A Risk-Based Approach to Assess the Operational Resilience of Transmission Grids. Applied Sciences. 2020; 10(14):4761. https://doi.org/10.3390/app10144761

Chicago/Turabian Style

Papic, Milorad, Svetlana Ekisheva, and Eduardo Cotilla-Sanchez. 2020. "A Risk-Based Approach to Assess the Operational Resilience of Transmission Grids" Applied Sciences 10, no. 14: 4761. https://doi.org/10.3390/app10144761

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop