Abstract
Air pollution in urban regions remains a crucial subject of study, given its implications on health and environment, where much effort is often put into monitoring pollutants and producing accurate trend estimates over time, employing expensive tools and sensors. In this work, we study the problem of air quality estimation in the urban area of Milan (IT), proposing different machine learning approaches that combine meteorological and transit-related features to produce affordable estimates without introducing sensor measurements into the computation. We investigated different configurations employing machine and deep learning models, namely a linear regressor, an Artificial Neural Network using Bayesian regularization, a Random Forest regressor and a Long Short Term Memory network. Our experiments show that affordable estimation results over the pollutants can be achieved even with simpler linear models, therefore suggesting that reasonably accurate Air Quality Index (AQI) measurements can be obtained without the need for expensive equipment.
1. Introduction
Nowadays, air pollution represents a major environmental problem, increasingly worsening and affecting more people every year. This is especially true in urban environments, where the majority of the industries and traffic reside, releasing into the air alarmingly large quantities of pollutants and particulate matter that become a severe health risk from exposure [1]. Recent estimates claim that 4.6 million people die each year from causes directly attributable to air pollution [2], with a total of 300,000 cases in Europe only. These figures appear surprisingly high when compared to other common death causes such as car crashes, which is approximately three times lower [3]. The high incidence of deaths caused by air pollution can be explained by the fact that more than 90% of the world population lives in places where the air quality exceeds the guideline limits established by the World Health Organization (WHO) [4].
Several studies [1,5,6] analysed the relation between air pollution and health issues, both on global and local scale over long periods of time, demonstrating for instance augmented risks of respiratory diseases, such as bronchitis and asthma, or even reduced life expectancy [7]. Furthermore, air pollution is one of the major factors contributing to climate change, especially in terms of global warming. Even considering the relatively brief period, average temperatures have already risen by °C since 1980 and data records from NASA report that 19 out of 20 warmest years have occurred between 2001 and the present day (https://climate.nasa.gov/). Besides the direct effects of greenhouse gases, several subsequent issues are also involved. For instance, warmer periods could increase the ozone () levels by 1 to 10 ppb during the next years, where drier regions can drastically increase the risk of wildfires, and consequently release significant source of carbon oxides and particulate matter [8].
For these and other reasons, a steadily growing concern from authorities, media and citizens has led to a broad consensus about the need of strong regulations in order to reduce the emissions of major pollutants in the shortest possible time. Together with important international treaties (e.g., Paris agreements (https://unfccc.int/process-and-meetings/the-paris-agreement/the-paris-agreement)), the European Union established a remarkable set of legislation aimed at setting strict legal limits and target values for the concentrations of major air pollutants to be reached by the Member States within the next decades (https://eur-lex.europa.eu/legal-content/EN/ALL/?uri=CELEX:32008L0050). Because of the high population density in the old country, the primary purpose of this document is the safeguard of the human health by setting limits for Particulate Matter ( and ), Sulphur Dioxide (), Benzene (), Carbon Monoxide (), Ozone (), Nitrogen Oxides (), Lead and other toxic heavy metals such as Arsenic and Cadmium. In order to comply to these directives, each country requires a large amount of sensors to be positioned in key areas, mostly depending on the distribution and density of infrastructures and buildings. These monitoring stations can be divided into different groups according to the emission sources, namely: traffic, industrial or background stations, or the region category. In detail, monitoring stations are categorised as: (i) urban stations if positioned in central city districts, (ii) suburban stations when localised in the surroundings, or (iii) rural stations in any other case. In most cases, the urban stations group is the most significant indicator of the air quality for major cities and therefore requires a higher degree of attention, translated in both equipment and maintenance costs: without including heavy calibration, deployment and administration estimates, professional devices can reach prices over EUR 10.000 for a single unit. Multiplying this value for the number of pollutants or atmospheric conditions and the number of districts to be monitored in a large city, the yearly expenses can quickly become non-trivial.
At the same time, pollution levels in urban environments can typically be traced back to a relatively small subset of factors, with the vast majority of the contribution deriving from vehicle emissions and surrounding industries. Moreover, several studies [5,9] show a strong correlation between weather condition and trends of various pollutants: ozone levels for instance are directly influenced by warmer climates and solar radiation levels because of photo-chemical reactions induced on other pollutants, while temperature inversion layers can trap colder polluted air on the surface.
Given the serious nature of this subject, many studies have been conducted over the years in order to estimate trends of pollutants or provide air quality forecasts for future hours or days. These include statistical approaches such as [10], where spatial correlations and seasonal patterns were exploited to estimate long-term trends of particulate matter () using a hierarchical model, based on Partial Least Squares regression. Other studies [11,12,13] investigated the applicability of recent machine learning approaches based on neural networks to this domain. In [11] different combination of Multi-Layer Perceptrons (MLP), periodic components and Self-Organising Maps are applied to hourly values of and meteorological features, showing that the best results can actually be achieved by directly applying the MLP on the original data. Other solutions propose to merge features from different domains and leverage the extreme adaptability of deep learning to extract relevant knowledge and thus provide a finer estimate of air quality. As an example in a urban environment, U-Air [12,14] exploits different kinds of big data thanks to a composite framework where temporal and spatial information are processed by two different models to provide a robust 48-h forecast of the Air Quality Index (AQI). In [13], a similar approach is adopted and improved with the addition of an Attention Pooling layer that dynamically adapts to the most relevant monitoring station for a fine-grained prediction.
Despite the accuracy of current state-of-the-art solutions, a major drawback of the listed systems is the high reliance on real-time sensor data, which strongly limits their use to a small part of urban and densely populated areas covered by monitoring stations. With reference to the systems and the maintenance costs, expanding the encompassed areas can be a slow process, if feasible at all.
In this work we propose to combine meteorological and traffic-related features with recent machine learning and deep learning models to obtain a robust estimate of both pollutants and AQI. As a case study, we combine three years of sensor and vehicle logs from the city of Milan, from 2013 to 2016, training different kind of models to predict the monitored air pollutants, namely Nitrogen Oxides (, ), Carbon Monoxide (), Benzene (), Ozone (), Black Carbon () and Particulate Matter (, ). Expanding on previous work [15], we adopt a series of machine and deep learning models to predict the evolving trends of the pollutants in time. The predictions are first compared with a subset of the actual sensor logs recorded from high-end monitoring stations as ground truth, then used to predict an Air Quality Index following European standards, assessing the accuracy in identifying the correct category. Despite the undeniable loss in terms of performance with solutions including the pollutants in the feature set, we show that accurate estimates can still be obtained for most pollutants and therefore a fairly accurate AQI can be predicted even when relying only on environmental information.
In summary, the contributions of this paper are as follows:
- We study the problem of air quality estimation in urban areas with a focus on environmental features, discussing the relations between meteorological measurements and vehicle transits with air pollutants;
- We test and propose a series of experiments conducted with different popular machine and deep learning models, highlighting advantages and drawbacks of each solution;
- We demonstrate the feasibility of this task, showing fairly robust estimations without introducing past measurements of pollutants in our experiments.
The paper is organised as follows. Section 2 introduces: (i) the data sources used for the experiments, describing the process of acquisition, preprocessing and analysis; (ii) the frameworks and tools used to manipulate the data; and (iii) the evaluation measures and the experiment setup adopted. Section 3 reports the results obtained from the adopted solutions discussing their performance. Lastly, in Section 4 concludes with a summary of the study and delineates possible future works.
2. Materials and Methods
This section describes the different data sources selected for our case study and the set of experiments conducted on the processed features. First, in Section 2 we discuss how we obtained the different sets of sensor measurements and vehicle transits and briefly describe the available information. In Section 2.2 we enumerate the different processing steps carried out to prepare the data for our tests. In Section 2.3, we introduce our testing methodology, listing the models employed for training and the motivation behind the choices. Lastly, in Section 2.4 we outline our testing environment, enumerating the tools and frameworks adopted, and in Section 2.5 we provide a thorough description of the different experiments and how they were implemented.
2.1. Data Sources and Acquisition
In this case study we used information collected in three years, from 2013 to 2016, limited to the central areas of Milan. In particular, we collected three different data sources: (i) meteorological data from different sensor types, such as temperature, humidity, pressure and wind speed, (ii) traffic data derived from the passage of vehicles recorded from fixed video cameras in a belt surrounding the city center, and (iii) the ground-truth pollutant trends, obtained from different monitoring stations mounted in fixed crucial points.
Regarding meteorological data, we obtained the sensor logs of seven different weather stations, mainly distributed around the borders of the city, as shown in Figure 1. The monitoring platforms and their respective data are provided by Agenzia Regionale per la Protezione dell’Ambiente (ARPA) Lombardia, the reference institution in the region for environmental protection. This and other kind of datasets have recently become freely available for download on the regional Open Data portal (https://www.dati.lombardia.it/). Logs are provided with yearly subdivisions in standard CSV files, where each one stores data corresponding to a single sensor, defined by three fields: the unique ID for the sensor, a timestamp of the measurement in local time and the corresponding value measured. Any other additional information related to the sensors is in fact explained by a descriptor file first indicating the unique ID, name and position of the specific platform, then enumerating the different sensors of which it is equipped, specifying their unique ID, type, their measurement interval, their unit of measure and the operator used to normalize the logs into a time series with regular intervals between samples. From these descriptors it is possible to trace the sensors back to the respective measured weather feature and thus group them in six different types, displayed in Table 1. Except for the pressure category that only presents a single sensor, every other class of meteorological feature is well represented by at least three time series, in the three-year period we analysed. In terms of data format, every sensor class utilises a standard measurement unit and contains records with a regular resolution of an hour, obtained by averaging the aggregation of the raw measurements. The only exception is represented by the precipitations category, which instead provides logs aggregated with a cumulative sum, indicating the total amount of millimeters of rain which fell every hour.
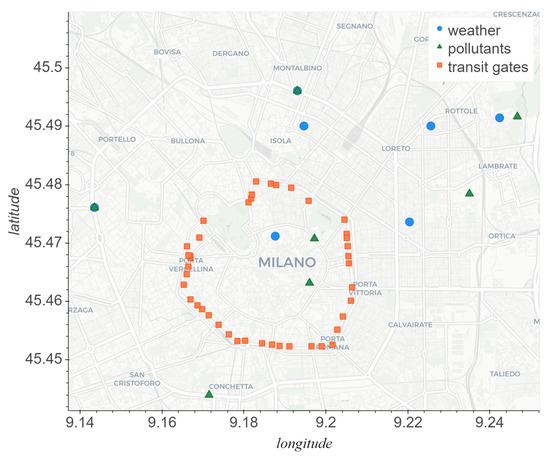
Figure 1.
Map displaying the distribution of weather (blue), pollutants (green) and transit (orange) sensor stations around the city center of Milan.

Table 1.
Weather sensors divided by feature type, with amount of unique sensors per group, unit of measurements, time interval between samples and aggregation type used to unify the data formats.
A similar procedure concerned the measurements of the pollutants. Data were once again provided by ARPA, freely available for download through the above-mentioned portal, and were subdivided into file descriptors, containing name, location and equipped sensors of the monitoring stations, together with individual CSV files containing yearly measurements of the individual sensors, identified by a unique ID. The positioning of these cells is visible in Figure 1. In total, exploring the three-year period considered for this work, we analysed 10 different pollutant categories, each one measured by at least one sensor in the central area of Milan.
The count of unique measurements varies greatly with the severity and the intrinsic relevance of the pollutant for the definition of an air quality index, which is typically identified by a combination of , and particulate matter, as described in Section 2.3. Specifically, nitrogen oxides (, ) are represented, respectively, by 8 and 7 unique sensors distributed around the city center, C6 and by 4, and particulate matter (, ) by 3, by 2. Lastly, and are represented by a single measurement only.
As for the meteorological data, logs for the pollutants provided by ARPA correspond to an hourly aggregation by average, with the exception of particulate matter ( and ), where measurements are stored with daily interval, representing a 24-h mean value. While this is sub-optimal given the consistency of the remaining data, it does not represent a major issue and it is somewhat expected since the vast majority of air quality indicators only make use of a daily average for particulate matter.
The last feature type employed in this work is represented by recorded hourly transits in the congestion charge surrounding the center of Milan. In this case, data is provided by Agenzia Mobilità Ambiente e Territorio (AMAT) (https://www.amat-mi.it/) and encompasses the C Area, corresponding to the urban region of Cerchia dei Bastioni. The area is accessible by a total of 42 gates, displayed in Figure 1, each one monitored by fixed cameras continuously monitoring and recording the plates of any vehicle entering the city center. The logs were cross-referenced with data from the regional Department of Motor Vehicles, in order to obtain, for each plate, a list of characteristics of the corresponding vehicle, including fuel type and potential category of European emission standard. The complete dataset is subdivided into three main CSV files: the first containing information about the monitoring gates, the second providing detailed information about vehicles and the last one providing the transit records in the city center, during the three-year period. Altogether, these files contain information about four main features: (i) the emission standard category, from Euro 0 to Euro 6; (ii) the fuel type, namely petrol, diesel, electricity, gas or hybrid; (iii) the category of vehicle, public transport, cargo or normal cars; and (iv) additional information such as whether the vehicle was authorized into the area, or whether it is a service vehicle or if it belongs to residents.
2.2. Data Preprocessing and Analysis
As introduced in the previous section, the available data appears scattered in many different physical files or presents different formats and configurations. In order to align the features into a single common representation for model training, we carried on an extensive multi-step preprocessing phase, combining (i) data aggregation (ii) data cleaning (iii) imputation and (iv) feature engineering. Considering the first point, aggregation was necessary for two main reasons: first and foremost, the collected data described above unfortunately presents a large number of randomly missing values, without any distinguishable pattern in terms of time periods with the exception of the transits, which include none of all the available features in four specific intervals, as described below. Second, the amount of sensors and their distribution on the territory was extremely limited in terms of covered surface, certainly not enough to conduct a proper spatial analysis. A bilinear interpolation of the values over time is typically applied to simulate a continuous distribution of the features, such as in U-Air [12], but this option was also discarded again because of the lack of data in many of the sensors equipped by the monitoring stations, for both weather and pollutants, as shown in Table 2. Therefore, in order to drastically reduce the amount of missing data while maintaining a coherent ground truth, we opted for a single time series for each sensor type, aggregating by timestamp and averaging when more than one value was present over the same timestamp. This operation is justified by the fact that, given the relative proximity of sensors, most records present extremely similar trends over time. The results, in terms of data coverage, are reported again in Table 2.

Table 2.
Total amount of missing values for weather and pollutant sensors. On the left, the count represents the amount w.r.t. total feature values, on the right, the result after mean aggregation among groups.
A similar process was carried out on traffic-related features: first, data from vehicle details were merged with transit records and subsequently aligned with the time resolution of the available sensors by summing the passages occurred in the same hour. Then, since spatial information was discarded in previous sets to reduce sparsity, transits from all the gates was summed up in order to obtain once again a single time series for each of the vehicle-related features. Therefore, the final aggregated dataset contains the sum of all the vehicle transits at any gate and during the same hour for every traffic-related feature, from the emission standards (euro-0 to euro-6) to vehicle types and fuel types.
Concerning the data cleaning phase, every available meteorological and aerial feature was checked for noticeable outliers. Because of the hourly aggregation of the original sensor logs and the aforementioned spatial reduction, little to no effort was required to check and limit the values into a reasonable range. Additionally, most of the feature sets already appear in predefined ranges, such as the humidity provided in percentage, while others inherently describe out of the ordinary yet crucial situations, such as the rainfall amount, which can only be checked for impossible values (e.g., negative records). During this phase we also discarded those features that still contained a large amount of missing data, namely wind direction which contained a single year of data out of three, and dropped transit entries representing unknown values (euro_na, fuel_na, vehicle_na). The latter were substituted with a single additional feature named total, representing the total amount of transits, regardless of the vehicle type. An analogous procedure was carried out on target variables. On the basis of the former analysis, we decided to exclude from the study both sulphur dioxide () and ammonia () measurements for three main reasons: first and foremost, both pollutants were represented by a single ground-truth sensor each which contained a large portion of missing data, as shown in Table 2. Second, the low correlation displayed by the two pollutants, visible in Figure A1, cannot justify a possible imputation phase over their respective time series, especially with an high percentage of data to be estimated. Third, our main objective is the estimation of an Air Quality Index where both categories are not among the required pollutants for its computation, thus not essential for our case study.
The aggregation procedure reduces the amount of missing information, nevertheless many features still remain incomplete or even unchanged in the particular case of transits, where the spanned missing intervals were the same across every record, as shown in Figure 2 and Table 3. While this does not represent a problem in most cases, it is preferable to maintain a continuous time series, especially for experiments with sequence-based models such as deep Recurrent Neural Networks. For consistency, we therefore opted for a domain-based imputation phase, during which existing features from the same domain (namely weather, pollutants and transits) are exploited to estimate missing values in the others. This decision was once again motivated by the extreme trend similarities among sensors of the same category, as reflected by the correlation matrices displayed in Appendix A.
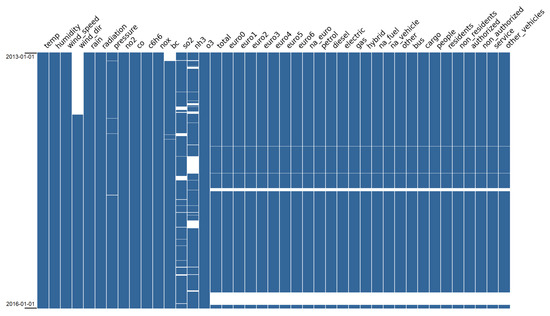
Figure 2.
Missing values in the aggregated hourly set over the three-year span, highlighted by the white areas.

Table 3.
Missing periods in the transits dataset with respective length.
In our work, we adopted an hybrid approach: considering the time series representing the evolution of a single feature and an empirically determined threshold of six hours, if a continuous sequence of missing values remains below the threshold, we simply impute by polynomial interpolation (with grade 2). Otherwise, we apply an iterative statistical imputation strategy, where the features with the least amount of missing values are estimated first, using all the others as input with a round-robin process. This allows for theoretically better results since at every step we maximise the amount of ground-truth information provided to the model. In our case, we exploited a linear regression approach with Bayesian Ridge regularisation. In the particular case of transits, an iterative procedure could not be applied since every feature was missing in the same intervals. Nevertheless, the same interpolation approach is employed for periods below the threshold, while for all the remaining ones we adopted a statistical approach for time series forecasting. Specifically, given the extreme regularity and the multiple seasonalities of transits, we used a Trigonometric, Box-Cox Transformation, ARMA Errors, Trend and Seasonal Components (TBATS) method to generate the periodical components, then scaled the result by mean and variance of the surrounding context in order to avoid large discontinuities between imputed and ground-truth values. This technique was applied to every missing period except the last one, as the time range of 52 days was exceedingly long for any forecast or estimation to be considered reliable. Instead, we opted for truncating the three-year span into a shorter albeit continuous testing period for every feature, starting from 01/03/2013 until 24/10/2015. This in practice excludes the last part of the dataset, but guarantees a full and regular time series.
Subsequently, we carried out the feature engineering phase. This operation is not strictly required, especially for deep sequence-based models, but can be extremely beneficial for simpler linear models. Specifically, we augmented the merged data set with (i) temporal features, (ii) lagged features and (iii) aggregated information. In the first case, for each record we introduced specific information about the month, day of the week and time of day, encoded using trigonometric functions in order to maintain their inherent cyclical trend. In practice, we exploited the decomposition documented in Equation (1) to generate the described pair of values, using the previously mentioned time intervals.
In the formulas, f represents the selected feature (month, day of the week or hour of the day), represents the time period required for a complete cycle, in this case respectively 12, 7 and 24. Additionally, we also employed a standard Radial Basis Function for each month i, shown again in Equation (1). This allows the models to capture average trend information in the period highlighted by the Gaussian function. As last time-related feature, we added a simple dummy variable set to 1 when the given day represented a public holiday and 0 otherwise.
Limited to and , we conducted an additional processing phase generating a parallel dataset by further reducing every feature to a daily resolution by averaging over the 24-h window. This is only required for particulate matter since, as reported in Table 2, it is the only category of target variables with daily resolution. While upscaling the respective time series could be considered as a viable option, the behaviour of particulate matter did not present strong correlations when compared with other air pollutants. Therefore, an harmonization procedure with the remaining features would have required different heavy assumptions on the daily trends of particulate matter that were simply not possible given the available data.
In order to assess which features are potentially significant for an accurate estimate of pollutants, we investigated the Pearson correlation coefficient [16] by means of a correlation matrix, a standard measure to quantify linear correlation between pairs of variables. The coefficient can assume values in the range , with indicating total negative correlation, total positive correlation and 0 no correlation at all. In Figure 3, correlation coefficients among target pollutants and feature variables are reported. It can be observed that, despite the weak values, most pollutants present a positive trend with the increase of transits. This is especially noticeable with particulate matter ( and ), where the correlation is stronger. With reference to the aforementioned aggregation, we must point out that the reported correlations with particulate matter refer to the dataset reduced to daily resolution, while all the other measures refer to the average hourly records.
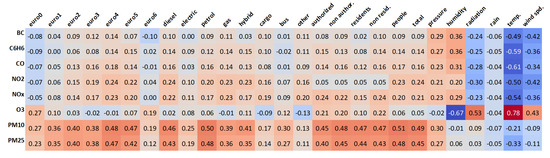
Figure 3.
Correlation matrix between target variables and selected features.
Confirming the statements reported in Section 1, meteorological features appear to be the most correlated with the targets, in particular temperature, wind speed and radiation negatively influence the trend of pollutants, while pressure and humidity present a weak positive correlation. In contrast with the other dependent variables, the Ozone () shows an opposite behaviour in most cases: it appears for instance strongly correlated with temperature, radiation and wind speed, while also noticeably correlated with humidity in a negative way. Another unexpected result is represented by the complete absence of linear correlation between rain and pollutants. Despite the weak coefficients, we maintained the feature, as the influence of rainfall on air pollutants is seldom immediate and may typically occur in the following hours or days, thus the apparent lack of linear correlation.
Likewise, we investigated the autocorrelation for each of the hourly pollutants, with the aim of defining suitable time windows for the estimation procedure. This measure can be defined as the correlation between a signal and its copy delayed over time, thus having the same range . As observable in Figure 4, every pollutant presents a high autocorrelation in a 72-h window, with strong spikes on the 24th and 48th mark. Therefore, limited to the target variables with hourly resolution, we augmented the set with lagged features selecting two time windows of 24 and 48 h. While a longer window could have been beneficial, these intervals should still allow for a thorough analysis over the importance of lagged variables in the estimation, and at the same time avoiding a feature explosion in the datasets. We note that this procedure is not required for recurrent models such as Long Short-Term Memory (LSTM) [17], as the inherently sequential architecture allows for time windows of arbitrary lengths, nevertheless we applied the same criteria by forcing the latter to assume the same values of the two intervals chosen. We also point out that this analysis did not take into consideration particulate matter because of the daily resolution of the signals. In this case, we opted for two simpler time windows with a lag of one and two days respectively.
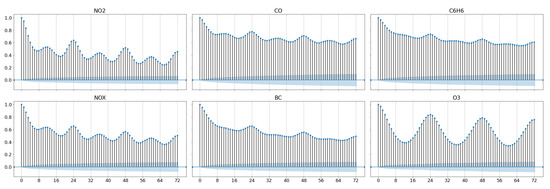
Figure 4.
Autocorrelation for the hourly pollutants considered in the case study, over a time window of 72 h.
2.3. Methodology
The main objective of this study is the estimation of an Air Quality Index (AQI) in an urban environment, exploiting data related to vehicle transits and meteorological features. While the process can be defined as a standard classification task using AQI levels as target categories, we opted instead for the definition of a regression problem over pollutants in order to assess the validity of the solution on each target variable. Moreover, the latter configuration can be reduced to a classification problem by computing the AQI over the regression result. The AQI estimate is computed in two steps: (i) independent estimation of each pollutant (, , , , , at hourly resolution, and , at daily resolution), and (ii) computation of the AQI according to the official European formula, by using the estimates of each pollutant. The approaches proposed for the aforementioned steps were evaluated with different dataset configurations, considering weather and traffic features at: (i) time t, (ii) from time to time t, and (iii) from to time t.
Formally, we can define this multi-step prediction pipeline as follows: given a set of aggregated features from two different domains, namely meteorological measurements and vehicle transit counts , temporal features , and a machine learning model g with parameters , the objective is to first provide an estimate for each pollutant i and time step t on the test set, such that , where w indicates a specific time window. Obtained the estimates , the goal is to evaluate a single global measure of air quality over the same data for each time step, named Air Quality Index (AQI), defined as where is a subset of the original pollutants and is a single integer value indicating the gravity of the air pollution. Specifically, we adopted a common European Air Quality Index (CAQI) which provides five different levels of severity based on three pollutants, namely , and , as detailed in Section 2.5.
Given the data described above, we trained the same set of regressors on every available feature for each pollutant. Specifically, we selected for this work four models with different characteristics: (i) a linear regressor with Bayesian Ridge Regularization, (ii) a Neural Network Using Bayesian Regularization (BRNN) (iii) a Random Forest Regressor (RF) [18], an ensemble model using decision trees as base estimators, and (iv) a Long-Short Term Memory (LSTM) model [19].
The first linear model can be seen as a standard Ordinary Least Squares (OLS) algorithm, with the addition on a regularization process that minimizes the weight estimates, therefore reducing the influence of strong outliers in most situations. In this particular case, the regularization uses a probabilistic approach similar to ridge regression, where the weights are assumed to follow a normal distribution around zero. Linear models represent the best compromise between performance and efficiency, for this reason they are typically employed as robust baseline [20].
Together with the linear model, we included a simple Neural Network with Bayesian Regularisation (BRNN) as second baseline. The motivation behind this model is twofold: first of all, previous work [15] had already shown encouraging results using this architecture. Second, it provided a good comparison between standard multi-layer perceptrons and recurrent neural networks.
The third approach selected, Random Forest, belongs to the category of ensemble models based on bagging. The latter technique involves the separate training of n weaker models, in this case standard decision trees, where the strong model is represented by the whole group and the regression output is obtained by averaging the results of each individual estimator. Formally, given a training set S, the bagging procedure generates n new sets such that by sampling the original data. Subsequently, n individual models are trained on each and their results are aggregated by averaging in regression tasks, or by majority voting in classification problems. Despite the high demand in terms of computational resources and training time, Random Forests (and bagging in general) typically provide robust solutions without suffering from overfitting like simpler regression trees, thanks to the sampling procedure and ensemble learning. Because of their versatility and resilience to outliers, RF models have already been successfully applied in many different regression tasks, from calibration of air pollutant sensors [21] to air quality estimation in urban environments [22,23].
Lastly, we employed a Deep Recurrent Neural Network (RNN), specifically a LSTM model. In general, RNNs inherently handle input sequences with varying length; however, the latter is particularly suited for the task given the internal architecture. LSTM units are in fact able to capture both long-term patterns and short-term variations thanks to a combined mechanism of input gates, where the information content from new examples is merged with the internal state of the network, and forget gates, where the decision of whether to keep or discard information from previous states is taken. Given their high adaptability to sequential inputs, LSTM models have been successfully applied to time series forecasting and estimation of air pollutants in different domains [17,24,25]. For our work, we made use of a LSTM network structured with three hidden layers with dimension 100, followed by a simple linear layer with a single output, corresponding to a specific estimated pollutant.
2.4. Frameworks and Tools
In this section we enumerate and briefly describe tools and hardware used in order to conduct the preprocessing and analysis steps addressed in Section 2.2 and the experiments described in the following paragraphs of this manuscript. As data were provided in CSV format, every preliminary phase from acquisition to aggregation and cleaning was carried out using a scientific Python 3.6 environment through a combination of pandas [26] and numpy [27] libraries, with the support of the statsmodels package [28] for time series analysis and matplotlib for data visualization. For the data imputation phase and the following experiments, we leveraged the popular scikit-learn library [29], which offers rich functionalities in many different machine learning domains, from data preprocessing to the metrics computation, and provides out-of-the-box robust implementations for many popular models and algorithms. Specifically, together with the previously mentioned packages, we used this library for data normalization, definition of the cross validation, other testing setups described in the next section and implementation of the Bayesian Ridge linear regressor. As deep learning counterpart, we employed the PyTorch framework [30], another extensive library providing a wide variety of features. In particular, the latter was leveraged for the implementation and training of the LSTM regressor. A detailed description of software libraries and respective versions is provided in Table 4. In order to carry out the experiments with the BRNN model, we also leveraged an R environment considering the lack of equivalent Python implementations. In this case, we maintained the same processing pipeline using the libraries listed in the right section of Table 4 to reproduce pandas and numpy functionalities, then we trained the model provided by the namesake package brnn. Once trained, the results were stored and evaluated in the Python pipeline, in an identical manner to the other solutions.

Table 4.
List of Python (top) and R (bottom) libraries and respective versions installed on the machine.
All the procedures and experiments described in this paper were performed on a Linux workstation equipped with an Intel Core i9-7940X processor with a base frequency of 3.10GHz and a total of 14 cores, 128GB of RAM and Nvidia GTX 1080Ti video cards, with CUDA 10.1 capabilities.
2.5. Experiments
In summary, the main goal of this work is AQI classfication. We tackled this problem by first defining a regression task on each individual pollutant, then merging the results using the index thresholds and computing an overall performance on air quality estimation. Therefore, in the following paragraphs the discussion will first focus on regression results and then move to the classification problem, analysing the estimates of the different models employed. The first regression task was carried out with different evaluation runs performed on each pollutant independently, using the same setup for each target variable with the only exception of particulate matter. In the latter configuration, the training procedure remained the same described below, with the only change of dataset employed, as stated in Section 2.2. For simplicity, in the following paragraphs we refer to the original set of time series with hourly resolution as Hourly Set (HSet), while referring to the daily-averaged data as Daily Set (DSet).
Despite the definition of a standard regression task, special care must be taken in the event of time series data. First, features in the training and test subdivisions are inherently dependent on time, threfore a random selection of a portion of samples cannot be considered a viable option as the temporal dependency must be respected. This is also crucial for training the LSTM model or any recurrent network in general, given their sequential nature.
Additionally, both meteorological trends, transit counts and consequently pollutant measurements are bound to change in the longer period. Considering the available information spanning almost three years, we had to take into account that even the same models may present extremely different results, depending on the training intervals and the test windows selected.
In order to assess the performance of the aforementioned models, we identified 3 folds of equal size over the three year interval, each one subsequently divided into training, validation and test sets. We maintained a continuous timeline in the second subdivision as well, by keeping the first as training, as validation and the remaining as test data. The presence of a validation set is useful to assess the number of iterations required to maximize the performance without overfitting, moreover provides a clear separation between train and test data, avoiding any possible time dependency. Every model was then fitted and evaluated independently and the final results were obtained by averaging the scores over the three splits.
We trained the linear model using the default tolerance threshold , the Random Forest model using 100 base estimators with maximum depth set to 8 to further reduce overfitting and the LSTM model using two layers of 100 hidden cells, using a dropout between hidden and linear layer to improve the generalization, with a drop rate set to . For this last training configuration we used an Adam optimizer with learning rate , iterating for 20 epochs with a batch size of 32. Lastly, the BRNN was initialized using the parameters defined in previous work in order to maintain a comparable setup.
In every testing scenario we employed a Mean Squared Error loss, then we computed on every model two common regression metrics in order to better assess and compare the results. Specifically, we computed the Root Mean Squared Error (RMSE), which better represents the actual error on the test set and the Symmetric Mean Average Percentage Error (sMAPE), which is an error-based measure expressed in percentage and therefore unbound from any value range. Formally these measures can be expressed as in Equation (2).
We precise that our current formulation for the sMAPE does not correspond to a percentage, but we kept a simpler range, where error rate, to improve readability. Completed and evaluated the regression problem, the AQI estimation performance still needs to be investigated. For this task, only a subset of the pollutants need to be taken into consideration, which typically consist of Nitrogen Dioxide (), Ozone () and particulate matter, in most cases referring to . Regarding the AQI, the European Environment Agency (EEA) defined a common metric, named Common Air Quality Index (CAQI), which is described by five different thresholds and computed on the pollutants listed above [31]. A subset of the complete table, including global indices and thresholds for individual pollutants are reported in Table 5.

Table 5.
Common Air Quality Index (CAQI) reference table. Indices of individual pollutants correspond to hourly concentrations (), except for the 24-h index for . The common index is defined as the worst quality among sub-components.
The CAQI can be computed with both hourly and daily concentrations. In order to compute the global index, the maximum value among pollutant concentrations must be taken.
Since our data contained hourly concentrations for every pollutant except particulate matter, we computed the hourly version using the daily mean of , using the ad hoc index provided by the CAQI. In order to evaluate the regression estimates through the AQI, we first computed the ground-truth indices using the real pollutant trends in the test set, then applied the same transformation to the estimated time series produced by the trained models. We defined the latter task as a standard multi-class categorization problem, employing the F1-score as metric for its robustness against unbalanced classes.
3. Results
In this section, the results obtained from the aforementioned tasks are presented. The discussion will first focus on regression results, analysing the advantages and drawbacks of the employed techniques over each pollutant and time window, for both Hourly Set and Daily Set, subsequently the AQI prediction estimates will be presented and assessed.
As summarized in Table 6, the results on the regression task over the pollutants with hourly resolution is in line with expectations. The performance on the Hourly Set without lagged variables, displayed on the columns marked with , highlights on average better results for simpler models: in every case, the best values in terms of RMSE were achieved by the linear model or the Random Forest regressor, with the only exception of where the BRNN obtained a slightly smaller error. The second configuration, indicated by , displays results obtained with lagged variables over a 24-h period. In this case, the longer window allowed the models to reach better estimates in most cases, with a relevant edge of RF in half of the considered pollutants. Here the exceptions are represented by the benzene (), where the linear model outperformed the other solutions, and the ozone (), where the LSTM surpassed the linear regressor by a small margin. These values might be explained by the higher autocorrelation of these two pollutants on the 24-h mark, visible in Table 4, together with the strong periodic patterns of the ozone influenced by solar radiation that could favour sequence-based solutions like LSTM.

Table 6.
Results of the adopted models on the Hourly Set. For each pollutant and model, RMSE and sMAPE metrics are provided, in three different scenarios: no lag, 24-h, and 48-h windows. Results highlighted in bold represent the best performing model w.r.t the pollutant and the window w.
Further increasing the time interval, as summarized in the last column (), does not seem to introduce a relevant advantage over previous solutions, as the error rates computed on the new estimates appear roughly the same. Again, the only exception is represented by the LSTM model, that obtained better results for the majority of pollutants, but most importantly consistently reduced its error with respect to the previous 24-h configuration. Not surprisingly, a deep recurrent neural network can outperform standard machine learning techniques taking advantage of the sequential structure of the data; however, we note that, even in this case, the results are only marginally better than, for instance, the linear regressor. This could be very well caused by the strong limitation on the time interval considered, nevertheless a longer window did not represent a viable comparison because of the feature explosion caused by the introduction of lagged variable in the other configurations.
The results over the Daily Set are shown in Table 7. In this case, we carried out the same evaluation procedure, running the models over the test set and computing the error metrics for each pollutant and estimator, in three different time windows corresponding to lags of one and two days, which are comparable with the 24 and 48-h shifts in the Hourly Set. Unfortunately, due to the lack of data and lower resolution of the available signals, the results are far from optimal, when compared to the hourly counterpart. However, the RMSE values presented are consistent with the data distribution, displayed in Table 8, and both linear and Random Forest regressors display good performances in the setups with window size and . In a similar manner to the Hourly Set, further increasing the interval explored did not translate into better estimates. In the specific case of LSTM, the small dataset with daily resolution was not enough to take advantage of the time series structure and the resulting performance are on par with simpler and faster models.

Table 7.
Results of the selected models on the Daily Set. The results are again presented with RMSE and sMAPE on different time windows, corresponding to no lag, one-day lag and two-days lag.

Table 8.
Descriptor values for target variables.
Given the regression estimates and their performances described in previous paragraphs, we analysed the results on the AQI classification task. In Table 9 the F1-scores resulted from the AQI computation over ground-truth and predicted pollutants are summarised, where each subsection refers to the same configuration of time intervals already applied on the previous tasks. In every subsection, the first columns represent a pollutant p and each row represents a model m. Consequently, each cell contains the F1-score of the Air Quality sub-index (Table 5) obtained from the ground truth of p and the estimates produced my m, on the same testing period of p. The last two columns of every block summarise instead the global AQI, defined as , where each represents a sub-index.

Table 9.
F1-scores obtained on the sub-indices of each pollutant, on the global indices CAQI and CAQI* (without ), using the same configurations with time windows equal to zero, one and two days.
The sub-indices are consistent with the performances described in the regression task: reached on average affordable F1-score, with the Random Forest obtaining the best score around , while was best predicted by the LSTM with F1-Score of . Reflecting the inferior regression performances on the previous analysis, worse performances were instead achieved on by every model in most cases. A few exceptions comprise the models trained on the 48-h window, where the F1-scores on average exceed the threshold, and the linear model on the 24-h configuration. This is again expected, as the lack of data negatively influenced the regression estimates, thus undermining the classification results as well.
Observing the global AQI results, presented in the penultimate column, we can observe the same result degradation caused by the bad estimates generated by some estimators. For this very reason, we introduced a last column identified with that presents the same global CAQI calculations, excluding the last pollutant, specifically . Despite its lack of practical use, this external measure allows for better assessments of the information loss (or gain) brought by the additional pollutant. From this last column it is possible to observe that, in the vast majority of the combinations, a decent AQI estimation is possible, within limits. Moreoever, the introduction of a lagged interval can be beneficial in some cases, especially for sequence-based solutions such as LSTM. Nevertheless, as already verified within the regression problem, a window size of 24 is sufficient to raise the estimates by a margin in terms of F1-score. On the other hand, standard machine learning models do not benefit as much from the introduction of lagged features, since for instance the RF solution can perform equally well in all the three interval setups.
Both the linear model on and the LSTM on obtain very good CAQI estimates around , thanks to better performances over the single pollutants, but most importantly thanks to better estimations over . Comparing the global score to the adjusted AQI, we can see that the absence of drastically reduces the results. The confusion matrices derived by these two solutions are reported in Figure 5 (linear and LSTM indicated by a and b respectively), together with an ensemble solution (c): this last configuration was achieved by selecting the best regressors over each pollutant. Specifically, we selected the RF regressor with 48-h configuration for , the LSTM with -hour configuration for and lastly the linear model over 24-h period as estimator for . This last ensemble allowed us to achieve a total F1-score , surpassing the single-model solutions achieved so far.
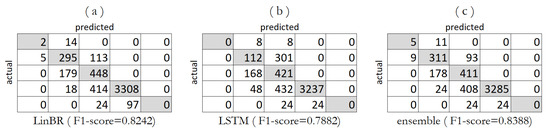
Figure 5.
CAQI Confusion matrices of the best models, specifically (a) the linear model (LinBR, w = 24), (b) the LSTM model (LSTM, w = 48) and (c) an "ensemble" result, given by using the best predictors for each pollutant: RF for , LSTM for , LinBR for .
In order to justify the extreme disparity between these higher scores and the extremely low estimates achieved in some cases, we note that the AQI results are strongly influenced by factors: (i) the air quality thresholds in Table 5 are not equally spaced, but the intervals between categories become wider with the increase of the pollutant measurements; (ii) the computed AQI presents a decreasing granularity and inherent class imbalance; in particular, the first levels are represented by a small fraction of samples, while higher levels contain the majority of the data points. This is clearly visible in the confusion matrices, where the AQI level 4 () contains more than 3000 instances.
4. Conclusions
This work presents a simple yet effective approach to air quality estimation in urban areas from local environmental an traffic information. We demonstrated that good estimates can be provided for most pollutants by only exploiting meteorological features, such as temperature and humidity, and urban-related features, such as vehicle transits, thanks to the strong correlations among them. Moreover, we thoroughly tested different classes of machine learning models, specifically a linear regressor and a Multi-Layer Perceptron with Bayesian regularization, a Random Forest regressor and a Long-Short Term Memory network. We demonstrated that decent results can still be achieved by simpler models, provided that a robust preprocessing and engineering phase is carried out on the available data. In fact, the linear model achieved scores comparable to more complex solutions such as RF and LSTM, especially when considering shorter window dimensions. For instance, the linear model obtained an F-measure of , and over the individual AQI sub-indices, that amounted to F1-score for the global AQI in the 24-h window configuration. Notably, the linear model surpassed any other solution by a large margin when considering daily measurements of and , where training data was scarce. For these reasons, this solution can be considered a robust lightweight option in the case of limited resources. Nevertheless, when the latter are available, deep recurrent neural networks such as LSTM can provide a relevant edge in terms of estimation performance, as their inherently sequential structure allow for the examination of longer time periods. This can lead to equal or even better results than standard approaches, as demonstrated by the consistently lower RMSE in most hourly pollutants over the 48-h windows. Despite the heavier computational demands, LSTM does not require extensive preprocessing phases such as the introduction of lagged variables, as the sequence length can be trivially modified. Therefore, LSTM-based solution can be considered a valid and versatile option for many different use cases.
Compared to most part of the literature where time series of air pollutants are included in the estimation for future forecasts, our approach provides results that are almost on par with other works. However, it has the advantage of providing AQI estimates in a completely sensor-free scenario, thus suggesting a an alternative methodology that can first of all reduce the costs for professional equipment and its maintenance. Furthermore, this technique can be applied in any urban region, after a prior calibration based on a small ground truth of sensor data.
Future works will involve satellite monitoring to expand the predictions on larger areas. For this task, coarser but more comprehensive aerial information could be exploited, such as data related to air pollutants provided by the Copernicus Sentinel-5P mission by Copernicus, a European project in collaboration with ESA for atmosphere monitoring. The latter could allow a more fine-grained estimation on larger areas, without the need for detailed on-ground measurements.
Author Contributions
Conceptualization, E.A., C.R., and A.F.; methodology, E.A., A.F., and C.R.; software, E.A.; validation, A.F. and C.R.; formal analysis, E.A.; data curation, E.A.; writing—original draft preparation, E.A. and A.F.; writing—review and editing, A.F. and C.R.; visualization, E.A.; supervision, A.F. and C.R.; project administration, C.R.; funding acquisition, C.R. All authors have read and agreed to the published version of the manuscript.
Funding
The APC was funded by LINKS Foundation.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Correlation Matrix Matrices among Features from the Same Domain
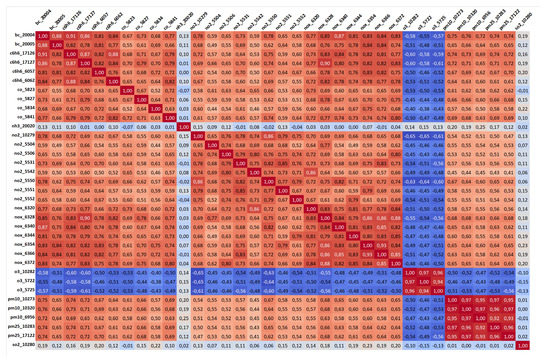
Figure A1.
Correlation among unique pollutant sensors.
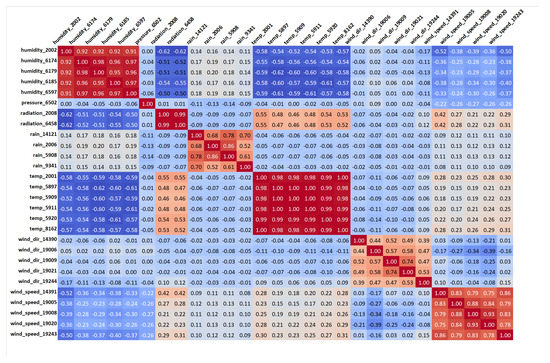
Figure A2.
Correlation matrix among unique weather sensors.
References
- Brunekreef, B.; Holgate, S.T. Air pollution and health. Lancet 2002, 360, 1233–1242. [Google Scholar] [CrossRef]
- World Health Organization. 7 million Premature Deaths Annually Linked to Air Pollution; World Health Organization: Geneva, Switzerland, 2014. [Google Scholar]
- World Health Organization. Global Status Report on Road Safety 2018; World Health Organization: Geneva, Switzerland, 2018. [Google Scholar]
- World Health Assembly. Health, Environment and Climate Change: Report by the Director-General; World Health Assembly: Geneva, Switzerland, 2018; 7p. [Google Scholar]
- De Sario, M.; Katsoujanni, K.; Michelozzi, P. Climate change, extreme weather events, air pollution and respiratory health in Europe. Eur. Respir. J. Off. J. Eur. Soc. Clin. Respir. Physiol. 2013, 42, 826–843. [Google Scholar] [CrossRef] [PubMed]
- Vanos, J.; Cakmak, S.; Kalkstein, L.; Yagouti, A. Association of weather and air pollution interactions on daily mortality in 12 Canadian cities. Air Qual. Atmos. Health 2015, 8, 307–320. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Chen, R.; Sera, F.; Vicedo-Cabrera, A.M.; Guo, Y.; Tong, S.; Coelho, M.S.; Saldiva, P.H.; Lavigne, E.; Matus, P.; et al. Ambient particulate air pollution and daily mortality in 652 cities. N. Engl. J. Med. 2019, 381, 705–715. [Google Scholar] [CrossRef] [PubMed]
- Jacob, D.J.; Winner, D.A. Effect of climate change on air quality. Atmos. Environ. 2009, 43, 51–63. [Google Scholar] [CrossRef]
- Battista, G.; de Lieto Vollaro, R. Correlation between air pollution and weather data in urban areas: Assessment of the city of Rome (Italy) as spatially and temporally independent regarding pollutants. Atmos. Environ. 2017, 165, 240–247. [Google Scholar] [CrossRef]
- Sampson, P.D.; Szpiro, A.A.; Sheppard, L.; Lindström, J.; Kaufman, J.D. Pragmatic estimation of a spatio-temporal air quality model with irregular monitoring data. Atmos. Environ. 2011, 45, 6593–6606. [Google Scholar] [CrossRef]
- Kolehmainen, M.; Martikainen, H.; Ruuskanen, J. Neural networks and periodic components used in air quality forecasting. Atmos. Environ. 2001, 35, 815–825. [Google Scholar] [CrossRef]
- Zheng, Y.; Liu, F.; Hsieh, H.P. U-Air: When Urban Air Quality Inference Meets Big Data. In Proceedings of the 19th SIGKDD Conference on Knowledge Discovery and Data Mining (KDD 2013), Chicago, IL, USA, 11–14 August 2013. [Google Scholar]
- Cheng, W.; Shen, Y.; Zhu, Y.; Huang, L. A Neural Attention Model for Urban Air Quality Inference: Learning the Weights of Monitoring Stations. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Zheng, Y.; Yi, X.; Li, M.; Li, R.; Shan, Z.; Chang, E.; Li, T. Forecasting Fine-Grained Air Quality Based on Big Data. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; Association for Computing Machinery: New York, NY, USA, 2015; pp. 2267–2276. [Google Scholar] [CrossRef]
- Rossi, C.; Farasin, A.; Falcone, G.; Castelluccio, C. A Machine Learning Approach to Monitor Air Quality from Traffic and Weather data. In Proceedings of the 2019 European Conference on Ambient Intelligence, Rome, Italy, 13–15 November 2019; Volume 2492, pp. 66–74. [Google Scholar]
- Flach, P. Machine Learning: The Art and Science of Algorithms That Make Sense of Data; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Tsai, Y.; Zeng, Y.; Chang, Y. Air Pollution Forecasting Using RNN with LSTM. In Proceedings of the 2018 IEEE 16th International Conference on Pervasive Intelligence and Computing (DASC), Athens, Greece, 12–15 August 2018; pp. 1074–1079. [Google Scholar]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Basagaña, X.; Triguero-Mas, M.; Agis, D.; Pérez, N.; Reche, C.; Alastuey, A.; Querol, X. Effect of public transport strikes on air pollution levels in Barcelona (Spain). Sci. Total Environ. 2018, 610–611, 1076–1082. [Google Scholar] [CrossRef] [PubMed]
- Zimmerman, N.; Presto, A.A.; Kumar, S.P.; Gu, J.; Hauryliuk, A.; Robinson, E.S.; Robinson, A.L.; Subramanian, R. A machine learning calibration model using random forests to improve sensor performance for lower-cost air quality monitoring. Atmos. Meas. Tech. 2018, 11, 291–313. [Google Scholar] [CrossRef]
- Yu, R.; Yang, Y.; Yang, L.; Han, G.; Move, O.A. RAQ–A random forest approach for predicting air quality in urban sensing systems. Sensors 2016, 16, 86. [Google Scholar] [CrossRef] [PubMed]
- Singh, K.P.; Gupta, S.; Rai, P. Identifying pollution sources and predicting urban air quality using ensemble learning methods. Atmos. Environ. 2013, 80, 426–437. [Google Scholar] [CrossRef]
- Huang, C.J.; Kuo, P.H. A Deep CNN-LSTM Model for Particulate Matter (PM(2.5)) Forecasting in Smart Cities. Sensors 2018, 18, 2220. [Google Scholar] [CrossRef] [PubMed]
- Bui, T.; Le, V.; Cha, S. A Deep Learning Approach for Air Pollution Forecasting in South Korea Using Encoder-Decoder Networks & LSTM. arXiv 2018, arXiv:1804.07891. [Google Scholar]
- McKinney, W. Data Structures for Statistical Computing in Python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010. [Google Scholar] [CrossRef]
- Oliphant, T. NumPy: A Guide to NumPy; Trelgol Publishing: Spanish Fork, UT, USA, 2006. [Google Scholar]
- Seabold, S.; Perktold, J. Statsmodels: Econometric and statistical modeling with python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Advances in Neural Information Processing Systems 32; Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2019; pp. 8024–8035. [Google Scholar]
- Van den Elshout, S.; Léger, K.; Heich, H. CAQI common air quality index—Update with PM2. 5 and sensitivity analysis. Sci. Total Environ. 2014, 488, 461–468. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).