Flow Visualization of Spinning and Nonspinning Soccer Balls Using Computational Fluid Dynamics
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods
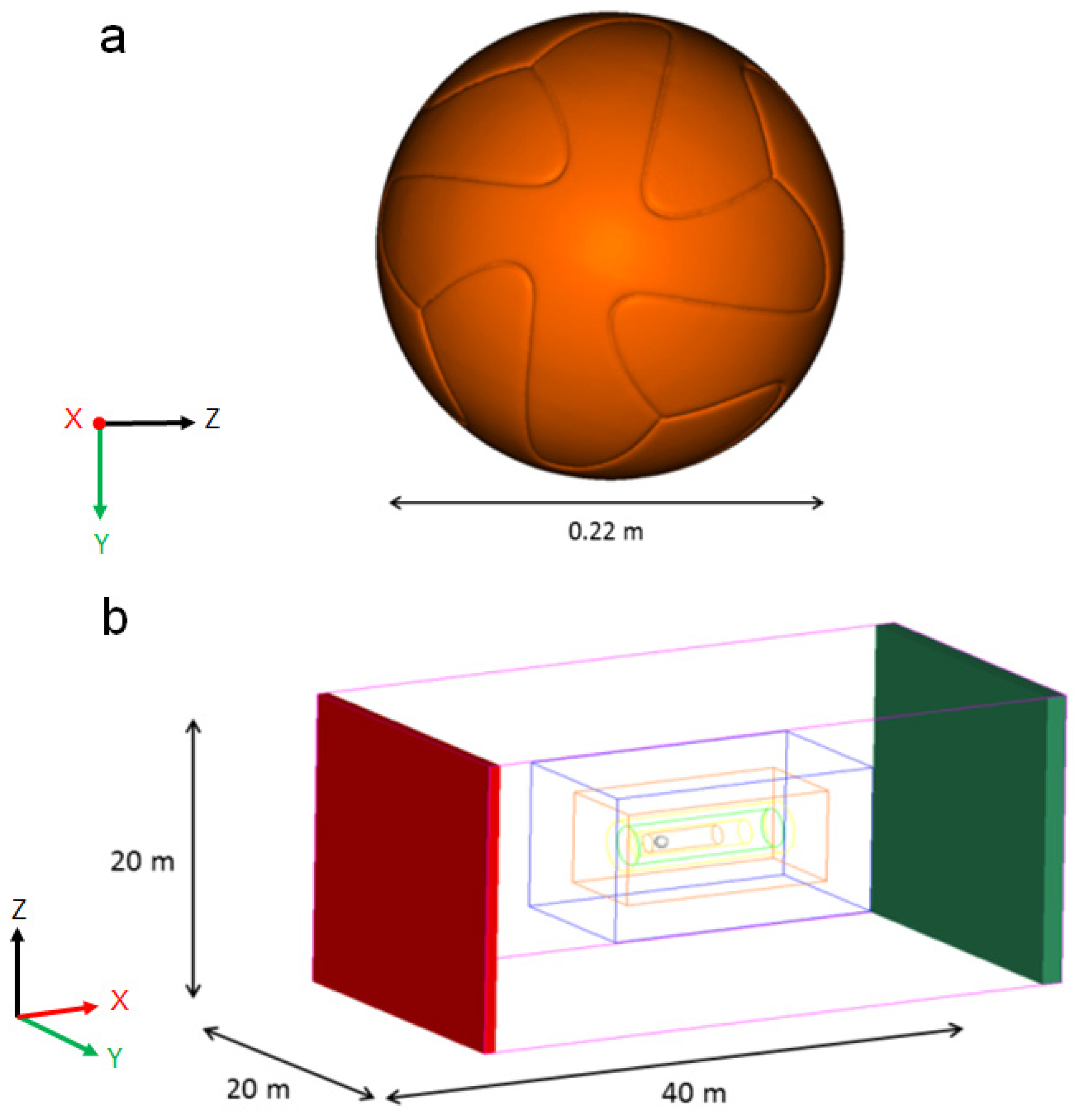
2.1. CFD Analysis Using the Lattice Boltzmann Method
2.2. Wind Tunnel Test
2.3. Free-Flight Test
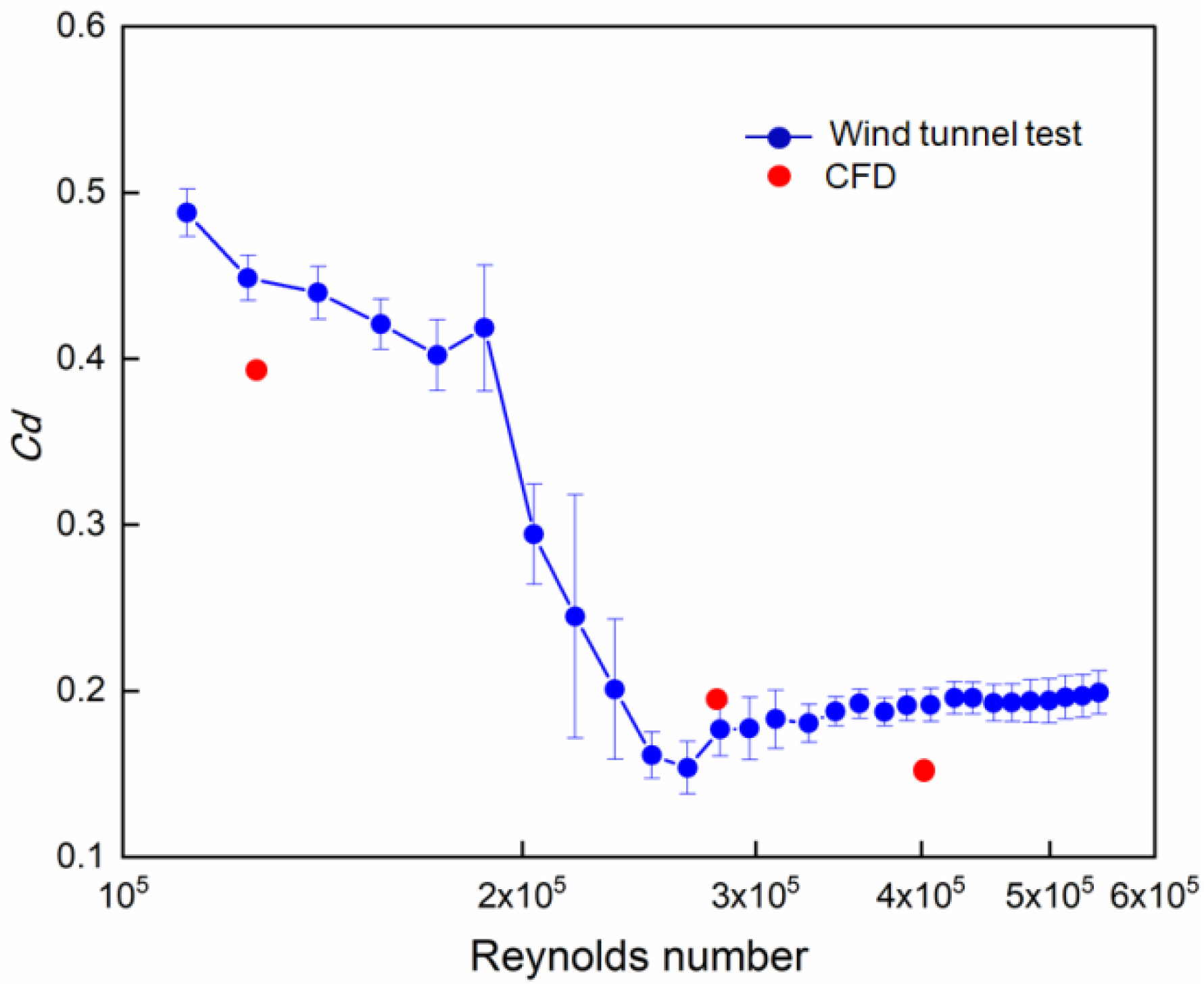
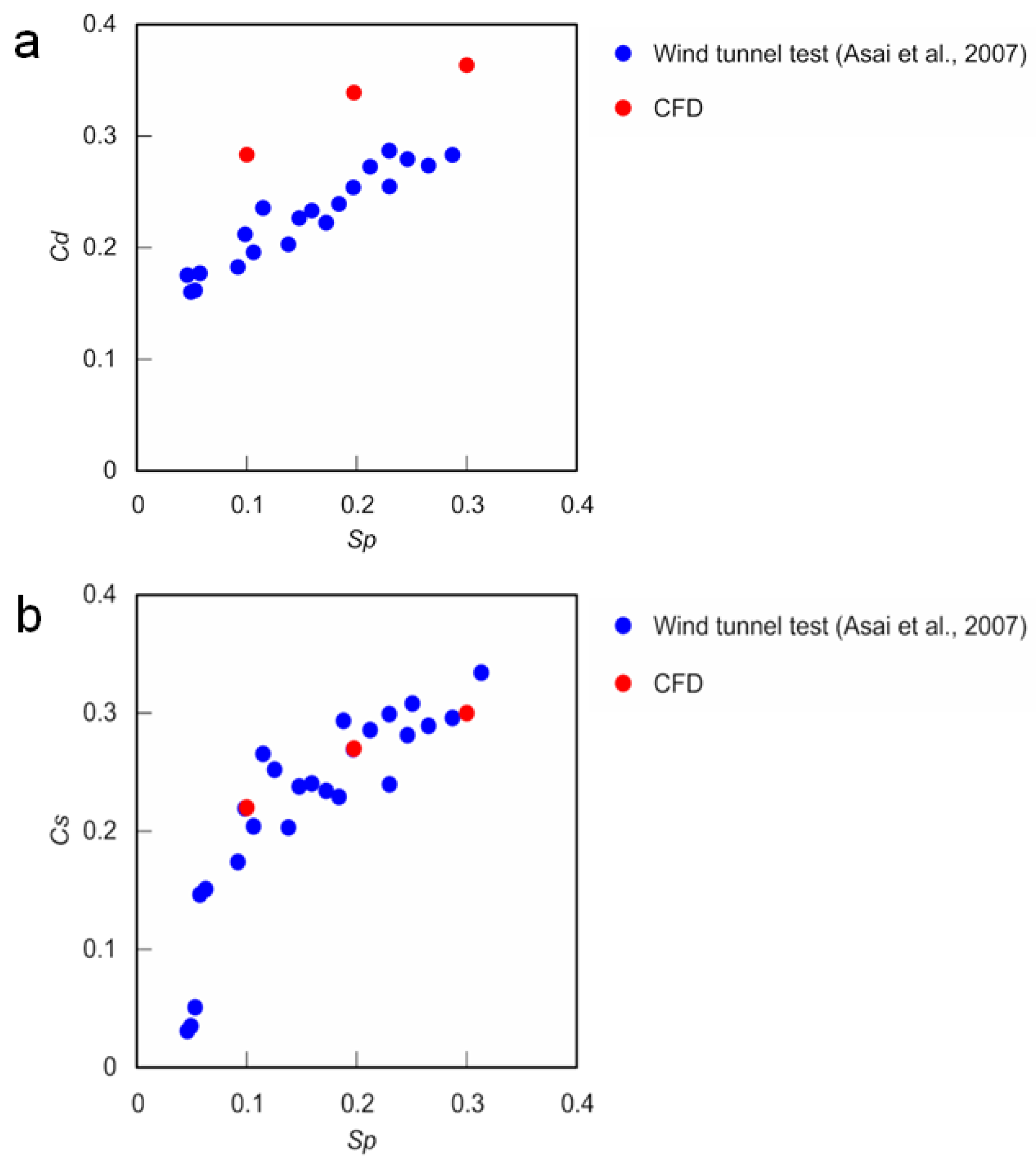
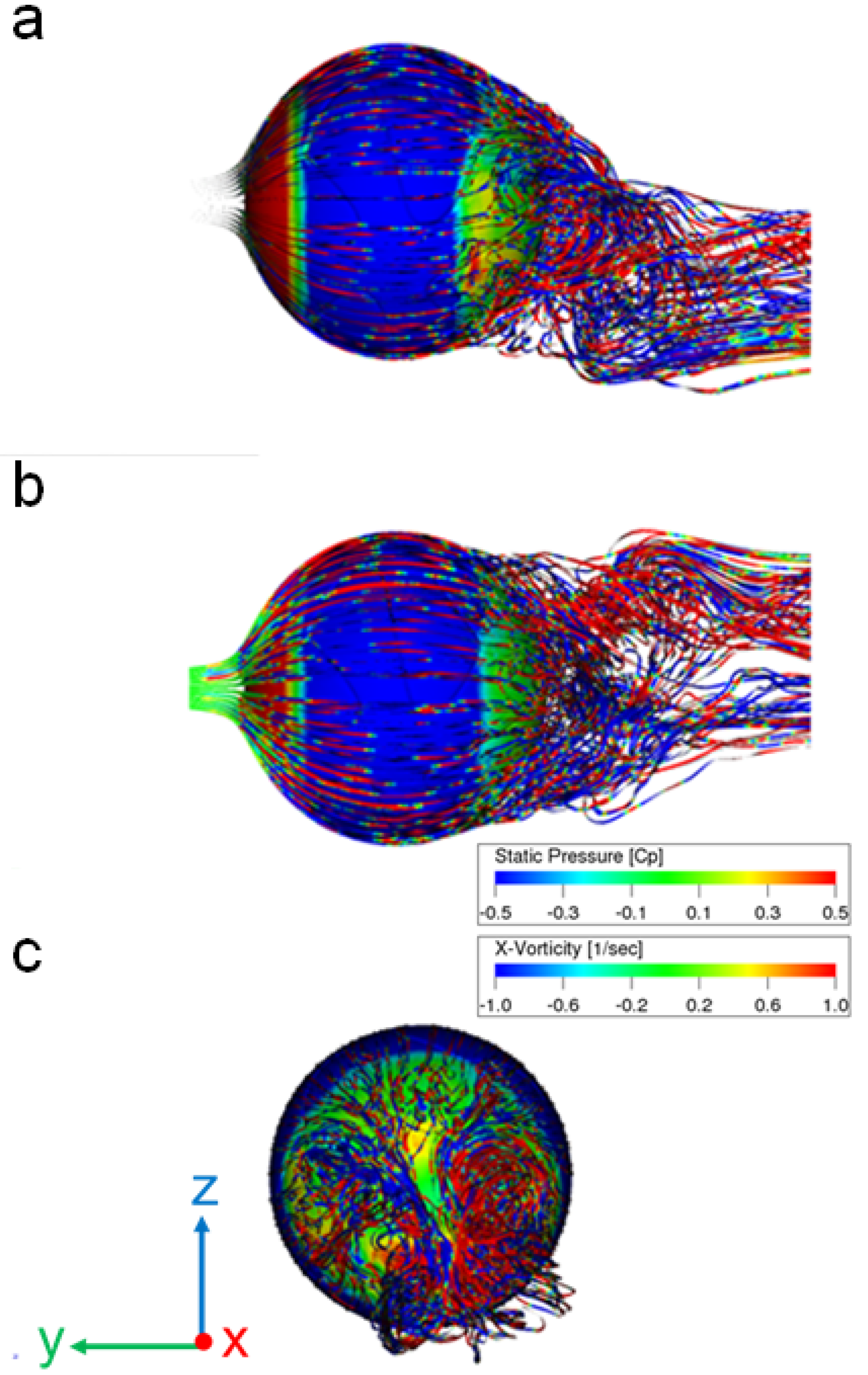
3. Results and Discussion
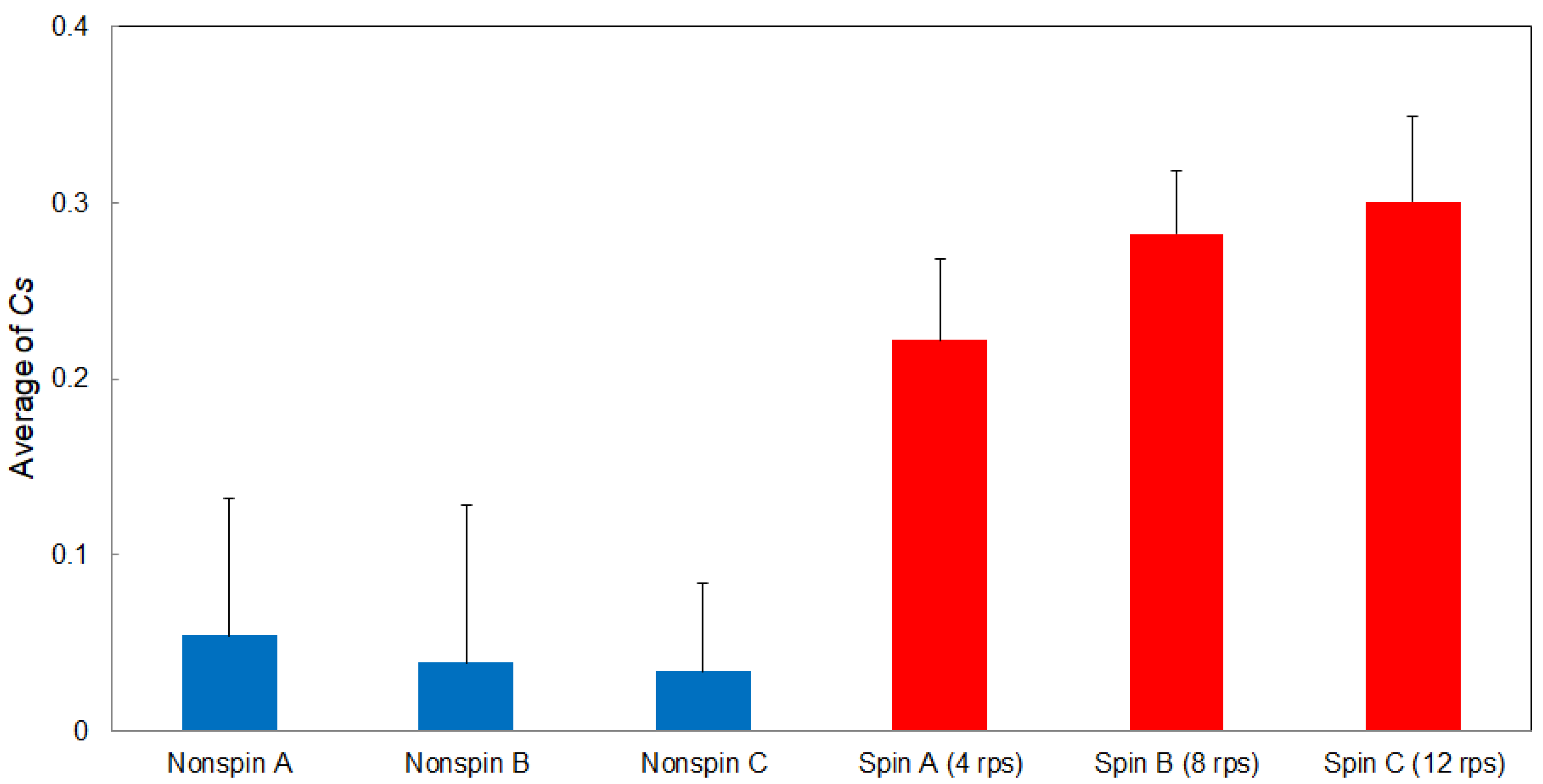
3.1. Steady Cd and Cs Obtained from CFD
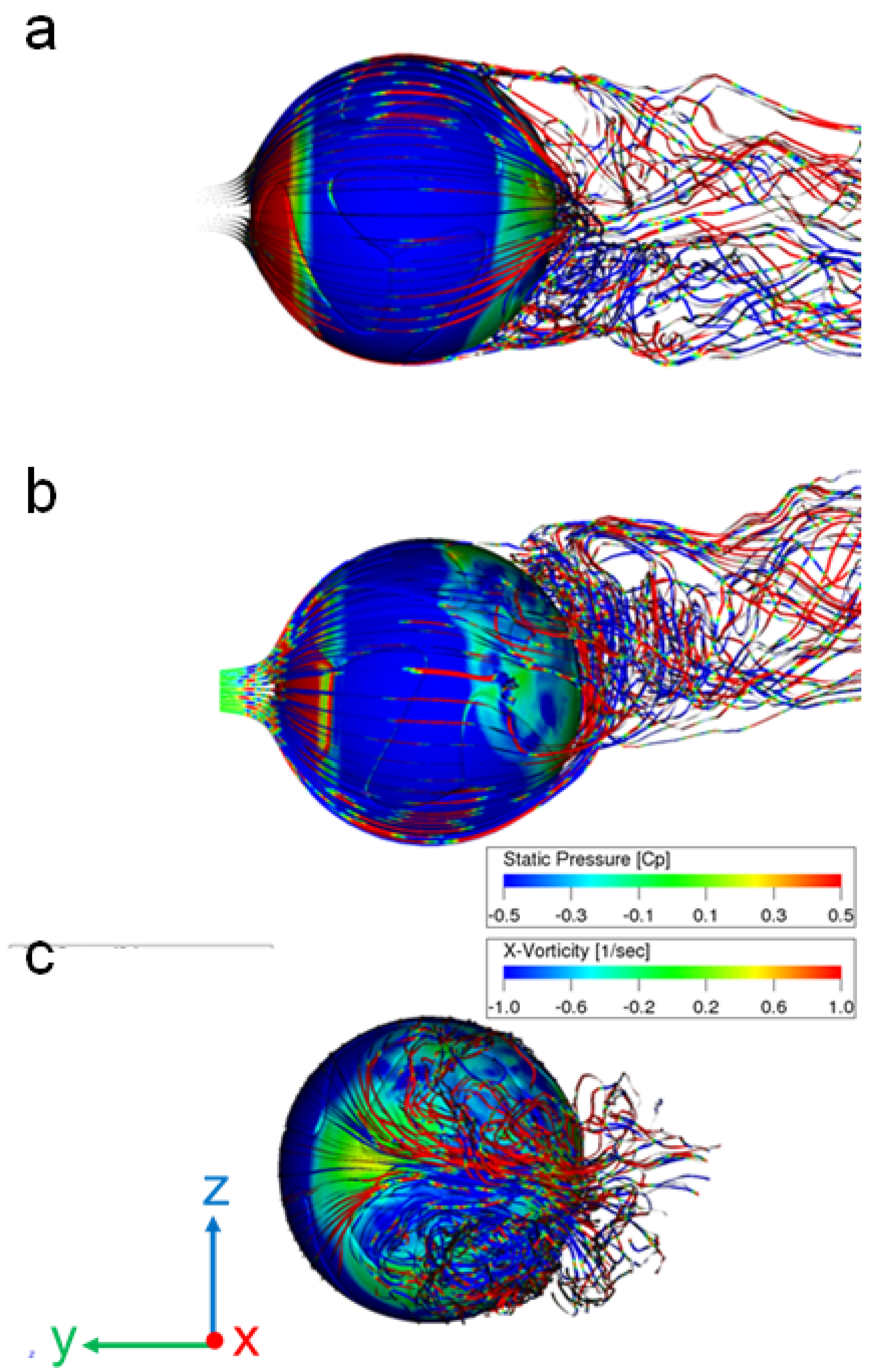
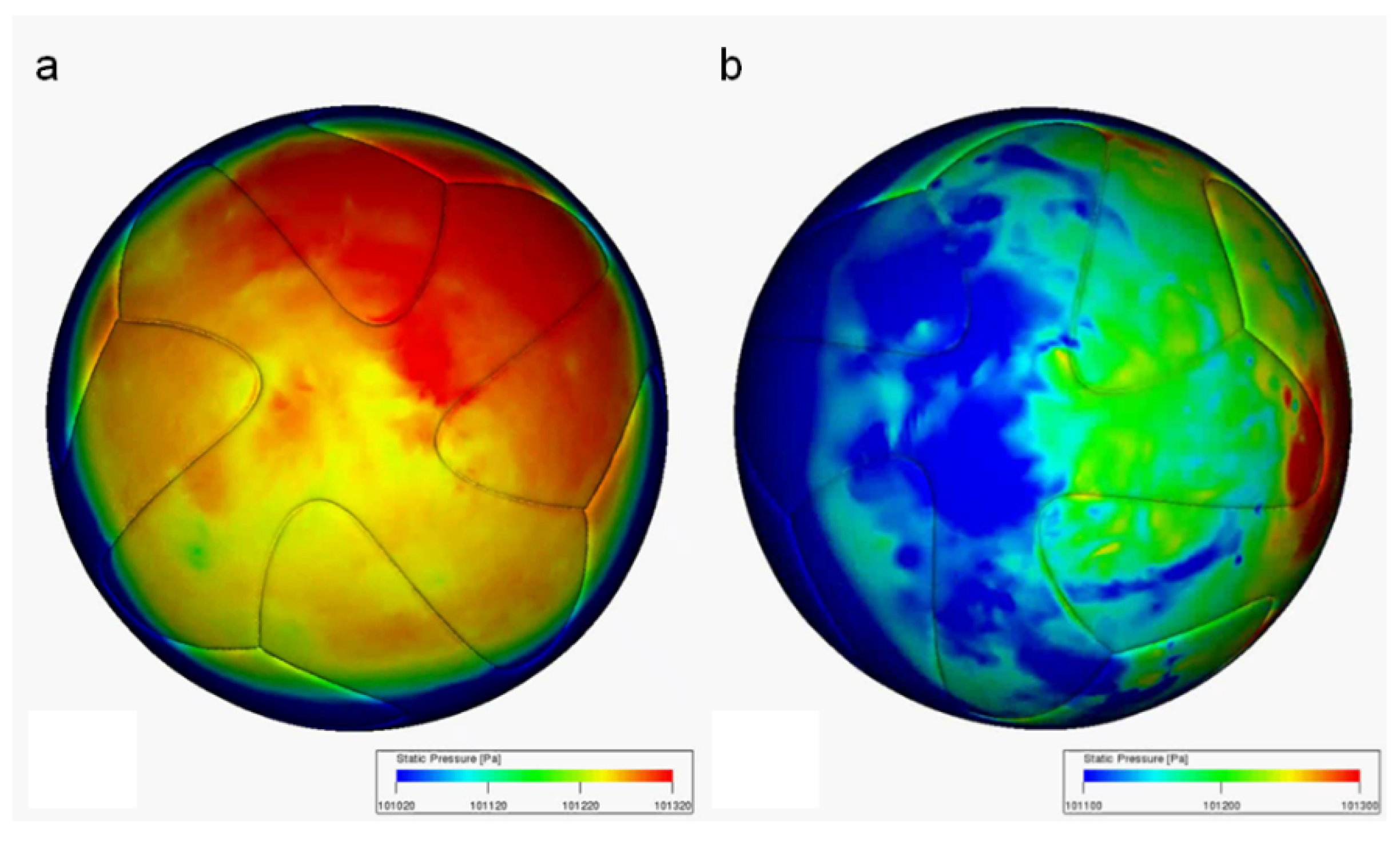
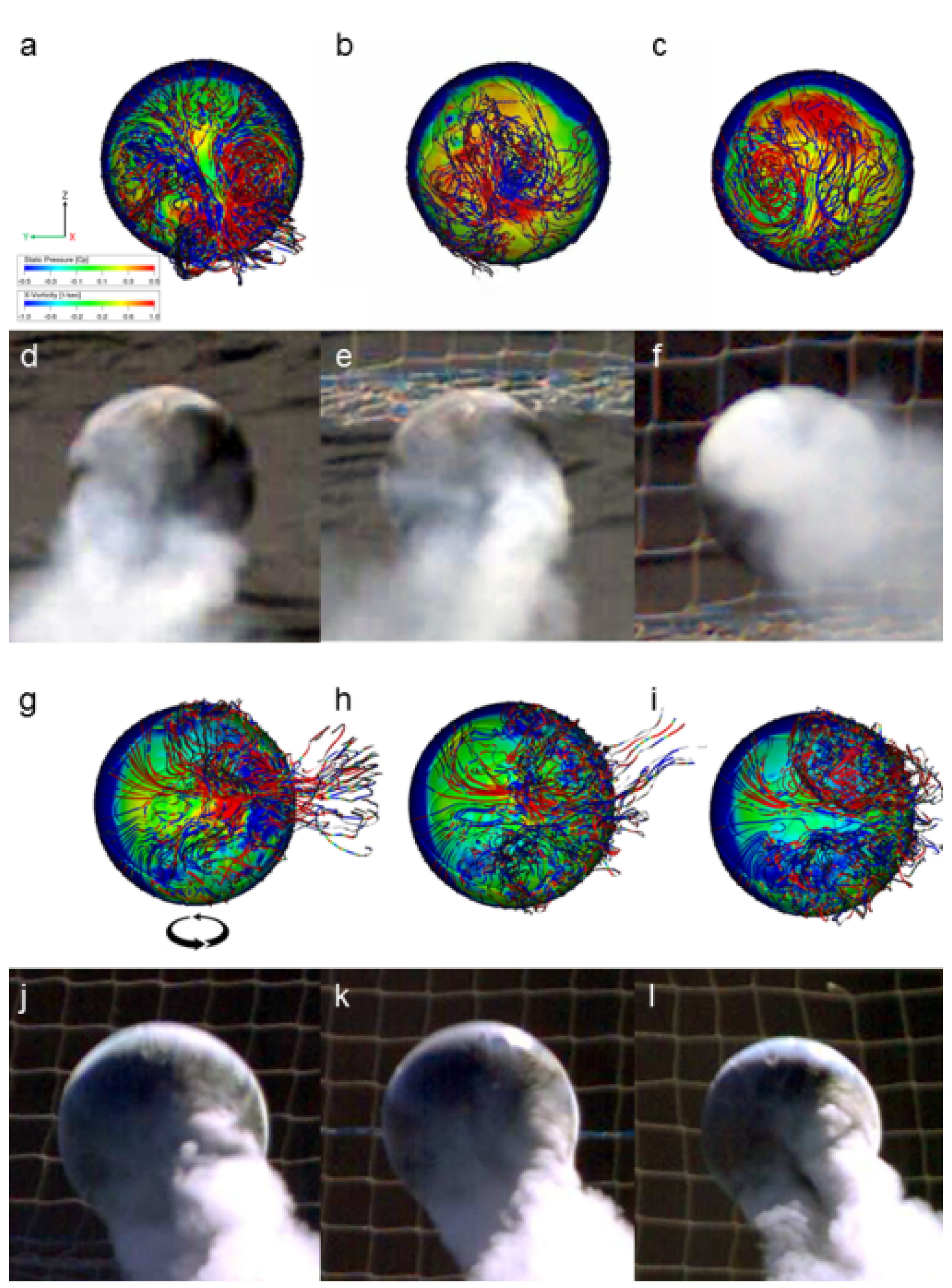
3.2. Flow Visualization from CFD
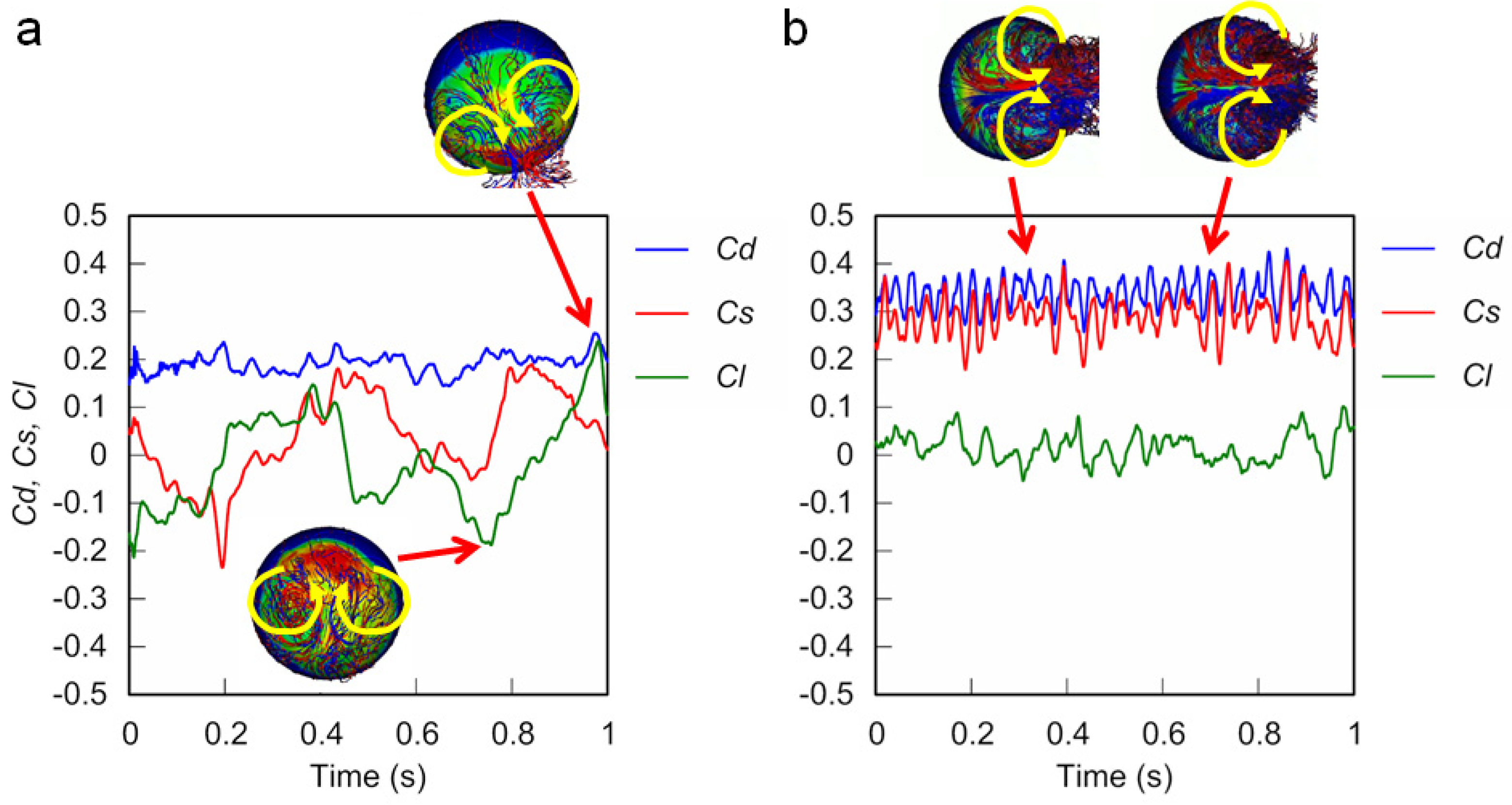
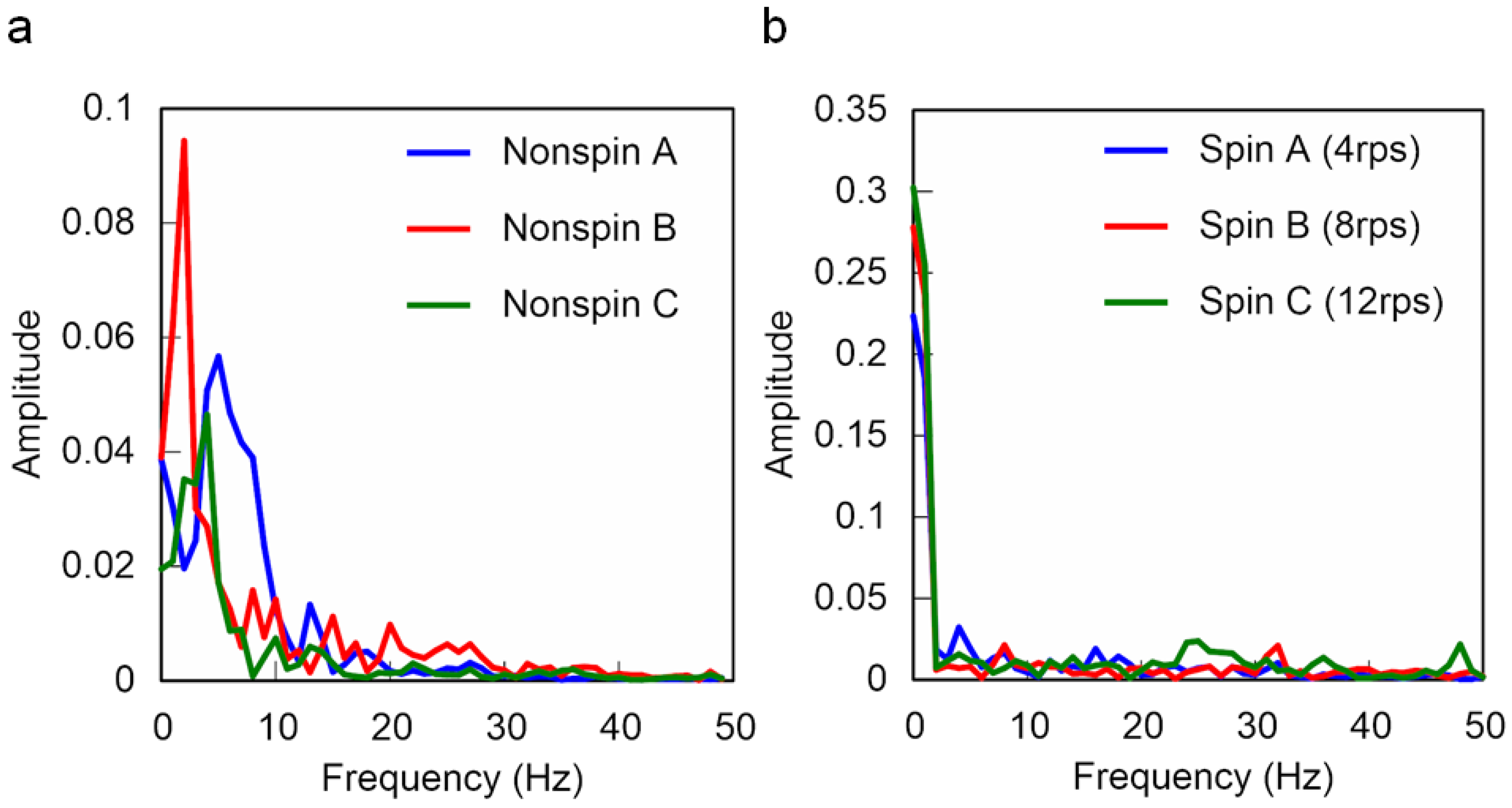
3.3. Unsteady Cd, Cs, and Cl Obtained using CFD
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Thomson, J.J. The dynamics of a golf ball. Nature 1910, 85, 2151–2157. [Google Scholar]
- Mehta, R.D.; Bentley, K.; Proudlove, M.; Varty, P. Factors affecting cricket ball swing. Nature 1983, 303, 787–788. [Google Scholar] [CrossRef]
- Davies, J.M. The aerodynamics of golf balls. J. Appl. Phys. 1949, 20, 821–828. [Google Scholar] [CrossRef]
- Bearman, P.W.; Harvey, J.K. Golf ball aerodynamics. Aeronaut. Q. 1976, 27, 112–122. [Google Scholar] [CrossRef]
- Watts, R.G.; Sawyer, E. Aerodynamics of a knuckleball. Am. J. Phys. 1975, 43, 960–963. [Google Scholar] [CrossRef]
- Watts, R.G.; Ferrer, R. The lateral force on a spinning sphere: Aerodynamics of a curveball. Am. J. Phys. 1987, 55, 40–44. [Google Scholar] [CrossRef]
- Štěpánek, A. The aerodynamics of tennis balls: The topspin lob. Am. J. Phys. 1988, 56, 138–142. [Google Scholar] [CrossRef]
- Wei, Q.; Lin, R.; Liu, Z. Vortex-induced dynamics loads on a non-spinning volleyball. Fluid Dyn. Res. 1988, 3, 231–237. [Google Scholar] [CrossRef]
- Mehta, R.D. Aerodynamics of sports balls. Annu. Rev. Fluid Mech. 1985, 17, 151–189. [Google Scholar] [CrossRef]
- Higuchi, H.; Kiura, T. Aerodynamics of knuckleball: Flow-structure interaction problem on a pitched baseball without spin. J. Fluid. Struct. 2012, 32, 65–77. [Google Scholar] [CrossRef]
- Hong, S.; Asai, T.; Seo, K. Visualization of air flow around soccer ball using a particle image velocimetry. Sci. Rep. 2015, 5, 15108. [Google Scholar] [CrossRef]
- Achenbach, E. Vortex shedding from spheres. J. Fluid Mech. 1974, 62, 209–221. [Google Scholar] [CrossRef]
- Saffman, P.G. Vortex Dynamics; Cambridge University Press: Cambridge, UK, 1992; ISBN 0960-2933. [Google Scholar]
- Leweke, T.; Dizès, S.L.; Williamson, C.H.K. Dynamics and instabilities of vortex pairs. Annu. Rev. Fluid Mech. 2016, 48, 1–35. [Google Scholar] [CrossRef]
- Widnall, S.E. The stability of a helical vortex filament. J. Fluid Mech. 1972, 54, 641–663. [Google Scholar] [CrossRef]
- Taneda, S. Visual observations of the flow past a sphere at Reynolds numbers between 104 and 106. J. Fluid Mech. 1978, 85, 187–192. [Google Scholar] [CrossRef]
- Makita, H. Forefront of wind-tunnel experiment on turbulence structure. J. Fluid Sci. Technol. 2007, 2, 525–534. [Google Scholar] [CrossRef][Green Version]
- Sengupta, K.T.; Singh, N.; Suman, V.K. Dynamical system approach to instability of flow past a circular cylinder. J. Fluid Mech. 2010, 656, 82–115. [Google Scholar] [CrossRef]
- Asai, T.; Seo, K.; Kobayashi, O.; Sakashita, R. Fundamental aerodynamics of the soccer ball. Sports Eng. 2007, 10, 101–109. [Google Scholar] [CrossRef]
- Passmore, M.; Spencer, A.; Tuplin, S.; Jones, R. Experimental studies of the aerodynamics of spinning and stationary footballs. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2008, 222, 195–205. [Google Scholar] [CrossRef]
- Goff, J.E.; Smith, W.H.; Carré, M.J. Football boundary-layer separation via dust experiments. Sports Eng. 2011, 14, 139–146. [Google Scholar] [CrossRef]
- Carré, M.J.; Asai, T.; Akatsuka, T.; Haake, S.J. The curve kick of a football II: Flight through the air. Sports Eng. 2002, 5, 183–192. [Google Scholar] [CrossRef]
- Kray, T.; Franke, J.; Frank, W. Magnus effect on a rotating soccer ball at high Reynolds numbers. J. Wind Eng. Ind. Aerodyn. 2014, 124, 46–53. [Google Scholar] [CrossRef]
- Barber, S.; Chin, S.B.; Carré, M.J. Sports ball aerodynamics: A numerical study of the erratic motion of soccer balls. Comput. Fluids 2009, 38, 1091–1100. [Google Scholar] [CrossRef][Green Version]
- Jalilian, P.; Kreun, P.K.; Makhmalbaf, M.M.; Liou, W.W. Computational aerodynamics of baseball, soccer ball and volleyball. Am. J. Sports Sci. 2014, 2, 115–121. [Google Scholar] [CrossRef]
- Chen, H. Volumetric formulation of the lattice Boltzmann method for fluid dynamics: Basic concept. Phys. Rev. E 1998, 58, 3955–3963. [Google Scholar] [CrossRef]
- Fares, E.; Nölting, S. Unsteady flow simulation of a high-lift configuration using a lattice Boltzmann approach. In Proceedings of the 49th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2011; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2011. AIAA 2011-869. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Cortelezzi, L.; Karagozian, A.R. On the formation of the counter-rotating vortex pair in transverse jets. J. Fluid Mech. 2001, 446, 347–373. [Google Scholar] [CrossRef]
- Devenport, W.J.; Rife, M.C.; Liapis, S.I.; Follin, G.J. The structure and development of a wing-tip vortex. J. Fluid Mech. 1996, 312, 67–106. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Proc. R. Soc. A Math. Phys. Eng. Sci. 1991, 434, 9–13. [Google Scholar] [CrossRef]
- Kotapati, R.; Keating, A.; Kandasamy, S.; Duncan, B.; Shock, R.; Chen, H. The lattice-Boltzmann-VLES method for automotive dynamics simulation, a review. SAE Tech. Pap. 2009, 26, 57. [Google Scholar] [CrossRef]
- Sun, C.; Zhang, R.; Chen, H. A PDE Sliding Mesh Algorithm for Turbulent Flow Simulations with PowerFLOW; Technical report EXA Corporation: Boston, MA, USA, 2009. [Google Scholar]
- Passmore, M.; Tuplin, S.; Stawski, A. The real-time measurement of football aerodynamic loads under spinning conditions. Proc. Inst. Mech. Eng. Part P J. Sports Eng. Technol. 2017, 231, 262–274. [Google Scholar] [CrossRef]
- Asai, T.; Seo, K. Aerodynamic drag of modern soccer balls. Springer Plus 2013, 2, 171. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Hong, S.; Asai, T. Effect of panel shape of soccer ball on its flight characteristics. Sci. Rep. 2014, 4, 5068. [Google Scholar] [CrossRef] [PubMed]
- Passmore, M.; Rogers, D.; Tuplin, S.; Harland, A.; Lucas, T.; Holmes, C. The aerodynamic performance of a range of FIFA-approved footballs. Proc. Inst. Mech. Eng. Part P J. Sports Eng. Technol. 2012, 226, 61–70. [Google Scholar] [CrossRef]
- Goverdhan, R.N.; Williamson, C.H.K. Vortex induced vibrations of a sphere. J. Fluid Mech. 2005, 531, 11–47. [Google Scholar] [CrossRef]
- Asai, T.; Kamemoto, K. Flow structure of knuckling effect in footballs. J. Fluid. Struct. 2011, 27, 727–733. [Google Scholar] [CrossRef][Green Version]
- Benjamin, B. Theory of the vortex breakdown phenomenon. J. Fluid Mech. 1962, 14, 593–629. [Google Scholar] [CrossRef]
- Lucca-Negro, O.; O’Doherty, T. Vortex breakdown: A review. Prog. Energy Combust. Sci. 2001, 27, 431–481. [Google Scholar] [CrossRef]
- Ortega, J.M.; Bristol, R.L.; Savaş, Ö. Experimental study of the instability of unequal-strength counter-rotating vortex pairs. J. Fluid Mech. 2003, 474, 35–84. [Google Scholar] [CrossRef]
- Mizota, T.; Kurogi, K.; Ohya, Y.; Okajima, A.; Naruo, T.; Kawamura, Y. The strange flight behaviour of slowly spinning soccer balls. Sci. Rep. 2013, 3, 1871. [Google Scholar] [CrossRef]
- Capone, A.; Klein, C.; Felice, F.D.; Miozzi, M. Phenomenology of a flow around a circular cylinder at subcritical and critical Reynolds numbers. Phys. Fluids 2016, 28, 74101. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asai, T.; Nakanishi, Y.; Akiyama, N.; Hong, S. Flow Visualization of Spinning and Nonspinning Soccer Balls Using Computational Fluid Dynamics. Appl. Sci. 2020, 10, 4543. https://doi.org/10.3390/app10134543
Asai T, Nakanishi Y, Akiyama N, Hong S. Flow Visualization of Spinning and Nonspinning Soccer Balls Using Computational Fluid Dynamics. Applied Sciences. 2020; 10(13):4543. https://doi.org/10.3390/app10134543
Chicago/Turabian StyleAsai, Takeshi, Yasumi Nakanishi, Nakaba Akiyama, and Sungchan Hong. 2020. "Flow Visualization of Spinning and Nonspinning Soccer Balls Using Computational Fluid Dynamics" Applied Sciences 10, no. 13: 4543. https://doi.org/10.3390/app10134543
APA StyleAsai, T., Nakanishi, Y., Akiyama, N., & Hong, S. (2020). Flow Visualization of Spinning and Nonspinning Soccer Balls Using Computational Fluid Dynamics. Applied Sciences, 10(13), 4543. https://doi.org/10.3390/app10134543





