A Linear Programming Method for Finding a Minimal Set of Axial Lines Representing an Entire Geometry of Building and Urban Layout
Abstract
1. Introduction
2. Background
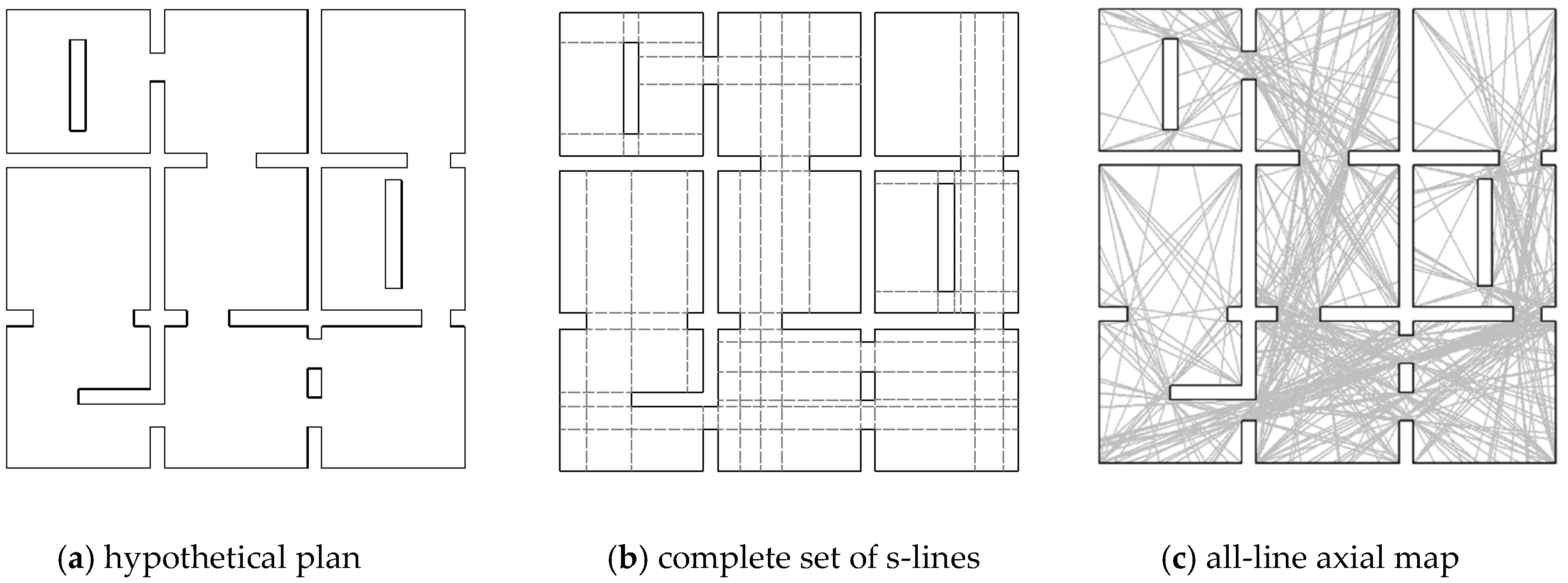
2.1. Axial Line Analysis Computation
2.2. Linear Programming
3. Methods
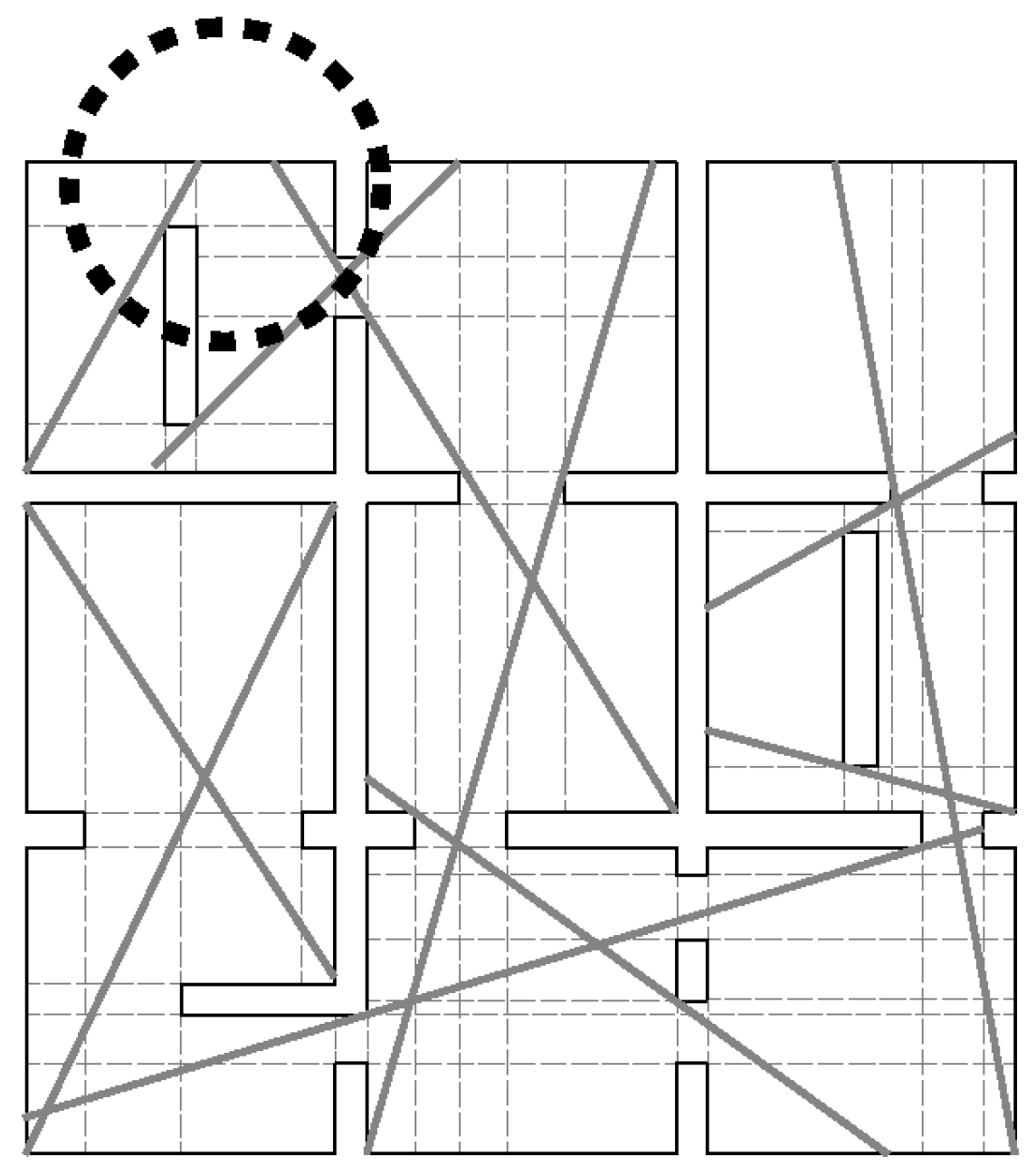
4. Problem Formulation
5. Implementation
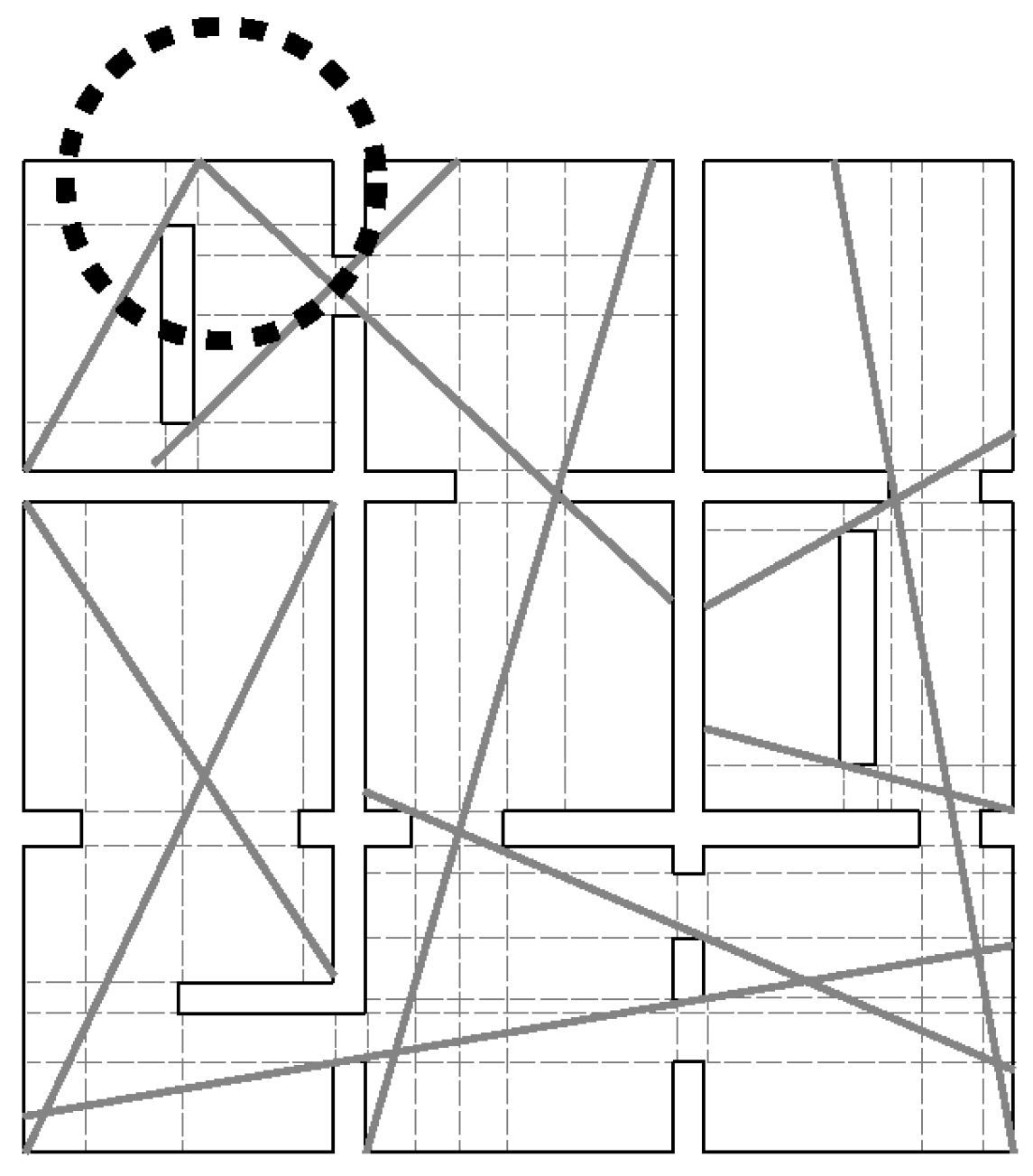
5.1. Problem-Solution Procedure
5.2. Modified Problem-Solution Procedure
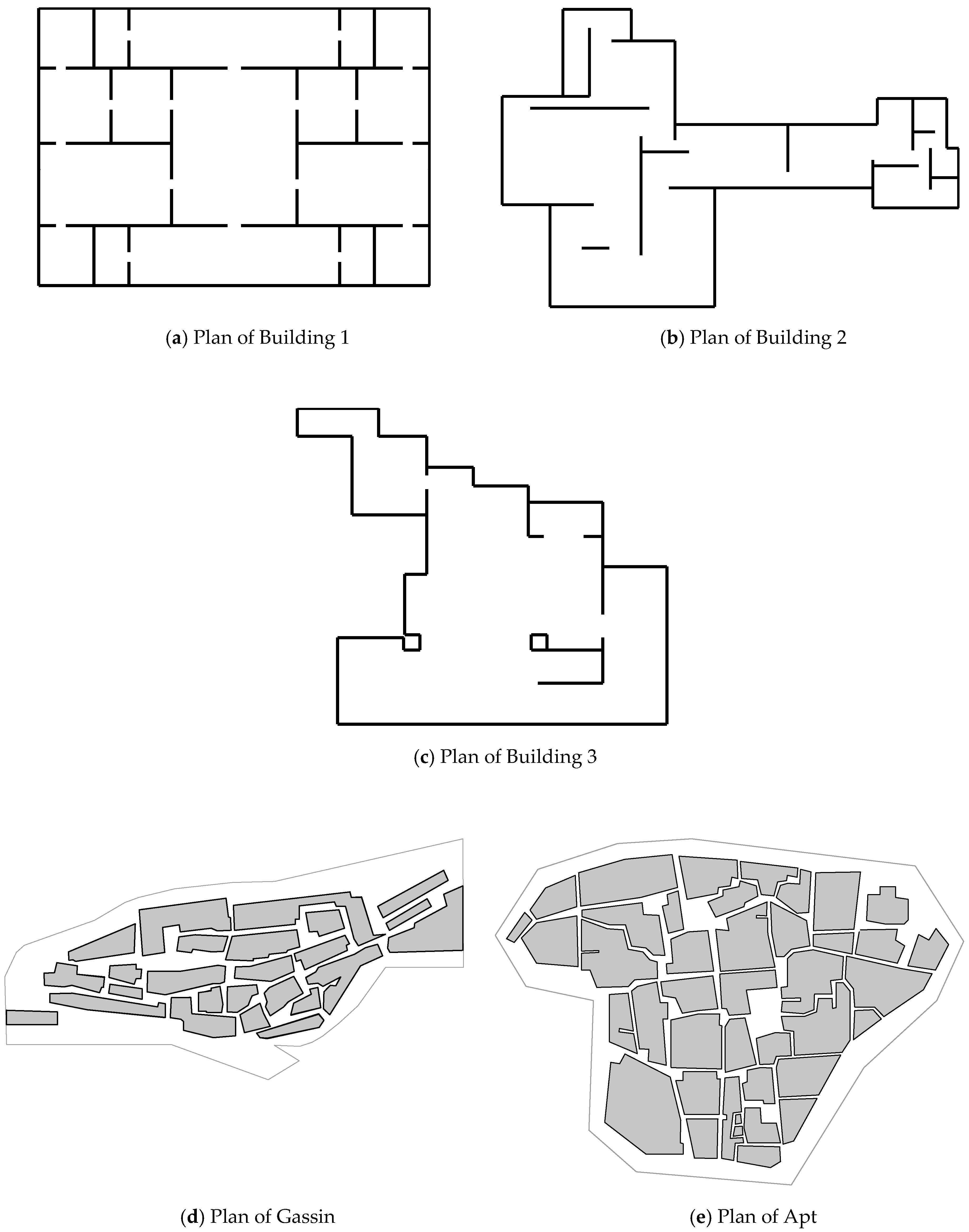
6. Computation
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hillier, B.; Hanson, J. The Social Logic of Space; Cambridge University Press: Cambridge, UK, 1984. [Google Scholar]
- Peponis, J.; Wineman, J.; Bafna, S.; Rashid, M.; Kim, S.H. On the generation of linear representation of spatial configuration. Environ. Plan. B Plan. Des. 1998, 25, 5595–5676. [Google Scholar] [CrossRef]
- Turner, A.; Penn, A.; Hillier, B. An algorithmic definition of the axial map. Environ. Plan. B Plan. Des. 2005, 32, 4254–4344. [Google Scholar] [CrossRef]
- Batty, M.; Rana, S. The automatic definition and generation of axial lines and axial maps. Environ. Plan. B Plan. Des. 2004, 31, 6156–6240. [Google Scholar] [CrossRef]
- Jiang, B.; Liu, X. Automatic generation of the axial lines of urban environments to capture what we perceive. Int. J. Geogr. Inf. Sci. 2010, 24, 5455–5458. [Google Scholar] [CrossRef]
- Liu, X.; Jiang, B. Defining and generating axial lines from street center lines for better understanding of urban morphologies. Int. J. Geogr. Inf. Sci. 2012, 26, 15211–15232. [Google Scholar] [CrossRef]
- Hillier, B.; Penn, A. Dense civilisations: The shape of cities in the 21st century. Appl. Energy 1992, 43, 416–426. [Google Scholar] [CrossRef]
- Penn, A.; Desyllas, J.; Vaughan, L. The space of innovation: Interaction and communication in the work environment. Environ. Plan. B Plan. Des. 1999, 26, 1932–2018. [Google Scholar] [CrossRef]
- Flemming, U. Wall representations of rectangular dissections and their use in automated space allocation. Environ. Plan. B Plan. Des. 1978, 5, 2152–2232. [Google Scholar] [CrossRef]
- Anderssen, R.S.; Ive, J.R. Exploiting structure in linear-programming formulations for land-use planning. Environ. Plan. B Plan. Des. 1982, 9, 3313–3339. [Google Scholar] [CrossRef]
- Anderssen, R.S.; Cocks, K.D.; Ive, J.R. Implications of the generalized upper bounding structure in land-use allocation. Environ. Plan. B Plan. Des. 1983, 10, 2072–2117. [Google Scholar] [CrossRef]
- Erkut, E.; Francis, R.L.; Lowe, T.J. A multi-median problem with inter-distance constraints. Environ. Plan. B Plan. Des. 1988, 15, 1811–1890. [Google Scholar] [CrossRef]
- ReVelle, C.; Snyder, S. A shortest path model for the optimal timing of forest harvest decisions. Environ. Plan. B Plan. Des. 1996, 23, 1651–1675. [Google Scholar] [CrossRef]
- Turner, J.; Wineman, J.; Psarra, S.; Jung, S.K.; Senske, N. Syntax 2D 1.3.7; Computer Software; University of Michigan: Ann Arbor, MI, USA, 2006. [Google Scholar]

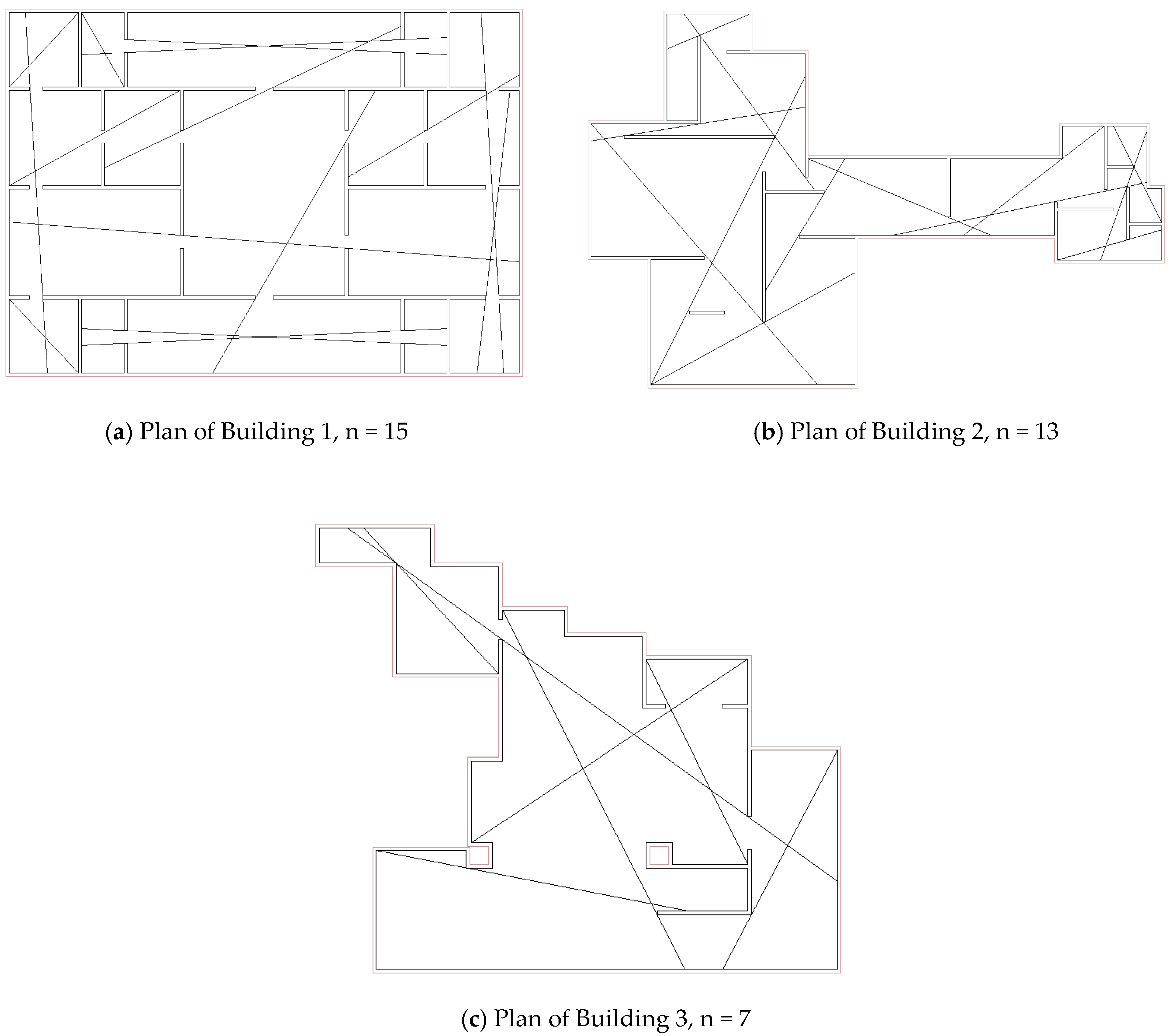
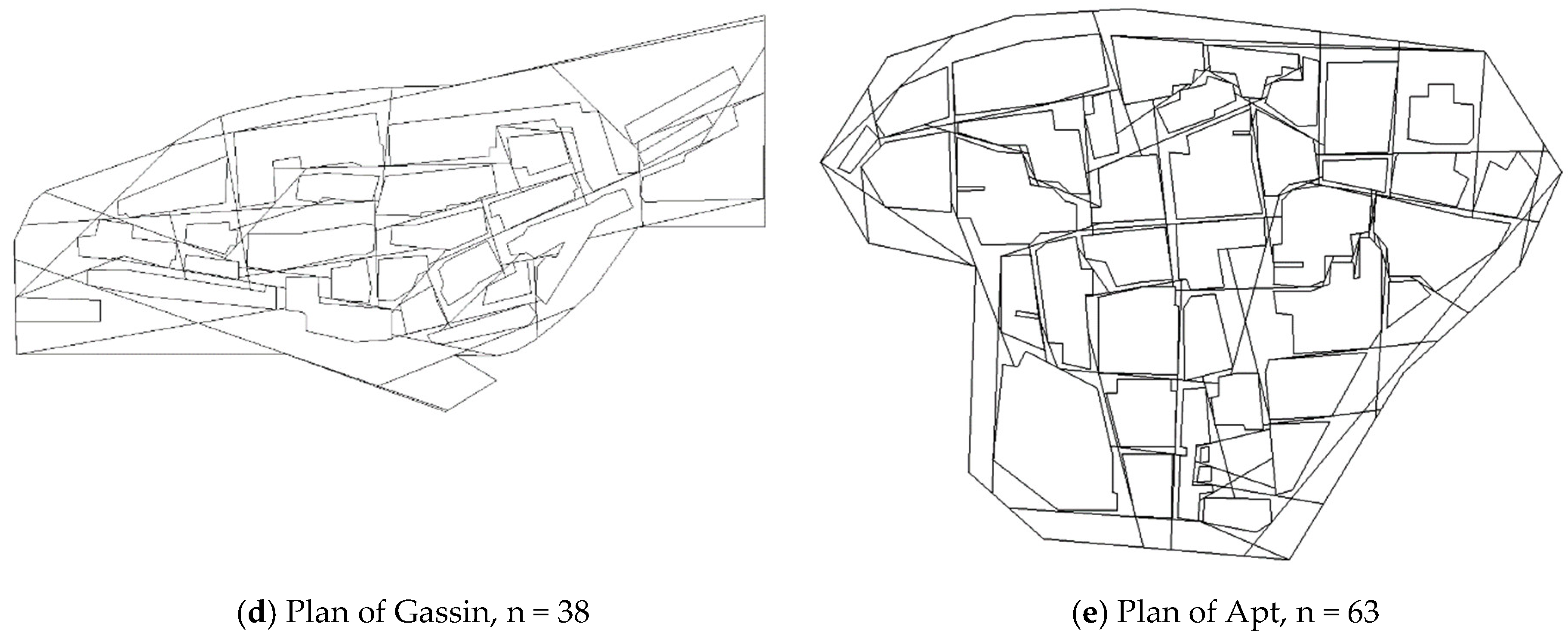
| Cases | Number of Axial Lines | Data Preparation and Problem Formulation (ms) | Solution (ms) |
|---|---|---|---|
| Building 1 | 692 | 110 | 30 |
| Building 2 | 184 | 10 | <1 |
| Building 3 | 225 | 10 | 10 |
| Gassin | 1124 | 532 | 1722 |
| Apt | 1296 | 740 | 124,389 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, S.K.; Kim, Y. A Linear Programming Method for Finding a Minimal Set of Axial Lines Representing an Entire Geometry of Building and Urban Layout. Appl. Sci. 2020, 10, 4273. https://doi.org/10.3390/app10124273
Jung SK, Kim Y. A Linear Programming Method for Finding a Minimal Set of Axial Lines Representing an Entire Geometry of Building and Urban Layout. Applied Sciences. 2020; 10(12):4273. https://doi.org/10.3390/app10124273
Chicago/Turabian StyleJung, Sung Kwon, and Youngchul Kim. 2020. "A Linear Programming Method for Finding a Minimal Set of Axial Lines Representing an Entire Geometry of Building and Urban Layout" Applied Sciences 10, no. 12: 4273. https://doi.org/10.3390/app10124273
APA StyleJung, S. K., & Kim, Y. (2020). A Linear Programming Method for Finding a Minimal Set of Axial Lines Representing an Entire Geometry of Building and Urban Layout. Applied Sciences, 10(12), 4273. https://doi.org/10.3390/app10124273





