Cycling Biomechanics and Its Relationship to Performance
Abstract
Featured Application
Abstract
1. Introduction
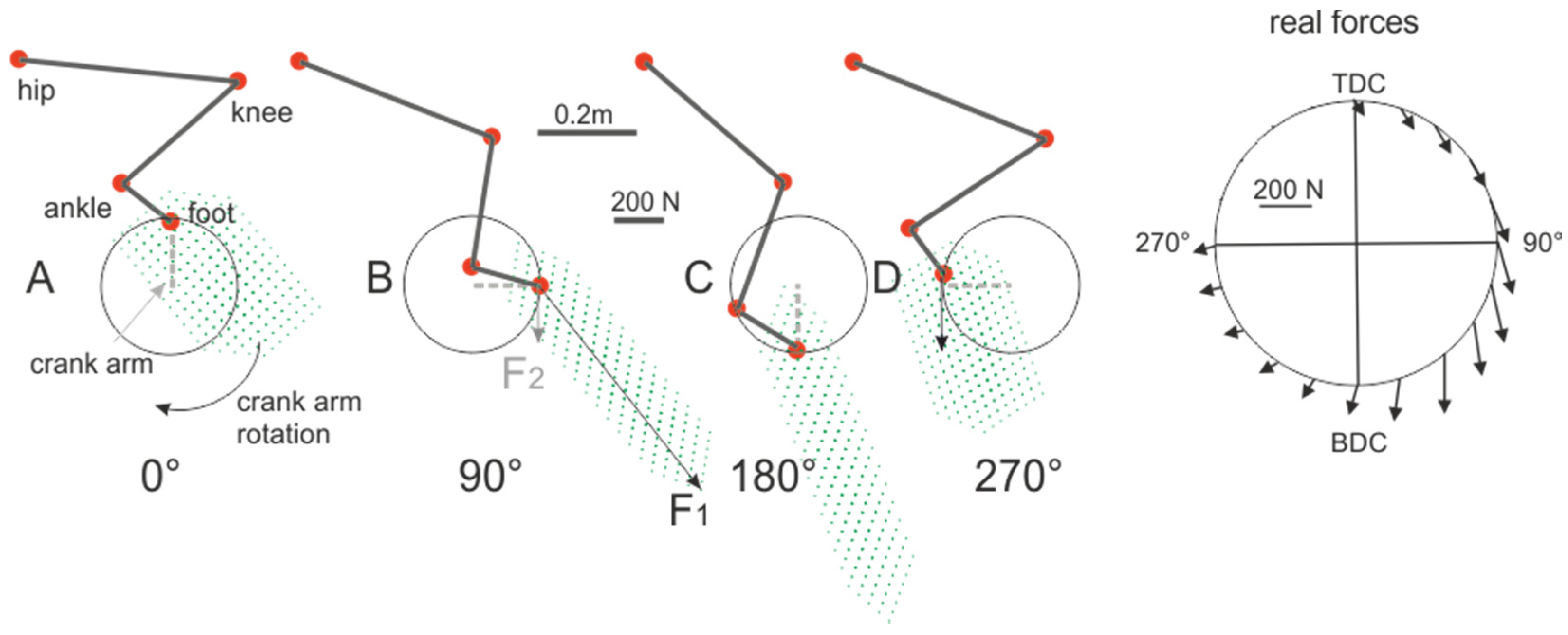
2. Crank Power-Output
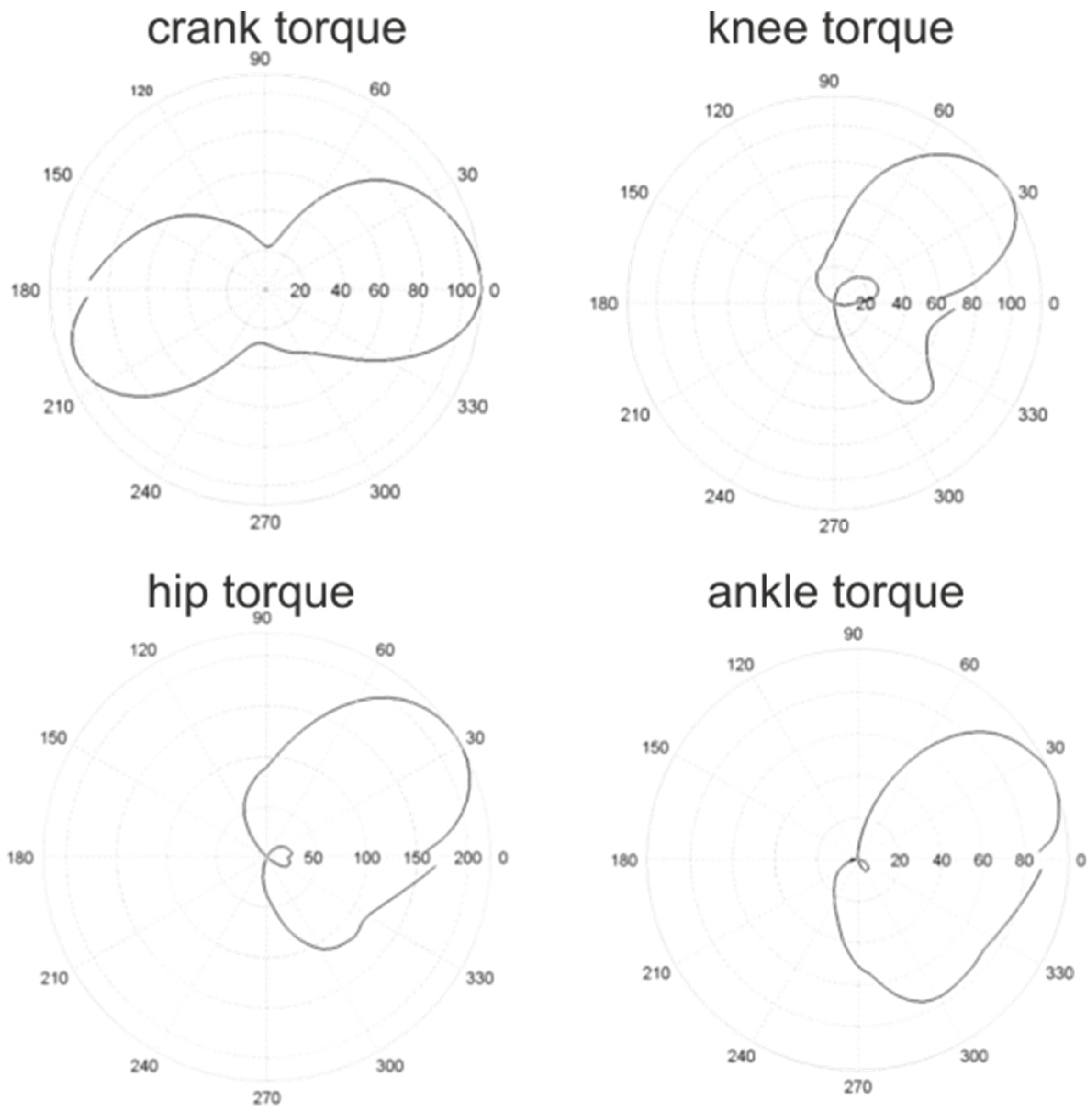
3. Joint Torque
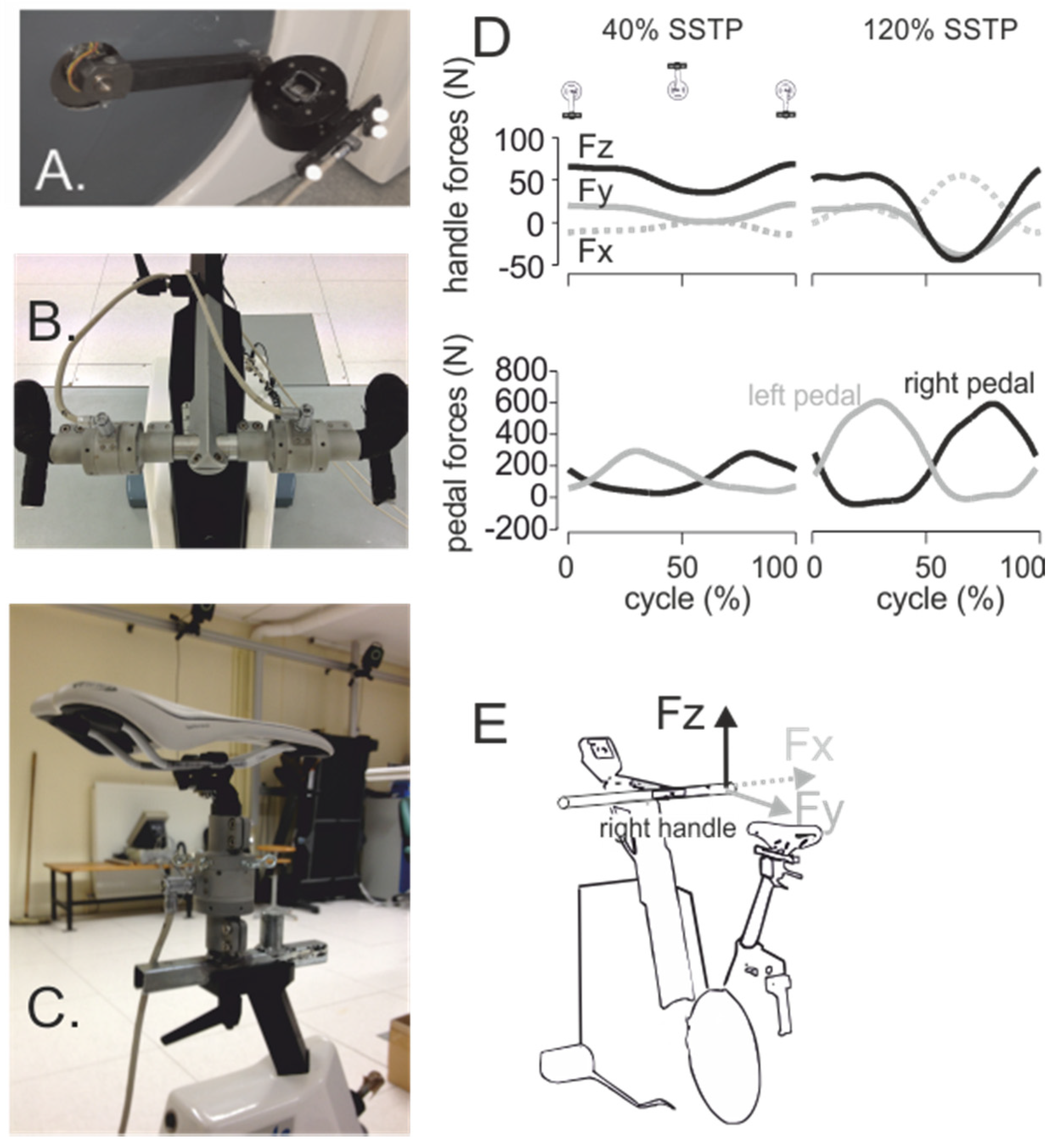
4. Seat and Handlebar Forces and the Role of the Upper Arms
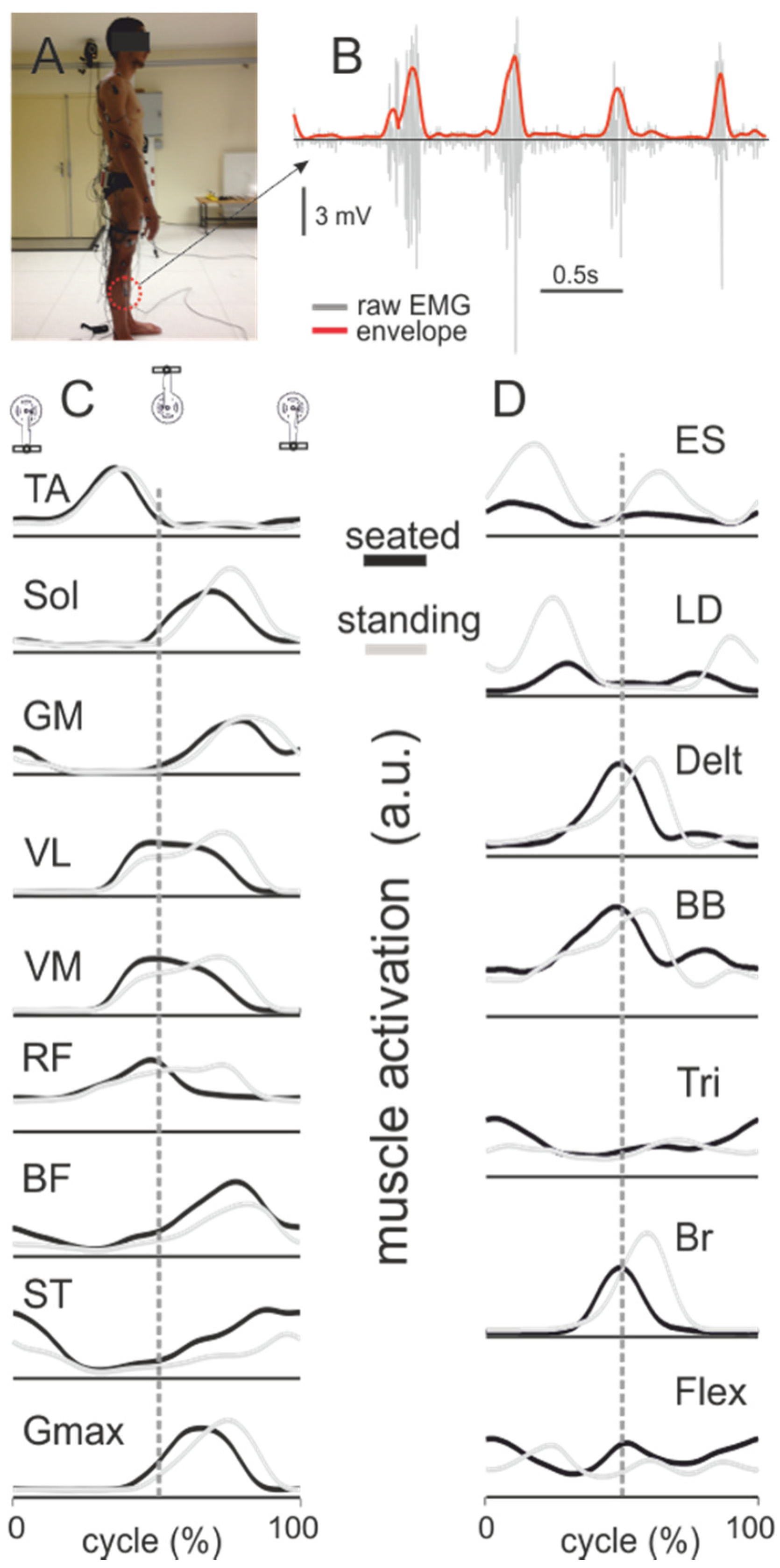
5. Electromyography
6. Measures of Muscle Fatigue
7. Measures of Muscle Mechanical Performance
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Swart, J.; Holliday, W. Cycling Biomechanics Optimization-the (R) Evolution of Bicycle Fitting. Curr. Sports Med. Rep. 2019, 18, 490–496. [Google Scholar] [CrossRef] [PubMed]
- Capostagno, B.; Lambert, M.I.; Lamberts, R.P. A Systematic Review of Submaximal Cycle Tests to Predict, Monitor, and Optimize Cycling Performance. Int. J. Sports Physiol. Perform. 2016, 11, 707–714. [Google Scholar] [CrossRef] [PubMed]
- Joyner, M.J.; Coyle, E.F. Endurance exercise performance: The physiology of champions. J. Physiol. 2008, 586, 35–44. [Google Scholar] [CrossRef] [PubMed]
- Spindler, D.J.; Allen, M.S.; Vella, S.A.; Swann, C. The psychology of elite cycling: A systematic review. J. Sports Sci. 2018, 36, 1943–1954. [Google Scholar] [CrossRef] [PubMed]
- Bernstein, N.A. The Coordination and Regulation of Movements; Pergamon Press: New York, NY, USA, 1967. [Google Scholar]
- Merkes, P.F.J.; Menaspa, P.; Abbiss, C.R. Power output, cadence, and torque are similar between the forward standing and traditional sprint cycling positions. Scand. J. Med. Sci. Sports 2020, 30, 64–73. [Google Scholar] [CrossRef] [PubMed]
- Patterson, R.P.; Moreno, M.I. Bicycle pedalling forces as a function of pedalling rate and power output. Med. Sci. Sports Exerc. 1990, 22, 512–516. [Google Scholar] [CrossRef]
- Hug, F.; Drouet, J.M.; Champoux, Y.; Couturier, A.; Dorel, S. Interindividual variability of electromyographic patterns and pedal force profiles in trained cyclists. Eur. J. Appl. Physiol. 2008, 104, 667–678. [Google Scholar] [CrossRef]
- Kautz, S.A.; Hull, M.L. A theoretical basis for interpreting the force applied to the pedal in cycling. J. Biomech. 1993, 26, 155–165. [Google Scholar] [CrossRef]
- Salomoni, S.; Tucker, K.; Hug, F.; McPhee, M.; Hodges, P. Reduced Maximal Force during Acute Anterior Knee Pain Is Associated with Deficits in Voluntary Muscle Activation. PLoS ONE 2016, 11, e0161487. [Google Scholar] [CrossRef]
- Bailey, M.P.; Maillardet, F.J.; Messenger, N. Kinematics of cycling in relation to anterior knee pain and patellar tendinitis. J. Sports Sci. 2003, 21, 649–657. [Google Scholar] [CrossRef]
- Bertucci, W.; Grappe, F.; Groslambert, A. Laboratory versus outdoor cycling conditions: Differences in pedaling biomechanics. J. Appl. Biomech. 2007, 23, 87–92. [Google Scholar] [CrossRef] [PubMed]
- Fintelman, D.M.; Sterling, M.; Hemida, H.; Li, F.X. Effect of different aerodynamic time trial cycling positions on muscle activation and crank torque. Scand. J. Med. Sci. Sports 2016, 26, 528–534. [Google Scholar] [CrossRef] [PubMed]
- Arpinar-Avsar, P.; Birlik, G.; Sezgin, O.C.; Soylu, A.R. The effects of surface-induced loads on forearm muscle activity during steering a bicycle. J. Sports Sci. Med. 2013, 12, 512–520. [Google Scholar]
- Gardner, A.S.; Martin, J.C.; Martin, D.T.; Barras, M.; Jenkins, D.G. Maximal torque- and power-pedaling rate relationships for elite sprint cyclists in laboratory and field tests. Eur. J. Appl. Physiol. 2007, 101, 287–292. [Google Scholar] [CrossRef] [PubMed]
- Nimmerichter, A.; Williams, C.; Bachl, N.; Eston, R. Evaluation of a field test to assess performance in elite cyclists. Int. J. Sports Med. 2010, 31, 160–166. [Google Scholar] [CrossRef]
- Hawley, J.A.; Noakes, T.D. Peak power output predicts maximal oxygen uptake and performance time in trained cyclists. Eur. J. Appl. Physiol. Occup. Physiol. 1992, 65, 79–83. [Google Scholar] [CrossRef]
- Bentley, D.J.; McNaughton, L.R.; Thompson, D.; Vleck, V.E.; Batterham, A.M. Peak power output, the lactate threshold, and time trial performance in cyclists. Med. Sci. Sports Exerc. 2001, 33, 2077–2081. [Google Scholar] [CrossRef]
- Zameziati, K.; Mornieux, G.; Rouffet, D.; Belli, A. Relationship between the increase of effectiveness indexes and the increase of muscular efficiency with cycling power. Eur. J. Appl. Physiol. 2006, 96, 274–281. [Google Scholar] [CrossRef]
- Davis, R.R.; Hull, M.L. Measurement of pedal loading in bicycling: II. Analysis and results. J. Biomech. 1981, 14, 857–872. [Google Scholar] [CrossRef]
- Sanderson, D.J.; Black, A. The effect of prolonged cycling on pedal forces. J. Sports Sci. 2003, 21, 191–199. [Google Scholar] [CrossRef]
- Garcia-Lopez, J.; Diez-Leal, S.; Ogueta-Alday, A.; Larrazabal, J.; Rodriguez-Marroyo, J.A. Differences in pedalling technique between road cyclists of different competitive levels. J. Sports Sci. 2016, 34, 1619–1626. [Google Scholar] [CrossRef] [PubMed]
- Ericson, M.O.; Nisell, R. Efficiency of pedal forces during ergometer cycling. Int. J. Sports Med. 1988, 9, 118–122. [Google Scholar] [CrossRef] [PubMed]
- Sanderson, D.J.; Hennig, E.M.; Black, A.H. The influence of cadence and power output on force application and in-shoe pressure distribution during cycling by competitive and recreational cyclists. J. Sports Sci. 2000, 18, 173–181. [Google Scholar] [CrossRef] [PubMed]
- Theurel, J.; Crepin, M.; Foissac, M.; Temprado, J.J. Effects of different pedalling techniques on muscle fatigue and mechanical efficiency during prolonged cycling. Scand. J. Med. Sci. Sports 2012, 22, 714–721. [Google Scholar] [CrossRef]
- Davis, B.L.; Vaughan, C.L. Phasic behavior of EMG signals during gait: Use of multivariate statistics. J. Electromyogr. Kinesiol. 1993, 3, 51–60. [Google Scholar] [CrossRef]
- De Marchis, C.; Schmid, M.; Bibbo, D.; Castronovo, A.M.; D’Alessio, T.; Conforto, S. Feedback of mechanical effectiveness induces adaptations in motor modules during cycling. Front. Comput. Neurosci. 2013, 7, 35. [Google Scholar] [CrossRef]
- Mornieux, G.; Gollhofer, A.; Stapelfeldt, B. Muscle coordination while pulling up during cycling. Int. J. Sports Med. 2010, 31, 843–846. [Google Scholar] [CrossRef]
- Korff, T.; Romer, L.M.; Mayhew, I.; Martin, J.C. Effect of pedaling technique on mechanical effectiveness and efficiency in cyclists. Med. Sci. Sports Exerc. 2007, 39, 991–995. [Google Scholar] [CrossRef]
- Bini, R.; Hume, P.; Croft, J.L.; Kilding, A. Pedal Force Effectiveness in Cycling: A Review of Constraints and Training Effects. J. Sci. Cycl. 2013, 2, 11–24. [Google Scholar]
- Kutch, J.J.; Valero-Cuevas, F.J. Muscle redundancy does not imply robustness to muscle dysfunction. J. Biomech. 2011, 44, 1264–1270. [Google Scholar] [CrossRef]
- Valero-Cuevas, F.J. A mathematical approach to the mechanical capabilities of limbs and fingers. Adv. Exp. Med. Biol. 2009, 629, 619–633. [Google Scholar] [CrossRef] [PubMed]
- Watier, B.; Costes, A.; Moretto, P. An Inverse Dynamic Study Suggests That Cyclists Marginally Use Hip Joint Torque at Maximal Power. In Proceedings of the Congress of the International Society of Biomechanics 2013, Natal, Brazil, 4–9 August 2013; Available online: https://media.isbweb.org/images/conferences/isb-congresses/2013/oral/sb-cycling.04.pdf (accessed on 8 May 2020).
- Martin, J.C.; Brown, N.A. Joint-specific power production and fatigue during maximal cycling. J. Biomech. 2009, 42, 474–479. [Google Scholar] [CrossRef] [PubMed]
- Zatsiorsky, V.M.; Zaciorskij, V.M. Kinetics of Human Motion; Human Kinetics: Champaign, IL, USA, 2002. [Google Scholar]
- Elmer, S.J.; Barratt, P.R.; Korff, T.; Martin, J.C. Joint-specific power production during submaximal and maximal cycling. Med. Sci. Sports Exerc. 2011, 43, 1940–1947. [Google Scholar] [CrossRef] [PubMed]
- McDaniel, J.; Behjani, N.S.; Elmer, S.J.; Brown, N.A.; Martin, J.C. Joint-specific power-pedaling rate relationships during maximal cycling. J. Appl. Biomech. 2014, 30, 423–430. [Google Scholar] [CrossRef]
- Bini, R.R.; Diefenthaeler, F.; Mota, C.B. Fatigue effects on the coordinative pattern during cycling: Kinetics and kinematics evaluation. J. Electromyogr. Kinesiol. 2010, 20, 102–107. [Google Scholar] [CrossRef]
- Mornieux, G.; Guenette, J.A.; Sheel, A.W.; Sanderson, D.J. Influence of cadence, power output and hypoxia on the joint moment distribution during cycling. Eur. J. Appl. Physiol. 2007, 102, 11–18. [Google Scholar] [CrossRef]
- Sanderson, D.J. The influence of cadence and power output on the biomechanics of force application during steady-rate cycling in competitive and recreational cyclists. J. Sports Sci. 1991, 9, 191–203. [Google Scholar] [CrossRef]
- Neptune, R.R.; Herzog, W. The association between negative muscle work and pedaling rate. J. Biomech. 1999, 32, 1021–1026. [Google Scholar] [CrossRef][Green Version]
- Gonzalez, H.; Hull, M.L. Multivariable optimization of cycling biomechanics. J. Biomech. 1989, 22, 1151–1161. [Google Scholar] [CrossRef]
- Marsh, A.P.; Martin, P.E.; Sanderson, D.J. Is a joint moment-based cost function associated with preferred cycling cadence? J. Biomech. 2000, 33, 173–180. [Google Scholar] [CrossRef]
- Costes, A.; Turpin, N.A.; Villeger, D.; Moretto, P.; Watier, B. Spontaneous change from seated to standing cycling position with increasing power is associated with a minimization of cost functions. J. Sports Sci. 2018, 36, 907–913. [Google Scholar] [CrossRef] [PubMed]
- Watier, B.; Costes, A.; Turpin, N.A. Modification of the spontaneous seat-to-stand transition in cycling with bodyweight and cadence variations. J. Biomech. 2017, 63, 61–66. [Google Scholar] [CrossRef]
- Turpin, N.A.; Costes, A.; Moretto, P.; Watier, B. Can muscle coordination explain the advantage of using the standing position during intense cycling? J. Sci. Med. Sport 2017, 20, 611–616. [Google Scholar] [CrossRef] [PubMed]
- Costes, A.; Turpin, N.A.; Villeger, D.; Moretto, P.; Watier, B. A reduction of the saddle vertical force triggers the sit-stand transition in cycling. J. Biomech. 2015, 48, 2998–3003. [Google Scholar] [CrossRef]
- Soden, P.D.; Adeyefa, B.A. Forces applied to a bicycle during normal cycling. J. Biomech. 1979, 12, 527–541. [Google Scholar] [CrossRef]
- Turpin, N.A.; Costes, A.; Moretto, P.; Watier, B. Upper limb and trunk muscle activity patterns during seated and standing cycling. J. Sports Sci. 2017, 35, 557–564. [Google Scholar] [CrossRef] [PubMed]
- Pedersen, P.K.; Sorensen, J.B.; Jensen, K.; Johansen, L.; Levin, K. Muscle fiber type distribution and nonlinear VO2-power output relationship in cycling. Med. Sci. Sports Exerc. 2002, 34, 655–661. [Google Scholar] [CrossRef]
- McDaniel, J.; Subudhi, A.; Martin, J.C. Torso stabilization reduces the metabolic cost of producing cycling power. Can. J. Appl. Physiol. 2005, 30, 433–441. [Google Scholar] [CrossRef]
- Costes, A.; Turpin, N.A.; Villeger, D.; Moretto, P.; Watier, B. Influence of Position and Power Output on Upper Limb Kinetics in Cycling. J. Appl. Biomech. 2016, 32, 140–149. [Google Scholar] [CrossRef]
- Baker, J.S.; Davies, B. Additional considerations and recommendations for the quantification of hand-grip strength in the measurement of leg power during high-intensity cycle ergometry. Res. Sports Med. 2009, 17, 145–155. [Google Scholar] [CrossRef]
- Dore, E.; Baker, J.S.; Jammes, A.; Graham, M.; New, K.; Van Praagh, E. Upper body contribution during leg cycling peak power in teenage boys and girls. Res. Sports Med. 2006, 14, 245–257. [Google Scholar] [CrossRef] [PubMed]
- Padulo, J.; Laffaye, G.; Bertucci, W.; Chaouachi, A.; Viggiano, D. Optimisation of starting conditions in track cycling. Sport Sci. Health 2014, 10, 189–198. [Google Scholar] [CrossRef]
- Dorel, S.; Couturier, A.; Hug, F. Influence of different racing positions on mechanical and electromyographic patterns during pedalling. Scand. J. Med. Sci. Sports 2009, 19, 44–54. [Google Scholar] [CrossRef] [PubMed]
- Savelberg, H.H.; Van de Port, I.G.; Willems, P.J. Body configuration in cycling affects muscle recruitment and movement pattern. J. Appl. Biomech. 2003, 19, 310–324. [Google Scholar] [CrossRef][Green Version]
- Duc, S.; Bertucci, W.; Pernin, J.N.; Grappe, F. Muscular activity during uphill cycling: Effect of slope, posture, hand grip position and constrained bicycle lateral sways. J. Electromyogr. Kinesiol. 2008, 18, 116–127. [Google Scholar] [CrossRef] [PubMed]
- Fintelman, D.M.; Sterling, M.; Hemida, H.; Li, F.X. Optimal cycling time trial position models: Aerodynamics versus power output and metabolic energy. J. Biomech. 2014, 47, 1894–1898. [Google Scholar] [CrossRef] [PubMed]
- Jansen, C.; McPhee, J. Predictive dynamic simulation of Olympic track cycling standing start using direct collocation optimal control. Multibody Syst. Dyn. 2020, 49, 53–70. [Google Scholar] [CrossRef]
- Milner-Brown, H.S.; Stein, R.B. The relation between the surface electromyogram and muscular force. J. Physiol. 1975, 246, 549–569. [Google Scholar] [CrossRef]
- Farina, D. Interpretation of the surface electromyogram in dynamic contractions. Exerc. Sport Sci. Rev. 2006, 34, 121–127. [Google Scholar] [CrossRef]
- Blake, O.M.; Champoux, Y.; Wakeling, J.M. Muscle coordination patterns for efficient cycling. Med. Sci. Sports Exerc. 2012, 44, 926–938. [Google Scholar] [CrossRef]
- Blake, O.M.; Wakeling, J.M. Estimating changes in metabolic power from EMG. Springerplus 2013, 2, 229. [Google Scholar] [CrossRef] [PubMed]
- Chapman, A.; Vicenzino, B.; Blanch, P.; Hodges, P. Do differences in muscle recruitment between novice and elite cyclists reflect different movement patterns or less skilled muscle recruitment? J. Sci. Med. Sport 2009, 12, 31–34. [Google Scholar] [CrossRef] [PubMed]
- Chapman, A.R.; Vicenzino, B.; Blanch, P.; Hodges, P.W. Patterns of leg muscle recruitment vary between novice and highly trained cyclists. J. Electromyogr. Kinesiol. 2008, 18, 359–371. [Google Scholar] [CrossRef] [PubMed]
- Candotti, C.T.; Loss, J.F.; Bagatini, D.; Soares, D.P.; da Rocha, E.K.; de Oliveira, A.R.; Guimaraes, A.C. Cocontraction and economy of triathletes and cyclists at different cadences during cycling motion. J. Electromyogr. Kinesiol. 2009, 19, 915–921. [Google Scholar] [CrossRef]
- Chapman, A.R.; Vicenzino, B.; Blanch, P.; Knox, J.J.; Hodges, P.W. Leg muscle recruitment in highly trained cyclists. J. Sports Sci. 2006, 24, 115–124. [Google Scholar] [CrossRef]
- Zatsiorsky, V.M.; Latash, M.L. What Is a Joint Torque for Joints Spanned by Multiarticular Muscles? J. Appl. Biomech. 1993, 9, 333–336. [Google Scholar] [CrossRef]
- MacIntosh, B.R.; Neptune, R.R.; Horton, J.F. Cadence, power, and muscle activation in cycle ergometry. Med. Sci. Sports Exerc. 2000, 32, 1281–1287. [Google Scholar] [CrossRef] [PubMed]
- Blake, O.M.; Wakeling, J.M. Muscle coordination limits efficiency and power output of human limb movement under a wide range of mechanical demands. J. Neurophysiol. 2015, 114, 3283–3295. [Google Scholar] [CrossRef]
- Gandevia, S.C. Spinal and supraspinal factors in human muscle fatigue. Physiol. Rev. 2001, 81, 1725–1789. [Google Scholar] [CrossRef]
- Doyle-Baker, D.; Temesi, J.; Medysky, M.E.; Holash, R.J.; Millet, G.Y. An Innovative Ergometer to Measure Neuromuscular Fatigue Immediately after Cycling. Med. Sci. Sports Exerc. 2018, 50, 375–387. [Google Scholar] [CrossRef] [PubMed]
- Turpin, N.A.; Guevel, A.; Durand, S.; Hug, F. Fatigue-related adaptations in muscle coordination during a cyclic exercise in humans. J. Exp. Biol. 2011, 214, 3305–3314. [Google Scholar] [CrossRef] [PubMed]
- Driss, T.; Lambertz, D.; Rouis, M.; Vandewalle, H. Influence of musculo-tendinous stiffness of the plantar ankle flexor muscles upon maximal power output on a cycle ergometre. Eur. J. Appl. Physiol. 2012, 112, 3721–3728. [Google Scholar] [CrossRef] [PubMed]
- Vandervoort, A.A.; McComas, A.J. A comparison of the contractile properties of the human gastrocnemius and soleus muscles. Eur. J. Appl. Physiol. Occup. Physiol. 1983, 51, 435–440. [Google Scholar] [CrossRef]
- Lepers, R.; Hausswirth, C.; Maffiuletti, N.; Brisswalter, J.; van Hoecke, J. Evidence of neuromuscular fatigue after prolonged cycling exercise. Med. Sci. Sports Exerc. 2000, 32, 1880–1886. [Google Scholar] [CrossRef] [PubMed]
- Kordi, M.; Goodall, S.; Barratt, P.; Rowley, N.; Leeder, J.; Howatson, G. Relation between Peak Power Output in Sprint Cycling and Maximum Voluntary Isometric Torque Production. J. Electromyogr. Kinesiol. 2017, 35, 95–99. [Google Scholar] [CrossRef] [PubMed]
- Dorel, S.; Guilhem, G.; Couturier, A.; Hug, F. Adjustment of muscle coordination during an all-out sprint cycling task. Med. Sci. Sports Exerc. 2012, 44, 2154–2164. [Google Scholar] [CrossRef] [PubMed]
- Turpin, N.A.; Costes, A.; Villeger, D.; Watier, B. Selective muscle contraction during plantarflexion is incompatible with maximal voluntary torque assessment. Eur. J. Appl. Physiol. 2014, 114, 1667–1677. [Google Scholar] [CrossRef]
- Kordi, M.; Folland, J.; Goodall, S.; Haralabidis, N.; Maden-Wilkinson, T.; Sarika Patel, T.; Leeder, J.; Barratt, P.; Howatson, G. Mechanical and morphological determinants of peak power output in elite cyclists. Scand. J. Med. Sci. Sports 2020, 30, 227–237. [Google Scholar] [CrossRef]
- Ashe, M.C.; Scroop, G.C.; Frisken, P.I.; Amery, C.A.; Wilkins, M.A.; Khan, K.M. Body position affects performance in untrained cyclists. Br. J. Sports Med. 2003, 37, 441–444. [Google Scholar] [CrossRef]
- Heil, D.P.; Derrick, T.R.; Whittlesey, S. The relationship between preferred and optimal positioning during submaximal cycle ergometry. Eur. J. Appl. Physiol. Occup. Physiol. 1997, 75, 160–165. [Google Scholar] [CrossRef]
- Barratt, P.R.; Martin, J.C.; Elmer, S.J.; Korff, T. Effects of Pedal Speed and Crank Length on Pedaling Mechanics during Submaximal Cycling. Med. Sci. Sports Exerc. 2016, 48, 705–713. [Google Scholar] [CrossRef] [PubMed]
- Hill, A.V. The heat of shortening and the dynamic constants of muscle. Proc. R. Soc. Lond. Ser. B-Biol. Sci. 1983, 126, 136–195. [Google Scholar]
- Hansen, E.A.; Andersen, J.L.; Nielsen, J.S.; Sjogaard, G. Muscle fibre type, efficiency, and mechanical optima affect freely chosen pedal rate during cycling. Acta Physiol. Scand. 2002, 176, 185–194. [Google Scholar] [CrossRef] [PubMed]
- Ansley, L.; Cangley, P. Determinants of “optimal” cadence during cycling. Eur. J. Sport Sci. 2009, 9, 61–85. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Turpin, N.A.; Watier, B. Cycling Biomechanics and Its Relationship to Performance. Appl. Sci. 2020, 10, 4112. https://doi.org/10.3390/app10124112
Turpin NA, Watier B. Cycling Biomechanics and Its Relationship to Performance. Applied Sciences. 2020; 10(12):4112. https://doi.org/10.3390/app10124112
Chicago/Turabian StyleTurpin, Nicolas A., and Bruno Watier. 2020. "Cycling Biomechanics and Its Relationship to Performance" Applied Sciences 10, no. 12: 4112. https://doi.org/10.3390/app10124112
APA StyleTurpin, N. A., & Watier, B. (2020). Cycling Biomechanics and Its Relationship to Performance. Applied Sciences, 10(12), 4112. https://doi.org/10.3390/app10124112




