Figure 1.
Schematic of the proposed see-through near-eye display (NED). W1, W2, H, T, and γ are the front width, back width, height, thickness and bevel angle of plano-concave lens, respectively.
Figure 1.
Schematic of the proposed see-through near-eye display (NED). W1, W2, H, T, and γ are the front width, back width, height, thickness and bevel angle of plano-concave lens, respectively.
Figure 2.
Optical path diagram for imaging the real object. R is the radius of curvature of the front surface of lens, sr the real object distance, and s′ the image distance.
Figure 2.
Optical path diagram for imaging the real object. R is the radius of curvature of the front surface of lens, sr the real object distance, and s′ the image distance.
Figure 3.
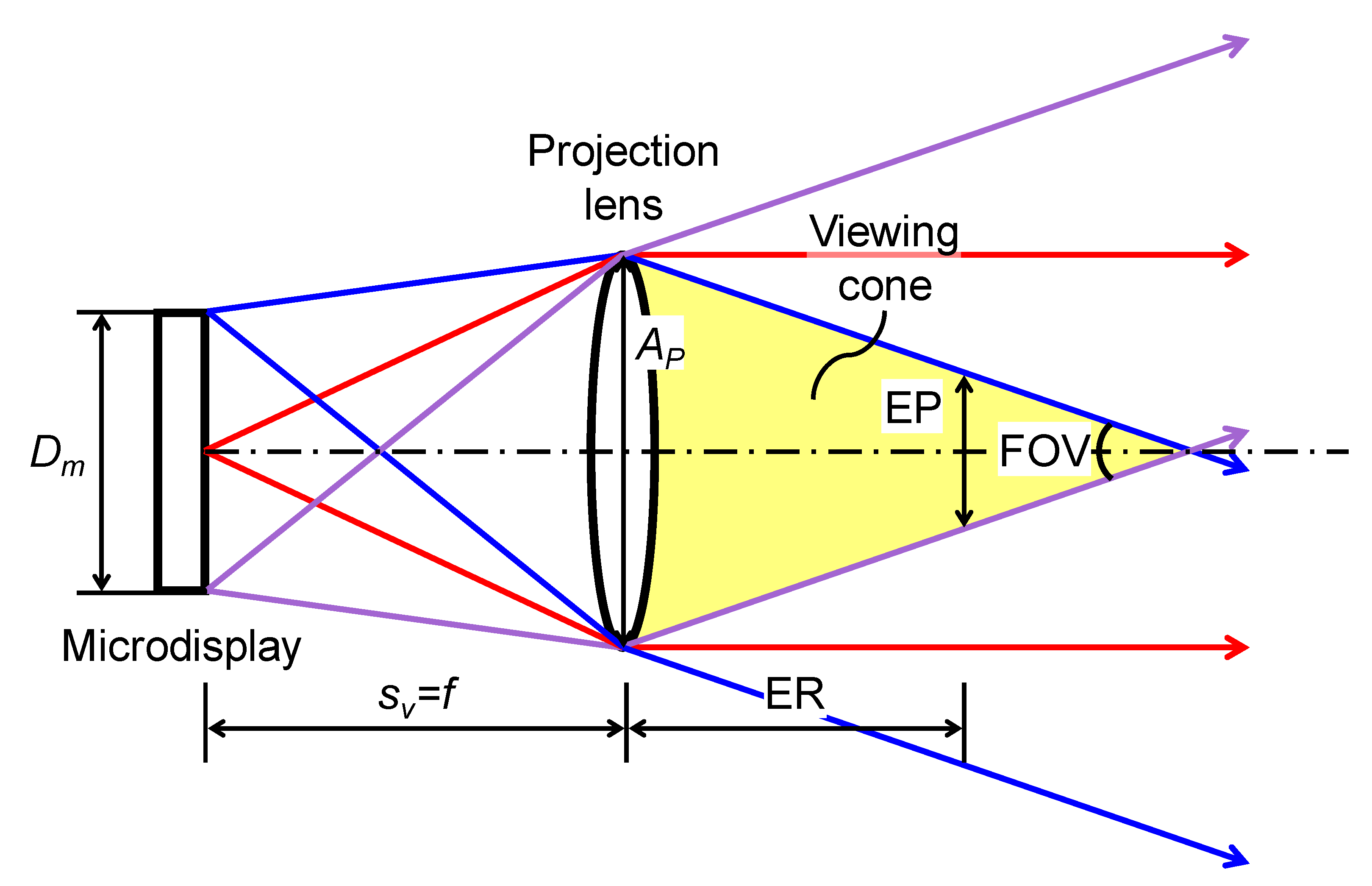
Optical path diagram of the pico projector. Dm is the size of the microdisplay, sv the virtual object distance, f the focal length of the projection lens, Ap the aperture of the projection lens, FOV the field of view, ER the eye relief, and EP the exit pupil.
Figure 3.
Optical path diagram of the pico projector. Dm is the size of the microdisplay, sv the virtual object distance, f the focal length of the projection lens, Ap the aperture of the projection lens, FOV the field of view, ER the eye relief, and EP the exit pupil.
Figure 4.
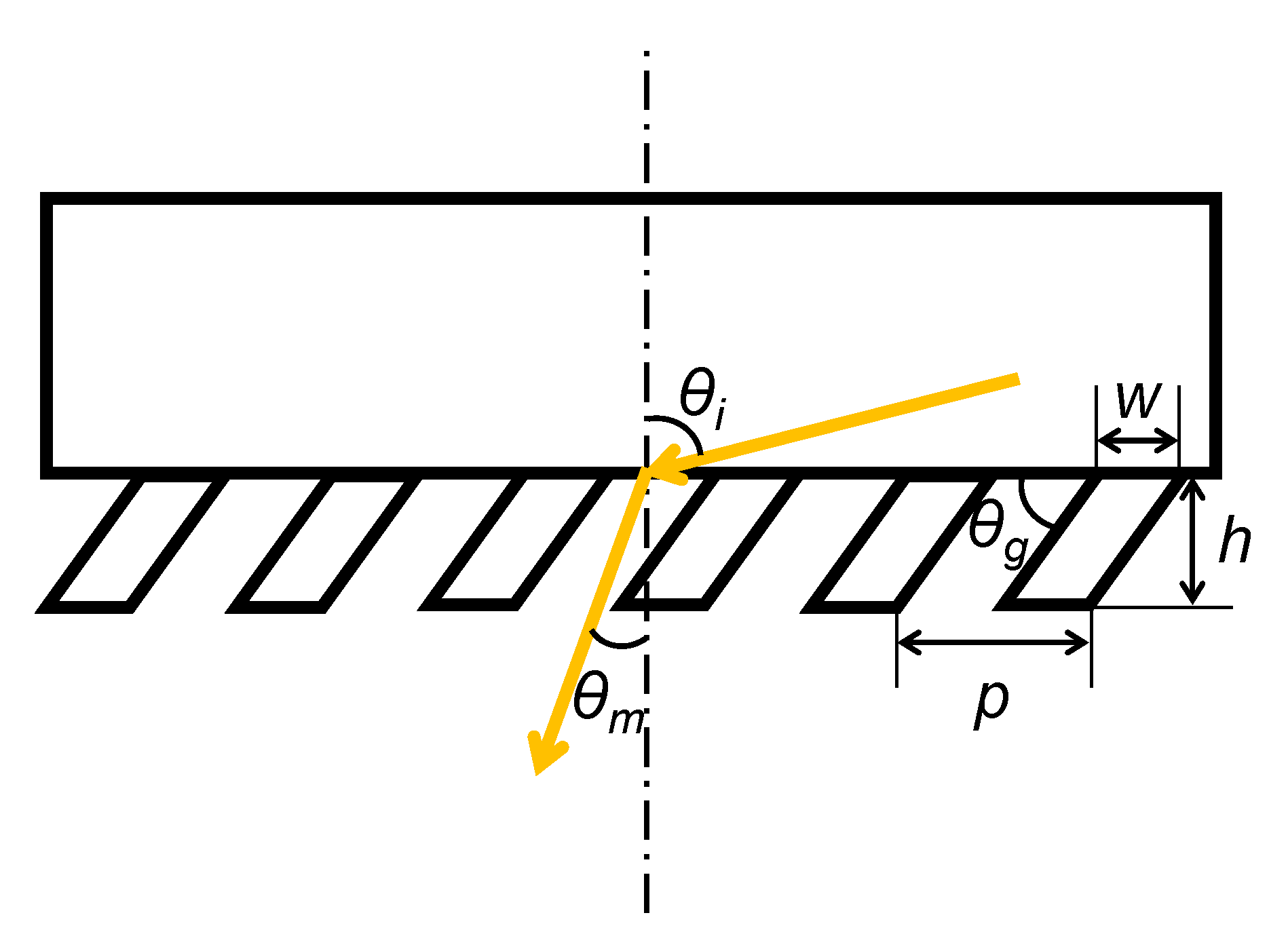
Cross-sectional profile of slanted grating. p is the grating period, h the grating height, w the grating width, θg the slant angle, θi the incident angle (relative to the grating normal), and θm the diffraction angle of mth order.
Figure 4.
Cross-sectional profile of slanted grating. p is the grating period, h the grating height, w the grating width, θg the slant angle, θi the incident angle (relative to the grating normal), and θm the diffraction angle of mth order.
Figure 5.
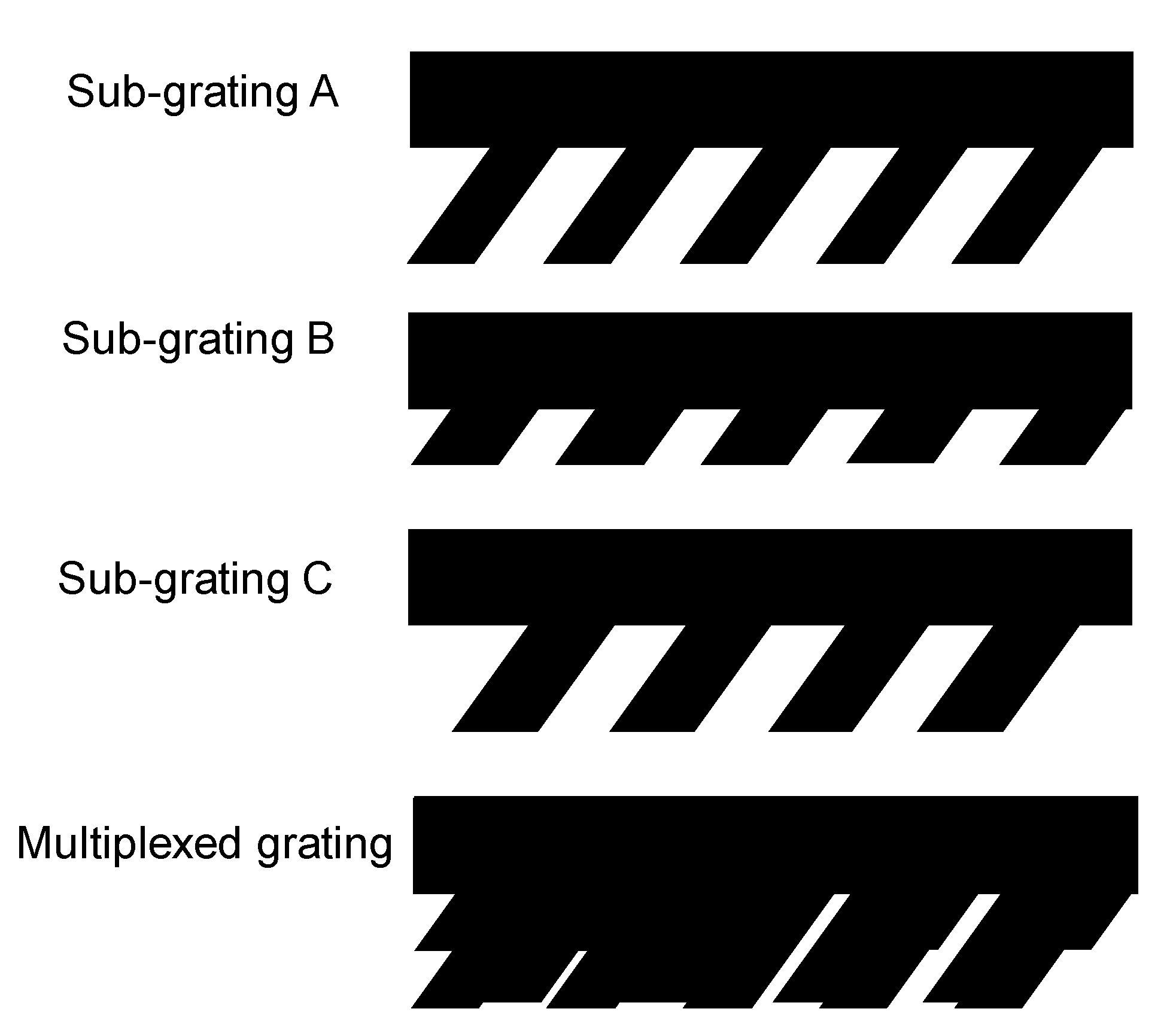
Decomposition of multiplexed grating into three sub-gratings. Say the periods of sub-gratings are pA, pB, and pC, respectively, then the collective period Pm of the multiplexed grating shall be the least common multiple of the above three.
Figure 5.
Decomposition of multiplexed grating into three sub-gratings. Say the periods of sub-gratings are pA, pB, and pC, respectively, then the collective period Pm of the multiplexed grating shall be the least common multiple of the above three.
Figure 6.
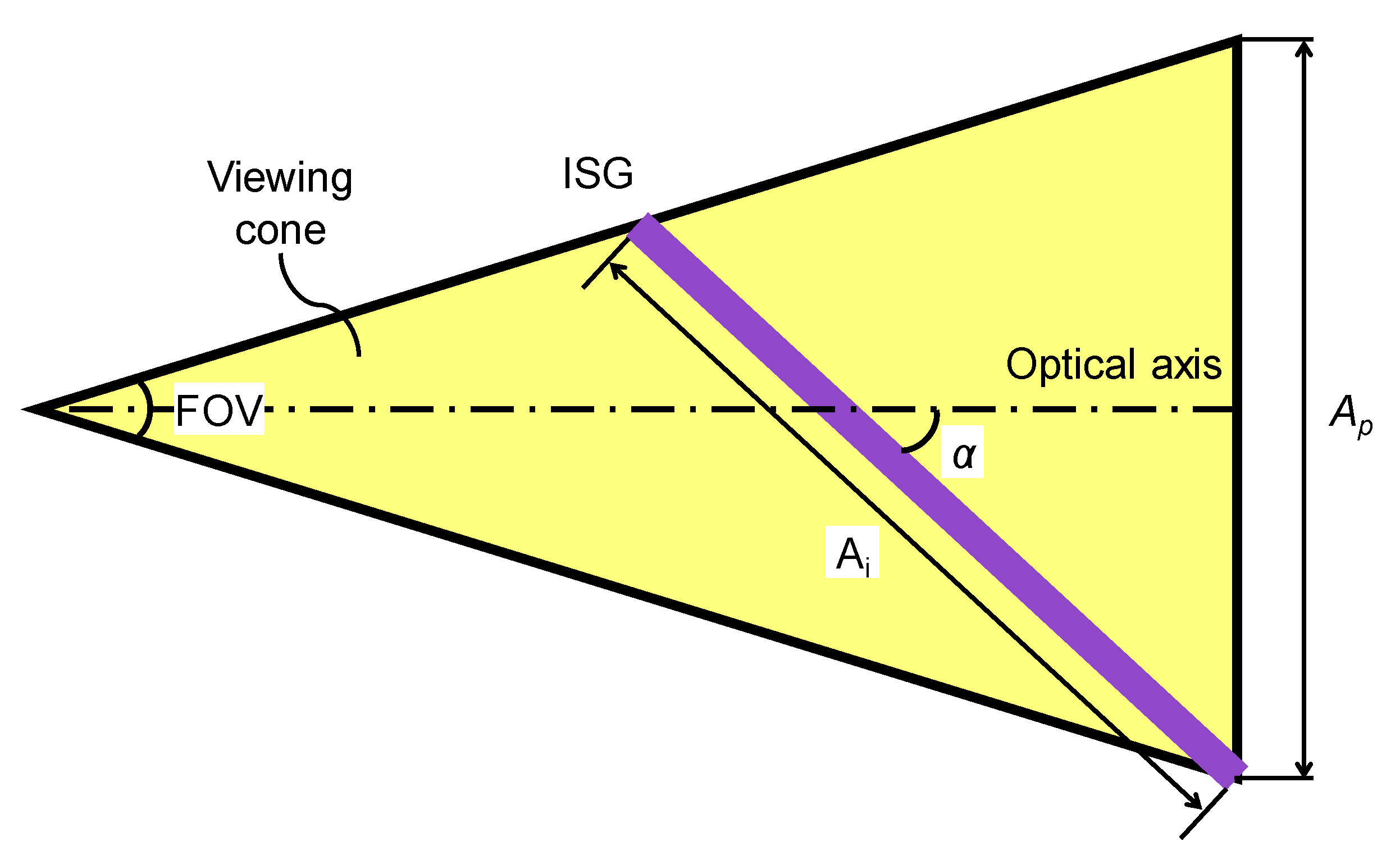
Illustration of the vertical expansion of the exit pupil by the in-coupling slanted grating (ISG). α is the angle between the optical axis of viewing cone and the plane of the ISG, Ap the aperture of the projection lens, Ai the vertical length of intersected exit pupil.
Figure 6.
Illustration of the vertical expansion of the exit pupil by the in-coupling slanted grating (ISG). α is the angle between the optical axis of viewing cone and the plane of the ISG, Ap the aperture of the projection lens, Ai the vertical length of intersected exit pupil.
Figure 7.
Illustration of the horizontal expansion of the exit pupil by the out-coupling slanted grating (OSG). β is the angle of beam incident to OSG, γ the bevel angle, Wi the width of the ISG, Ao the horizontal length of elongated exit pupil.
Figure 7.
Illustration of the horizontal expansion of the exit pupil by the out-coupling slanted grating (OSG). β is the angle of beam incident to OSG, γ the bevel angle, Wi the width of the ISG, Ao the horizontal length of elongated exit pupil.
Figure 8.
Diffraction efficiencies (DEs) of all possible diffraction orders combined of the ISG and OSG calculated with respect to the wavelength. The average DEs of the ISG and OSG over the entire spectrum (460 to 660 nm) are 48.0% and 16.7%, respectively.
Figure 8.
Diffraction efficiencies (DEs) of all possible diffraction orders combined of the ISG and OSG calculated with respect to the wavelength. The average DEs of the ISG and OSG over the entire spectrum (460 to 660 nm) are 48.0% and 16.7%, respectively.
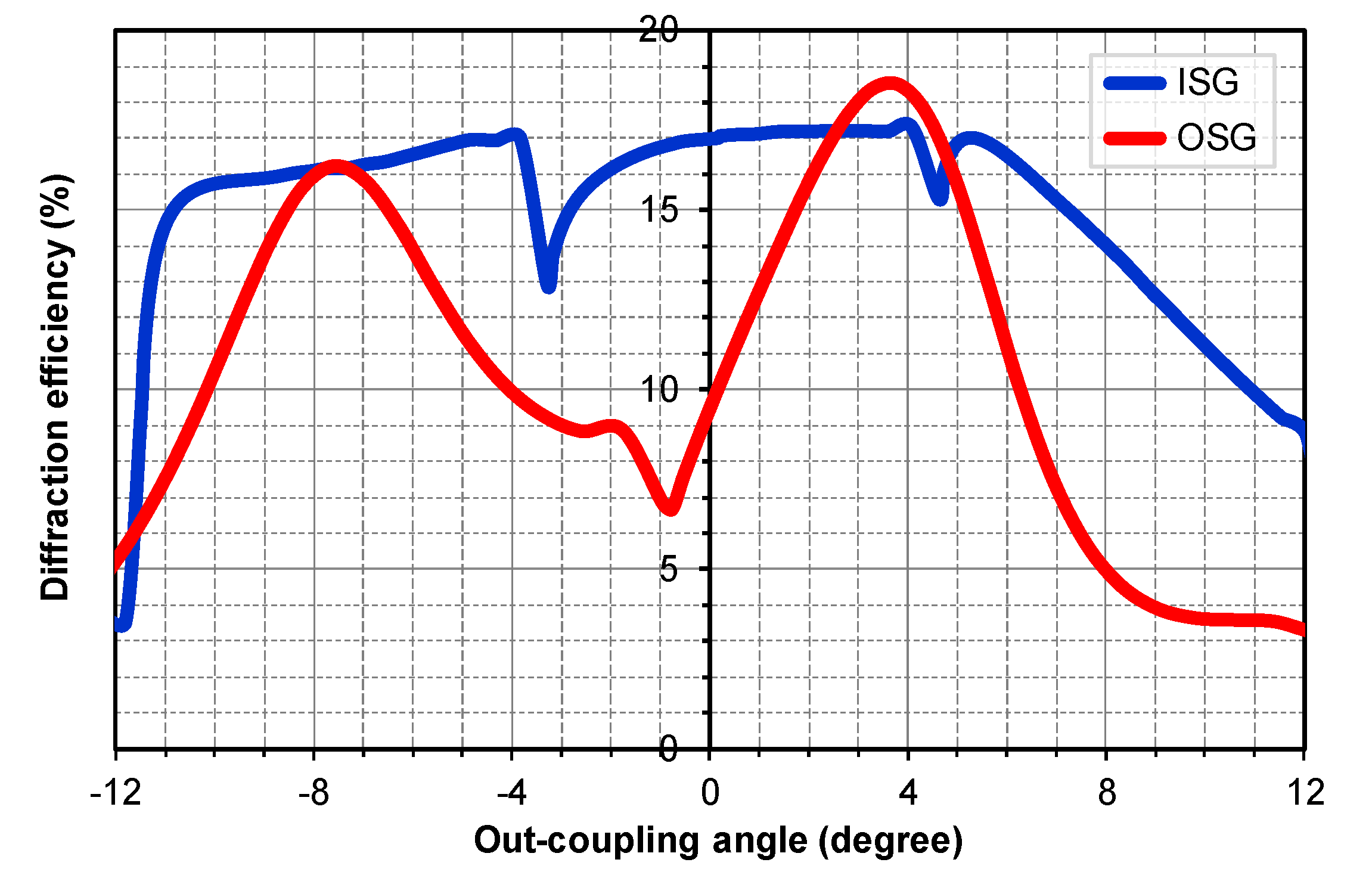
Figure 9.
Diffraction efficiencies of the ISG and OSG calculated with respect to the out-coupling angle for the wavelength of 565 nm. The average DEs of the ISG and OSG over the full horizontal/vertical FOV (±12°) are 14.40% and 10.53%, respectively.
Figure 9.
Diffraction efficiencies of the ISG and OSG calculated with respect to the out-coupling angle for the wavelength of 565 nm. The average DEs of the ISG and OSG over the full horizontal/vertical FOV (±12°) are 14.40% and 10.53%, respectively.
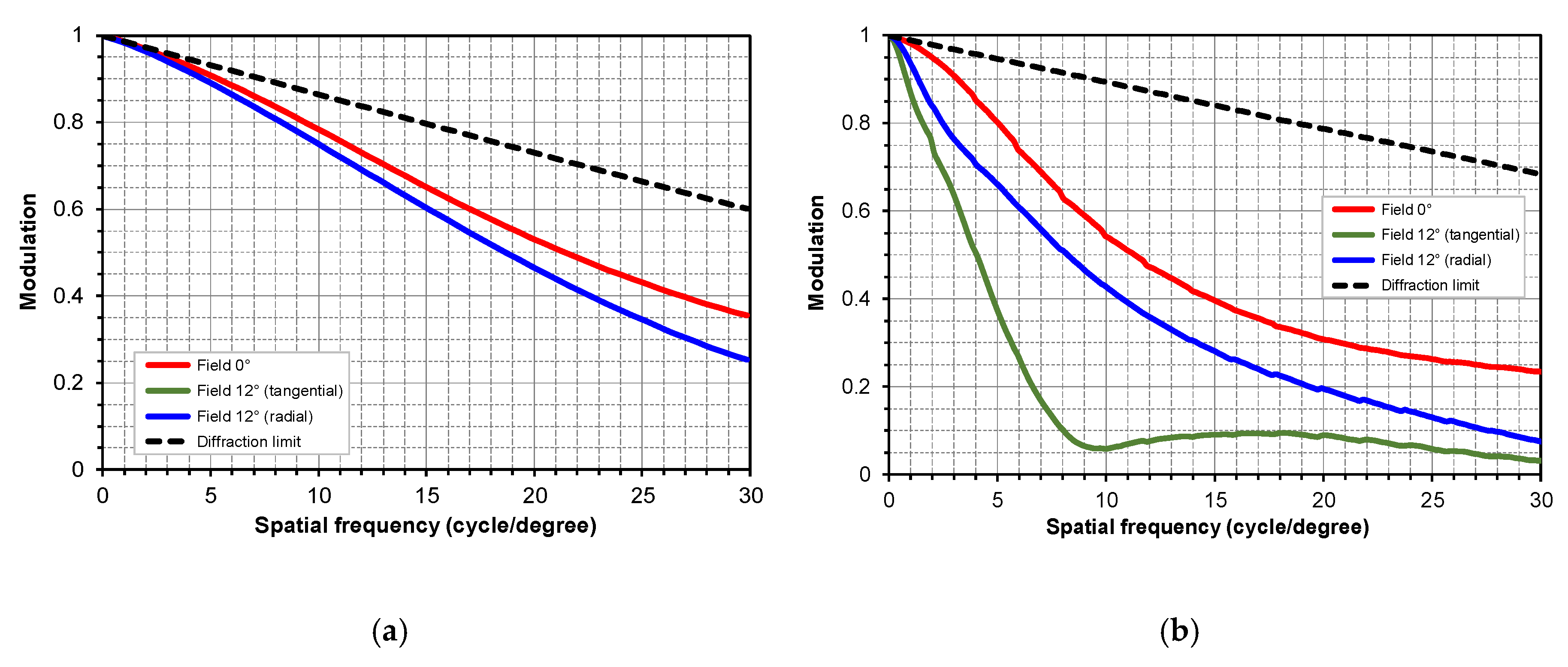
Figure 10.
Calculated MTFs of (a) real and (b) virtual images. At the spatial frequency of 30 cycle/degree, MTFs for all fields of the real and virtual images are above 0.252 and 0.032, respectively.
Figure 10.
Calculated MTFs of (a) real and (b) virtual images. At the spatial frequency of 30 cycle/degree, MTFs for all fields of the real and virtual images are above 0.252 and 0.032, respectively.
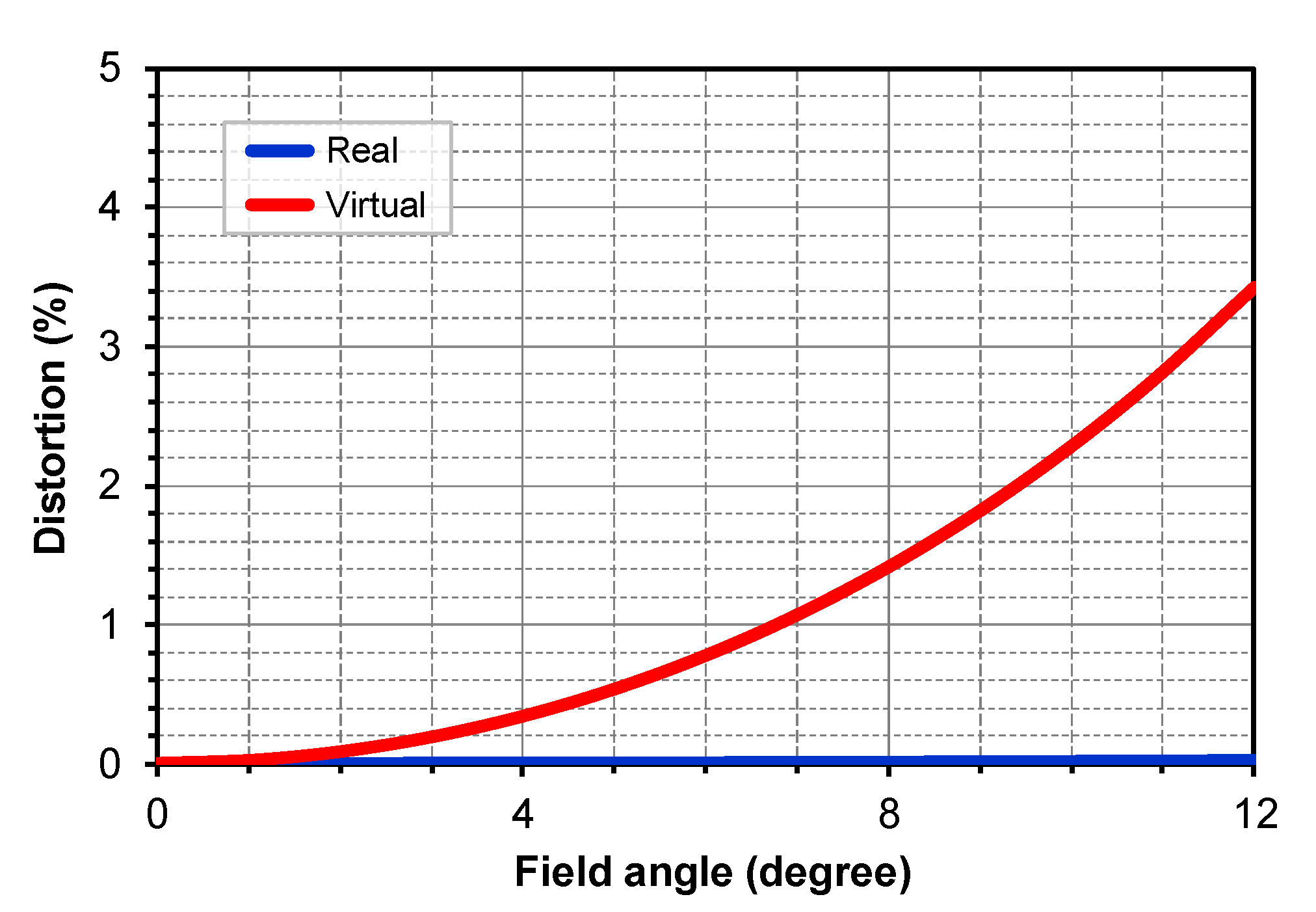
Figure 11.
Calculated distortion with respect to the field angle. It can be seen that the distortions are 0.02% and 3.4% for the real and virtual images, respectively.
Figure 11.
Calculated distortion with respect to the field angle. It can be seen that the distortions are 0.02% and 3.4% for the real and virtual images, respectively.
Figure 12.
(a) Original (photographer: C. P. Chen, location: Peterhof Grand Palace, St. Petersburg, Russia), (b) real, and (c) virtual images. Compared to the original one, the real image is virtually lossless, while the virtual image has a mild pincushion distortion and slightly decreased brightness.
Figure 12.
(a) Original (photographer: C. P. Chen, location: Peterhof Grand Palace, St. Petersburg, Russia), (b) real, and (c) virtual images. Compared to the original one, the real image is virtually lossless, while the virtual image has a mild pincushion distortion and slightly decreased brightness.
Table 1.
Parameters for the plano-concave lens.
Table 1.
Parameters for the plano-concave lens.
| Object | Parameter | Value |
|---|
| Plano-concave lens | W1 | 46 mm |
| W2 | 47.93 mm |
| H | 30 mm |
| T | 7.47 mm |
| γ | 75.52° |
| Pw | −3 m−1 |
| n@565 nm | 1.5880 1 |
| R | 0.1960 m |
Table 2.
Parameters of the pico projector.
Table 2.
Parameters of the pico projector.
| Object | Parameter | Value |
|---|
| Microdisplay | Dm (diagonal) | 0.233 inch |
| Dm (horizontal/vertical) | 0.165 inch |
| Resolution | 640 × 640 |
| Pixel size | 6.5 µm |
| CR | 100,000 |
| Projection lens | f | 10 mm |
| FOV (diagonal) | 33° |
| FOV (horizontal/vertical) | 24° |
| Aperture | 6 mm |
| ER | 12 mm |
| EP | 1 mm |
Table 3.
Optical surfaces used in the simulation of the real image.
Table 3.
Optical surfaces used in the simulation of the real image.
| Surface | Surface Type | Radius (mm) | Thickness (mm) | Refractive Index 1 | Semi-Aperture (mm) |
|---|
| real object | sphere | infinity | infinity | | |
| 1 | asphere | −196.0000 | 7.4700 | 1.5880 | 1.5000 |
| 2 | sphere | infinity | −336.2359 | | 2.6760 |
| real image | sphere | infinity | 0 | | 99.7948 |
Table 4.
Optical surfaces used in the simulation of the virtual image.
Table 4.
Optical surfaces used in the simulation of the virtual image.
| Surface | Surface Type | Radius (mm) | Thickness (mm) | Refractive Index 1 | Semi-Aperture (mm) |
|---|
| virtual image | sphere | infinity | infinity | | |
| 1 | asphere | 4.1494 | 3.6000 | 1.7258 | 3.0000 |
| 2 | asphere | 4.1379 | 10.0000 | | 2.2399 |
| microdisplay | sphere | infinity | 0.0000 | | 3.4613 |
Table 5.
Detailed parameters of aspherical surfaces for the real image.
Table 5.
Detailed parameters of aspherical surfaces for the real image.
| Surface | Y Radius (mm) | Conic Constant (K) | 4th Order Coefficient (A) | 6th Order Coefficient (B) | 8th Order Coefficient (C) |
|---|
| 1 | −196.0000 | 0.0000 | 0.0003 | −0.0001 | 2.7720 × 10−5 |
Table 6.
Detailed parameters of aspherical surfaces for the virtual image.
Table 6.
Detailed parameters of aspherical surfaces for the virtual image.
| Surface | Y Radius (mm) | Conic Constant (K) | 4th Order Coefficient (A) | 6th Order Coefficient (B) | 8th Order Coefficient (C) | 10th Order Coefficient (D) | 12th Order Coefficient (E) |
|---|
| 1 | 4.1494 | −0.1154 | 0.0003 | 5.7069 × 10−7 | 6.9614 × 10−6 | −5.4048 × 10−7 | 2.1806 × 10−8 |
| 2 | 4.1379 | −0.6547 | 0.0055 | 0.0003 | 0.0003 | −6.7023 × 10−5 | 9.9782 × 10−6 |
Table 7.
Optimized parameters of the ISG and OSG.
Table 7.
Optimized parameters of the ISG and OSG.
| Object | Sub-Object | Parameter | Value |
|---|
| ISG | Sub-grating A | p | 511 nm |
| h | 1015.80 nm |
| θg | 29.31° |
| w | 55.67 nm |
| Sub-grating B | p | 587 nm |
| h | 637.79 nm |
| θg | 29.31° |
| w | 272.30 nm |
| Sub-grating C | p | 688 nm |
| h | 697.85 nm |
| θg | 29.31° |
| w | 244.51 nm |
| Multiplexed grating | Pm | 19.95 μm |
| OSG | Sub-grating A | p | 317 nm |
| h | 702.98 nm |
| θg | 42.413° |
| w | 128.67 nm |
| Sub-grating B | p | 364 nm |
| h | 440.53 nm |
| θg | 42.413° |
| w | 237.36 nm |
| Sub-grating C | p | 427 nm |
| h | 633.81 nm |
| θg | 42.413° |
| w | 310.07 nm |
| Multiplexed grating | Pm | 12.39 μm |