COVID-19: A Comparison of Time Series Methods to Forecast Percentage of Active Cases per Population
Abstract
1. Introduction
2. Related Work
3. Description of Time Series Models
3.1. ARIMA: Auto-Regressive Integrated Moving Average
3.2. Holt–Winters Additive Model (HWAAS): Exponential Smoothing with Additive Trend and Additive Seasonality
3.3. TBAT
3.4. Prophet: Automatic Forecasting Procedure
3.5. DeepAR: Probabilistic Forecasting with Auto-Regressive Recurrent Networks
3.6. N-Beats: Neural Basis Expansion Analysis for Interpretable Time Series Forecasting
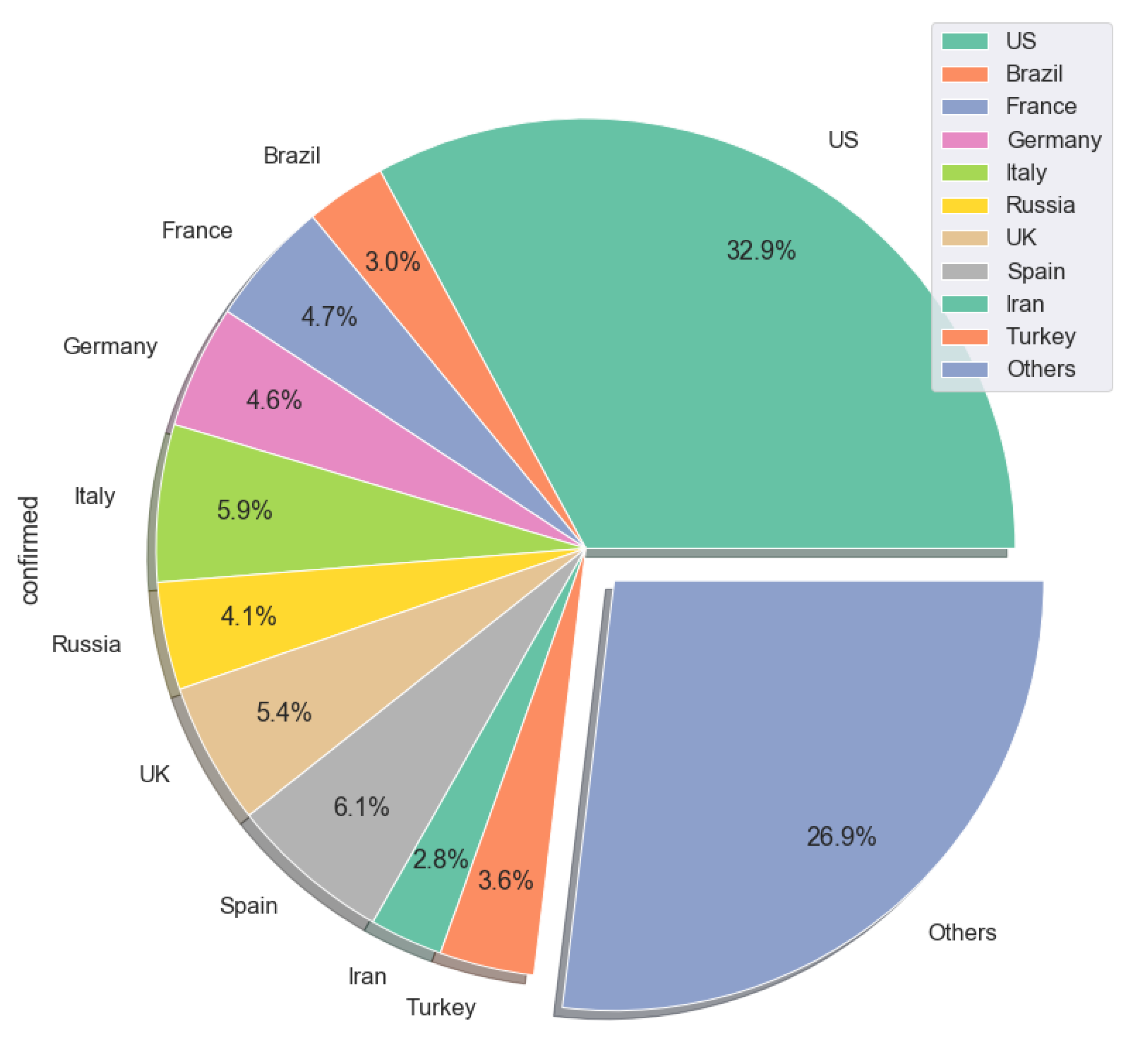
4. COVID-19 Data: Deaths, Confirmed, Recovered
- 1
- The number of confirmed COVID-19 cases
- 2
- The number of recovered COVID-19 patients
- 3
- The death toll due to COVID-19
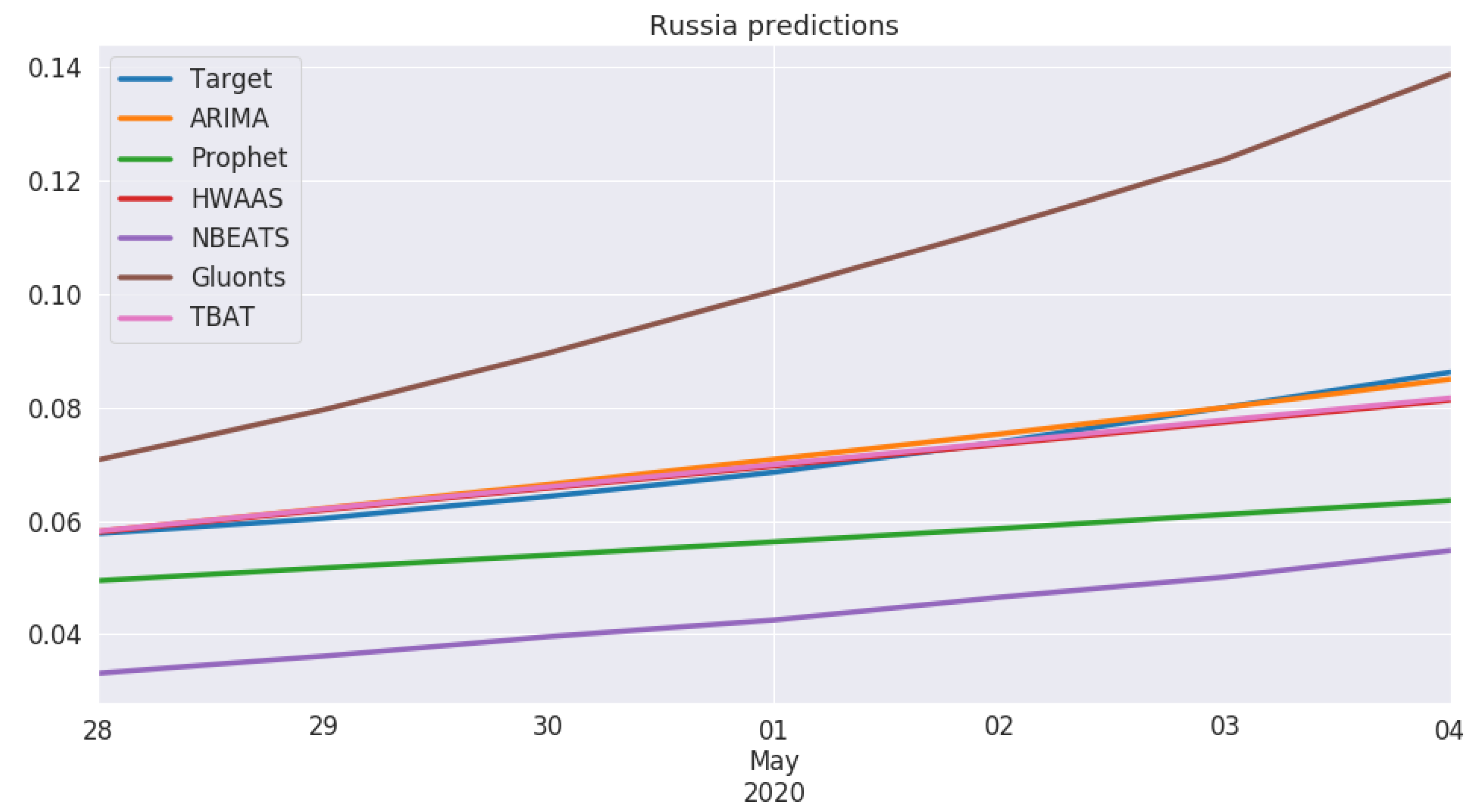
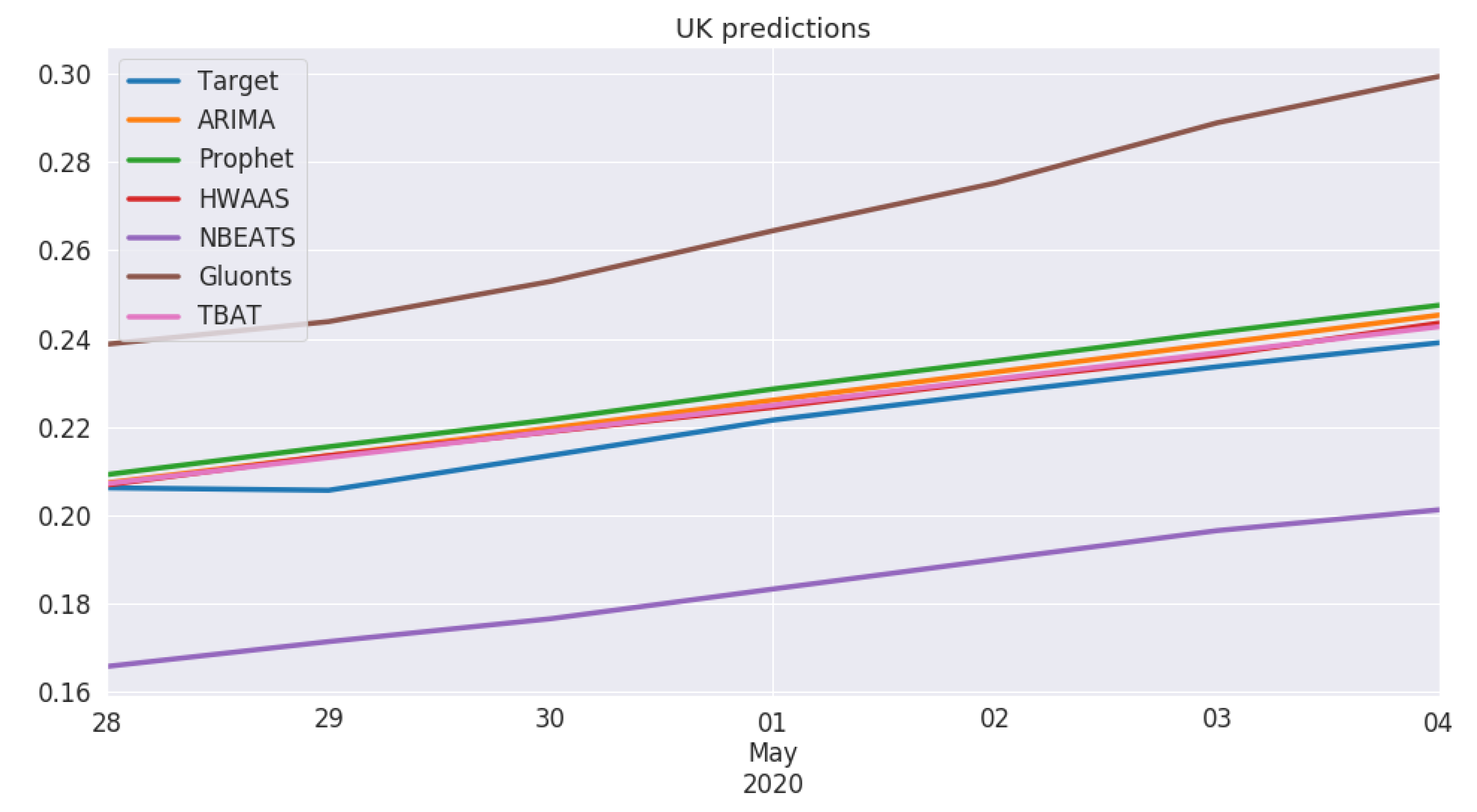
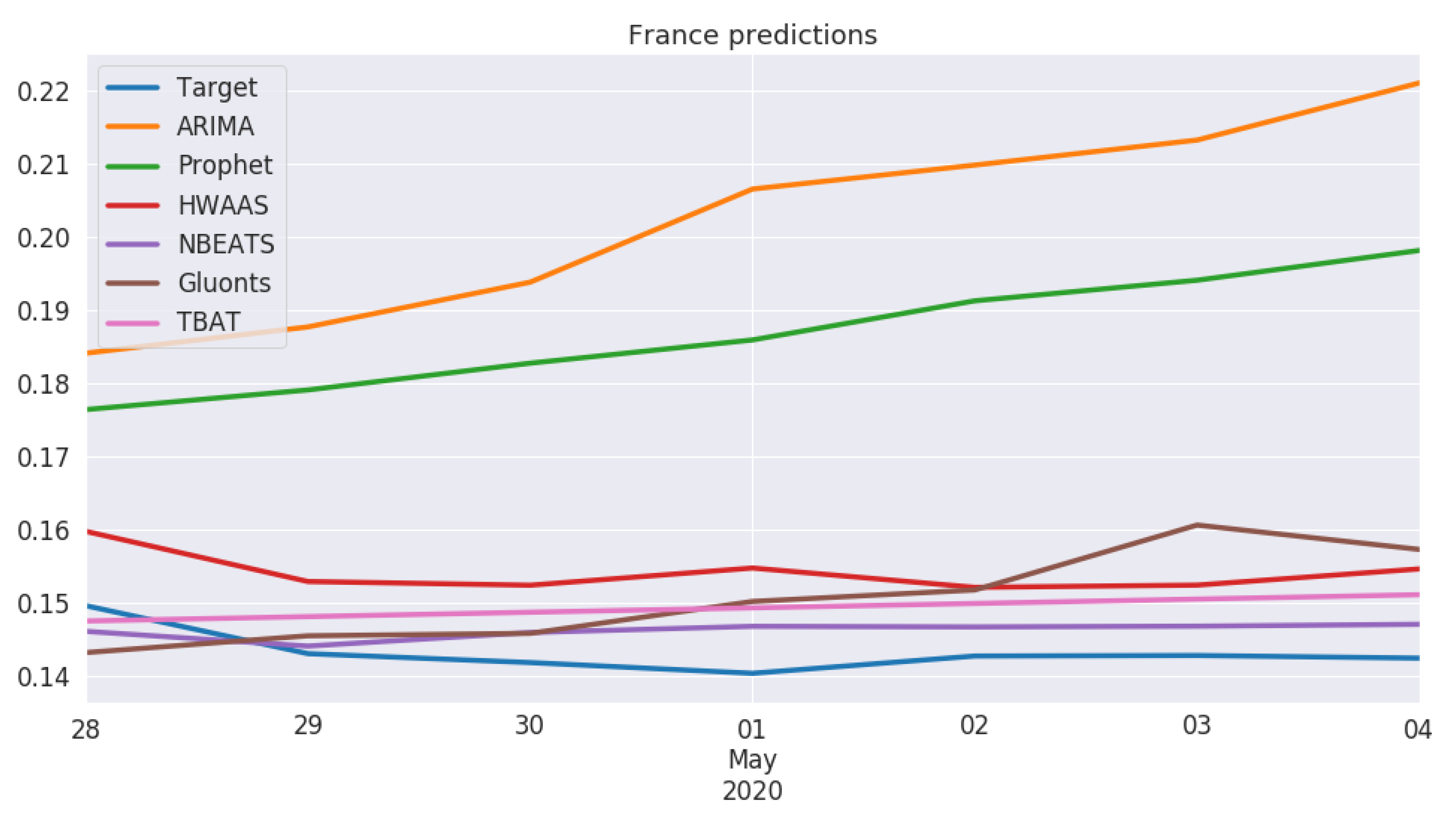
5. Experiments and Results
5.1. Modeling Process
5.2. Model Performance
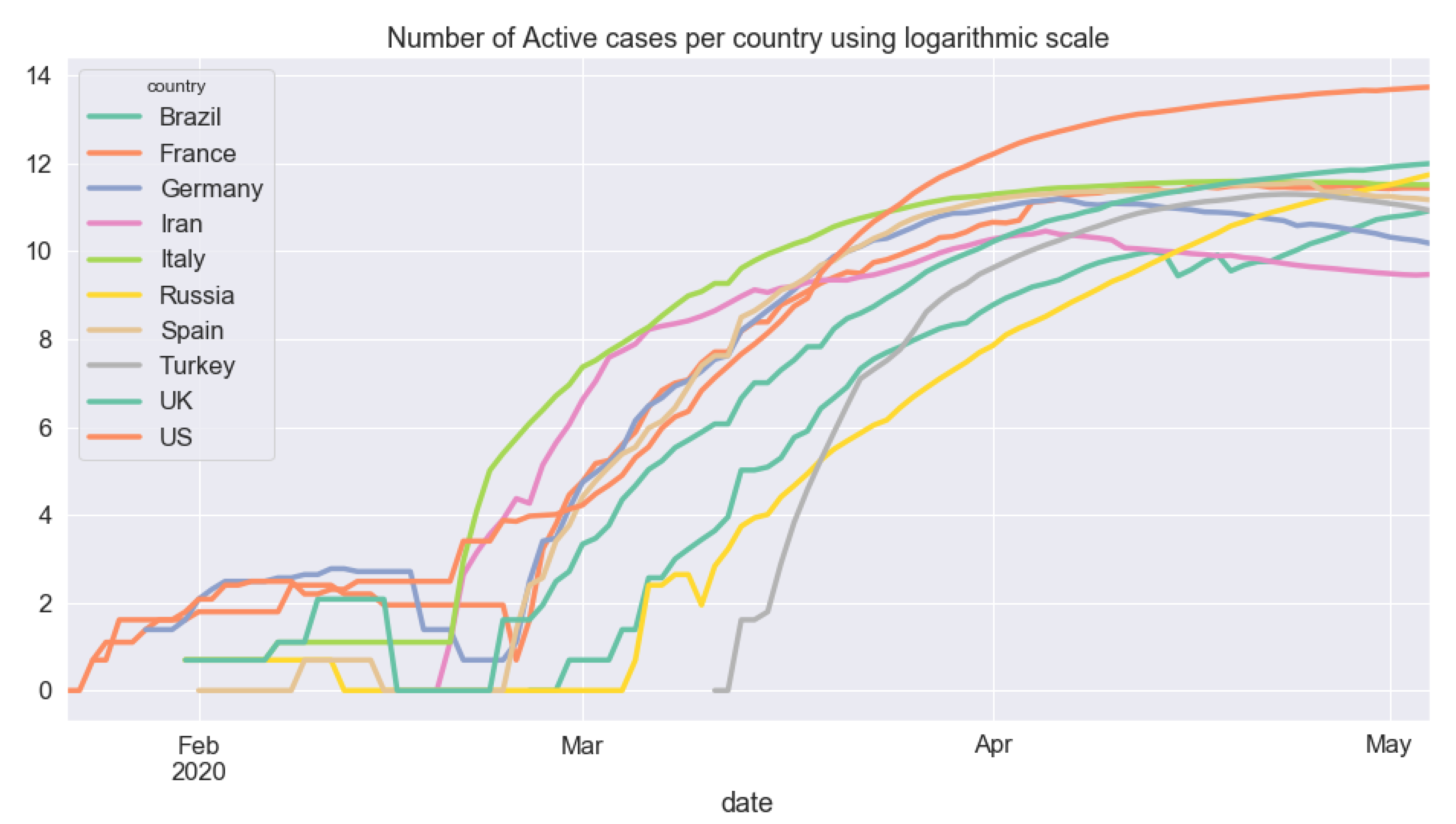
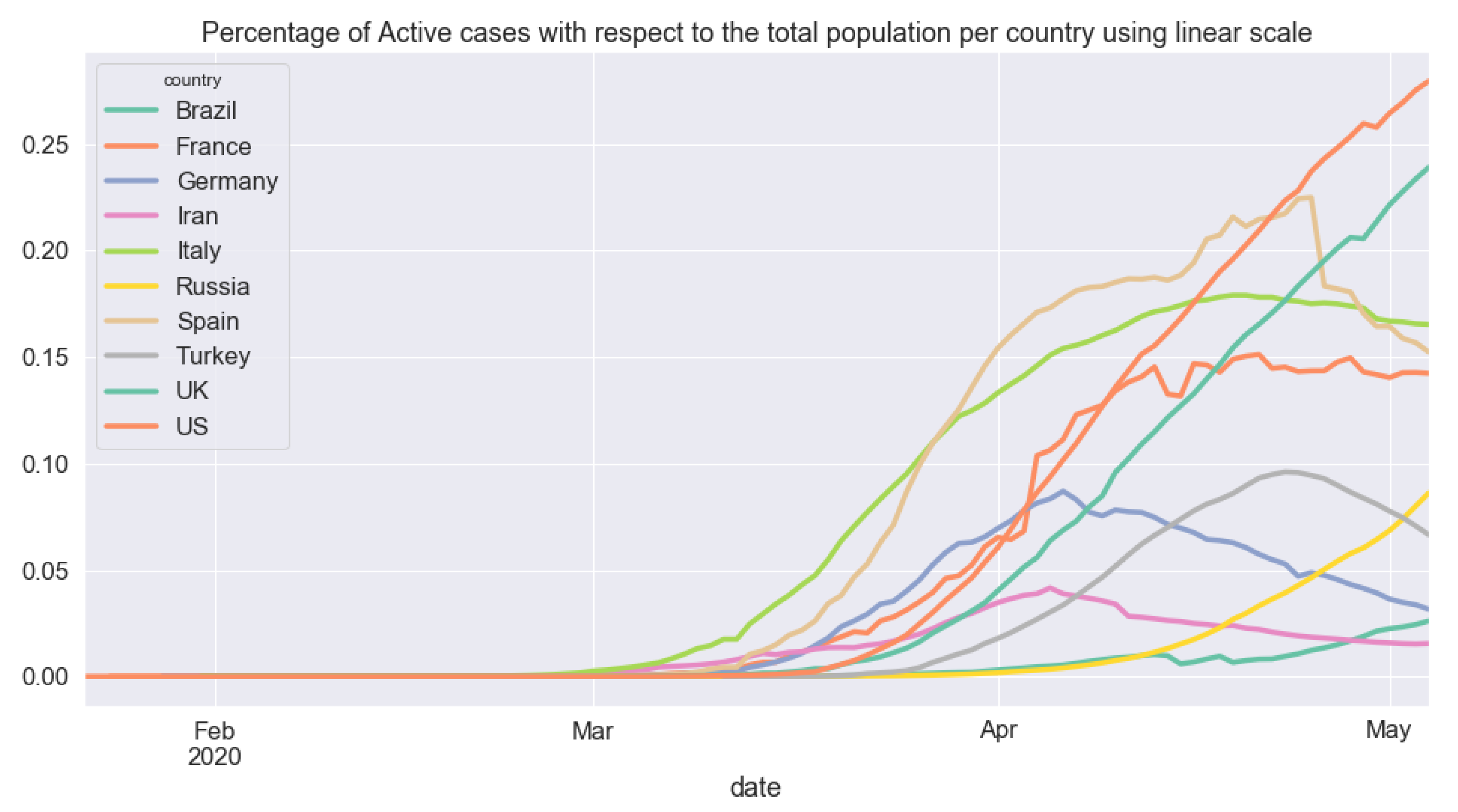
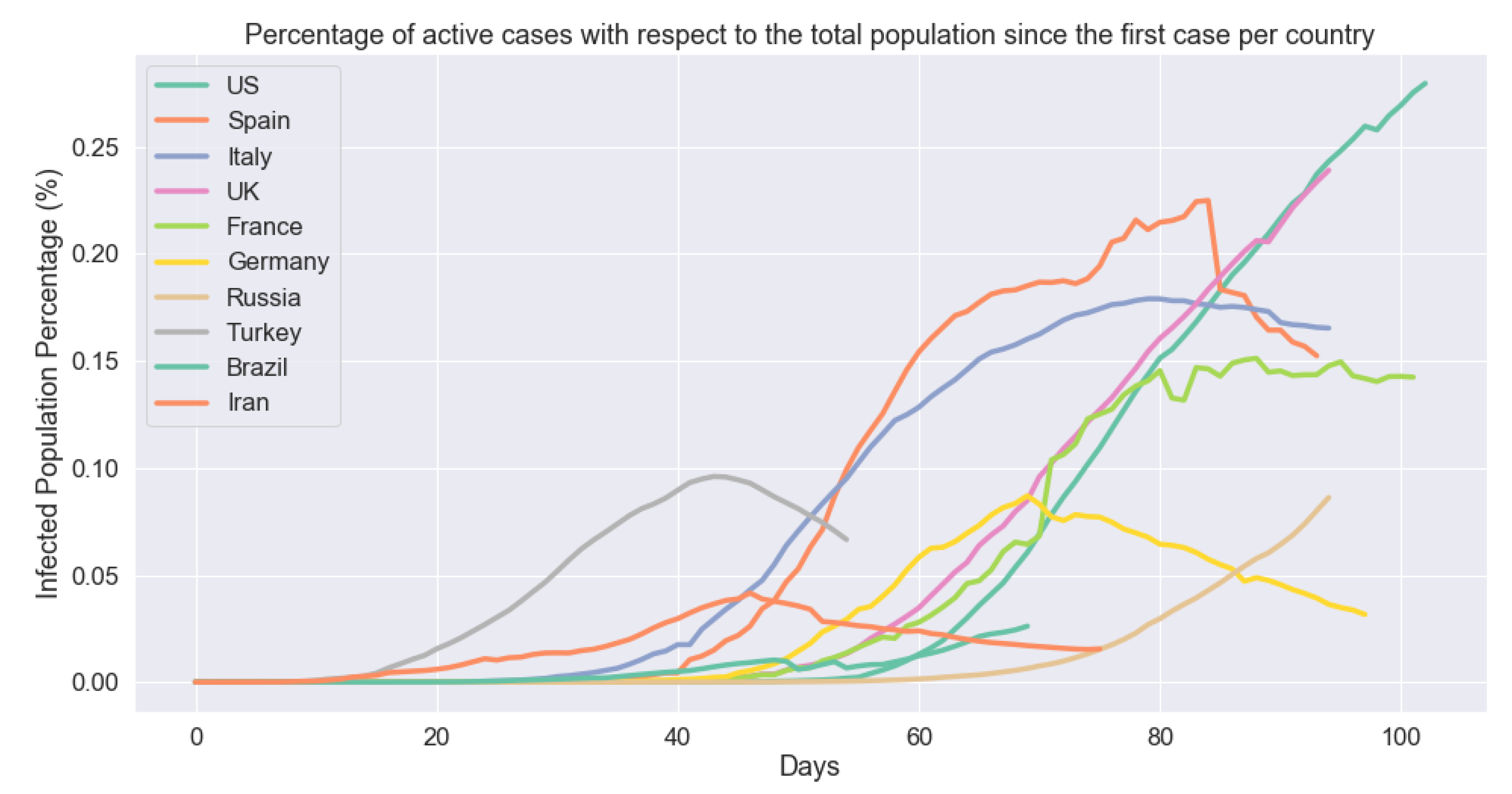
5.3. Cross-Country Comparison
- 1
- Country-specific climatic and geographical characteristics
- 2
- Different population-related attributes such as population density among the different countries
- 3
- Discrepancies in testing and measuring procedures and therefore data collection among the different countries
- 4
- Diversity in terms of quarantine and other social distancing measures implemented in the different countries as well as the timing, duration and severity of such measures
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- World Health Organization. Naming the Coronavirus Disease (COVID-19) and the Virus that Causes it. World Health Organization. 2020. Available online: https://www.who.int/emergencies/diseases/novel-coronavirus-2019/technical-guidance/naming-the-coronavirus-disease- (accessed on 2 May 2020).
- Coronaviridae Study Group. The species Severe acute respiratory syndrome-related coronavirus: Classifying 2019-nCoV and naming it SARS-CoV-2. Nat. Microbiol. 2020, 5, 536. [Google Scholar] [CrossRef]
- Lu, H.; Stratton, C.W.; Tang, Y.W. Outbreak of Pneumonia of Unknown Etiology in Wuhan China: The Mystery and the Miracle. J. Med Virol. 2020, 92, 401–402. [Google Scholar] [CrossRef]
- Fernandes, N. Economic Effects of Coronavirus Outbreak (COVID-19) on the World Economy. 2020. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3557504 (accessed on 4 May 2020).
- J. CSSE. Coronavirus COVID-19 Global Cases by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University (JHU). 2020. Available online: https://coronavirus.jhu.edu/map.html (accessed on 4 May 2020).
- McCloskey, B.; Zumla, A.; Ippolito, G.; Blumberg, L.; Arbon, P.; Cicero, A.; Endericks, T.; Lim, P.L.; Borodina, M.; M.G.E. Group. Mass gathering events and reducing further global spread of COVID-19: A political and public health dilemma. Lancet 2020, 395, 1096. [Google Scholar] [CrossRef]
- Preiser, W.; Van Zyl, G.; Dramowski, A. COVID-19: Getting ahead of the epidemic curve by early implementation of social distancing. S. Afr. Med J. 2020, 110, 1. [Google Scholar] [CrossRef]
- Klompas, M. Coronavirus Disease 2019 (COVID-19): Protecting hospitals from the invisible. Ann. Intern. Med. 2020, 172, 619–620. [Google Scholar] [CrossRef]
- WHO. Laboratory Testing for Coronavirus Disease 2019 (COVID-19) in Suspected Human Cases: Interim Guidance, 2 March 2020; Technical report. WHO: Geneva, Switzerland, 2020. [Google Scholar]
- Roser, M.; Ritchie, H.; Ortiz-Ospina, E. Coronavirus Disease (COVID-19)–Statistics and Research. Our World Data 2020. Available online: https://ourworldindata.org/coronavirus (accessed on 4 May 2020).
- Petherick, A. Developing antibody tests for SARS-CoV-2. Lancet 2020, 395, 1101–1102. [Google Scholar] [CrossRef]
- Vogel, G. New Blood Tests for Antibodies Could Show True Scale of Coronavirus Pandemic. Science 2020, 19. Available online: https://www.sciencemag.org/news/2020/03/new-blood-tests-antibodies-could-show-true-scale-coronavirus-pandemic (accessed on 4 May 2020). [CrossRef]
- Pang, J.; Wang, M.X.; Ang, I.Y.H.; Tan, S.H.X.; Lewis, R.F.; Chen, J.I.P.; Gutierrez, R.A.; Gwee, S.X.W.; Chua, P.E.Y.; Yang, Q.; et al. Potential rapid diagnostics, vaccine and therapeutics for 2019 novel coronavirus (2019-nCoV): A systematic review. J. Clin. Med. 2020, 9, 623. [Google Scholar] [CrossRef]
- Box, G.; Jenkins, G. Time Series Analysis Forecasting and Control/’Holden Day, San Francisco, California, 1970; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Chatfield, C. The Holt–Winters forecasting procedure. J. R. Stat. Soc. Ser. 1978, 27, 264–279. [Google Scholar] [CrossRef]
- De Livera, A.M.; Hyndman, R.J.; Snyder, R.D. Forecasting time series with complex seasonal patterns using exponential smoothing. J. Am. Stat. Assoc. 2011, 106, 1513–1527. [Google Scholar] [CrossRef]
- Taylor, S.J.; Letham, B. Forecasting at scale. Am. Stat. 2018, 72, 37–45. [Google Scholar] [CrossRef]
- Salinas, D.; Flunkert, V.; Gasthaus, J.; Januschowski, T. DeepAR: Probabilistic forecasting with autoregressive recurrent networks. Int. J. Forecast. 2019. [Google Scholar] [CrossRef]
- Alexandrov, A.; Benidis, K.; Bohlke-Schneider, M.; Flunkert, V.; Gasthaus, J.; Januschowski, T.; Maddix, D.C.; Rangapuram, S.; Salinas, D.; Schulz, J.; et al. Gluonts: Probabilistic time series models in python. arXiv 2019, arXiv:1906.05264. [Google Scholar]
- Oreshkin, B.N.; Carpov, D.; Chapados, N.; Bengio, Y. N-BEATS: Neural basis expansion analysis for interpretable time series forecasting. arXiv 2019, arXiv:1905.10437. [Google Scholar]
- Chadsuthi, S.; Modchang, C.; Lenbury, Y.; Iamsirithaworn, S.; Triampo, W. Modeling seasonal leptospirosis transmission and its association with rainfall and temperature in Thailand using time–series and ARIMAX analyses. Asian Pac. J. Trop. Med. 2012, 5, 539–546. [Google Scholar] [CrossRef]
- Hanf, M.; Adenis, A.; Nacher, M.; Carme, B. The role of El Ni no southern oscillation (ENSO) on variations of monthly Plasmodium falciparum malaria cases at the cayenne general hospital, 1996–2009, French Guiana. Malar. J. 2011, 10, 100. [Google Scholar] [CrossRef] [PubMed]
- Song, X.; Xiao, J.; Deng, J.; Kang, Q.; Zhang, Y.; Xu, J. Time series analysis of influenza incidence in Chinese provinces from 2004 to 2011. Medicine 2016, 95, e3929. [Google Scholar] [CrossRef]
- Adhikari, R.; Agrawal, R.K. An introductory study on time series modeling and forecasting. arXiv 2013, arXiv:1302.6613. [Google Scholar]
- Yin, R.; Luusua, E.; Dabrowski, J.; Zhang, Y.; Kwoh, C.K. Tempel: Time-series mutation prediction of influenza A viruses via attention-based recurrent neural networks. Bioinformatics 2020, 36, 2697–2704. [Google Scholar] [CrossRef]
- Lee, K.; Agrawal, A.; Choudhary, A. Forecasting Influenza Levels Using Real-time Social Media Streams. In Proceedings of the 2017 IEEE International Conference on Healthcare Informatics (ICHI), Park City, UT, USA, 23–26 August 2017; pp. 409–414. [Google Scholar]
- Zhang, Y.; Yakob, L.; Bonsall, M.B.; Hu, W. Predicting seasonal influenza epidemics using cross-hemisphere influenza surveillance data and local Internet query data. Sci. Rep. 2019, 9, 1–7. [Google Scholar] [CrossRef]
- Soebiyanto, R.P.; Adimi, F.; Kiang, R.K. Modeling and predicting seasonal influenza transmission in warm regions using climatological parameters. PLoS ONE 2010, 5, e9450. [Google Scholar] [CrossRef]
- Dominguez, A.; Mu noz, P.; Martínez, A.; Orcau, A. Monitoring mortality as an indicator of influenza in Catalonia, Spain. J. Epidemiol. Community Health 1996, 50, 293–298. [Google Scholar] [CrossRef] [PubMed]
- Roosa, K.; Lee, Y.; Luo, R.; Kirpich, A.; Rothenberg, R.; Hyman, J.; Yan, P.; Chowell, G. Real-time forecasts of the COVID-19 epidemic in China from 5 February to 24 February 2020. Infect. Dis. Model. 2020, 5, 256–263. [Google Scholar] [PubMed]
- Yang, Z.; Zeng, Z.; Wang, K.; Wong, S.S.; Liang, W.; Zanin, M.; Liu, P.; Cao, X.; Gao, Z.; Mai, Z.; et al. Modified SEIR and AI prediction of the epidemics trend of COVID-19 in China under public health interventions. J. Thorac. Dis. 2020, 12, 165. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Feng, W.; Quan, Y.H. Trend and forecasting of the COVID-19 outbreak in China. J. Infect. 2020, 80, 469–496. [Google Scholar]
- Hu, Z.; Ge, Q.; Jin, L.; Xiong, M. Artificial intelligence forecasting of covid-19 in china. arXiv 2020, arXiv:2002.07112. [Google Scholar]
- Al-qaness, M.A.; Ewees, A.A.; Fan, H.; Abd El Aziz, M. Optimization method for forecasting confirmed cases of covid-19 in China. J. Clin. Med. 2020, 9, 674. [Google Scholar] [CrossRef]
- Fanelli, D.; Piazza, F. Analysis and forecast of COVID-19 spreading in China, Italy and France. Chaos Solitons Fractals 2020, 134, 109761. [Google Scholar] [CrossRef]
- Wu, J.T.; Leung, K.; Leung, G.M. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: A modelling study. Lancet 2020, 395, 689–697. [Google Scholar] [CrossRef]
- Anastassopoulou, C.; Russo, L.; Tsakris, A.; Siettos, C. Data-based analysis, modelling and forecasting of the COVID-19 outbreak. PLoS ONE 2020, 15, e0230405. [Google Scholar] [CrossRef]
- Zhang, S.; Diao, M.; Yu, W.; Pei, L.; Lin, Z.; Chen, D. Estimation of the reproductive number of novel coronavirus (COVID-19) and the probable outbreak size on the Diamond Princess cruise ship: A data-driven analysis. Int. J. Infect. Dis. 2020, 93, 201–204. [Google Scholar] [CrossRef]
- IHME COVID-19 Health Service Utilization Forecasting Team. Forecasting COVID-19 impact on hospital bed-days, ICU-days, ventilator-days and deaths by US state in the next 4 months. medRxiv 2020. [Google Scholar] [CrossRef]
- Petropoulos, F.; Makridakis, S. Forecasting the novel coronavirus COVID-19. PLoS ONE 2020, 15, e0231236. [Google Scholar] [CrossRef] [PubMed]
- Yule, G.U. Why do we sometimes get nonsense-correlations between Time-Series?–a study in sampling and the nature of time-series. J. R. Stat. Soc. 1926, 89, 1–63. [Google Scholar] [CrossRef]
- Wold, H. A Study in Analysis of Stationary Time Series. J. R. Stat. Soc. 1939, 102, 295. [Google Scholar]
- McKenzie, E. General exponential smoothing and the equivalent ARMA process. J. Forecast. 1984, 3, 333–344. [Google Scholar] [CrossRef]
- Kane, M.J.; Price, N.; Scotch, M.; Rabinowitz, P. Comparison of ARIMA and Random Forest time series models for prediction of avian influenza H5N1 outbreaks. BMC Bioinform. 2014, 15, 276. [Google Scholar] [CrossRef]
- Zhang, G.P. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Kalekar, P.S. Time series forecasting using holt-winters exponential smoothing. Kanwal Rekhi Sch. Inf. Technol. 2004, 4329008, 1–13. [Google Scholar]
- Chatfield, C.; Yar, M. Holt-Winters forecasting: Some practical issues. J. R. Stat. Soc. Ser. 1988, 37, 129–140. [Google Scholar] [CrossRef]
- Gelper, S.; Fried, R.; Croux, C. Robust forecasting with exponential and Holt–Winters smoothing. J. Forecast. 2010, 29, 285–300. [Google Scholar]
- Harvey, A.; Koopman, S.J.; Riani, M. The modeling and seasonal adjustment of weekly observations. J. Bus. Econ. Stat. 1997, 15, 354–368. [Google Scholar]
- Box, G.E.; Cox, D.R. An analysis of transformations. J. R. Stat. Soc. Ser. 1964, 26, 211–243. [Google Scholar] [CrossRef]
- Hyndman, R.; Koehler, A.B.; Ord, J.K.; Snyder, R.D. Forecasting with Exponential Smoothing: The State Space Approach; Springer Science & Business Media: Berlin, Germany, 2008. [Google Scholar]
- Harvey, A.C.; Peters, S. Estimation procedures for structural time series models. J. Forecast. 1990, 9, 89–108. [Google Scholar] [CrossRef]
- Hutchinson, G.E. An Introduction to Population Ecology; Number 504: 51 HUT; John Wiley & Sons: Hoboken, NJ, USA, 1978. [Google Scholar]
- Harvey, A.C.; Shephard, N. Estimation and Testing of Stochastic Variance Models; Technical report. Suntory and Toyota International Centres for Economics and Related: London, UK, 1993. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. LSTM Can Solve Hard Long Time Lag Problems. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 1997; pp. 473–479. [Google Scholar]
- Graves, A. Generating sequences with recurrent neural networks. arXiv 2013, arXiv:1308.0850. [Google Scholar]
- Oord, A.v.d.; Dieleman, S.; Zen, H.; Simonyan, K.; Vinyals, O.; Graves, A.; Kalchbrenner, N.; Senior, A.; Kavukcuoglu, K. Wavenet: A generative model for raw audio. arXiv 2016, arXiv:1609.03499. [Google Scholar]
- Zaremba, W.; Sutskever, I.; Vinyals, O. Recurrent neural network regularization. arXiv 2014, arXiv:1409.2329. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Cleveland, R.B.; Cleveland, W.S.; McRae, J.E.; Terpenning, I. STL: A seasonal-trend decomposition. J. Off. Stat. 1990, 6, 3–73. [Google Scholar]
- Novel Corona Virus 2019 Dataset. Available online: https://www.kaggle.com/sudalairajkumar/novel-corona-virus-2019-dataset (accessed on 4 May 2020).
- Population by Country Dataset—2020. Available online: https://www.kaggle.com/tanuprabhu/population-by-country-2020 (accessed on 4 May 2020).
- Friedman, M. A comparison of alternative tests of significance for the problem of m rankings. Ann. Math. Stat. 1940, 11, 86–92. [Google Scholar] [CrossRef]
- Holm, S. A simple sequentially rejective multiple test procedure. Scand. J. Stat. 1979, 6, 65–70. [Google Scholar]
| US | Spain | Italy | UK | France | |
|---|---|---|---|---|---|
| ARIMA | 0.007421 | 0.080094 | 0.005628 | 0.005484 | 0.060824 |
| Prophet | 0.013877 | 0.065433 | 0.019217 | 0.007634 | 0.044482 |
| HWAAS | 0.172957 | 0.031497 | 0.006616 | 0.004366 | 0.011007 |
| NBEATS | 0.036958 | 0.050492 | 0.008645 | 0.037623 | 0.004220 |
| Gluonts | 0.044805 | 0.108842 | 0.043551 | 0.046134 | 0.010549 |
| TBAT | 0.009873 | 0.029295 | 0.005810 | 0.004310 | 0.007003 |
| Germany | Russia | Turkey | Brazil | Iran | |
| ARIMA | 0.006431 | 0.001536 | 0.004442 | 0.004194 | 0.002628 |
| Prophet | 0.037139 | 0.014681 | 0.044595 | 0.009279 | 0.016281 |
| HWAAS | 0.004586 | 0.002295 | 0.000887 | 0.005717 | 0.001046 |
| NBEATS | 0.013192 | 0.027078 | 0.018265 | 0.010870 | 0.003745 |
| Gluonts | 0.057523 | 0.034479 | 0.093839 | 0.002836 | 0.002277 |
| TBAT | 0.003389 | 0.002193 | 0.001946 | 0.005621 | 0.000425 |
| Rank | Algorithm |
|---|---|
| 1.70000 | TBAT |
| 2.90000 | ARIMA |
| 2.90000 | HWAAS |
| 4.10000 | NBEATS |
| 4.60000 | Prophet |
| 4.80000 | Gluonts |
| Comparison | Statistic | Adjusted p-Value | Result |
|---|---|---|---|
| TBAT vs Gluonts | 3.70521 | 0.00106 | H0 is rejected |
| TBAT vs Prophet | 3.46616 | 0.00211 | H0 is rejected |
| TBAT vs NBEATS | 2.86855 | 0.01237 | H0 is rejected |
| TBAT vs ARIMA | 1.43427 | 0.30299 | H0 is accepted |
| TBAT vs HWAAS | 1.43427 | 0.30299 | H0 is accepted |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papastefanopoulos, V.; Linardatos, P.; Kotsiantis, S. COVID-19: A Comparison of Time Series Methods to Forecast Percentage of Active Cases per Population. Appl. Sci. 2020, 10, 3880. https://doi.org/10.3390/app10113880
Papastefanopoulos V, Linardatos P, Kotsiantis S. COVID-19: A Comparison of Time Series Methods to Forecast Percentage of Active Cases per Population. Applied Sciences. 2020; 10(11):3880. https://doi.org/10.3390/app10113880
Chicago/Turabian StylePapastefanopoulos, Vasilis, Pantelis Linardatos, and Sotiris Kotsiantis. 2020. "COVID-19: A Comparison of Time Series Methods to Forecast Percentage of Active Cases per Population" Applied Sciences 10, no. 11: 3880. https://doi.org/10.3390/app10113880
APA StylePapastefanopoulos, V., Linardatos, P., & Kotsiantis, S. (2020). COVID-19: A Comparison of Time Series Methods to Forecast Percentage of Active Cases per Population. Applied Sciences, 10(11), 3880. https://doi.org/10.3390/app10113880







