Performance Evaluation of Two Machine Learning Techniques in Heating and Cooling Loads Forecasting of Residential Buildings
Abstract
1. Introduction
2. Case Study
3. Methods
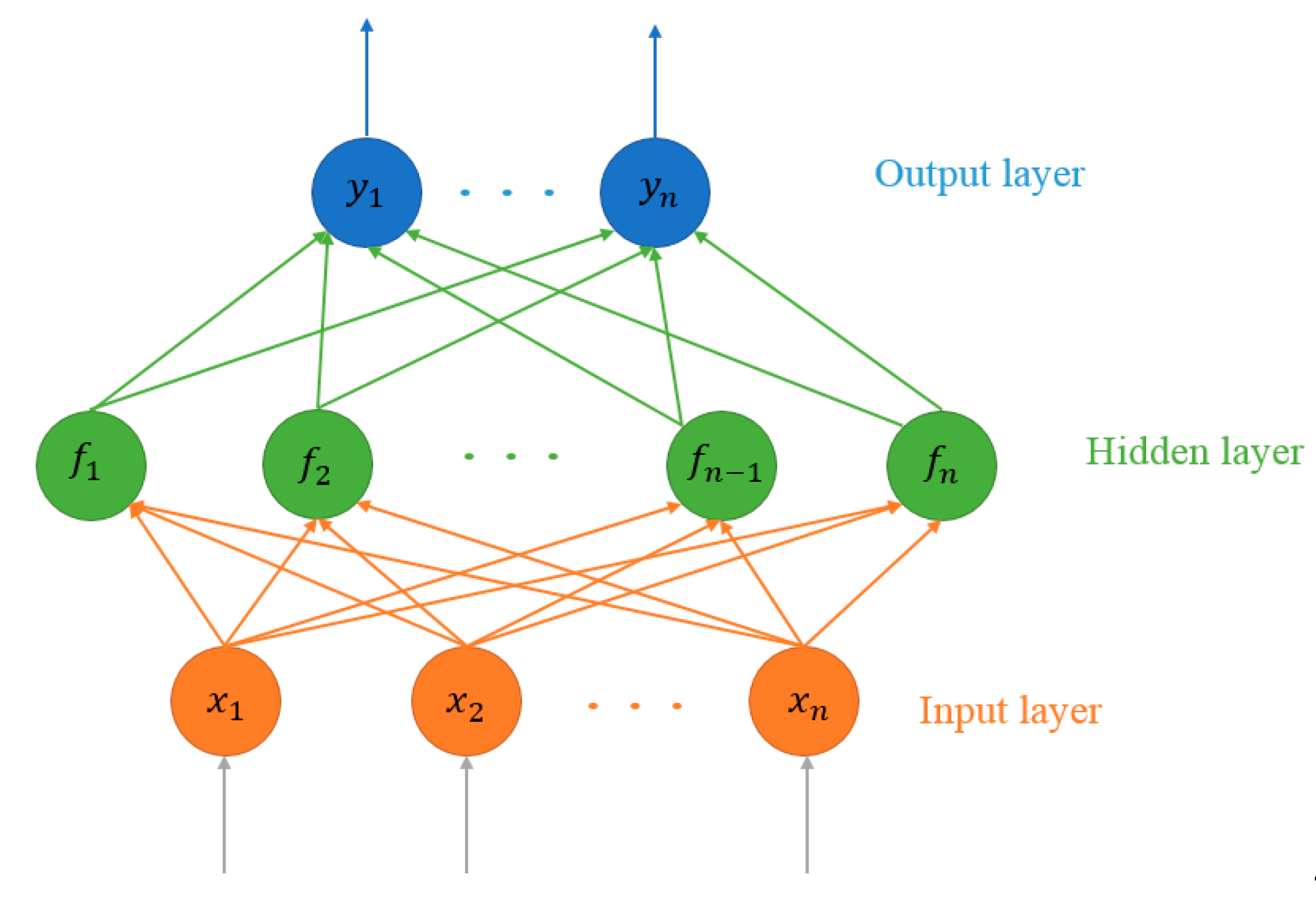
3.1. Multilayer Perceptron (MLP)
3.2. Support Vector Regression (SVR)
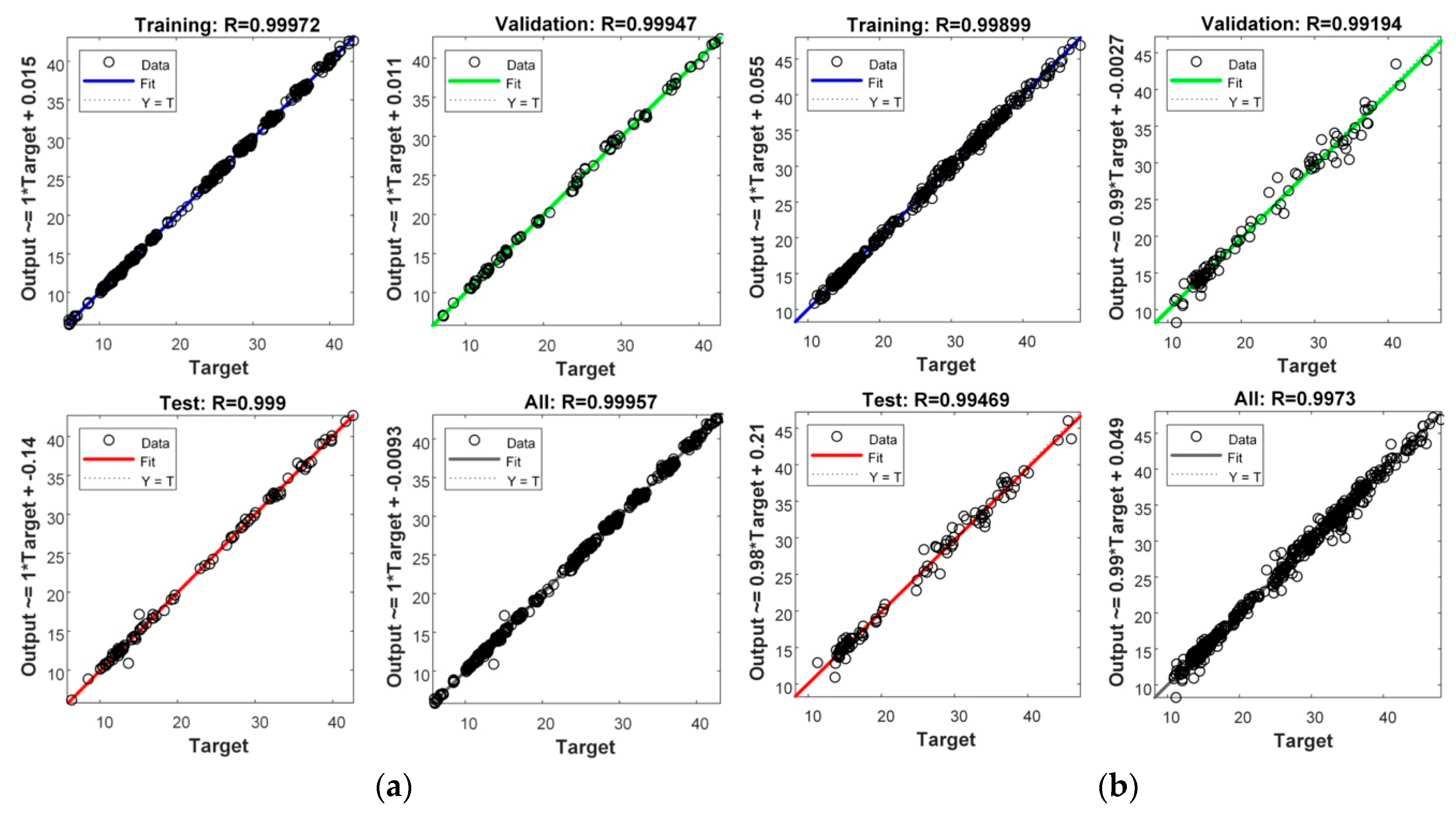
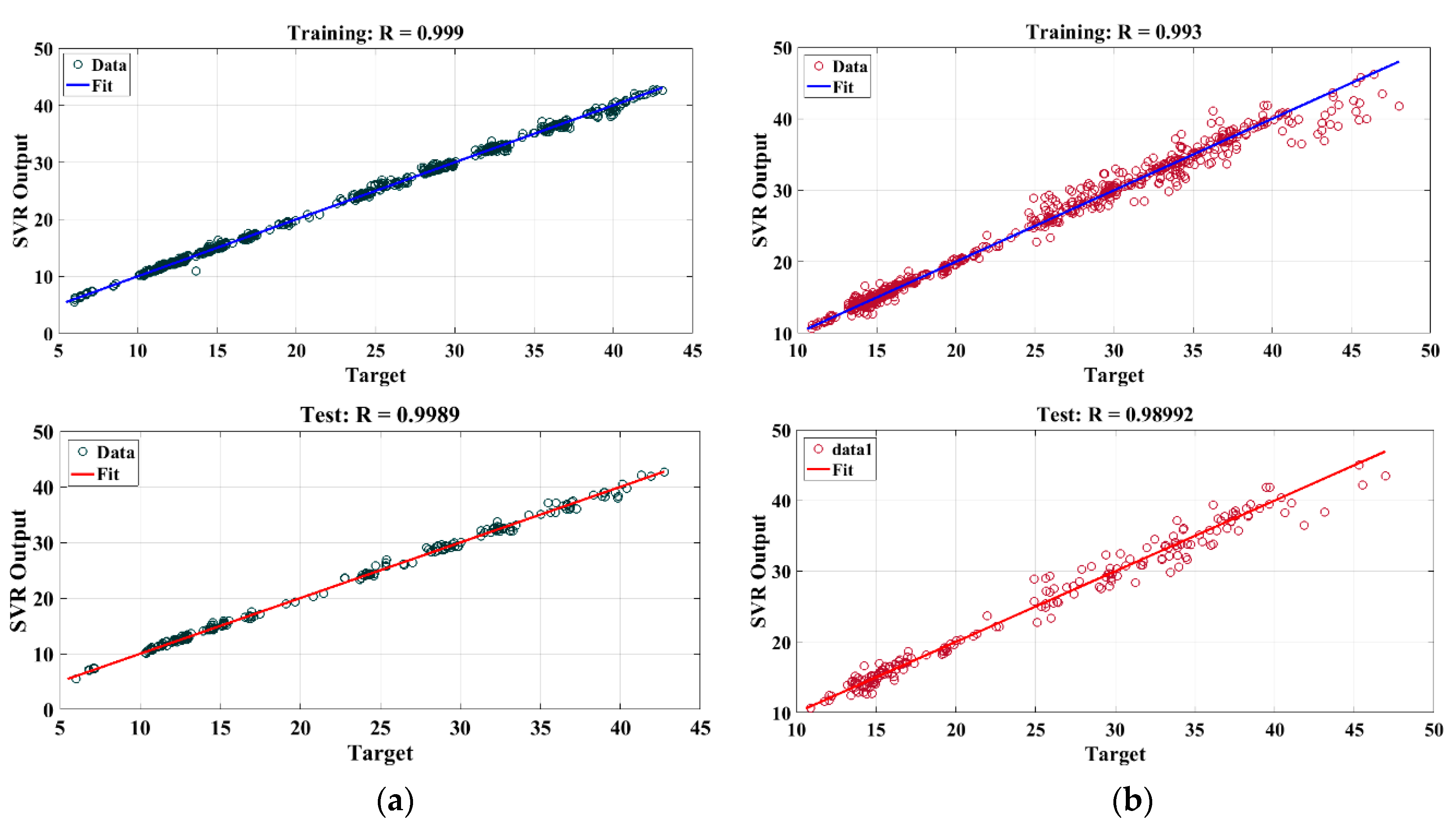
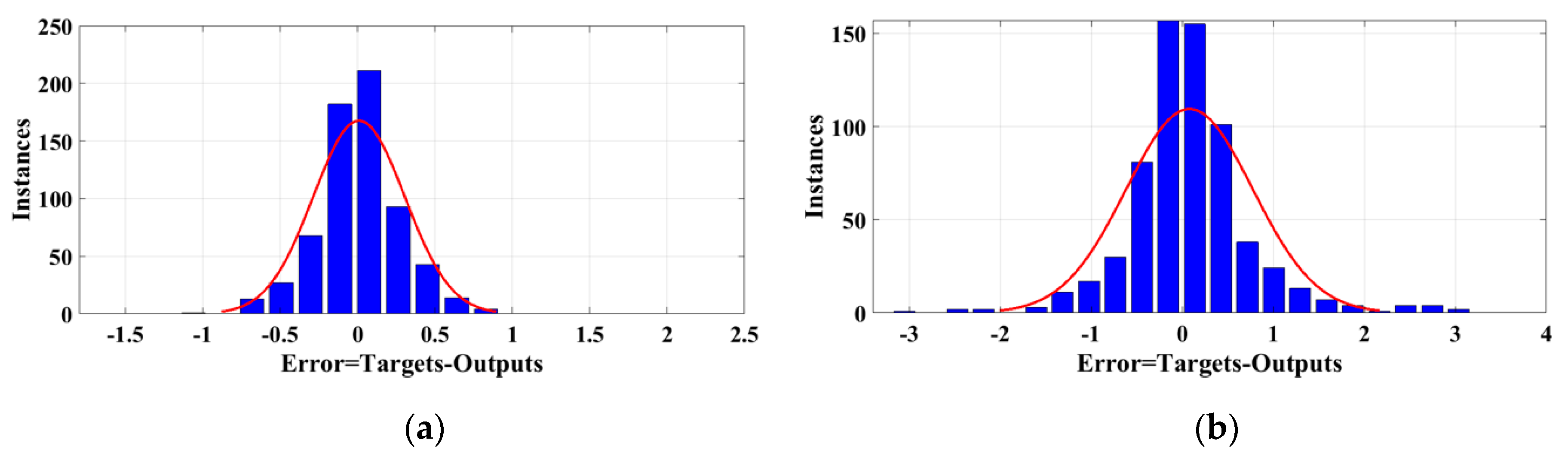
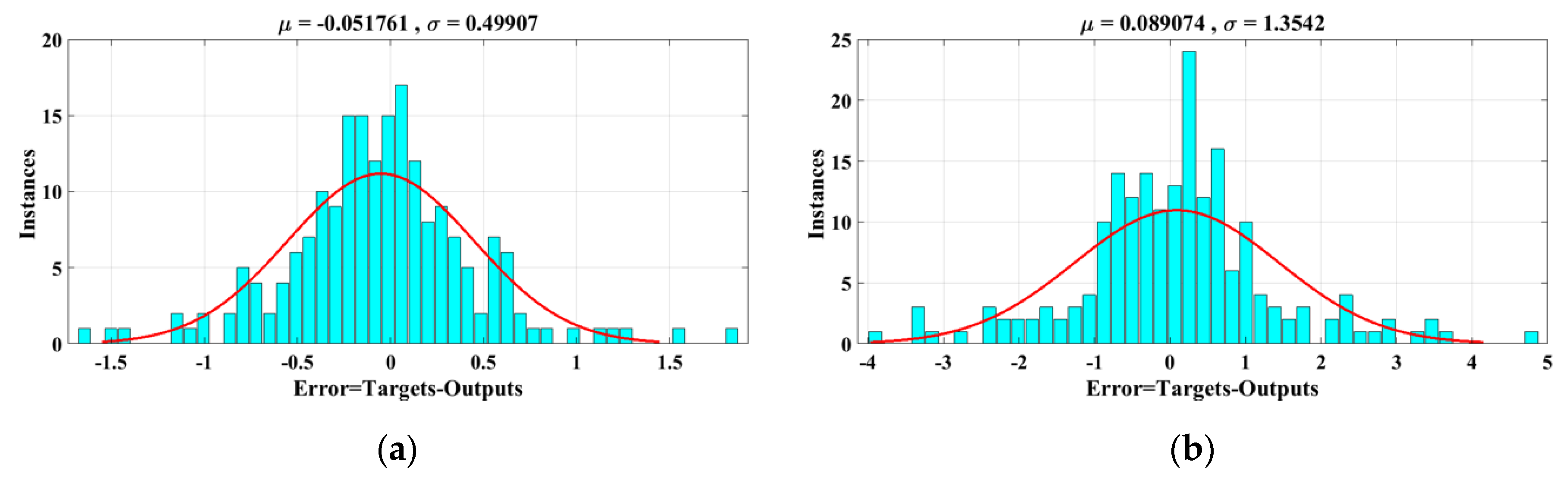
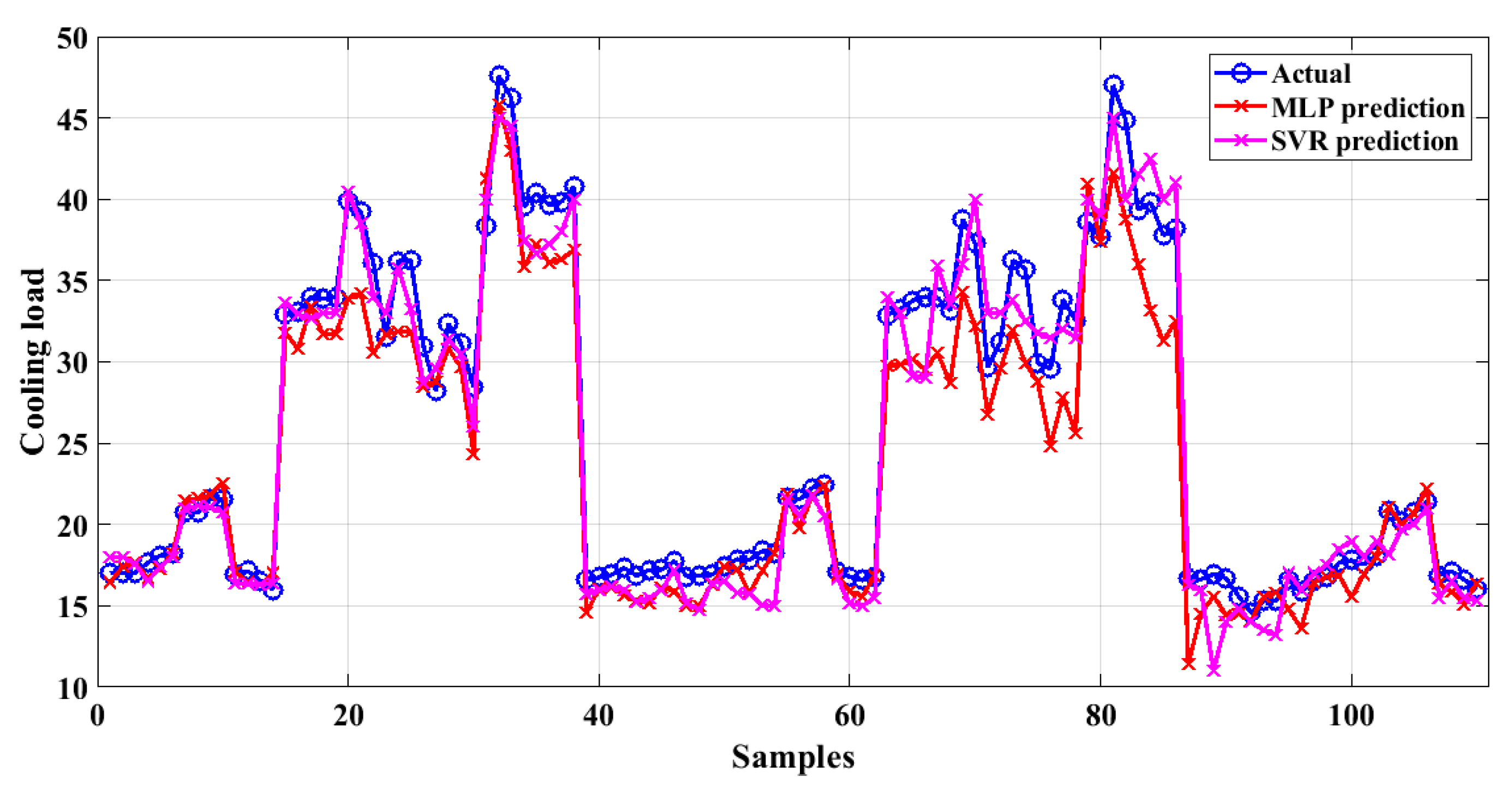
4. Simulation and Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dadon, I. Planning the Second Generation of Smart Cities: Technology to handle the pressures of urbanization. IEEE Electrif. Mag. 2019, 7, 6–15. [Google Scholar] [CrossRef]
- Pérez-Lombard, L.; Ortiz, J.; Pout, C. A review on buildings energy consumption information. Energy Build. 2008, 40, 394–398. [Google Scholar] [CrossRef]
- Moradzadeh, A.; Sadeghian, O.; Pourhossein, K.; Mohammadi-Ivatloo, B.; Anvari-Moghaddam, A. Improving Residential Load Disaggregation for Sustainable Development of Energy via Principal Component Analysis. Sustainability 2020, 12, 3158. [Google Scholar] [CrossRef]
- Wei, Y.; Zhang, X.; Shi, Y.; Xia, L.; Pan, S.; Wu, J.; Han, M.; Zhao, X. A review of data-driven approaches for prediction and classification of building energy consumption. Renew. Sustain. Energy Rev. 2018, 82, 1027–1047. [Google Scholar] [CrossRef]
- Abd Alla, S.; Bianco, V.; Tagliafico, L.A.; Scarpa, F. Life-cycle approach to the estimation of energy efficiency measures in the buildings sector. Appl. Energy 2020, 264, 114745. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, X. A hybrid method of dynamic cooling and heating load forecasting for office buildings based on artificial intelligence and regression analysis. Energy Build. 2018, 174, 293–308. [Google Scholar] [CrossRef]
- Di Foggia, G. Energy efficiency measures in buildings for achieving sustainable development goals. Heliyon 2018, 4, e00953. [Google Scholar] [CrossRef]
- Shi, E.; Jabari, F.; Anvari-Moghaddam, A.; Mohammadpourfard, M.; Mohammadi-Ivatloo, B. Risk-Constrained Optimal Chiller Loading Strategy Using Information Gap Decision Theory. Appl. Sci. 2019, 9, 1925. [Google Scholar] [CrossRef]
- Nebot, À.; Mugica, F. Energy performance forecasting of residential buildings using fuzzy approaches. Appl. Sci. 2020, 10, 720. [Google Scholar] [CrossRef]
- Yang, L.; Yan, H.; Lam, J.C. Thermal comfort and building energy consumption implications—A review. Appl. Energy 2014, 115, 164–173. [Google Scholar] [CrossRef]
- Mansour-Saatloo, A.; Agabalaye-Rahvar, M.; Mirzaei, M.A.; Mohammadi-Ivatloo, B.; Zare, K. Robust scheduling of hydrogen based smart micro energy hub with integrated demand response. J. Clean. Prod. 2020, 267, 122041. [Google Scholar] [CrossRef]
- Mirzaei, M.A.; Yazdankhah, A.S.; Mohammadi-Ivatloo, B. Stochastic security-constrained operation of wind and hydrogen energy storage systems integrated with price-based demand response. Int. J. Hydrogen Energy 2019, 44, 14217–14227. [Google Scholar] [CrossRef]
- Jozi, A.; Pinto, T.; Praça, I.; Vale, Z. Decision support application for energy consumption forecasting. Appl. Sci. 2019, 9, 699. [Google Scholar] [CrossRef]
- Zhou, Y.; Wu, J.; Long, C. Evaluation of peer-to-peer energy sharing mechanisms based on a multiagent simulation framework. Appl. Energy 2018, 222, 993–1022. [Google Scholar] [CrossRef]
- Cui, S.; Wang, Y.-W.; Xiao, J.-W. Peer-to-Peer Energy Sharing among Smart Energy Buildings by Distributed Transaction. IEEE Trans. Smart Grid 2019, 10, 6491–6501. [Google Scholar] [CrossRef]
- Kneifel, J. Life-cycle carbon and cost analysis of energy efficiency measures in new commercial buildings. Energy Build. 2010, 42, 333–340. [Google Scholar] [CrossRef]
- Penna, P.; Prada, A.; Cappelletti, F.; Gasparella, A. Multi-objectives optimization of Energy Efficiency Measures in existing buildings. Energy Build. 2015, 95, 57–69. [Google Scholar] [CrossRef]
- Macas, M.; Moretti, F.; Fonti, A.; Giantomassi, A.; Comodi, G.; Annunziato, M.; Pizzuti, S.; Capra, A. The role of data sample size and dimensionality in neural network based forecasting of building heating related variables. Energy Build. 2016, 111, 299–310. [Google Scholar] [CrossRef]
- Jing, Z.; Cai, M.; Pipattanasomporn, M.; Rahman, S.; Kothandaraman, R.; Malekpour, A.; Paaso, E.A.; Bahramirad, S. Commercial Building Load Forecasts with Artificial Neural Network. In Proceedings of the 2019 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 18–21 February 2019; pp. 1–5. [Google Scholar]
- Zhang, L.; Wen, J. A systematic feature selection procedure for short-term data-driven building energy forecasting model development. Energy Build. 2019, 183, 428–442. [Google Scholar] [CrossRef]
- Le, L.T.; Nguyen, H.; Dou, J.; Zhou, J. A comparative study of PSO-ANN, GA-ANN, ICA-ANN, and ABC-ANN in estimating the heating load of buildings’ energy efficiency for smart city planning. Appl. Sci. 2019, 9, 2630. [Google Scholar] [CrossRef]
- Kwok, S.S.K.; Lee, E.W.M. A study of the importance of occupancy to building cooling load in prediction by intelligent approach. Energy Convers. Manag. 2011, 52, 2555–2564. [Google Scholar] [CrossRef]
- Fan, C.; Ding, Y. Cooling load prediction and optimal operation of HVAC systems using a multiple nonlinear regression model. Energy Build. 2019, 197, 7–17. [Google Scholar] [CrossRef]
- Chaudhuri, T.; Soh, Y.C.; Li, H.; Xie, L. A feedforward neural network based indoor-climate control framework for thermal comfort and energy saving in buildings. Appl. Energy 2019, 248, 44–53. [Google Scholar] [CrossRef]
- Yu, Z.; Haghighat, F.; Fung, B.C.M.; Yoshino, H. A decision tree method for building energy demand modeling. Energy Build. 2010, 42, 1637–1646. [Google Scholar] [CrossRef]
- Roy, S.S.; Samui, P.; Nagtode, I.; Jain, H.; Shivaramakrishnan, V.; Mohammadi-ivatloo, B. Forecasting heating and cooling loads of buildings: A comparative performance analysis. J. Ambient Intell. Humaniz. Comput. 2020, 11, 1253–1264. [Google Scholar] [CrossRef]
- Chou, J.-S.; Bui, D.-K. Modeling heating and cooling loads by artificial intelligence for energy-efficient building design. Energy Build. 2014, 82, 437–446. [Google Scholar] [CrossRef]
- Bacher, P.; Madsen, H.; Nielsen, H.A.; Perers, B. Short-term heat load forecasting for single family houses. Energy Build. 2013, 65, 101–112. [Google Scholar] [CrossRef]
- Yu, J.; Bae, M.; Bang, H.-C.; Kim, S.-J. Cloud-based building management systems using short-term cooling load forecasting. In Proceedings of the 2013 IEEE Globecom Workshops (GC Wkshps), Atlanta, GA, USA, 9–13 December 2013; pp. 896–900. [Google Scholar]
- Favre, L.; Schafer, T.M.; Robyr, J.-L.; Niederhäuser, E.-L. Intelligent algorithm for energy, both thermal and electrical, economic and ecological optimization for a smart building. In Proceedings of the 2018 IEEE International Energy Conference (ENERGYCON), Limassol, Cyprus, 3–7 June 2018; pp. 1–5. [Google Scholar]
- Ben-Nakhi, A.E.; Mahmoud, M.A. Cooling load prediction for buildings using general regression neural networks. Energy Convers. Manag. 2004, 45, 2127–2141. [Google Scholar] [CrossRef]
- Tsanas, A.; Xifara, A. Accurate quantitative estimation of energy performance of residential buildings using statistical machine learning tools. Energy Build. 2012, 49, 560–567. [Google Scholar] [CrossRef]
- Haykin, S.S. Neural Networks and Learning Machines/Simon Haykin; Prentice Hall: New York, NY, USA, 2009. [Google Scholar]
- Moradzadeh, A.; Khaffafi, K. Comparison and evaluation of the performance of various types of neural networks for planning issues related to optimal management of charging and discharging electric cars in intelligent power grids. Emerg. Sci. J. 2017, 1, 201–207. [Google Scholar]
- Moradzadeh, A.; Pourhossein, K. Early Detection of Turn-to-Turn faults in Power Transformer Winding: An Experimental Study. In Proceedings of the 2019 International Aegean Conference on Electrical Machines and Power Electronics (ACEMP) & 2019 International Conference on Optimization of Electrical and Electronic Equipment (OPTIM), Istanbul, Turkey, 27–29 August 2019; pp. 199–204. [Google Scholar]
- Seo, D.K.; Eo, Y.D. Multilayer Perceptron-Based Phenological and Radiometric Normalization for High-Resolution Satellite Imagery. Appl. Sci. 2019, 9, 4543. [Google Scholar] [CrossRef]
- Thimm, G.; Fiesler, E. High-order and multilayer perceptron initialization. IEEE Trans. Neural Netw. 1997, 8, 349–359. [Google Scholar] [CrossRef] [PubMed]
- Moradzadeh, A.; Pourhossein, K. Application of Support Vector Machines to Locate Minor Short Circuits in Transformer Windings. In Proceedings of the 2019 54th International Universities Power Engineering Conference (UPEC), Bucharest, Romania, 3–6 September 2019; pp. 1–6. [Google Scholar]
- Zhang, J.; Liao, Y.; Wang, S.; Han, J. Study on driving decision-making mechanism of autonomous vehicle based on an optimized support vector machine regression. Appl. Sci. 2018, 8, 13. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Taghavifar, H.; Mardani, A. A comparative trend in forecasting ability of artificial neural networks and regressive support vector machine methodologies for energy dissipation modeling of off-road vehicles. Energy 2014, 66, 569–576. [Google Scholar] [CrossRef]
- Choubin, B.; Khalighi-Sigaroodi, S.; Malekian, A.; Kişi, Ö. Multiple linear regression, multi-layer perceptron network and adaptive neuro-fuzzy inference system for forecasting precipitation based on large-scale climate signals. Hydrol. Sci. J. 2016, 61, 1001–1009. [Google Scholar] [CrossRef]


| Mathematical Symbol | Variables |
|---|---|
| Relative compactness | |
| Surface area | |
| Wall area | |
| Roof area | |
| Overall height | |
| Orientation | |
| Glazing area | |
| Glazing area distribution | |
| Heating load | |
| Cooling load |
| Heating Load | Cooling Load | |||||||
|---|---|---|---|---|---|---|---|---|
| R | MSE | RMSE | MAE | R | MSE | RMSE | MAE | |
| MLP | 0.9993 | 0.2335 | 0.4832 | 0.4118 | 0.9824 | 6.896 | 2.626 | 2.0973 |
| SVR | 0.9979 | 0.7838 | 0.8853 | 0.7780 | 0.9878 | 3.024 | 1.7389 | 1.4762 |
| Data Type | References | Heating Load (R) | Cooling Load (R) |
|---|---|---|---|
| Used data in this paper | MLP in this paper | 0.9993 | 0.9824 |
| SVR in this paper | 0.9979 | 0.9878 | |
| DNN [14] | 0.9805 | 0.9976 | |
| GBM [14] | 0.9853 | 0.9853 | |
| GPR [14] | 0.9984 | 0.9913 | |
| MPMR [14] | 0.8802 | 0.8955 | |
| ANN [15] | 0.9980 | 0.9840 | |
| CART [15] | 0.9960 | 0.9810 | |
| GLR [15] | 0.9950 | 0.9830 | |
| CHAID [15] | 0.9950 | 0.9810 | |
| GA-ANN [18] | 0.9800 | - | |
| PSO-ANN [18] | 0.9720 | - | |
| ICA-ANN [18] | 0.9700 | - | |
| ABC-ANN [18] | 0.9730 | - | |
| Different data | GRNN [28] | - | 0.9640 |
| PENN [20] | - | 0.9500 | |
| MLR [20] | - | 0.7510 | |
| AR [20] | - | 0.8370 | |
| ARX [20] | - | 08640 | |
| MNR (initial prediction) [20] | - | 0.8990 | |
| MNR (final calibration) [20] | - | 0.9580 | |
| ANN [21] | 0.9900 | - | |
| Decision tree [22] | 0.92 | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moradzadeh, A.; Mansour-Saatloo, A.; Mohammadi-Ivatloo, B.; Anvari-Moghaddam, A. Performance Evaluation of Two Machine Learning Techniques in Heating and Cooling Loads Forecasting of Residential Buildings. Appl. Sci. 2020, 10, 3829. https://doi.org/10.3390/app10113829
Moradzadeh A, Mansour-Saatloo A, Mohammadi-Ivatloo B, Anvari-Moghaddam A. Performance Evaluation of Two Machine Learning Techniques in Heating and Cooling Loads Forecasting of Residential Buildings. Applied Sciences. 2020; 10(11):3829. https://doi.org/10.3390/app10113829
Chicago/Turabian StyleMoradzadeh, Arash, Amin Mansour-Saatloo, Behnam Mohammadi-Ivatloo, and Amjad Anvari-Moghaddam. 2020. "Performance Evaluation of Two Machine Learning Techniques in Heating and Cooling Loads Forecasting of Residential Buildings" Applied Sciences 10, no. 11: 3829. https://doi.org/10.3390/app10113829
APA StyleMoradzadeh, A., Mansour-Saatloo, A., Mohammadi-Ivatloo, B., & Anvari-Moghaddam, A. (2020). Performance Evaluation of Two Machine Learning Techniques in Heating and Cooling Loads Forecasting of Residential Buildings. Applied Sciences, 10(11), 3829. https://doi.org/10.3390/app10113829








