Time-Series Prediction of the Oscillatory Phase of EEG Signals Using the Least Mean Square Algorithm-Based AR Model
Abstract
:1. Introduction
2. Materials and Methods
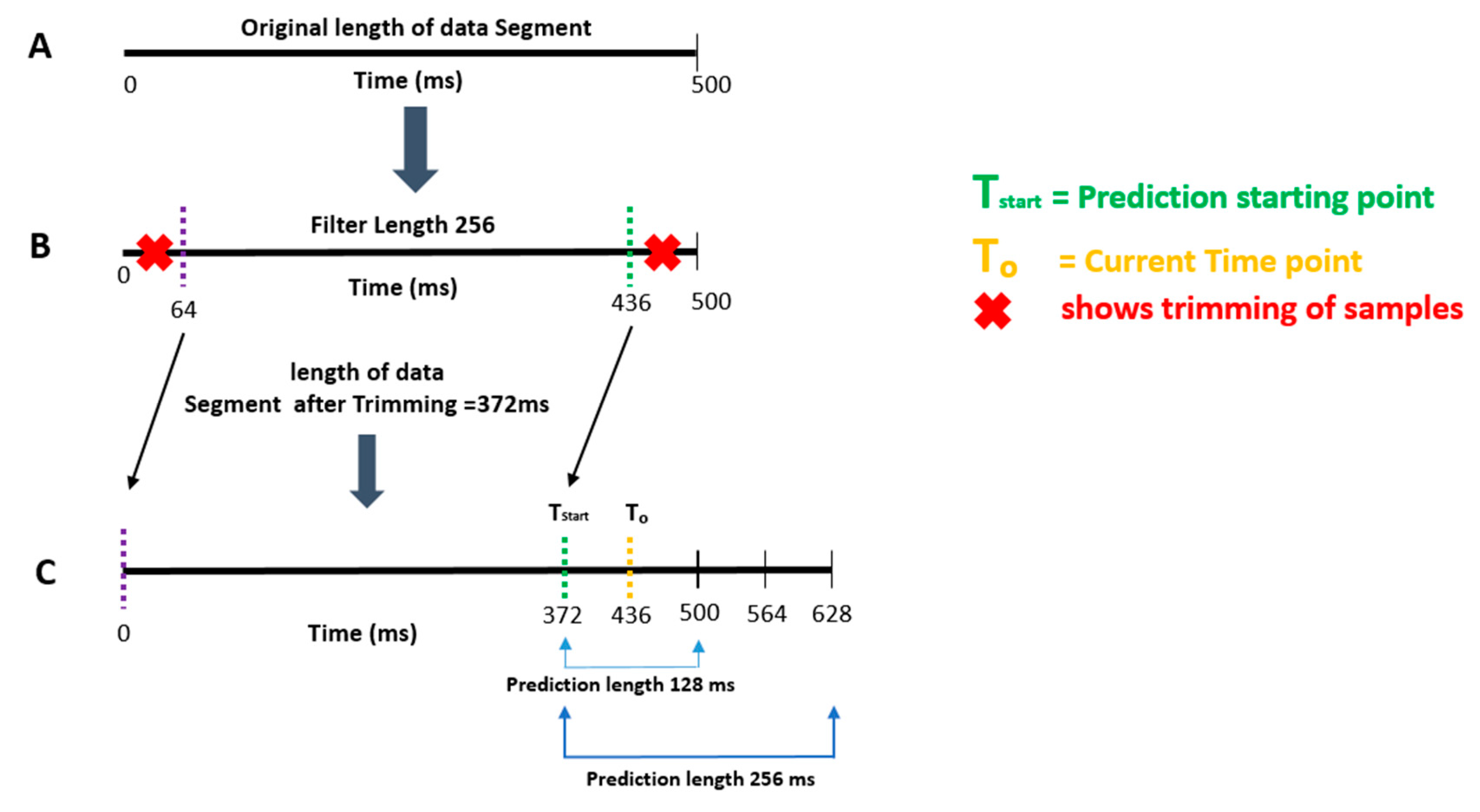
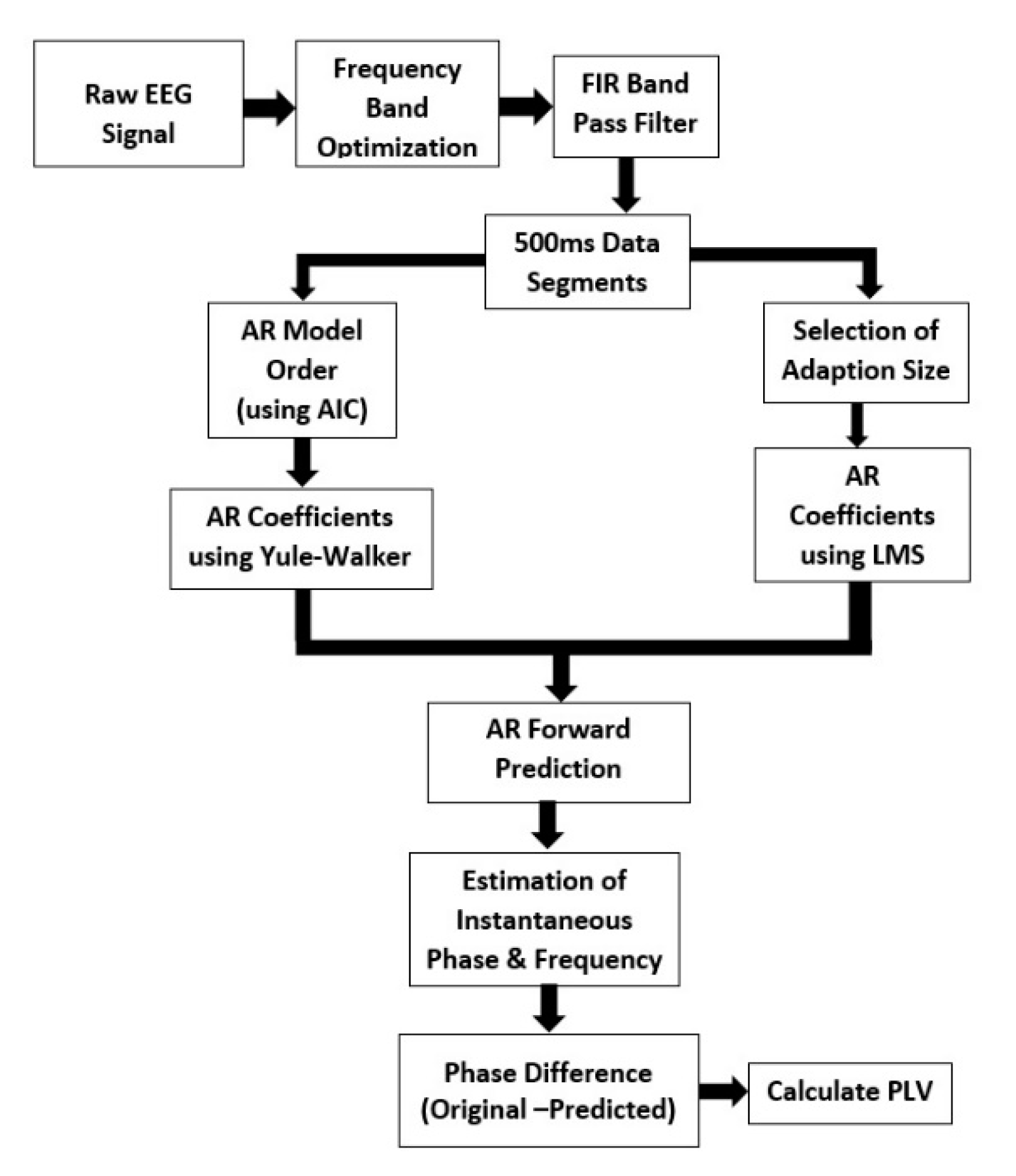
2.1. Algorithm Outline
- Re-reference the raw data and then downsample to 500 Hz.
- Optimize the frequency band (8–13 Hz) based on the peak/central frequency of each individual. The individual alpha frequency (IAF) is linked to the maximum EEG power within the alpha range. After finding the IAF, a passband for a band-pass filter is chosen. The low cutoff frequency for the band-pass filter is IAF-1 and high cutoff frequency is IAF+1.
- Apply a two-pass finite impulse response (FIR) band-pass filter with a filter order of 128 and the passband chosen in step 2 [28].
- Segment the data into 500 ms epochs.
- Compute the optimal AR model order using Akaike’s Information Criterion (AIC).
- Compute AR coefficients using the Yule–Walker equations.
- Select the adaptation size/learning rate of LMS.
- Select the number of filter taps (same as the AR model order).
- Compute the coefficients using LMS and then use those coefficients to predict the next sample until the prediction length in the AR equation.
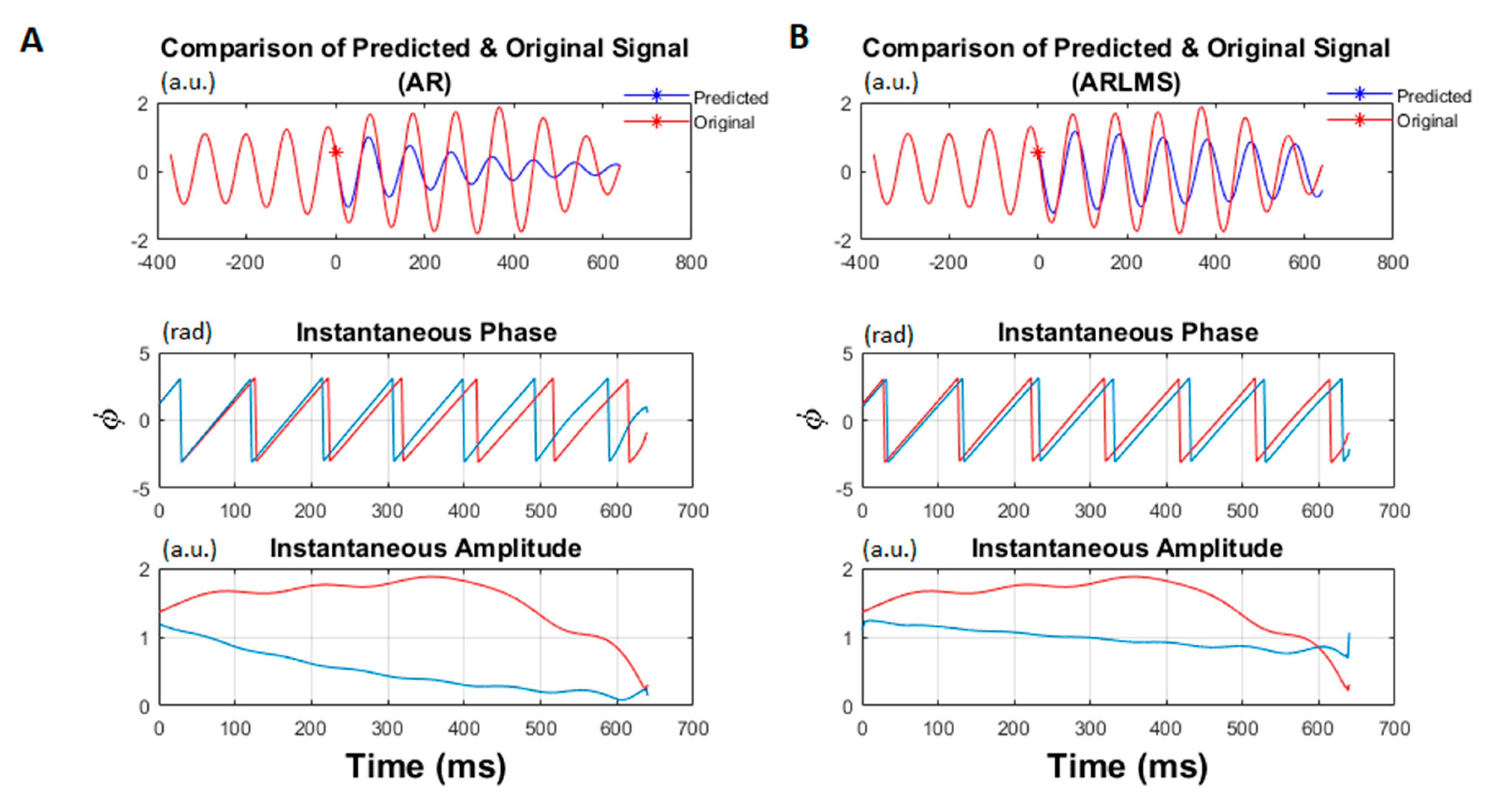
- Calculate the time-series forward prediction for twice the prediction length (256 ms) for the LMS-based AR model (See Figure 1).
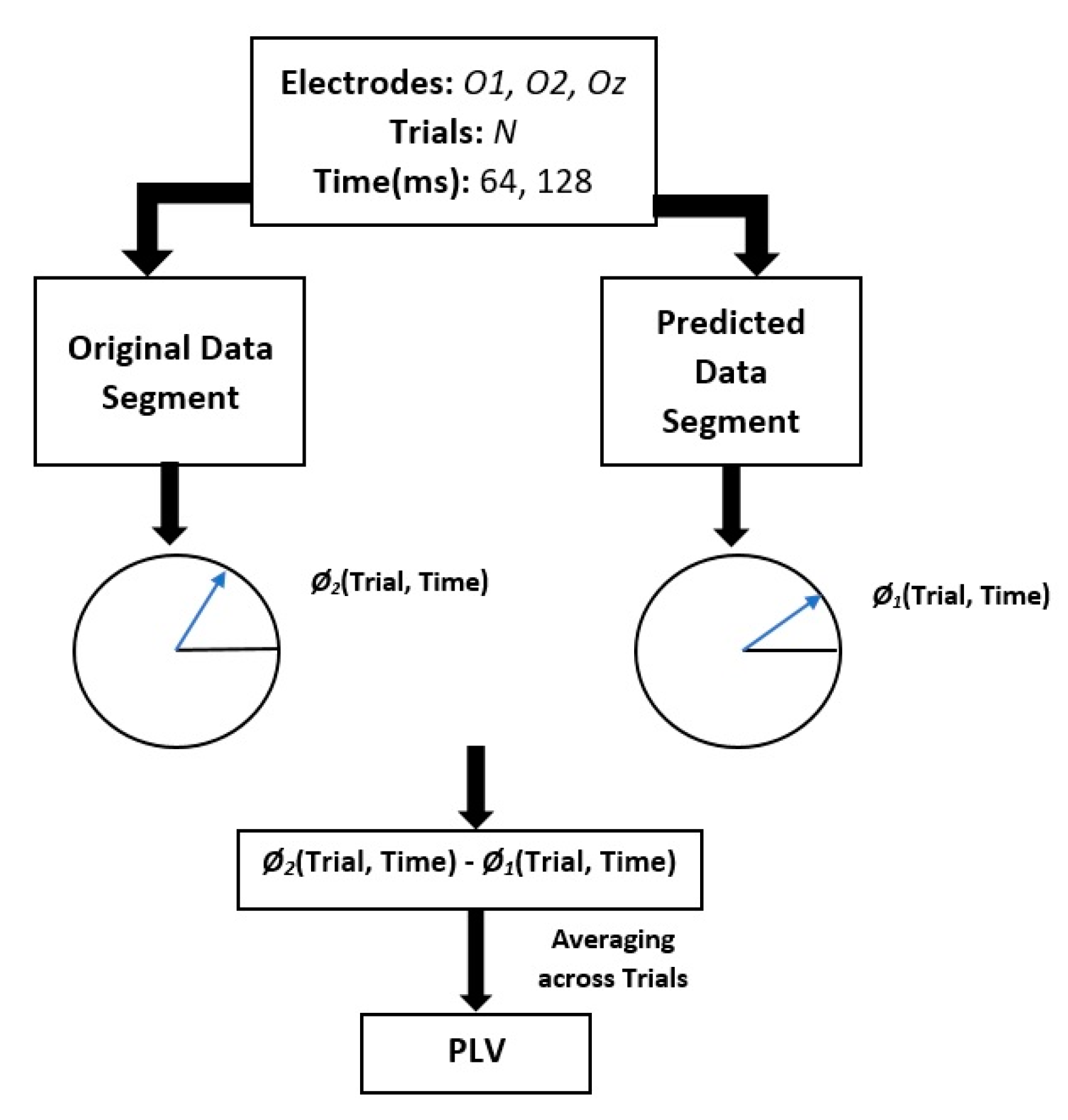
- Compute the means of the predicted segment and original segment and subtract the respective means from the predicted segment and original segment.
- Estimate the instantaneous phase and frequency of the original and predicted data segments by calculating the analytic signal via the Hilbert transform.
- Compute the phase difference between the original and predicted data segments.
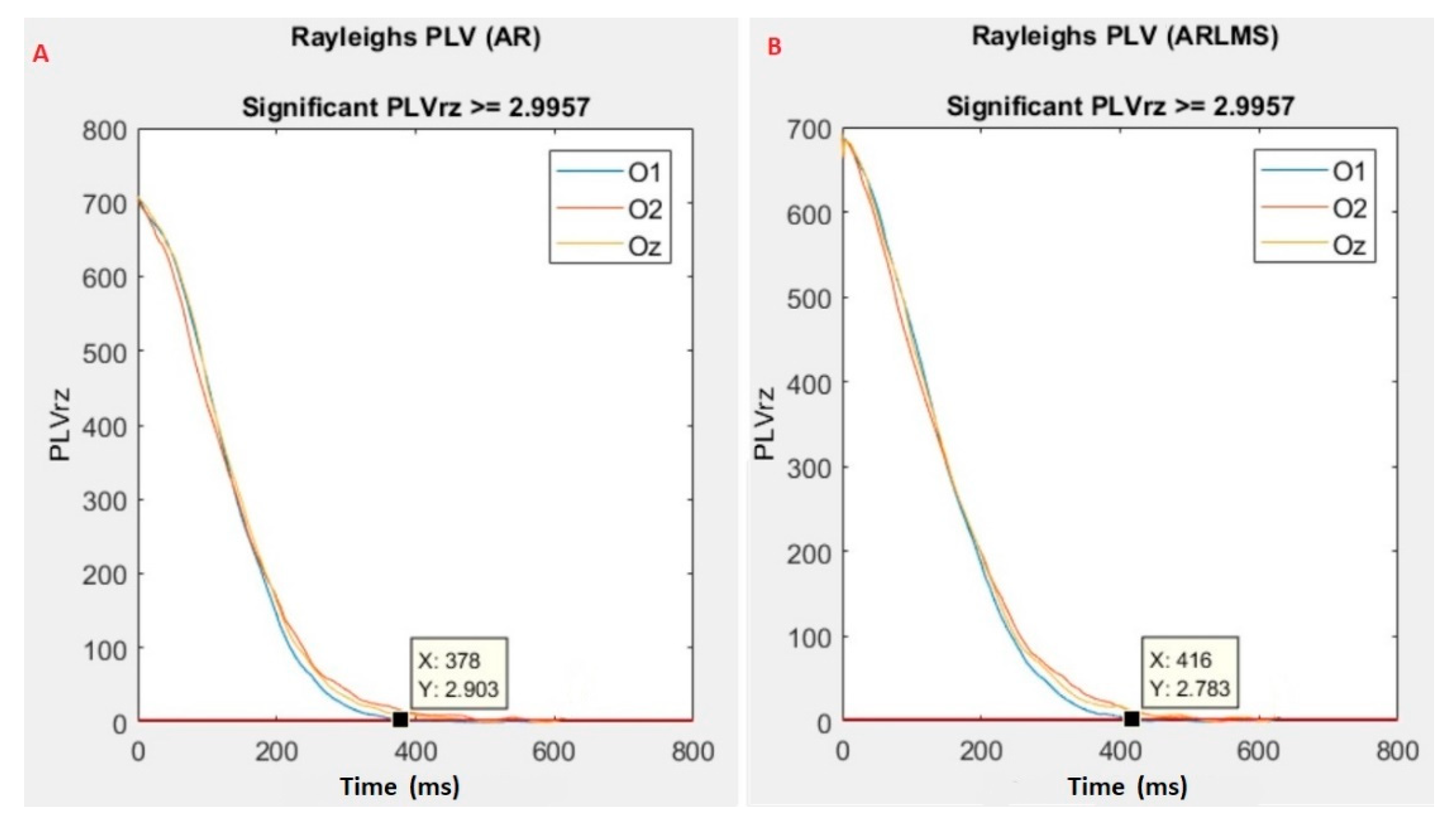
- Calculate the phase locking value (PLV) between the original and predicted data.
2.2. Autoregressive (AR) Model
2.3. Least Mean Square (LMS)
2.4. Instantaneous Frequency and Phase
2.5. Participants
2.6. EEG Recording and Preprocessing
2.7. Statistical Analysis
3. Results
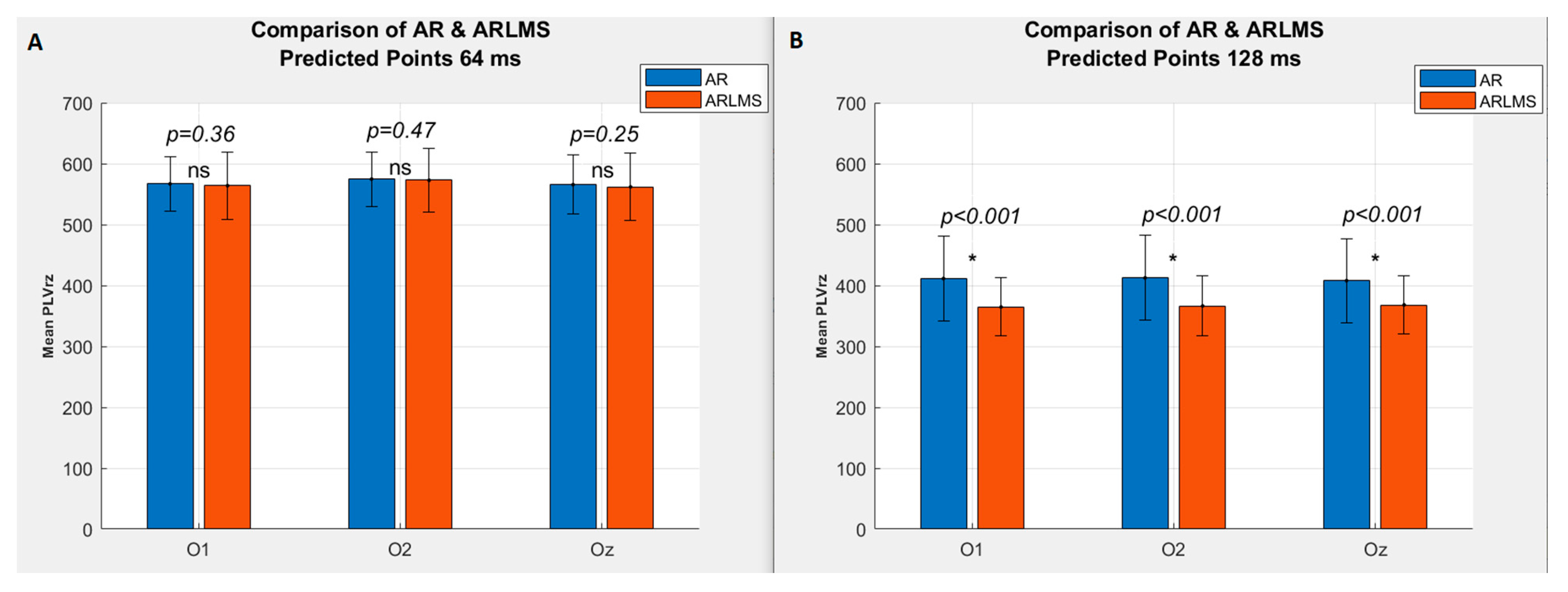
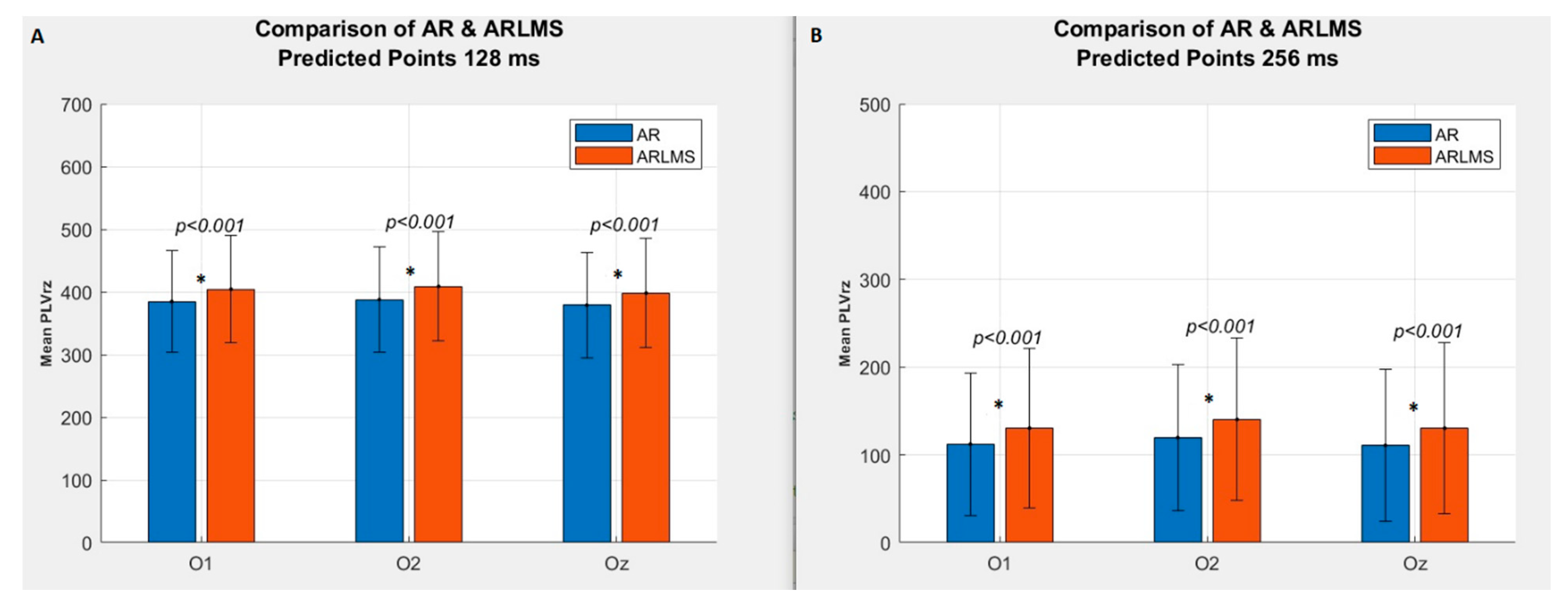
3.1. Shorter Prediction Length
3.2. Twice Prediction Length
3.3. Sampling Points Crossing the Significant Rayleigh’s Z Value
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Data Availability
References
- Womelsdorf, T.; Schoffelen, J. Modulation of neuronal interactions through neuronal synchronization. Science 2007, 316, 1609–1612. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mathewson, K.E.; Lleras, A. Pulsed out of awareness: EEG alpha oscillations represent a pulsed- inhibition of ongoing cortical processing. Front. Psychol. 2011, 2, 99. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Klimesch, W.; Sauseng, P. EEG alpha oscillations: The inhibition–timing hypothesis. Brain. Res. Rev. 2007, 53, 63–88. [Google Scholar] [CrossRef] [PubMed]
- Jensen, O.; Mazaheri, A. Shaping functional architecture by oscillatory alpha activity: Gating by inhibition. Front. Hum. Neurosci. 2010, 4, 186. [Google Scholar] [CrossRef] [Green Version]
- Thut, G.; Nietzel, A. α-Band electroencephalographic activity over occipital cortex indexes visuospatial attention bias and predicts visual target detection. J. Neurosci. 2006, 26, 9494–9502. [Google Scholar] [CrossRef] [Green Version]
- Gratton, G.; Villa, A.E.P. Functional correlates of a three-component spatial model of the alpha rhythm. Brain Res. 1992, 582, 159–162. [Google Scholar] [CrossRef]
- Worden, M.S.; Foxe, J. Anticipatory biasing of visuospatial attention indexed by retinotopically specific-band electroencephalography increases over occipital cortex. J. Neurosci. 2000, 20, 63. [Google Scholar] [CrossRef] [Green Version]
- Pfurtscheller, G.; Neuper, C. Event-related synchronization of mu rhythm in the EEG over the cortical hand area in man. Neurosci. Lett. 1994, 174, 93–96. [Google Scholar] [CrossRef]
- Hanslmayr, S.; Aslan, A. Prestimulus oscillations predict visual perception performance between and within subjects. Neuroimage 2007, 37, 1465–1473. [Google Scholar] [CrossRef]
- Van Dijk, H.; Schoffelen, J. Prestimulus oscillatory activity in the alpha band predicts visual discrimination ability. J. Neurosci. 2008, 28, 1816–1823. [Google Scholar] [CrossRef] [Green Version]
- Lerga, J.; Saulig, N.; Mozetic, V.; Lerga, R. Number of EEG signal components estimated using the short-term Rényi entropy. In Proceedings of the 2016 International Multidisciplinary Conference on Computer and Energy Science (SpliTech), Split, Croatia, 13–15 July 2016. [Google Scholar]
- Lerga, J.; Saulig, N. Algorithm based on the short-term Rényi entropy and IF estimation for noisy EEG signals analysis. Comput. Biol. Med. 2017, 80, 1–13. [Google Scholar] [CrossRef]
- Jadav, G.M.; Lerga, J. Adaptive filtering and analysis of EEG signals in the time-frequency domain based on the local entropy. EURASIP J. Adv. Signal Process. 2020, 2020, 1–18. [Google Scholar]
- Khan, N.A.; Mohammadi, M.; Ali, S. Instantaneous frequency estimation of intersecting and close multi-component signals with varying amplitudes. Signal Image Video Process. 2019, 13, 517–524. [Google Scholar] [CrossRef]
- Mathewson, K.E.; Gratton, G. To see or not to see: Prestimulus α phase predicts visual awareness. J. Neurosci. 2009, 29, 2725–2732. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- VanRullen, R.; Busch, N. Ongoing EEG phase as a trial-by-trial predictor of perceptual and attentional variability. Front. Psychol. 2011, 2, 60. [Google Scholar] [CrossRef] [Green Version]
- Busch, N.A.; Dubois, J. The phase of ongoing EEG oscillations predicts visual perception. J. Neurosci. 2009, 29, 7869–7876. [Google Scholar] [CrossRef] [PubMed]
- Pavlides, C.; Greenstein, Y.J. Long-term potentiation in the dentate gyrus is induced preferentially on the positive phase of θ-rhythm. Brain Res. 1988, 439, 383–387. [Google Scholar] [CrossRef]
- Hölscher, C.; Anwyl, R. Stimulation on the positive phase of hippocampal theta rhythm induces long-term potentiation that can be depotentiated by stimulation on the negative phase in area CA1 in vivo. J. Neurosci. 1997, 17, 6470–6477. [Google Scholar] [CrossRef]
- Hyman, J.M.; Wyble, B.P. Stimulation in hippocampal region CA1 in behaving rats yields long-term potentiation when delivered to the peak of theta and long-term depression when delivered to the trough. J. Neurosci. 2003, 23, 11725–11731. [Google Scholar] [CrossRef]
- Chen, L.L.; Madhavan, R. Real-time brain oscillation detection and phase-locked stimulation using autoregressive spectral estimation and time-series forward prediction. IEEE Trans. Biomed. Eng. 2011, 60, 753–762. [Google Scholar] [CrossRef] [Green Version]
- Roux, S.G.; Cenier, T. A wavelet-based method for local phase extraction from a multi-frequency oscillatory signal. J. Neurosci. Methods 2007, 160, 135–143. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brunner, C.; Scherer, R. Online control of a brain-computer interface using phase synchronization. IEEE Trans. Biomed. Eng. 2006, 53, 2501–2506. [Google Scholar] [CrossRef] [PubMed]
- Marzullo, T.C.; Lehmkuhle, M.J. Development of closed-loop neural interface technology in a rat model: Combining motor cortex operant conditioning with visual cortex microstimulation. IEEE Trans. Neural Syst. Rehabil. Eng. 2010, 18, 117–126. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Anderson, W.S.; Kossoff, E.H. Implantation of a responsive neurostimulator device in patients with refractory epilepsy. Neurosurg. Focus 2008, 25, E12. [Google Scholar] [CrossRef] [PubMed]
- Anderson, W.S.; Kudela, P. Phase-dependent stimulation effects on bursting activity in a neural network cortical simulation. Epilepsy. Res. 2009, 84, 42–55. [Google Scholar] [CrossRef] [Green Version]
- Zrenner, C.; Desideri, D. Real-time EEG-defined excitability states determine efficacy of TMS-induced plasticity in human motor cortex. Brain Stimul. 2018, 11, 374–389. [Google Scholar] [CrossRef]
- Schaworonkow, N.; Triesch, J. EEG-triggered TMS reveals stronger brain state-dependent modulation of motor evoked potentials at weaker stimulation intensities. Brain Stimul. 2019, 12, 110–118. [Google Scholar] [CrossRef]
- Tseng, S.-Y.; Chen, R.-C. Evaluation of parametric methods in EEG signal analysis. Med. Eng. Phys. 1995, 17, 71–78. [Google Scholar] [CrossRef]
- Pardey, J.; Roberts, S.; Tarassenko, L. A review of parametric modelling techniques for EEG analysis. Med. Eng. Phys. 1996, 18, 2–11. [Google Scholar] [CrossRef]
- Koo, B.; Gibson, J.D.; Gray, S.D. Filtering of colored noise for speech enhancement and coding. In Proceedings of the International Conference on Acoustics, Speech, and Signal Processing, Glasgow, UK, 23–26 May 1989. [Google Scholar] [CrossRef]
- Lim, J.; Oppenheim, A. All-pole modeling of degraded speech. IEEE Trans. Signal. Process. 1978, 26, 197–210. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1978, 19, 465–471. [Google Scholar] [CrossRef]
- Wu, W.R.; Chen, P.C. Adaptive AR modeling in white Gaussian noise. IEEE Trans. Signal Process. 1997, 45, 1184–1192. [Google Scholar] [CrossRef]
- Widrow, B.; Stearns, D.S. Adaptive Signal Processing, 1st ed.; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1985. [Google Scholar]
- Poularikas, A.D.; Ramadan, Z.M. Adaptive Filtering Primer with MATLAB, 1st ed.; CRC Press: Boca Raton, FL, USA, 2006; pp. 101–135. [Google Scholar]
- Boashash, B. Estimating and interpreting the instantaneous frequency of a signal. I. Fundamentals. Proc. IEEE 1992, 80, 520–538. [Google Scholar] [CrossRef]
- Suetani, H.; Kitajo, K. A manifold learning approach to mapping individuality of human brain oscillations through beta-divergence. Neurosci. Res. 2020. [Google Scholar] [CrossRef] [PubMed]
- Kitajo, K.; Sase, T. Consistency in macroscopic human brain responses to noisy time-varying visual inputs. bioRxiv 2019, 645499. [Google Scholar] [CrossRef]
- Sase, T.; Kitajo, K. The metastable human brain associated with autistic-like traits. bioRxiv 2019, 855502. [Google Scholar] [CrossRef] [Green Version]
- Delorme, A.; Makeig, S. EEGLAB: An open source toolbox for analysis of single-trial EEG dynamics including independent component analysis. J. Neurosci. Methods 2004, 134, 9–21. [Google Scholar] [CrossRef] [Green Version]
- Lachaux, J.P.; Rodriguez, E. Measuring phase synchrony in brain signals. Hum. Brain. Mapp. 1999, 8, 194–208. [Google Scholar] [CrossRef] [Green Version]
- Fischer, N. Statistical Analysis of Circular Data; Cambridge UP: Cambridge, UK, 1993. [Google Scholar] [CrossRef]
- Zarubin, G.; Gundlach, C. Real-time phase detection for EEG-based tACS closed-loop system. In Proceedings of the 6th International Congress on Neurotechnology, Electronics and Informatics, Seville, Spain, 20–21 Spetember 2018. [Google Scholar] [CrossRef]
- Bajaj, V.; Pachori, R.B. Separation of rhythms of EEG signals based on Hilbert-Huang transformation with application to seizure detection. In Proceedings of the International Conference on Hybrid Information Technology, Daejeon, Korea, 23–25 August 2012. [Google Scholar] [CrossRef]
- Lin, C.F.; Zhu, J.D. Hilbert-Huang transformation-based time-frequency analysis methods in biomedical signal applications. Proc. Inst. Mech. Eng. Part H 2012, 226, 208–216. [Google Scholar] [CrossRef]
- Le Van Quyen, M. Comparison of Hilbert transform and wavelet methods for the analysis of neuronal synchrony. J. Neurosci. Methods 2001, 111, 83–98. [Google Scholar] [CrossRef]
- Mansouri, F.; Dunlop, K. A fast EEG forecasting algorithm for phase-locked transcranial electrical stimulation of the human brain. Front. Neurosci. 2017, 11, 401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Oh, S.L.; Jahmunah, V. Deep convolutional neural network model for automated diagnosis of schizophrenia using EEG signals. Appli. Sci. 2019, 9, 2870. [Google Scholar] [CrossRef] [Green Version]
- Oh, S.L.; Hagiwara, Y. A deep learning approach for Parkinson’s disease diagnosis from EEG signals. Neural Comput. Appl. 2018, 1–7. [Google Scholar] [CrossRef]
- Li, F.; Li, X. A Novel P300 Classification Algorithm Based on a Principal Component Analysis-Convolutional Neural Network. Appli. Sci. 2020, 10, 1546. [Google Scholar] [CrossRef] [Green Version]
- Li, F.; He, F. A Novel Simplified Convolutional Neural Network Classification Algorithm of Motor Imagery EEG Signals Based on Deep Learning. Appli.Sci. 2020, 10, 1605. [Google Scholar] [CrossRef]
- Aldayel, M.; Ykhlef, M. Deep Learning for EEG-Based Preference Classification in Neuromarketing. Appl. Sci. 2020, 10, 1525. [Google Scholar] [CrossRef] [Green Version]
- Xiang, L.; Guoqing, G. A convolutional neural network-based linguistic steganalysis for synonym substitution steganography. Math. Biosci. Eng. 2020, 17, 1041–1058. [Google Scholar] [CrossRef]
- McIntosh, J.; Sajda, P. Estimation of phase in EEG rhythms for real-time applications. arXiv 2019, arXiv:1910.08784. [Google Scholar]
- Sezer, O.B.; Gudelek, M.U. Financial time series forecasting with deep learning: A systematic literature review: 2005–2019. Appl. Soft. Comput. 2020, 90, 106181. [Google Scholar] [CrossRef] [Green Version]
- Song, X.; Liu, Y.; Xue, L. Time-series well performance prediction based on Long Short-Term Memory (LSTM) neural network model. J. Petrol. Sci. Eng. 2020, 186, 106682. [Google Scholar] [CrossRef]
- Memarzadeh, G.; Keynia, F. A new short-term wind speed forecasting method based on fine-tuned LSTM neural network and optimal input sets. Energ. Convers. Manag. 2020, 213, 112824. [Google Scholar] [CrossRef]
- Karevan, Z.; Suykens, J.A.K. Transductive LSTM for time-series prediction: An application to weather forecasting. Neural Netw. 2020, 125, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Monesi, M.J.; Accou, B.; Martinez, J.M.; Francart, T.; Hamme, H.V. An LSTM Based Architecture to Relate Speech Stimulus to EEG. arXiv 2020, arXiv:2002.10988. [Google Scholar]
- Bandara, K.; Bergmeir, C.; Smyl, S. Forecasting across time series databases using recurrent neural networks on groups of similar series: A clustering approach. Expert. Sys. Appl. 2020, 140, 112896. [Google Scholar] [CrossRef] [Green Version]
| Subjects | Results of Channel O1 800 ms | |
|---|---|---|
| Autoregressive (AR) Model | Least Mean Square (LMS)-based AR Model | |
| Time Points | Time Points | |
| 1. | 424 | 446 |
| 2. | 368 | 392 |
| 3. | 536 | 550 |
| 4. | 492 | 484 |
| 5. | 382 | 416 |
| 6. | 420 | 578 |
| 7. | 452 | 456 |
| 8. | 678 | 752 |
| 9. | 392 | 370 |
| 10. | 694 | * |
| 11. | 630 | 678 |
| 12. | 506 | 556 |
| 13. | 702 | 618 |
| 14. | 524 | 522 |
| 15. | 796 | * |
| 16. | 644 | 598 |
| 17. | 528 | 578 |
| 18. | * | 778 |
| 19. | 566 | 598 |
| 20. | 660 | 714 |
| 21. | 452 | 406 |
| Prediction Time Point (ms) | p-Value | AR Model | LMS-Based AR Model |
|---|---|---|---|
| Rayleigh’s Z Value (Mean Values) | |||
| 64 | p < 0.001 | 582 | 568 |
| 128 | p < 0.001 | 384 | 403 |
| 256 | p < 0.001 | 113 | 131 |
| 340 | p = 0.010 | 50.5 | 61.18 |
| 400 | p = 0.070 | 29 | 35 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shakeel, A.; Tanaka, T.; Kitajo, K. Time-Series Prediction of the Oscillatory Phase of EEG Signals Using the Least Mean Square Algorithm-Based AR Model. Appl. Sci. 2020, 10, 3616. https://doi.org/10.3390/app10103616
Shakeel A, Tanaka T, Kitajo K. Time-Series Prediction of the Oscillatory Phase of EEG Signals Using the Least Mean Square Algorithm-Based AR Model. Applied Sciences. 2020; 10(10):3616. https://doi.org/10.3390/app10103616
Chicago/Turabian StyleShakeel, Aqsa, Toshihisa Tanaka, and Keiichi Kitajo. 2020. "Time-Series Prediction of the Oscillatory Phase of EEG Signals Using the Least Mean Square Algorithm-Based AR Model" Applied Sciences 10, no. 10: 3616. https://doi.org/10.3390/app10103616
APA StyleShakeel, A., Tanaka, T., & Kitajo, K. (2020). Time-Series Prediction of the Oscillatory Phase of EEG Signals Using the Least Mean Square Algorithm-Based AR Model. Applied Sciences, 10(10), 3616. https://doi.org/10.3390/app10103616







