Continuous Variable Quantum Secret Sharing with Fairness
Abstract
1. Introduction
2. CVQSS Scheme with Fairness
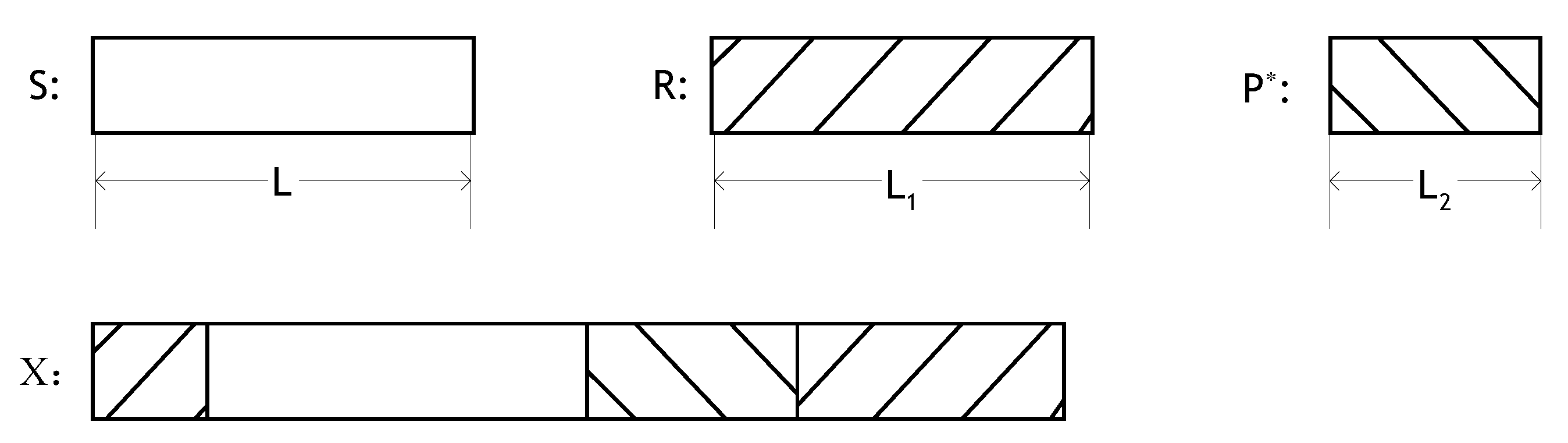
2.1. Chinese Remainder Theorem
2.2. Verifying Function for CVQSS
2.3. (2,2)-CVQSS Scheme with Fairness
2.3.1. Initialization
2.3.2. Distribution
2.3.3. Recovery
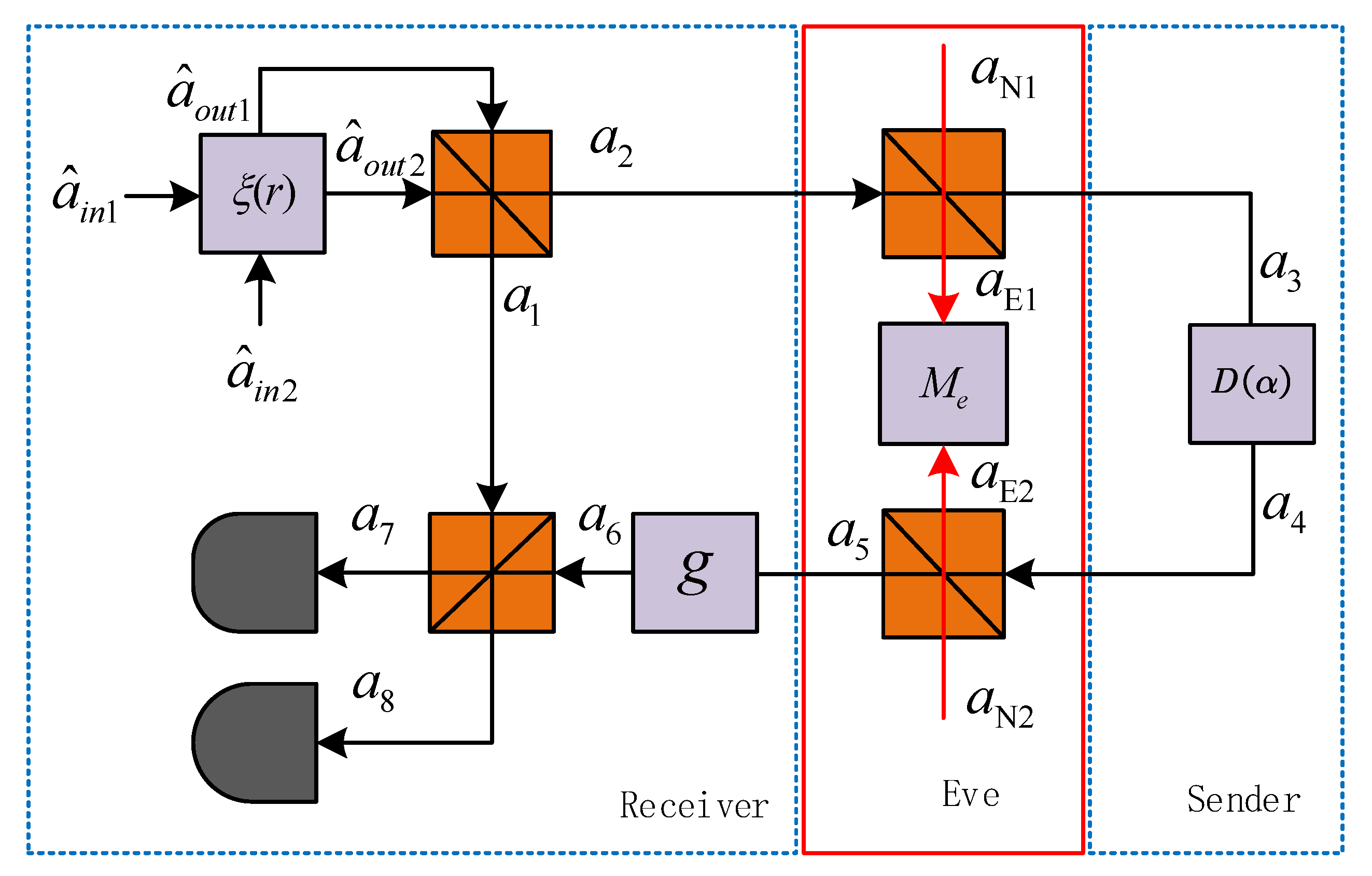
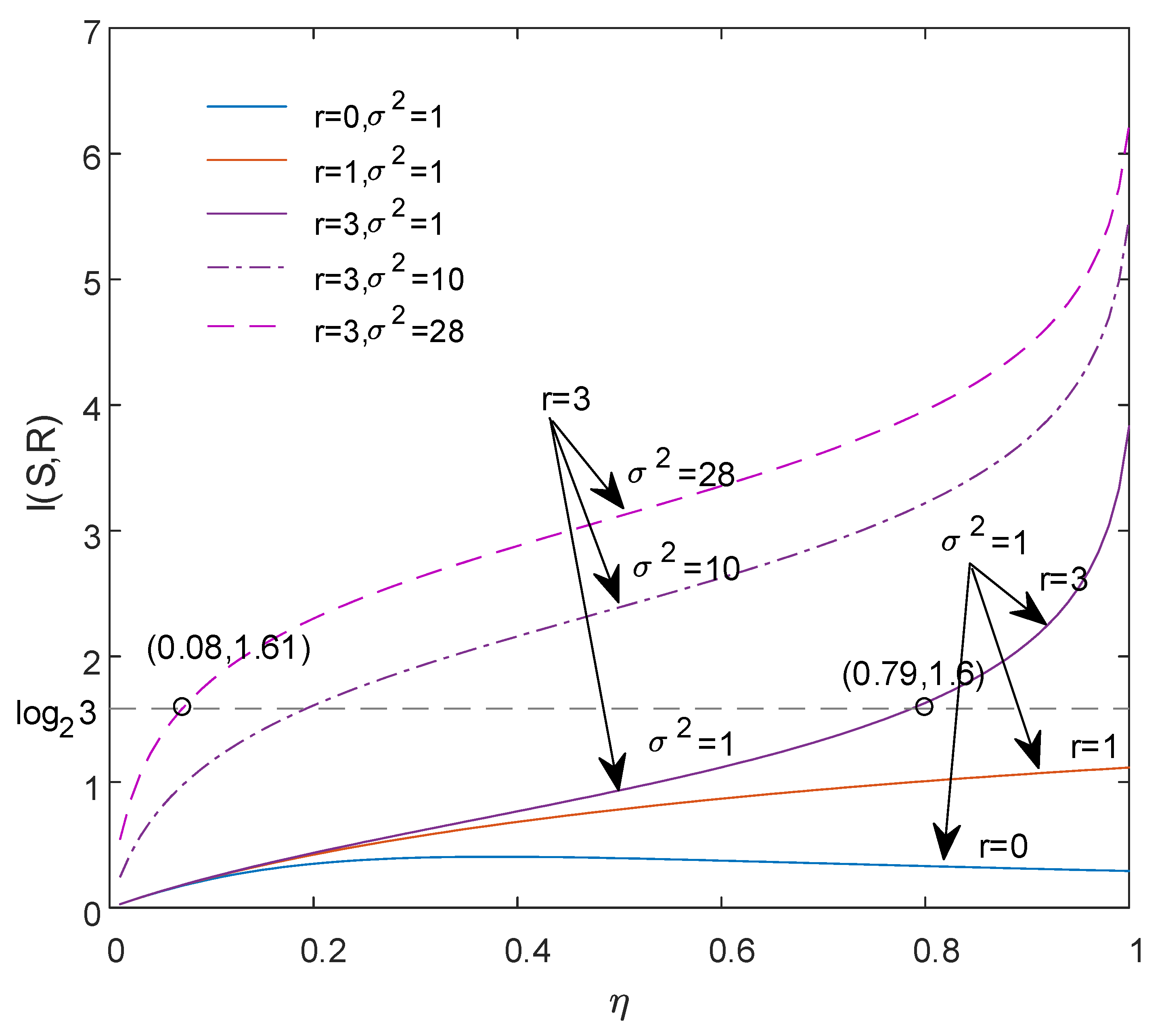
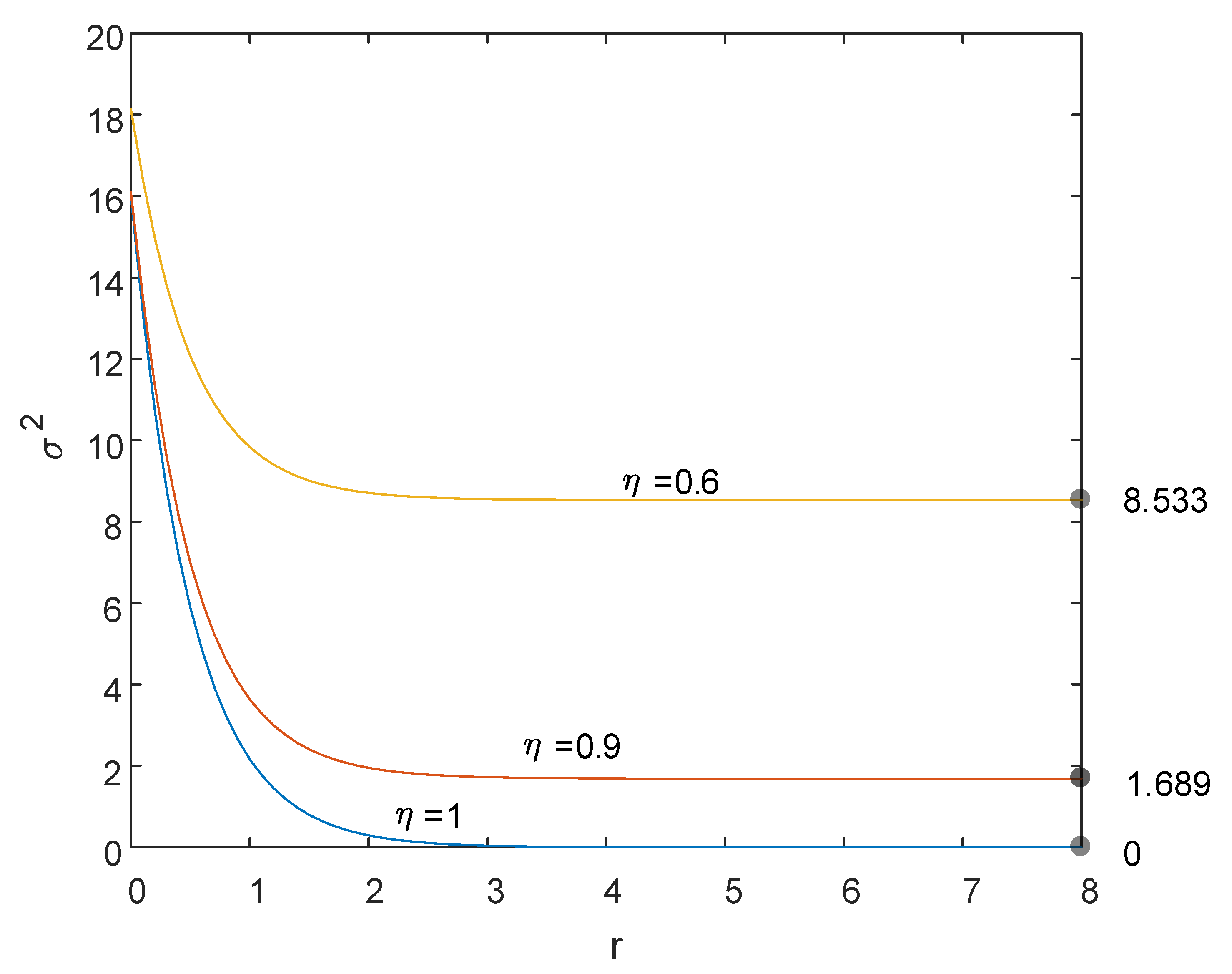
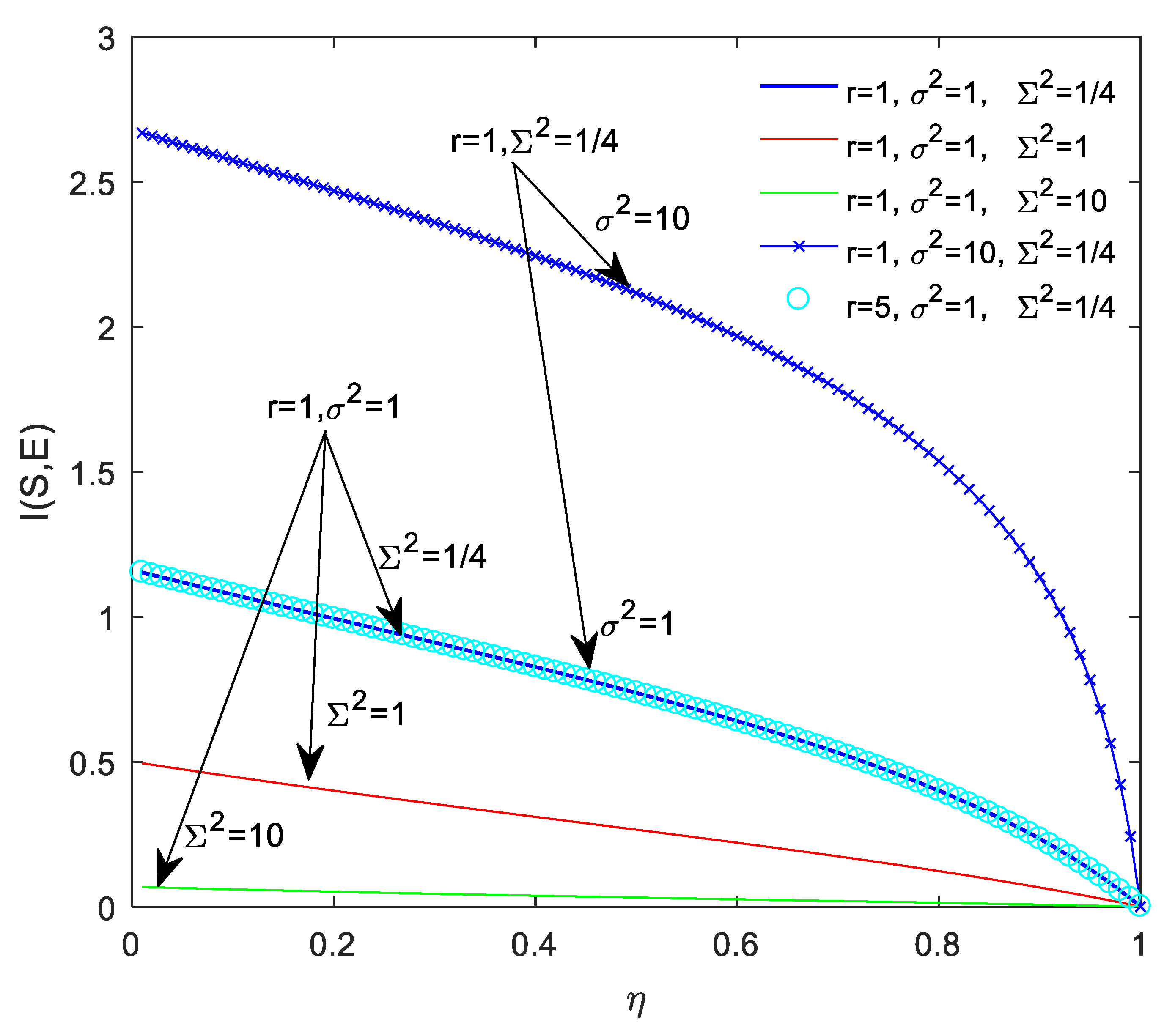
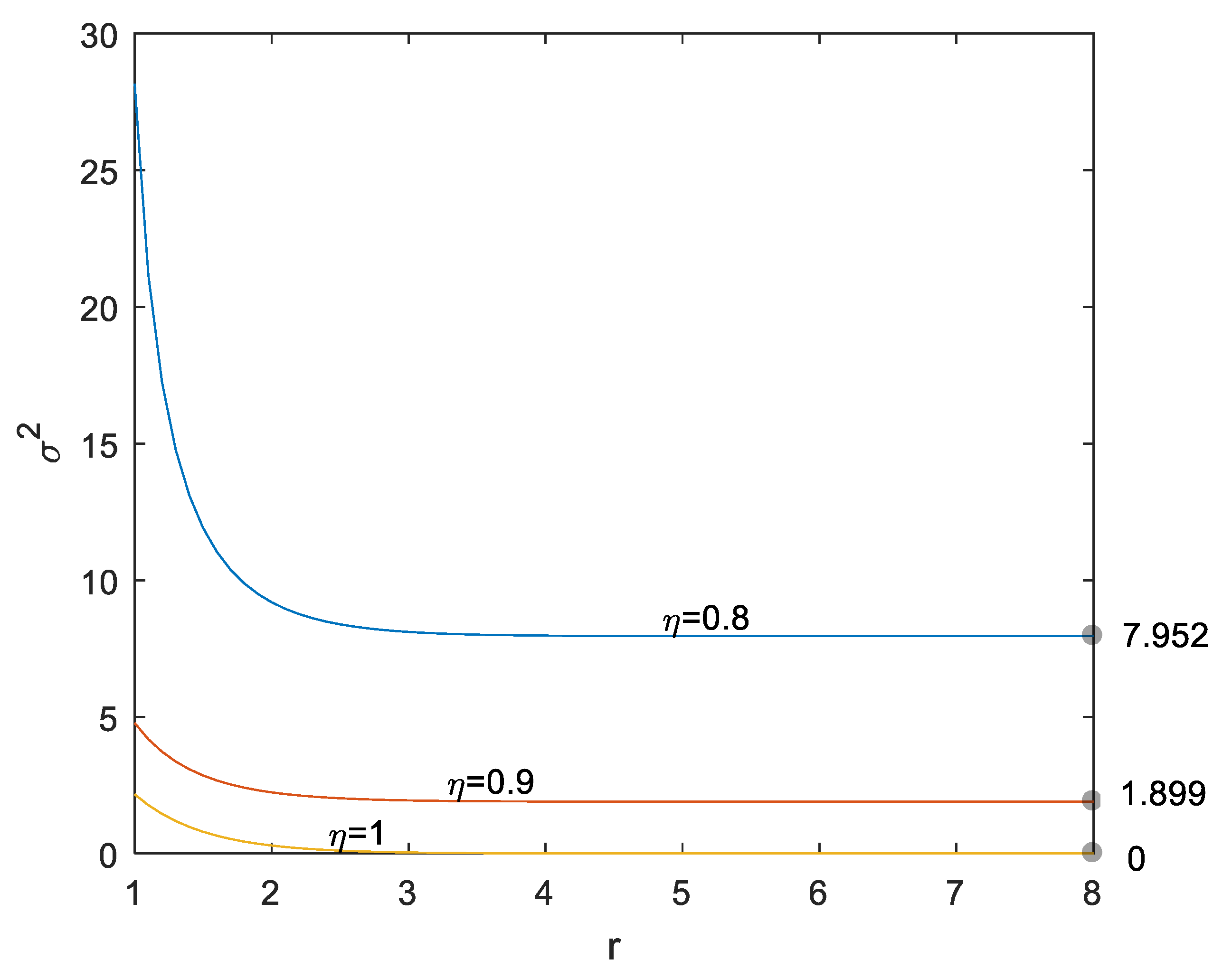
3. Security Analysis
3.1. No Attack
3.2. Internal Attack
3.3. Fairness Property
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hillery, M.; Bužek Berthiaume, A. Quantum secret sharing. Phys. Rev. A 1999, 59, 1829. [Google Scholar] [CrossRef]
- Karlsson, A.; Koashi, M.; Imoto, N. Quantum entanglement for secret sharing and secret splitting. Phys. Rev. A 1999, 59, 162. [Google Scholar] [CrossRef]
- Zhang, Z.; Man, Z. Multiparty quantum secret sharing of classical messages based on entanglement swapping. Phys. Rev. A 2005, 72, 022303. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, K.; Peng, K. Multiparty secret sharing of quantum information based on entanglement swapping. Phys. Lett. A 2004, 324, 420–424. [Google Scholar] [CrossRef]
- Guo, Y.; Liao, Q.; Huang, D.; Zeng, G. Quantum relay schemes for continuous-variable quantum key distribution. Phys. Rev. A 2017, 95, 042326. [Google Scholar] [CrossRef]
- Guo, Y.; Xie, C.; Huang, P.; Li, J.; Zhang, L.; Huang, D.; Zeng, G. Channel-parameter estimation for satellite-to-submarine continuous-variable quantum key distribution. Phys. Rev. A 2018, 97, 052326. [Google Scholar] [CrossRef]
- Guo, Y.; Ye, W.; Zhong, H.; Liao, Q. Continuous-variable quantum key distribution with non-Gaussian quantum catalysis. Phys. Rev. A 2019, 99, 032327. [Google Scholar] [CrossRef]
- Feng, Y.; Shi, R.; Guo, Y. Arbitrated quantum signature scheme with continuous-variable squeezed vacuum states. Chin. Phys. B 2018, 27, 020302. [Google Scholar] [CrossRef]
- Guo, Y.; Feng, Y.; Zeng, G. Quantum anonymous voting with unweighted continuous-variable graph states. Quantum Inf. Process 2016, 15, 3327–3345. [Google Scholar] [CrossRef]
- Lance, A.M.; Symul, T.; Bowen, W.P.; Tyc, T.; Sanders, B.C.; Lam, P.K. Continuous variable (2, 3) threshold quantum secret sharing schemes. New J. Phys. 2003, 5, 4. [Google Scholar] [CrossRef]
- Shi, R.; Su, Q.; Guo, Y. Quantum secret sharing based on Chinese remainder theorem. Commun. Theor. Phys. 2011, 55, 573. [Google Scholar]
- Guo, Y.; Zhao, Y. High-efficient quantum secret sharing based on the Chinese remainder theorem via the orbital angular momentum entanglement analysis. Quantum Inf. Process. 2013, 12, 1125–1139. [Google Scholar] [CrossRef][Green Version]
- Kang, Y.; Liao, Q.; Geng, J.; Guo, Y. Continuous Variable Quantum Secret Sharing with Chinese Remainder Theorem. Int. J. Theor. Phys. 2019, 58, 3986–3997. [Google Scholar] [CrossRef]
- Liu, F.; Su, Q.; Wen, Q. Eavesdropping on multiparty quantum secret sharing scheme based on the phase shift operations. Int. J. Theor. Phys. 2014, 53, 1730–1737. [Google Scholar] [CrossRef]
- Qin, S.J.; Gao, F.; Wen, Q.Y.; Zhu, F.-C. Cryptanalysis of the Hillery-Bužek-Berthiaume quantum secret-sharing protocol. Phys. Rev. A 2007, 76, 062324. [Google Scholar] [CrossRef]
- Gao, F.; Qin, S.J.; Wen, Q.Y.; Zhu, F.-C. A simple participant attack on the protocol. Quantum Inf. Comput. 2007, 7, 329–334. [Google Scholar]
- Lin, H.Y.; Harn, L. Fair reconstruction of a secret. Inf. Process. Lett. 1995, 55, 45–47. [Google Scholar] [CrossRef]
- Liu, F.; Qin, S.J.; Wen, Q.Y. A quantum secret-sharing protocol with fairness. Phys. Scr. 2014, 89, 075104. [Google Scholar] [CrossRef]
- Maitra, A.; De, S.J.; Paul, G.; Pal, A.K. Proposal for quantum rational secret sharing. Phys. Rev. A 2015, 92, 022305. [Google Scholar] [CrossRef]
- He, G.; Zeng, G. Quantum encryption protocol based on continuous variable EPR correlations. Commun. Theor. Phys. 2006, 46, 61. [Google Scholar]
- Gong, L.H.; Song, H.C.; He, C.S.; Liu, Y.; Zhou, N.-R. A continuous variable quantum deterministic key distribution based on two-mode squeezed states. Phys. Scr. 2014, 89, 035101. [Google Scholar] [CrossRef]
- Ma, S.; Li, X.; Xie, J.; Li, F.-L. Two-mode squeezed states of two separated nitrogen-vacancy-center ensembles coupled via dissipative photons of superconducting resonators. Phys. Rev. A 2019, 99, 012325. [Google Scholar] [CrossRef]
- Downing, C.A.; Carreño, J.C.L.; Laussy, F.P.; del Valle, E.; Fernández-Domínguez, A.I. Quasichiral interactions between quantum emitters at the nanoscale. Phys. Rev. Lett. 2019, 122, 057401. [Google Scholar] [CrossRef] [PubMed]
- Asmuth, C.; Bloom, J. A modular approach to key safeguarding. IEEE Trans. Informat. Theory 1983, 29, 208. [Google Scholar] [CrossRef]
- Shannon, C.E. Communication theory of secrecy systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- He, G.; Zhu, J.; Zeng, G. Quantum secure communication using continuous variable Einstein-Podolsky-Rosen correlations. Phys. Rev. A 2006, 73, 012314. [Google Scholar] [CrossRef]
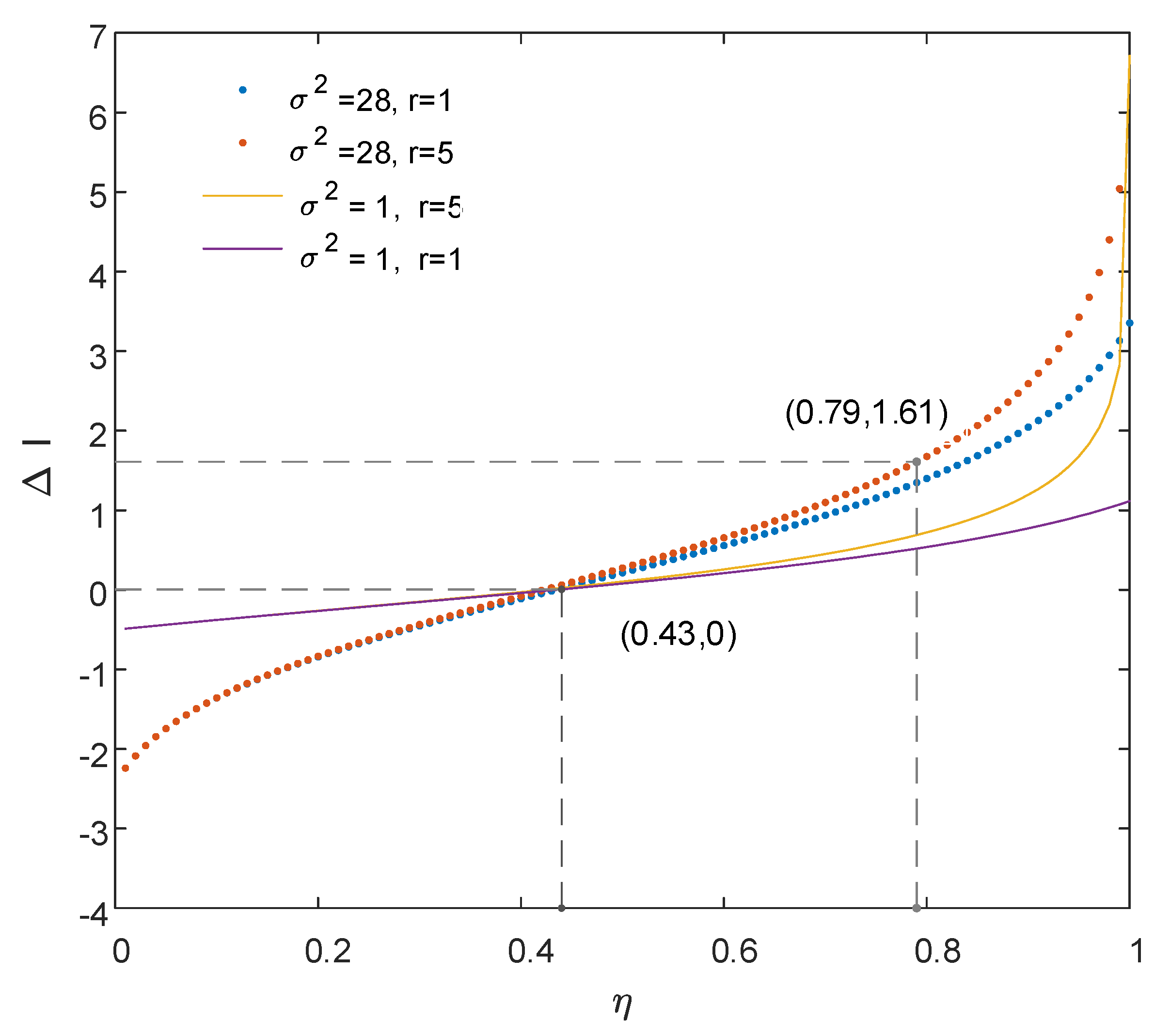
| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 1 | 0 | 1 | |
| 0 | 1 | 2 | 0 | 1 | 2 |
| 1/3 | 0 | 1/3 | 0 | 1/3 | 0 | |
| 0 | 1/3 | 0 | 1/3 | 0 | 1/3 |
| 1/2 | 0 | 0 | 1/2 | 0 | 0 | |
| 0 | 1/2 | 0 | 0 | 1/2 | 0 | |
| 0 | 0 | 1/2 | 0 | 0 | 1/2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, Y.; Guo, Y.; Zhong, H.; Chen, G.; Jing, X. Continuous Variable Quantum Secret Sharing with Fairness. Appl. Sci. 2020, 10, 189. https://doi.org/10.3390/app10010189
Kang Y, Guo Y, Zhong H, Chen G, Jing X. Continuous Variable Quantum Secret Sharing with Fairness. Applied Sciences. 2020; 10(1):189. https://doi.org/10.3390/app10010189
Chicago/Turabian StyleKang, Ye, Ying Guo, Hai Zhong, Guojun Chen, and Xiaojun Jing. 2020. "Continuous Variable Quantum Secret Sharing with Fairness" Applied Sciences 10, no. 1: 189. https://doi.org/10.3390/app10010189
APA StyleKang, Y., Guo, Y., Zhong, H., Chen, G., & Jing, X. (2020). Continuous Variable Quantum Secret Sharing with Fairness. Applied Sciences, 10(1), 189. https://doi.org/10.3390/app10010189





