Measurement of Structural Loads Using a Novel MEMS Extrinsic Fabry–Perot Strain Sensor
Abstract
1. Introduction
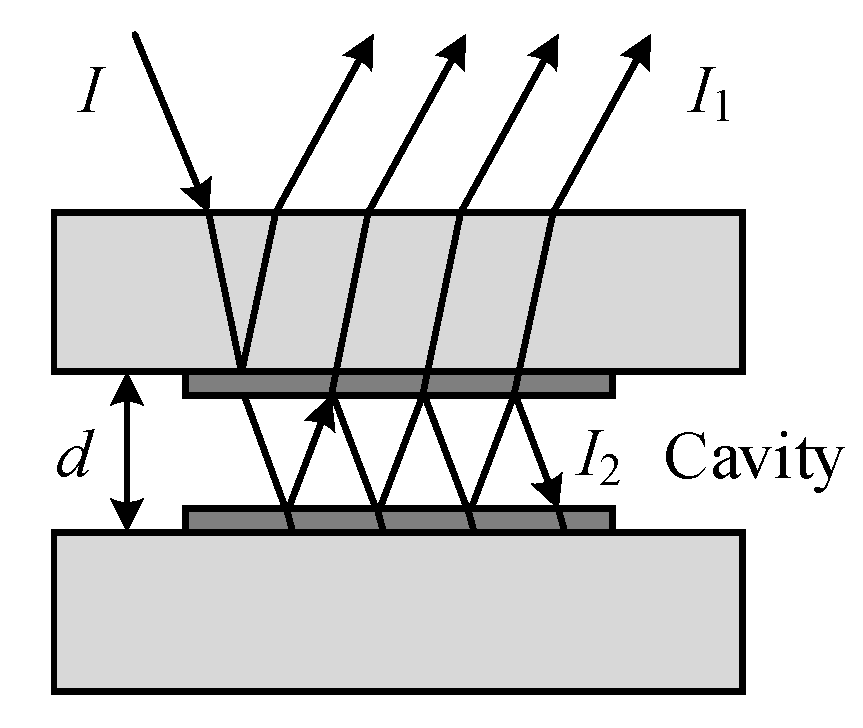
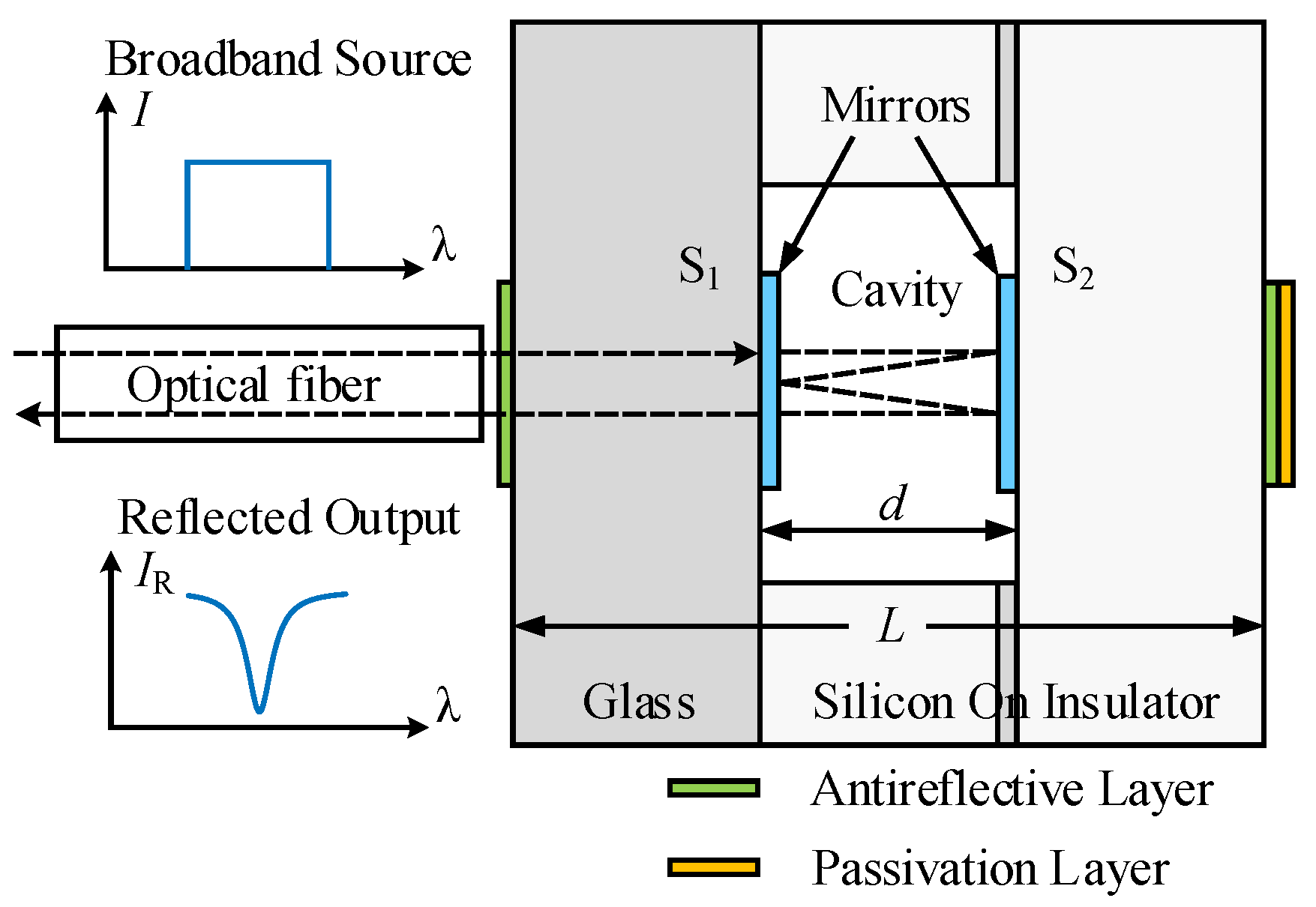
2. Principle of Operating
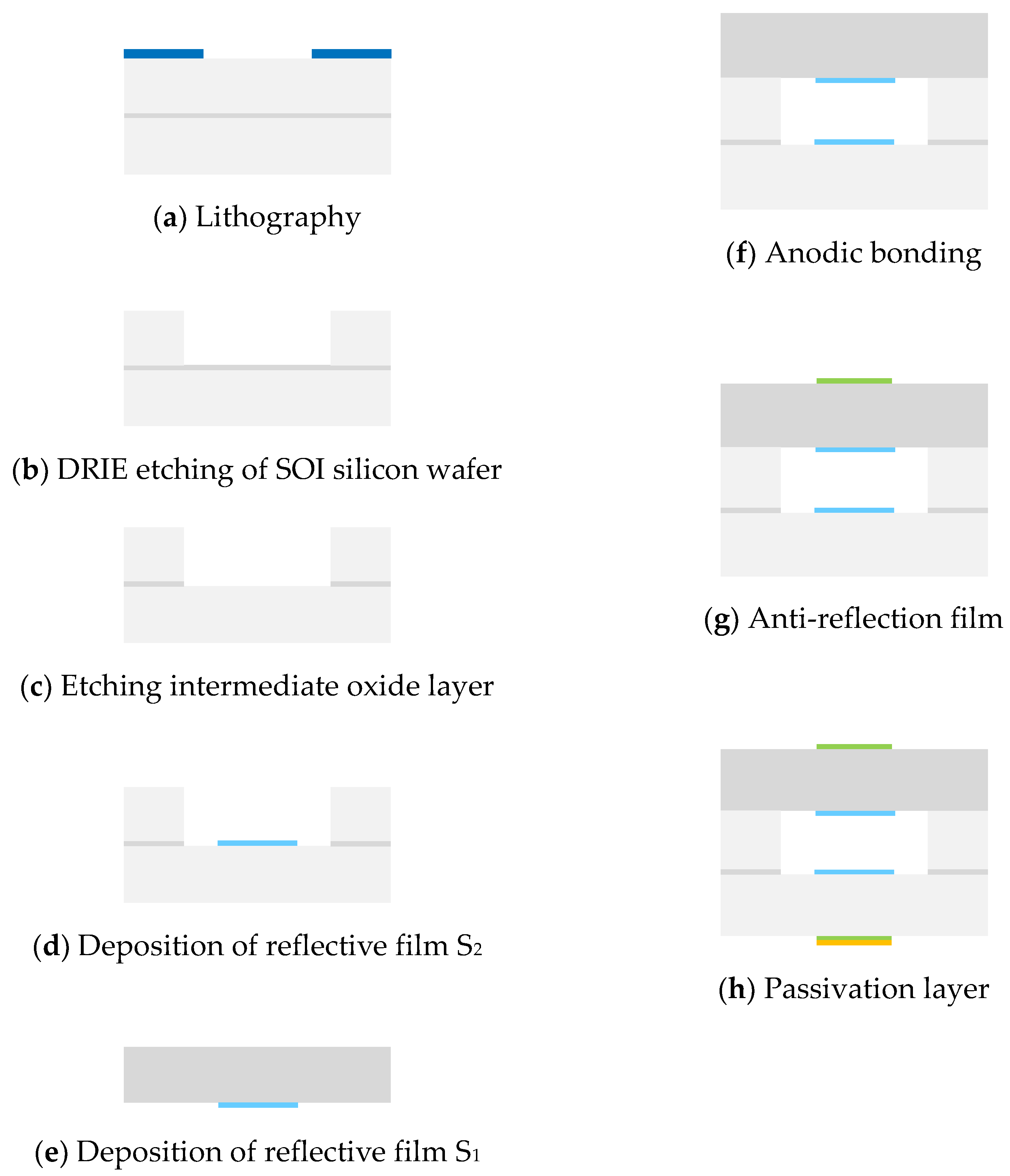
3. Sensor Fabrication
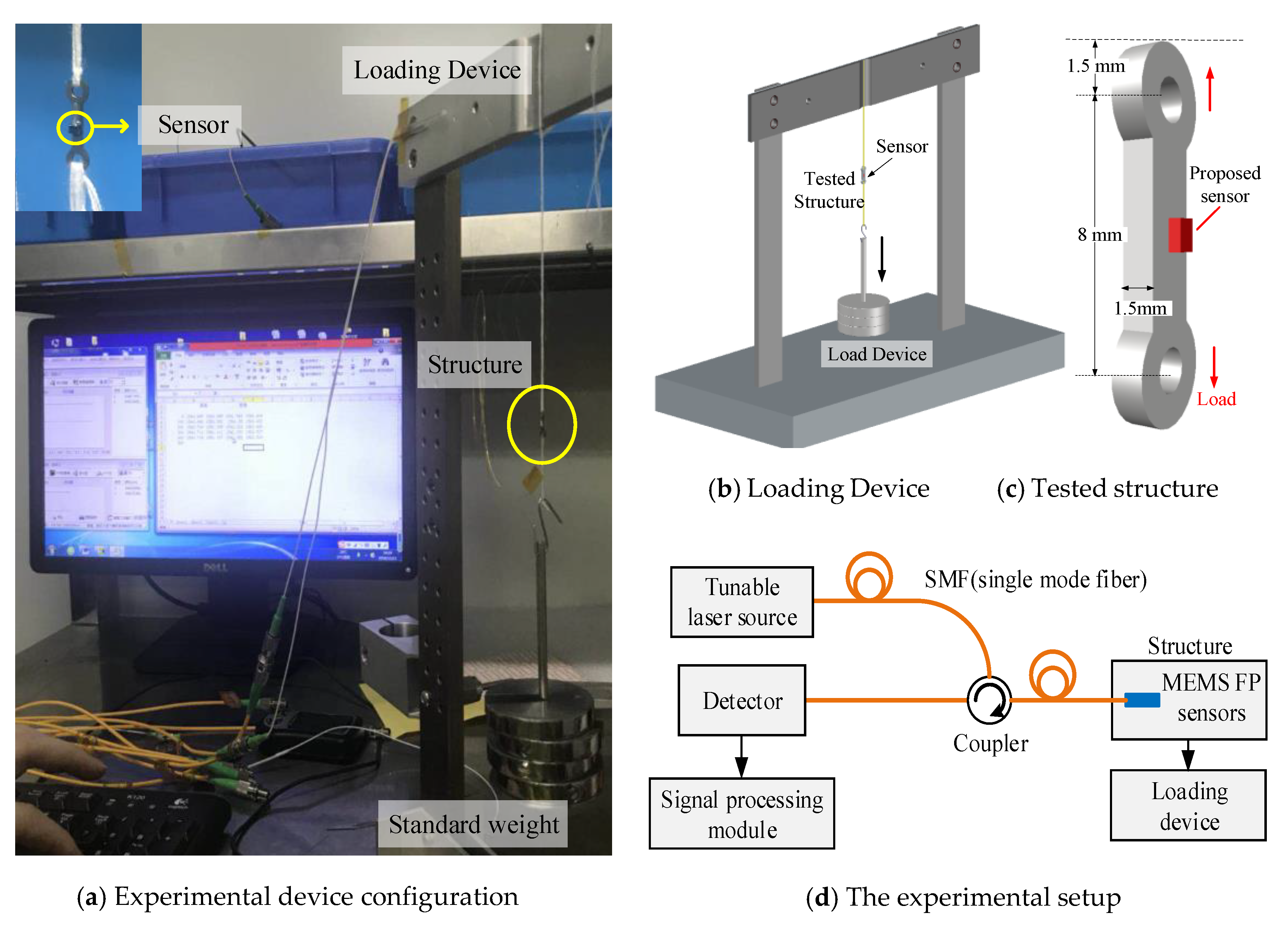
4. Experimental Setup and Discussion
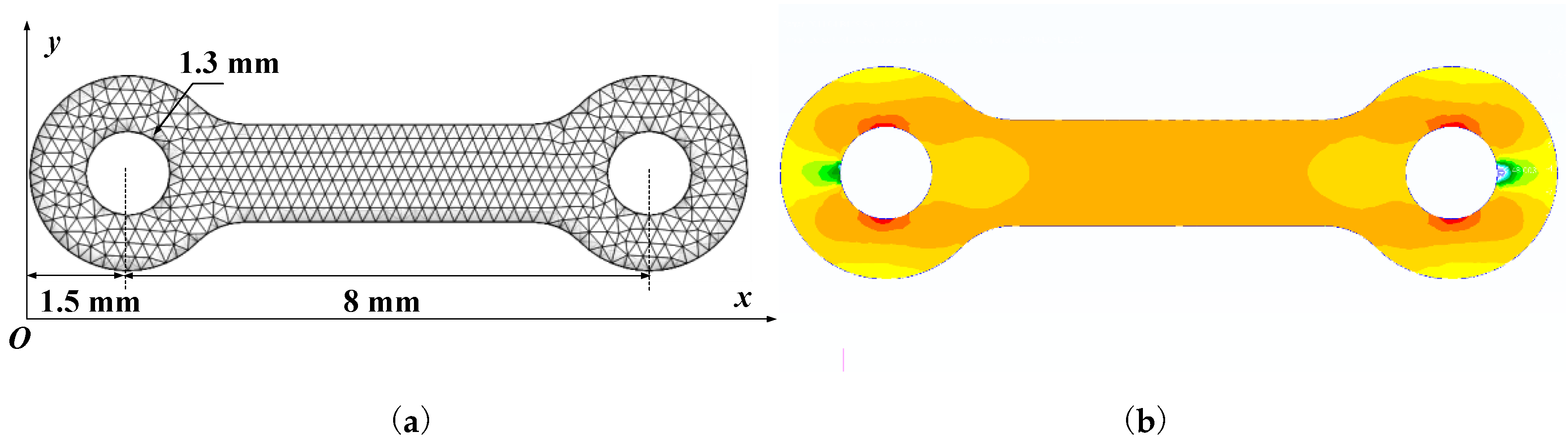
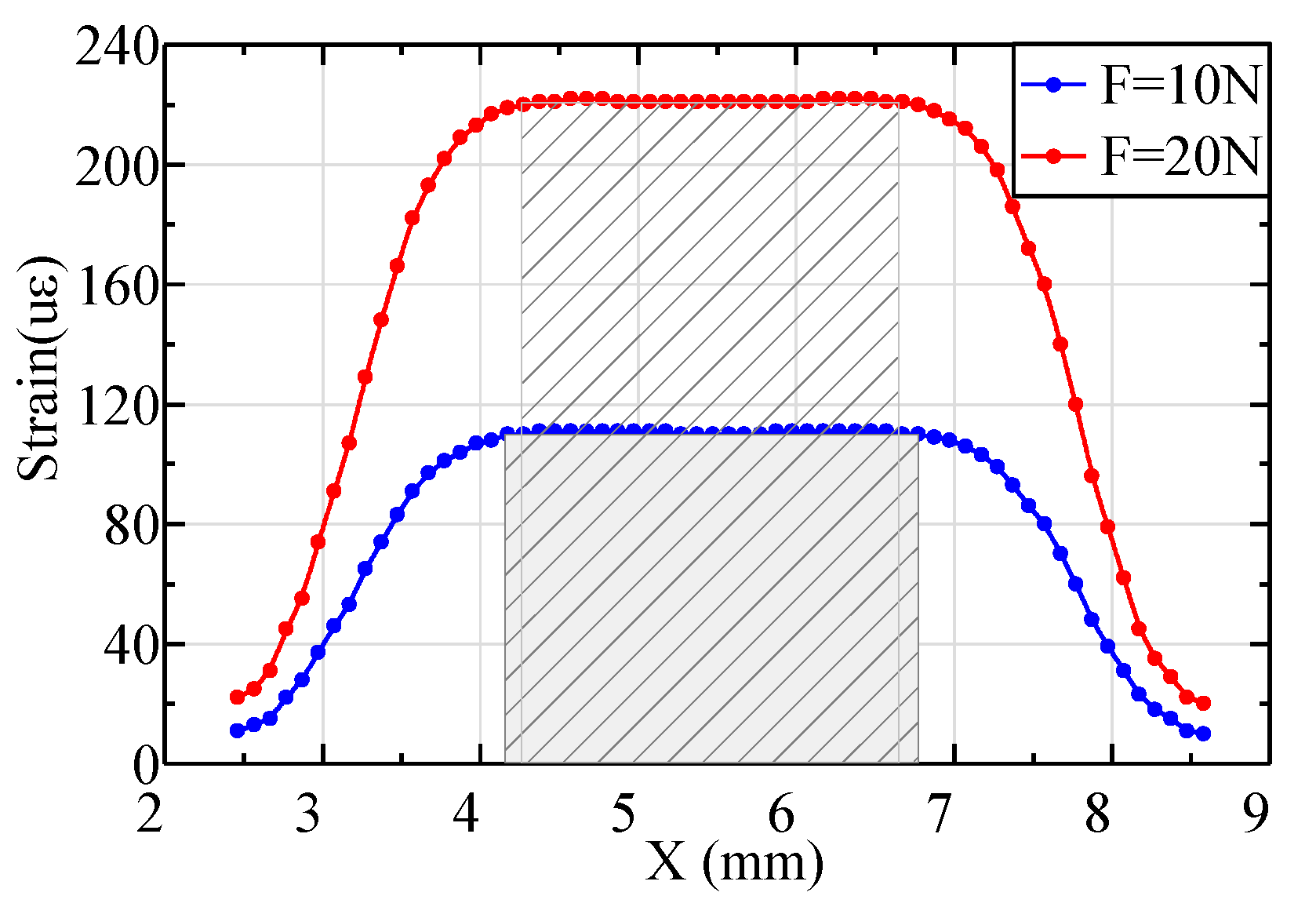
4.1. Sensor Placement
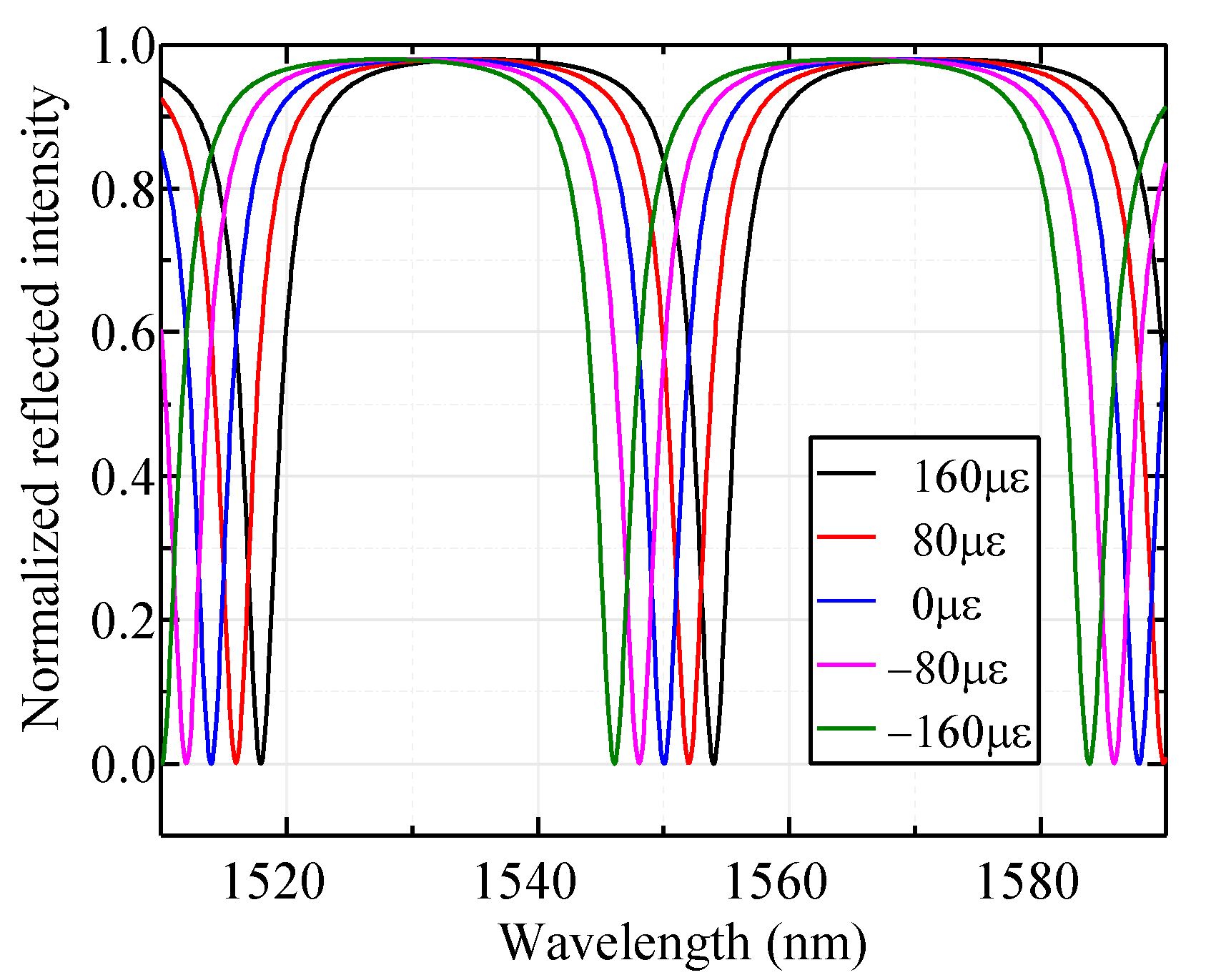
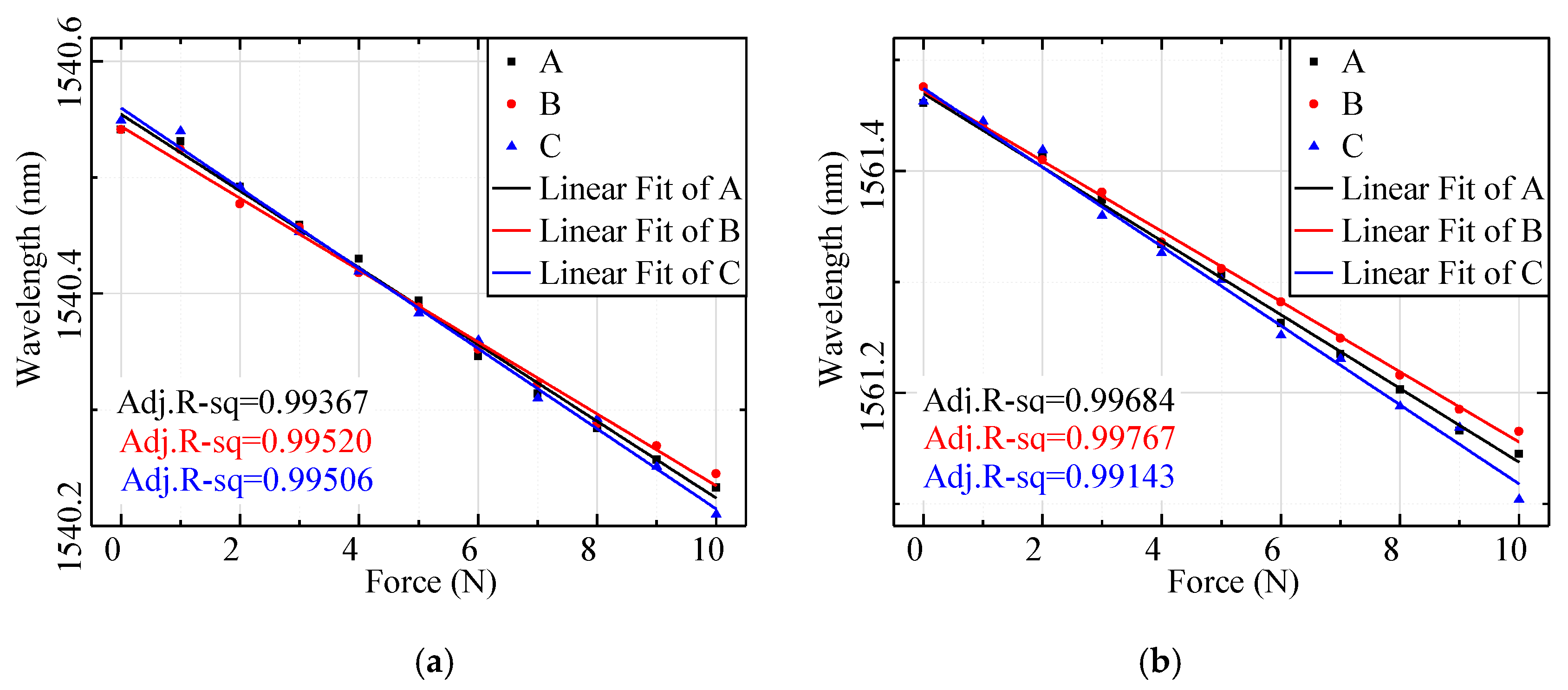
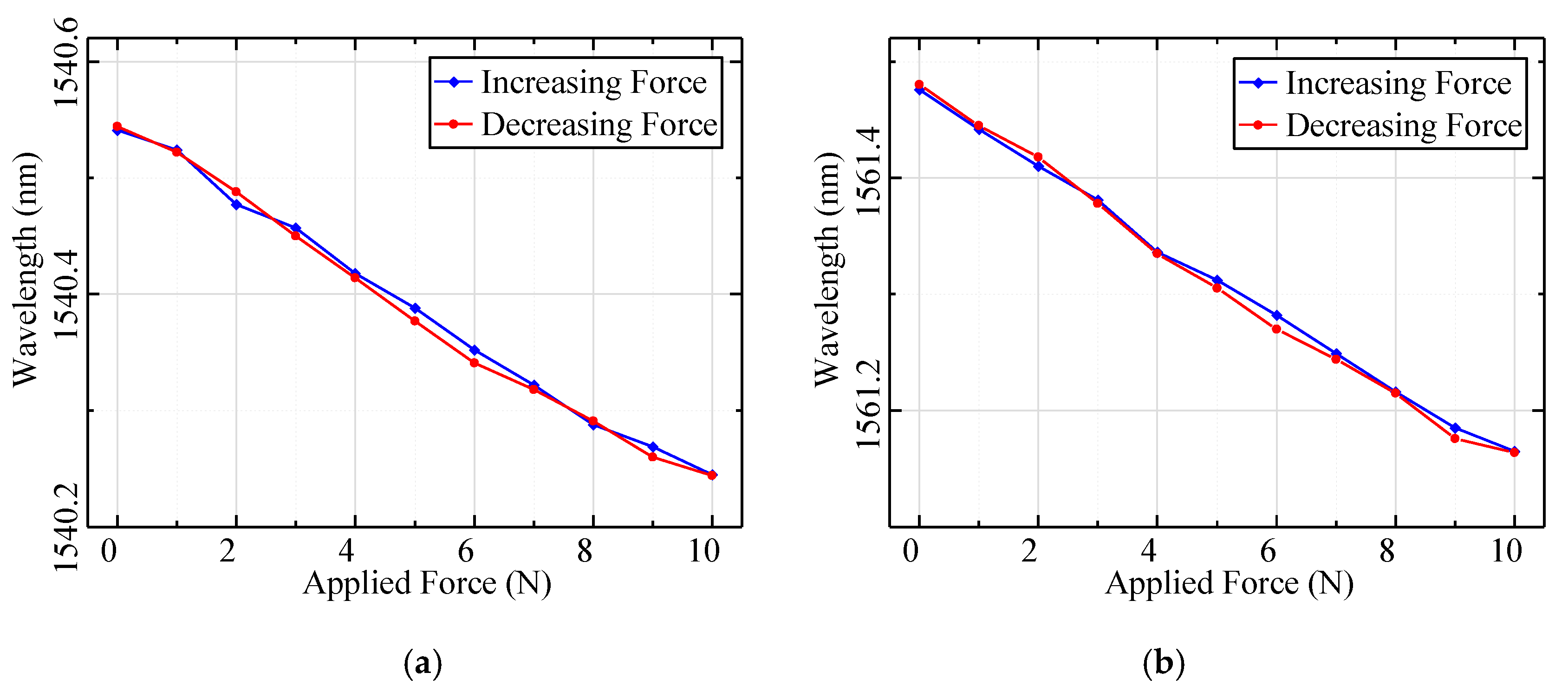
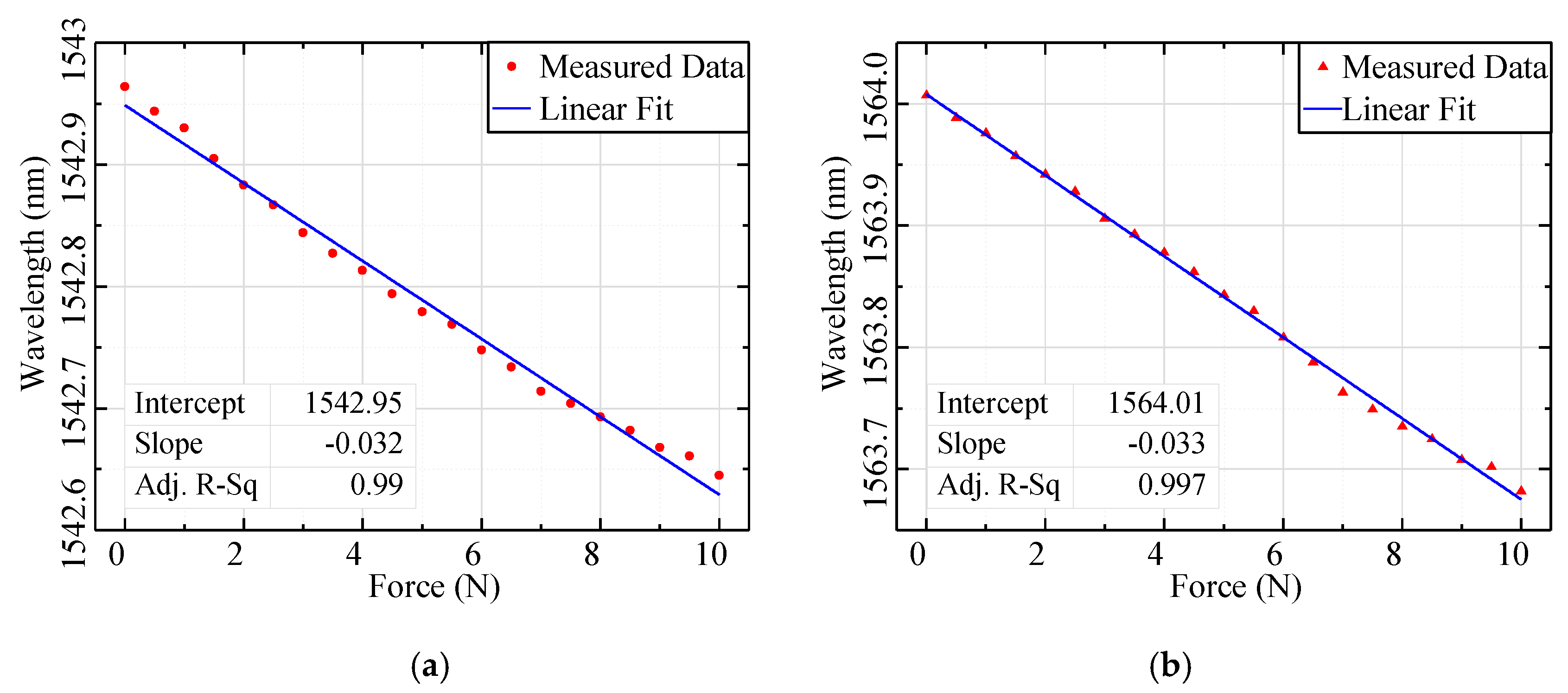
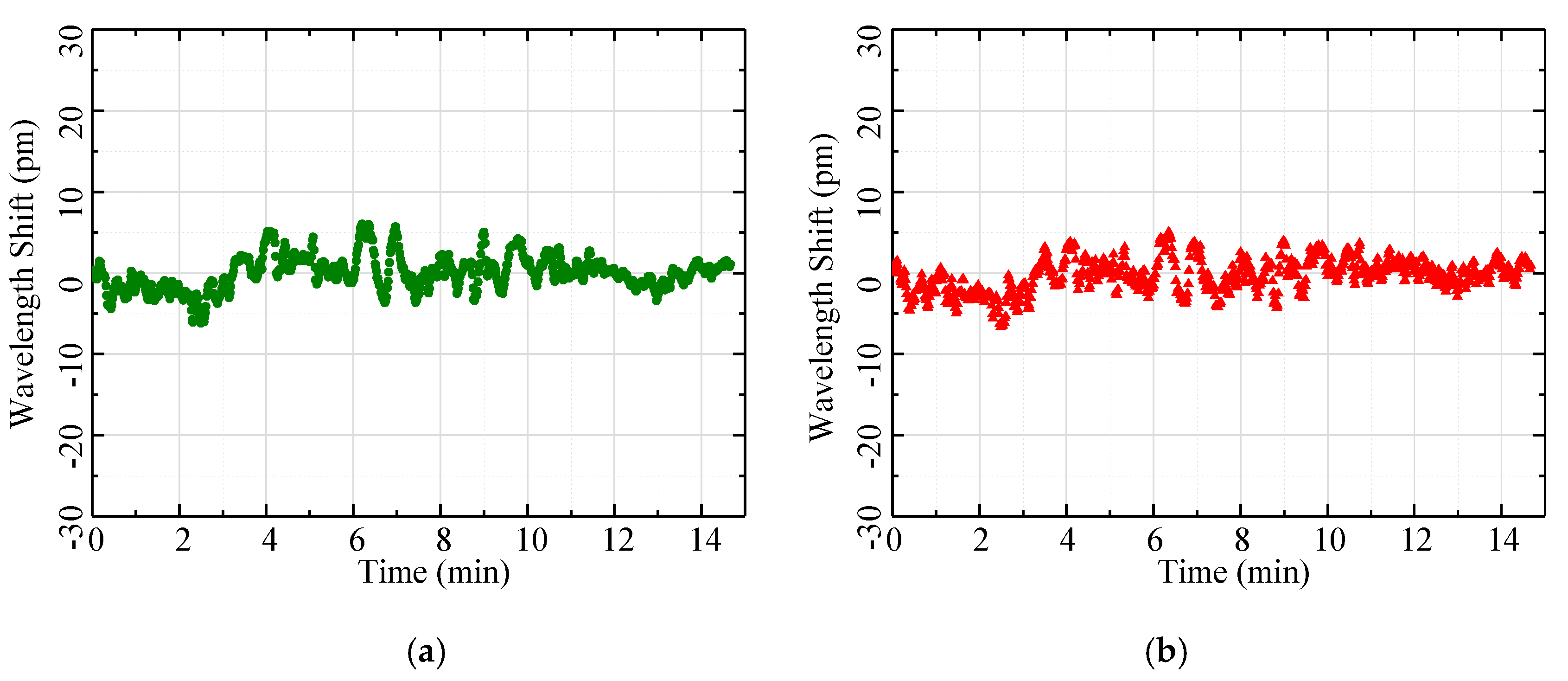
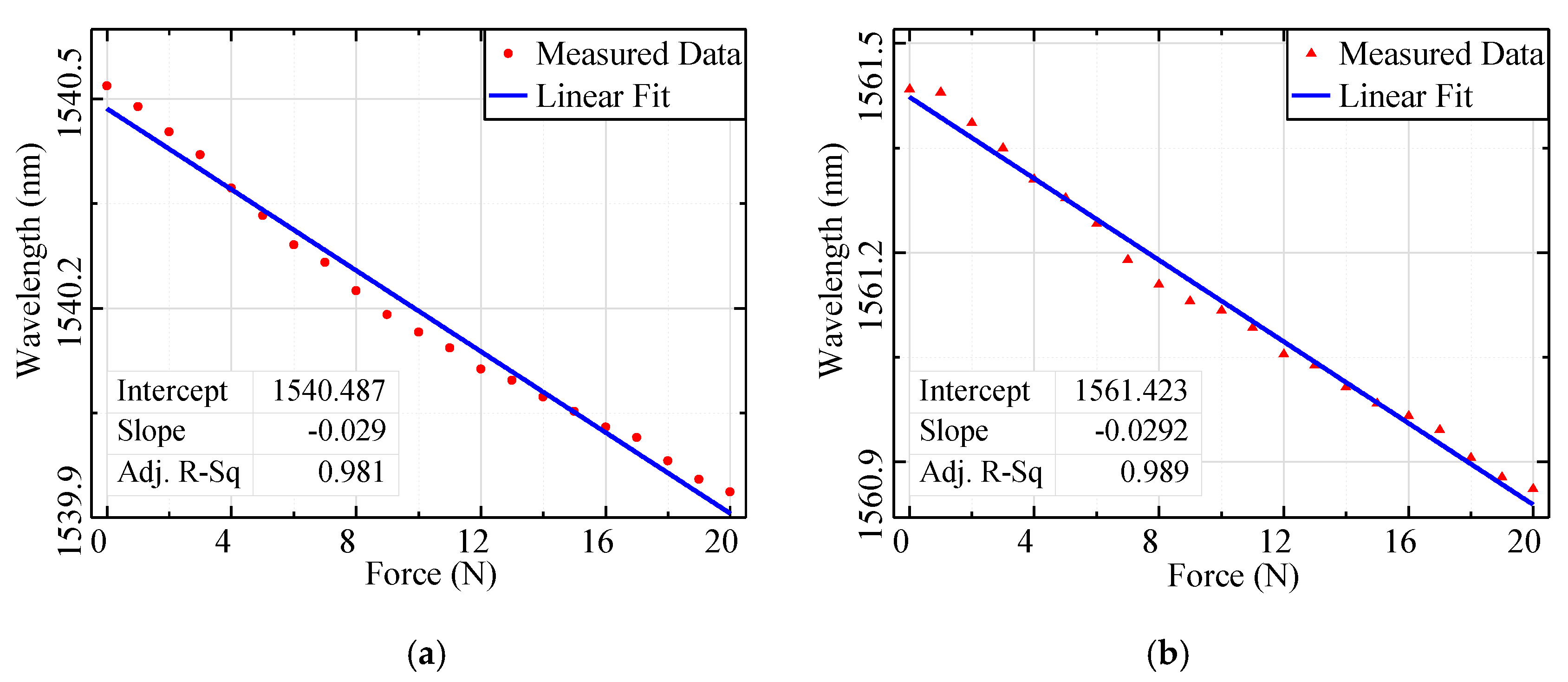
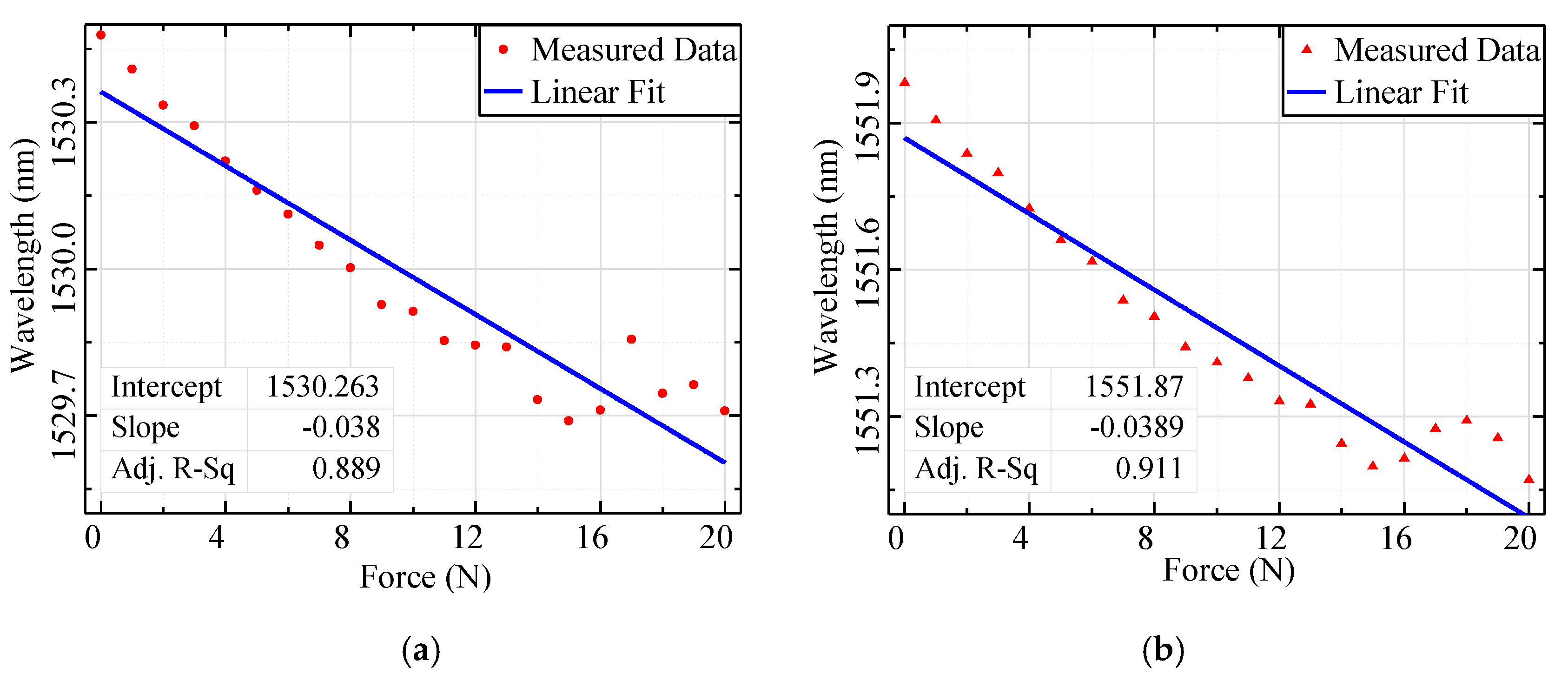
4.2. Measurement and Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Di Sante, R. Fiber Optic Sensors for Structural Health Monitoring of Aircraft Composite Structures: Recent Advances and Applications. Sensors 2015, 15, 18666–18713. [Google Scholar] [CrossRef] [PubMed]
- Ramakrishnan, M.; Rajan, G.; Semenova, Y.; Farrell, G. Overview of Fiber Optic Sensor Technologies for Strain/Temperature Sensing Applications in Composite Materials. Sensors 2016, 16, 99. [Google Scholar] [CrossRef] [PubMed]
- Pena, F.; Strutner, S.M.; Richards, W.L.; Piazza, A.; Parker, A.R. Evaluation of Embedded FBGs in Composite Overwrapped Pressure Vessels for Strain based Structural Health Monitoring. In Proceedings of the Industrial and Commercial Applications of Smart Structures Technologies 2014, San Diego, CA, USA, 10 March 2014. [Google Scholar]
- Geng, T.; Li, J.; Yang, W.; An, M.; Zeng, H.; Yang, F.; Cui, Z.; Yuan, L. Simultaneous measurement of temperature and strain using a long-period fiber grating with a micro-taper. Opt. Rev. 2016, 23, 657–661. [Google Scholar] [CrossRef]
- Lee, B.H.; Kim, Y.H.; Park, K.S.; Eom, J.B.; Kim, M.J.; Rho, B.S.; Choi, H.Y. Interferometric Fiber Optic Sensors. Sensors 2012, 12, 2467–2486. [Google Scholar] [CrossRef] [PubMed]
- Her, S.-C.; Yang, C.-M. Dynamic Strain Measured by Mach-Zehnder Interferometric Optical Fiber Sensors. Sensors 2012, 12, 3314–3326. [Google Scholar] [CrossRef]
- Xiao, S.; Wu, B.; Dong, Y.; Xiao, H.; Yao, S.; Jian, S. Strain and Temperature Discrimination using Two sections of PMF in Sagnac interferometer. Opt. Laser Technol. 2019, 113, 394–398. [Google Scholar] [CrossRef]
- Templeton, E.H.; Davis, M.A.; Pedrazzani, J.R.; Ohanian, O.J. Distributed High Temperature Measurement for Monitoring Bleed Air Lines and other Aircraft Structures. In Proceedings of the AIAA Information Systems-AIAA Infotech @ Aerospace, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar]
- Forbes, B.; Vlachopoulos, N.; Hyett, A.J. The application of distributed optical strain sensing to measure the strain distribution of ground support members. Facets 2018, 3, 195–226. [Google Scholar] [CrossRef]
- Lu, Z.; Cao, Y.; Wang, G.; Ran, Y.; Feng, X.; Guan, B.O. High-Resolution Displacement Sensor Based on a Chirped Fabry–Pérot Interferometer Inscribed on a Tapered Microfiber. Appl. Sci. 2019, 9, 403. [Google Scholar] [CrossRef]
- Zhang, T.; Liu, Y.; Yang, D.; Wang, Y.; Fu, H.; Jia, Z.; Gao, H. Constructed fiber-optic FPI-based multi-parameters sensor for simultaneous measurement of pressure and temperature, refractive index and temperature. Opt. Fiber Technol. 2019, 49, 64–70. [Google Scholar] [CrossRef]
- Li, H.; Deng, H.; Zheng, G.; Shan, M.; Zhong, Z.; Liu, B. Reviews on corrugated diaphragms in miniature fiber-optic pressure sensors. Appl. Sci. 2019, 9, 2241. [Google Scholar] [CrossRef]
- Zhao, Y.; Xia, F.; Chen, M.; Tong, R.; Peng, Y. Optical fiber axial contact force sensor based on bubble-expanded Fabry–Pérot interferometer. Sens. Actuators A Phys. 2018, 272, 318–324. [Google Scholar] [CrossRef]
- Arata, J.; Nitta, T.; Nakatsuka, T.; Kawabata, T.; Matsunaga, T.; Haga, Y.; Harada, K.; Mitsuishi, M. Optic Force Sensor for a Surgical Device Using a Fabry-Perot Interferometer. Appl. Sci. 2019, 9, 3454. [Google Scholar] [CrossRef]
- Favero, F.C.; Araujo, L.; Bouwmans, G.; Finazzi, V.; Villatoro, J.; Pruneri, V. Spheroidal Fabry-Perot microcavities in optical fibers for high-sensitivity sensing. Opt. Express 2012, 20, 7112–7118. [Google Scholar] [CrossRef] [PubMed]
- Frazão, O.; Aref, S.H.; Baptista, J.M.; Santos, J.L.; Latifi, H.; Farahi, F.; Kobelke, J.; Schuster, K. Fabry-pérot cavity based on a suspended-core fiber for strain and temperature measurement. IEEE Photonics Technol. Lett. 2009, 21, 1229–1231. [Google Scholar] [CrossRef]
- Yan, L.; Gui, Z.; Wang, G.; An, Y.; Gu, J.; Zhang, M.; Liu, X.; Wang, Z.; Wang, G.; Jia, P. A micro bubble structure based fabry–perot optical fiber strain sensor with high sensitivity and low-cost characteristics. Sensors 2017, 17, 555. [Google Scholar] [CrossRef]
- Domingues, M.F.; Rodriguez, C.A.; Martins, J.; Tavares, C.; Marques, C.; Alberto, N.; André, P.; Antunes, P. Cost-effective optical fiber pressure sensor based on intrinsic Fabry-Perot interferometric micro-cavities. Opt. Fiber Technol. 2018, 42, 56–62. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, T.; Wang, Y.; Yang, D.; Liu, X.; Fu, H.; Jia, Z. Simultaneous measurement of gas pressure and temperature with integrated optical fiber FPI sensor based on in-fiber micro-cavity and fiber-tip. Opt. Fiber Technol. 2018, 46, 77–82. [Google Scholar] [CrossRef]
- Wang, Y.; Liao, C.R.; Wang, D.N. Embedded coupler based on selectively infiltrated photonic crystal fiber for strain measurement. Opt. Lett. 2012, 37, 4747–4749. [Google Scholar] [CrossRef]
- Liu, Y.; Lang, C.; Wei, X.; Qu, S. Strain force sensor with ultra-high sensitivity based on fiber inline Fabry-Perot micro-cavity plugged by cantilever taper. Opt. Express 2017, 25, 7797–7806. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, D.N.; Chen, W.P. Crescent shaped Fabry-Perot fiber cavity for ultra-sensitive strain measurement. Sci. Rep. 2016, 6, 1–9. [Google Scholar] [CrossRef]
- Liu, H.; Liu, B. High-Sensitivity Fabry-Pérot Strain Senor Based on Fusion Splicing Photonic Crystal Fiber and Single Mode Fiber. In Proceedings of the 2018 11th International Symposium on Communication Systems, Networks & Digital Signal Processing (CSNDSP), Budapest, Hungary, 18–20 July 2018; pp. 1–4. [Google Scholar]
- Liu, S.; Wang, Y.; Liao, C.; Wang, G.; Li, Z.; Wang, Q.; Zhou, J. High-sensitivity strain sensor based on in-fiber improved Fabry-Perot interferometer. Opt. Lett. 2014, 39, 2121–2124. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Yang, D.; Yuan, Y.; Xu, J.; Li, D.; Zhao, J. Strain and high-temperature discrimination using a Type II fiber Bragg grating and a miniature fiber Fabry-Perot interferometer. Appl. Opt. 2016, 55, 6341–6345. [Google Scholar] [CrossRef] [PubMed]
- Ge, Y.; Cai, K.; Wang, T.; Zhang, J. MEMS pressure sensor based on optical Fabry-Perot interference. Optik 2018, 165, 35–40. [Google Scholar] [CrossRef]
- Abeysinghe, D.C.; Dasgupta, S.; Boyd, J.T.; Jackson, H.E. A novel MEMS pressure sensor fabricated on an optical fiber. IEEE Photonics Technol. Lett. 2001, 13, 993–995. [Google Scholar] [CrossRef]
- Pang, C.; Bae, H.; Gupta, A.; Bryden, K.; Yu, M. MEMS Fabry-Perot sensor interrogated by optical system-on-a-chip for simultaneous pressure and temperature sensing. Opt. Express 2013, 21, 21829. [Google Scholar] [CrossRef]
- Eugene, H. Interference. In Optics, 5th ed.; Murchana, B., Vikash, T., Trudy, K., Vikram, K., Eds.; Pearson Education: Edinburgh Gate, UK, 2017; pp. 436–441. [Google Scholar]
- Set, S.Y.; Jablonski, M.K.; Hsu, K.; Goh, C.S.; Kikuchi, K. Rapid amplitude and group-delay measurement system based on intra-cavity-modulated swept-lasers. IEEE Trans. Instrum. Meas. 2004, 53, 192–196. [Google Scholar] [CrossRef]
- Beer, F.P.; Johnston, E.R., Jr.; Dewolf, J.T.; Mazurek, D.F. Stress and Strain—Axial Loading. In Mechanics of Materials, 6th ed.; McGraw-Hill: New York, NY, USA, 2012; pp. 56, 67. [Google Scholar]
- Moradi, M. Strain Transfer Analysis of Surface-Bonded MEMS Strain Sensors. IEEE Sens. J. 2013, 13, 637–643. [Google Scholar] [CrossRef]
- Fang, Z.; Chin, K.K.; Qu, R.; Cai, H. Fiber grating and related devices. In Fundamentals of Optical Fiber Sensors; John Wiley & Sons: Hoboken, NJ, USA, 2012; pp. 249–250. [Google Scholar]
- Agidew, T.F.; Secco, E.L.; Maereg, A.T.; Reid, D.; Nagar, A.K. Fiber Optic-Based Force Sensor for Bio-Mimetic Robotic Finger. In Proceedings of the IEEE SENSORS, Glasgow, UK, 29 October–1 November 2017. [Google Scholar]
| Materials Physical Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Young’s modulus of the structure | 107 | GPa | |
| Poisson’s ratio of the structure | 0.34 | ||
| Density of the structure | 4.62 | g/cm3 | |
| Length of the structure | 11 | mm | |
| Width of the structure | 1.5 | mm | |
| Thickness of the structure | 0.55 | mm |
| Case | Minimum (N) | Maximum (N) | Increment (N) | Sensor Location |
|---|---|---|---|---|
| 1 | 0 | 10 | 1 | Center (5.5 mm) |
| 2 | 0 | 10 | 0.5 | Center (5.5 mm) |
| 3 | 5 | 5 | - | Center (5.5 mm) |
| 4 | 0 | 20 | 1 | Center (5.5 mm) |
| 5 | 0 | 20 | 1 | Bottom (7.0 mm) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, Y.; Zeng, J.; Huang, J.; Zhong, S.; Cheng, Z.; Liang, D. Measurement of Structural Loads Using a Novel MEMS Extrinsic Fabry–Perot Strain Sensor. Appl. Sci. 2020, 10, 18. https://doi.org/10.3390/app10010018
Bai Y, Zeng J, Huang J, Zhong S, Cheng Z, Liang D. Measurement of Structural Loads Using a Novel MEMS Extrinsic Fabry–Perot Strain Sensor. Applied Sciences. 2020; 10(1):18. https://doi.org/10.3390/app10010018
Chicago/Turabian StyleBai, Yufang, Jie Zeng, Jiwei Huang, Shaolong Zhong, Zhuming Cheng, and Dakai Liang. 2020. "Measurement of Structural Loads Using a Novel MEMS Extrinsic Fabry–Perot Strain Sensor" Applied Sciences 10, no. 1: 18. https://doi.org/10.3390/app10010018
APA StyleBai, Y., Zeng, J., Huang, J., Zhong, S., Cheng, Z., & Liang, D. (2020). Measurement of Structural Loads Using a Novel MEMS Extrinsic Fabry–Perot Strain Sensor. Applied Sciences, 10(1), 18. https://doi.org/10.3390/app10010018





