An Algorithm to Manage Transportation Logistics That Considers Sabotage Risk

Abstract

This paper presents an algorithm to solve the multilevel location–allocation problem when sabotage risk is considered (MLLAP-SB). Sabotage risk is the risk that a deliberate act of sabotage will happen in a living area or during the transportation of a vehicle. This can change the way decisions are made about the transportation problem when it is considered. The mathematical model of the MLLAP-SB is first presented and solved to optimality by using Lingo v. 11 optimization software, but it can solve only small numbers of test instances. Second, two heuristics are presented to solve large numbers of test instances that Lingo cannot solve to optimality within a reasonable time. The original differential evolution (DE) algorithm and the extended version of DE—the modified differential evolution (MDE) algorithm—are presented to solve the MLLAP-SB. From the computational result, when solving small numbers of test instances in which Lingo is able to find the optimality, DE and MDE are able to find a 100% optimal solution while requiring much lower computational time. Lingo uses an average 96,156.67 s to solve the problem, while DE and MDE use only 104 and 90 s, respectively. Solving large numbers of test instances where Lingo cannot solve the problem, MDE outperformed DE, as it found a 100% better solution than DE. MDE has an average 0.404% lower cost than DE when using a computational time of 90 min. The difference in cost between MDE and DE changes from 0.08% when using 10 min to 0.54% when using 100 min computational time. The computational result also explicitly shows that when sabotage risk is integrated into the method of solving the problem, it can reduce the average total cost from 32,772,361 baht to 30,652,360 baht, corresponding to a 9.61% reduction.

1. Introduction

Managing logistics and operating costs is the most important issue for managers to think about. Operating a logistics system includes managing transportation and inventory. Transportation in the real world not only has traveling costs, which include fuel costs, but in some areas special issues need to be considered. For example, in three southern provinces of Thailand, bombings often occur due to conflict among different groups. These three provinces are Narathiwat, Pattanee, and Yala. Their main business is selling palm. There are many palm fields that need to have palm collected at collecting points and then transported to factories, which will transform palm into the final product. All along this route there is a risk of bombing, which can generate sabotage risk and costs besides the transportation costs. Decision-makers face the problem that if they consider only costs, this will affect the safety of people who are involved in logistical activities. Therefore, the management of the logistical system in this special area needs to be reconsidered.

Palm is one of many sources of renewable energy. Energy is an important factor for the development of businesses, industries, and logistics. Most energy that we use comes from fossil fuels and is not renewable. This is one of the main causes of global warming. Therefore, renewable energy from plants is a good option that many countries are interested in. Sugar cane, cassava, and oil palms are renewable energy plants that can be grown in certain geographic locations in some countries. For example, Brazil was one of the leading countries that grew sugarcane to produce ethanol fuel in 2012 and 2013 (Bargos et al. 2016). In addition, a case study investigating growing energy plants was performed by Bojić et al. (2013), and the optimal siting and size of bioenergy facilities using geographically dependent renewable resources was studied by Sultana and Kumar (2012).

Thailand is the only country in the world that can grow all three renewable energy plants all year round, especially oil palms. Oil palms play an important role in the transportation industry and are supported by the government to be grown in many areas according to the oil palm industry development plan. Starting from 2012 until 2021 in the three southern border provinces, the plan is to establish stability, to reduce social inequality, and to create peace. Information from 2004 to 2012 shows that 14,074 violent incidents occurred in the provinces, including 2478 bomb explosions in civilian areas and transportation routes. Narathiwat, one of the three southern border provinces, had the most violent incidents, 5021. These facts threaten palm producers when palms are being delivered to both palm-collecting centers and palm oil extraction factories. A study by Krahomwong (2016) shows that the most important problem for the industry is transporting oil palms in the three southern border provinces. Narathiwat has the largest area of oil palm cultivation and the biggest logistics problem as well. The high transportation cost in this province is due to improper palm-collecting center locations, causing higher costs for oil palm manufacturers and palm-collecting centers themselves. Because of the unpeaceful incidents in the three southern border provinces, the authors would like to present a solution that can decrease operating costs and risks. We will focus on Narathiwat Province and explore three important aspects in order to set mathematic conditions. The aspects are as follows:

(1)

The lowest total operating cost.

(2)

The lowest emission from transportation.

(3)

The lowest risk of sabotage that might happen along transportation routes and at palm-collecting centers.

Managing transportation logistics for peaceful conditions needs to be reconsidered. Generally, the only things decision-makers need to consider when making decisions about transportation logistics are the total operating or transportation costs. Aside from making decisions on transportation logistics under sabotage risk for the area or the road that is normally used to transport the goods, under these conditions decision-makers face the difficulty of making decisions regarding the risk while keeping the cost as low as possible.

This case study is very complicated, and several factors need to be carefully considered in order to reach a break-even point for the investment. Metaheuristic algorithms are applied and used in a lot of research, and the differential evolution algorithm (DE), another method, has gained a lot of attention and can effectively solve problems, such as truck sequencing problems in cross-docking operations in a study by Liao et al. (2012) and the dynamic berth allocation problem in a study by Şahin and Kuvvetli (2016).

The differential evolution (DE) algorithm was first proposed by Storn and Price (1997). It is presented to solve over continuous optimization. Since then, DE has been successfully used to solve various combinatorial optimizations, such as by Pitakaso (2015); Pitakaso and Sethanan (2016) used DE to solve assembly line balancing, Storn and Price (1995) and Nearchou (2006) applied DE to solve machine layout, Lampinen and Zelinka (1999) used DE to solve the manufacturing problem, and Sethanan and Pitakaso (2016b) used it to solve generalized assignment problems.

Many researchers have been successful at using DE to solve transportation problems such as Vehicle Routing Problem (VRP) (Boon et al. 2015; Huan and Jeichang 2012; Akkararungruangkul and Kaewman 2018) and VRP with pickup and delivery system (Mingyong and Erbia 2010). The location routing problem (LRP) is also a problem that some researchers are interested in, such as Su et al. (2016) and Drexl and Schneider (2015). Thongdee and Pitakaso (2015) successfully employed the original DE to solve the multilevel location–allocation problem (MLLAP). They used DE to find a good location to establish an ethanol plant using bagasse and tapioca waste as the raw material, and these two materials are delivered from the sugar factory and tapioca starch. The objective function is to minimize total distance to reduce environmental impact. In our study, we solve a problem in the same class as MLLAP, but besides being interested in environmental impact, sabotage risk is our main interest, because the case study is in an area where the risk of a deliberate act is quite high. Therefore, the decision-making of MLLAP will shift the interest so that not only the distance between point to point is interesting but also the risk of bombs.

DE has been successfully applied to many combinatorial optimizations. This because it is simple to apply to solve problems and uses only a few parameters. Many researchers have tried to improve the efficiency of DE by adding a few behaviors to the original DE and calling it modified DE (MDE). Pitakaso and Sethanan (2016) suggested using a good combination of different mutations and recombination formula. Yong et al. (2018) presented a new strategy to select a solution for the mutation process. Wang et al. (2016) introduced the use of cumulative population distribution with the DE mechanism. Sethanan and Pitakaso (2016a) added more steps to the original DE to introduce a local search strategy by using reborn vectors. The computational results show that adding new attributes can improve the efficiency of DE, because MDE outperforms the original DE in finding good solutions.

From the review we can see that introducing new behaviors to DE can increase the solution quality. Among the studies mentioned above, some add more intensification behavior to search more intensively in some interested areas (Sethanan and Pitakaso 2016a, 2016b), and some use more diversification with the original DE to enhance its capability to explore more searching space (Wang et al. 2016; Yong et al. 2018); both ways are successful. In this paper, the original DE has both diversification and intensification behavior. The proposed heuristics will first be searched for intensively, and when a better solution cannot be found within the predefined condition, the process that can enhance the capability of the diversification behavior of DE will be used. Therefore, this paper has two main contributions: (1) a new class of MLLAP is introduced, MLLAP-SB, and (2) new attributes of DE are introduced so that the original DE has more diversified behavior.

The paper is organized as follows: Section 2 presents the problem definition and mathematics in which the authors can see the whole body of the proposed problem; Section 3 presents the proposed heuristics in which the differential evolution (DE) algorithm is explained; and Section 4 and Section 5 are the computational results and conclusion.

2. Problem Description and Mathematical Formulation

The model used to solve the location–allocation problem of supporting renewable energy cultivation in the three southern border provinces has two levels of decision-making. From the starting point of the research of Nanthasamroeng et al. (2008) and Mayachearw (2012), who studied the mentioned problem, we now investigate the activities and areas for growing oil palms in more detail. The increase in products under current circumstances is shown in Figure 1.

• Indices
  $i=$ Oil palm producer number 1, 2, …, n has a certain number of oil palms each day
  $j=$ Area chosen to be a palm-collecting center
  $l=$ Oil palm factory
• Decision Variables

  $q_{ij}$ Number of oil palms of producer $i$ sent to palm-collecting center $j$ (kg)

  $Q{a}_{jl}$ Number of oil palms collected at palm-collecting center $j$ sent to factory $l$ (kg)

  $x_{ij}=\{\begin{array}{l}1ifproducerisendspalmstocollectingcenterj\\ 0otherwise\end{array}$

  $z_j=\{\begin{array}{l}1ifcollectingcenterjischosen\\ 0otherwise\end{array}$

  $y_{jl}=\{\begin{array}{l}1ifcollectingcenterjsendspalmstofactoryl\\ 0otherwise\end{array}$

• Parameters

  $d_{ij}$	Distance from producer $i$ to palm-collecting center $j$ (km)
  $d_{ji}$	Distance from palm-collecting center $j$ back to producer $i$ (km)
  $G{o}_{jl}$	Distance from palm-collecting center $j$ to factory $l$ (km)
  $G{o}_{lj}$	Distance from factory $l$ back to palm-collecting center $j$ (km)
  $n_i$	Number of transportation rounds by each producer $i$
  $A{p}_i$	Number of palms producer $i$ can send each day (kg)
  $c_i$	Existing transportation cost of producer $i$ (baht/km)
  $C{o}_j$	Existing transportation cost of palm-collecting center $j$ (baht/km)
  $l{a}_j$	Land price of each palm-collecting center $j$ (baht)
  $A{d}_j$	Surface adjustment cost of palm-collecting center $j$ (baht)
  $B{u}_j$	Construction cost of palm-collecting center $j$ (baht)
  $O{v}_j$	Other costs of palm-collecting center $j$ (baht)
  $f{1}_i$	Emission factor from using diesel fuel to transport oil palms by producer $i$ (baht/km)
  $f{2}_j$	Emission factor from using diesel fuel to transport oil palms by palm-collecting center $j$ (baht/km)
  $R_{ij}$	Possibility of bomb explosion on route from producer $i$ to palm-collecting center $j$
  $R_{ji}$	Possibility of bomb explosion on route from palm-collecting center $j$ back to producer $i$
  $Po{p}_{ij}$	Average population density on route from producer $i$ to palm-collecting center $j$ that has sabotage risk
  $Po{p}_{ji}$	Average population density on route from palm-collecting center $j$ back to producer $i$ that has sabotage risk
  $R{R}_{jl}$	Possibility of bomb explosion on route from palm-collecting center $j$ to factory $l$
  $PP{O}_{jl}$	Average population density on route from palm-collecting center $j$ to factory $l$ that has sabotage risk
  $N{N}_j$	Possibility of bomb explosion at palm-collecting center $j$
  $P{P}_j$	Average population density at palm-collecting center $j$ that has sabotage risk
  $g$	Distance of bomb explosion affecting population with a radius of 0.1 km using formula $\mathsf{\pi }{r}^2$
  $Tr{p}_j$	Number of routes for transferring palms from palm-collecting center to factory (integer)
  $Ca{p}_j$	Capability of palm-collecting center $j$
  $V_j$	Capability of vehicles of palm-collecting center $j$ (kg)
  $Fa{c}_l$	Capability of factory $l$ (kg)
  $M$	Maximum amount of oil palm producer
  $Bomb$	Compensation costs from sabotage (baht)

2.1. Objective Function

The objective function is the sum of the lowest total operating cost, the cost of emitting pollution from transportation, the cost of securing transportation routes, and the lowest cost of operating a palm-collecting center that has sabotage risk.

$$\begin{array}{c}Min{\displaystyle {\displaystyle \sum }_{i=1}^I}{\displaystyle {\displaystyle \sum }_{j=1}^J}{x}_{ij}\left(d_{ij}+d_{ji}\right)c_i{n}_i+{\displaystyle {\displaystyle \sum }_{j=1}^J}{\displaystyle {\displaystyle \sum }_{l=1}^L}{y}_{jl}\left(G{o}_{jl}+G{o}_{lj}\right)C{o}_{j}Tr{p}_j\\ +{\displaystyle {\displaystyle \sum }_{j=1}^J}{z}_j\left(l{a}_j+A{d}_j+B{u}_j+O{v}_j\right)+{\displaystyle {\displaystyle \sum }_{i=1}^I}{\displaystyle {\displaystyle \sum }_{j=1}^J}f{1}_i{x}_{ij}\left(d_{ij}+d_{ji}\right)n_i\\ +{\displaystyle {\displaystyle \sum }_{j=1}^J}{\displaystyle {\displaystyle \sum }_{l=1}^L}f{2}_j{y}_{jl}\left(G{o}_{jl}+G{o}_{lj}\right)Tr{p}_j+[Bomb({\displaystyle {\displaystyle \sum }_{i=1}^I}{\displaystyle {\displaystyle \sum }_{j=1}^J}\left(\left(R_{ij}Po{p}_{ij}\right)+\left(R_{ji}Po{p}_{ji}\right)\right)g{x}_{ij}{n}_i\\ +{\displaystyle {\displaystyle \sum }_{j=1}^J}{\displaystyle {\displaystyle \sum }_{l=1}^L}2\left(R{R}_{jl}gPP{O}_{jl}{y}_{jl}Tr{p}_j\right)+{\displaystyle {\displaystyle \sum }_{j=1}^J}N{N}_{j}P{P}_{j}g{z}_j)]\end{array}$$

(1)

2.2. Constraint Functions

The constraints are the limitations and conditions of the decision variables the decision-maker needs to take care of. The objective function needs to be minimized when all constraints addressed below are satisfied.

$${{\displaystyle \sum }}_{j=1}^J{x}_{ij}=1{\forall }_i$$

(2)

$${{\displaystyle \sum }}_{j=1}^J{q}_{ij}=A{p}_i{\forall }_i$$

(3)

$${{\displaystyle \sum }}_{i=1}^I{x}_{ij}{q}_{ij}\le Ca{p}_j{\forall }_j$$

(4)

$$q_{ij}\le M{x}_{ij}{\forall }_{i,j}$$

(5)

$${\displaystyle \sum }_{j=1}^J{z}_j\ge 1$$

(6)

$$x_{ij}\le z_j{\forall }_{i,j}$$

(7)

$${{\displaystyle \sum }}_{l=1}^L{y}_{jl}\le 1{\forall }_j$$

(8)

$$Q{a}_{jl}\le M{y}_{jl}{\forall }_{i,j}$$

(9)

$${{\displaystyle \sum }}_{j=1}^J{y}_{jl}Q{a}_{jl}\le Fa{c}_l{\forall }_l$$

(10)

$$Tr{p}_j\ge \frac{{{\displaystyle \sum }}_{i=1}^I{q}_{ij}{z}_j}{V_j}{\forall }_j,Integer$$

(11)

$${{\displaystyle \sum }}_{l=1}^{L}Q{a}_{jl}={{\displaystyle \sum }}_{i=1}^I{q}_{ij}{\forall }_j$$

(12)

The objective function (Equation (1)) consists of eight parts. The first part shows the total cost of transferring palms from producer $i$ to palm-collecting center $j$. The second part shows the cost of transferring palms from palm-collecting center $j$ to factory $l$. The third part is the cost of land investment, surface adjustment, construction, and other operating costs at palm-collecting center $j$. The first three parts focus on the lowest total operating process, while the fourth and fifth parts concentrate on fee rates for emitting carbon dioxide. The sixth part shows the level of safety of transferring palms from producer $i$ to palm-collecting center $j$. The seventh part shows the level of safety of transferring palms from palm-collecting center $j$ to factory $l$. The last part shows the possibility of a bomb explosion at the palm-collecting center.

Constraint function (2) ensures that all producers send their palms to a palm-collecting center. Constraint function (3) ensures that each producer sends the palms on hand to palm-collecting center $j$. Constraint function (4) ensures that the number of palms producer $i$ sends to palm-collecting center $j$ does not exceed the capacity of palm-collecting center $j$. Constraint function (5) states that if no palms from producer $i$ are being sent to the palm-collecting center $\left(x_{ij}=0\right)$, then the number of palms being sent must equal 0 $\left(q_{ij}=0\right)$. Constraint function (6) advises that palm-collecting center $j$ has more than one location. Constraint function (7) states that if palm-collecting center $j$ is open, there must be producer $i$ sending its palms to the center. Constraint function (8) ensures that a palm-collecting center must send all palms to factory $l$. Constraint function (9) states that if the palms at palm-collecting center $j$ are not sent to a factory $\left(y_{ij}=0\right)$, then the number of palms being sent must equal 0 $\left(Q{a}_{jl}=0\right)$. Constraint function (10) ensures that the number of palms from palm-collecting center $j$ must not exceed the capacity of factory $l$. Constraint function (11) represents the limit of transportation routes from palm-collecting center $j$ to factory $l$. Finally, constraint function (12) ensures that the number of palms sent from palm-collecting center $j$ to factory $l$ must equal the total number palm-collecting center $j$ had on hand.

3. Proposed Heuristics

Generally, the differential evolution (DE) algorithm comprises four steps: (1) generating the initial solution, (2) performing the mutation process, (3) performing the recombination process, and (4) performing the selection process. In our modified DE (MDE), one step is added to these general steps. When the best solution is not updated for the predefined iterations (in our pretest, the best value of the unchanged solution is 25 iterations), the best solution will produce the offspring vectors. The offspring vectors will be increased and reduced using our designed mechanism, which will be explained later. This step is called the best vector reproduction process; thus, in total, the MDE is composed of five steps: (1) generating the initial solution, (2) performing the mutation process, (3) performing the recombination process, (4) performing the selection process, and (5) performing the best vector reproduction process.

DE was first developed to solve continuous optimization. To let DE be applicable to combinatorial optimization, it is necessary to design a decoding method well.

The flowchart of the proposed heuristics is shown in Figure 2.

From Figure 2, we can explain the process step-by-step as follows:

(1)

Generate the initial population (NP) according to the size of D-dimensional vectors that are set by the number of producers, the number of palm-collecting centers in the candidate process, and the number of oil palm factories. This step can be executed by generating random numbers [0, 1] in an array in each vector, as shown in

Table 1. Encoding random numbers [0, 1] in each vector.

	Farmer					Collecting Center					Factory
	1	2	3	4	5	1	2	3	4	5	1	2
	14	11	13	4	4	20	20	20	20	20	35	35
NP1	0.266	0.377	0.910	0.609	0.282	0.921	0.737	0.044	0.084	0.016	0.841	0.860

.

The vector generated in Table 1 has D-dimensions that have to be divided into three groups. The first group is the vector for the farmer: Table 1 has five farmers (the name of the farmer is shown in the first row, while the second row shows the demand of each farmer, and the third row is the randomly generated number). The second group is the information of the collecting center: in rows 1, 2, and 3, this is the name of the collecting center, its capacity, and the randomly generated number, respectively. The last group is the factory details, which are its name, its capacity, and the randomly generated number. The vector in Table 1 can be decoded by using decoding methods. The decoding method is composed of five steps, as follows:

(a)

Arrange the values of random numbers in each group in ascending order. From

Table 2. Arranging random numbers in each vector.

Order	1	2	3	4	5	1	2	3	4	5	1	2
	Farmer					Collecting Center					Factory
Producers	1	5	2	4	3	5	4	3	2	1	1	2
	14	4	11	4	13	20	20	20	20	20	35	35
NP1	0.266	0.282	0.377	0.609	0.910	0.016	0.084	0.044	0.737	0.921	0.841	0.860

, the order of the field is 1, 5, 2, 4, and 3, which have 14, 4, 11, 4, and 13 tons of palm available in the field, respectively. The order of the collection center is 5, 4, 3, 2, and 1. All the collecting centers in the example have a capacity of 20 tons. Finally, the factory order is 1 and 2, each of which has a capacity of 35 tons.

(b)

Assign the farm in the first order of the farmer group to the first collecting center in this group, and this farm and collecting center will be assigned to the first list in the factory group. The second farmer in the farmer order is assigned to the first collecting center as long as it has enough capacity; if it does not have enough capacity, the second collecting center in the list will be used. This mechanism is also used with the factory level. From step 1, field 1 (14 tons) will be assigned to collecting center 5 (20 tons). Field 1 has 14 tons available; therefore, collecting center 5 has 6 tons of available space for the next field to be assigned in. Thus, field 5 can be assigned to collecting center 5. Resulting from that, collecting center 5 has 2 tons remaining, which means that if no field can be assigned to collecting center 5, then collecting center 5 is closed. After the collecting center is closed, we will decide to transport palm to another factory, and collecting center 5 will deliver the product to factory 1, which is first on the factory list.

(c)

Repeat step 2 until all farms are assigned. At this step, all fields will be assigned to exactly one collecting center, and the assigned collecting center will deliver the product to one of the factories. The result is shown in

Table 3. Assignment results of fields, collecting centers, and factories.

Factory	Collecting Center	Fields	#Round of Truck
1	5 (18 tons)	1, 5	2 (15, 3)
	4 (15 tons)	2, 4	1 (15)
2	3 (13 tons)	3	1 (15)

.

(d)

Determine the number of rounds of trucks (30 tons) that will be used to deliver palms from the collecting center to the factory (delivery of palms from the farmer to the collecting center means the direct shipping form of the farmer to the collecting center and its parameters). For example, collecting center 5 has a total 18 tons of palm to deliver. Therefore, it needs 2 rounds, because the truck has 15-ton capacity. On the first round, the truck will deliver 15 tons, and the remaining 3 tons will be delivered in the second round. Results of calculating numbers of rounds are shown in Table 3.

Table 3 shows that factory 1 will serve collecting centers 5 and 4, while factory 2 will serve collecting center 3. Collecting center 5 will get palm from fields 1 and 5. Fields 2 and 4 will deliver palm to collecting center 4, and field 3 will deliver product to collecting center 3. Finally, collecting centers 5, 4, and 3 have 2, 1, and 1 rounds of trucking, respectively, to transport their product to the assigned factory.

(e)

Calculate the total cost of the solution constructed in steps 1–4. In this step, all important data will be collected and calculated, such as distance, investment to open the collecting center, and the sabotage cost. The distance from fields to collecting centers is shown in

Table 4. Distance from fields to collection centers (km).

Field	1	2	3	4	5
1	56	54	12	43	32
2	45	45	12	67	23
3	8	43	2	16	89
4	98	45	41	31	6
5	12	23	17	54	24

. The distance from collecting centers to factories is shown in

Table 5. Distance from collecting centers to factories (km).

Factory	1	2
Field
1	65	44
2	32	98
3	23	45
4	54	23
5	34	2

. The average density of population living along the road from fields to collecting centers and from collecting centers to factories (within a radius of 0.1 km) is shown in

Table 6. Average population along connections of fields to collecting centers (people/km).

Field	1	2	3	4	5
1	140	170	65	200	210
2	45	57	245	432	123
3	189	165	234	176	176
4	200	400	140	300	130
5	200	300	120	80	90

and

Table 7. Average population along connections of collecting centers to factories (people/km).

Factory	1	2
Field
1	140	320
2	320	98
3	230	450
4	540	230
5	340	200

, respectively. The possibility of having a bomb in each road connection is shown in

Table 8. Probability of bomb occurring between fields and collecting centers.

Field	1	2	3	4	5
1	0.1	0.07	0.08	0.15	0.06
2	0.2	0.12	0.14	0.08	0.1
3	0.2	0.07	0.09	0.08	0.02
4	0.08	0.4	0.01	0.03	0.04
5	0.08	0.12	0.19	0.2	0.02

and

Table 9. Probability of bomb occurring between fields and collecting centers.

Factory	1	2
Field
1	0.02	0.04
2	0.01	0.34
3	0.02	0.07
4	0.06	0.06
5	0.02	0.1

. The investment cost of collecting centers 1, 2, 3, 4, and 5 is 1000, 1200, 1100, 1000, and 1300 baht, respectively.

The emission cost of transport is 4 baht per km (converting carbon dioxide emission to baht), and the fuel cost is 5 baht per km. The investment cost is 3400 baht when collecting centers 3, 4, and 5 are in operation. The total distance of the connection between all fields to collecting centers is 312 km (two ways), and the total distance between fields and factories is 334 km. Note that the distance from collecting center 5 to factory 1 is two-way transport, and each way has to go two rounds; thus, the total distance used in this plan is 646 km, which costs 3300 baht, and this generates a total emission cost of 2584 baht (4 baht per km). The total density of people who could possibly be affected in the transport is calculated from the number of people in the connection multiplied by the probability of having a bomb along that road. For example, the connection from field 1 to collecting center 5 has a population of 210, and the probability a bomb will occur is 0.06; thus, the probability that people will be affected by the bomb is 12.6, and each will need 1500 baht to recover when they are injured. Thus, the cost of this connection is 18,900 baht (this method can also be applied to the connection between collection centers and factories). The results show that the total sabotage cost is 292,080 baht. Thus, the total cost for this plan is 301,364 baht.

(2)

Perform the mutation process.

The NP mutant vector $V_{i,j,G}$ is the value adjustment within the same vector using function (13). In each target vector of NP, it will make a random selection $\left(r_1,r_2,\mathrm{and}{r}_3\right)$, and the $F$ value equals 2.0 (Qin et al. 2009; Sethanan and Pitakaso 2016b):

$$V_{i,j,G}=X_{r_1,j,G}+F\left(X_{r_2,j,G}-X_{r_3,j,G}\right)$$

(13)

(3)

Perform the recombination process.

Each NP trial vector $V_{i,j,G}$ is the result of the recombination process using function (14) between target vectors of each present NP and mutant vectors with the possibility of crossing set $Cr$ at 0.8 (Qin et al. 2009; Sethanan and Pitakaso 2016b) in order to change values in each vector:

$$U_{i,j,G}=\{\begin{array}{c}{V}_{i,j,G}ifran{d}_{i,j}\le Crorj=Irand\\ X_{i,j,G}ifran{d}_{i,j}>Crorj\ne Irand\end{array}$$

(14)

Set $ran{d}_{i,j}$ as a random number that has a value between [0, 1], which is within a target vector. In each present NP and mutant vector, $Irand$ is a random selection of the position that changes value in both vectors. If the value of $ran{d}_{i,j}$ is less than or equal to that of $Cr$ in position $j$ of both of these vectors, the mutant value in this position will be in a trial vector. On the other hand, if the value of $ran{d}_{i,j}$ is more than that of $Cr$ in the position, the value in this position will be in a trial vector.

(4)

Perform the selection process by using Equation (15) to determine the target vector of the next processing round $\left(X_{i,j,G+1}\right)$ that can be selected from the better vector, a current target vector $\left(X_{i,j,G+1}\right)$ or a trail vector $\left(U_{i,j,G}\right)$:

$$X_{i,j,G+1}=\{\begin{array}{l}{U}_{i,j,G}iff\left(U_{i,j,G}\right)\le f\left(X_{i,j,G}\right)\\ X_{i,j,G}otherwise\end{array}$$

(15)

(5)

If the best solution is not changed within the predefined iteration, then perform the best vector reproduction process. This process can be executed by generating a new vector (NV) of DE. The reproduction of the best vector is performed using Equation (1), but the first two vectors (r₁ and r₂) are selected from the current set of vectors (NP), and the last vector is newly randomly generated. If the new vector cannot find the new best solution, then the number of vectors that will be reproduced is increased one vector at a time. If the new vector is not able to find a new best solution when the number of the new vectors generated reaches the maximum limitation that can be calculated form Equation (16), it will reduce the number of NV until it is reduced to one. When NV is equal to 1, the reproduction process is terminated. The termination condition of the reproduction process can be both when NV reaches 1 and when it finds a new best solution. An example of increasing and reducing NV is shown in

Table 10. Format using the number of populations in each iteration.

Number of Iterations to Find Results	Number of Populations in Each Iteration
1	$N{P}_{\mathrm{i}}^{\prime }\left(1\right)$	Number of population increased
2	$N{P}_{\mathrm{i}}^{\prime }\left(1\right)$, $N{P}_{\mathrm{i}}^{\prime }\left(2\right)$
3	$N{P}_{\mathrm{i}}^{\prime }\left(1\right)$, $N{P}_{\mathrm{i}}^{\prime }\left(2\right)$, $N{P}_{\mathrm{i}}^{\prime }\left(3\right)$
4	$N{P}_{\mathrm{i}}^{\prime }\left(1\right)$, $N{P}_{\mathrm{i}}^{\prime }\left(2\right)$, $N{P}_{\mathrm{i}}^{\prime }\left(3\right)$, $N{P}_{\mathrm{i}}^{\prime }\left(4\right)$
5	$N{P}_{\mathrm{i}}^{\prime }\left(1\right)$, $N{P}_{\mathrm{i}}^{\prime }\left(2\right)$, $N{P}_{\mathrm{i}}^{\prime }\left(3\right)$, $N{P}_{\mathrm{i}}^{\prime }\left(4\right)$, $N{P}_{\mathrm{i}}^{\prime }\left(5\right)$
6	$N{P}_{\mathrm{i}}^{\prime }\left(1\right)$, $N{P}_{\mathrm{i}}^{\prime }\left(2\right)$, $N{P}_{\mathrm{i}}^{\prime }\left(3\right)$, $N{P}_{\mathrm{i}}^{\prime }\left(4\right)$	Number of population decreased
7	$N{P}_{\mathrm{i}}^{\prime }\left(1\right)$, $N{P}_{\mathrm{i}}^{\prime }\left(2\right)$, $N{P}_{\mathrm{i}}^{\prime }\left(3\right)$
8	$N{P}_{\mathrm{i}}^{\prime }\left(1\right)$, $N{P}_{\mathrm{i}}^{\prime }\left(2\right)$
9	$N{P}_{\mathrm{i}}^{\prime }\left(1\right)$

.

$$Po{p}_{\mathrm{gr}}=\underset{\mathrm{Number}\mathrm{of}\mathrm{population}\mathrm{increased}}{\underbrace{\left(\frac{Npop}{2}\times \left(Npop+1\right)\right)}}+\underset{\mathrm{Number}\mathrm{of}\mathrm{population}\mathrm{decreased}}{\underbrace{\left(\frac{Npop}{2}\times \left(Npop-1\right)\right)}}$$

(16)

• Set
  • $Po{p}_{\mathrm{gr}}$ = Number of added vectors
  • $N_{pop}$ = Number of initial population

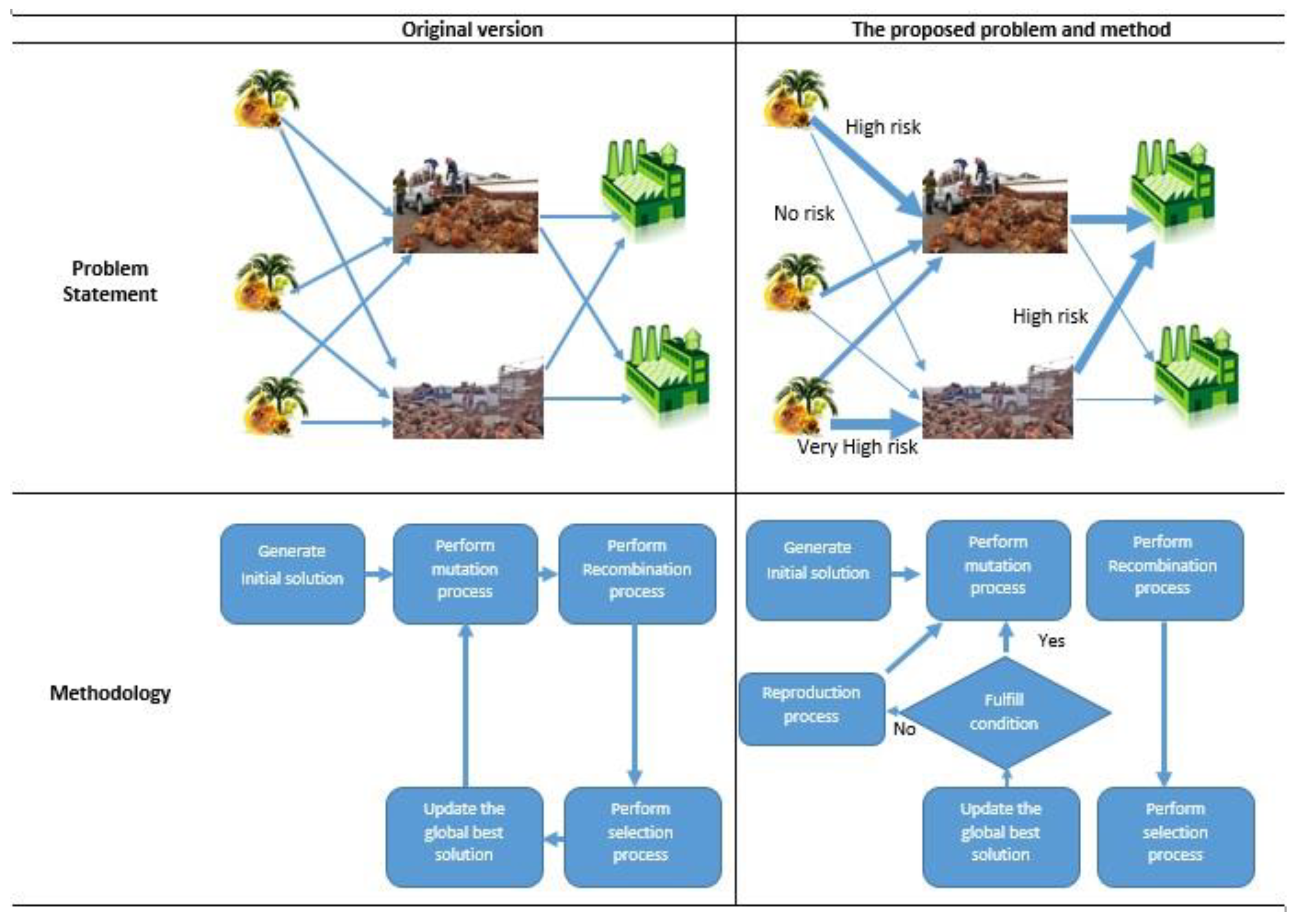
Figure 3 depicts the proposed problem and heuristics that we designed to solve the multilevel location–allocation problem. The original version of the problem does not take sabotage risk into account in the model solving, while the proposed problem integrates sabotage risk into the model so that the decision-maker can make better decisions. In the proposed methodology, a reproduction process has been added to introduce new generated vectors to the system, so the proposed algorithm has more diversification in searching the new solution to allow it to escape from the local optimal. The reproduction process will be applied only when the algorithm cannot fulfill the predefined search conditions, as the algorithm can find a better solution within the predefined iterations.

4. Computational Results

In this research, we present an MDE that is efficient at solving a multilevel location–allocation problem. In the case study, we compare the efficiency of the optimal solution from Lingo v.11 to the traditional DE and our MDE. The proposed heuristics involve coding in Dev C++ using PC Intel Core i3 CPU 3.70 GHz Ram DDR4 8 GB.

In testing to find the most efficient results of these four algorithms, we compared the computation time for instance tests with 5, 10, 20, and 50 farms. Each size randomly generates three sets of parameters; thus, we have 12 random test instances and one real case study. The case study has 77 farms. The number of potential collecting centers is equal to the number of farms, and the number of factories varies from one to five. Each instance test was repeated five times. The best among all solutions was taken as representative of the proposed method. Thus, our first experiment was executed to compare the efficiency of the proposed heuristics with the results generated by Lingo v.11.

Table 11. Comparing results of DE and MDE algorithms with the optimal solution generated by Lingo v.11.

Instance	Lingo v.11		DE		MDE
	Cost (Baht)	Time (s)	Cost (Baht)	Time (s)	Cost (Baht)	Time (s)
5.1	17,563,210	38	17,563,210	10	17,563,210	9
5.2	17,756,540	54	17,756,540	13	17,756,540	11
5.3	17,481,870	49	17,481,870	11	17,481,870	12
10.1	23,165,420	466,760	23,165,420	158	23,165,420	119
10.2	23,223,900	36,633	23,223,900	179	23,223,900	160
10.3	23,223,900	73,406	23,223,900	252	23,223,900	229
Average		96,156.67		104		90

shows the results comparing the proposed method (DE and MDE) with the optimal solution generated from Lingo v.11. Lingo is executed until it finds an optimal solution, while DE and MDE collect the time to find the optimal solution, which is equal to the result generated by Lingo as the stopping criterion.

From Table 11, we can see that, on average, Lingo can find an optimal solution in 96,156.67 s, while DE and MDE can find an optimal solution within 104 s. The computational time of Lingo is dramatically increased when the number of farms is 10. This means that Lingo cannot find the solution in the remaining test instances. In the next simulation result, we compare the performance of the MDE and DE algorithms with a larger number of test instances. In this experiment, we execute DE and MDE in six test instances (20 and 50 farms) and one real case study (77 farms). The stopping criterion is 90 min computational time, and the results are shown in

Table 12. Results of seven test instances of DE and MDE using 90 min computational time.

Test Instance	Result (Baht)
	DE (a)	MDE (b)	%dif
20.1	35,067,350	35,012,940	0.16
20.2	35,118,530	35,030,880	0.25
20.3	35,034,940	35,024,930	0.028
50.1	30,483,050	30,253,650	0.76
50.2	36,368,650	36,133,690	0.65
50.3	35,469,520	30,192,920	0.91
Case study	12,925,850	12,917,510	0.06
Average	31,495,413	30,652,360	0.404

Note: %dif = [(a − b)/a] × 100%.

.

From Table 12, in this group of problems, DE has an average cost of 25,997,859 baht, while MDE has an average cost of 25,923,139 baht. When we calculate the percentage difference of DE and MDE, there is a 0.404% difference, but MDE requires 100% lower cost than DE, which means that the modified version of DE outperforms the original DE.

From

Table 13. Percentage difference in cost between DE and MDE using 10, 30, 40, 60, 80, and 100 min as the stopping criterion.

Time (min)	10	30	40	60	80	100
Instance
20.1	0.0	0.12	0.25	0.28	0.39	0.59
20.3	−0.03	0.12	0.12	0.29	0.37	0.39
20.3	−0.01	0.24	0.18	0.24	0.30	0.48
50.1	0.04	0.08	0.89	0.13	0.43	0.43
50.2	0.10	0.12	0.12	0.32	0.28	0.95
50.3	0.32	0.28	0.18	0.19	0.32	0.33
Case study	0.14	0.43	0.25	0.43	0.12	0.59
Average	0.08	0.20	0.28	0.27	0.32	0.54

, the results show that when we run long enough, MDE outperforms DE. The next question is whether there is some sense that DE outperforms MDE. The experiment was executed with the second group of data. For the stopping criterion we used computational time, which is set to 10, 30, 40, 60, 80, and 100 min, and the results of the simulation are shown in Table 13. The simulation was executed five times, and the best solution is representative of the simulation. Percentage difference between cost generated from DE and MDE is calculated from Equation (17):

$$\%diff=\frac{CostgeneratedfromDE-CostgeneratedfromMDE}{CostGeneratedfromDE}\times 10$$

(17)

From Table 13, we can see that only in instances 20.2 and 20.3 did DE have a better solution than MDE when run for 10 min; in all other instances, MDE outperformed DE. Figure 4 shows the plot of average percent difference between DE and MDE.

From Figure 4, we can see that when using longer computational time, the gap between DE and MDE is greater, except with computational time of 40 and 60 min, in which the performance of DE and MDE differs the least. When the runtime from 60 min is increased, the performance of MDE is higher again. From this, we can conclude that when using longer computational time, DE will be stuck in the local optimal, while MDE can escape from the local optimal and generate a better solution.

The last experiment focuses on a strategy to deal with transportation logistics when sabotage risk is considered and the question of whether it is different when we do not take risk into account in the decision model. This experiment was executed using MDE to solve the second group of problems. MDE-1 is MDE that takes the last two terms from the objective function (Equation (1)), but after MDE-1 finishes the simulation (90 min run), the best solution is used to calculate the total cost, including sabotage cost, while MDE is the original version that uses Equation (1) as the objective function.

Table 14. Results of MDE and MDE-1.

Test Instances	Result (Baht)
	MDE (a)	Sub (b)	% Sub (c)	MDE-1 (a)	Sub (b)	% Sub (c)
20.1	35,012,940	26,259,705	63.58	38,769,768	32,954,303	82.42
20.2	35,030,880	24,871,925	65.00	37,576,269	21,939,828	69.03
20.3	35,024,930	11,908,476	48.28	36,887,763	29,879,088	78.29
50.1	30,253,650	19,664,872	61.69	31,324,479	23,806,605	79.19
50.2	36,133,690	21,318,877	61.77	36,987,895	29,960,195	78.30
50.3	30,192,920	20,229,256	53.42	32,878,129	29,590,317	83.92
Case study	12,917,510	9,817,308	68.26	14,982,224	11,386,491	76.00
Average	30,652,360	19,152,917	60.29	32,772,361	25,645,261	78.17

MDE-1 (ignoring sabotage cost in the objective function) has 78.17% sabotage cost when compared with total cost, while MDE has 60.29% sabotage cost. This means MDE-1 has 6.9% higher cost than MDE.

shows the results of MDE and MDE-1 for total cost (including sabotage cost), sabotage cost, and the percent of sabotage cost generated from MDE and MDE-1. Percent of sabotage cost can be calculated with Equation (18):

$$c=\frac{b}{a}\times 100\%$$

(18)

5. Conclusions

This paper presents a modified DE (MDE) to solve the multistage location–allocation problem when considering sabotage risk as the constraint. The proposed algorithm adds one more step to the original version of DE, which is the best vector reproduction process, and this gives MDE better efficiency, which can be seen in Table 12; it generates better solutions than the original DE in all test instances. This is because when MDE cannot find an improved solution, it will escape from the local optimal by introducing a new vector to the system, and this vector will lead the new search space. Searching for new solutions from the new search space will increase the chances of finding better solutions for the algorithm. At the same time, diversification of the original DE is improved by the reproduction process; therefore, MDE outperforms the original DE.

The difference between MDE and DE becomes larger (solution quality of MDE is greater than that of DE) when using longer computational time. The difference is 0.08% when using 10 min computational time and 0.54% when using 100 min computational time (see Table 13 and Figure 4). This means that when the computational time is longer, the performance of MDE is better.

Comparing DE and MDE with the optimal solution generated from Lingo v.11 (see Table 11), we can see that both can find the optimal solution the same as Lingo, but using less computational time (Table 11). Lingo uses an average of 96,156.67 s to explore the optimal solution for a small number of test instances, while DE and MDE use only 140 and 90 s, respectively. This shows that DE and MDE are indeed suitable for this kind of problem, even when the problem size is small, although sometimes the heuristics need more time to find a better solution than Lingo. However, in this case, even though the problem size is small, our proposed heuristics generated the same result as Lingo but used much less computational time. This was because the decoding method is effective at finding a good solution in a short computational time.

Managing transportation logistics in the multilevel location–allocation problem when there is sabotage cost, we need to take care of it in order to generate lower total cost (see Table 14). MDE has been used to solve the integration model of transportation logistics when sabotage risk is considered. MDE-1 is the same method, but solves the transportation logistics model without considering the risk. MDE generates an average total cost of 30,652,360 baht, while MDE-1 generates an average total cost of 32,772,361 baht for large numbers of test instances. This means that when we consider sabotage risk in the model, we can reduce cost by 9.61%, even we use the same method to solve the problem. Therefore, when the special cost term occurs in the objective function, the decision-maker has to take care of it carefully to get the most effective methodology to get the best answer for the firm.

From the computational results, MDE can generate better solutions than the original version. This is because its ability to escape from the local optimal is better than that of DE, by introducing a new random vector. This is because we add the process of enhancing the diversification behavior of DE. Thus, a more effective process to increase diversification of the algorithm can be added. The algorithm’s designer can also add new DE processes to intensify the algorithm so that it will have more diversification and intensification behavior. Another point that can be further studied is to formulate the problem as a multi-objective model so that multiple cost terms in the problem can be easily traced.