Strategy under Ambiguity, and a New Type of Decision Dilemma

Abstract

In this exploratory study, we challenge real decision makers to make choices in strategic games involving ambiguity, and to rationalize those choices. Such games are unique because they are not optimizable; however, the challenge such decisions represent—making choices over irreversible resource commitments in a competitive context and without complete information—is only growing in frequency in our modern business context. As such, our goal is to improve our understanding of real strategic decision making facing irreducible uncertainty, and then to identify ways to improve the outcomes. The challenge is that there are no theoretical solutions for these problems. (While such work has offered solutions, those have always involved watered-down problems—in terms of a lack of true uncertainty or a lack of true optimization). Thus, we approach the challenge from an experimental methodology as one alternative path toward improving outcomes. We do so by considering the influence of decision and decision-maker characteristics on the behaviors displayed while confronting these problems, with an eye on identifying vulnerabilities. We find that such characteristics correlate with expected behaviors, and that there exists potential room for improvements in the observed strategizing. The results of our study on the behaviors witnessed across three variants of our prototypical game—that represent increasing levels of complexity in the underlying ambiguity—have implications for theory and for practice, where one such conceptual implication involves the discovery of an entirely new form of the decision dilemma.

1. Introduction

Strategizing under ambiguity (SuA) is an underdeveloped area of research, but one that represents an increasingly important challenge to managerial decision makers (e.g., Einhorn and Hogarth 1986). SuA problems are doubly difficult because they not only involve imperfect information arising from the simultaneity of rival choices, but they also involve incomplete information over the probabilities of the possible states of the world (where the interdependent payoffs occur based on the choices made). Further, organizations are more and more likely to find themselves confronting such problems—i.e., decisions entailing competitive non-risk uncertainties (Knight 1921) that they cannot simply ignore, delay, or otherwise escape—as their economic futures engage with greater complexities and disruptions. Such SuA problems are, by definition, non-optimizable while also being of significant performative importance (e.g., Petkova et al. 2014; Srivastava 2015). Unfortunately, they have been effectively ignored in management research because they do not allow for the kind of calculable answers and simple prescriptions that are more likely to be published. Thus, studies such as this one are needed to address the outstanding issues by confronting these unavoidable managerial challenges directly, starting with an analysis of how real decision makers deal with prototypical examples of such SuA problems.

SuA problems are not simple or trivial. Making a decision under ambiguity means not knowing, or being able to know, what the future entails prior to having to choose an action—e.g., in terms of the probabilities of known possible outcome states, or in terms of the full set of those states, or in terms of the payoffs of possible choices that could occur in those states, or in terms of the complete set of those choices, or in terms of some combination of those (e.g., Packard et al. 2017). Further, making a strategic decision entails irreversible resource commitments that involve rival-interdependent rewards, affecting both the firm’s absolute and relative performance levels, perhaps even at an existential intensity. Together, such ambiguity and interdependency make for very challenging problems.

Conceptual research has avoided confronting these problems directly. Instead, ‘tricks’ have been applied to remove the unknowable ambiguity or to switch the goal of optimization to something else. To the former, unknowable probabilities have been replaced by questionable subjective prior beliefs so that expected values can be calculated (e.g., Savage 1954). To the latter, heuristics—such as the maximin rule—have replaced value maximization (e.g., Hertwig et al. 2019). (Other approaches include outright violating the unknowability assumption by suggesting that the unknowns can be made known through active search or experimentation (e.g., Rindova and Courtney 2020)). All such approaches that avoid confronting real unknowables by converting them into knowables; however, can be dangerously inaccurate while also providing false confidence to decision makers.

Our exploratory study places the research on a more accurate and practical path; we do so by analyzing how real decision makers approach unavoidable versions of a prototypical SuA decision problem. As such, we offer a contrast to past work that has skirted the exploration of the full challenge of decisions involving both irreducible uncertainty and rivalry simultaneously. This allows us to identify potential areas for improvement as well as possible drivers of real behaviors, drivers involving both decision and decision-maker characteristics. Our study on SuA problems differs from past approaches in two ways: First, it builds on recent experimental studies that reveal how important the specific form and intensity of ambiguous choices are in driving decision behavior (Aggarwal and Mohanty 2021). We do so by adding to the knowledge about behaviors under differing intensity levels of SuA problems (where the intensity is based on choice complexity). Second, it involves not only identifying choices but also the self-reported rationales behind those choices. Such supplemental data provide new insight into how the boundedness of rationality affects behaviors when decision makers face non-optimizable decision problems of varying complexity.

We analyze the research question: Under the assumption of bounded rationality and given a SuA problem, how do decision makers and decision characteristics affect behaviors and generate strategic vulnerabilities? Our analysis focuses on specifics—on the decision characteristic of the level of intensity of the probabilistic ambiguity involved (i.e., how complex the ambiguity is to assess), on several demographic and psychographic decision-maker characteristics (e.g., gender; experience/training; ambiguity-avoidance), and on the relevant decision-making behaviors (i.e., choices made, rationalizations given, consistency of choices with the expressed rationales, population variance over choices, and the projected vulnerability of average choices to exploitation by alternative decision strategies).

We address the research question empirically using primary data. Our research method is an experimental survey that requires participants to make choices across several similar SuA problems, providing their rationales for each, in addition to their background information. This is primarily a treatment effects study, focusing on the treatment of three levels of intensity of a prototypical SuA decision, a decision defined by a specific type of game structure where Ellsbergian ambiguity1 can occur. Data were collected through the survey, online, in real time. In order to control for the type of decision makers who would be confronted by such problems in the real world, access to the survey was filtered for participant quality, including for a minimum level of ability to play standard game-theoretic models correctly.

The data are analyzed statistically, using OLS regression and means and variance differences testing, in order to identify significant correlations and discrepancies—ones that could provide new insights into decision-maker behaviors, both at the individual and population levels. That basic analysis is supplemented by a Monte Carlo simulation to identify possible weaknesses in the average decision strategy used by the population.

Our results are interpreted by comparing them to a set of expectations over how the three games will be played based on prior research (see below). The results indicate that decision makers are bounded in rationality and that boundedness likely influences how decision characteristics affect behavior—with more intense ambiguity problems generating more confusion and inconsistent play. The results also indicate that decision-maker characteristics, such as gender, can affect behavior for these problems (as they have for less difficult experimental games in past studies). Further, the results indicate that there are potential ways to exploit the average decision behaviors observed when real agents are confronted by such challenging problems.

The results advance the literature on SuA by providing new insights into behavioral patterns and drivers at the individual and population levels for these unique decision problems (e.g., regarding what individual and decision characteristics correlate with which choices and rationales). The results also entail implications for practice—with new insights into how to improve the decision-making process for these challenging problems (e.g., from who should be making the decisions to how the decisions should be modeled and analyzed to avoid possible exploitation by rivals).

Below, after reviewing the most related literature, we move on to describe our methods and materials. We then describe a survey that includes these games as well as questions about the characteristics of the decision-making participants. We detail how this survey was administered and what data were collected. We analyze the decisions made in the games, the reasons given for making them, and the factors influencing the choices and patterns across the choices. We discuss the results, including any surprises, in addition to implications for theory and practice in light of the exploratory nature of this study.

2. Related Literature on SuA Decision Problems

Little research exists on the SuA decision problem proper—i.e., on taking actions that involve interdependent payoffs under incomplete information. The majority of related literature on addressing decision-making under non-risk uncertainty is non-strategic in nature and seeks either to transform its unknowables into knowables in order to apply probability-based analysis or to prepare for the unknowable outcomes through building organizational robustness. To the former, there are significant streams of theoretical and experimental empirical work based on subjective probability estimates and the expected utility analysis that follows (e.g., Savage 1954). More recently, there has been a push to revisit and relabel the six ways that Knight (1921) suggested that non-risk uncertainties, such as ambiguity, can be faced. These ways include attempting to control it, shape it, or diversify it (e.g., Cerreia-Vioglio et al. 2013; Gollier 2014; Rindova and Courtney 2020). Further, while those ways have optimistic descriptions, none can actually guarantee a best, or even better, decision choice. The main reason is that by the definition of non-risk uncertainty, these problems must remain un-optimizable—because the expected values of all pertinent choices simply cannot be computed (Hansson 1996; Hodgson 2011; Ramoglou 2021).

There is a recent stream of literature analyzing how perceived forms of more specific SuA problems are addressed in reality by engineers and policy makers. For example, Marchau et al. (2019) describe several ways for preparing organizations to react better once the uncertainty has been revealed and its outcomes realized. Scenario planning logic is behind several approaches for reducing redundancies and increasing organizational robustness to imaginable futures (e.g., Machina 2014) and for those decision makers trying to deal with possible black swan events (Taleb 2012). In the management literature, such work is less visible, although some analysis is starting to appear where the core unknowability of a decision cannot be transformed but instead must be confronted by managers directly (e.g., Arend 2020a). In the decision-making literature, there has also been recent research to establish that there are many distinct forms of ambiguity, and that decision-maker behavior is affected not only by which form is presented but also by the level of ambiguity perceived in that form (Aggarwal and Mohanty 2021).

There is also some conceptual work on ways to analyze the unoptimizable decisions by envisioning a range of possibilities—in order to represent the ambiguity involved—so that the trade-offs between the possible benefits and costs to such uncertain futures can be made more systematically (e.g., using information gap decision theory—Ben-Haim 2006). Another stream of literature addresses ambiguous problems by applying heuristics instead of optimization-focused analysis, allowing often better use of what knowledge is provided in SuA problems to obtain to a ‘solution’—one that maximizes something simpler than value (e.g., minimum possible payoff)—that is computable by even very boundedly rational decision makers (e.g., Hertwig et al. 2019; Kozyreva and Hertwig 2021; Mousavi and Gigerenzer 2014). This approach is ecologically inspired, using the idea that entities and their environments co-evolve based on blunt and speedy reactions. Other relevant work considers the way the problem itself may influence whether and how any ambiguity (or rivalry) in a problem is perceived, analyzed, and action upon (e.g., Hansson 1996; Kuhlthau 1993).

Further related literature focuses further on ambiguity aversion—i.e., what people will pay to avoid decisions involving unknowable probabilities relative to similar problems involving either only risk or certainty (e.g., Ellsberg’s (1961) original urn-problem experiments; Budescu et al. 2002; Heath and Tversky 1991). Such research appears to reveal that ambiguity aversion differs from risk aversion as a concept and in terms of behavior—a result that supports Knight’s (1921) differentiation between risk and uncertainty; however, there has been a relative vacuum of such behavioral economic research on how real decision makers actually play multi-party games involving ambiguity that they cannot avoid; that is the gap that we intend to begin to fill here (answering the calls for such work—e.g., Aflaki 2013).

3. Materials and Methods

We address our research question in a straightforward manner. We use the simplest representative SuA game (i.e., a game involving only two choices, one rival, and one ambiguity) that can be varied by intensity level (i.e., involving three distinct levels of complexity). This game is also presented in a very recognizable and understandable format to survey takers as a standard way of depicting a strategic decision. We also use a regular survey questionnaire—in terms of asking about common demographic and background factors. We provide a reasonable range of possible rationales for them to consider when making their choices, which helps them think about why they are choosing what they are choosing rather than simply responding without any analysis. (This also provides a basis for assessing the confusion at the individual and population levels brought on by greater ambiguity intensity.).

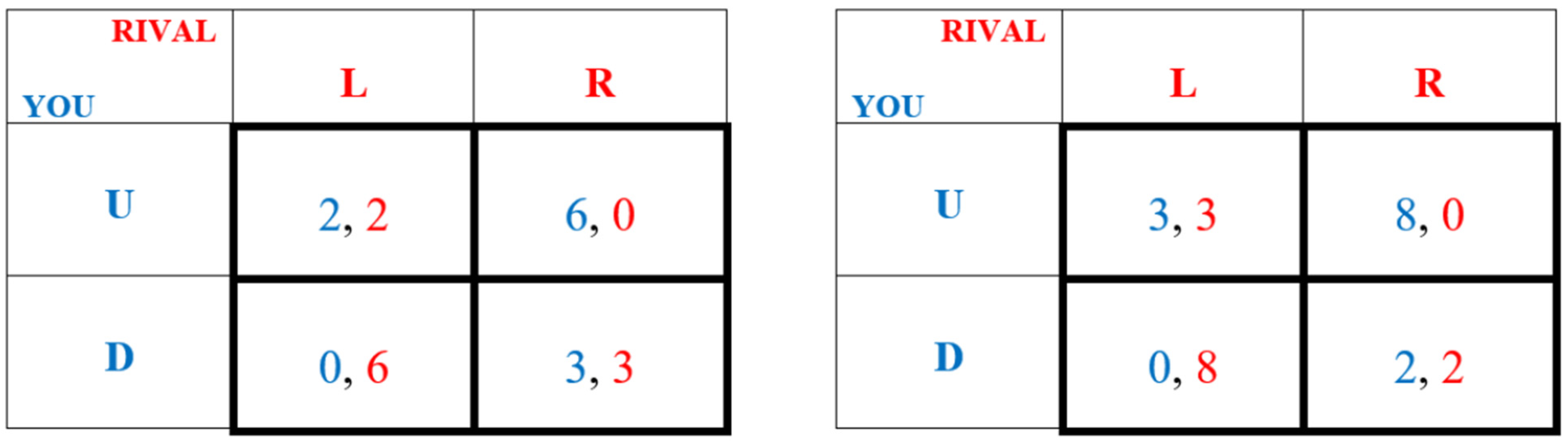
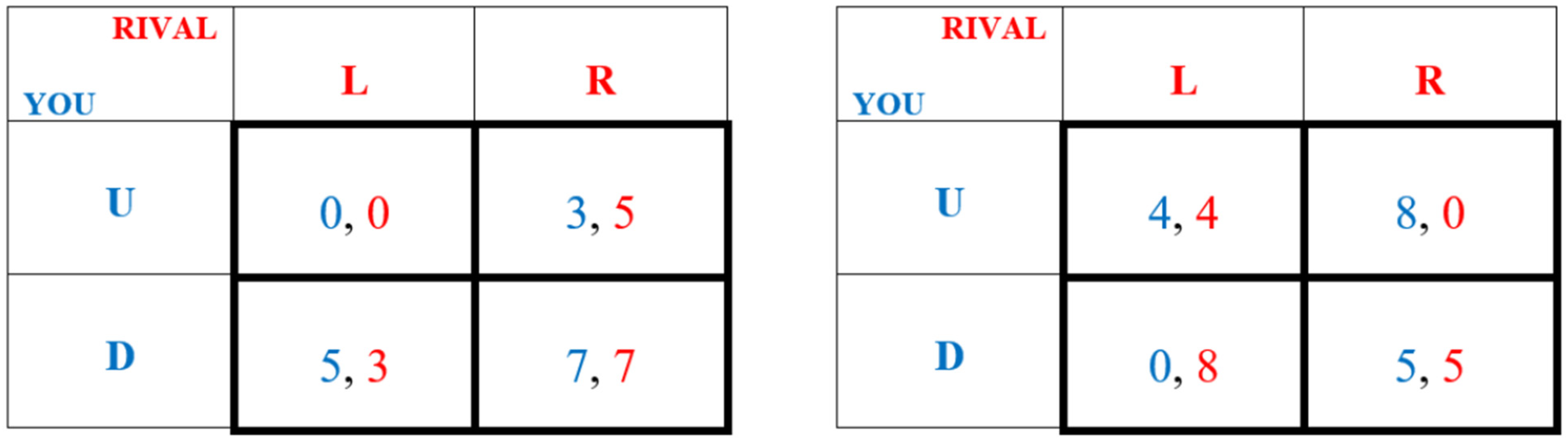
3.1. Specification of the SuA Game Structure

We chose a recently described game structure as the common basis for three specific variants of our focal SuA decision problem. In a recent piece in PLOS ONE, a structure for the implied game was introduced (Arend 2020b). The basic structure consists of two bookend games that define the interior game being played. That interior implied game has its normal form payoff matrix generated by the payoff matrices of the bookend games as the weighted sum of the probability of playing each where the weights add up to one—the full probability space.2 Figure 1, Figure 2 and Figure 3 depict the three variants used in our survey here. What makes these problems ambiguous is that the value of p (i.e., the probability of playing the left-side game) is ex ante unknowable, as is its distribution, and that distribution’s distribution, and so on. Players do not know the value of p, and have no basis for assuming it is drawn from a uniform or normal or bimodal or any other type of distribution; they are explicitly informed that its value can range from 0 to 1, inclusive.

INSTRUCTIONS: You are playing a GAME composed of the TWO GAMES depicted. A LOTTERY will identify which of the two games provides the payoffs. There are 101 tickets in the lottery, each with one number on it, ranging from 0 to 100; however, any ticket can have any number on it. So, all tickets could have the number 0 or 22 or 77 or 100 on them, or 50 could have the number 0 and 51 could have the number 100, and so on. In other words, predicting the outcome of the lottery is impossible; however, whatever one ticket is chosen will determine how probable it will be that the left-most game determines payoffs. If the ticket chosen has 0 written on it, the right-most game will determine the payoffs; if the ticket chosen has 50 written on it, each game has an equal chance of determining the payoffs. You and your rival will NOT know the outcome of the lottery prior to having to make your choice. So, given each game has an uncertain chance of determining the payoff outcome, what is your choice? (Assume that You and your rival choose your best option without knowing what the other has chosen.).

We chose to depict and analyze the Ellsbergian form of ambiguity—i.e., probabilistic ambiguity—because it is the most researched and well-known form of Knight’s (1921) types of non-risk uncertainty. We chose it because it is easy to understand (which is important in an experiment), because it can easily provide variants (for testing different treatments), and because it appears more realistic than other types of uncertainty (as people can envision real problems of unknowable but bounded possible probability parameter values in business and in engineering). We chose it because it leaves the unoptimizable unknowability intact. Indeed, in such decision problems, there are no rationally justified ways to reduce the given uncertainty even though the decision-maker must choose an available option in the face of it.

We chose this form of SuA problem because it presents a single but robust challenge for decision makers to focus on—it captures both the ambiguity and interdependency required, and it is adjustable. Further, our SuA problem even looks like the common 2 × 2 games that are often used in these types of study, which makes this experiment more likely to be understood by its participants. We chose this set of games (i.e., the three variants) so that they were easily understandable and comparable to participants of the experiment. Restricting the games to depict only two symmetric players (i.e., the decision maker and her rival) and only two possible choices each is the most simple-yet-robust way to represent strategic interaction, and is the standard base format in game theory analysis. Further restricting the variants to involve only two bookends also provided the simplest case for the experiment where participants only needed to consider one focal probability level and its possible values.

The variants of these probabilistic-ambiguity bookend problems (sometimes termed ‘games’ or ‘problem variants’ below) ranged in complexity from simple to difficult. The first SuA problem (depicted in Figure 1) involves uncertainty over the value of p, but it actually does not involve any ambiguity of choice. Regardless of the level of p, the best choice is apparent and unambiguous because the same dominant choice occurs for each bookend. The second SuA problem (depicted in Figure 2) involves both uncertainty over p and over the best choice (i.e., U, D, or a Mix). Each of its bookends has a different dominant strategy, so the value of p determines the best choice. If one actually varies the probability value from 0 to 1, there exists a wide range of p where U is best and where D is best, with only a relatively very small crossover range (approximately 2% of the space) where a mix is best (i.e., best as entailing the highest payoff value given the level of p). The third SuA problem (depicted in Figure 3) is similar to the second (i.e., in that there exists a true ambiguity over choice), but entails a much wider range where a mixed strategy is best (approximately 44% of the space). Essentially, the challenge to the decision maker increases across the variants—moving from there being one best option (in Figure 1) to two best possible options (Figure 2) to three best possible options (in Figure 3)3.

In the experiment, the choices of gameplay are simplified to three: U, D, or Mix (i.e., rather than allowing any specification of that mix, such as 30% U and 70% D). The set of reasons for the choice in a decision problem is also simplified, here to six possible rationales: it is the dominant strategy; it provides the maximum expected value; it maximizes the maximum possible value (i.e., is maximax); it maximizes the minimum possible value (i.e., is maximin); it feels right; do not know. Only the first four are logical and verifiable rationales.

3.2. Expectations of Real Play in SuA Game Problems

Given the exploratory nature of this research, in lieu of arguing hypotheses, we explain our expectations of the choices and patterns of choices across the three specific SuA decision problems played in the experiment. We begin by noting that, based on past behavioral economics studies, it has been proven that real decision makers, when choosing among alternatives in an experimental setting, will not often play with coldly rational and focused optimization strategies (e.g., Axelrod 1984; Ellsberg 1961); however, they will play, on average, in boundedly rational ways that produce acceptable payoffs (and, in expanding-pie games, this approach often produces superior and mutually beneficial outcomes—e.g., Meyer and Banks 1997). As such, our expectations are consistent with the idea that the majority of participants will exhibit rational behavior—although bounded—even when facing problems with no optimal solutions. We translate the effects of that prediction of boundedly rational decision making to our three SuA problem variants below.

In the first SuA problem variant (see Figure 1), we expect that a significant majority of real decision makers will identify the unambiguous best choice (i.e., U) and identify an appropriate rationale (e.g., that it is dominant). Each bookend has a visible dominant strategy, and even with the added complexity of an unknown p, most participants will correctly identify that choice. That said, due to the usual population variance in boundedness, we also expect that a non-trivial number will be nonetheless mistaken, even though U is dominant, has the highest expected value and is also the maximax and maximin option, because human subjects are prone to a non-zero level of error when making decisions in such experimental settings.

Of the two remaining SuA problem variants—the ones involving actual ambiguous choices—we expect that the more complex one will involve a greater variance of choice. The third variant is the problem with three wide ranges of p that each favor a different choice (U, D, and Mix) where the natural reference point of p = ½ has Mix as its best choice rather than one of the two pure strategies (as the second variant does). So, because there are three attractive possible choices, and because a boundedly rational calculation short-cut (i.e., of identifying the favored choice at the midpoint of p-values) points to a non-pure strategy, we expect significantly less consistency of choice among real decision makers for this problem variant. Specifically, that reduced consistency should present itself in a measurable way—through a relatively higher variance across the three choices (taken across the sample of participants) when the behavior in the SuA problem third variant is compared to that in the second variant.

We also understand, from past research that uses surveys involving game theory experiments or hypothetical strategic choices, that decision-maker characteristics will correlate significantly with specific choices and choice patterns (e.g., Francioni et al. 2015). Because our experiment involves choices under explicit uncertainty, we expect that particular decision-maker characteristics will correlate with observed behaviors. For example, because males do not like to admit ignorance (e.g., Turk et al. 1998), we expect that their indicated rationales for their choices to be negatively correlated with such admissions. We also expect education and experience related to game theory and to the expected-value calculation to affect the choices and rationales in a positive manner given the implied greater training and familiarity involved (e.g., Hershey and Walsh 2000). Finally, we expect that a participant’s general ambiguity avoidance level will affect choices in a similar way. These decision makers will put in the extra calculative effort and rationalization—as a substitute for paying extra to avoid ambiguity avoidance (e.g., Alary et al. 2013)—and realize more positive choices and rationales.

Further, we understand from previous behavioral economics research—for example, on playing the prisoner’s dilemma (PD) game—that real decision makers’ choices will be exploitable by alternative strategies (e.g., by a fully rational strategy—see Axelrod 1984). From that same research, however, we also know that real decision makers tend to do well in expanding-pie games (such as the PD) when playing against each other, producing higher expected-average payoffs than when alternative strategies—the ones used to exploit the naïve strategies (e.g., playing D in the PD)—are solely pursued (e.g., Meyer and Banks 1997). We expect similar outcomes for our experiment. First, we expect that the average choice profile in the SuA games will be exploitable. Second, we expect that those average choice profiles will involve higher payoffs when played against themselves than the payoffs from the exploiting strategies when played against themselves.

3.3. Empirical Methods

We used Amazon’s MTurk service to access, filter, incentivize, and pay our survey participants. We restricted the sample to those MTurk Workers with more experience (5000 or more tasks completed), higher quality (97% and above approval ratings), and who were more likely to understand multi-step instructions in English (accessing MTurk from the US, UK, and other high-English-fluency EU and island nations). The full sample was obtained over three waves (of sizes 10, 100, and 90) posted within a ten-day period from late December 2020 to early January 2021. Two filter questions were used in order to only allow those respondents presenting a basic understanding of game theory and optimization (i.e., able to identify a dominant strategy in a three-choice, two-player normal-form game, and able to calculate an expected value of a simple bet) to partake in the main survey, where they had to answer all questions seriously in order to be paid the full amount.

Because we are interested in finding how decision and decision-maker characteristics affect decision behavior, we collected data on the SuA problem ambiguity intensity, the demographics and psychographics of the participants, and on the choices made and the rationales they claimed supported those choices. This provided the analysis materials we needed to determine the significance and direction of the relationships of interest at both the individual and population (sample) levels.

3.3.1. Dependent Variables

The experiment included the three SuA problem variants described above. The main dependent variables (DVs) involved the possible choices for each problem (among U, D, and Mix) and the rationales indicated for their choices (of the six available, as listed above). The DVs analyzed below specify the problem variant (1, 2, or 3), along with either a focal choice (U or D) or a possible rationale (dominant, expected value maximization, maximin/maximax, or gut feel/ignorance) or both. The DVs (indicated by the string of symbols in italics) used are as follows: choice1 = U (the correct choice in game variant 1); rationale1 = dom (the correct rationale of ‘dominant’ in game variant 1); choice2 = D (the most popular choice in game variant 2); game2 = D&eV (the most popular choice and consistent rationale of ‘expected value’ maximization in game variant 2); rationale2 = unk (the rationales in game variant 2 of gut feel or ignorance); choice3 = U (the most popular choice in game variant 3); game3 = U&max (the most popular choice with two consistent rationales—maximax or maximin—in game variant 3); rationale3 = unk (the rationales in game variant 3 of gut feel or ignorance).

3.3.2. Independent Variables

The experiment was contained in a survey that included several decision-maker characteristics, some of which were alluded to above. The main independent variables (IVs) were: male (1 = yes, 0 = no); age; US-id (identify as American: 1 = yes, 0 = no); college (education level at college undergraduate or better: 1 = yes, 0 = no); GT-exposure (exposure to game theory: 5-point Likert scale from 1 = none to 5 = expert); eV-experience (experience calculating expected values: 5-point Likert scale from 1 = none to 5 = a great deal); options-experience (experience keeping open or building options: 5-point Likert scale from 1 = none to 5 = a great deal); ambiguity-aversion (measure of how much of a loss to take when selling an Ellsbergian bet with the distribution of the distribution being a fair lottery with expected value $1 and bounds from $0 to $2: where selling for $0.95 translates to 0.05 for this measure). One supplemental IV was used to analyze the second and third SuA problem variant’s DVs, and is based on the first problem’s DVs—game1score (measured as =2 if choice1 was U and rationale1 was ‘dominant’, as = 1 if choice1 was U but rationale1 was not ‘dominant’, and, as = 0 if choice1 was not U). This was included as a means of controlling for the level of rationality (based on observed behavior playing the one variant where that could be measured).

4. Results

4.1. Descriptive Statistics

Table 1. Descriptive statistics.

	Variable	Mean	StdDev	Min	Max	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
1	choice1 = U	0.880	0.326	0	1
2	rationale1 = dom	0.350	0.478	0	1	0.239
3	choice2 = D	0.705	0.457	0	1	0.166	0.084
4	game2 = D&eV	0.345	0.477	0	1	0.171	0.107	0.469
5	rationale2 = unk	0.205	0.405	0	1	−0.041	−0.191	−0.242	−0.369
6	choice3 = U	0.670	0.471	0	1	0.134	0.091	0.129	0.196	−0.065
7	game3 = U&max	0.290	0.455	0	1	0.033	0.085	−0.022	0.000	0.030	0.449
8	rationale3 = unk	0.150	0.358	0	1	−0.060	−0.132	−0.066	−0.128	0.515	−0.182	−0.268
9	male	0.645	0.480	0	1	−0.017	−0.047	−0.022	0.077	−0.193	0.013	−0.102	−0.098
10	age	37.805	10.404	18	71	−0.002	−0.097	0.010	−0.137	0.067	0.019	0.017	0.123	−0.103
11	US-id	0.920	0.272	0	1	0.061	−0.015	0.133	0.020	0.013	−0.089	−0.096	0.021	−0.103	0.037
12	college	0.765	0.425	0	1	0.122	0.011	0.107	0.129	−0.128	−0.013	−0.088	−0.097	−0.042	−0.029	0.010
13	GT-exposure	2.245	0.848	1	5	0.034	0.060	−0.072	0.039	−0.162	0.015	−0.094	−0.089	0.104	0.017	−0.089	0.328
14	eV-experience	2.580	0.887	1	5	−0.001	−0.090	−0.047	0.166	−0.165	0.039	−0.095	−0.085	0.238	−0.011	0.047	0.190	0.538
15	options-experience	2.520	0.961	1	5	0.104	−0.004	−0.049	0.034	−0.030	0.015	−0.036	0.006	0.032	0.090	−0.071	0.374	0.453	0.511
16	ambiguity-aversion	0.184	0.353	−1	1	−0.014	0.040	0.049	0.055	0.047	0.099	0.179	−0.129	−0.072	0.053	−0.039	−0.137	−0.184	−0.113	−0.109
17	game1score	1.225	0.645	0	2			0.158	0.171	−0.158	0.130	0.085	−0.125	−0.049	−0.066	0.046	0.065	0.046	−0.071	0.045	0.038

provides the descriptive statistics for the variables used in our analysis. All variables have reasonable means and variances, and maximized ranges. Almost all IVs have high correlations with at least one of the DVs, mostly in sensible directions (e.g., college is highly positively correlated with good choices and negatively with admitted ignorance; game1score is highly correlated with good choices in game variants two and three). Several of the IVs show high correlations with each other relating to education and experience or exposure; regardless, the regressions indicated no issues with multicollinearities (i.e., as tolerances for the regressions were all above 0.5).

4.2. Empirical Outcomes

To determine whether our four expectations were met or not, we analyzed the data as follows: In terms of the first part of the first expectation, 88%—a significant majority4—chose the unambiguously best strategy (U), with 85% identifying one of the four possible consistent rationales (i.e., dominant, highest expected value, maximax, and maximin), but with only 35% identifying the most correct rationale for that choice (i.e., being the dominant strategy).

In terms of the second expectation, an analysis of the differences in the variances of choices in the last two problem variants (where 1 = U, 2 = D, 3 = Mix), the standard deviation for choice2 (at 0.54) was significantly lower than that for choice3 (at 0.68), based on a comparison test F-statistic (of 0.63, with a significance level of 0.001). That result supports the second expectation that the more complex problem will cause greater variance among the strategies chosen. (Additionally, the most popular choice dropped in consensus level by 5-percent from problem variant 2 to problem variant 3).

In terms of the third expectation,

Table 2. Probit analyses.

DV	choice1 = U				rationale1 = dom
IVs	Coeft	Error	z	|z| > Z*	Coeft	Error	z	|z| > Z*
constant	0.440	0.749	0.59	0.557	0.095	0.580	0.16	0.870
male	0.053	0.266	0.20	0.841	−0.071	0.202	−0.35	0.725
age	−0.002	0.012	−0.15	0.881	−0.014	0.009	−1.52	0.127
US-id	0.412	0.402	1.02	0.306	0.078	0.348	0.22	0.823
college	0.289	0.290	1.00	0.319	−0.037	0.244	−0.15	0.879
GT-exposure	0.006	0.179	0.03	0.974	0.261	0.141	1.86	0.064
eV-experience	−0.120	0.162	−0.74	0.460	−0.289	0.146	−1.98	0.048
options-experience	0.200	0.158	1.27	0.206	0.056	0.122	0.46	0.645
ambiguity-aversion	−0.028	0.335	−0.08	0.932	0.212	0.269	0.79	0.432
chi-sq			5.110	0.746			8.255	0.409
pseudo-R2			0.035				0.032
DV	choice2 = D				game2 = D&eV				rationale2 = unk
IVs	Coeft	Error	z	|z| > Z*	Coeft	Error	z	|z| > Z*	Coeft	Error	z	|z| > Z*
constant	−0.403	0.638	−0.63	0.528	−1.174	0.650	−1.81	0.071	0.524	0.722	0.73	0.468
male	0.035	0.212	0.16	0.870	0.119	0.211	0.56	0.573	−0.506	0.225	−2.25	0.025
age	0.005	0.010	0.50	0.620	−0.015	0.010	−1.57	0.117	0.003	0.010	0.33	0.739
US-id	0.506	0.343	1.48	0.140	−0.049	0.364	−0.13	0.893	−0.003	0.393	−0.01	0.993
college	0.510	0.249	2.05	0.040	0.524	0.259	2.02	0.043	−0.357	0.268	−1.33	0.182
GT-exposure	−0.153	0.147	−1.04	0.297	−0.162	0.147	−1.11	0.268	−0.149	0.154	−0.97	0.332
eV-experience	0.043	0.146	0.30	0.766	0.404	0.149	2.71	0.007	−0.232	0.158	−1.47	0.142
options-experience	−0.113	0.128	−0.88	0.377	−0.146	0.128	−1.14	0.256	0.186	0.138	1.34	0.179
ambiguity-aversion	0.176	0.275	0.64	0.523	0.312	0.290	1.08	0.281	0.041	0.314	0.13	0.896
game1score	0.324	0.151	2.14	0.033	0.410	0.156	2.63	0.008	−0.417	0.170	−2.46	0.014
chi-sq			13.440	0.144			22.967	0.006			21.795	0.010
pseudo-R2			0.055				0.089				0.107
DV	choice3 = U				game3 = U&max				rationale3 = unk
IVs	Coeft	Error	z	|z| > Z*	Coeft	Error	z	|z| > Z*	Coeft	Error	z	|z| > Z*
constant	0.242	0.646	0.38	0.707	−0.004	0.644	−0.01	0.995	−0.566	0.741	−0.76	0.445
male	0.007	0.203	0.03	0.974	−0.256	0.209	−1.22	0.222	−0.267	0.243	−1.10	0.272
age	0.004	0.009	0.40	0.692	0.000	0.009	0.03	0.973	0.014	0.011	1.34	0.180
US-id	−0.538	0.387	−1.39	0.165	−0.488	0.344	−1.42	0.156	0.030	0.436	0.07	0.945
college	−0.047	0.249	−0.19	0.851	−0.207	0.245	−0.84	0.398	−0.388	0.289	−1.34	0.179
GT-exposure	−0.034	0.143	−0.24	0.812	−0.092	0.144	−0.64	0.524	−0.115	0.171	−0.67	0.500
eV-experience	0.135	0.142	0.95	0.341	−0.038	0.149	−0.25	0.799	−0.157	0.171	−0.92	0.357
options-experience	−0.038	0.123	−0.31	0.760	0.055	0.129	0.42	0.672	0.190	0.146	1.30	0.193
ambiguity-aversion	0.349	0.274	1.28	0.202	0.629	0.293	2.14	0.032	−0.732	0.341	−2.15	0.032
game1score	0.296	0.149	1.99	0.046	0.184	0.153	1.20	0.231	−0.281	0.183	−1.54	0.123
chi-sq			8.275	0.507			13.451	0.143			15.693	0.074
pseudo-R2			0.033				0.056				0.093

depicts the Probit regressions that were run to determine whether decision-maker characteristics correlated significantly with observed behaviors. While only a few specific regression runs were significant over the discrete choices made in the problem variants, most runs did have at least one decision-maker characteristic with significant correlation. That result provided weak support for the third expectation.

The fourth expectation was much more complicated to assess, and entailed two parts: The first part entailed determining whether the average choice profile for the survey across U, D, and Mix (e.g., 70% U and 30% D) was exploitable. The second part entailed determining whether that profile provided higher payoffs when played against itself than the exploiting choice profile played against itself. The average choice profile for a game was computed by taking the number of U’s and adding half the number of Mix’s and dividing by the total number of valid participant choices for that game (i.e., Mix was interpreted as half U and half D) to give the percent U, with the remainder being the percent D for that game. Given the average choice profile for a game, we could then play it against either pure profile (100% U or 100% D) or against itself to determine payoffs in that game. That left the issue of playing one strategy profile against another in a way that was sufficiently representative to address the fourth expectation.

Because we cannot simulate an unknowable distribution for p, theoretically, we cannot test either of these parts of the fourth expectation. Practically we can try to do so, though through a Monte Carlo-type simulation; we can assess the two parts of this expectation in a fair and representative simulated manner, by using a randomizer to choose the distribution for choosing p (i.e., one randomizer chooses 0 < k < 1, where k is the cutoff between choosing the left-side and right-side game where a second randomizer chooses another value between 0 and 1 to be compared to k) and then use that mechanism to actually choose the p for any simulated run of a game so that the payoffs to each player could then be computed based on their choices (for that one run of the game). We can then play that simulated game 20,000 times and record the average payoffs for each strategy profile when playing against another in order to address the fourth expectation.

Both games were exploitable by playing only U against the choice profile observed. (Note, here exploitable means that the exploiting strategy—i.e., playing 100% U—enjoys a much higher relative average payoff than the average choice profile strategy when played against each other across the simulation.) Playing the averaged choice profile strategies against themselves produced an estimated 5.07 payoff in game two and an estimated 5.41 payoff in game three, levels that far exceeded those when the exploiting profile strategy [U] was solely played against itself. In fact, these choice profile strategy payoffs were both near the top of possible payoff levels for any strategy profile that included both choices.5. These basic results provide semi-strong support for expectation four.

5. Discussion

We conducted this exploratory study in order to gain a deeper understanding of the challenges that SuA problems pose to real decision makers. We specified three variants of a game-based decision problem that involved Ellsbergian-type ambiguity in the form of an unknowable focal value (of probability). We paid participants (Amazon MTurk workers) to play those variants. They chose among three strategies in each game, identifying the rationale underlying their choices. Most of our general expectations were met: decision makers are not fooled by a probabilistically ambiguous problem with an unambiguously best choice; decision makers are more confused by more complex ambiguity; decision maker personal characteristics often correlate with their choices; the average decision choice profile is exploitable but also fares well when played against itself. The study also revealed a few surprises that we identify and comment on below, including the discovery of a new type of choice dilemma and the unwarranted apparent confidence-as-consensus expressed by real decision makers when confronted by real ambiguity.

It is not surprising that when one digs into the details of specific problems involving specific ambiguities that several new insights can emerge that were not visible when only generalities were being considered. We describe four such surprising insights below, including what appears to be a new form of dilemma in games.

First, these SuA problems are quite sensitive to specifications; for example, slight changes in payoff levels of the bookend games can flip what the popular choice and its underlying rationale will be for the SuA problem itself. The three variants we chose produced a wide variety of behaviors, although they were similar in many ways (e.g., no negative payoffs were involved; all bookend games had dominant strategy solutions). Further, that sensitivity was not easily explained, as neither decision-maker characteristics nor simple heuristics (e.g., maximin) appeared to be consistent predictors of the majority choices of strategy or rationale. While there were some broad patterns that were predictable (see expectation two), it appears that SuA problems are not easy to solve, nor do they lend to easy explanations for real decision-maker behaviors. This insight appears to imply that each such problem needs to be analyzed separately.

Second, just as with any other games that include the possibility of inefficient outcomes (e.g., co-ordination games), there exist ways, ex ante, to improve the future outcomes for all parties. In the case of our SuA game, it is possible to improve the range of payoff outcomes and eliminate most of the core ambiguity through the use of enforceable partnership contracts. (Note that was not an option in the experiment). For example, in game two, if both players could commit to playing D, then the possible payoff range reduces from being 0-to-8 to being 5-to-7. Thus, as with other problems (e.g., the PD), the costs to alter the problem given (e.g., by negotiating a cooperative contract prior to choosing game strategies) may be worthwhile for all parties to seriously consider.

Third, a new type of choice dilemma arose in the analysis of expectation four. It is a dilemma that differs from the PD. In the PD, the dominant strategy [defection] is Pareto inefficient (i.e., because if both players could commit to playing cooperation, each would be better off than they are in the DD-equilibrium condition). In our SuA game two’s problem, a different inefficiency arises. The pure strategy [D] has the largest p range of higher absolute payoffs (a right-hand range of 5/9th of the full unitary p-space)—so choosing D is the dominant strategy for more than half of all possible p values. That said, playing D can be ‘exploited’ by the other pure strategy [U] within a majority of the p range (a left-hand range of 4/5th of the entire unitary p-space), where that exploitation entails lower absolute payoffs to the focal player (than also playing D) but higher relative payoffs than the other player (i.e., where the payoff from playing U to the rival’s D is greater than what the rival gets playing D to the firm’s U). Given p is unknowable, it is unclear whether the gain in absolute payoffs from one choice should trump the relative payoff gain from the other choice, especially in a strategically competitive situation. Unlike in the PD, this SuA game has no consistently dominant strategy nor any Pareto optimality ex ante. In the PD, defection provides both the highest-absolute-payoff against a rival playing the other strategy of cooperation and the highest-relative-payoff. In other words, our analysis has revealed a completely new type of dilemma to the game theory literature, and one that decision makers facing a SuA problem may confront—that we will name as the arend dilemma.6

Fourth, the analysis of the first three expectations also implies a question about whether decision makers consciously acknowledge the realities of the ambiguities that they face. Despite the actual choice-related ambiguities in the second and third games, when real decision makers were forced to choose among strategies, it appears that an unexpected consensus forms to a pure choice (i.e., U or D, with an average consensus of 68.8%) rather than a mixed option (i.e., Mix, with an average preference of 11.3%) when the latter appeared the more appropriate strategy. This over-confidence was also noted in the fact that most of the players did not indicate a consistent rationale for their choice of strategy. Those results—revealing a significant level of confusion behind the actions taken—appear to show an under-appreciation of the uncertainty the decision makers faced, as only 19% on average admitted ignorance as a rationale—which was really the most appropriate rationale option available.7 Further, recall, this is a very explicit and simplified representation of uncertainty relative to what they may face in reality (which makes such inappropriate over-confidence even more likely to be observed in the field).

5.1. Discussion of Implications

We begin with specific implications based on the results of testing our four expectations; we then speak to the broader theoretical and practical implications.

The analysis of expectation one implies that it is important for decision makers to analyze a given SuA decision problem to see whether ambiguity actually exists over the focal choice regardless of whether it exists elsewhere (i.e., over the focal probability). There is no need to make finding a solution any harder than it needs to be if one choice is better than others, irrespective of an unknowable probability. The results underlying expectation one relate to the literature in two ways: First, decision makers behaved in a boundedly rational manner, consistent with past experimental outcomes (e.g., Kahneman and Tversky 1979; Simon 1957) while supporting the new expectation that participants can understand—on the whole—a prototypical SuA problem. Second, how such a new problem is presented can affect the level of ambiguity perceived and acted upon (e.g., Hansson 1996; Kuhlthau 1993), here in our first variant, with a new way of presenting the ambiguity as a probability issue that did not affect the best choice.

The analysis of expectation two implies that more complex problems require more complex approaches. While few individual decision makers appear to have noticed the increase in the complexity of the ambiguity between games two and three (i.e., based on their indicated choices and rationales), on average their confusion increased, some of which could have been alleviated with greater calculative effort as part of a more complex approach (e.g., in identifying the p-range where Mix was better, or that U was the maximax and maximin choice in game three). The results underlying expectation two relate to the literature on bounded rationality: they provided support for the notion that problems that challenge rationality more (i.e., entail higher levels of ambiguity intensity-as-complexity) lead to more confusion and variance in decision behaviors (e.g., Weil 2010), where this was shown with a new-to-that-literature problem in this study.

The analysis of expectation three implies that some decision-maker characteristics may influence choices and rationales, but with little consistency. That indicates it may be useful to be aware of such factors in order to control them in oneself and to exploit them in rivals.8 The results underlying expectation three relate to the wider literature on decision making that supports the idea that individual-level characteristics can influence behaviors in predictable ways (e.g., in general (Francioni et al. 2015), and with characteristics related to gender (Yang and Zhu 2016) or to training/experience (Hershey and Walsh 2000) specifically), where that extends to our new SuA decision problem as well.

Looking across the first three expectations, it appears that players under-appreciated the uncertainty that they faced. They displayed unwarranted confidence when confronting ambiguity. This appears to indicate a lack of training in what to do about such uncertainties, in addition to a vulnerability that could be exploitable. (For example, in the real world, if some parties do not see a real uncertainty in a specific, possibly beneficial investment, then it may be effective to underpay them to take it on—or insure it—for you).

The analysis of expectation four implies that such strategic exploitation is indeed very possible, even if it has only been supported in an artificial or simulated form in our study. That insight implies that more analysis over the SuA problem is important (e.g., in identifying what the upside payoff choices are for the ranges of p values). It is important to understand how one’s strategy can be exploited (and how one can exploit a rival’s) in these situations where players are less trained and seemingly less aware of the true nature of the challenges they face. The results underlying expectation four relate to the behavioral literature on strategic game playing: We also find, but in a new game, that the average strategy used by real decision makers is exploitable but yet highly rewarding when played against itself (e.g., Meyer and Banks 1997)—as standard expanding-pie game experiments have shown in the past. This outcome appears to support the idea that social beings have an ingrained ability to make decisions, even in the face of uncertainty, that tend to avoid mutually destructive consequences (e.g., Miller 1993).

We conducted this exploratory study because a gap exists in the theory (and their consequent prescriptions) relevant to effectively dealing with SuA problems in cases where that ambiguity is well-defined but irreducible prior to decision making. Exploration studies such as ours not only provide empirical insights into how real decisions are made (here when confronting ambiguity) but also provide some basis for inductive theorizing. For example, one new insight to theorizing emerging from our study appears to be that both the quality and quantity of the uncertainty matter to how such ambiguity is (and should be) dealt with. This is new because previous research has pointed to it being primarily a quality or a quantity rather than both (e.g., Lipshitz and Strauss 1997).9 That insight comes from interpreting expectations one and two together.

In terms of theorizing through the use of models, a major implication from our analysis of SuA problems is the importance of limiting the prescriptions about SuA until a specific SuA problem is described. Further, the inability to optimize—caused by the ambiguity involved—does not usually mean that all hope is lost regarding how to limit the impact of the uncertainty; there often exist feasible options for rewriting the game (e.g., that explore legal avenues for cooperation) in order to reduce given ambiguities (e.g., by shifting up and also minimizing the range of the affected possible payoffs).

For practice, the results of our study imply that firms would be well-served to consider the following four recommendations: First, take SuA problems on a case-by-case basis, making an effort to understand any ambiguities involved and what the full range of options are for addressing them, prior to trying to resolve them. That may involve identifying any dilemmas, in addition to mapping out scenarios within the uncertainty-relevant bounds, in order to make better decisions. Given the bounded rationality at play, it is important to attend to the less-complicated, more routine tasks of perceiving and setting up what the problem is by identifying every uncertainty and complication involved—regardless of how a problem is initially presented to the firm—in order to make the next, more difficult tasks (e.g., of analysis) less confusing and less mistake-prone. In our study, that would mean noticing that the first SuA problem presented did not actually involve an ambiguous choice (a realization that would translate into an easier analysis for finding the best option).

Second, appreciate the traits and aversions that the firm’s decision makers have that could affect their choices, and adjust staffing as necessary. Aside from staffing, the incentives offered to the decision makers who confront SuA problems need to be specially written to assure personal alignment with the organization’s goals (e.g., to default to a maximin rule under existential threats to the organization). Choosing who does what in the decision-making process should account for personal traits (e.g., experience, aversions, and possibly even gender), especially when there is no time to recheck work. When possible, a post-mortem should be conducted on SuA problems so that managers can learn about what occurred and why, in order to improve the process for the next challenge (and possibly to reduce any biases, implicit or not, that affect choices under uncertainty) (Kelley and Caplan 1993).

Third, presuming that the SuA problem has been correctly identified, for example, in terms of its intensity level, firms need to allocate the appropriate resources for the decision at hand—directing more personnel and analysis into the more challenging, more ambiguous problems (in order to compensate for any limitations caused by individual bounded rationality). In other words, for these non-standard problems, it is recommended that firms have flexibility built into their processes (e.g., besides having flexibility on allocating who does what, also being flexible on allocating how many people do that).

Fourth, because relatively little is known about dealing with these types of problems, other than that they tend to be addressed by exploitable strategies (on average), it is important to understand the firm’s positioning with the rivals involved in any specific SuA decision. If it is more important in the short-term to beat a rival in the present SuA game—outperform them in a relative way—then that may entail a different choice than if it is more important to maximize absolute performance or to keep the industry competition away from potentially mutually destructive interactions. (Incentive systems would also need to be adjusted to align possibly short-term interests of a manager with the longer-term interests of the organization.) In other words, for these types of SuA problems—where short-term goals may conflict with long-term goals—firms need to fully understand the trade-offs involved (including how reputational effects may influence future interactions—in terms of which rivals or partners will be involved and how they will act given what the firm did in the past). This may be a useful check on these choices in the decision-making process—i.e., at the stage where larger firm constraints and wider strategic interests need to influence the ultimate behaviors engaged in (e.g., Jones 1991).

5.2. Limitations

As with any exploratory study, especially one that is experiment-based, the specificity of the data and their analysis produce significant limitations on the generalizability of the results. Our study involved a limited sample size (N = 200) of a pseudo-random population (i.e., of experienced, qualified MTurk workers, mostly located in the US, who could answer two basic game theory filter questions), who responded at a specific period in time (i.e., late 2020–early 2021). So, we caution extending the results to dissimilar populations. Our study involved a relatively small set of decision-maker characteristics and SuA problem variants. So, we caution extending the results to dissimilar problem variants and other specific personality traits. Regardless, our results are solidly based on the recorded data and are robust to limited alternative specifications. We recommend future work to build on this exploratory study in order to address these generalizability concerns and to add new insights.

5.3. Summary and Look Forward

There remains much ground to cover on this topic of decision making in SuA problems. Our exploratory study provides one effective approach (i.e., using specific games sharing a common structure, focusing on one variant at a time, exploring the choices of real decision makers) for constructing a foundation of understanding. From that foundation, the investigation into more complex and real SuA problems can be performed (e.g., perhaps involving more than one uncertainty, or where the uncertainties are interdependent, or where one is sequentially linked to another in the ‘next’ problem). Such investigations should provide new suggestions for how SuA decision processes can be improved, building on some of our recommendations here (e.g., about staffing, pre-analysis clarifications, weighing short-term versus long-term goals, and more). So, we look forward to such follow-on work that moves us away from hypothetical generalities applied to under-specified problems and towards necessarily more precise descriptions and deeper analyses. Such work will lead the field more quickly towards the uncovering of new and valuable insights into the mysteries and confusions currently enshrouding the best ways to address non-risk uncertainties in the strategic decisions we must confront in the future.