Geometric Factor as the Characteristics of the Three-Dimensional Process of Volume Changes of Heavy Soils

Abstract

During simulation of a water regime of heavy soils, it is necessary to know the isotropy parameters of any volume changes. Volume changes appear in both vertical and horizontal directions. In vertical directions, they appear as a topsoil movement, and in horizontal directions as the formation of a crack network. The ratio between horizontal and vertical change is described using the geometric factor, r_s. In the present paper, the distribution of volume changes to horizontal and vertical components is characterized by the geometric factor, in selected soil profiles, in the East Slovakian Lowland. In this work the effect of soil texture on the value of the geometric factor and thus, on the distribution of volume changes to vertical and horizontal components was studied. Within the hypothesis, the greatest influence of the clay soil component was shown by the geometric factor value. New information is obtained on the basis of field and laboratory measurements. Results will be used as inputs for numerical simulation of a water regime for heavy soils in the East Slovakian Lowland.

1. Introduction

Heavy soils are characterized by a high content of clay particles which, due to moisture changes, cause volume changes in soil. When moisture increases, soil swells, and on drying, soil shrinks. Volumetric changes occur in a three-dimensional process, that in the vertical direction reflects the vertical movement of the soil surface, and in the horizontal plane the formation of cracks. The degree of distribution of soil volume changes to horizontal and vertical components depends on the isotropic properties of the soil environment [1,2,3,4]. The presence of cracks in conditions of heavy soils creates a two-domain soil environment, which significantly affects hydrological processes, especially in extreme meteorological conditions, highlighting the importance of studying this three-dimensional process [5,6,7,8,9]. Due to expected climatic changes, it is assumed that an increased frequency of extreme meteorological events will occur.

The aim of the paper is to characterize the distribution of volume changes to horizontal and vertical components in selected soil profiles in the East Slovakian Lowland (ESL) using a geometric factor. Based on the obtained results, the next goal is to verify the hypothesis concerning any effect of texture on the value of the geometric factor and thus, on the degree of distribution of volume changes to vertical and horizontal components. Within the hypothesis, it is assumed that the clay soil component has the greatest influence on the geometric factor value [10,11]. Results will be used as inputs for numerical simulation of water regimes of heavy soils in the ESL [12,13,14,15,16,17].

2. Materials and Methods

The procedure for determining isotropic soil volume expansion is based on laboratory determination of volume changes in clay-loam soil, for a precisely defined geometry of soil sample volume at the initial state of the experiment, and in the drying process under controlled conditions. Drying of isotropic soil samples is accompanied by volumes changes caused by horizontal and vertical shrinkage. Horizontal shrinking under natural conditions causes crack formations and vertical changes followed by decrease of soil surface area. From this point of view, laboratory results of studied volume changes should be interpreted for natural conditions. Previous studies [18,19,20] have mentioned one possible approach.

Figure 1 is a plot of soil sample saturation in the form of a cube with an edge length, z_s. Soil sample saturation is represented by a broken line. Its volume is $V_s=z_s^3$. After isotropic shake, the saturated sample is reduced by volume $\Delta V$ per cube, as per $z=z_s-\Delta z$ for edge length and volume $V=z^3$. Based on the above, it is possible to formulate a relationship

$$\frac{V}{V_s}=\frac{V_s-\Delta V}{V_s}=\frac{z^3}{z_s^3}=\frac{{\left(z_s-\Delta z\right)}^3}{z_s^3}.$$

(1)

On the basis of Equation (1) and Figure 1, it is possible to deduce the relationship between volume change of sample and change in sample height, i.e., by changing the volume in the vertical direction and in the horizontal plane.

$$1-\frac{\Delta V}{V_s}={\left[1-\frac{\Delta z}{z_s}\right]}^3.$$

(2)

For most soils in natural conditions, according to Equation (2), it is possible to consider isotropic shrinkage. Therefore, it is possible to substitute a the geometric factor r_s for 3 without greater loss of accuracy. We can then present a generalized version of the equation in the form

$$1-\frac{\Delta V}{V_s}={\left[1-\frac{\Delta z}{z_s}\right]}^{r_s}.$$

(3)

Mathematical expression of the relationship between volume change of sample and its vertical decrease can then be expressed in the form

$$\Delta z=z_s-\left[{\left(\frac{V}{V_s}\right)}^{\frac{1}{r_s}}\right]z_s.$$

(4)

Total change in soil volume is represented by ΔV = ΔV_v + ΔV_h, while ΔV_v = $z_s^2$ Δz. From the above and from Equation (4), the relation follows

$$\Delta V_h=\Delta V-z_s^2\Delta z,$$

(5)

$$\Delta V_h=V_s\left[{\left(\frac{V}{V_s}\right)}^{\frac{1}{r_s}}-\frac{V}{V_s}\right].$$

(6)

In accordance with Equation (1), Equation (2) can be interpreted as follows. In the case of shrinking without cracks, r_s = 1. In the case of crack formation and without decrease, r_s → ∞. For all other cases, for formation of drained cracks and a surface decrease, occurring simultaneously, the following values are distinguished: r_s = 3 for isotropic shrinking; 1 < r_s < 3, while vertical movement is more prevalent than horizontal shrinking. If r_s > 3, then the formation of cracks is more prevalent than vertical movement.

Considering that during the drying, the change of sample height in the direction of the vertical axis of sampling is measured, and volume of soil sample saturated by water, and volume of dried soil sample is measured also, it is possible to calculate the geometric factor r_s from Equation (4). By adjusting the equation, we get a relationship for calculating the geometric factor in the following shape.

$$r_s=\frac{\log (\frac{V}{V_s})}{\log \left[\frac{-\left(\Delta z)+z_s\right)}{z_s}\right]}.$$

(7)

From Equation (5), based on these theoretical considerations and experimental field and laboratory measurements, the geometric factor of volume expansion was determined as a quantifier of the distribution of total volume changes to horizontal and vertical components.

Another part of this research consists of two stages. In the first stage, r_s values were quantified for characteristic profiles on the ESL. In the second stage, the correlation between values of the geometric factor and content of clay (r_s < 0.002 mm), dust (r_s = 0.002–0.050 mm) and sandy particles (r_s = 0.050–2.000 mm) in soil were investigated. Investigated soil layers were classified in terms of isotropic volume changes.

To assess this correlation, models that best describe the tightness of correlation relationships were selected. As a criterion for selecting a model, the correlation coefficient value was used.

In addition, the relationship between $r_s\mathrm{and}{V}_h$ has been shown, based on measurements of $V,V_s,Z_s,\Delta z$ and Equation (6).

Measurements were made on the ESL in 11 sampling profiles from 10 different locations, the location of which is shown in Figure 2. Sampling points were selected to characterize the soil environment of the ESL. As part of the fieldwork, intact soil samples were taken by the swab probe method and placed into collecting rollers. The volume of withdrawal rollers was 100 cm³ with a diameter of 5.6 cm. The geometric dimensions of soil samples during shaking were measured by a micrometer. The size of shrinking versus percentage saturation for Michalovce is shown in

Table 1. Soil sample measurements and calculation of r_s in the Michalovce locality.

Layer [cm]	Rolle Number	zs [m]	Vs [m3]	V [m3]	Z [m]	∆z [m]	rs [-]	$\overline{r_s}$ [-]	∆z [%]	∆V [%]
	88	4.38	101.02	80.44	4.06	0.32	2.98		7.36	20.38
0–10	507	4.30	100.97	81.58	4.07	0.30	3.04	2.93	6.77	19.20
	511	4.33	101.25	84.29	4.11	0.28	2.76		6.43	16.75
	78	4.30	100.87	85.90	4.16	0.20	3.41		4.59	14.80
10–20	527	4.30	100.31	86.11	4.15	0.22	2.96	3.05	5.03	14.16
	530	4.33	100.51	86.28	4.13	0.23	2.79		5.33	14.16
	504	4.30	100.04	87.84	4.16	0.19	2.91		4.37	12.20
20–30	525	4.33	100.51	88.92	4.18	0.18	2.94	3.09	4.08	11.53
	533	4.37	100.85	88.79	4.21	0.16	3.40		3.67	11.96
	74	4.36	100.63	87.16	4.16	0.20	3.10		4.53	13.38
30–40	87	4.37	101.01	87.19	4.21	0.16	3.94	3.36	3.66	13.69
	515	4.34	100.42	85.93	4.13	0.22	3.03		5.01	14.43
	76	4.36	100.83	90.10	4.26	0.11	4.59		2.41	10.64
40–50	80	4.37	101.15	90.61	4.28	0.10	5.00	4.58	2.17	10.42
	519	4.38	99.70	90.35	4.28	0.10	4.15		2.34	9.37
	84	4.37	100.97	90.57	4.24	0.13	3.60		2.97	10.30
50–60	506	4.35	100.41	91.39	4.25	0.10	4.04	4.07	2.30	8.98
	536	4.36	99.79	92.12	4.28	0.08	4.57		1.72	7.68
	81	4.36	100.43	93.63	4.33	0.03	-		0.69	6.78
60–70	529	4.36	100.13	92.82	4.30	0.06	5.45	5.27	1.38	7.30
	535	4.37	101.05	93.35	4.30	0.07	5.08		1.55	7.62
	85	4.38	100.96	95.62	4.33	0.05	4.70		1.14	5.29
70–80	505	4.36	100.79	93.73	4.31	0.06	5.46	4.76	1.32	7.01
	534	4.36	100.39	93.45	4.28	0.08	4.12		1.72	6.91

Legend: z_s—sample height in a saturated state; V_s—volume of the saturated sample; V—sample volume after shrinkage; Z—height after drying, ∆Z—change of sample height; r_s—geometric factor; $\overline{r_s}—$layer average of the geometric factor; ∆V—total change in sample volume.

, in the last column on the right. The largest measured volume changes were around 40%. Soil samples were saturated under laboratory conditions to full water capacity, and after measuring their geometric dimensions, were dried at 30 °C gradually until the weight changes were approaching the measurement error. The last drying was carried out at 105 °C. All necessary data for calculating the variables of Equation (7) were obtained by measuring the geometric dimensions of the soil samples after drying. Soil samples were taken at depths of 0.10 m to 0.80 m at all locations except the Milhostov site. At the Milhostov site, samples were taken from depths of soil up to 1.60 m.

3. Results

The results of the measurements and calculations were divided into two parts in accordance with the methodological procedure. In the first part, geometric factor values were quantified. In the Michalovce profile in Table 1, the values of the soil sample volume changes, and values of the geometric factor r_s, are shown. In Table 1, for three successive layers of 0.1 m intervals, the height of the water-saturated rollers, their saturated volumes and these values after drying, are given. For each measurement, a calculated value of r_s and then an average value of the geometric factor for each layer are calculated, according to Equation (7). From Table 1, percentage volume change, and change in vertical dimension (Δz) of individual samples, as well as their average values in each layer, are obvious. In

Table 2. Texture characteristics of studied soil profiles in Michalovce. Analogously, all examined profiles were characterized.

Layer [cm]	I. Fraction <0.001 mm	Clay [%]	Silt [%]	Sand [%]
0–10	28.07	31.85	56.08	12.07
10–20	27.19	31.04	59.27	9.69
20–30	27.29	31.14	58.42	10.44
30–40	27.61	31.63	59.89	8.48
40–50	23.09	26.66	60.83	12.51
50–60	19.78	22.73	60.67	16.60
60–70	18.35	20.89	63.53	15.59
70–80	16.94	19.27	56.33	24.40

, each layer of each collection site is characterized by texture composition. All eleven sites were processed analogously.

Table 3. Profile evaluation by the average r_s value.

Locality [cm]	Coordinates	rs in Layer [-]				I. Fraction	Clay	Profile Rating
		Max	Min	Max-Min	Avg	<0.001 mm	<0.002 mm
Michalovce	N48°44.255′ E21°56.664′	5.3	2.9	2.3	3.9	23.54	26.90	1
Milhostov	N48°40.185′ E21°44.248′	5.9	2.8	3.1	3.9	27.28	29.15	1
Pribeník	N48°23.688′ E21°59.547′	3.4	2.9	0.5	3.1	29.70	31.90	1
Senné	N48°39.802′ E22°02.892′	4.4	2.6	1.8	3.0	51.03	54.84	2
Sírnik	N48°30.538′ E21°48.830′	4.8	2.7	2.0	3.3	30.55	35.18	1
Somotor 1	N48°23.748′ E21°48.471′	10.0	3.8	6.2	5.3	23.72	25.89	1
Somotor 2	N48°23.173′ E21°48.237′	3.0	1.7	1.3	2.3	18.30	20.15	3
Horeš	N48°22.540′ E21°53.907′	3.9	2.7	1.2	3.1	41.19	43.74	1
Kamenec	N48°21.048′ E21°48.877′	3.4	2.2	1.2	2.8	29.81	32.11	3
Vysoká	N48°36.796′ E22°06.898′	13.0	3.0	10.0	5.7	11.27	12.88	1
Zatín	N48°28.725′ E21°54.918′	3.4	2.9	0.5	3.4	28.45	31.55	1

Legend: 1—formation of cracks (r_s > 3); 2—isotropic shrinkage (r_s = 3), 3—vertical movement 1< r_s <3.

summarizes values of the geometric factor in all eleven investigated soil profiles. The table also shows coordinates of individual field profiles. Results indicate that, in the examined profiles, volume change predominantly results in the formation of cracks (r_s > 3.0). Only in Senné was an isotropic shrinkage identified (r_s = 3.0). In two profiles, the predominance of vertical movements over crack formation was identified (Kamenec (2.8), Somotor 2 (2.3)). The highest value (r_s = 13.0) was identified in the locality of Vysoká [21]. Vysoká also had the highest variation range. The lowest value (r_s = 1.7) was found in Somotor 2.

The second part of this research focused on a correlation analysis between the values of the geometric factor and the components of the texture of the soil samples. In addition, the shape of dependence between r_s and V_h is shown based on volumetric measurements.

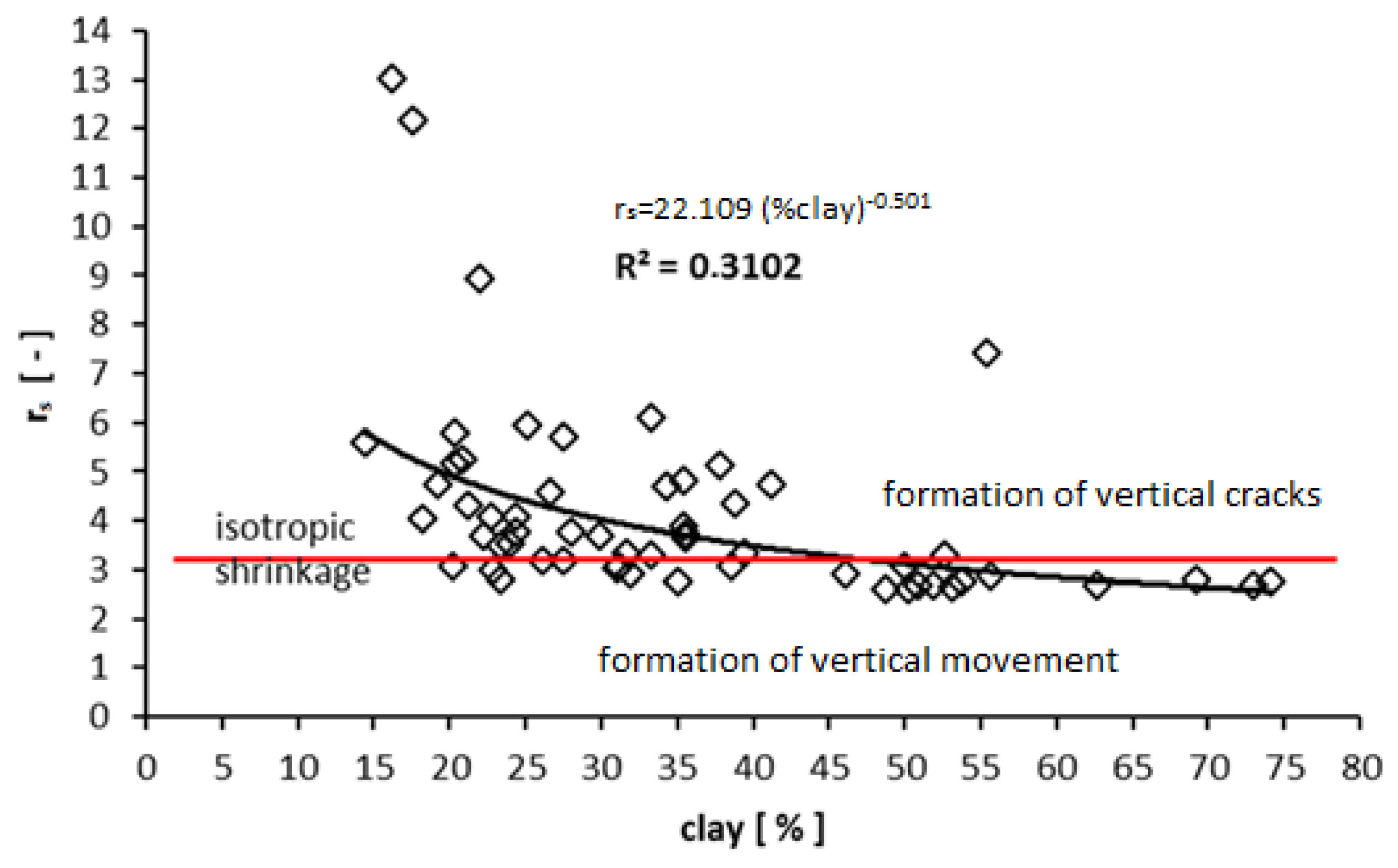
Figure 3 represents an analysis of the effect of the clay particle fraction, which is represented by a particle fraction of <0.002 mm for the geometric factor values. The geometric factor in this case is the average value of soil layers from which soil samples were taken for grain analysis. The effect of the content of clay particles on r_s is obvious from this picture. In this case a correlation was identified R = 0.56. The result can be interpreted as a significant influence of clay content in soil on the geometric factor, and on the distribution of total volume change to vertical and horizontal components. The figure shows that clay, and clay soil (45% to 55% clay content), are isotropic in terms of volume change. In addition, vertical movement slightly outweighs horizontal plane movement with an increase in the clay content of soils, and the variability of this movement decreases. The geometric factor oscillates slightly below the isotropic boundary. As the proportion of clay in soils decreases, the variability of r_s is significantly increased.

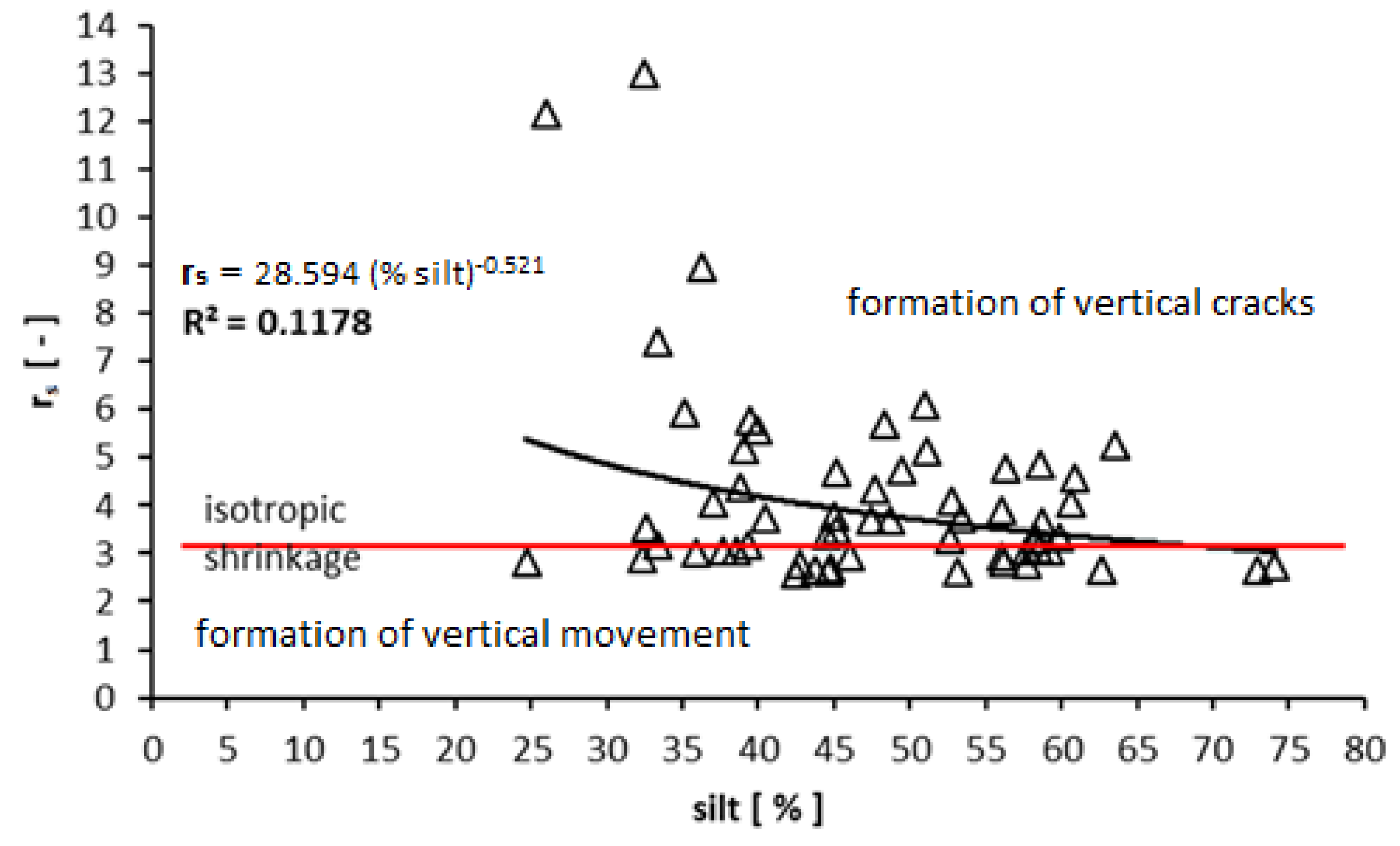
Figure 4 shows the relationship between r_s and silt particles in the soil samples. The Correlation coefficient, R = 0.34, is insignificant. The greatest variability of r_s was found to be between 30 and 40% for silt particles. Increasing the particle ratio caused the variability of r_s to decrease, and r_s values tended to approach the value of “3” from above, i.e., to the value of isotropic volume change.

Similar results are documented in Figure 5. Here, the relationship between r_s and the sand content in soil can be seen. The correlation coefficient of R = 0.36 is insignificant. The difference between the sand content in soil and silt content in soil, is the evenly distribution of sand content variability. The sand content trend in soil, increasing with the geometric factor, is opposite to that of the silt content in soil, which decreases with an increase in the geometric factor. In both cases, the r_s values oscillate around the isotropic shrinkage value, or are higher than the isotropic shrinkage value.

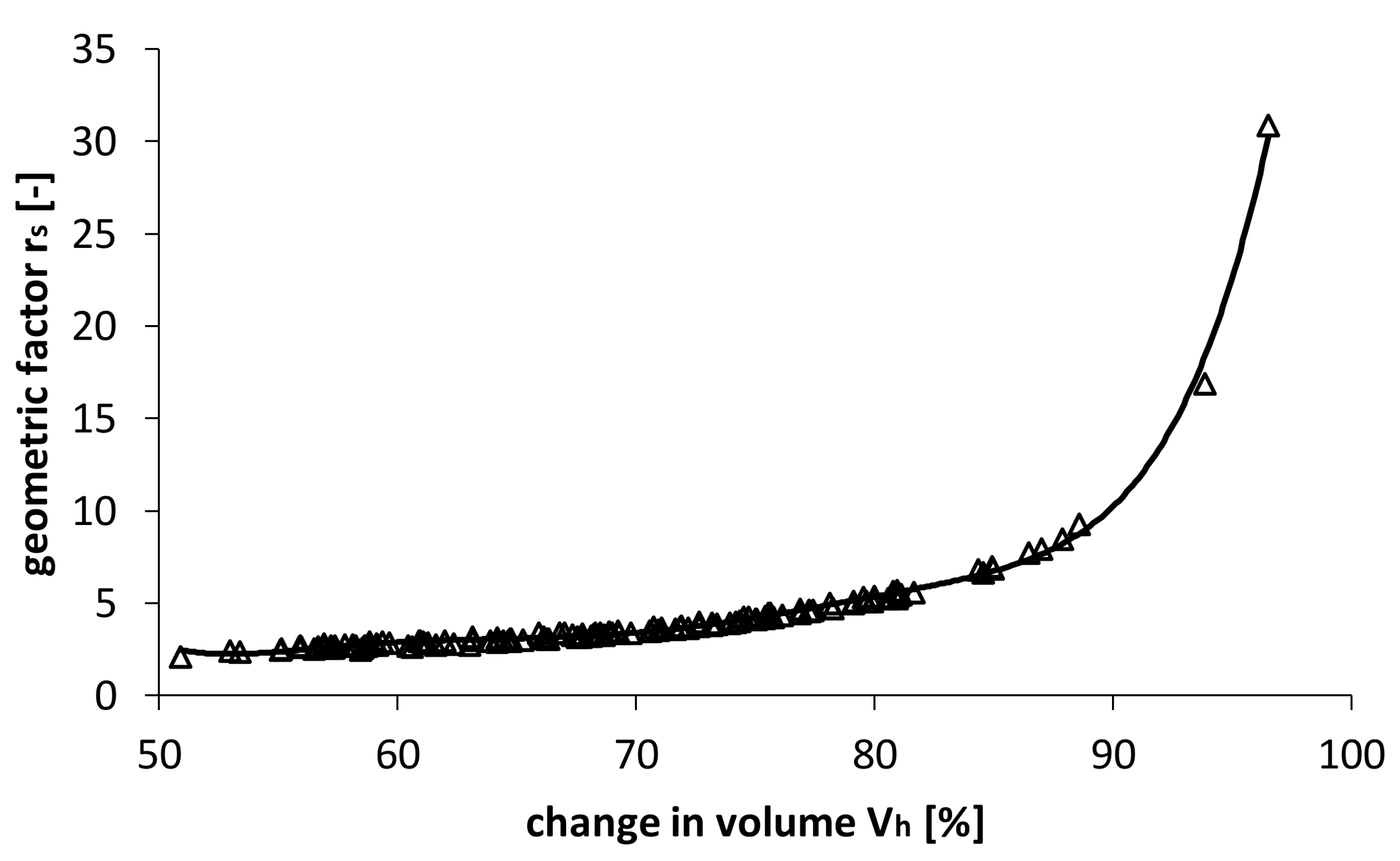
Figure 6 shows the relationship between the volume change in the horizontal direction V_h, and the geometric factor, r_s, with the volume change V_h being expressed as a percentage of the total measured volume change. The graph shows the effect of the geometric factor on the behavior of volumetric changes and their distribution to horizontal and vertical components. With an increase in r_s, more of the total volume change is due to the horizontal component.

4. Discussion

There may be several causes of the observed anisotropy of soil, when its volume was changed. It can be assumed that this is due to inequalities that occur in sedimentation processes, and the inhomogeneity of clay minerals that are sources of volume changes in soils. The primary condition causing volume change, is the presence of clay minerals and water. Crystals of clay mineral are composed of platelet formations (consisting of silicon tetrahedra and aluminum octahedra) ranging from 1 (montmorillonite) to a theoretically unlimited number (kaolinite). Individual plates have a very small valency (0.5–1.0 nm) and a high specific surface area (15 m²·g⁻¹—kaolinite, 80 m²·g⁻¹—illite; 800 m²·g⁻¹—montmorillonite). The size of the specific surface of these plates is closely related to the size of the volume changes. The larger the specific surface, the greater the ability to swell. The surface of the clay mineral plates carries a negative electrical charge that can attract water molecules. Consequently, with the increasing the surface area of clay mineral crystals, the more water molecules can bind. With an increasing water content, swelling of such a clay occurs. Drying will return the clay to its original volume. The abilities of individual minerals to assimilate water into their structure, and thus increase their volume, are different. Kaolinite clays are relatively inactive (they have low ability to bind water), illite clays have low to moderate swelling ability, and montmorillonite clays are highly expansive, and in their pure form (under laboratory conditions), can change volume by 1400–2000% (Na-montmorillonite). Pore size and pore distribution in soil is another factor influencing volume change. Presence of organic components in soil may also have a significant effect on volume changes.

Under natural conditions, clay minerals do not occur in pure form but in mixed structures. Therefore, it is necessary to know the species composition of clay minerals for a detailed assessment of these processes. Their determination is difficult. Information on the species composition of clay minerals is insufficient for the ESL.

For these reasons, further research on the ESL should aim to determine the species composition of clay minerals in characteristic soil species. These findings will help to avoid possible mistakes in determining cracked porosity based on physical clay content. This is the reason for paying increased attention to identifying the species composition of clay minerals in the soils of the ESL.

In this context, it is necessary to be aware that the amount and distribution of volumetric changes to horizontal and vertical components also have an indirect influence on the presence of silt and sand in soil. The representation of any of the textural components of clay, silt and sand, is a linear combination of the remaining two, provided that the granularity is accurately determined. If one of them is increased in soil, the remaining two are reduced. Silt and sand do not cause volume changes, but the increased soil content reduces clay content and volume change. This creates an inhomogeneous environment in terms of volume change and the associated geometric factors. The anisotropy of volume changes increases followed by the increased variability of the geometric factor. If there are large amounts of silt and sand or a reduction in clay, then soil is lighter and volume changes disappear, respectively. These changes are not measurable. With an increase in clay content and a decrease in silt and sand content, volume changes begin to display characteristics of isotropic shrinkage, i.e., r_s = 3. With isotropic shrinkage, the impacts of silt and sand gradually disappear. Changes in r_s across the vertical soil profile may be related to an increase or decrease in soil clay content. This is common under the ESL conditions. This may be associated with the impact of superficial soil layers. Sedimentation processes can have a significant impact on the anisotropy of volumetric changes and changes in the geometric factor, r_s, across vertical soil profiles in lowland conditions. This is especially true when platelet clay particles are predominately oriented in one direction.

The degree of influence of individual grain fractions on the geometric factor is related to the size of the grains and the pore size. The smaller the particles in the porous material, the more homogeneous it is, and the value r_s approximates or oscillates around the value “3”. The upper limit of clay particle size (2 μm) is 25 times smaller than the upper limit of dust particle size (50 μm) and 1000 times less than the upper limit of sand particle size (2000 μm). These variation ranges cause r_s to deviate from the value “3”, i.e., to deviate from isotropic shrinkage and thus increases the variability of r_s.

5. Conclusions

In this paper, values of the geometric factor, r_s, were quantified in characteristic soil profiles. Based on this, soil profiles were evaluated for the distribution of volume changes to horizontal and vertical components. In one case, isotropic volume changes were identified in Senné. This was the locality with the highest content of clay minerals of all investigated localities. Vertical volume changes dominated in two locations. In the remaining eight locations, horizontal volume changes dominated, i.e., crack formation and thus the formation of a two-domain soil system (crack and soil matrix) [22,23,24,25]. Summaries of the results are shown in Table 3.

The effect of texture on the geometric factor was analyzed. A high correlation between measured horizontal volume changes and the geometric factor has been demonstrated. The results are graphically shown in Figure 3, Figure 4, Figure 5 and Figure 6. All results were obtained from experimental measurements in the field and in the laboratory.

To focus further research on this subject area, we recommend paying increased attention to identifying the species composition of clay minerals in the soils of the ESL.

The results of this analysis will be used for numerical simulation of the water regime and its prognosis under heavy soil conditions in the ESL.