Industrial-Scale Wastewater Nano-Aeration and -Oxygenation and Dissolved Air Flotation: Electric Field Nanobubble and Machine Learning Approaches to Enhanced Nano-Aeration and Flotation

Abstract

Substantial boosts in the low-energy nano-oxygenation of incoming process water were achieved at a municipal wastewater treatment plant (WWTP) upstream of activated sludge (AS) aeration lanes on a single-pass basis by means of an electric field nanobubble (NB) generation method (with unit residence times of the order of just 10–15 s). Both ambient air and O₂ cylinders were used as gas sources. In both cases, it was found that the levels of dissolved oxygen (DO) were maintained far higher for much longer than those of conventionally aerated water in the AS lane—and at DO levels in the optimal operational WWTP oxygenation zone of about 2.5–3.5 mg/L. In the AS lanes themselves, there were also excellent conversions to nitrate from nitrite, owing to reactive oxygen species (ROS) and some improvements in BOD and E. coli profiles. Nanobubble-enhanced Dissolved Air Flotation (DAF) was found to be enhanced at shorter times for batch processes: settlement dynamics were slowed slightly initially upon contact with virgin NBs, although the overall time was not particularly affected, owing to faster settlement once the recruitment of micro-particulates took place around the NBs—actually making density-filtering ultimately more facile. The development of machine learning (ML) models predictive of NB populations was carried out in laboratory work with deionised water, in addition to WWTP influent water for a second class of field-oriented ML models based on a more narrow set of more easily and quickly measured data variables in the field, and correlations were found for a more facile prediction of important parameters, such as the NB generation rate and the particular dependent variable that is required to be correlated with the efficient and effective functioning of the nanobubble generator (NBG) for the task at hand—e.g., boosting dissolved oxygen (DO) or shifting Oxidative Reductive Potential (ORP).

1. Introduction

A major and fundamental challenge is limited (typically below Henry’s Law) solubility in many liquids, e.g., gases, such as oxygen, and especially hydrogen, in water. In ecosystems and the environment, a lack of dissolved oxygen (DO) is a major reason for fish kills and water bodies being blighted by algal blooms, sometimes in addition to a lack of the effectiveness of activated sludge (AS) processes in water treatment or poor results in irrigation.

Nanobubbles (NBs) are nanoscale gas bubbles than can exist on solid surfaces or in bulk liquids. They have attracted significant attention in the last decade [1,2,3] due to their long-time (meta)stability and high potential for real-world applications. The effects of several commercial applications of nanobubbles have been identified to date, such as the improved performance of fine-particle flotation [4,5,6,7,8] and the superior mass transfer of gases in separation and reaction engineering [6,9,10]. Nanobubbles have shown potential for use in water treatment [11,12], in sterilisation by applying ozone gas [13,14,15], and in accelerating the metabolism in shellfish and vegetables [16,17,18]. NBs have considerable potential to be used for soil remediation for soil polluted by organic chemicals in combination with bioremediation [19,20].

More recent studies on NBs in water treatment and flotation have shown, for instance, NB-enhanced floatation operations in seawater desalination as being promising, with a more effective separation of dissolved ions and suspended solids via mechanisms such as collisions, attachment, and detachment [21] in the flotation process. The possibility of optimising NB-mediated flotation phenomena in mineral recovery, as well as flotation kinetics per se, has been explored in terms of the optimal surfactant deployment strategy, as well as in consideration of how best to generate and detect NBs (e.g., ultrasonication, hydrodynamic cavitation, electrolysis, etc.) [22]. There has also been a greater appreciation and more detailed study recently of micro-nanobubbles, such as, inter alia, higher mass transfer rates and collision efficiency, which renders them especially promising for water treatment applications like disinfection and flotation [23]. If anything, these more recent explorations of NBs and their potential to improve water treatment and flotation processes offer more efficient and cost-effective solutions vis-à-vis the status quo of aeration bubbling approaches [21,22,23].

Nanobubbles, when generated properly and efficiently, allow bottlenecks of gas accommodation in liquids to be tackled. Following the fundamental discovery of bulk nanobubble and nano-droplet formation in Coulombic fields to gas–liquid systems, there was a striking finding of supersaturated gas present in liquid in NB form [24], borne of electric field dipolar coupling mechanics [25]. This highly novel, disruptive, and additive-free electrostriction-based approach lends itself to many industrial and environmental applications, some of which have been explored recently, often in a forward-looking way [24].

In any event, in more general terms, according to their nucleation media and history, nanobubbles, which cover both nanoscale bubbles and droplets, are the gas-containing components in the more general case, in what one might usefully refer to as the nano-phase [24]. They can be broadly categorised as either surface- or bulk-type. Compared to their bulk counterparts, surface nanobubbles have been the subject of many more studies [1], and they are found on the majority of aqueous surfaces, where they can persist for weeks at a time [24]. In the majority of aqueous solutions, bulk nanobubbles are present and may be continuously produced by agitation and ambient natural light [1,16]. In sharp contrast to thermodynamic predictions, surface NBs typically shrink, although they maintain their metastability when dissolved gas levels are decreased [15,16]. On the other hand, the size of bulk NBs allows them to react to ions and additives, and they usually have diameters between 50 and 200 nm. As previously mentioned, the presence of bulk NBs is of great industrial and ecological interest because, depending on their generation method and bulk liquid conditions, their occasional long life and stability observed frequently surpass the residence time of many processes, including recirculation aeration systems or, more generally, water-body aeration, and aeration cycles in activated sludge tanks for wastewater treatment. Nanobubbles generated via electrostriction are particularly seen to have a long life [21,22,23,25].

Traditional mechanical generation approaches to nanobubble formation present challenges including, amongst others, substantial energy usage, a lack of operational agility, and general complications, and the differences between these earlier NB generation approaches vis-à-vis the breakthrough electrostriction method are discussed in greater detail in Ref. [24]. In stark contrast, in the disruptive electrostriction approach [24], applying Coulombic fields via covered electrodes to liquid–gas (or, indeed, partially mutually immiscible) mixtures leads to the immediate generation and accumulation of nanobubbles in the liquid in a low-energy manner [24]—“sucking in” the guest molecules in the transient negative-pressure region via spatial density fluctuation at the liquid–guest interface [24]. These thick-skinned nanobubbles have notable ecological and commercial properties [24], boosting sustainability.

It is important to understand that, in actual (sludge-) nanobubble-aerated systems, or any oxygen-consuming process/species (brewing, plants, algae, fish, etc.), as opposed to standard ones—of Standard Oxygen Transfer Efficiency (SOTE), Standard Oxygen Transfer Rate (SOTR), etc.—the Aeration Efficiency (AE) in “nanobubbly” systems would be expected to outstrip that of other conventional systems. The reason for this is largely kinetic, in that the “reservoirs” or “batteries” of air NBs in both standard and actual sludge-activated systems achieve about 2.5–3.5 mg/L of DO (at a high energy cost of continuous aeration, naturally, under WWTP conditions)—that is, not in NB form. In contrast, it is no better than the 1.5–2 mg/L obtained for other methods (and often a great deal worse than that). However, the real difference lies in actual system performance, as in the case of real bacterial sludge activation in a WWTP: in this case, the 1.5–2 mg/L of DO is depleted rapidly, as the bacteria “feed off” DO, always hungry for more—with DO dropping quickly to 1 mg/L and below. In contrast, as we shall see shortly, our activated sludge trials showed that DO remained at 3–3.5 mg/L, as oxygen departed the NB to make up for the initial depletion of molecularly solvated oxygen (“DO”)—maintaining the DO level at a high value of 3–3.5 mg/L. As a result, microbes appeared to work substantially faster in reducing the BOD, COD, and ammonia levels. In effect, these NB “batteries” serve as a “feedback-control” system to regulate and maintain (high, essentially somewhat supersaturated) DO levels.

In the present study, we explore NB-based aeration strategies in the context of WWTP operations, as well as in activated sludge microbial cultures, assessing aeration and energetic effectiveness, as well as implications for settlement dynamics and Dissolved Air Flotation. In so doing, we also consider advances in the development of machine learning (ML) models—in progressing from laboratory work using Dynamic Light Scattering (DLS) facilities on deionised water to ML model training and the use of real-world field trial experiences—rooted in the monitoring of data. This allows for a second class of field-oriented ML models based on a more narrow set of more easily and quickly measured data variables that can be measured in the field, and correlations can be made for a more facile prediction of important parameters, such as the nanobubble (NB) generation rate and the particular dependent variable that is required to be correlated with the efficient and effective functioning of the nanobubble generator (NBG) for the task at hand—e.g., boosting DO, shifting Oxidative Reductive Potential (ORP), etc.

2. Methodology

An approximately 180–200 L/min WWTP influent water flow was put through a sidestream on a continuous-flow AquaB wastewater-processing unit (cf. Figure 1), including a variable flow control slurry pump for the purpose of facilitating this trial at the Ballykelly WWTP in Northern Ireland. Gas flow (whether air or O₂—vide infra) was about 80 L/min at 6 bar g and was delivered to a gas delivery manifold at the bottom of the electrostriction chamber using a compressor—in other words, a driving force of about 4 bar above the approximately 2 bar g operating pressure of the unit. There is vortex-enhanced electrostriction caused by upstream Venturi screw meso/microbubble generation from 40 L/min of the atmospheric air drawn through, and this converts the mother microbubbles into a sub-population of nanobubbles.

The mechanism of nanobubble generation in the present study is mediated by a DC static electric field, as detailed in Ref. [24]. Here, once a population of upstream-generated macro- and mesoscale bubbles comes into contact with sheathed electrodes in which this DC static electric field is imparted, we generate a derivative sub-population of nanobubbles from electrostriction action on the original population of bubbles: in short, the densification of water around the larger upstream bubbles mediated by the static field leads to a partial vacuum around these bubbles, which serves to suck fluid pockets of gas into a population of satellite nanoscale bubbles surrounding the periphery of the original macro/mesobubbles.

The already-mentioned compressed gas supplied through a manifold connection at the bottom of the electrostriction column went upwards as a countercurrent gas supply line of generated microbubbles—followed by their conversion to nanobubbles on the internal electrode bank. The power draw of the electrostriction itself from the main AC was only about 7 Watts: the vast bulk of that is AC-to-DC conversion overhead. There is additional power needed for pumping and air compressors, although this is very low considering the impressive levels of aeration that may be achieved very rapidly (cf. Results)—of the order of 0.8 kW. Bearing in mind that a pumping station is, of course, already there at WWTPs for transfer into the AS lanes, it may not always be necessary to supply additional NB generator pumping in explicit power draw budgets, although, to be fair, a typical, industry guideline Venturi-draw power equivalence allowance of about 0.3–0.5 kW may be allowed to account for additional equivalent pressure drops.

Figure 2 shows a couple of typical size distributions from Dynamic Light Scattering via a Malvern Zetasizer Pro using filtered water passed through the nanobubble generator (such that the derived count rate is less than 100 k.c.p.s. [24]); in any event, this water source shows no such nanoscale light scattering features prior to its passage (i.e., well below any instrument detection limits). For these examples, the typical diameter ranges are around 85–105 nm. The scale is up to 10 microns, and it is just these nanobubble features which are present (with no detectable level of microbubbles); as such, light scattering does not detect larger meso and macrobubbles.

3. Results and Discussion

3.1. Single-Pass Oxygenation from Air and O₂

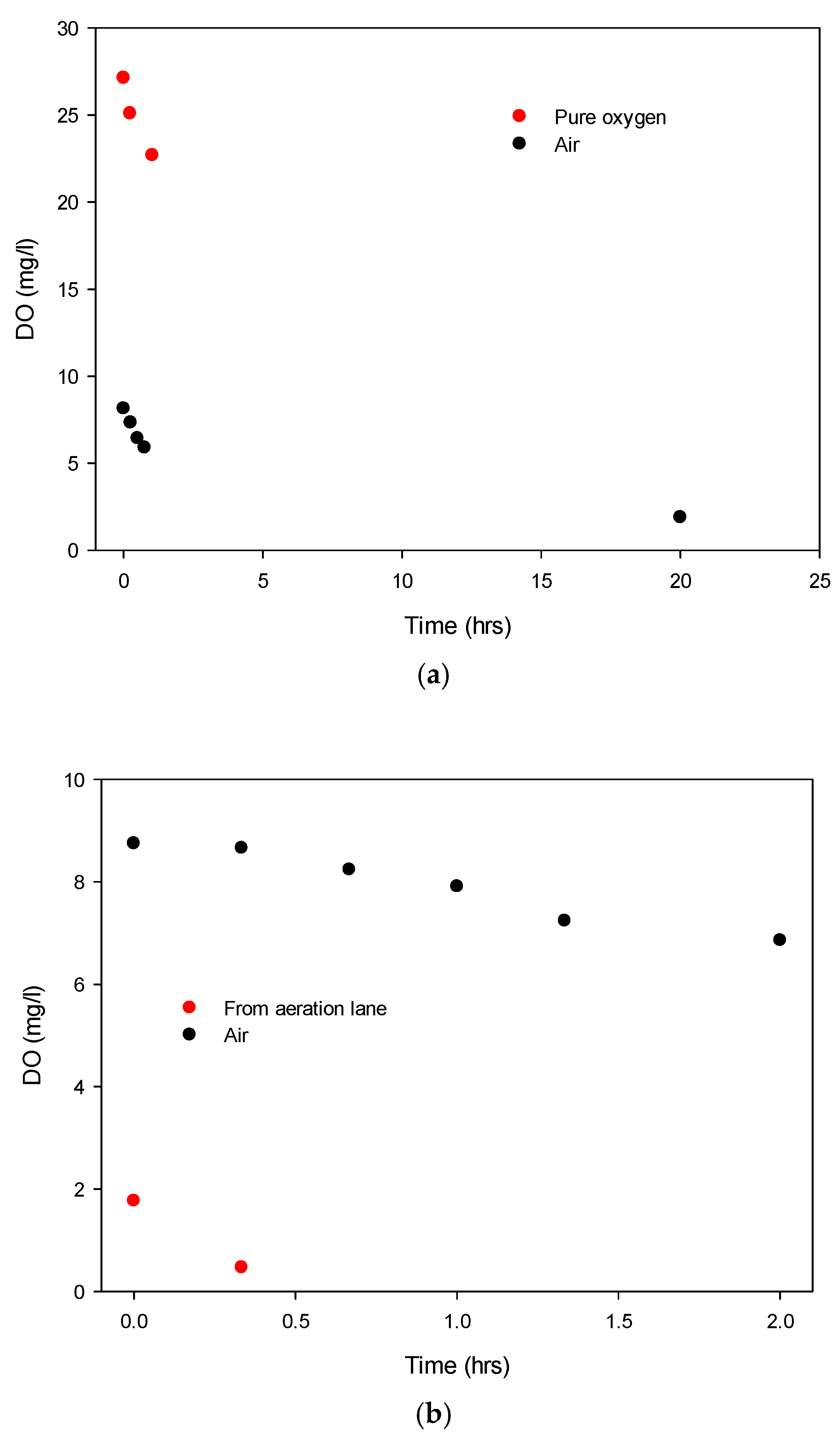
Before discussing the most promising low-energy NB oxygenation results, let us state the intrinsic deoxygenation rate of water sampled from the WWTP AS lanes, for background context: at 11 °C, DO dropped from 0.77 to 0.47 mg/L in 20 min (cf. Figure 3b). This results in a negative exponential decay/relaxation time, τ, of 0.675 h (i.e., 40.5 min) for the exp(−t/τ) oxygen depletion relationship as a result of microbial consumption. As an aside, for exponential decay, as a rule of thumb for quick mental arithmetic, one relaxation time decays the initial level by a bit over two-thirds; 95% is lost after three such time “periods” have elapsed—i.e., two hours in this example results in a loss of 95% of the oxygen pumped in by the blowers in the aeration lane, without continuous re-aeration. As we shall see, we obtain far longer intrinsic relaxation times for DO levels in nano-oxygenated samples, owing to the previously discussed reservoir effect of the NB state.

In Figure 3b, a second typical example of air showing the DO drop versus time for a single passage of incoming wastewater (DO < 0.1 mg/L) in shown in black (with the microbial culture again absent)—showing a relaxation time of about 16 h. For comparison, the red curve shows wastewater from the activated-sludge aeration lane not treated with nanobubbles, with the initial DO of ~1.9 ± 0.16 mg/L decaying much more quickly, as the present microbial culture consumes the dissolved oxygen much more quickly—this is slowed substantially by the presence of NBs in aeration lane wastewater.

With single-pass NB aeration from air (with the aid of a compressor), we routinely achieved (with a residence time of 10–15 s through the unit) DO boosts from <0.1 mg/L to 8.1–8.3 mg/L (corresponding to 0.3 to 73–76% of Henry’s Law level at 10–11 °C)—a typical example is shown in Figure 3a,b. However, these DO levels were maintained higher for much longer: a relaxation time of 13.9 ± 2.7 h (averaged over six readings, arising from an 8.11 ± 0.20 mg/L decay to 1.92 ± 0.05 mg/L over 20 h, although the temperature was higher at 15.5 °C on the second day, compared to 10.6 °C). In any event, this is twenty times longer than the intrinsic relaxation time in the AS lane itself without NBs (compare Figure 3a vs. Figure 3b).

Considering statistical hypothesis testing and the distribution of the DO data and time evolutions thereof, normal/random distributions were seen, and the standard deviations were quite similar, supporting the validity of ANOVA testing and the validity of pairwise Student’s t-testing. Using ANOVA testing passing 99% confidence levels (at 99.2% on the Fisher F-distribution), we can conclude that NB-based aeration has led to a significant boost in long-lived oxygenation. Naturally, as there was not an AS culture presence in the nano-aerated influent water source, this comparison is slightly dramatic. However, we also carried out AS nano-aeration, which also showed the maintenance of DO levels at 3–3.5 mg/L for two to three times longer in the AS samples than with conventional aeration, with microbes appearing to operate at a metabolic rate around 2–3% above that of the conventional aeration of the AS samples. Measured over five cases, the aeration retention time boost was 2.39 ± 0.41, passing the Student’s t-test results at the 95% confidence level (at ~97%, single-tailed). This constant NB reservoir/battery-fed replenishment is simply Fick’s Law (kinetics) in action, resulting in the maintenance of the liquid-phase fugacity of oxygen in the conventionally dissolved state (thermodynamics), subject to microbial oxygen demand. Still, maintaining a target DO level of 3–3.5 mg/L for, typically, double or more the time in AS samples is striking—pointing to the substantial additional levels of nano-dissolved oxygen, realised in a very-low-energy way compared to mechanical fine-bubble systems and AS lane mechanical aerator blowers.

This striking low-energy and efficient oxygenation is explained, once again, by the reservoir effect, with the NBs’ additional oxygen supply in the nano-dissolved state providing oxygen release (via Fick’s Law) as the microbial population consumes local DO (and promoting the chemical potential driving force based on oxygen). DO probes cannot detect nanobubbles in any direct way—but we estimate that there is a further 5–8 mg/L in the NB state initially [24] (which is depleted over tens of hours by influent water oxygen demand), above and beyond the measured DO level. These data have not yet been verified independently by other research groups in published form, although efforts are underway.

There was 27.13 ± 0.71 mg/L O₂ as a cylinder-fed gas, declining to 22.7 ± 0.56 mg/L over a little over an hour. In contact with air, this corresponds to 243 to 201% of Henry’s Law level at about 10.5 °C, and indeed, for near-pure O₂, we would expect the initial DO levels to reach above 200%, given that the electrostriction chamber also has a certain residence time of air therein. In any event, the DO depletion decay time here was about 5.8 ± 0.9 h. This shows that if O₂ is readily available in the nano-dissolved state in any event (beyond measured DO), then it is very useful indeed to boost DO. However, the longer relaxation time of simply using single-pass air, as opposed to pure O₂ (13.7 h vs. 5.8 h), arises due to the enhanced level of oxygen in the NBs [24].

Comparing the DO decay dynamics shown in Figure 3 with other fine-bubble aeration approaches, a conventional Xylem Sanitaire Silver II fine-bubble sparger–aerator was used as a control to aerate 200 L of filtered municipal water in comparison to 200 L passed through the NB generator shown in Figure 1. After 1 min of operation for each configuration, the relaxation times for DO decay were found to be 63.6 ± 3.1 and 2.35 ± 0.26 h for nanobubble and fine-bubble aeration, respectively.

Commenting on these observed results in terms of nanobubble-based explanations, in cleaner water with lower BOD and COD, it is evident that the reservoir effect of curtailed and slower Fick’s Law transfer of NB-borne oxygen to the regularly dissolved (Henry’s Law) state—in an effort to realise closer NB and Henry’s Law state fugacity equilibration—suppresses the decay of DO. In contrast, the meso and microbubbles imparted by regular fine-bubble generators in such sparger–diffusers are dissipated relatively rapidly—within no more than a few hours by Stokesian bubble rising/buoyancy dissipation. In this case/comparison, one can see that DO (reflective of individual molecular solvation in a Henry’s Law state) decays around 25 times faster than it does for nanobubble aeration, given that Stokes’ Law has led to the rapid decay of any meso/microbubble reservoirs. In short, the slowness of release of nanobubbles, especially in cleaner water with low BOD and COD, leads to a far slower decay of DO, as these long-lived stores of gas release O₂ molecules far more slowly—with less thermodynamic driving force for Fick’s Law transfer.

3.2. Settlement and Dissolved Air Flotation

The settlement dynamics were slowed slightly initially upon contact with virgin NBs, although the overall time was not particularly affected, owing to faster settlement once the recruitment of micro-particulates took place around the NBs—actually making density-filtering ultimately more facile. Rising and settling are shown in Figure 4.

The reason why there was some initial rise upwards is a result of the same principle behind nano-aeration enhancing Dissolved Air Flotation (DAF)—at least initially. This is a vivid illustration of carrier agency: there is a time lag whilst nano- and macro-particulates are attracted to the electrostatically attractive and naked surfaces of virgin, newly nucleated/created nanobubbles. This is simply a result of molecular diffusion and rearrangement forming an entourage or micron-sized colony—which is now subject to buoyancy forces and either rises or settles according to its aggregate density compared to the surrounding water. After this time has elapsed, settlement was then observed to occur quite rapidly, and there was no particular difference in settlement timescales. Still, this shows the potential for judiciously timed DAF operations, which is of interest to many WWTP operators.

Some water analysis is useful here, in the guise of an analysis on the Stirred Specific Volume Index (SSVI): this is related to an increase in the time taken prior to settling with incremental increases after each successive pass of NB generation—as shown in

Table 1. Stirred Specific Volume Index and associated settling time for each NB generation pass.

Sample	Time (min/s)	SSVI (mL/g)
Initial	11:40	108
1st Pass	12:20	115
2nd Pass	13:30	108
3rd Pass	14:45	108

.

It can be seen that there is a slight increase in sludge volume after the generation of virgin NBs, although it is not clear whether further settlement densification might take place given more time. There was little difference vis-à-vis the initial composition for more passes. Taken together, these results show that the increasing NB population resulting from the second and third passes for non-virgin NBs leads to slightly slower settlement, although there is a final acceleration in the latter stages of apparently more ordered settlement.

Aside from the more qualitative flotation analysis of Figure 4, considering the flotation kinetics of conventional aeration spargers vis-à-vis NB-treated water from the system in Figure 1, we measured mass removal times (via skimming) over an hour from 2.5 g/L of added 0.1 mm PETG beads to 10 L sampled from municipal water passed through the generator, as well as those exposed to a conventional Xylem Sanitaire Silver II fine-bubble sparger–aerator as a control, using 1 min of running in both cases (cf. Figure 5). It can be seen that, after an initial relaxation time of around 3–4 min, the kinetics of NB-enhanced removal is of the order of 40% greater vis-à-vis fine-bubble approaches to DAF.

By way of further NB-based explanations, and commenting more broadly, if anything, these overall DAF observations in Figure 4 and Table 1, albeit preliminary, may well have positive implications for a reduction in Total Suspended Solids (TSS) and the densification of solids. If so, as seemingly suggested, this will enhance solid removal processing a great deal. Although various disparate fine- and nanobubble providers make such general settlement-related claims, their usage of energy-inefficient and biofouling membranes as the bubble generation approach, together with resultant thin-skinned bubbles, renders these less suitable: the bulk-like density of these bubbles and faster Stokes’ Law rising speeds makes them shorter-lived and less able to sustain enhanced oxygenation and settlement properties.

3.3. Nitrate, Nitrite, and Ammonia

There were good conversions to nitrate from, inter alia, nitrite—owing to reactive oxygen species (ROS)—cf.

Table 2. (a) Highlights for air-fed NBs; % change is relative to the initial sample. (b) Highlights for oxygen-fed NBs.

(a)
mg/L	Initial Sample	Passage Without NB Generation	1st Pass	2nd Pass	3rd Pass
Ammonia	16	16	16 (0)	14 (−13)	13 (−19)
BOD, mg/L	37	34	15 (−60)	18 (−51)	10 (−73)
COD, mg/L	300	285	85 (−72)	68 (−77)	81 (−73)
Nitrate, mg/L	0.41	0.48	1.52 (270)	2.9 (610)	3.52 (760)
Nitrite, mg/L	0.53	0.47	0.093 (−82)	0.26 (−51)	0.19 (−64)
pH	7.01	7.00	7.00 (0)	7.04 (0)	6.99 (0)
Total nitrogen, mg/L	17.4	17.2	16 (−8)	15 (−14)	14.1 (−19)
Total oxidised nitrogen, mg/L	0.9	1.0	1.6 (78)	3.2 (260)	3.7 (310)
(b)
mg/L	Initial Sample	Passage Without NB Generation	1st Pass	% Change
Ammonia	11	11	10	−9.1
BOD, mg/L	37	33	23	−38
COD, mg/L	120	116	96	−20
Nitrate, mg/L	0.41	0.46	3.11	660
Nitrite, mg/L	0.83	0.78	0.094	−89
pH	6.97	6.98	7.00	0.43
Total nitrogen, mg/L	12.9	12.8	11.5	−11
Total oxidised nitrogen, mg/L	1.2	1.3	3.2	170

. The values of initial samples are also compared to those for the passage without the generation of NBs, i.e., with the electric field action disabled—it is clear that neither of these control cases is equivalent to the case of NB generation. Over multiple passes, nitrite levels fell from 0.53 mg/L (N) to 0.09–0.1 mg/L (N) after the second pass. The ammonia level was already quite low in the initial sample at 16 mg/L (N) incoming into the AS lanes, and this was unchanged after one pass but dropped to 14 and 12 mg/L (N) after the second and third passes, respectively. Similarly, and very encouragingly, conversion to nitrate improved from the first to second/third pass.

For single-pass pure-oxygen usage, the nitrite conversion to nitrate is rather spectacular (albeit with other nitrogen sources also playing a part—catalysed especially by pure oxygen), whilst ammonia oxidation (despite influent levels not being problematic) is also notable—all of which are seen in the substantial increase in total oxidised nitrogen. BOD and COD reduction is also meaningful and important, and this study recommends leveraging this reduction if possible.

As can be seen in Table 2, there were improvements in ammonia, nitrate, nitrite, BOD, and COD, and the percentage change data is instructive—with pure oxygenation being very useful, when available.

Commenting on NB-based explanations for these observed phenomena, the decline in nitrite levels from 0.53 mg/L (N) to 0.09–0.1 mg/L (N) after the second pass suggests a reorganisation of the NBs from the virgin state to a revised population in terms of ROS activity for oxidation chemistry (i.e., in going to the second pass instead for the first instance of non-virgin nanobubbles). The decrease in the ammonia level from 16 mg/L (N) incoming into the AS lanes to 14 and 12 mg/L (N) after the second and third passes, respectively, is also consistent with the reorganisation of non-virgin NBs (and the associated boost in ROS populations from that process). Similarly, the conversion to nitrate improved in going from the first to second/third pass—pointing to rises in ROS activity via the reorganisation of non-virgin NBs. Effectively, passage through the generator on subsequent passes helps to break up some of the corona/cloaks enveloping the NBs (cf. flotation/settlement dynamics in Figure 4 and Figure 5), which leads them to boost the ROS population and the accompanying oxidative activity. This is seen explicitly in the level of oxidised N increasing from 2.5 to 4.4 mg/L (or 0.9 to 3.7 mg/L) over three passes, with the major step change upon the second pass (i.e., the first occasion that non-virgin NB colonies and their electrostatically adsorbed colonies are disrupted); in parallel, there is a slight drop in the total N population from 24 to 22 mg/L (or 17.4 to 14.1 mg/L).

The largest improvements were seen in BOD, COD, and the nitrite-to-nitrate conversion upon the primary aeration on the first pass in the very creation of virgin nanobubbles in the first instance. However, the more subtle effects of reactive oxygen species (ROS) tend to be apparent with the subsequent passes in terms of the oxidation of ammonia in dealing with non-virgin NBs.

3.4. Multi-Pass Operations for Oxygenation

Multiple-pass operations through a continuous flow NB generator are a WWTP option; indeed, laser light scattering (DLS) [24] shows subtle effects on shifting NB populations from the virgin NB state. This was the most notable change and feature of multiple passes, as opposed to any meaningful boost in the already very impressive levels of DO enhancement seen in the production of virgin NBs on the first pass. The reason as to why DO did not increase substantially on the subsequent passes is that the NB population had already been created with nano-dissolved oxygen (not detected by DO probes—ipso facto), as confirmed by DLS; therefore, given that there was only about 45–60 min between successive passes, there was not a meaningful amount of time to allow DO to drop much (bearing in mind a typical nano-aerated relaxation time of 13.7 h—and 40 h for a 95% loss of DO—as per the earlier clarification on the nature of exponential decay for first-order microbial DO consumption dynamics). We note that in the AS lane itself, in that one-hour inter-pass time (due to the filling and emptying of the intermediate IBC), the batch DO declines by over three-quarters—i.e., exp(−1/0.675) = 0.22—although this is of course expedited due to the explicit presence of the AS culture itself with its very substantial microbial oxygen demand.

As an WWTP operational policy note, the benefits of multiple passes appear mostly in going from the first to the second pass, in terms of the maximal return of enhanced ROS/oxidative capacity, e.g., in relation to the nitrogen balance phenomenon. This is due to the first disruption of the non-virgin NBs and ensuing/concomitant ROS generation. The benefits to enhanced DO are less clear vis-à-vis multi-pass operation, in that the creation of virgin NBs in residence times of only 10–15 s via effective combined hydrodynamic turbulence and bubble-mixing strategies with electrostriction delivers the high nano-dissolved state in the 5–8 mg/L region of nano-dissolved DO, sidestepping Henry’s Law for tens of hours in influent water (with longer residual aeration also seen in AS samples in the general ~3 ± 0.25 mg/L range), and the NBs’ Fick’s Law oxygen diffusion characteristics dominate DO relaxation kinetics. To put this more in layman’s terms, oxygen spillover from the NBs maintains the high DO levels for far longer in the nano-dissolved state, so DO is available to be fed to “hungry” microbes (see below too with respect to COD and BOD).

3.5. Other Characterisation of NB Water Samples and Discharge Analysis

For treatment water, there was an apparent improvement in COD, BOD, and E. coli profiles, which was especially seen after the first pass for the generation of virgin NBs that accompanied low-energy (nano-)oxygenation. BOD and COD fell by about two- and four-fold, respectively, due to very effective oxygenation by virgin NBs. However, we also note some level of discrepancy between the lab results, so this is only a tentative conclusion; further testing is needed here, admittedly. E. coli. levels were almost halved by the third pass (falling from 2.91 to 1.66 × 10⁶ MPN/100 mL), although further research is needed, as is the case with BOD and COD observations. Intriguingly, the total number of coliforms did not decline by nearly the same amount (i.e., from 6.49 to 5.48 × 10⁶ MPN/100 mL—or by only 15%); this is highly encouraging, as E. coli. is undesirable, whereas the microbiology of the coliforms is important to support the overall health and effectiveness of activated sludge cultures.

In terms of NB-based explanations, microbiologically, this NB oxygenation appears to be beneficial. In addition, phosphorus levels declined by the order of 10% and more so on subsequent passes—albeit less dramatic than nitrogen balance effects, owing to more demanding oxidation phenomena.

3.6. Development of Laboratory-Based Neural Network Models

Having observed positive aeration and DAF phenomena in a WWTP context, unambiguous positive effects in influent water processing, and subsequent AS-based phenomena of prolonged aeration for lower aerator energy (of the order of 25%, albeit preliminary), another potential positive course of study involves considering how one may deploy neural networks (NNs) in an attempt to use easier-to-measure approaches to gauge the level of NB production per se (as opposed to just the headline level of traditionally dissolved oxygen, which might potentially be misleading [24]). This is important, given the level of ROS and electrostatic activity shift imparted by the generation of electric-field-generated nanobubbles [24,26,27], in terms of a signature of nanobubble activity on the nanobubbly water; indeed, NN models may facilitate the advent of Model-Based Control (MBC) and the boosting of NB-enhanced WWTP operational performance with overall aeration energy minimisation. Of course, this requires the development of from-scratch NN models for NB generation estimation. AquaB granted trial access to its commercial machine learning model software for NB generation performance to allow select results to be reported on, albeit without details of parameters and functional forms.

This NN model development starting point was used for deionised (DI) water and suitably filtered municipal water and for making connections (i.e., developing correlative models with) to the NB population (as the dependent variable) as measured by multi-angle DLS methods in the Malvern NTA Pro—which tends to show more consistent results than the Zetasizer Pro, given that the image analysis approach tends to be more consistent than a back-transform of the raw scattering light intensity signal, especially when taken in auto-correlation form [24]. For this purpose, a smaller-scale AquaB submersible NB generator suited for the laboratory is used—as shown in Figure 6—as well as an AquaB pipe flow model [24].

In terms of the municipal water source, a water reverse osmosis filter with three stages made by AquaClear Ltd. was applied to tap water in the Dublin area, and filtering was performed until the derived count rate in a Malvern Zetasizer Pro (made by Malvern Panalytical) was just under the 100 k.c.p.s. threshold to minimise the number of impurities that scatter light. For reproducibility and to enable the detection of acceptable levels of statistical error, this is crucial. It was discovered that background water samples did not contain any NBs when they were not run through water-flow-based NB generators or combined with submersible units.

In the case of the flow units, a Malvern Nanosight Pro was also used for comparison purposes in order to use the NTA particle/bubble-tracking approach as an arguably more consistent bubble-counting/detection metric than Zetasizer Pro multi-angle DLS (MA-DLS). The lower concentration detection limits for both types of Malvern instruments were on the order of around 10⁶ NBs per mL for the relatively clean, filtered tap water (to slightly below a practical and feasible 100 k.c.p.s. threshold—a light scattering quality threshold).

The NBGs were then operated with both water sources at a range of temperatures from 2 to 40 °C in an effort to clarify several plausible dependent variables, including the water source and the level of flow turbulence (as per Reynolds number) for pipe flow, on the DLS-derived NB population (as the dependent variable), with DO and ORP as secondary dependent variables when using air as the NB generating fluid. A list of potential independent variables was identified—in the sense that they might subsequently show some level of inter-correlation—which must be explored; see

Table 3. Candidates for independent variables prior to inter-correlation investigations. X means that a feature was present as a candidate variable for examination.

Variable	Batch Mode (Submersible)	Continuous Mode (Flow)
DC Voltage	X	X
Water flowrate (Reynolds number)		X
Water volume	X
Air flowrate	X	X
Water temperature	X	X
pH	X	X
Electrical conductivity	X	X
Water source	X	X

.

In each case—batch (submersible) and continuous flow (pipe model)—a two-level factorial design was set up, using a 2⁷⁻⁴_III-factorial design on a full-foldover alias structure symmetry—meaning that anything greater than the main effects interacting with two-way interactions can be eliminated (i.e., resolution III)—and main effects were disentangled from two-way interactions to gain a less ambiguous picture of their true underlying importance. This was performed in an effort to gauge the most important variables affecting the NB population (and, later, DO and ORP shift, which are partly correlated with the NB population as alternative field-measurable independent variables—i.e., as context-dependent, partially reliable proxies for the NB population—to be used and interpreted with care). Inter-collinearity correlation analysis was performed for these respective variables to assess information overlap, and it was found that the level of inter-correlation was relatively low—somewhat by design in independent variable selection (thus eliminating the need for, e.g., Principal Component Analysis—which simplifies matters).

The following main effects and two-way interactions were found from the 2⁷⁻⁴_III-factorial/foldover analysis, and the two symbolic expressions below show what essentially independent variables map onto the two NB population (dependent) variables, i.e., those that are causally linked (statistically):

Batch (NB pop.) ← Voltage, volume, air rate, temp., water source, temp. x voltage.

Pipe flow (NB pop.) ← Voltage, water flowrate, air rate, temp., water source, temp. x voltage, water flowrate x voltage.

All of these passed ANOVA and Fisher F-statistic statistical significance tests at the 95% level of certainty. The training and test sets of the data were chosen at random from the full accumulated data-set at approximately a ratio of 85:15% of the data quantity.

Multiple-variable (least-squares) linear regression models were then constructed for these models, and the level of r² performance was good at about 91 and 93% for the batch and pipe flow models, respectively, in terms of predictive performance outside of the training data (and also still significant in both cases with respect to the χ²-testing procedure for the requisite number of the degrees of freedom of the main effects and two-factor interactions).

Prior to discussing equivalent neural network fits for these models, we can consider the linear regression model fits to the DO and ORP shift analogues (arising from formal 2⁷⁻⁴_III-factorial/foldover analysis). It was found that DO was less correlated to the NB population—unsurprisingly, as DO probes (e.g., optical, load resistance, etc.) do not measure the presence of NBs directly. Rather, it is titration methods that tend to more completely measure at least a good portion of the NB population. We found that the ORP shift is a more accurate and correlated proxy variable to be used for the NB population [24,26,27], as it captures, relatively directly, the oxidative effect of the created NB population by the electric field approach (in terms of, e.g., electro-generated reactive oxygen species). Therefore, we also constructed equivalent statistically significant regression models for the ORP shift:

Batch (ORP shift) ← Voltage, volume, air rate, temp., temp. x voltage.

Pipe flow (ORP shift) ← Voltage, water flowrate, air rate, temp., temp. x voltage.

As we can see, the ORP shift tends to be a more robust, if imperfect, field measure of the presence of NBs and their population, as it is—crucially—less sensitive to the water source—to the point of being almost agnostic. The techno-commercial implications of this are hugely positive for field deployment and monitoring-and-control systems, in that DLS measurement is a highly technically specialised art/métier, requiring expensive and long-lead-time equipment and highly experienced laboratory personnel in time lag measurements, which work the best with clean water sources (highly filtered tap water or DI water being the best) to avoid meso- and microscopic particulates and dirt corrupting the raw laser scattering intensity signal and undermining the sound detection of nanoscale features (e.g., nanobubbles). In terms of the ORP model’s predictive statistical quality, the test set’s r² performance was strong at around 93 and 96% for the batch and pipe flow models, respectively, with parallel χ²-test metrics also showing strong statistically significant goodness-of-fit performance for the associated number of main-effects/two-way degrees of freedom. Bearing in mind the democratic price of a good-quality ORP probe, and that reasonable measurements can be taken in a matter of minutes, this is a pragmatic measurement approach to take for real-world unit operations (vide infra).

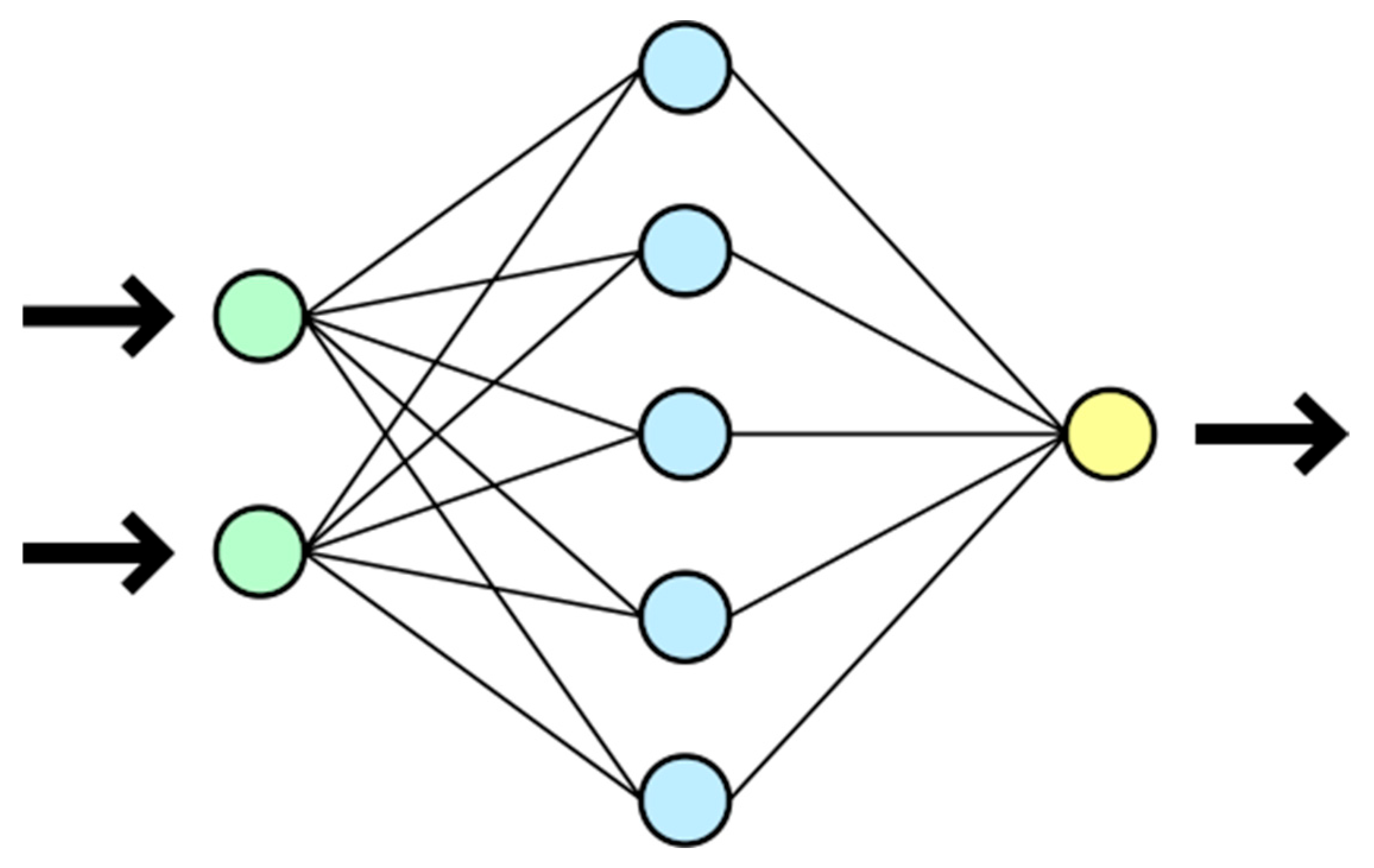
Having identified the appropriate independent variables using factorial/foldover approaches and eliminated inter-correlation problems, AI modelling was further used for the NB population and ORP shift metrics under both batch and flow modalities, in an attempt to improve performance over the by-now-trained multiple-variable linear regression models. Machine learning was then carried out by way of training neural networks for the above 2 × 2 sets of regression models, and a high-level overview of the neural network architecture is shown in Figure 7. The form of the gradient descent approach was experimented with to minimise the square of the predictive deviations—favouring the back-propagation method. This allowed the weight functions to be adapted efficiently during the training process.

The training, validation, and test sets of the data were chosen at random from the full accumulated data suite at roughly a ratio of 70:20:10% of the data quantity. Using this approach, even better 2 × 2 model performance was obtained on the external test set compared to regression models, as shown in

Table 4. Summary of coefficients of determination of models, with all passing χ²-tests for d.o.f. used.

Model	Linear Regression r2	Neural Network r2
NB pop, batch (sub)	91.2	94.1
NB pop, flow (pipe)	93.1	95.8
ORP shift, batch (sub)	93.3	96.1
ORP shift, flow (pipe)	95.9	97.6

.

Obviously, the prima facie correlative link (i.e., causal) established between the ORP shift and NB population is both essential and reassuring for the pragmatic and industrial use of the ORP shift as an accessible field measurement technique in either real-time or close-to-real-time approaches, in the real world, or in the wild, outside of the research lab in industrial nanobubble generators. This can aid in subsequent explorations.

3.7. Development of Field-Based Models

Having established the ORP shift as a robust metric highly (causally) correlated with the NB population, the goal of field testing for ML/NN model development is to gather as much all-year-round data as possible for outdoor operations—where seasonal variations can often be a factor—so that this can be taken into account in fit-for-purpose, outdoor-oriented field usage ORP shift models.

To this end, we applied NN fitting, as is evident in

Table 5. Candidates for field deployment independent variables prior to inter-correlation investigations. X means that a feature was present as a candidate variable for examination.

Variable	Submersible	Flow Mode
DC Voltage	X	X
Water flowrate (Reynolds number)		X
Water volume	X
Air flowrate	X	X
Water temperature	X	X
Level of suspended solids (wt %)	X	X
Water salinity—total dissolved solids	X	X
Chlorophyll level	X	X

, for the following modified set of easier-to-measure data (neglecting pH, as it was not found to be overly influential on the ORP shift or NB population for the laboratory investigations).

The 2⁷⁻⁴_III-factorial/foldover analysis led to the following field-rated NN models for the ORP shift (as a proxy for NB population and associated oxidative potency). The models are as follows:

Batch (ORP shift) ← Voltage, volume, air rate, temp., susp. solids, salinity, temp. x voltage, temp. x chlorophyll.

Pipe flow (ORP shift) ← Voltage, water flowrate, air rate, temp., susp. solids, salinity, temp. x voltage, temp. x salinity.

It can be seen that chlorophyll takes on a two-factor interaction importance in its relationship with temperature for water-body aeration, which is perhaps not particularly surprising, given the importance of chlorophyll in reservoirs and lakes (and, of course, its temperature sensitivity and, therefore, seasonality). Conversely, in turbulent-flow situations, where water is (by definition) much less stagnant (and chlorophyll levels are generally lower), there is a greater two-factor interaction between salinity and temperature.

Using the same training/validation/test split approach in the data partitioning as before, neural network r² values of 88.2 and 89.6% performance are obtained for the submersible/batch and pipe/continuous flow cases, respectively (with χ²-testing showing goodness of fit for the degrees of freedom used in the factorial-determined models). This was typically 2–3% better than that of the corresponding linear regression models directly from 2⁷⁻⁴_III-factorial/foldover analysis. Although this is not quite as good as their laboratory ORP shift counterparts (either for linear regression or neural network approach), it must be kept in mind that the R&D laboratory is a much more highly controlled environment, where essentially complete control and mastery over the experiment itself and measurement procedures can be asserted at will.

4. Conclusions

In this WWTP field trial, we showed that low-energy NB oxygenation with virgin NBs on a first-pass basis is highly effective, whilst multiple-pass options present interesting strategies for enhanced oxidation and nitrogen management strategies. With the appropriate handling of flotation/settlement phenomena (also of interest to DAF), NB water is of much interest in relation to AS. In the context of discharge analysis from the AS tanks and overall WWT per se, as the final effluent, we see that oxygenation within only 10–15 s of residence time for influent processing achieves a great deal of positive and promising results (with less need for blower usage in the AS tank channels, owing to longer residual oxygenation therein by NBs). Still, consent to discharge limits are not reached with just this treatment alone—and nor would that be expected, as the AS culture very much still has to conduct its work. In brief and at a high level, NBs in WWT are meant to support more facile aeration/oxygenation for AS (and possibly also for well-scoop-timed DAF) and (abiotic, Ammanox-avoiding) oxidation phenomena.

A further high-level comparison of NB oxygenation approaches with more established aeration techniques is warranted by way of conclusions. Certainly, in the past decade or so, the water treatment industry has seen the rise of the membrane aeration biofilter (MABF), for instance, as a good example of an innovative water treatment technology [28], as well as continual improvements in the development and performance of fine-bubble diffusers. In Section 3.1, a comparison was made between DO decay dynamics for NB oxygenation (from air) versus fine-bubble aeration, whilst Section 3.2 showed superior flotation kinetics for DAF-type impurity mass removal. In comparison specifically with MABF approaches, the absence of a membrane and/or filter in the presently studied electric field approach, ipso facto, is a crucial—even existential—point of difference vis-à-vis MABF and other current water treatment approaches. This results in, inter alia, substantially lower energy costs for oxygen transfer together with much less onerous maintenance burden.

In any event, as a result of the present study, future OPEX-/CAPEX-conscious recommendations are as follows:

-

Consider the dilution of a single-pass air NB output stream (with greater dilution of O₂-supplied NB if near-pure O₂ is already available and at hand). Dilute until DO is about two-thirds of the desired optimal operational range in the AS lanes—bearing in mind whether additional levels of nano-dissolved oxygen are present that the DO probes cannot detect.

-

Run this into the AS lanes and monitor/record the reduced power draw from the blowers, keeping the DO command–control system and set-points working as usual.

-

With energy savings in mind, consider just a mixer set-up for agitation instead, with reduced blower capacity.

-

Prior to entry into the WWTP, monitor ammonia and nitrite. If their levels are higher than usual, run a double-pass arrangement upstream of the AS lane for enhanced oxidation and nitrogen management.

-

Also consider submersible nanobubble generators in the AS lanes for low-energy aeration. It will be necessary to assess biofouling performance over longer-term operation, despite the encouraging results so far with the oxidative potency of electric field nanobubble biofilm suppression [24,26,27].

Given the positive results of the WWTP deployment of electric field NB generators, one must consider NN model integration therewith. A graphical user interface and control system firmware can be added to the AquaB offering, for both local and remote use (both near and far from the installed unit), subject to ongoing data acquisition and model improvement negotiations. In this way, NN-enabled MBC performance maximisation can be deployed to optimise NB-enhanced WWTP performance, with aerator blower energy minimisation.