Analysis of Uncertainty in the Depth Profile of Soil Organic Carbon
Abstract
:1. Introduction
2. Materials and Methods
2.1. Bayesian Regression
2.2. Deterministic Error Analysis
2.3. SOC Depth Profile
3. Results
3.1. Deterministic Regression Model
3.2. Comparison with Bayesian Regression
3.3. Application to Regional Data
4. Discussion
- (a)
- When the power law model is used with error-free coefficients, the transfer of uncertainty (σ or CV) is entirely determined by the exponent, i.e., the coefficient as demonstrated mathematically by differential error analysis.
- (b)
- If a model is fitted to the scatterplot by regression, there is added uncertainty due to errors in the estimation of the coefficients. Once again, only the shape coefficient for the power law model matters and not the scaling coefficient, . In the latter case, only a translation is involved with the scaling coefficient, .
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Biggs, A.J.W.; Grundy, M.J. The need for better links between pedology and soil carbon research in Australia. Soil Res. 2010, 48, 1–6. [Google Scholar] [CrossRef]
- Hicks Pries, C.E.; Castanha, C.; Porras, R.; Torn, M.S. The whole-soil carbon flux in response to warming. Science 2007, 355, 1420–1423. [Google Scholar] [CrossRef]
- Refsgaard, J.C.; van der Sluijs, J.P.; Højberg, A.L.; Vanrolleghem, P.A. Uncertainty in the environmental modelling process—A framework and guidance. Environ. Model. Softw. 2007, 22, 1543–1556. [Google Scholar] [CrossRef]
- Robinson, N.J.; Benke, K.K.; Norng, S. Identification and interpretation of sources of uncertainty in soils change in a global systems-based modelling process. Soil Res. 2015, 53, 592–604. [Google Scholar] [CrossRef]
- Heuvelink, G.B.M.; Burrough, P.A. Developments in statistical approaches to spatial uncertainty and its propagation. Int. J. Geog. Inf. Sci. 2002, 16, 111–113. [Google Scholar] [CrossRef]
- Brown, J.D.; Heuvelink, G.B.M. Assessing Uncertainty Propagation Through Physically based Models of Soil Water Flow and Solute Transport. In Encyclopedia of Hydrological Sciences; Anderson, M., McDonnell, J., Eds.; Wiley & Sons: Chichester, UK, 2005. [Google Scholar]
- Hamilton, A.J.; Basset, Y.; Benke, K.K.; Grimbacher, P.S.; Miller, S.E.; Novotný, V.; Samuelson, G.A.; Stork, N.E.; Weiblen, G.D.; Yen, J.D. Quantifying uncertainty in estimation of tropical arthropod species richness. Am. Nat. 2010, 176, 90–95. [Google Scholar] [CrossRef] [PubMed]
- Hamilton, A.J.; Novotny, V.; Waters, E.K.; Basset, Y.; Benke, K.K.; Grimbacher, P.S.; Miller, S.E.; Samuelson, G.A.; Weiblen, G.D.; Yen, J.D.; et al. Estimating global arthropod species richness: Refining probabilistic models using probability bounds analysis. Oecologia 2013, 171, 357–365. [Google Scholar] [CrossRef] [PubMed]
- Benke, K.K.; Robinson, N.J. Quantification of Uncertainty in Mathematical Models: The Statistical Relationship between Field and Laboratory pH Measurements. Appl. Environ. Soil Sci. 2017, 2017, 1–12. [Google Scholar] [CrossRef]
- Benke, K.K.; Norng, S.; Robinson, N.J.; Benke, L.R.; Peterson, T.J. Error propagation in computer models: Analytic approaches, advantages, disadvantages and constraints. Stoch. Environ. Res. Risk Assess. 2018, 32, 2971–2985. [Google Scholar] [CrossRef]
- Kuczera, G.; Parent, E. Monte Carlo Assessment of Parameter Uncertainty in Conceptual Models: The Metropolis Algorithm. J. Hydrol. 1998, 211, 69–85. [Google Scholar] [CrossRef]
- Kavetski, D.; Kuczera, G.; Franks, S.W. Bayesian Analysis of Input Uncertainty in Hydrological Modelling: 1. Theory. Water Resour. J. 1998, 42, W03407. [Google Scholar]
- Vrugt, J.A.; Gupta, H.V.; Bouten, W.; Sorooshian, S. The Shuffled Complex Evolutionary Metropolis Algorithm for optimisation and uncertainty assessment of hydrological parameters. Water Resour. Res. 2003, 39, 1201. [Google Scholar] [CrossRef]
- Qian, S.S.; Stow, C.A.; Borsuk, M.E. On Monte Carlo Methods for Bayesian inference. Ecol. Model. 2003, 159, 269–277. [Google Scholar] [CrossRef]
- Carlin, B.P.; Louis, T.A. Bayesian Methods for Data Analysis, 3rd ed.; Chapman and Hall: Boca Raton, FL, USA, 2008. [Google Scholar]
- Box, G.E.P.; Cox, D.R. An analysis of transformations revisited, rebutted. J. Amer. Stat. Assoc. 1982, 77, 209–210. [Google Scholar] [CrossRef]
- Geman, S.; Geman, D. Stochastic Relaxation, Gibbs Distributions, and the Bayesian Restoration of Images. IEEE Tran. Pattern Anal. Mach. Intell. 1984, 6, 721–741. [Google Scholar] [CrossRef] [PubMed]
- Helton, J.C. Uncertainty and Sensitivity Analysis Techniques for Use in Performance Assessment for Radioactive Waste Disposal. Reliab. Eng. Syst. Saf. 1993, 42, 327–367. [Google Scholar] [CrossRef]
- Mandel, J. The Statistical Analysis of Experimental Data; Dover Publications Inc.: New York, NY, USA, 1984. [Google Scholar]
- Parratt, L.G. Probability and Experimental Errors in Science; Dover Publications Inc.: New York, NY, USA, 1971. [Google Scholar]
- Taylor, J.R. An Introduction to Error Analysis; University Science Books: Sausalito, CA, USA, 1997. [Google Scholar]
- Freund, J.E. Mathematical Statistics; Prentice-Hall: Englewood Cliffs, NJ, USA, 1971. [Google Scholar]
- McBratney, A.B. On variation, uncertainty and informatics in environmental soil management. Aust. J. Soil Res. 1992, 30, 913–935. [Google Scholar] [CrossRef]
- Bishop, T.F.A.; Minasny, B.; McBratney, A.B. Uncertainty analysis for soil-terrain models. Int. J. Geog. Inf. Sci. 2006, 20, 117–134. [Google Scholar] [CrossRef]
- Heuvelink, G.B.M. Realistic quantification of input, parameter and structural errors of soil process models. In Proceedings of the Solutions for a Changing World, 19th World Congress of Soil Science, Brisbane, Australia, 1–6 August 2010. [Google Scholar]
- Malone, B.P.; McBratney, A.B.; Minasny, B. Empirical estimates of uncertainty for mapping continuous depth functions of soil attributes. Geoderma 2011, 160, 614–625. [Google Scholar] [CrossRef]
- Goidts, E.; van Wesmael, B.; Crucifix, M. Magnitude and sources of uncertainties in soil organic carbon (SOC) stock assessments at various scales. Eur. J. Soil Sci. 2009, 60, 723–729. [Google Scholar] [CrossRef]
- Li, M.; Zhang, X.; Pang, G.; Han, F. The estimation of soil organic carbon distribution and storage in a small catchment area of the Loess Plateau. Catena 2013, 101, 11–16. [Google Scholar] [CrossRef]
- Panda, D.K.; Singh, R.; Kundu, D.K.; Chakraborty, H.; Kumar, A. Improved Estimation of Soil Organic Carbon Storage Uncertainty Using First-Order Taylor Series Approximation. Soil Sci. Soc. Am. J. 2008, 72, 1708–1711. [Google Scholar] [CrossRef]
- Rayment, G.E.; Lyons, D.J. Soil Chemical Methods: Australia; CSIRO Publishing: Collingwood, Australia, 2011. [Google Scholar]
- Gill, P.E.; Murray, W.; Wright, M.H. The Levenberg-Marquardt Method. In Practical Optimization; Academic Press: London, UK, 1981. [Google Scholar]
- Kvålseth, T.O. Cautionary note about R 2. Am. Stat. 1985, 39, 279–285. [Google Scholar] [CrossRef]
- Bayes, T. An essay towards solving a problem in the doctrine of chances. Phil. Trans. Roy. Soc. Lond. 1763, 53, 1393–1442. [Google Scholar] [CrossRef]
- Freni, G.; Mannina, G. Bayesian approach for uncertainty quantification in water quality modelling: The influence of prior distribution. J. Hydrol. 2010, 392, 31–39. [Google Scholar] [CrossRef]
- Robertson, F.; Crawford, D.; Partington, D.; Oliver, I.; Rees, D.; Aumann, C.; Armstrong, R.; Perris, R.; Davey, M.; Moodie, M.; et al. Soil organic carbon in cropping and pasture systems of Victoria, Australia. Soil Res. 2016, 54, 64–77. [Google Scholar] [CrossRef]
- Hoyle, F.C.; D’Antuono, M.; Overheu, T.; Murphy, D.V. Capacity for increasing soil organic carbon stocks in dryland agricultural systems. Soil Res. 2013, 51, 657–667. [Google Scholar] [CrossRef]
- Murphy, B.W. Impact of soil organic matter on soil properties—A review with emphasis on Australian soils. Soil Res. 2015, 53, 605–635. [Google Scholar] [CrossRef]
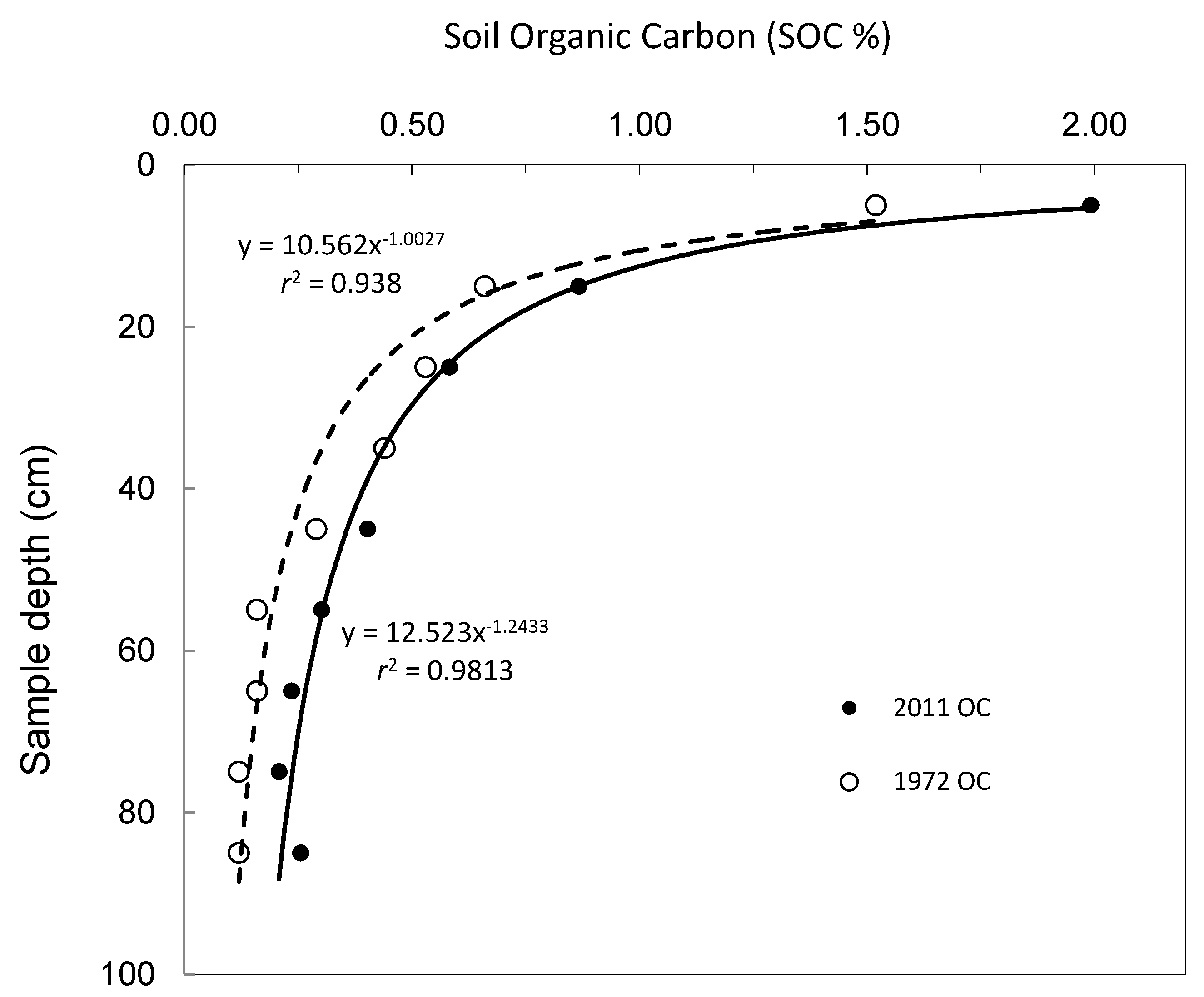

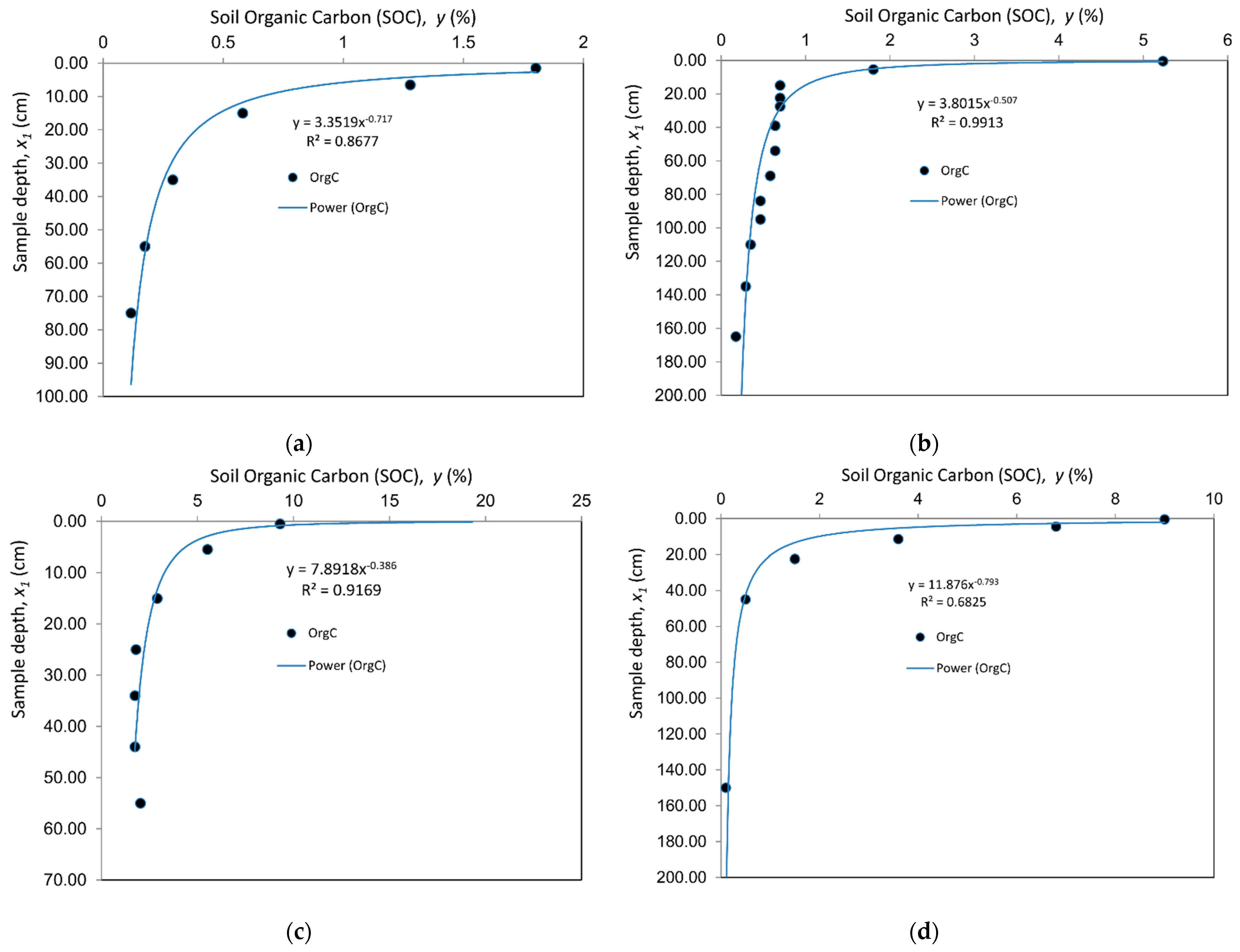
| Date | Parameter | Frequentist | Bayesian | Excel 2003 |
|---|---|---|---|---|
| (Year) | (Levenberg–Marquardt) | (MCMC) | (Transform) | |
| 2011 | 6.925 | 6.948 | 7.241 | |
| 0.773 | 0.774 | 0.789 | ||
| 1972 | 5.329 | 5.518 | 8.435 | |
| 0.773 | 0.787 | 0.936 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Robinson, N.; Benke, K. Analysis of Uncertainty in the Depth Profile of Soil Organic Carbon. Environments 2023, 10, 29. https://doi.org/10.3390/environments10020029
Robinson N, Benke K. Analysis of Uncertainty in the Depth Profile of Soil Organic Carbon. Environments. 2023; 10(2):29. https://doi.org/10.3390/environments10020029
Chicago/Turabian StyleRobinson, Nathan, and Kurt Benke. 2023. "Analysis of Uncertainty in the Depth Profile of Soil Organic Carbon" Environments 10, no. 2: 29. https://doi.org/10.3390/environments10020029
APA StyleRobinson, N., & Benke, K. (2023). Analysis of Uncertainty in the Depth Profile of Soil Organic Carbon. Environments, 10(2), 29. https://doi.org/10.3390/environments10020029








