The Distributed Practice Effect on Classroom Learning: A Meta-Analytic Review of Applied Research
Abstract
1. Introduction
1.1. The Case for Distributed Practice
1.2. Bridging the Research–Practice Divide
1.3. The Present Review
2. Method
2.1. Eligibility Criteria
2.2. Search Strategy
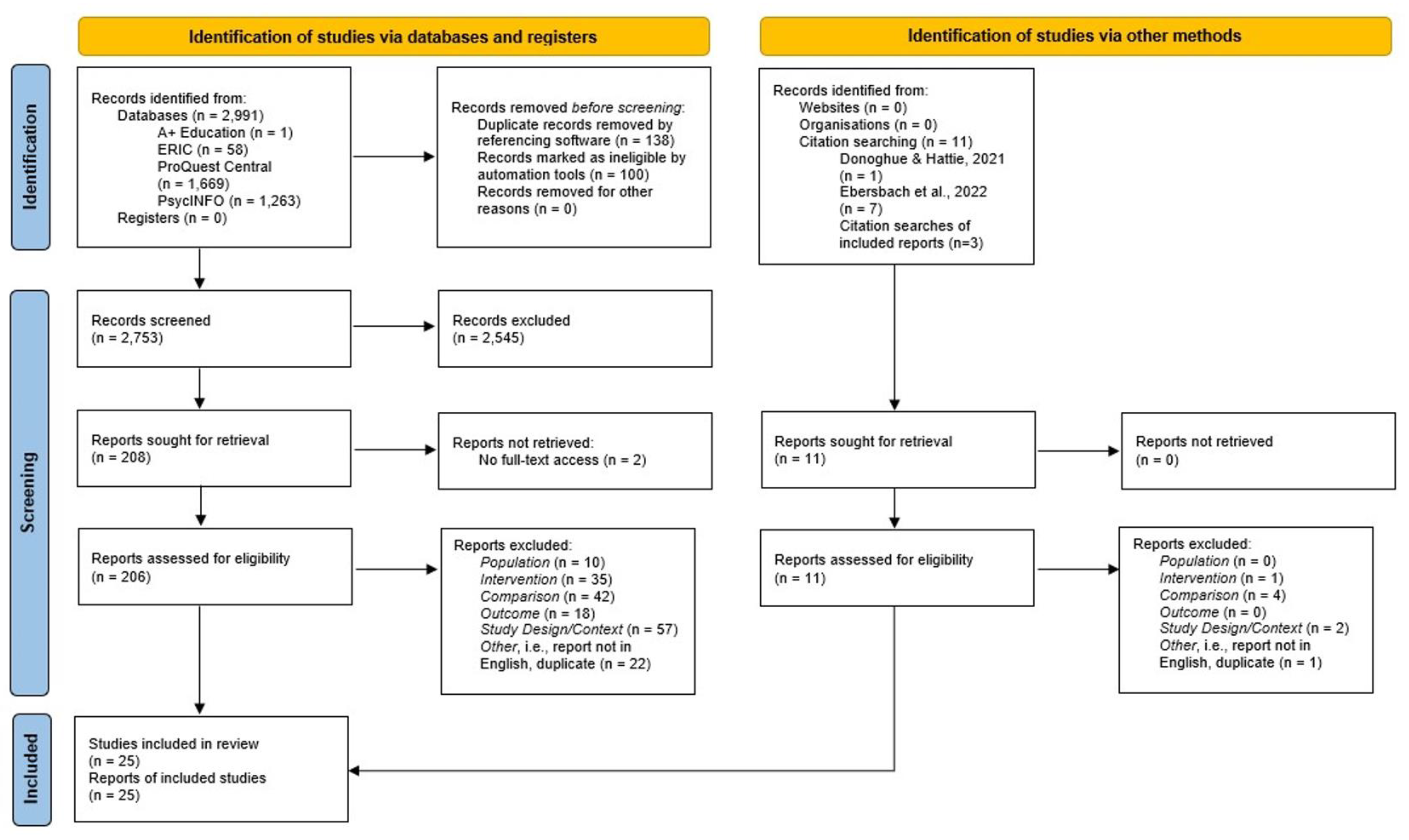
2.3. Selection Process
2.4. Data Items and Collection
2.5. Synthesis Methods
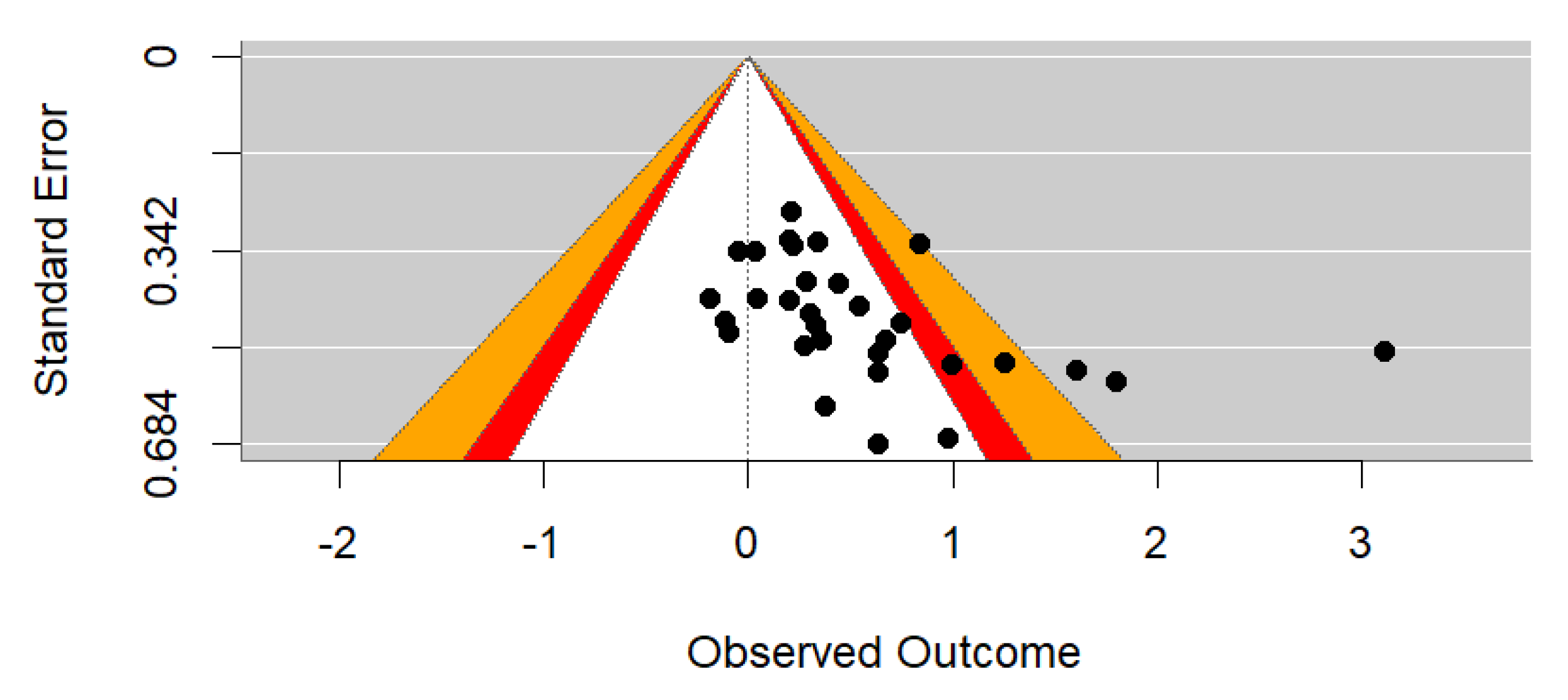
2.6. Bias and Certainty Assessment
3. Results
3.1. Screening
3.2. Included Studies
3.2.1. Included in Review
3.2.2. Included in Analysis
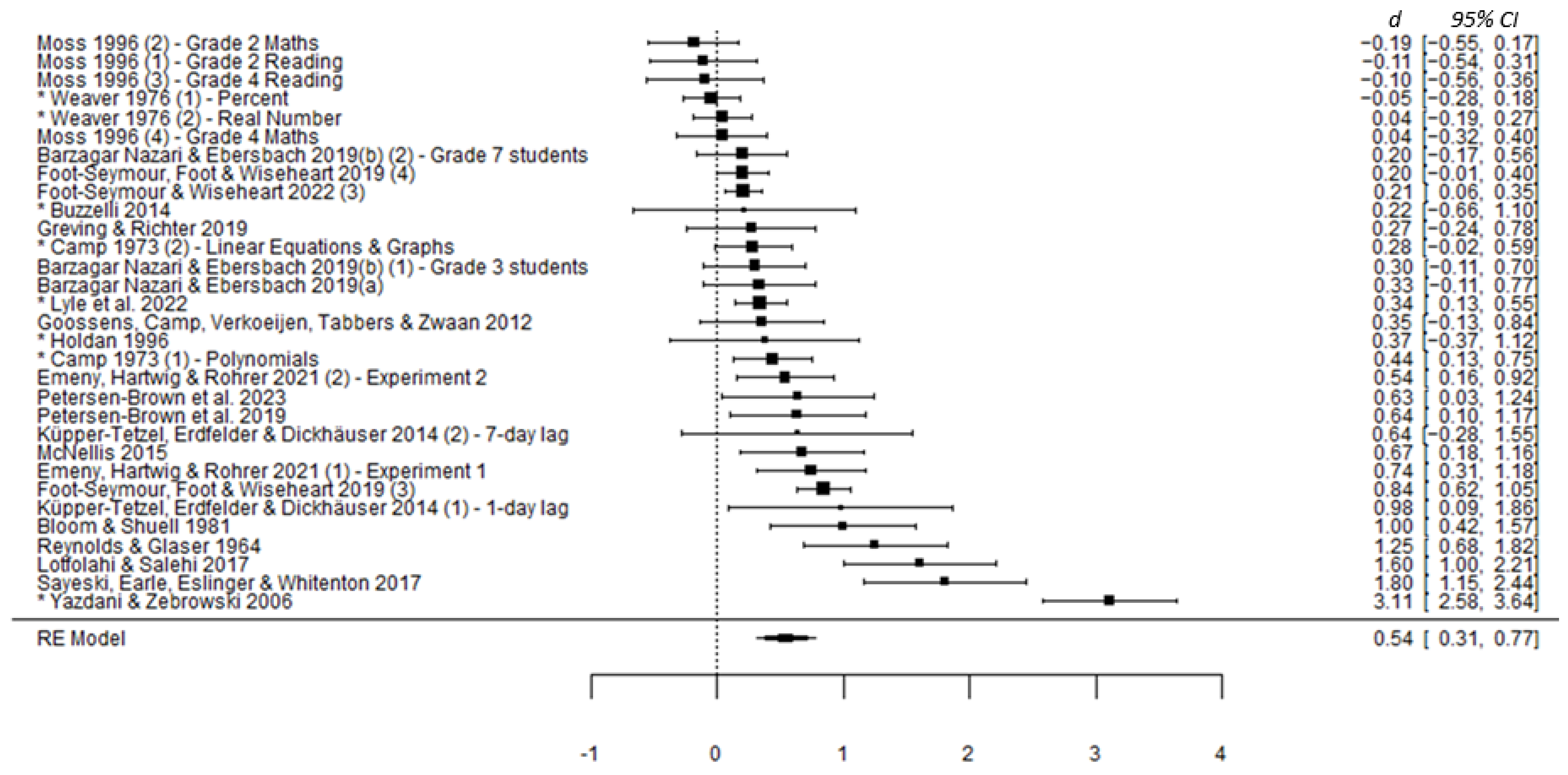
3.3. Synthesis
3.3.1. Preliminary Analysis
3.3.2. Main Analysis
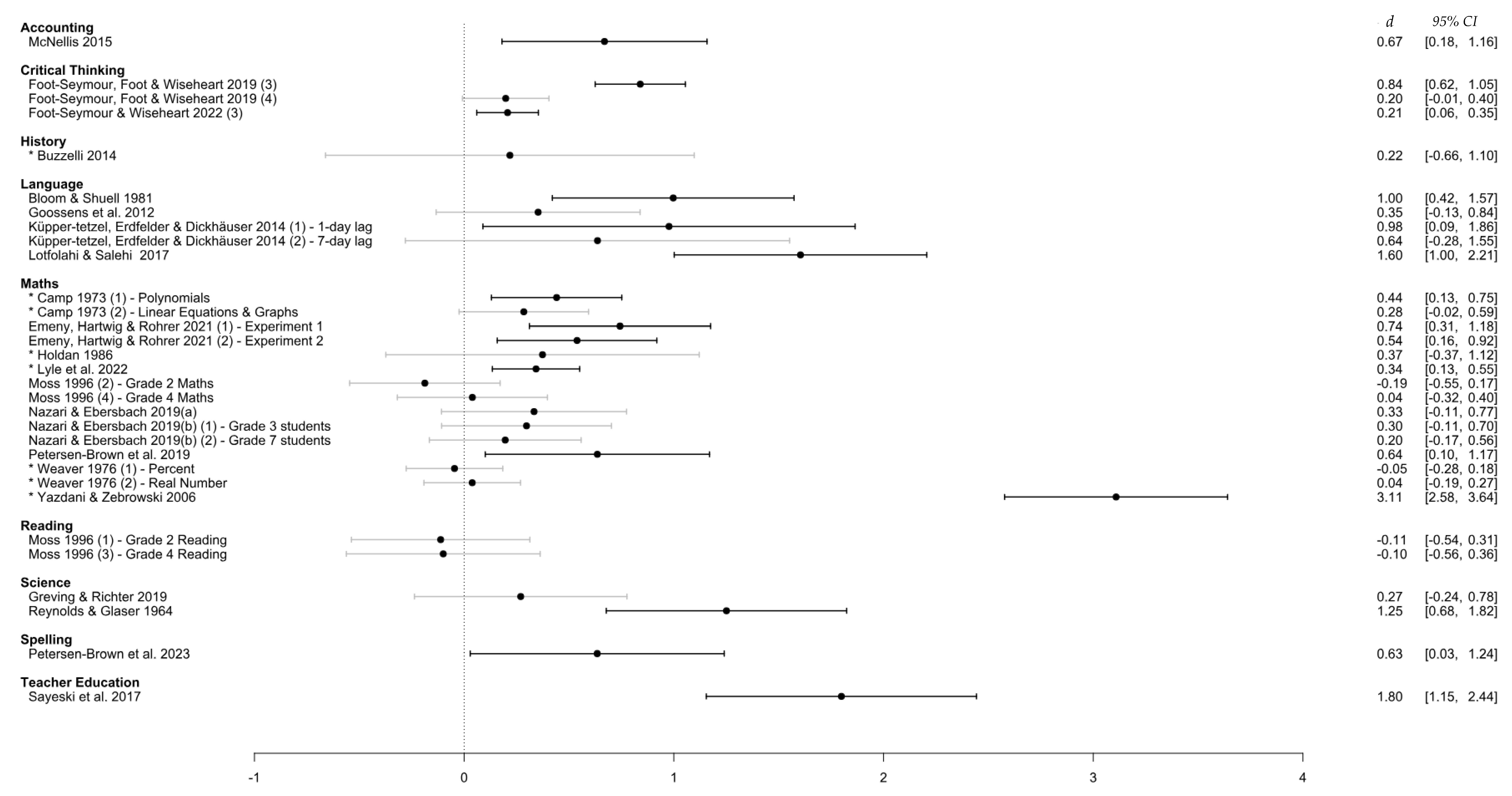
3.3.3. Moderator Analysis
3.4. Key Variables
3.4.1. Learning Domain
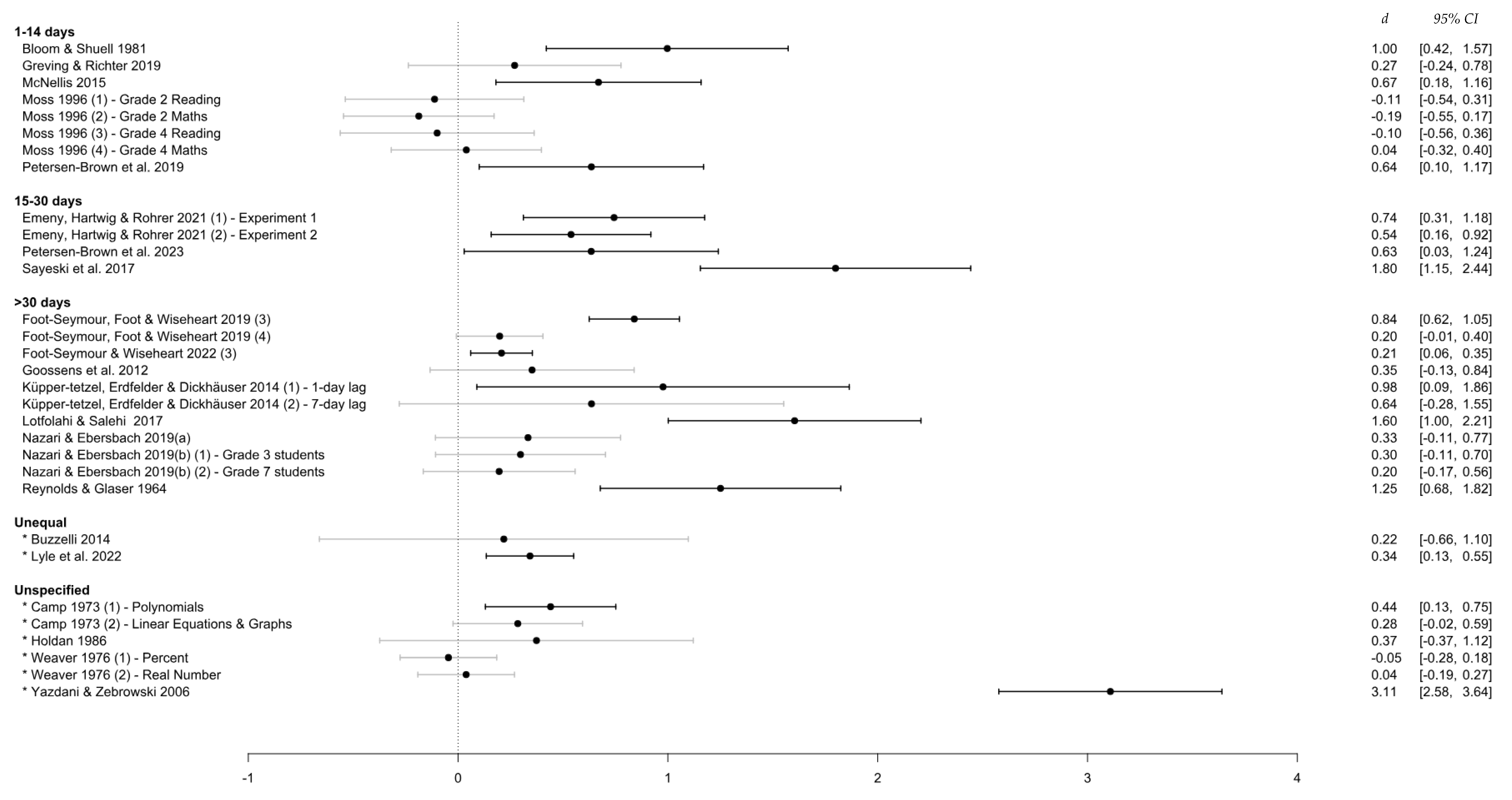
3.4.2. Retention Interval
3.4.3. Interstudy Interval
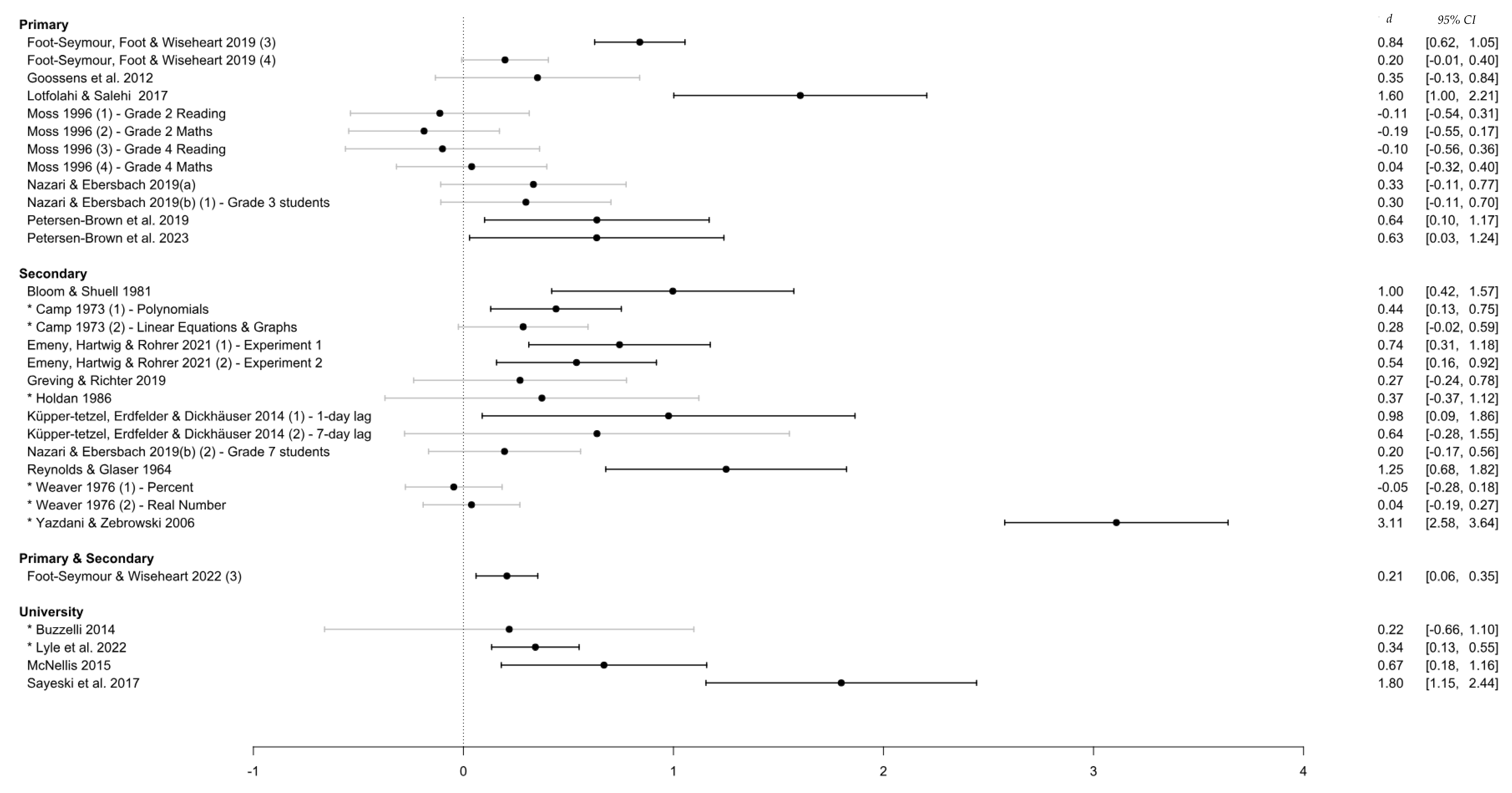
3.4.4. Education Level
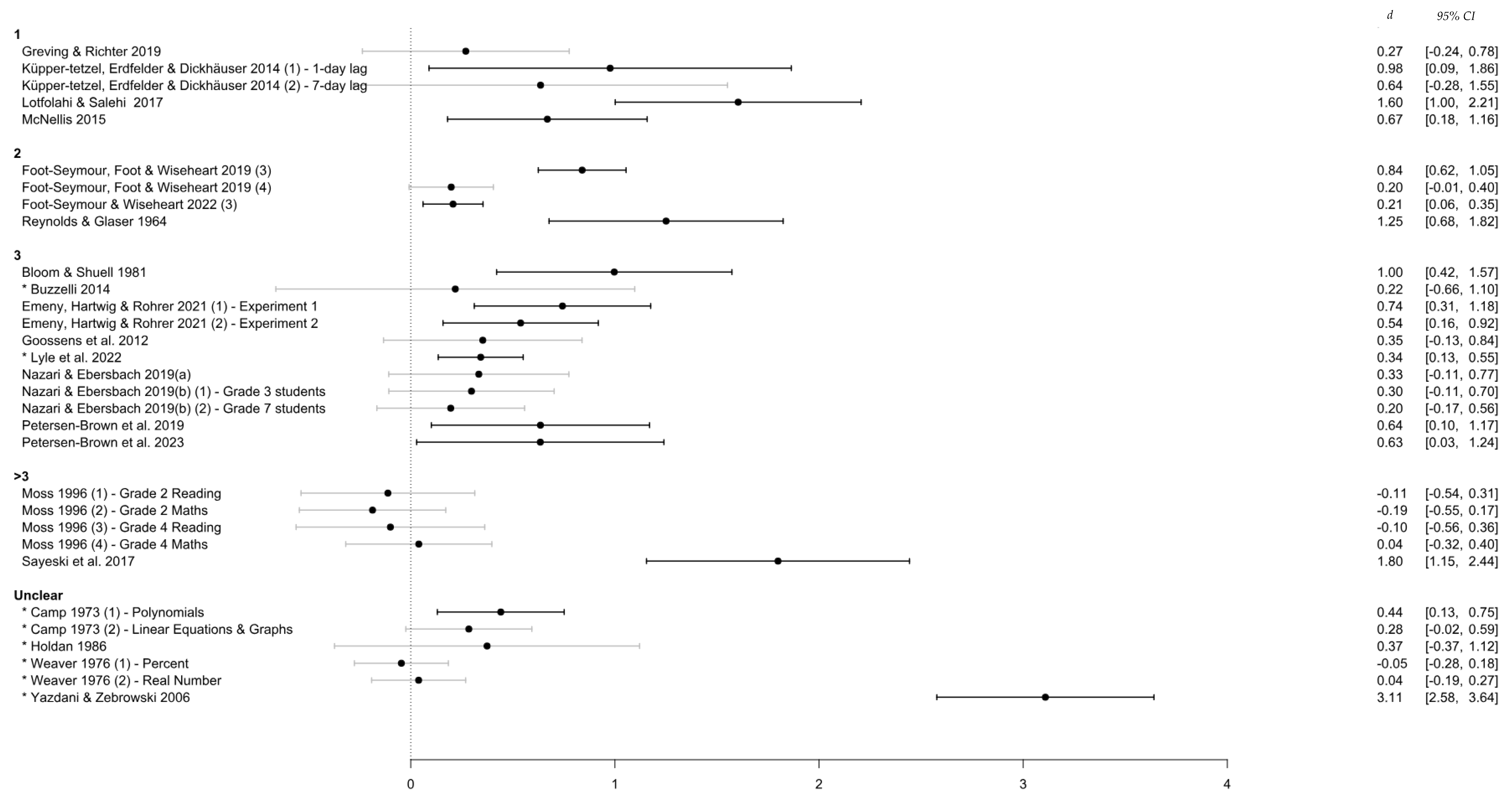
3.4.5. Number of Re-Exposures
3.5. Key Themes
3.5.1. The ‘Practice’ in Distributed Practice
3.5.2. Feedback in Practice and the Role of Technology
3.5.3. Distributed Practice as a Teaching or Learning Strategy?
4. Discussion
4.1. The Overall Effect
4.2. Timing as a Factor
4.3. Learning Domain and Level
4.4. Limitations
4.5. Implications
4.5.1. Educational Implications
4.5.2. Research Implications
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Database | Search Syntax | Search Fields |
|---|---|---|
| A+ Education (Informit) | (“spacing effect” OR “distribut* practi?e”~1 OR “spac* practi?e”~1 OR “mass* practi?e”~1 OR “distribut* learn*”~1 OR “spac* learn*”~1 OR “mass* learn*”~1) AND (class* OR stud* OR learn OR appli*) | Default |
| ERIC | (“spacing effect” OR “(distribut* OR spac* OR mass*) N/1 practi#e” OR “(distribut* OR spac* OR mass*) N/1 learn*”) AND (class* OR stud* OR appli*) | Default (All Fields+ text) |
| PsycINFO (Ovid) | ((spacing effect or ((distribut* or spac* or mass*) adj practi#e) or ((distribut* or spac* or mass*) adj learn*)) and (class* or stud* or appli*)) | Default (Title, Abstract, Heading Word, Table of Contents, Key Concepts, Original Title, Tests & Measures, Mesh Word) |
| ProQuest Central (ProQuest) | (“spacing effect” OR “(distribut* OR spac* OR mass*) N/1 practi#e” OR “(distribut* OR spac* OR mass*) N/1 learn*”) AND (class* OR stud* OR appli*) | Default (All Fields+ text) |
References
- Agarwal, P. K., Nunes, L. D., & Blunt, J. R. (2021). Retrieval practice consistently benefits student learning: A systematic review of applied research in schools and classrooms. Educational Psychology Review, 33(4), 1409–1453. [Google Scholar] [CrossRef]
- Anderson, J., & Boyle, C. (2015). Inclusive education in Australia: Rhetoric, reality and the road ahead. Support for Learning, 30(1), 4–22. [Google Scholar] [CrossRef]
- Australian Curriculum Assessment and Reporting Authority. (n.d.). F-10 curriculum: Mathematics—Key ideas. Available online: https://www.australiancurriculum.edu.au/f-10-curriculum/mathematics/key-ideas/ (accessed on 1 October 2023).
- * Barzagar Nazari, K., & Ebersbach, M. (2018). Distributed practice: Rarely realized in self-regulated mathematical learning. Frontiers in Psychology, 9, 2170. [Google Scholar] [CrossRef]
- * Barzagar Nazari, K., & Ebersbach, M. (2019a). Distributed practice in mathematics: Recommendable especially for students on a medium performance level? Trends in Neuroscience and Education, 17, 100122. [Google Scholar] [CrossRef]
- * Barzagar Nazari, K., & Ebersbach, M. (2019b). Distributing mathematical practice of third and seventh graders: Applicability of the spacing effect in the classroom. Applied Cognitive Psychology, 33(2), 288–298. [Google Scholar] [CrossRef]
- Benson, W. L., Dunning, J. P., & Barber, D. (2022). Using distributed practice to improve students’ attitudes and performance in statistics. Teaching of Psychology, 49(1), 64–70. [Google Scholar] [CrossRef]
- Berliner, D. C. (2002). Comment: Educational research: The hardest science of all. Educational Researcher, 31(8), 18–20. [Google Scholar] [CrossRef]
- Bjork, E. L., & Bjork, R. A. (2011). Making things hard on yourself, but in a good way: Creating desirable difficulties to enhance learning. In M. A. Gernsbacher, R. W. Pew, & J. R. Pomerantz (Eds.), Psychology and the real world: Essays illustrating fundamental contributions to society (pp. 55–64). Worth Publishers. [Google Scholar]
- * Bloom, K. C., & Shuell, T. J. (1981). Effects of massed and distributed practice on the learning and retention of second-language vocabulary. The Journal of Educational Research, 74(4), 245–248. [Google Scholar] [CrossRef]
- Breckwoldt, J., Ludwig, J. R., Plener, J., Schroder, T., Gruber, H., Peters, H., Breckwoldt, J., Ludwig, J. R., Plener, J., Schroder, T., Gruber, H., & Peters, H. (2016). Differences in procedural knowledge after a “spaced” and a “massed” version of an intensive course in emergency medicine, investigating a very short spacing interval. BMC Medical Education, 16, 249. [Google Scholar] [CrossRef]
- * Buzzelli, A. A. (2014). Twitter in the classroom: Determining the effectiveness of utilizing a microblog for distributed practice in concept learning [Doctoral dissertation, Robert Morris University]. [Google Scholar]
- * Camp, J. S. (1973). The effects of distributed practice upon learning and retention in introductory algebra. Dissertation Abstracts International Section A: Humanities and Social Sciences, 34(5-A), 2455–2456. [Google Scholar]
- Cepeda, N. J., Coburn, N., Rohrer, D., Wixted, J. T., Mozer, M. C., & Pashler, H. (2009). Optimizing distributed practice: Theoretical analysis and practical implications. Experimental Psychology, 56(4), 236–246. [Google Scholar] [CrossRef] [PubMed]
- Cepeda, N. J., Pashler, H., Vul, E., Wixted, J. T., & Rohrer, D. (2006). Distributed practice in verbal recall tasks: A review and quantitative synthesis. Psychological Bulletin, 132(3), 354–380. [Google Scholar] [CrossRef]
- Cepeda, N. J., Vul, E., Rohrer, D., Wixted, J. T., & Pashler, H. (2008). Spacing effects in learning: A temporal ridgeline of optimal retention. Psychological Science, 19(11), 1095–1102. [Google Scholar] [CrossRef] [PubMed]
- Deeks, J. J., Higgins, J. P. T., & Altman, D. G. (2023). Chapter 10: Analysing data and undertaking meta-analyses. In J. P. T. Higgins, & J. Thomas (Eds.), Cochrane handbook for systematic reviews of intervention (version 6.4). Cochrane. Available online: https://training.cochrane.org/handbook/current (accessed on 2 June 2023).
- Dempster, F. N. (1988). The spacing effect: A case study in the failure to apply the results of psychological research. American Psychologist, 43(8), 627–634. [Google Scholar] [CrossRef]
- Department of Education and Training. (2020). High impact teaching strategies: Excellence in teaching and learning. Available online: https://www.education.vic.gov.au/school/teachers/teachingresources/practice/improve/Pages/hits.aspx (accessed on 12 April 2023).
- Donoghue, G. M., & Hattie, J. A. C. (2021). A meta-analysis of ten learning techniques. Frontiers in Education, 6, 581216. [Google Scholar] [CrossRef]
- Donovan, J. J., & Radosevich, D. J. (1999). A meta-analytic review of the distribution of practice effect: Now you see it, now you don’t. Journal of Applied Psychology, 84(5), 795–805. [Google Scholar] [CrossRef]
- Dunlosky, J., & Rawson, K. A. (2015). Practice tests, spaced practice, and successive relearning: Tips for classroom use and for guiding students’ learning. Scholarship of Teaching and Learning in Psychology, 1(1), 72–78. [Google Scholar] [CrossRef]
- Dunlosky, J., Rawson, K. A., Marsh, E. J., Nathan, M. J., & Willingham, D. T. (2013). Improving students’ learning with effective learning techniques: Promising directions from cognitive and educational psychology. Psychological Science in the Public Interest, 14(1), 4–58. [Google Scholar] [CrossRef]
- Ebbinghaus, H. (1885/1913). Memory: A contribution to experimental psychology. Teachers College, Columbia University. [Google Scholar]
- * Ebersbach, M., & Barzagar Nazari, K. (2020). Implementing distributed practice in statistics courses: Benefits for retention and transfer. Journal of Applied Research in Memory and Cognition, 9(4), 532–541. [Google Scholar] [CrossRef]
- Ebersbach, M., Lachner, A., Scheiter, K., & Richter, T. (2022). Using spacing to promote lasting learning in educational contexts. Zeitschrift für Entwicklungspsychologie und Pädagogische Psychologie, 54(4), 151–163. [Google Scholar] [CrossRef]
- * Emeny, W. G., Hartwig, M. K., & Rohrer, D. (2021). Spaced mathematics practice improves test scores and reduces overconfidence. Applied Cognitive Psychology, 35(4), 1082–1089. [Google Scholar] [CrossRef]
- * Foot-Seymour, V., Foot, J., & Wiseheart, M. (2019). Judging credibility: Can spaced lessons help students think more critically online? Applied Cognitive Psychology, 33(6), 1032–1043. [Google Scholar] [CrossRef]
- * Foot-Seymour, V., & Wiseheart, M. (2022). Judging the credibility of websites: An effectiveness trial of the spacing effect in the elementary classroom. Cognitive Research: Principles and Implications, 7, 5. [Google Scholar] [CrossRef]
- Foster, N. L., Mueller, M. L., Was, C., Rawson, K. A., & Dunlosky, J. (2019). Why does interleaving improve math learning? The contributions of discriminative contrast and distributed practice. Memory & Cognition, 47, 1088–1101. [Google Scholar]
- Gerbier, E., & Toppino, T. C. (2015). The effect of distributed practice: Neuroscience, cognition, and education. Trends in Neuroscience and Education, 4(3), 49–59. [Google Scholar] [CrossRef]
- Gjerde, V., Vegard Havre, P., Holst, B., & Kolstø, S. D. (2022). Problem solving in basic physics: Effective self-explanations based on four elements with support from retrieval practice. Physical Review Physics Education Research, 18(1), 010136. [Google Scholar] [CrossRef]
- * Goossens, N. A., Camp, G., Verkoeijen, P. P., Tabbers, H. K., & Zwaan, R. A. (2012). Spreading the words: A spacing effect in vocabulary learning. Journal of Cognitive Psychology, 24(8), 965–971. [Google Scholar] [CrossRef]
- * Greving, C. E., & Richter, T. (2019). Distributed learning in the classroom: Effects of rereading schedules depend on time of test. Frontiers in Psychology, 9, 2517. [Google Scholar] [CrossRef]
- Greving, C. E., & Richter, T. (2021). Beyond the distributed practice effect: Is distributed learning also effective for learning with non-repeated text materials? Frontiers in Psychology, 12, 685245. [Google Scholar] [CrossRef]
- * Grote, M. G. (1995). Distributed versus massed practice in high school physics. School Science and Mathematics, 95(2), 97–101. [Google Scholar] [CrossRef]
- Gurung, R. A. R., & Burns, K. (2019). Putting evidence-based claims to the test: A multi-site classroom study of retrieval practice and spaced practice. Applied Cognitive Psychology, 33(5), 732–743. [Google Scholar] [CrossRef]
- Hattie, J. A. C., & Donoghue, G. M. (2016). Learning strategies: A synthesis and conceptual model. npj Science of Learning, 1, 16013. [Google Scholar] [CrossRef] [PubMed]
- Higgins, J. P. T., Li, T., & Deeks, J. J. (2023). Choosing effect measures and computing estimates of effect. In J. P. T. Higgins, & J. Thomas (Eds.), Cochrane handbook for systematic reviews of intervention (version 6.4). Cochrane. Available online: https://training.cochrane.org/handbook/current (accessed on 2 June 2023).
- * Holdan, E. G. (1986). A comparison of the effects of traditional, exploratory, distributed, and a combination of distributed and exploratory practice on initial learning, transfer, and retention of verbal problem types in first-year algebra. Dissertation Abstracts International Section A: Humanities and Social Sciences, 46(9-A), 2542. Available online: http://ovidsp.ovid.com/ovidweb.cgi?T=JS&PAGE=reference&D=psyc2&NEWS=N&AN=1986-55259-001 (accessed on 16 May 2023).
- Janiszewski, C., Noel, H., & Sawyer, A. G. (2003). A meta-analysis of the spacing effect in verbal learning: Implications for research on advertising repetition and consumer memory. Journal of Consumer Research, 30(1), 138–149. [Google Scholar] [CrossRef]
- Kang, S. H. K. (2016). Spaced repetition promotes efficient and effective learning. Policy Insights from the Behavioral and Brain Sciences, 3(1), 12–19. [Google Scholar] [CrossRef]
- Kapler, I. V., Weston, T., & Wiseheart, M. (2015). Spacing in a simulated undergraduate classroom: Long-term benefits for factual and higher-level learning. Learning and Instruction, 36, 38–45. [Google Scholar] [CrossRef]
- * Küpper-tetzel, C. E., Erdfelder, E., & Dickhäuser, O. (2014). The lag effect in secondary school classrooms: Enhancing students’ memory for vocabulary. Instructional Science, 42(3), 373–388. [Google Scholar] [CrossRef]
- Lakens, D. (2013). Calculating and reporting effect sizes to facilitate cumulative science: A practical primer for t-tests and ANOVAs. Frontiers in Psychology, 4, 863. [Google Scholar] [CrossRef]
- Lee, T. D., & Genovese, E. D. (1988). Distribution of practice in motor skill acquisition: Learning and performance effects reconsidered. Research Quarterly for Exercise and Sport, 59(4), 277–287. [Google Scholar] [CrossRef]
- Lindsey, R. V., Shroyer, J. D., Pashler, H., & Mozer, M. C. (2014). Improving students’ long-term knowledge retention through personalized review. Psychological Science, 25(3), 639–647. [Google Scholar] [CrossRef]
- Lonergan, R., Cumming, T. M., & O’Neill, S. C. (2022). Exploring the efficacy of problem-based learning in diverse secondary school classrooms: Characteristics and goals of problem-based learning. International Journal of Educational Research, 112, 101945. [Google Scholar] [CrossRef]
- * Lotfolahi, A. R., & Salehi, H. (2017). Spacing effects in vocabulary learning: Young EFL learners in focus. Cogent Education, 4(1), 1287391. [Google Scholar] [CrossRef]
- Lyle, K. B., Bego, C. R., Hopkins, R. F., Hieb, J. L., & Ralston, P. A. S. (2019). How the amount and spacing of retrieval practice affect the short-and long-term retention of mathematics knowledge. Educational Psychology Review, 32(1), 277–295. [Google Scholar] [CrossRef]
- * Lyle, K. B., Bego, C. R., Ralston, P. A., & Immekus, J. C. (2022). Spaced retrieval practice imposes desirable difficulty in calculus learning. Educational Psychology Review, 34(3), 1799–1812. [Google Scholar] [CrossRef]
- Maddox, G. B. (2016). Understanding the underlying mechanism of the spacing effect in verbal learning: A case for encoding variability and study-phase retrieval. Journal of Cognitive Psychology, 28(6), 684–706. [Google Scholar] [CrossRef]
- * McNellis, C. J. (2015). Re-conceptualizing instruction on the statement of cash flows: The impact of different teaching methods on intermediate accounting students’ learning. Advances in Accounting Education, 17, 115–144. [Google Scholar]
- Microsoft Corporation. (2023). Microsoft excel. (Version 2032). Microsoft Corporation. [Google Scholar]
- * Moss, V. D. (1996). The efficacy of massed versus distributed practice as a function of desired learning outcomes and grade level of the student. Dissertation Abstracts International Section B: The Sciences and Engineering, 56(9-B), 5204. Available online: http://ovidsp.ovid.com/ovidweb.cgi?T=JS&PAGE=reference&D=psyc3&NEWS=N&AN=1996-95005-375 (accessed on 16 May 2023).
- Namaziandost, E., Murad Hassan Mohammed, S., & Masoumeh Izadpanah, S. (2020). The effects of spaced versus massed distribution instruction on EFL learners’ vocabulary recall and retention. Cogent Education, 7(1), 1792261. [Google Scholar] [CrossRef]
- Namaziandost, E., Nasri, M., Fariba Rahimi, E., & Mohammad Hossein, K. (2019). The impacts of spaced and massed distribution instruction on EFL learners’ vocabulary learning. Cogent Education, 6(1), 1661131. [Google Scholar] [CrossRef]
- Namaziandost, E., Razmi, M. H., Atabekova, A., Shoustikova, T., & Kussanova, B. H. (2023). An account of Iranian intermediate EFL learners’ vocabulary retention and recall through spaced and massed distribution instructions. Journal of Education, 203(2), 275–284. [Google Scholar] [CrossRef]
- Page, M. J., McKenzie, J. E., Bossuyt, P. M., Boutron, I., Hoffmann, T. C., Mulrow, C. D., Shamseer, L., Tetzlaff, J. M., Akl, E. A., Brennan, S. E., Chou, R., Glanville, J., Grimshaw, J. M., Hrobjartsson, A., Lalu, M. M., Li, T., Loder, E. W., Mayo-Wilson, E., McDonald, S., … Moher, D. (2021). The PRISMA 2020 statement: An updated guideline for reporting systematic reviews. BMJ, 372, 71. [Google Scholar] [CrossRef] [PubMed]
- Pappas, M. L. (2009). Inquiry and 21st-century learning. School Library Monthly, 25(9), 49–51. [Google Scholar]
- Peters, J. L., Sutton, A. J., Jones, D. R., Abrams, K. R., & Rushton, L. (2008). Contourenhanced meta-analysis funnel plots help distinguish publication bias from other causes of asymmetry. Journal of Clinical Epidemiology, 61(10), 991–996. [Google Scholar] [CrossRef]
- * Petersen-Brown, S., Lundberg, A. R., Ray, J. E., Dela Paz, I. N., Riss, C. L., & Panahon, C. J. (2019). Applying spaced practice in the schools to teach math vocabulary. Psychology in the Schools, 56(6), 977–991. [Google Scholar] [CrossRef]
- * Petersen-Brown, S., Riese, A. M., Schneider, M. M., Ray, J. E., & Clonkey, H. R. (2023). Applying distributed practice in the schools to enhance retention of spelling words. Psychology in the Schools, 60(9), 3486–3503. [Google Scholar] [CrossRef]
- Pomerance, L., Greenberg, J., & Walsh, K. (2016). Learning about learning: What every new teacher needs to know. National Centre on Teacher Quality. Available online: https://www.nctq.org/publications/Learning-About-Learning:-What-Every-New-Teacher-Needs-to-Know (accessed on 12 April 2023).
- R Core Team. (2023). R: A language and environment for statistical computing. R Foundation for Statistical Computing. Available online: https://www.R-project.org/ (accessed on 20 April 2023).
- * Reynolds, J. H., & Glaser, R. (1964). Effects of repetition and spaced review upon retention of a complex learning task. Journal of Educational Psychology, 55(5), 297–308. [Google Scholar] [CrossRef]
- Robinson, A. G. (1979). A compared difference in pupil performance as a function of teacher presented material (1-1), peer (cross-age) presented material, teacher presented material (1-5), and massed and spaced scheduling of instruction. Dissertation Abstracts International Section A: Humanities and Social Sciences, 39(11-A), 6701–6702. Available online: http://ovidsp.ovid.com/ovidweb.cgi?T=JS&PAGE=reference&D=psyc2&NEWS=N&AN=1980-51592-001 (accessed on 16 May 2023).
- Rohrer, D., & Pashler, H. (2010). Recent research on human learning challenges conventional instructional strategies. Educational Researcher, 39(5), 406–412. [Google Scholar] [CrossRef]
- Saavedra, A. R., & Opfer, V. D. (2012). Learning 21st-century skills requires 21st-century teaching. The Phi Delta Kappan, 94(2), 8–13. [Google Scholar] [CrossRef]
- * Sayeski, K. L., Earle, G. A., Eslinger, R., & Whitenton, J. N. (2017). Teacher candidates’ mastery of phoneme-grapheme correspondence: Massed versus distributed practice in teacher education. Bulletin of the Orton Society, 67(1), 26–41. [Google Scholar] [CrossRef]
- Schopfel, J., & Rasuli, B. (2018). Are electronic theses and dissertations (still) grey literature in the digital age? A FAIR debate. The Electronic Library, 36(2), 208–219. [Google Scholar] [CrossRef]
- Sobel, H. S., Cepeda, N. J., & Kapler, I. V. (2011). Spacing effects in real-world classroom vocabulary learning. Applied Cognitive Psychology, 25(5), 763–767. [Google Scholar] [CrossRef]
- Sterne, J. A., Sutton, A. J., Ioannidis, J. P., Terrin, N., Jones, D. R., Lau, J., Carpenter, J., Rucker, G., Harbord, R. M., Schmid, C. H., Tetzlaff, J., Deeks, J. J., Peters, J., Macaskill, P., Schwarzer, G., Duval, S., Altman, D. G., Moher, D., & Higgins, J. P. (2011). Recommendations for examining and interpreting funnel plot asymmetry in meta-analyses of randomised controlled trials. BMJ, 343, d4002. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, Y., & Dekeyser, R. (2017). Exploratory research on second language practice distribution: An Aptitude × Treatment interaction. Applied Psycholinguistics, 38(1), 27–56. [Google Scholar] [CrossRef]
- Svihla, V., Wester, M. J., & Linn, M. C. (2017). Distributed practice in classroom inquiry science learning. Learning: Research and Practice, 4(2), 180–202. [Google Scholar] [CrossRef]
- Sweller, J. (2010). Cognitive load theory: Recent theoretical advances. In J. L. Plass, R. Brünken, & R. Moreno (Eds.), Cognitive load theory (pp. 29–47). Cambridge University Press. [Google Scholar]
- Taylor, K., & Rohrer, D. (2010). The effects of interleaved practice. Applied Cognitive Psychology, 24(6), 837–848. [Google Scholar] [CrossRef]
- The EndNote Team. (2023). EndNote. (Version 20.6). Clarivate. [Google Scholar]
- van Merrienboer, J. J. G., Kirschner, P. A., & Kester, L. (2003). Taking the load off a learner’s mind: Instructional design for complex learning. Educational Psychologist, 38(1), 5–13. [Google Scholar] [CrossRef]
- Viechtbauer, W. (2010). Conducting meta-analyses in {R} with the {metafor} package. Journal of Statistical Software, 36(3), 1–48. [Google Scholar] [CrossRef]
- * Weaver, J. R. (1976). The relative effects of massed versus distributed practice upon the learning and retention of eighth grade mathematics. Dissertation Abstracts International Section A: Humanities and Social Sciences, 37(5-A), 2698. [Google Scholar]
- Wilson, D. B. (n.d.). Practical meta-analysis effect size calculator. Available online: https://campbellcollaboration.org/research-resources/effect-size-calculator.html (accessed on 16 June 2023).
- Wiseheart, M., Küpper-Tetzel, C. E., Weston, T., Kim, A. S. N., Kapler, I. V., & Foot-Seymour, V. (2019). Enhancing the quality of student learning using distributed practice. In J. Dunlosky, & K. A. Rawson (Eds.), The Cambridge handbook of cognition and education (pp. 550–584). Cambridge University Press. [Google Scholar]
- * Yazdani, M., & Zebrowski, E. (2006). Spaced reinforcement: An effective approach to enhance the achievement in plane geometry. Journal of Mathematical Sciences and Mathematics Education, 1, 37–43. [Google Scholar]
- Ysseldyke, J. E., & Pickholtz, H. (1975). Dissertation research in school psychology: 1967–73. Journal of School Psychology, 13(3), 264–271. [Google Scholar] [CrossRef]

| Inclusion | Exclusion | |
|---|---|---|
| Population | Study participants enrolled in primary, secondary, or tertiary education | Participants drawn exclusively from special populations (e.g., autistic, intellectual disability, etc.) |
| Intervention | Distributed or spaced practice with interstudy intervals of at least 1 day | Interstudy intervals of less than 1 day |
| Comparison | Massed practice conditions with time spent studying equal to that of spaced practice conditions | Comparison to other learning strategies |
| Outcomes | Measures of retention (e.g., percentage correctly recalled) or transfer of information learnt (e.g., percentage correctly applied). Where retention was measured more than once, data were extracted from the longest retention interval measured in both the comparison and intervention conditions | Qualitative outcomes (e.g., teacher and/or student perceptions of effectiveness) |
| Study design and context | Studies conducted in the classroom using classroom-relevant learning materials | Studies using learning materials with no clear connections to specific syllabi or curriculum |
| Analysis | Potential Data Inaccuracies | Studies | Effect Sizes | Effect Size [95% CI] | I2 (%) | |
|---|---|---|---|---|---|---|
| Unequal Retention Intervals | Non-Independent Effect Sizes | |||||
| 1 | Included | Included All | 22 | 31 | 0.54 [0.31, 0.77] | 92.13 |
| 2 | Included | Averaged | 22 | 25 | 0.63 [0.36, 0.89] | 94.93 |
| 3 | Excluded | Included All | 16 | 23 | 0.51 [0.31, 0.72] | 83.88 |
| 4 | Excluded | Averaged | 16 | 19 | 0.57 [0.36, 0.78] | 84.68 |
| Learning Domain | Effect Size [95% CI] |
|---|---|
| Accounting | 0.67 [0.18, 1.16] |
| Critical Thinking | 0.41 [0.00, 0.82] |
| History | 0.22 [0.00, 0.44] |
| Language | 0.91 [0.44, 1.3] |
| Math | 0.46 [0.09, 0.84] |
| Reading | −0.11 [−0.42, 0.21] |
| Science | 0.75 [−0.21, 1.71] |
| Spelling | 0.63 [0.03, 1.24] |
| Teacher Education | 1.80 [1.15, 2.44] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mawson, R.D.; Kang, S.H.K. The Distributed Practice Effect on Classroom Learning: A Meta-Analytic Review of Applied Research. Behav. Sci. 2025, 15, 771. https://doi.org/10.3390/bs15060771
Mawson RD, Kang SHK. The Distributed Practice Effect on Classroom Learning: A Meta-Analytic Review of Applied Research. Behavioral Sciences. 2025; 15(6):771. https://doi.org/10.3390/bs15060771
Chicago/Turabian StyleMawson, Rhys D., and Sean H. K. Kang. 2025. "The Distributed Practice Effect on Classroom Learning: A Meta-Analytic Review of Applied Research" Behavioral Sciences 15, no. 6: 771. https://doi.org/10.3390/bs15060771
APA StyleMawson, R. D., & Kang, S. H. K. (2025). The Distributed Practice Effect on Classroom Learning: A Meta-Analytic Review of Applied Research. Behavioral Sciences, 15(6), 771. https://doi.org/10.3390/bs15060771







