Few studies have examined the ability of children between the ages of three and five years old to solve fraction problems without formal instruction [
1]. Starting from birth, humans have the capacity to mentally discriminate between different numerosities, an ability known as our number sense [
2]. During development, number knowledge gives us an understanding of the cardinal principle, meaning that the final word in a count sequence represents the amount of the entire set. This understanding has been linked to more advanced ideas such as fairness and equivalence and some researchers believe these judgments could be a longitudinal predictor of how well a child performs in arithmetic [
3]. Thus, numerical knowledge is a critical cognitive milestone as it allows children to understand notions of fairness and equal sharing between one or more parties [
3]. In addition, cognitive development around this age also displays a corresponding protracted time course with fine motor development [
4]. Supporting research [
4,
5] proposes that these two facets of development are in some way intertwined. Furthermore, recent research supports an active sensorimotor system presence when working with numbers, suggesting a link between embodied cognition and mathematical reasoning [
6].
1.1. Development of Numerical and Arithmetical Skills
The approximate number system (ANS) model suggests that we are born with the tools (intuitions regarding numbers and sets) for number processing and that through the development of new symbol systems we can build upon our foundational system of number sense [
8]. Although a consensus of researchers agree on the notion of such system, it is still up for debate whether arithmetical ability arises from innate, specific cognitive skills or whether it is due to general cognitive abilities such as memory and reasoning. Authors such as Dehaene and Butterworth believe that it could be a result of our evolution, since animals such as parrots, dolphins, dogs, and monkeys can distinguish between different numerosities and even perform basic arithmetical operations. Perhaps the similarities seen between us and various animal species suggests that number approximation is a result of certain evolutionary pressures, resulting in the emergence of an internal brain system dedicated to rudimentary arithmetic.
Dehaene [
8] suggests that in order for us to acquire and represent information about numerical quantities, there must be a specific cerebral circuit that facilitates this processing. Studies using lesion methods often indicate the presence of a dedicated neural system for number sense, identifying the inferior parietal region as a significant node in the circuit of the number sense system [
8,
9]. This network might be present in both hemispheres of the intraparietal cortex and it is thought to be involved in mental manipulation of numerical quantities, since this region displays activation while an individual performs various number processing tasks [
2,
10].
Lesion studies also identify the angular gyrus as a critical brain region for normal arithmetical performance; and if this area or the intraparietal region is damaged, then one would show deficits in numerical processing and arithmetic [
8]. Specifically, damage to the inferior parietal region can result in impaired internal representations of quantities and an inability to comprehend the actual meaning of numbers [
8]. Additionally, research conducted on individuals with developmental dyscalculia, a disorder associated with difficulty in understanding number concepts, facts, and procedures, also supports Dehaene’s argument. Evidence shows that several forms of cognitive difficulties may interfere with mathematics performance, but they are not causal features in dyscalculia. These examples indicate an innate specific capacity for acquiring arithmetical skills rather than it being a learned process throughout the course of development.
Converging evidence presented by [
11] suggests that the strong association between number sense and perception and action supports the presence of a ‘sensorimotor numerosity system’ that resides in the parietal cortex. It is important to note the many similarities seen between these two systems pertaining to their proximity to each other and the large number of shared cortical regions during these two processes. This review provides examples of this interaction from neuroimaging studies, highlighting the parietal cortex to be active in both numerosity perception and action areas pertaining to eye and hand movements. We agree that in order to fully understand numerosity, it is critical to evaluate possible motor mechanisms involved in building foundational symbolic mathematical skills.
The ANS system gives us the ability to mentally represent numbers and recognize the magnitude of both symbolic (Arabic numerals, number words) and non-symbolic (unrelated dots patterns, random sticks patterns) numbers [
12]. As we get older, we develop strategies to use language and symbolization to understand and work with numbers [
12]. One strategy that has been extensively researched is the idea of a numerospatial “mental number line” that allows us to manipulate and calculate numbers in our head [
13]. This potentially inherited system represents the idea that the difference between two consecutive numbers is the same regardless of their positions on the number line [
14]. Because the mental number line helps put the weight of quantity onto an Arabic numeral, it seems to be vital for future arithmetical thinking and for calculating numbers in one’s head. With the use of language, the mental number line allows us to conceptualize numbers on a more abstract level by expanding the semantic range of the concept of number [
13]. In this sense, language allows ANS representations (e.g., “five” and 5) to be mapped onto exact symbolic representations, thus reinforcing the strength between Arabic numerals and number words [
2,
9].
We use our number sense as a fundamental parameter by which we make sense of our world [
8]. If this ability is compromised, then one could have trouble understanding and working with numbers later on. It is no surprise that having a solid foundational knowledge of mathematics is vital for future academic performance, careers, and managing day to day responsibilities such as balancing a check book. For these reasons, it is important to identify deficits early on and help educators come up with creative ways to help a child with a learning disability. However, knowing how to represent numbers does not necessarily give people the ability to solve complex, higher-order mathematics problems [
12]. In regard to arithmetic, it is still unclear whether we use numerical representations to manipulate numbers themselves; some researchers suggest that the ANS is active only at the early stages of our development [
12,
13].
Interestingly, the study by [
14] found that ANS acuity was a significant predictor of mathematics achievement at 5 years of age, but not at 7 years of age. Gimbert et al. [
15] suggests that a reason for this is that as mathematical thinking advances, children begin to rely less on their ANS and more on other cognitive mechanisms. The researchers suggest that after the ANS relationship is formed, working memory assumes a larger role in mathematical reasoning [
15]. Results from this study suggest that the age range between 5 and 7 may be an important transitional period where the brain seems to be switching gears from relying on ANS to working memory when working with numbers. Gimbert et al. [
15] suggests that a reason for this switch from the ANS to working memory is that after we learn the magnitude of numbers, we then learn how to manipulate them while keeping in mind arithmetical rules. The differences shown between these ages suggest specific developmental processes and important changes in cognition are happening that can potentially predict an individual’s success in learning mathematics [
15].
The study by Chu et al. [
14] found that preschool-aged children have capabilities for both numerical abstraction and numerical reasoning. Numerical abstraction (also known as enumeration) involves a set of cognitive skills that are used to acquire representations of numerosities of sets and these skills adhere to one-to-one correspondences [
14]. We use this when counting and two types of enumeration exist: subitizing and counting. Subitizing is rapid, precise, and accurate, and we use it when counting less than four items [
16]. Counting is more error prone and takes longer to process, 250–350 ms per item, rather than subitizing, 40–100 ms per item [
16]. Typically developing children as young as three years old have an understanding of small numerosities (up to four items) and know that counting is a way to find the total number of items in a set [
9]. Enumeration is thought to give young children the tools needed to form representations of numerical quantities and discriminate different sets of numbers from each other [
16].
1.2. Fractional Knowledge
In the initial stages of learning arithmetic, children are actively making use of their counting skills, which allows them to know that numbers have both a sequence and a numerosity (cardinal) meaning [
9]. Our knowledge of fractions begins with a whole-number bias that we learn through counting and sharing [
17]. Learning activities that include the number line are beneficial for teaching fraction concepts because it provides children with an integrated spatial structure to represent both whole and part number magnitudes [
18,
19] Theoretically, the mental number line should aid in our understanding fraction magnitude concepts because it draws on pre-existing associations between numerical magnitudes and spatial locations [
19]. In addition, it also helps students see that there are an infinite number of fractions lying between whole numbers [
18,
19]. As a result, activities that emphasize the importance of the number line when working with part–whole relationships can make it easier for students to critically think about proportions and the arithmetical relationships between two or more fractions [
19].
People use different strategies when working with fractions and a finding from Fazio et al. [
18] indicates that people with difficulties concerning fraction magnitude comparison showed both a lack of conceptual understanding of correct procedures and a failure to recall correct procedures. This lack of a conceptual understanding can hinder progression in mathematics and effects can last throughout adulthood [
18]. High-paying jobs in STEM exemplify this because they generally require an individual to have substantial competency in mathematics. Careers in engineering, software development, medicine, etc., all require an advanced level of proficiency in mathematics and many of the mathematical demands in these jobs are built upon fractions. These demands are omnipresent in higher-level fields of mathematics learned after fractions such as prealgebra, algebra, and trigonometry, so a solid base knowledge of these concepts is needed for success in these areas [
18]. Consequentially, but not surprisingly, adults lacking a strong fractional knowledge foundation are at a loss because attempts at working with equations in these areas without understanding the fractions involved would be futile [
18].
1.3. Executive Functioning
In the review by Cameron, Brock, Murrah, Bell, Worzalla, Grissmer, andand Morrison [
20], researchers state that it is important to consider the effects of executive functioning on aspects of academic performance. Executive functioning is defined as the higher-level cognitive processes that facilitate new ways of behaving and optimizes an individual’s approach to novel situations [
20]. This is essential to our understanding of mathematical cognition because executive functioning is often associated with mechanisms of working memory, in addition to problem solving, planning, and coordinating responses that require recall and organization of newly learned information in novel ways [
21].
Individuals with a deficiency in mathematics tend to have problems with acquiring the basic skills needed to solve arithmetic and more contextualized assignments such as word problems, especially when these students also have problems with reading [
22]. Low achievement in these areas often reflects the possible difficulties students with a learning disability in mathematics or reading have with memory and novel information processing [
10]. If there were deficits in working memory, then it would be especially difficult to learn arithmetic, primarily because working memory is responsible for short-term storage of information and allows us to hold that information in our mind and work with it [
23,
24]. Deficits in working memory (i.e., managing, storing, and integrating more than one set of information) are common in children with various learning disorders [
10].
Cognitive and metacognitive processes such as effectively processing, diagramming, and solving multistep mathematics equations are necessary when solving mathematics problems because they allow us to maintain and manipulate information while also keeping in mind the rules of arithmetic [
10]. In addition, research suggests that a higher executive functioning processing capacity overall would allow someone to learn concepts and pay attention in class more efficiently [
22]. This is significant especially in the classroom because behaviors that facilitate learning (following directions and sustaining attention) serve as the basis for excelling in the traditional school setting [
20].
Visual representations, such as diagrams, seem to help students better understand mathematical concepts [
25]. The use of diagrams has also been shown to be beneficial in managing, storing, and integrating information from math problems that require several steps [
25]. Furthermore, visuospatial capacities appear to be largely active when learning a new mathematical skill and applying it later [
25]. In regard to teaching mathematics, the use of visual representations can increase both mathematical understanding and processing of information, and therefore using these aides in a meaningful way can function as an instructional scaffolding strategy for students [
25].
1.4. Fine Motor Ability
Fine motor ability entails how we coordinate precise movements of small muscles in our hands through eye coordination [
20]. Without it, we would not be able to grasp a pencil, tie our shoelaces, or brush our teeth [
26]. The review by Cameron et al. [
20] indicates that fine motor activities play a significant role in the development of a child because they take up a substantial amount of a typical preschooler or kindergartener’s school day. For example, the researchers conducting this observational study of kindergarten classrooms found that 46% of the school day was devoted to fine motor activities. These activities included tasks such as writing, using scissors to cut paper, bean counting tasks, and playing with toys such as building blocks and Legos. Tests that are designed to evaluate fine motor ability commonly involve tasks with visual, cognitive, and manual dexterity demands (e.g., drawing a picture with a pencil) and also assesses an individual’s capability for understanding spatial organization (e.g., building with blocks) [
20].
Fine motor ability is controlled by the cerebral cortex, basal ganglia, and cerebellum [
26]. These areas are also increasingly being associated with mechanisms of executive functions such as working memory and general reasoning skills [
25]. The cerebellum is an example of this development, being traditionally thought to coordinate motor movements but is also increasingly associated with cognitive functions such as sustaining attention [
4]. For example, Diamond [
4] found the cerebellum to be the most active when an individual is presented with novel, cognitive tasks. In addition, one could also credit the cerebellum with a role in numerical cognition because children eventually learn about quantity through motor-based interactions with their environment; an example of this is pointing and counting on your fingers [
27].
The idea that the prefrontal cortex plays a role in both motor functions and cognitive functions is also gaining traction [
4]. The prefrontal cortex is most often implicated with executive functions; however, increasing data show that this might not be its only function [
4,
5]. Grissmer et al. [
5] suggests that it might also be involved in numerous other functions such as coordinating complex motor, emotional, or cognitive activities that requires action from several parts of the brain [
5]. Functional neuroimaging studies provide evidence that when a cognitive task is being performed, activation in the dorsolateral region of the prefrontal cortex increases along with the cerebellum [
4]. The primary motor cortex is also important because observations suggest that it becomes activated when solving numerical problems [
4]. In short, consistent evidence that displays activation in the motor areas of the brain has shown to be a significant indicator to understanding how we solve mathematics problems [
4,
6]. These findings add significance to the proposition that fine motor skills and cognitive abilities are more related than previously thought and even possibly intertwined.
1.5. Gestures and Counting
There is a large body of evidence showing that our fingers play a major role in counting and arithmetic [
28]. The act of using your fingers to count may play an essential role in learning the basics of numbers because when a child enters preschool, counting is typically taught by showing an explicit motor behavior where one is instructed to watch their fingers move while counting [
29]. This association extends beyond just learning how to count because children’s arithmetical skills are best predicted by how well they perform in finger discrimination task [
28,
29]. This could be viewed as a cognitive advantage because the act of using finger gestures is assumed to ground thought in action by reducing demands on working memory [
30]. Perhaps this reduction in cognitive workload allows the brain to multitask more efficiently, thus assisting mechanisms necessary for paying attention and participating in classroom instruction.
Numerous behavioral and neuroimaging studies have confirmed that mental arithmetic relies on pre-existing representations in the sensorimotor system. However, many questions remain. One association still open to interpretation regards the possible overlap between brain areas involved in mental arithmetic and those involved in finger discrimination. Many researchers agree that perhaps fingers constitute a useful means for obtaining and communicating arithmetic knowledge because they offer a physical counterpart for mental operations. Whichever the case, it is widely agreed that these fine motor systems give us the essential motor skills to solve mathematics problems in school and these associations typically extend into adulthood.
Gesturing during mathematics instruction can help students better retain concepts because it can contribute representational, supplemental information that may not be conveyed by verbal language alone [
20,
31]. Interestingly, a growing amount of research suggests that mathematical processes are supported by the sensorimotor system [
29]. Future examination of the neural systems involved when an individual solves mathematical problems is necessary because more data are needed to prove that a dedicated sensorimotor circuit is in place and is active when we work with mathematical concepts [
29].
The studies by Susan Goldin-Meadow imply that the use of hand gestures during math instruction can facilitate learning [
30,
31]. These studies indicate that the use of gestures can reflect an individual’s cognitive state and perhaps can play a causal role in learning mathematics [
25,
32]. In order to distinguish this from a correlational to a causal relationship, the use of gesture can be manipulated in studies when instructing children to use or restrict gestures while solving math problems [
25]. Perhaps gesturing plays a role in memory and learning in both children and adults because they can aid in retaining knowledge in a way that decreases demands on working memory, freeing up cognitive resources that can be used elsewhere [
31]. This finding is especially beneficial to children with a learning disability in mathematics because representational gestures have been associated with learning when solving math problems. These children often struggle with working memory, so encouraging the use of gestures during math instruction may be a helpful intervention to decrease cognitive load and facilitate learning by helping children extract information from their own hand movements during counting tasks [
31].
1.6. Fine Motor Skills and Cognitive Development
Previous literature has also shown that fine motor ability is a strong predictor of academic performance [
4,
5,
24]. Cameron et al. [
20] suggest that if a child has a deficit in fine motor development, often times their overall academic performance suffers as well. As a result, those children are more likely to take longer to complete assignments and fall behind in school [
20]. Additionally, most activities that build or demonstrate cognitive skills also involve fine motor tasks (e.g., reading and writing) [
5]. Fine motor ability is implicated in reading because it requires finely tuned psychomotor control necessary for eye tracking and directing one’s eye movements during word tracking [
5]. In like manner, fine motor control over the hands as well is necessary for hand–eye coordination when writing [
5]. Concurrent research also implies that cognitive and motor functions display equally protracted time courses during development [
4]. Evidence for this comes from studies such as Diamond [
4], which demonstrate that both motor and cognitive systems are affected when there are genetic or environmental perturbations.
One reason why studying preschoolers is important to our understanding of cognitive development is because when a child is young, they are most amendable to learning [
20]. This time point is often called the “sensitive period” and can be described as the optimum window of opportunity for brain malleability and is thought to occur just before or around the age of seven years old [
26]. This part of a child’s life is when they are the most receptive to cognitive development and these changes often extend into adolescence and adulthood [
26]. During this sensitive period, the method in which an individual learns mathematics can drastically alter future mathematics performance due to the fact that they are actively developing the foundation for mathematical reasoning and are beginning to scaffold fractional understanding concepts [
27]. In addition, researchers who have explored the long-term effects of early interventions have concluded that the early years are the most cost-effective time to intervene [
20]. Moreover, identifying and fixing these kinds of deficits in a child’s development during these years could provide a strong base for future mathematics reasoning abilities.
1.7. Fair Sharing
A critical cognitive milestone during the preschool years is the concept of fairness [
3]. This hallmark of social cooperation is defined as the ability to share items in a way that agrees with standard principles of justice [
3]. Children this age show a dilemma when it comes to fair sharing because although they understand codes of fairness by 3 years of age, they do not always exhibit these behaviors [
33]. This “moral hypocrisy” known as the knowledge–behavior gap, assumes that children know they should share resources fairly but are often reluctant to when sharing deals with the first person [
33]. Chernyak et al. [
3] suggest that this is a cognitive process that is poorly understood, but perhaps it can be explained by the insufficient cognitive resources hypothesis. They state that although children generally understand number cardinality (the number of items in a set) at this age, they might be missing the cognitive abilities that enable them to behave in accordance with social expectancies [
3]. These resources may still be in early development, and tasks such as resource distribution require the coordination of advanced behavioral and cognitive abilities that may not be fully established yet [
3].
Furthermore, results from [
3] suggest that numerical cognition plays a role in sharing behaviors. For example, in order to state that a distribution is fair, the child must have numerical cognition systems in place that allow them to understand the rule of cardinality [
3]. If the child distributes two batteries to one flashlight and two batteries to another flashlight, then that distribution would be fair because it shows cardinal equivalence [
3]. This may help explain the cognitive mechanisms at work when conceptualizing ideas such as fairness and equality.
Cwikla [
34] was interested in young children’s naïve understanding of fair sharing and the differences in strategies used for solving contextual problems before they had any formal instruction in school. Children this age are likely sharing and partitioning snacks and toys amongst their siblings and peer groups, so she also questioned whether these problems are best presented in the context of fair sharing. Upon reviewing the literature, Cwikla found that minimal empirical evidence exists as to whether three, four, and five-year-old children can understand or acquire such fractional concepts before formal instruction in school where the whole-number bias is established. Previous research [
9] suggests that children have some knowledge about partitioning objects when they first enter school, adding to the claim that our number sense is somewhat innate. Cwikla tested children aged three to six on how well they described and illustrated their attempts at fair sharing tasks. She would read a question such as “Chris wanted to share six crackers with his three friends. How could he do this fairly?” and prompt the child to draw the items and show how they would share them fairly. All of these questions were framed socially, using the snack-sharing context as something the child would find familiar. Student work from this study shows that prekindergarten students have the ability to consider, illustrate, and explain fair-sharing tasks with mixed fraction solutions. Although children at this age may not use the proper mathematical language to express their solution to these problems, they still more often than not understand when something has been fairly distributed. These results suggest that preschool-aged children have an intuitive understanding of fractional quantity and understand the notions of “fairness” and “sharing” before formal mathematics instruction.
1.8. Current Study
The purpose of the current study is to use these findings to extend the work of Cwikla [
34] by examining whether general developmental factors of age and fine motor ability predict the development of fractional reasoning and fair sharing concepts in preschool-aged children. Because a child’s implicit knowledge of simple arithmetic is supported by the approximate number system, it is important to identify the cognitive mechanisms that facilitate the development of numerical reasoning [
15]. The ability to consider the parts and the whole simultaneously appear around age six or seven, although evidence [
34] suggests that the age of acquisition may be earlier. In addition, we investigated whether children who show signs of weak fine motor skills also have lower scores on our measure of cognitive abilities such as fractional reasoning and subitizing. Understanding the precursors of fraction understanding and the cognitive load that goes into solving problems involving fractions will allow researchers to gain more insight into this relationship which can potentially help teach educators the most effective and evidence-based ways of promoting a solid foundation for numerical reasoning.
The current study proposes that the development of mathematical competence, specifically fractional reasoning, is a multifaceted process that requires integration from executive functioning skills, fine motor ability, and the use of gestures. Indeed, if the neural substrates for enumeration are overlapping with those of fine motor control, as suggested by Soylu, then one would expect a significant correlation between these two behaviours to develop early on when basic counting is so critical for math task performance. The ability to control and direct the operations of the hand and fingers may result in better counting performance but may not directly influence mathematical cognition. This study examines video recordings of the gestures made during a dot counting task to yield an objective measure of fine motor ability that goes beyond that of motoric speed, and looks for signs of overall fine motor development as well as motor/cognitive synchrony. This is assessed through ratings of the child’s hand morphology, accuracy of gestures, and synchrony of both gestures and spoken word.
 Question 1. 3 keys and 3 locks
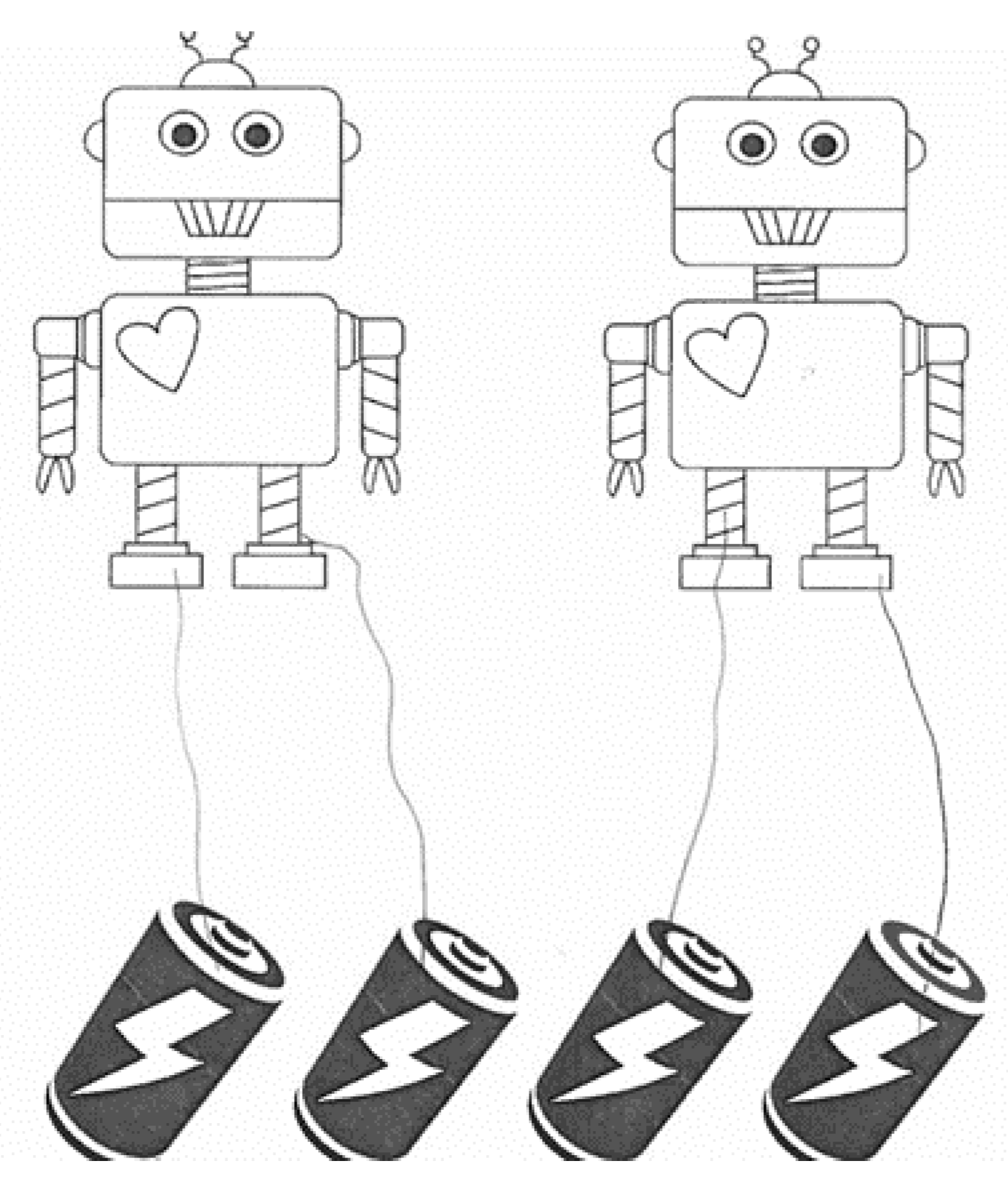
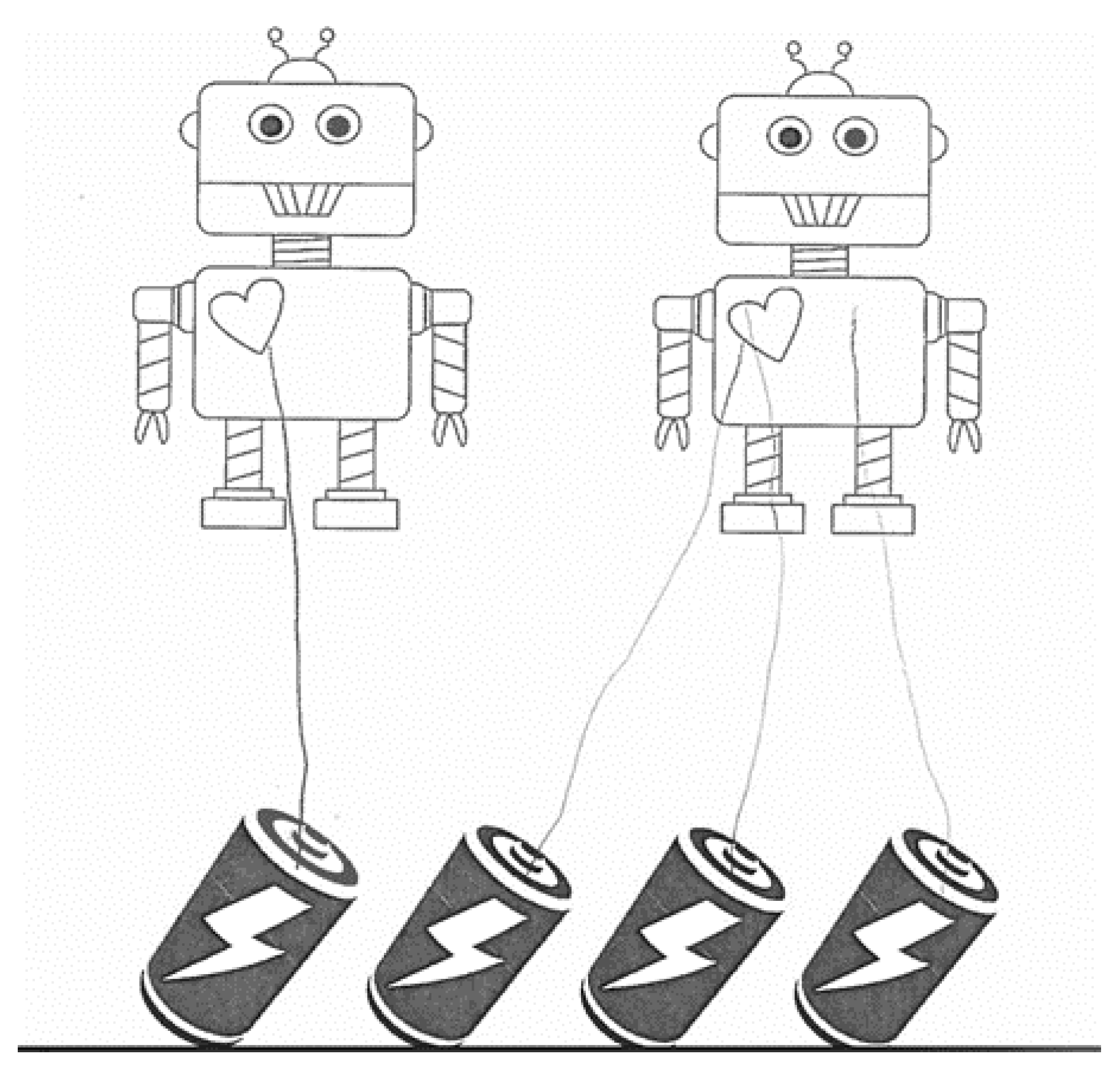
Question 1. 3 keys and 3 locks Question 2. 2 robots and 4 batteries
Question 2. 2 robots and 4 batteries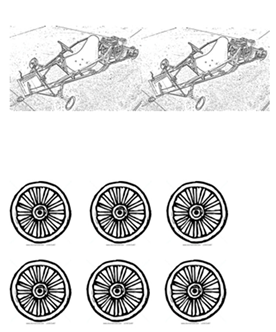 Question 3. 2 go-karts and 6 wheels
Question 3. 2 go-karts and 6 wheels Question 4. Cut rope evenly and distribute
Question 4. Cut rope evenly and distribute Question 5. 2 tents and 5 pieces of cloth
Question 5. 2 tents and 5 pieces of cloth Question 6. 2 kids and 2 hats
Question 6. 2 kids and 2 hats Question 7. 2 kids and 4 oars
Question 7. 2 kids and 4 oars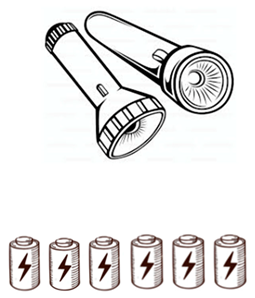 Question 8. 2 flashlights and 6 batteries
Question 8. 2 flashlights and 6 batteries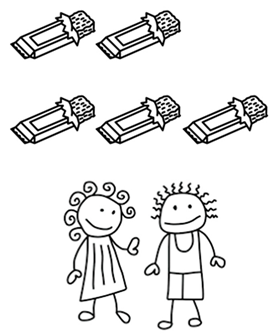 Question 9. 2 kids and 5 energy bars
Question 9. 2 kids and 5 energy bars